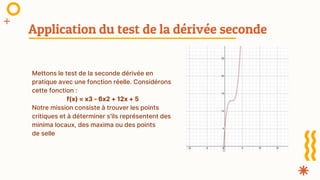
Le test de la dérivée seconde est un outil utilisé pour analyser le comportement d'une fonction autour des points critiques en utilisant la dérivée seconde f''(x). Il permet de déterminer si ces points sont des minima locaux, des maxima locaux ou des points de selle, selon que f''(x) est positif, négatif ou nul. L'application pratique de ce test sur une fonction donnée illustre la façon de trouver et d'interpréter les points critiques.

1. Test de la
derivée seconde

2. 01
Qu'est-ce que le test de
la dérivée seconde ?

3. Le test de la dérivée seconde est un outil puissant pour comprendre le comportement
d'une fonction autour des points critiques. Il s'appuie sur la dérivée seconde d'une
fonction, désignée par f''(x). Voici le lien essentiel :
Qu'est-ce que le test de la dérivée seconde ?
● Si f''(x) est positive à un point critique, cela suggère que la fonction a un minimum
local à ce point
● Si f''(x) est négative, cela implique un maximum local
● Et si f''(x) est égal à zéro, le test n'est pas concluant, ce qui indique la présence
possible d'un point de selle
Essentiellement, le test de la deuxième dérivée t'indique si la fonction est courbée vers
le haut (concave vers le haut) ou vers le bas (concave vers le bas) à un point critique

4. Mettons le test de la seconde dérivée en
pratique avec une fonction réelle. Considérons
cette fonction :
f(x) = x3 - 6x2 + 12x + 5
Notre mission consiste à trouver les points
critiques et à déterminer s'ils représentent des
minima locaux, des maxima ou des points
de selle
Application du test de la dérivée seconde

5. Étape 1 : trouver les points critiques
Fixe f'(x) à zéro et résous pour x afin de
trouver les points critiques :
3x^2 - 12x + 12 = 0
Une fois que tu auras résolu pour x, tu
auras les points critiques suivants
Commence par calculer les dérivées
première et seconde de f(x). La
première dérivée, f'(x), nous donne les
points critiques :
f'(x) = 3x^2 - 12x + 12

6. Étape 2 : utiliser le test de la dérivée seconde
Calculez f''(c)
Si f''(c) est positif, cela
indique un minimum local
à x=c
Si f''(c) est négatif, cela
suggère un maximum
local
Si f''(c) est égal à zéro, le
test n'est pas concluant,
ce qui indique la présence
possible d'un point de selle
En appliquant ce test à chaque point critique, vous pouvez déterminer la nature des
extrema

7. CRÉDITS : Ce modèle de présentation a été créé par Slidesgo, comprenant des icônes
de Flaticon, des infographies et des images de Freepik et du contenu de Swetha Tandri
Merci !
Avez-vous des questions ?
votreemail@freepik.com
+91 620 421 838
votresite.com
Veuillez conserver cette diapositive pour l’attribution

8. Ressources alternatives
Voici un assortiment de ressources alternatives dans le même style que ce modèle :
Vecteurs
● Modern new year party banners with abstract design

9. Ressources
Avez-vous aimé les ressources de ce modèle ? Obtenez-les sur ces sites Web :
Vecteurs
● Flat design minimal makeup artist landing page

10. Instructions for use
If you have a free account, in order to use this template, you must credit Slidesgo by keeping the Thanks slide. Please
refer to the next slide to read the instructions for premium users.
As a Free user, you are allowed to:
● Modify this template.
● Use it for both personal and commercial projects.
You are not allowed to:
● Sublicense, sell or rent any of Slidesgo Content (or a modified version of Slidesgo Content).
● Distribute Slidesgo Content unless it has been expressly authorized by Slidesgo.
● Include Slidesgo Content in an online or offline database or file.
● Offer Slidesgo templates (or modified versions of Slidesgo templates) for download.
● Acquire the copyright of Slidesgo Content.
For more information about editing slides, please read our FAQs or visit our blog:
https://slidesgo.com/faqs and https://slidesgo.com/slidesgo-school

11. As a Premium user, you can use this template without attributing Slidesgo or keeping the Thanks slide.
You are allowed to:
● Modify this template.
● Use it for both personal and commercial purposes.
● Hide or delete the “Thanks” slide and the mention to Slidesgo in the credits.
● Share this template in an editable format with people who are not part of your team.
You are not allowed to:
● Sublicense, sell or rent this Slidesgo Template (or a modified version of this Slidesgo Template).
● Distribute this Slidesgo Template (or a modified version of this Slidesgo Template) or include it in a database or in
any other product or service that offers downloadable images, icons or presentations that may be subject to
distribution or resale.
● Use any of the elements that are part of this Slidesgo Template in an isolated and separated way from this
Template.
● Register any of the elements that are part of this template as a trademark or logo, or register it as a work in an
intellectual property registry or similar.
For more information about editing slides, please read our FAQs or visit our blog:
https://slidesgo.com/faqs and https://slidesgo.com/slidesgo-school
Instructions for use (premium users)

12. This presentation has been made using the following fonts:
Patua One
(https://fonts.google.com/specimen/Patua+One)
Inter
(https://fonts.google.com/specimen/Inter)
Fonts & colors used
#da622e #fdfcf8 #882e06 #ffa900

13. Create your Story with our illustrated concepts. Choose the style you like the most, edit its colors, pick
the background and layers you want to show and bring them to life with the animator panel! It will
boost your presentation. Check out how it works.
Storyset
Pana Amico Bro Rafiki Cuate

14. You can easily resize these resources without losing quality. To change the color, just ungroup the resource and click
on the object you want to change. Then, click on the paint bucket and select the color you want. Group the resource again
when you’re done. You can also look for more infographics on Slidesgo.
Use our editable graphic resources...

17. JANUARY FEBRUARY MARCH APRIL MAY JUNE
PHASE 1
PHASE 2
Task 1
Task 2
Task 1
Task 2
JANUARY FEBRUARY MARCH APRIL
PHASE 1
Task 1
Task 2

20. You can resize these icons without losing quality.
You can change the stroke and fill color; just select the icon and click on the paint bucket/pen.
In Google Slides, you can also use Flaticon’s extension, allowing you to customize and add even more icons.
...and our sets of editable icons

21. Educational Icons Medical Icons

22. Business Icons Teamwork Icons

23. Help & Support Icons Avatar Icons

24. Creative Process Icons Performing Arts Icons

25. Nature Icons

26. SEO & Marketing Icons

27. Add the title here
Text 1 Text 2 Text 3
Text 4 Text 5 Text 6
2016 2017 2018 2019 2020
“Despite being red,
Mars is actually a
very cold place”
“Mercury is the
smallest planet in
the Solar System”
“Neptune is the
farthest planet from
the Sun”
“Saturn is a gas
giant and has
several rings”
“Venus is the
second planet from
the Sun and is
terribly hot”
Premium infographics

28. “Despite being red,
Mars is actually a
very cold place”
“Jupiter is the
biggest planet in the
entire Solar System”
“Saturn is a gas
giant and has
several rings”
75%
Premium infographics
“Mercury is the
smallest planet in the
Solar System”
TITLE 1
75%

29. Digital Marketing
Premium Icons

30. Online Learning
Premium Icons

31. Laboratory
Premium Icons

32. Goals & Results
Premium Icons

33. Infographic Elements
Premium Icons