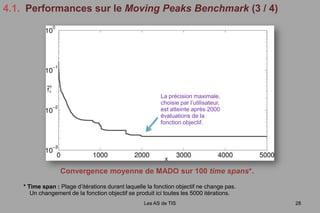
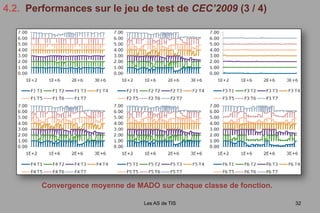
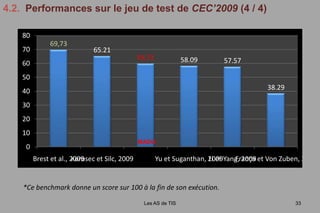
Le document présente les travaux de Julien Lepagnot sur le développement de l'algorithme d'optimisation dynamique Mado, sous la supervision d'un comité académique. Il explore l'optimisation statique et dynamique, ainsi que des métaheuristiques variées, tout en fournissant une analyse des performances de Mado. Les résultats montrent que Mado performe bien dans des contextes dynamiques, malgré quelques limitations avec certains types de fonctions, notamment celles à hauts multimodalités.

1. Atelier scientifique de l'équipe TIS du LISSIAnalyse des performances de l'algorithme d'optimisation dynamique MADOJulien Lepagnot, doctorant en 2ème annéeSous la direction de: A. Nakib, H. Oulhadj et P. SiarryLes AS de TIS1

2. Plan de l’exposéIntroductionMembres de l’équipeL’optimisation statiqueLes métaheuristiquesL’optimisation dynamiqueLa thèseChoisir les bons ingrédientsMise au point d’une nouvelle métaheuristiqueDescription de MADOAnalyse des performancesConclusions et perspectivesLes AS de TIS2

3. Plan de l’exposéIntroductionMembres de l’équipeL’optimisation statiqueLes métaheuristiquesL’optimisation dynamiqueLa thèseChoisir les bons ingrédientsMise au point d’une nouvelle métaheuristiqueDescription de MADOAnalyse des performancesConclusions et perspectivesLes AS de TIS3

4. 1.1. Membres de l’équipeLes AS de TIS4Patrick SIARRY – Professeur des universitésHamouche OULHADJ – Maître de conférencesAmir NAKIB – ATER et consultant R&DJulien LEPAGNOT – Doctorant en 2ème annéeDomaines de recherche : Optimisation, métaheuristiques, applications de l’optimisation dans le domaine biomédical, modélisation…Recalage d’angiographies rétiniennesSegmentation d’images biomédicalesAvant recalageAprès recalageTranslationImage IRM originaleImage segmentée

5. 1.2. L’optimisation statique (1 / 2)Les AS de TIS5Problème d’optimisation statiqueFormaliser le problème en terme de fonction objectif à maximiser ou minimiser. Soit :un espace de recherche S

6. une fonction objectif fDans le cas d’une minimisation, on cherche la position s* telle que :s* = arg min( f(s)\ s Î S )Dans le cas d’une maximisation, on se ramène à un problème de minimisation :Maximiser f Minimiser – f

7. 1.2. L’optimisation statique (2 / 2)Les AS de TIS6Le problème de tournées de véhiculesLe problème d’affectation de tâchesmachine 1machine 2machine 3DépôtchargechargechargeCompression du signalRecalage d’imagesmodélisation viaune métaheuristiqueAvant recalageAprès recalageTranslation

8. Les AS de TIS71.3. Les métaheuristiques (1 / 4)Classification des méthodes d'optimisation statique

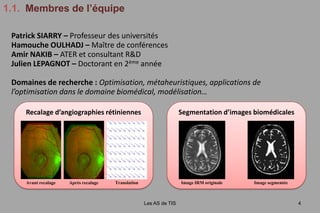
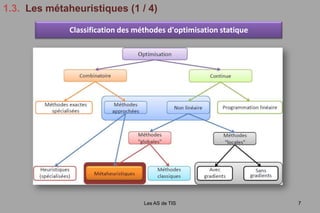
9. 1.3. Les métaheuristiques(2 / 4)Les AS de TIS8Exemple : Algorithmes évolutionnaires [Holland, 1973]COMPETITION entre agentsReposent sur la compétition au sens de DarwinPopulationcourantePopulation dedescendantsCroisementEvaluationSélectionMutationPopulation dedescendants mutésPopulationévaluée

10. 1.3. Les métaheuristiques(3 / 4)Les AS de TIS9Exemple : Colonies de fourmis [Dorigo et al., 1996]INTELLIGENCE EN ESSAIM : COOPERATION INDIRECTE entre agents (via l’environnement)

11. 1.3. Les métaheuristiques (4 / 4)Les AS de TIS10Exemple : Les essaims particulaires [Kennedy et Eberhart, 1995]INTELLIGENCE EN ESSAIM : COOPERATION DIRECTE entre agentsVers sa meilleureperformanceL’OEP simule le comportement social d’un essaim de « particules »A chaque itération t, chaqueparticule i se définit par :

12. sa position

13. sa vitesseω, c1, c2, coefficients de confiance et r1, r2Î ]0, 1]NouvellepositionPositionactuelleVers la meilleureperformance del’essaimVers le pointaccessible avec lavitesse courante

14. 1.4. L’optimisation dynamique (1 / 4)Les AS de TIS11Problème d’optimisation dynamiqueDans le cas dynamique, la fonction objectif est susceptible de changer au cours du temps. On a :un espace de recherche S

15. une fonction objectif f

16. le temps tDans le cas d’une minimisation, on cherche la position s* telle que :s* = arg min( f(s,t)\ s Î S )

17. 1.4. L’optimisation dynamique (2 / 4)Les AS de TIS12retraitpanneLe problème de tournées de véhiculesLe problème d’affectation de tâchesajoutajoutretraitmachine 1machine 2machine 3DépôtchargechargeCompression du signalEstimation du mouvement dans une séquenceNouveau modèleà chaque battementpeu de différences entreles décalages consécutifs(repartir de l’ancienne solution)

18. 1.4. L’optimisation dynamique (3 / 4)Les AS de TIS13Techniques d’optimisation dynamiqueAdaptation des métaheuristiques d’optimisation statique

19. 1.4. L’optimisation dynamique (4 / 4)Les AS de TIS14Benchmarks (tests standards) :Le « MovingPeaks Benchmark » [J. Branke, 1999](beaucoup d’auteurs l’utilisent)

20. Un ensemble de fonctions de test proposées par W. TFAILIau LISSI durant sa thèse en 2007(n'est pas très utilisé)

21. La compétition de CEC’2009 [Trondheim, Norvège, May 2009](en émergence)Plan de l’exposéIntroductionL’équipeL’optimisationLes métaheuristiquesL’optimisation dynamiqueLa thèseChoisir les bons ingrédientsMise au point d’une nouvelle métaheuristiqueDescription de MADOAnalyse des performancesConclusions et perspectivesLes AS de TIS15

22. 2.1. Choisir les bons ingrédientsLes AS de TIS16

23. 2.2. Mise au point d’une nouvelle métaheuristiqueLes AS de TIS17Agents de recherche locale coordonnés, archivage des optima trouvés :

24. PSO : Impossible de rattacher la méthode à cette classe

25. Fourmis : Pas de phéromones, impossible aussi

26. Evolutionnaires : Impossible aussi

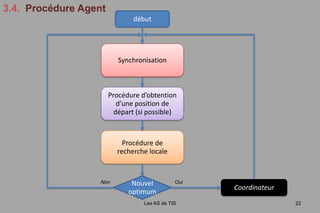
27. Programmation à Mémoire Adaptative [E. Taillard, 1997] : Tentative……échouée

28. Multi-Agent :Multi-Agent DynamicOptimizationMADOHill Climbing à pas adaptatifHill Climbing à pas adaptatifHill Climbing à pas adaptatifHill Climbing à pas adaptatifPseudo-parallélisme des recherches locales

29. Plan de l’exposéIntroductionLa thèseDescription de MADOStructure générale de MADOStructure d’un agent de MADOLa population initiale d’agentsProcédure AgentDétection de changementAnalyse des performancesSur le MovingPeaks BenchmarkSur le jeu de test de CEC’2009Conclusions et perspectivesLes AS de TIS18

30. 3.1. Structure générale de MADOLes AS de TIS19InitialisationModule de mémoireCoordinateurArchive …Module de gestion des agentsAgent 1Agent 2Agent iGestionnaire de l'archiveMémoire localeMémoire localeMémoire localeCritère d’arrêt satisfait ?NonOuiFin

31. 3.2. Structure d’un agent de MADOLe voisinage d’un agent est constitué d’un nombre N de solutions situées :à une distance de l’agent égale à son pas.

32. à égale distance les unes des autres.Le pas d’un agent :correspond ainsi à la distance entre sa solution courante et ses voisines.

33. est adapté à chaque déplacement de l’agent.Espace de rechercheRayon =pas de l’agentSolutions appartenantau voisinage de l’agent.La solution courante, sur laquelle se trouve l’agent.Les AS de TIS20

34. 3.3. La population initiale d’agentsA l’initialisation, le coordinateur ordonne la création de na agents, et les dispose de façon « régulière » dans l’espace de recherche.Espacer au maximum les na agents entre eux, dans l’hyperrectangleT.Sur cette figure, na = 5, et l’espace est à 2 dimensions.Espace de recherchenormalisé1 maxreHyperrectangleT oùsont placés lesagents maxre maxre maxre 1 =Agent2 na maxre01Les AS de TIS21

35. Les AS de TIS223.4. Procédure AgentdébutSynchronisationProcédure d’obtention d’une position de départ (si possible)Procédure de recherche localeNouveloptimumNonOuiCoordinateur

36. 3.4. Procédure Agent détailléeDébutSynchronisationDemande d’une nouvelle position et d’un nouveau pas au coordinateurOuiNonTrop proche d’autres agents?Peut trouver une meilleure solution voisine?Attente que tous les autres agents entrent dans un état SynchronisationOuiNonSynchronisationSe déplacer sur la meilleure solution voisineAdapter le pas par le produit scalaire cumuléObtention d’une nouvelle position et d’un nouveau pasRéduire le pasCritère d’arrêt d’une recherche locale satisfait?OuiNonEnvoi de l’optimum local trouvé au coordinateurLes AS de TIS23