Télécharger pour lire hors ligne
Téléchargé parSylvain Hallé
La quantification du premier ordre en logique temporelle
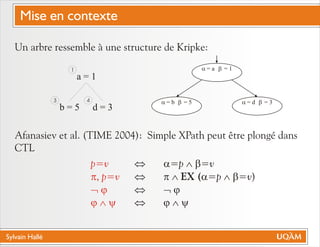
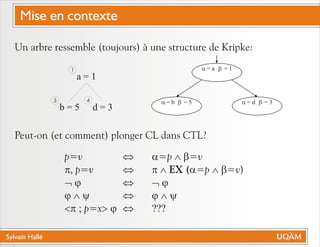
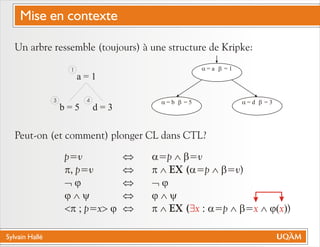
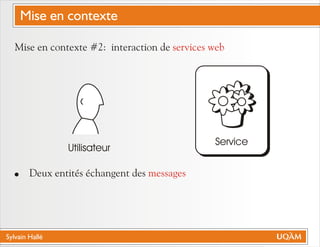
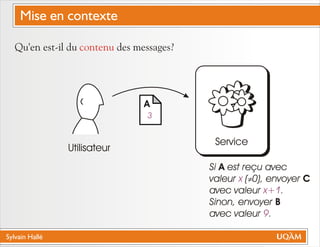
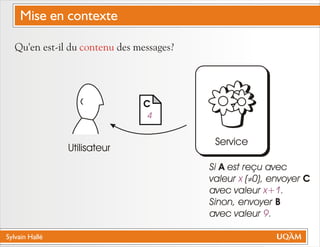
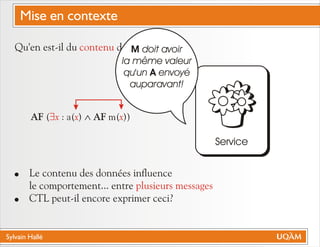
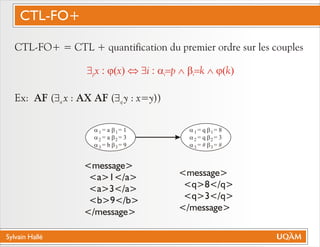
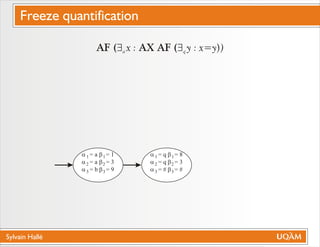
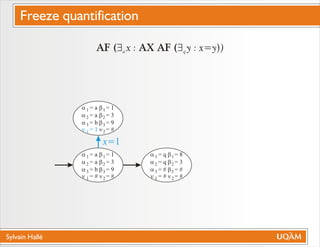
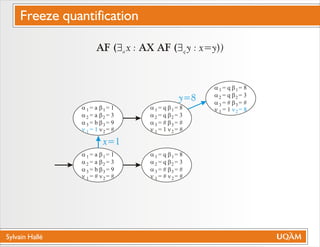
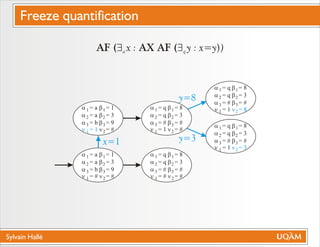
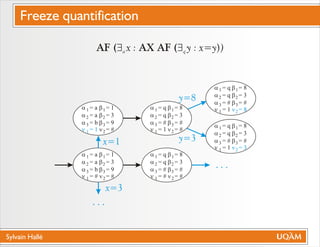
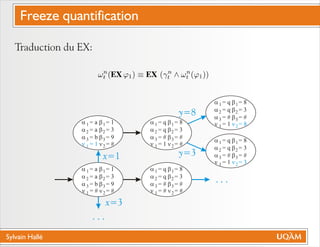
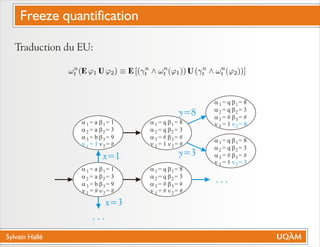
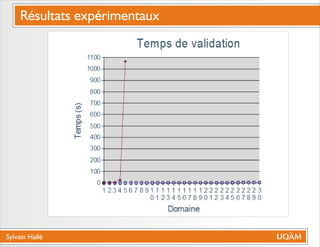
Le document de Sylvain Hallé explore la quantification du premier ordre en logique temporelle, notamment à travers son application aux documents XML et aux services Web. Il discute des interactions entre entités échangées ainsi que des contraintes définies par la logique temporelle, s'intéressant à des problèmes tels que la vérification de messages et la structure des arbres en relation avec la logique temporelle. L'auteur propose des approches pour le model checking de ctl-fo+, tout en évaluant la complexité et les techniques de quantification.
La quantification du premier ordre en logique temporelle
- 1. Sylvain Hallé Sylvain Hallé Lab Universitédu Québec à Montréal Montréal, CANADA Laboratoire de téléinformatique UQAM La quantification du premier ordre en logique temporelle: applications aux documents XML et aux services web
- 2. Sylvain Hallé Mise encontexte Mise en contexte #1: requêtes sur documents XML Arbre de couples paramètre-valeur: cas particulier de document XML On considère un sous-ensemble de XPath 1.0: Ex.: a=1/b=5 ou a=2/d=3 a = 1 b = 5 d = 3 1 3 4 <a>1 <b>5</b> <d>3</d> </a> p : p=v | p, p=v j : Ø j | j Ù j | p
- 3. Sylvain Hallé Mise encontexte Un arbre ressemble à une structure de Kripke: Afanasiev et al. (TIME 2004): Simple XPath peut être plongé dans CTL a = 1 b = 5 d = 3 1 3 4 a = a b = 1 a = b b = 5 a = d b = 3 p=v p, p=v Ø j j Ù y Û a=p Ù b=v Û p Ù EX (a=p Ù b=v) Û Ø j Û j Ù y
- 4. Sylvain Hallé Mise encontexte On étend Simple XPath ( : Ex: <; a=x> <a=x ; b=y> x y Utilité: propriétés de configurations réseau (et autres) Þ Í XPath 2.0) ¹ CL a = 1 b = 5 d = 3 1 3 4 p : p=v | p, p=v j : Ø j | j Ù j | <p ; p=x> j | x=y
- 5. Sylvain Hallé Un arbreressemble (toujours) à une structure de Kripke: Peut-on (et comment) plonger CL dans CTL? a = 1 b = 5 d = 3 1 3 4 a = a b = 1 a = b b = 5 a = d b = 3 p=v Û a=p Ù b=v p, p=v Û p Ù EX (a=p Ù b=v) Ø j Û Ø j j Ù y Û j Ù y <p ; p=x> j Û ??? Mise en contexte
- 6. Sylvain Hallé Un arbreressemble (toujours) à une structure de Kripke: Peut-on (et comment) plonger CL dans CTL? a = 1 b = 5 d = 3 1 3 4 p=v Û a=p Ù b=v p, p=v Û p Ù EX (a=p Ù b=v) Ø j Û Ø j j Ù y Û j Ù y <p ; p=x> j Û p Ù EX ( a=p Ù b= Ù j( ))$x : x x a = a b = 1 a = b b = 5 a = d b = 3 Mise en contexte
- 7. Sylvain Hallé Un arbreressemble (toujours) à une structure de Kripke: Peut-on (et comment) plonger CL dans CTL? a = 1 b = 5 d = 3 1 3 4 p=v Û a=p Ù b=v p, p=v Û p Ù EX (a=p Ù b=v) Ø j Û Ø j j Ù y Û j Ù y <p ; p=x> j Û p Ù EX ( a=p Ù b= Ù j( ))$x : x x a = a b = 1 a = b b = 5 a = d b = 3 Mise en contexte
- 8. Sylvain Hallé Mise encontexte #2: interaction de ! Deux entités échangent des services web messages Utilisateur Service Mise en contexte
- 9. Sylvain Hallé Mise encontexte #2: interaction de ! Deux entités échangent des services web messages A Utilisateur Service Mise en contexte
- 10. Sylvain Hallé Mise encontexte #2: interaction de ! Deux entités échangent des services web messages B Utilisateur Service Mise en contexte
- 11. Sylvain Hallé Mise encontexte #2: interaction de ! Deux entités échangent des services web messages D Utilisateur Service Mise en contexte
- 12. Sylvain Hallé Mise encontexte #2: interaction de ! Deux entités échangent des services web messages D Utilisateur Service Mise en contexte
- 13. Sylvain Hallé Mise encontexte #2: interaction de ! Deux entités échangent des services web messages Utilisateur Service Impossible d'envoyer D après avoir envoyé un A ! Mise en contexte
- 14. Sylvain Hallé Mise encontexte #2: interaction de ! Deux entités échangent des ! L'interaction possède une mémoire (memoryful behaviour) services web messages Utilisateur Service Impossible d'envoyer D après avoir envoyé un A ! Mise en contexte
- 15. Sylvain Hallé Mise encontexte #2: interaction de ! Deux entités échangent des ! L'interaction possède une mémoire (memoryful behaviour) services web messages Utilisateur Service Impossible d'envoyer D après avoir envoyé un A ! Comment le savoir? Mise en contexte
- 16. Sylvain Hallé Mise encontexte #2: interaction de ! Deux entités échangent des ! L'interaction possède une mémoire (memoryful behaviour) ! Deutsch, Sui, Vianu (PODS 2006): utiliser une logique temporelle (disons CTL) pour définir les contraintes services web messages Utilisateur Service Impossible d'envoyer D après avoir envoyé un A ! Comment le savoir? Mise en contexte
- 17. Sylvain Hallé Mise encontexte #2: interaction de ! Deux entités échangent des ! L'interaction possède une mémoire (memoryful behaviour) ! Deutsch, Sui, Vianu (PODS 2006): utiliser une logique temporelle (disons CTL) pour définir les contraintes services web messages Service Impossible d'envoyer D après avoir envoyé un A ! AG (a AX AG d)® Ø Mise en contexte
- 18. Sylvain Hallé Qu'en est-ildu des messages?contenu Service Utilisateur Mise en contexte
- 19. Sylvain Hallé Qu'en est-ildu des messages?contenu A 3 Service Utilisateur Mise en contexte
- 20. Sylvain Hallé Qu'en est-ildu des messages?contenu A 3 Service Utilisateur Si A est reçu avec valeur ( 0), envoyer C avec valeur . Sinon, envoyer B avec valeur . x x+1 9 ¹ Mise en contexte
- 21. Sylvain Hallé Qu'en est-ildu des messages?contenu C 4 Service Utilisateur Si A est reçu avec valeur ( 0), envoyer C avec valeur . Sinon, envoyer B avec valeur . x x+1 9 ¹ Mise en contexte
- 22. Sylvain Hallé Qu'en est-ildu des messages? ! Le contenu des données influence le comportement contenu Service C 4 Si A est reçu avec valeur ( 0), envoyer C avec valeur . Sinon, envoyer B avec valeur . x x+1 9 ¹ Utilisateur Mise en contexte
- 23. Sylvain Hallé Qu'en est-ildu des messages? ! Le contenu des données influence le comportement contenu M 6 Service Utilisateur Mise en contexte
- 24. Sylvain Hallé Qu'en est-ildu des messages? ! Le contenu des données influence le comportement contenu Service M 6 Utilisateur Mise en contexte
- 25. Sylvain Hallé Service M 6 Qu'en est-ildu des messages? ! Le contenu des données influence le comportement... entre contenu plusieurs messages Utilisateur M doit avoir la même valeur qu'un A envoyé auparavant! Mise en contexte
- 26. Sylvain Hallé Qu'en est-ildu des messages? ! Le contenu des données influence le comportement... entre contenu plusieurs messages Service M 6 Utilisateur M doit avoir la même valeur qu'un A envoyé auparavant! Comment le savoir? Mise en contexte
- 27. Sylvain Hallé Qu'en est-ildu des messages? ! Le contenu des données influence le comportement... entre ! CTL peut-il encore exprimer ceci? contenu plusieurs messages Service M 6 Utilisateur M doit avoir la même valeur qu'un A envoyé auparavant! Comment le savoir? Mise en contexte
- 28. Sylvain Hallé Qu'en est-ildu des messages? ! Le contenu des données influence le comportement... entre ! CTL peut-il encore exprimer ceci? contenu plusieurs messages Service M doit avoir la même valeur qu'un A envoyé auparavant! AF ( : a( ) AF m( ))$x x xÙ Mise en contexte
- 29. Sylvain Hallé Qu'en est-ildu des messages? ! Le contenu des données influence le comportement... entre ! CTL peut-il encore exprimer ceci? contenu plusieurs messages Service M doit avoir la même valeur qu'un A envoyé auparavant! AF ( : a( ) AF m( ))$x x xÙ Mise en contexte
- 30. Sylvain Hallé Deux contextes: !Plongement de XPath/XQuery en CTL ! Vérification de transactions de services web Même besoin: ! et plusieurs éléments d'un (ou plusieurs) document(s) XML... ! ... = quantification du premier ordre en logique temporelle (ici CTL) Comment faire? extraire comparer Mise en contexte
- 31. Sylvain Hallé Hallé, Villemaire,Cherkaoui, Tremblay (WS-FM 2007): = structure de Kripke "spéciale" ! Les états contiennent k ! ... = messages XML d'arité ! ... (pas de hiérarchie (pour le moment)) workflow messaging model couples paramètre-valeur bornée plats <message> <a>1</a> <a>3</a> <b>9</b> </message> <message> <q>8</q> <q>3</q> </message> a a a = a = a = b b b b = 1 = 3 = 9 1 2 3 1 2 3 a a a = q = q = # b b b = 8 = 3 = # 1 2 3 1 2 3 Workflow messaging model
- 32. Sylvain Hallé CTL-FO+ =CTL + quantification du premier ordre sur les couples Ex: AF ($ x : AX AF ($ y : x=y))a q <message> <a>1</a> <a>3</a> <b>9</b> </message> <message> <q>8</q> <q>3</q> </message> a a a = a = a = b b b b = 1 = 3 = 9 1 2 3 1 2 3 a a a = q = q = # b b b = 8 = 3 = # 1 2 3 1 2 3 $ x : j(x) Û $i : a=p Ù b=k Ù j(k)p i i CTL-FO+
- 33. Sylvain Hallé Model checkingde CTL-FO+ sur un workflow messaging model? Complexité du model checking (domaines finis): (Hallé et al., EDOC 2007) pas pire que LTL Trois solutions: 1. Nouveau model checker 2. Adapter model checker existant 3. Retraduire le problème en CTL classique PSPACE-complet Þ Model checking de CTL-FO+
- 34. Sylvain Hallé Tentative #1:quantification Transformer une formule quantifiée comme: en pour toutes les valeurs du domaine de x. Devient formule CTL classique. idée (on verra plus loin). explicite Mauvaise Model checking de CTL-FO+
- 35. Sylvain Hallé Tentative #2:quantification Adaptation d'une idée de Alur et Henzinger (1994) Utilisée comme moyen de la quantification du premier ordre en CTL Principe: ajouter des variables d'état au système qui vont "geler" la valeur d'une autre variable d'état à un moment précis freeze simuler Model checking de CTL-FO+
- 36. Sylvain Hallé AF ($x : AX AF ($ y : x=y))a q a a a = a = a = b b b b = 1 = 3 = 9 1 2 3 1 2 3 a a a = q = q = # b b b = 8 = 3 = # 1 2 3 1 2 3 Freeze quantification
- 37. Sylvain Hallé AF ($x : AX AF ($ y : x=y))a q a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Freeze quantification
- 38. Sylvain Hallé AF ($x : AX AF ($ y : x=y))a q a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 x=1 Freeze quantification
- 39. Sylvain Hallé AF ($x : AX AF ($ y : x=y))a q a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 x=1 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Freeze quantification
- 40. Sylvain Hallé AF ($x : AX AF ($ y : x=y))a q a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 8 1 2 3 1 1 2 3 2 x=1 y=8 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Freeze quantification
- 41. Sylvain Hallé AF ($x : AX AF ($ y : x=y))a q a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 3 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 8 1 2 3 1 1 2 3 2 x=1 y=8 y=3 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Freeze quantification
- 42. Sylvain Hallé AF ($x : AX AF ($ y : x=y))a q a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 3 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 8 1 2 3 1 1 2 3 2 x=1 . . . y=8 y=3 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Freeze quantification
- 43. Sylvain Hallé AF ($x : AX AF ($ y : x=y))a q a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 3 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 8 1 2 3 1 1 2 3 2 x=1 x=3 . . . . . . y=8 y=3 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Freeze quantification
- 44. Sylvain Hallé Hallé, Villemaire,Cherkaoui, IEEE TSE 2008: on peut systématiser cette construction Workflow messaging model M + variables et qualificatif workflow messaging model M' Deuxième étape: on se débarrasse de la quantification dans la formule Formule CTL-FO+ j formule CTL y' Garde: "les t premières variables sur n ont pris une valeur" Þ Þ freeze Freeze quantification
- 45. Sylvain Hallé Traduction récursivew: paramétrisée par n (nombre total de variables quantifiées) et t (nombre de variables freeze qui ont déjà une valeur) Connecteurs booléens et égalité: direct Freeze quantification
- 46. Sylvain Hallé Traduction duEX: a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 3 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 8 1 2 3 1 1 2 3 2 x=1 x=3 . . . . . . y=8 y=3 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Freeze quantification
- 47. Sylvain Hallé Traduction duAF: a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 3 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 8 1 2 3 1 1 2 3 2 x=1 x=3 . . . . . . y=8 y=3 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Freeze quantification
- 48. Sylvain Hallé Traduction duAF: a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 3 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 8 1 2 3 1 1 2 3 2 x=1 x=3 . . . . . . y=8 y=3 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Généralisation: Si on remplace par true, on retrouve la définition classique i.e. le garde est un "filtre" Freeze quantification
- 49. Sylvain Hallé Traduction duEU: a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 3 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 8 1 2 3 1 1 2 3 2 x=1 x=3 . . . . . . y=8 y=3 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Freeze quantification
- 50. Sylvain Hallé Traduction dela quantification existentielle: a a a n = a = a = b = # b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = a = a = b = 1 b b b n = 1 = 3 = 9 = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = # b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 3 1 2 3 1 1 2 3 2 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = 8 1 2 3 1 1 2 3 2 x=1 x=3 . . . . . . y=8 y=3 a a a n = q = q = # = 1 b b b n = 8 = 3 = # = # 1 2 3 1 1 2 3 2 Freeze quantification
- 51. Sylvain Hallé Théorème (Halléet al., IEEE TSE 2008): ssi Traduction exponentielle... ...mais s'il en existe une meilleure => P = NP Minute! La quantification explicite était elle aussi une traduction exponentielle! CTL-FO+ PSPACE-complet CTL EXPTIME Freeze quantification
- 52. Sylvain Hallé Quantification expliciteFreeze quantification - Formule dépend du - Formule indépendante domaine du domaine - Petit système - Grand système - Grande formule - Petite formule On dit qu'un model checker est optimisé pour de grands espaces d'états, mais des formules (relativement) courtes. Est-ce vrai? Comparaison
- 53. Sylvain Hallé Formules CTL-FO+tirées d'un scénario de commerce électronique F1- "Un même produit ne peut apparaître que dans un seul message dans toute la transaction" (2 quantificateurs) F2- "Chaque produit dans une commande apparaît plus tard dans une confirmation de commande" (4 quantificateurs) F3- "Au moins un produit est acheté" (6 quantificateurs) Get all stocks Get stock details Place buy order(s) Place sell order(s) Confirm buy order(s) Confirm sell order(s) Cash transfer Cancel transaction Customer Online stock trading Résultats expérimentaux
- 54.
- 55.
- 56. Sylvain Hallé Out ofmemory (exp) Résultats expérimentaux
- 57. Sylvain Hallé Quantification explicite:plus appropriée (et plus efficace) pour des formules avec peu de quantificateurs (< 3) Quantification freeze: seule méthode qui donne des temps raisonnables pour toutes les formules >10000 fois plus rapide dans certains cas Conclusion
- 58. Sylvain Hallé S. Hallé,R. Villemaire, O. Cherkaoui, B. Ghandour. (2007). Model- checking Data-Aware Temporal Workflow Properties with CTL- FO+. Proc. EDOC 2008, IEEE Computer Society. S. Hallé, R. Villemaire, O. Cherkaoui, J. Tremblay, B. Ghandour. (2007). Extending Model Checking to Data-Aware Temporal Properties of Web Services. Proc. WS-FM 2008, Springer LNCS 4937. S. Hallé, R. Villemaire, O. Cherkaoui. Specifying and Validating Data-aware Temporal Web Service Properties. IEEE Transactions on Software Engineering (en révision). Références