Calcul des colonnes en acier de classe 4 soumises au feu - Rapport PFE

AUTEUR : MOHAMED AHATRI
TUTEUR : JEAN MARC FRANSSEN
MASTER SCIENCES DU FEU ET INGENIERIE DE LA SECURITE INCENDIE
ET
MASTER EN SCIENCES ET TECHNIQUES EN GENIE CIVIL
SUJET
Calcul des colonnes en acier de classe 4 soumises au feu
Soutenu le : 18/07/2014
Membres du Jury :
M. Olivier VAUQUELIN
M. Fabien CANDELIER
M. Eric CASALE
Année Universitaire 2013/2014
UNIVERSITE ABDEL MALEK ESSAADI
FACULTE DES SCIENCES ET TECHNIQUES DE
TANGER
UNIVERSITE D’AIX MARSEILLE
UNIMECA
UNIVERSITE DE LIEGE
STRUCTURAL ENGINEERING

2

Remerciement
En gratitude et témoignage de ma profonde reconnaissance, je tiens à remercier tout d’abord,
la faculté des sciences et techniques de Tanger (FSTT) et l’institut mécanique de Marseille
(UNIMECA) qui m’ont aidé à progresser en me permettant d’approfondir mes connaissances
théoriques, et de réaliser un stage de recherche.
Je remercie tout particulièrement mes professeurs de la FSTT M. Abdeslam DRAOUI, M.
Adil HAFIDI ALAOUI et M. Mokhtar MABSSOUT ainsi que mes professeurs de l’Institut
Mécanique de Marseille, M. Olivier VAUQUELIN, M. Fabien CANDELIER et M. Eric
CASALE pour l’aide et les conseils qu’ils m’ont prodigué tout au long de cette année.
Je tiens à remercier et à témoigner toute ma reconnaissance à mon encadrant, M. Jean-Marc
FRANSSEN, pour ses informations précieuses, son expérience qui m’ont permis d’évoluer
rapidement dans mon stage et son intérêt considérable porté pour mon travail. M.Anthony SCIFO
et M. Thomas GERNAY pour leur aide et leur soutien.
Je remercie aussi mes parents et amis, et qui m’ont aidé et encouragé tout au long de ce
stage.
Je remercie aussi toutes les personnes qui ont contribué, de près ou de loin, à l’expérience
enrichissante et pleine d’intérêt, et à la réussite de mon travail de stage.
Enfin, Je remercie les honorables membres du jury d’avoir accepté de juger mon travail et
toute personne ayant participée de près ou de loin à son élaboration.
3

Résumé
Le présent document constitue la synthèse de mon travail dans le cadre du Projet de Fin
d’Etudes effectué à l’Université de Liège(Ulg) au sein du département Structural Engineering
(SE), dont l’objectif est le calcul des colonnes en acier carbone de classe 4 soumises au feu.
La première étape du projet a été réalisée par le laboratoire d’Ulg. Cette dernière consistait à
réaliser huit essais sur des colonnes en acier carbone de classe 4 en situation d’incendie. Ces huit
essais ont été réalisés par le service SE afin de valider un modèle numérique utilisant le logiciel
SAFIR[1].
Une analyse paramétrique des poteaux métalliques en profilés soudés de classe 4 soumise au
feu a été réalisée. Le calcul des premiers modes de vibrations par le logiciel CAST3M du
CEA[2] à partir du logiciel RUBY[Annexe 1-2] a été mené pour générer les fichiers de donnée.
Ensuite, les calculs ont été lancée de manière automatique en utilisant des éléments finis non
linéaires de type coque du logiciel SAFIR. Enfin, les résultats ont été récupérés et organisés dans
une base de données.
Et pour terminer, on a élaboré un modèle simple de dimensionnement applicable en bureau
d’études qui a été calibré sur les résultats numériques
Ce rapport se veut donc le témoin de cette activité à la fois académique et professionnelle,
réalisée dans le cadre de ma formation à l’institut mécanique de Marseille (UNIMECA). Il
présente pour moi une opportunité de traiter un problème réel dont les enjeux sont énormes et
directement mesurables.
4

Abstract
This document is a summary of my master project conducted at the University of Liège (Ulg)
in the Structural Engineering (SE) department, whose objective is the calculation of Class 4
carbon steel columns subjected to fire.
The first step of the project was conducted by the Ulg laboratory. Eight tests were performed
on class 4 carbon steel columns in order to validate a numerical model in SAFIR software[1].
A parametric analysis of metal studs with welded profiles of class 4 exposed to fire was
performed. The calculation of the first vibration modes was performed using CAST3M CEA[2]
software from RUBY software[Annexe 1-2] to generate the data.
Then, the calculations have been launched automatically using nonlinear finite elements,
shell type of SAFIR software. The results were collected and organized into a database.
And finally, we have developed a simple model of dimensioning applicable in engineering
offices, and which has been calibrated on the numerical results.
This report thus witnesses this activity both academic and professional, conducted as part of
my training at the Mechanical Institute of Marseille (UNIMECA). It presents an opportunity for
me to deal with a real problem which stakes are high and directly measurable.
5

Notation
𝑁𝑏,𝑓𝑖,𝑡𝑡,𝑅𝑑 : La résistance de la section à la compression uniforme
𝑁𝑝𝑝𝑙𝑎𝑎𝑠𝑡𝑡𝑖𝑐 : La résistance plastique de la section transversale.
𝑁𝑐𝑟 : La résistance critique de la section transversale.
𝑏 : Largeur de la semelle
ℎ𝑛𝑢𝑚 : Hauteur de l’âme dans le modèle numérique.
ℎ𝑤 = ℎ : Hauteur de l’âme.
𝑡 𝑤 : Épaisseur de l’âme.
𝑡𝑓 : Épaisseur de la semelle.
𝑏 𝑒𝑓𝑓 : La largeur efficace de la semelle
ℎ 𝑛𝑢𝑢𝑚𝑒𝑓𝑓 : La hauteur efficace de l’âme.
𝜀𝜀 : Coefficient de 𝑓𝑓𝑦𝑦
𝜀𝜀 𝜃 : Coefficient de 𝑓𝑓𝑦𝑦 au cas d’incendie
𝑓𝑓𝑦𝑦 : Limite d’élasticité de l’acier à température normale.
𝑓𝑓𝑦𝑦𝜃 : Limite d’élasticité de l’acier à température élevée pour les sections de classe 1,2, et3.
𝑓𝑓𝑦𝑦02 : Limite d’élasticité de l’acier à température élevée pour les sections de classe 4.
χ 𝑓𝑖 ∶Cofficient de réduction pour la courbe de flambement global.
𝐴 𝑒𝑓𝑓 : Section efficace d’une colonne (classe 4).
Figure 1 : Paramètre d’un profilé reconstitué soudé
6

𝑘𝑦𝑦𝜃 : Coefficient réducteur de la limite d’élasticité de l’acier à température élevée pour les classes
1,2, et 3.
𝑘02,𝜃𝑎𝑎 : Coefficient réducteur de la limite d’élasticité de l’acier à température élevée pour les
classes 4.
𝑘 𝐸𝜃 : Module d’élasticité longitudinale à température élevée.
λ� 𝜃 : Élancement réduit pour le flambement.
λ 𝑠𝑡𝑡𝑟𝑜𝑛𝑔 : Valeur d’élancement selon l’axe fort pour déterminer l’élancement réduit.
λ 𝑤𝑒𝑎𝑎𝑘 : Valeur d’élancement selon l’axe faible pour déterminer l’élancement réduit.
𝐼: Moment d’inertie de section transversale
L : Longueur de la colonne.
∆𝑙
𝑙� : Dilatation thermique
𝐶𝑎𝑎 : Chaleur spécifique
λ𝑎𝑎 : Conductivité thermique
𝐸𝐸 : Module de l’élasticité longitudinale de l’acier (E= 210 000 MPa).
𝐿 𝑟𝑎𝑎𝑡𝑡𝑖𝑜𝑆𝑡𝑡𝑟 : Rapport de la longueur de flambement selon l'axe fort sur la longueur de la colonne
𝐿 𝑟𝑎𝑎𝑡𝑡𝑖𝑜𝑛𝑊 : Rapport de la longueur de flambement selon l'axe faible sur la longueur de la colonne
𝜌 : Rendement d’une section.
λ� 𝑝𝑝 : Elancement réduit pour le voilement local.
Ψ : Coefficient de distribution de contraintes.
𝐾 𝜎 : Coefficient de voilement de paroi de section
7

Liste des figures
FIGURE 1 : PARAMETRE D’UN PROFILE RECONSTITUE SOUDE ......................................................................................6
FIGURE 2 : COMPARAISON DES RESULTATS NUMERIQUES ET EXPERIMENTAUX........................................................21
FIGURE 3 : ENCHAINEMENT DES LOGICIELS.................................................................................................................22
FIGURE 4 : RELATION CONTRAINTE-DEFORMATION POUR L’ACIER AU CARBONE AUX TEMPERATURES ELEVEES. ...25
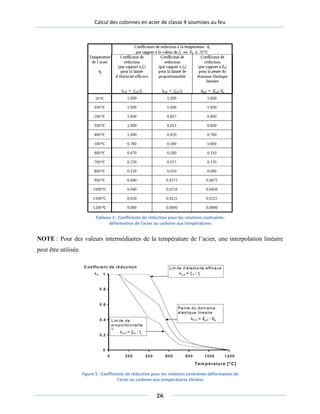
FIGURE 5 : COEFFICIENTS DE REDUCTION POUR LES RELATIONS CONTRAINTE-DEFORMATION DE L’ACIER AU
CARBONE AUX TEMPERATURES ELEVEES............................................................................................................26
FIGURE 6 : DILATATION THERMIQUE DE L’ACIER AU CARBONE EN FONCTION DE LA TEMPERATURE ......................28
FIGURE 7 : CHALEUR SPECIFIQUE DE L’ACIER AU CARBONE EN FONCTION DE LA TEMPERATURE .............................29
FIGURE 8 : CONDUCTIVITE THERMIQUE DE L’ACIER AU CARBONE EN FONCTION DE LA TEMPERATURE...................30
FIGURE 9: EVOLUTION DE LA TEMPERATURE EN FONCTION DU TEMPS.....................................................................31
FIGURE 10 : MAILLAGE DE LA COLONNE......................................................................................................................32
FIGURE 11 : CONDITIONS AUX LIMITES PENDANT L'ESSAI..........................................................................................34
FIGURE 12 : CONDITIONS AUX LIMITES - MODELE NUMERIQUES...............................................................................34
FIGURE 13 : LA TOLERANCE DE L'IMPERFECTION GLOBALE EN1090-2 [6]...................................................................36
FIGURE 14 : LA TOLERANCE DE L'IMPERFECTION LOCALE –ÂME DE PROFILE SOUDE EN1090-2 ...............................36
FIGURE 15 : LA TOLERANCE DE L'IMPERFECTION LOCALE –SEMELLE DE PROFILE SOUDE EN1090-2.........................37
FIGURE 16 : DISTRIBUTION DES CONTRAINTES RESIDUELLES POUR DES SECTIONS EN H RECONSTITUEES SOUDEES 37
FIGURE 17 : LES ZONES DES REPARTITIONS DES CONTRAINTES RESIDUELLES POUR LA SECTION RECONSTITUEE
SOUDEE ...............................................................................................................................................................38
FIGURE 18 : LA DISTRIBUTION ET LA REPARTITION DES CONTRAINTES RESIDUELLES.................................................40
FIGURE 19 : CHARGES DE RUINE SANS ET AVEC CR POUR DIFFERENTES LONGUEURS DE COLONNE .........................41
FIGURE 20 : CHARGES DE RUINE SANS ET AVEC CR CORRIGEES POUR DIFFERENTES LONGUEURS DE COLONNE......42
FIGURE 21 : EVOLUTION DE LA CHARGE APPLIQUEE SUR LES COLONNES D’ACIER EN FONCTION DU TEMPS ...........42
FIGURE 22 : PARAMETRES DE LA COLONNE.................................................................................................................43
FIGURE 23 : EXEMPLE D’UNE COURBE (CHARGE-LONGUEUR) REPRESENTANT LE SAUT A 4M...................................44
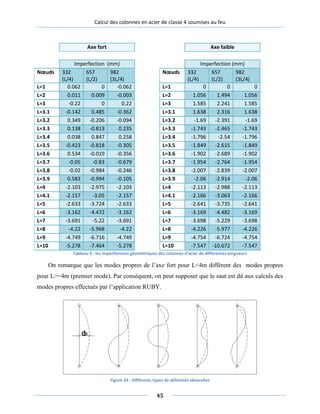
FIGURE 24 : DIFFERENTS TYPES DE DEFORMES OBSERVEES........................................................................................45
FIGURE 25 : MOYENNES DES RAPPORTS DES CHARGES DE RUINE DES METHODES ANALYTIQUES ET NUMERIQUE EN
FONCTION DE LA NUANCE D’ACIER.....................................................................................................................51
FONCTION DE LA TEMPERATURE ........................................................................................................................52
FONCTION DE LA LONGUEUR..............................................................................................................................53
FONCTION DE HNUM/TW ...................................................................................................................................54
FONCTION DE B/TF..............................................................................................................................................54
FIGURE 30 : DENSITE DE PROBABILITE DE LA LOI NORMALE(GAUSS) POUR LES RAPPORTS DES CHARGES DE RUINE55
FIGURE 31 : COMPARAISON DES RESULTATS NUMERIQUES SAFIR ET ANALYTIQUES DE LA METHODE EC3..............56
FIGURE 32 : COMPARAISON DES RESULTATS NUMERIQUES SAFIR ET ANALYTIQUES DE LA METHODE D'AVEIRO1..57
FIGURE 33 : COMPARAISON DES RESULTATS NUMERIQUES SAFIR ET ANALYTIQUES DE LA METHODE D'AVEIRO2...58
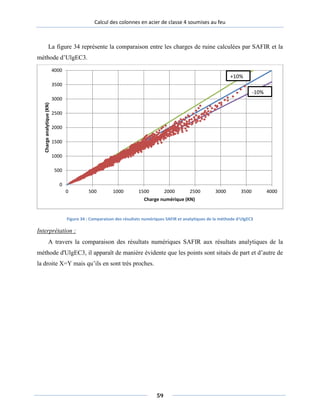
FIGURE 34 : COMPARAISON DES RESULTATS NUMERIQUES SAFIR ET ANALYTIQUES DE LA METHODE D'ULGEC3....59
FIGURE 35 : COMPARAISON DES RESULTATS NUMERIQUES SAFIR ET ANALYTIQUES DE LA METHODE D'ULGAV......60
8

FIGURE 36 : FONCTION DE REPARTITION DE LA LOI NORMALE POUR LES RAPPORTS DES CHARGES DE RUINE ........61
FIGURE 37 : CHARGE DE RUINE CALCULEE PAR SAFIR EN FONCTION DE LA LONGUEUR POUR UNE COLONNE DE
FY=460 MPA, T=650°C, TW=4MM, ET TF= 14MM OU LE FLAMBEMENT SELON L’AXE FAIBLE...........................62
FIGURE 38 : CHARGE DE RUINE CALCULEE PAR SAFIR EN FONCTION DE LA LONGUEUR POUR UNE COLONNE DE
FY=355 MPA, T=750°C, TW=4MM, ET TF= 6MM OU LE FLAMBEMENT SELON L’AXE FORT ...............................62
9

Liste des tableaux
TABLEAU 1 : PAROIS COMPRIMEES INTERNES (AME)..................................................................................................16
TABLEAU 2 : PAROIS COMPRIMEES EN CONSOLE (SEMELLE) ......................................................................................17
TABLEAU 3 : COEFFICIENTS DE REDUCTION POUR LES RELATIONS CONTRAINTE-DEFORMATION DE L’ACIER AU
CARBONE AUX TEMPERATURES..........................................................................................................................26
TABLEAU 4 : COEFFICIENTS DE REDUCTION POUR L’ACIER AU CARBONE POUR LE CALCUL DES SECTIONS DE CLASSE
4 AUX TEMPERATURES ELEVEES..........................................................................................................................27
TABLEAU 5 : TAILLE DES MAILLES DE CHAQUE ELEMENT............................................................................................33
TABLEAU 6 : : LES IMPERFECTIONS GEOMETRIQUES UTILISEES SELON LES DEUX PARTENAIRES...............................39
TABLEAU 7 : CHARGES DE RUINE CALCULEES PAR LES DEUX LOGICIELS ABAQUS/SAFIR............................................39
TABLEAU 8 : COMPARAISON DES CHARGES DE RUINE AVEC ET SANS APPLICATION D’EFFORT DE TRACTION...........43
TABLEAU 9 : LES IMPERFECTIONS GEOMETRIQUES DES COLONNES D’ACIER DE DIFFERENTES LONGUEURS ............45
TABLEAU 10 : CLASSIFICATION DE LA SECTION POUR LA SEMELLE .............................................................................46
TABLEAU 11 : CLASSIFICATION DE LA SECTION POUR L’AME ......................................................................................46
TABLEAU 12 : CLASSIFICATION DE LA SECTION POUR LA SEMELLE .............................................................................49
TABLEAU 13 : CLASSIFICATION DE LA SECTION POUR L’AME ......................................................................................49
TABLEAU 14 : LA MOYENNE GENERALE DE TOUS LES RAPPORTS DES CHARGES DE RUINE ET LEURS ECARTS TYPE ..55
10

Table de matière
REMERCIEMENT..................................................................................................................................................... 3
RESUME ................................................................................................................................................................. 4
ABSTRACT .............................................................................................................................................................. 5
NOTATION.............................................................................................................................................................. 6
LISTE DES FIGURES ................................................................................................................................................. 8
LISTE DES TABLEAUX ............................................................................................................................................ 10
TABLE DE MATIERE............................................................................................................................................... 11
INTRODUCTION.................................................................................................................................................... 13
CHAPITRE I : ETAT DE L’ART .......................................................................................................................... 14
1. GENERALITES ......................................................................................................................................................14
2. METHODE D’EUROCODE3 ..................................................................................................................................14
3. METHODES D’AVEIRO...........................................................................................................................................17
3.1. Méthode d’Aveiro 1 (Méthode non simplifiée).......................................................................................17
3.2. Méthode d’Aveiro (Méthode simplifiée).................................................................................................20
4. PARTIE EXPERIMENTALE DU PROJET..........................................................................................................................20
5. LOGICIELS ET APPLICATIONS UTILISES.......................................................................................................................21
CHAPITRE II : PROPRIETES DES MATERIAUX..................................................................................................... 23
1. GENERALITES ......................................................................................................................................................23
2. PROPRIETES MECANIQUES DES ACIERS AU CARBONE ....................................................................................................24
2.1. Propriétés de résistance et de déformation ...........................................................................................24
2.2. Masse volumique....................................................................................................................................24
3. PROPRIETES THERMIQUES DES ACIERS AU CARBONE.....................................................................................................27
3.1. Dilatation thermique..............................................................................................................................27
3.2. Chaleur spécifique ..................................................................................................................................28
3.3. Conductivité thermique..........................................................................................................................29
CHAPITRE III : ANALYSE PARAMETRIQUE – COURBE DE FLAMBEMENT ......................................................... 31
1. MODELE ELEMENTS FINIS POUR L’ANALYSE PARAMETRIQUE..........................................................................................31
1.1. Géométrie de la colonne et paramètres utilisés.....................................................................................31
1.2. Eléments finis utilisés dans le modèle ....................................................................................................32
1.3. Imperfections géométriques initiales .....................................................................................................35
1.4. Les contraintes résiduelles......................................................................................................................37
2. COMPARAISON DES RESULTATS ULG AVEC LE PARTENAIRE TECNALIA...........................................................................38
2.1. Comparaison des imperfections ULG/TECNALIA ....................................................................................38
2.2. Comparaison de la charge de ruine ULG/TECNALIA...............................................................................39
3. AMELIORATION DES APPLICATIONS UTILISEES .............................................................................................................40
3.1. Modification des Contraintes résiduelles(CR).........................................................................................40
11

3.2. Exécution du logiciel SAFIR.....................................................................................................................42
3.3. Modes propres dans RUBY .....................................................................................................................43
CHAPITRE IV : NOUVELLES PROPOSITIONS.................................................................................................... 46
1. PREMIERE PROPOSITION : METHODE ULGEC3 ...........................................................................................................46
2. DEUXIEME PROPOSITION : METHODE ULGAV.............................................................................................................49
3. RESULTATS .........................................................................................................................................................51
3.1. Flambement selon l’axe fort...................................................................................................................51
3.2. Flambement selon l’axe faible................................................................................................................61
3.3. Points suspects .......................................................................................................................................61
CONCLUSION........................................................................................................................................................ 63
BIBLIOGRAPHIES .................................................................................................................................................. 64
ANNEXES.............................................................................................................................................................. 65
ANNEXE 1 : LOGICIELS ET APPLICATIONS UTILISES................................................................................................ 66
ANNEXE 2 : RESULTATS : FLAMBEMENT SELON L’AXE FAIBLE............................................................................... 72
ANNEXE 3 : APPLICATION DES METHODES SUR LA BASE DONNEES DE TECNALIA................................................. 78
ANNEXE 4 : EXTRAIT DE LA BASE DE DONNEES (SAFIR)......................................................................................... 80
ANNEXE 5 : EXTRAIT DE LA BASE DE DONNEES (ABAQUS) .................................................................................... 89
12

Introduction
Quand une structure en acier carbone est exposée à un incendie, la température dans ses
éléments augmente et leur résistance et rigidité sont considérablement réduites, ce qui conduits la
plupart du temps à une nouvelle classe de section transversale. De cette manière le flambement
peut apparaître d’autant plus facilement que lorsque la température augmente.
L’objectif de ce travail est de trouver un nouveau modèle de calcul pour remplacer le modèle
actuel de l’EUROCODE3 [EN 1993-1-2] concernant les colonnes d’acier carbone de classe 4
exposées à un incendie. En effet la formulation actuelle de l’EUROCODE3 est trop sécuritaire, et
cela conduit donc à une consommation inutile en acier dans certaines situations.
On construit une base de données à partir des simulations effectuées sur les poteaux
métalliques soumis au feu par le logiciel SAFIR et à partir de cette base de données, on cherche à
développer un modèle simple qui sera calibré sur cette base de données.
Le projet présenté portera sur « le calcul des colonnes en acier carbone de classe 4 soumises
au feu ».
A cet effet, le présent rapport est scindé en quatre parties qui présenteront l’intégralité des
aspects théoriques et pratiques :
- La première partie est dédiée à présenter tous ce que été faite sur le projet et les
logiciels utilisés.
- La deuxième partie présente le comportement, les propriétés mécaniques, ainsi que
thermiques de l’acier carbone en situation d’incendie.
- La troisième partie, consiste à construire une base de données des résultats calculés par
le logiciel SAFIR.
- La quatrième partie est consacrée à l’élaboration d’un modèle de calcul simple de
dimensionnement applicable en bureau d’études.
13

Chapitre I : Etat de l’art
1. Généralités
Les anciennes recherches ont été faites sur le problème de flambement des colonnes d’acier
carbone de classe 4 à haute température. La commission européenne a validé un modèle proposé
dans l’EUROCODE3 qui est trop sécuritaire, ainsi il y a deux autres modèles ont été développés
par l’université d’AVEIRO de Portugal auxquelles il a été proposé de modifier la section
efficace, où il a été pris en compte le voilement local par la modification d’un paramètre qui
dépend des fois de la température réelle et d'autres fois d'une température fixe de 700°C. Dans la
suite de ce travail on étudiera en détail la méthode d’EUROCODE3 qui existe ainsi que les deux
autres d’AVEIRO.
2. Méthode d’EUROCODE3
Selon l’EUROCODE EN 1993-1-2, la résistance au flambement à l’instant t d’un élément en
compression de classe 4 soumis au feu est déterminée à partir de :
𝑁𝑏,𝑓𝑖,𝑡𝑡,𝑅𝑑 =
χ 𝑓𝑖 ∗ 𝐴 𝑒𝑓𝑓 ∗ 𝑘02,𝜃𝑎𝑎 ∗ 𝑓𝑓𝑦𝑦
𝛾 𝑀,𝑓𝑖
Où :
χ 𝑓𝑖 : Facteur de réduction pour le flambement par flexion en situation d’incendie.
𝑘02,𝜃𝑎𝑎 : Facteur de réduction de la limite d’élasticité de l’acier à la température 𝜃𝜃𝑎𝑎 pour des
sections de classe 4.
Pour calculerχ 𝑓𝑖 , il faut prendre le minimum entre le coefficient de réduction pour le flambement
selon l’axe fort et selon l’axe faible :
χ 𝑓𝑖 =
1
𝜑𝜃𝜃
+ � 𝜑𝜃𝜃
2 − λ�𝜃𝜃
2
Avec :
14

𝜑 𝜃 =
1
2
(1 + �𝛼 ∗ λ� 𝜃� + λ� 𝜃
2
)
Et
𝛼 = 0.65 ∗ �235
𝑓𝑓𝑦𝑦
�
L’élancement réduit λ� 𝜃 pour la température𝜃𝜃𝑎𝑎, est donné par l’expression :
λ� 𝜃 = λ ∗ �
𝑘02
𝑘 𝐸
�
Et
λ = max(λstrong ; λ 𝑤𝑒𝑎𝑎𝑘)
Avec :
𝐼𝑛𝑒𝑟𝑡𝑖𝑒 𝑠𝑒𝑙𝑜𝑛 𝑙′
𝑎𝑥𝑒𝑓𝑓𝑜𝑟𝑡 𝐼 =
𝑡 𝑤 ∗ ℎ 𝑛𝑢𝑢𝑚
3
12
+ 2 ∗ (
𝑏 ∗ 𝑡𝑓
3
12
+ 𝑏 ∗ 𝑡𝑓 ∗
ℎ 𝑛𝑢𝑢𝑚
2
4
)
𝐶ℎ𝑎𝑟𝑔𝑒 𝐶𝑟𝑖𝑡𝑖𝑞𝑢𝑒 𝑠𝑒𝑙𝑜𝑛 𝑙′
𝑎𝑥𝑒𝑓𝑓𝑜𝑟𝑡 𝑁𝑐𝑟 =
𝜋2
∗ 𝐸𝐸 ∗ 𝐼
(𝐿 ∗ 𝐿 𝑟𝑎𝑎𝑡𝑡𝑖𝑜𝑆𝑡𝑡𝑟)2
𝐸𝐸𝑙𝑎𝑛𝑐𝑒𝑚𝑒𝑛𝑡 𝑠𝑒𝑙𝑜𝑛 𝑙′
𝑎𝑥𝑒𝑓𝑓𝑜𝑟𝑡 λ 𝑠𝑡𝑡𝑟𝑜𝑛𝑔 = �
𝐴 𝑒𝑓𝑓 ∗ 𝑓𝑓𝑦𝑦
𝑁𝑐𝑟
�
Et :
𝐼𝑛𝑒𝑟𝑡𝑖𝑒 𝑠𝑒𝑙𝑜𝑛 𝑙′
𝑎𝑥𝑒 𝑓𝑓𝑎𝑖𝑏𝑙𝑒 𝐼 = �2 ∗
𝑡𝑓 ∗ 𝑏3
12
� + (
ℎ 𝑛𝑢𝑢𝑚 ∗ 𝑡 𝑤
3
12
)
𝐶ℎ𝑎𝑟𝑔𝑒 𝐶𝑟𝑖𝑡𝑖𝑞𝑢𝑒 𝑠𝑒𝑙𝑜𝑛 𝑙′
𝑎𝑥𝑒𝑓𝑓𝑎𝑖𝑏𝑙𝑒 𝑁𝑐𝑟 =
𝜋2
∗ 𝐸𝐸 ∗ 𝐼
(𝐿 ∗ 𝐿 𝑟𝑎𝑎𝑡𝑡𝑖𝑜𝑊)2
𝐸𝐸𝑙𝑎𝑛𝑐𝑒𝑚𝑒𝑛𝑡 𝑠𝑒𝑙𝑜𝑛 𝑙′
𝑎𝑥𝑒𝑓𝑓𝑜𝑟𝑡 λ 𝑤𝑒𝑎𝑎𝑘 = �
𝑁𝑐𝑟
�
Il est essentiel de déterminer les aires efficaces des éléments comprimés plans en utilisant le
tableau 1 pour les parois internes et le tableau 2 pour les parois en console. La détermination de
l’aire efficace de la zone comprimée d’une plaque dont l’aire de la section brute vaut A,
s’effectue au moyen de l’équation suivante :
𝐴 𝑒𝑓𝑓 = 𝜌 ∗ 𝐴
15

Où ρ est le coefficient réducteur pour le voilement de plaque.
Le coefficient réducteur ρ peut être considéré comme suit :
• Parois comprimées internes :
𝜌 = 1 𝑝𝑜𝑢𝑟 𝜆� 𝑝 ≤ 0.673
𝜌 =
𝜆� 𝑝 − 0.055(3 + ψ)
𝜆� 𝑝
2 ≤ 1 𝑝𝑜𝑢𝑟 𝜆� 𝑝 ≥ 0.673 𝑎𝑣𝑒𝑐 (3 + ψ) ≥ 0
• Parois comprimées en console :
𝜌 = 1 𝑝𝑜𝑢𝑟 𝜆� 𝑝 ≤ 0.748
𝜌 =
𝜆� 𝑝 − 0.188
𝜆� 𝑝
2 ≤ 1 𝑝𝑜𝑢𝑟 𝜆� 𝑝 ≥ 748
𝐴𝑣𝑒𝑐 ∶ 𝜆̅ 𝑝𝑝 = �
𝑓𝑓 𝑦
𝑁 𝑐𝑟
=
𝑏�
𝑡�
28.4∗𝜀𝜀∗� 𝐾 𝜎
Tableau 1 : parois comprimées internes (âme)
16

3. Méthodes d’Aveiro
Les chercheurs de l’université Aveiro de Portugal ont développé deux modèles auxquelles il
a été proposé de modifier la section efficace, où il a été pris en compte le voilement local par la
modification d’un paramètre qui dépend des fois de la température réelle et d'autres fois d'une
température fixe de 700°C.
3.1. Méthode d’Aveiro 1 (Méthode non simplifiée)
Si Classe de la section >= 3
𝜀𝜀 = �235
𝑓𝑓𝑦𝑦
�
Tableau 2 : Parois comprimées en console (semelle)
17

𝑟𝑙𝑜𝑐 = 𝜃𝜃
𝑘02𝐴𝑣𝑒𝑖𝑟𝑜 = 𝑘02−𝐴𝑣𝑒𝑖𝑟𝑜𝜃(𝑟𝑙𝑜𝑐)
𝑘𝑦𝑦𝐴𝑣𝑒𝑖𝑟𝑜 = 𝑘𝑦𝑦𝜃(𝑟𝑙𝑜𝑐)
𝑟𝑙𝑜𝑐 = 𝑘02𝐴𝑣𝑒𝑖𝑟𝑜
𝑘 𝑦𝐴𝑣𝑒𝑖𝑟𝑜
�
C'est là où se passe la modification de la méthode Aveiro. Le rapport ne dépend pas de la
température.
Le coefficient réducteur ρ pour calculer l’air efficace peut être considéré comme suit :
• Parois comprimées internes (Âme) :
𝜌 =
(𝜆̅𝑝𝑝 + 𝛼 𝜃) 𝛽 𝜃 − (3 + ψ)
(𝜆̅𝑝𝑝 + 𝛼 𝜃)2∗𝛽 𝜃
≤ 1 𝑠𝑖𝑛𝑜𝑛 𝜌 = 1
Avec : 𝛼 𝜃 = 0.9 − (0.315 ∗ 𝑟𝑙𝑜𝑐
𝜀𝜀 𝜃
� )
𝛽 𝜃 = 2.3 − (1.1 ∗ 𝑟𝑙𝑜𝑐)
Donc la hauteur efficace : ℎ 𝑒𝑓𝑓 = ℎ 𝑛𝑢𝑢𝑚 ∗ 𝑡 𝑤
Avec : ℎ 𝑛𝑢𝑢𝑚 = ℎ + 𝑡𝑓
• Parois comprimées en console (Semelle) :
𝜌 =
(𝜆̅𝑝𝑝 + 𝛼 𝜃) 𝛽 𝜃 − 0.188
Avec : 𝛼 𝜃 = 1.1 − (0.63 ∗ 𝑟𝑙𝑜𝑐
𝜀𝜀 𝜃
� )
𝛽 𝜃 = 2 − (1.1 ∗ 𝑟𝑙𝑜𝑐)
Donc la largeur efficace : 𝑏 𝑒𝑓𝑓 = 𝑏 ∗ 𝑡𝑓
Avec ∶ 𝜆� 𝑝 = �
𝑓𝑦
𝑁 𝑐𝑟
=
𝑏�
𝑡𝑡�
28.4∗𝜀∗�𝐾 𝜎
Si Classe de la section = 1 ou 2
𝑏 𝑒𝑓𝑓 = 𝑏 ℎ 𝑒𝑓𝑓 = ℎ 𝑛𝑢𝑢𝑚
𝐴 𝑒𝑓𝑓 = �ℎ 𝑒𝑓𝑓 ∗ 𝑡 𝑤� + 2 ∗ (𝑏 𝑒𝑓𝑓 ∗ 𝑡𝑓)
𝑓𝑓𝑦𝑦 𝜃
= 𝑘𝑦𝑦 ∗ 𝑓𝑓𝑦𝑦
On voit que même pour les classes 4, le coefficient réducteur 𝑘𝑦𝑦 a été utilisé au lieu de 𝑘02.
18

𝑁𝑝𝑝𝑙𝑎𝑎𝑠𝑡𝑡𝑖𝑐 = 𝐴 𝑒𝑓𝑓 ∗ 𝑓𝑓𝑦𝑦 𝜃
Selon la méthode d’Aveiro, la résistance au flambement à l’instant t d’un élément en
compression de soumis au feu est déterminé à partir :
𝑁𝐴𝑣1 = χ 𝑓𝑖 ∗ 𝐴 𝑒𝑓𝑓 ∗ 𝑁 𝑝𝑙𝑎𝑠𝑡𝑖𝑐
Il convient de prendre la valeur de χ 𝑓𝑖 égale à la plus petite des valeurs de χ𝑦𝑦,𝑓𝑖 et χ 𝑧,𝑓𝑖
déterminées selon l’expression :
χ 𝑓𝑖 =
1
𝜑𝜃𝜃
+ � 𝜑𝜃𝜃
2 − λ�𝜃𝜃
2
Avec : 𝜑 𝜃 =
1
2
(1 + �𝛼 ∗ λ� 𝜃� + λ� 𝜃
2
)
Et 𝛼 = 0.65 ∗ �235
𝑓𝑓𝑦𝑦
�
L’élancement réduit λ� 𝜃 pour la température 𝜃𝜃𝑎𝑎, est donné par l’expression :
λ� 𝜃 = λ ∗ �
𝑘𝑦𝑦
𝑘 𝐸
�
Et λ = max(λstrong ; λ 𝑤𝑒𝑎𝑎𝑘)
Le moment d’inertie selon l’axe fort :
𝐼 =
3
12
+ 2 ∗ (
𝑏 ∗ 𝑡𝑓
3
12
+ 𝑏 ∗ 𝑡𝑓 ∗
2
4
)
La résistance Critique selon l’axe fort :
𝑁𝑐𝑟 =
𝜋2
∗ 𝐸𝐸 ∗ 𝐼
Elancement selon l’axe fort :
λ 𝑠𝑡𝑡𝑟𝑜𝑛𝑔 = �
𝑁𝑐𝑟
�
Et :
19

Le moment d’inertie selon l’axe faible 𝐼 = �2 ∗
𝑡𝑡 𝑓∗𝑏3
12
� + (
ℎ 𝑛𝑢𝑚∗𝑡𝑡 𝑤
3
12
)
La résistance Critique Selon l’axe faible 𝑁𝑐𝑟 =
𝜋2∗𝐸∗𝐼
(𝐿∗𝐿 𝑟𝑎𝑡𝑖𝑜𝑊)2
Elancement selon l’axe faible λ 𝑤𝑒𝑎𝑎𝑘 = �
𝑁𝑐𝑟
�
3.2. Méthode d’Aveiro (Méthode simplifiée)
La deuxième méthode simplifiée d’Aveiro suit les mêmes démarches de la première en
modifiant le rloc =700 °C au lieu de rloc =𝜃𝜃.
4. Partie expérimentale du projet
L'un des principaux objectifs du projet est la création d'une gamme complète des éléments
d’épreuve expérimentale sur le comportement au feu des éléments en acier de profilés soudées ou
profilés laminées (sous forme de I et H) de classe 4 en effectuant un certain nombre d'essais au
feu.
Dans ce travail dédié aux colonnes de section I et H avec des sections minces soumises à une
compression axiale et à une compression axiale combinée à la flexion à une température élevée, 8
essais expérimentaux ont été réalisés. Ces 8 essais comportent 6 colonnes reconstituées soudées
avec des sections transversales constantes et variables et 2 colonnes laminés à chaud avec une
section constante.
Les essais au feu consistent à appliquer une charge mécanique jusqu'à atteindre un certain
rapport de charge (en pourcentage de la charge de ruine à froid) pour les éléments en acier et en
chauffant ensuite ce dernier au moins jusqu'à la rupture mécanique.
La colonne est chauffée sur toute sa longueur. Cette procédure est la même pour les huit
essais.
Ces tests sont conçus de telle sorte que la ruine est induite par un flambement global tout au
long de l'axe faible ou fort éventuellement combiné avec un voilement local des sections des
parois.
20

Les fabricants de profilés en acier sont Linda (Luxembourg) pour les échantillons soudés et
les échantillons laminés à chaud ont été fournis par Desmo (République tchèque).
Après les 8 essais effectués au sein du laboratoire, Un modèle numérique dans le logiciel
SAFIR a été calibré de manière à reproduire au mieux le comportement de ces huit colonnes.
En comparant ces résultats numériques et expérimentaux, on se rend compte que les résultats
obtenus sont très proche. On peut donc conclure la validité du modèle
5. Logiciels et Applications Utilisés
SAFIR est un logiciel qui permet de calculer la résistance de structures par la méthode des
éléments finis. On fait recours à l’utilisation des logiciels tiers non seulement pour la
modélisation des structures que l’on souhaite calculer, mais aussi pour l’affichage des résultats
Figure 2 : Comparaison des résultats numériques et expérimentaux
21

après que SAFIR ait réalisé les calculs. Pour cela, il est possible d’utiliser le logiciel GID comme
pré-processeur et le logiciel DIAMOND comme post-processeur.
Dans ce projet, vu qu’on travaille sur la même structure qui est une colonne d’acier carbone
avec différentes sections, un ingénieur du service SE de l’université de Liège a créé une
application VB s’appelant « MAILLEUR » [Annexe 1-1] pour créer les modèles des colonnes.
On retrouve l’enchainement des logiciels utilisés sur la figure 3.
Pour plus de détails sur les logiciels et applications utilisés, veuillez voir la partie Annexe 1.
MAILLEUR VB FICHIER IN
RUBY
Base de données
Fichier txt
SAFIR FICHIER OUTFICHIER
RUBY.IN
Matlab
Excel
DIAMOND
OUTPUT
READER VB
Sortie
Entrée
Figure 3 : Enchainement des logiciels
22

Chapitre II : Propriétés des matériaux
1. Généralités
L’acier est un matériau ininflammable. L’acier ne brûle pas et ne dégage ni chaleur, ni
fumée. Cependant, à des températures comme celles que l’on peut rencontrer en cas d’incendie
dans un bâtiment, l’acier perd une partie de sa résistance et de sa rigidité.
N’importe quelle résistance au feu peut être atteinte en prenant les bonnes mesures. En outre,
l’acier offre une grande sécurité pour les raisons suivantes:
L’acier est un matériau de construction prévisible. Contrairement à certains autres
matériaux de construction comme la maçonnerie et le béton, les caractéristiques intrinsèques de
l’acier à haute température sont déterminées précisément et il n’existe que de faibles variations.
L’acier est aussi un matériau de construction déformable. À haute température, tous les
matériaux subissent des déformations thermiques importantes. Ces déformations engendrent des
charges supplémentaires dans la construction. Pour reprendre ces déformations et ces charges, un
matériau ne doit pas tant être résistant, mais surtout déformable. Contrairement à un matériau
friable, comme le béton par exemple, l’acier en est parfaitement capable.
L’acier prévient par d’importantes déformations avant de céder éventuellement.
Normalement, les pompiers et autres services de secours peuvent déduire de l’évolution des
déformations si le bâtiment est sur le point de s’écrouler. La rupture friable et soudaine, qui peut
se produire avec le béton et les constructions en maçonnerie par exemple, est très rare dans le cas
de constructions en acier.
L’acier est un matériau facilement quantifiable. Les EUROCODE3s concernant le
calcul de la résistance au feu de l’acier sont basés sur des décennies de recherches scientifiques
poussées. Le comportement dans la construction est bien connu et tous les phénomènes possibles
sont prévisibles avec précision. Le risque qu’une autre forme de rupture que celle prévue lors de
la conception se produise est de ce fait très réduit dans le cas des constructions en acier.
23

2. Propriétés mécaniques des aciers au carbone
2.1. Propriétés de résistance et de déformation
Pour les vitesses d’échauffement comprises entre 2 et 50 K/min, il est utile de déterminer les
propriétés de résistance et de déformation de l’acier aux températures élevées à partir de la
relation contraintes-déformations donnée dans la figure 4.
NOTE : Pour les règles contenues dans la présente norme, il est supposé que les vitesses
d’échauffement se situent dans les limites spécifiées.
Il est nécessaire d’utiliser la relation donnée dans la figure 4 pour déterminer les résistances à
la traction, à la compression, à la flexion ou au cisaillement.
Le tableau 3 donne les facteurs de réduction pour les relations contrainte-déformation pour
l’acier aux températures élevées donnée dans la figure 4. Ces facteurs de réduction sont définis de
la façon suivante :
- Limite d’élasticité efficace, par rapport à la limite d’élasticité à 20°C : 𝑘𝑦𝑦,𝜃 =
𝑓𝑓𝑦𝑦,𝜃
𝑓𝑓𝑦𝑦
�
- Limite de proportionnalité, par rapport à la limite d’élasticité à 20°C : 𝑘𝑝𝑝,𝜃 =
𝑓𝑓𝑝𝑝,𝜃
𝑓𝑓𝑦𝑦
�
- Pente du domaine élastique linéaire, par rapport à la pente à 20°C : 𝑘 𝐸,𝜃 =
𝐸𝐸𝑎𝑎,𝜃
𝐸𝐸𝑎𝑎
�
NOTE : La variation de ces coefficients de réduction en fonction de la température est illustrée
sur la figure 5.
2.2. Masse volumique
La masse volumique de l’acier 𝜌𝑎𝑎 peut être considérée comme indépendante de la température de
l’acier. La valeur suivante peut être adoptée : 𝜌𝑎𝑎 = 7850 𝑘𝑔/𝑚3
24

Figure 4 : Relation contrainte-déformation pour l’acier au carbone aux températures élevées.
Légende : - 𝑓𝑓𝑦𝑦, 𝜃𝜃 Limite d’élasticité efficace.
- 𝑓𝑓𝑝𝑝, 𝜃𝜃 Limite de proportionnalité. - 𝐸𝐸𝑎𝑎, 𝜃𝜃 Pente du domaine élastique linéaire.
- 𝜀𝜀𝑝𝑝, 𝜃𝜃 Déformation à la limite de proportionnalité. - 𝜀𝜀𝑦𝑦, 𝜃𝜃 Déformation plastique.
- 𝜀𝜀𝑡𝑡, 𝜃𝜃 Déformation limite en élasticité. - 𝜀𝜀𝑢𝑢, 𝜃𝜃 Déformation ultime.
25

NOTE : Pour des valeurs intermédiaires de la température de l’acier, une interpolation linéaire
peut être utilisée.
Figure 5 : Coefficients de réduction pour les relations contrainte-déformation de
l’acier au carbone aux températures élevées
Tableau 3 : Coefficients de réduction pour les relations contrainte-
déformation de l’acier au carbone aux températures
26

Les coefficients de réduction pour la résistance des aciers au carbone par rapport à la limite
d’élasticité à 20°C pour les sections de classe 4 peuvent être pris dans le Tableau 4.
NOTE : Pour des valeurs intermédiaires de la température de l’acier, une interpolation linéaire
peut être utilisée.
3. Propriétés thermiques des aciers au carbone
3.1. Dilatation thermique
On détermine la dilatation thermique de l’acier (
∆𝑙
𝑙
) par l’intermédiaire des expressions
suivantes :
- Pour 20℃ ≤ 𝜃𝜃𝑎𝑎 < 750℃ ∶
∆𝑙
𝑙� = 1.2 ∗ 10−5
𝜃𝜃𝑎𝑎 + 0.4 ∗ 10−8
𝜃𝜃𝑎𝑎
2
− 2.416 ∗ 10−4
Tableau 4 : Coefficients de réduction pour l’acier au carbone pour le calcul
des sections de classe 4 aux températures élevées
27

- Pour 750℃ ≤ 𝜃𝜃 𝑎 < 860℃ ∶
∆𝑙
𝑙� = 1.1 ∗ 10−2
- Pour 860℃ ≤ 𝜃𝜃𝑎𝑎 ≤ 1200℃ ∶
∆𝑙
𝑙� = 2 ∗ 10−5
𝜃𝜃𝑎𝑎 − 6.2 ∗ 10−3
Où : 𝑙 ∶ Longueur à 20°C.
∆𝑙 ∶ Dilatation induite par la température.
𝜃𝜃𝑎𝑎 ∶ Température de l’acier [°C].
NOTE : La variation de la dilatation thermique en fonction de la température est illustrée dans la
figure 6.
3.2. Chaleur spécifique
Afin de déterminer la chaleur spécifique de l’acier 𝐶𝑎𝑎 on fait appel aux expressions
suivantes :
Figure 6 : Dilatation thermique de l’acier au carbone en fonction de la température
28

- Pour 20℃ ≤ 𝜃𝜃𝑎𝑎 < 600℃ ∶
𝐶𝑎𝑎 = 425 + 7.73 ∗ 10−1
𝜃𝜃𝑎𝑎 − 1.69 ∗ 10−3
𝜃𝜃𝑎𝑎
2
+ 2.22 ∗ 10−6
𝜃𝜃𝑎𝑎
3
𝐽/𝑘𝑔𝐾
- Pour 600℃ ≤ 𝜃𝜃𝑎𝑎 < 735℃ ∶
𝐶𝑎𝑎 = 666 +
13002
738 − 𝜃𝜃𝑎𝑎
𝐽/𝑘𝑔𝐾
- Pour 735℃ ≤ 𝜃𝜃𝑎𝑎 < 900℃ ∶
𝐶𝑎𝑎 = 545 +
17820
𝜃𝜃𝑎𝑎 − 731
𝐽/𝑘𝑔𝐾
- Pour 900℃ ≤ 𝜃𝜃𝑎𝑎 < 1200℃ ∶
𝐶𝑎𝑎 = 650 𝐽/𝑘𝑔𝐾
Où : 𝜃𝜃𝑎𝑎 ∶ Température de l’acier [°C].
NOTE : La variation de la chaleur spécifique en fonction de la température est illustrée dans la
figure 7.
3.3. Conductivité thermique
Il convient de déterminer la conductivité thermique de l’acier λ𝑎𝑎 au moyen des expressions
suivantes :
Figure 7 : Chaleur spécifique de l’acier au carbone en fonction de la
température
29

- Pour 20℃ ≤ 𝜃𝜃𝑎𝑎 < 800℃ ∶
λ𝑎𝑎 = 54 − 3.33 ∗ 10−2
𝜃𝜃𝑎𝑎 𝑊/𝑚𝐾
- Pour 800℃ ≤ 𝜃𝜃𝑎𝑎 ≤ 1200℃ ∶
λ𝑎𝑎 = 27.3 𝑊/𝑚𝐾
Où : 𝜃𝜃𝑎𝑎 ∶ Température de l’acier [°C].
NOTE : La variation de la conductivité thermique en fonction de la température est illustrée dans
la figure 8.
Figure 8 : Conductivité thermique de l’acier au carbone en fonction de
la température
30

Chapitre III : Analyse paramétrique – Courbe
de flambement
1. Modèle éléments finis pour l’analyse paramétrique
1.1. Géométrie de la colonne et paramètres utilisés
1.1.1. Dimensions de la colonne
- Nous avons étudié 250 types de colonnes de différentes sections et longueur.
- Les paramètres étudiés sont :
- Longueur : 1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9 – 10m.
- Epaisseur de l’âme : 4 – 6 – 8 – 10 – 12mm.
- Epaisseur de la semelle : 6 – 8 – 10 – 12 – 14mm
- La hauteur de l’âme h et la largeur de la semelle b sont toujours fixe :
h = 500 mm et b = 250mm
1.1.2. Evolution de la température dans les colonnes
Cinq températures ont été considérées : 350 – 450 – 550 – 650 -750 °C.
Lors des simulations cette température est supposée constante au cours du temps.
0
50
100
150
200
250
300
350
400
0 60 120 180 240 300
Température(°C)
Temps (s)
Figure 9: Evolution de la température en fonction du temps
31

1.1.3. Nuance d’acier
Quatre types d’acier ont été utilisés : S235 – S275 – S355 – S460.
1.2. Eléments finis utilisés dans le modèle
Des éléments finis de type coque ont été utilisés. Chaque élément de coque contient quatre
nœuds, dont chacun d’entre eux possède six degrés de liberté.
1.2.1. Discrétisation de la colonne
Pour la discrétisation de la colonne, nous avons utilisé la discrétisation quadrilatéral en
discrétisant la longueur sur 100, la hauteur sur 14 et le largueur sur 12 éléments.
Figure 10 : maillage de la colonne
32

Le tableau ci-dessous représente la discrétisation de chaque partie :
Tableau 5 : Taille des mailles de chaque élément
1.2.2. Conditions aux limites
Dans le modèle numérique, la colonne est libre en rotation autour de l'axe faible et l’axe fort
au niveau des deux extrémités. Le déplacement vertical à l'extrémité supérieur a été laissé libre
afin de permettre la contraction due à la charge de compression verticale tandis que ce
déplacement vertical est bloqué à l'autre extrémité. Les déplacements horizontaux sont bloqués
aux deux extrémités afin d'empêcher le mouvement de la section d'extrémité entière. Les
conditions aux limites de ce modèle sont illustrées dans la figure ci-dessous.
Largueur de la semelle Hauteur de l’âme
Longueur de la colonne
33

La figure 12 illustre les conditions aux limites mises en œuvre dans SAFIR afin de modéliser
les conditions aux limites décrites ci-dessus.
Figure 11 : Conditions aux limites
pendant l'essai
Figure 12 : Conditions aux limites -
modèle numériques
34

Les flèches bleues illustrent les degrés de libertés de rotation bloqués et les flèches rouges
illustrent les degrés de libertés de translation bloqués.
Une plaque épaisse de 500 mm est utilisée aux deux extrémités de la colonne. La plaque au
sommet de la colonne est utilisée afin de transmettre de manière uniforme la charge appliquée de
manière ponctuelle pour éviter le voilement local, et la plaque au fond est utilisée pour permettre
le mouvement de rotation de la colonne autour de l'axe faible.
1.3. Imperfections géométriques initiales
Les imperfections géométriques sont la déviation du profil par rapport à la géométrie parfaite.
Les imperfections géométriques comprennent le défaut de rectitude le long du profil, le défaut de
planéité des parois et le vrillage d’une section à l’autre. La technique communément adoptée afin
de définir la distribution des imperfections initiales est de réaliser une analyse linéaire de
flambement et puis d’utiliser un des modes propres, choisi selon un critère spécifique, comme la
forme initiale. L’utilisation des imperfections maximales pour un mode propre de flambement est
une estimation conservative car les imperfections maximales ne sont pas périodiques le long de
l’élément. Le pire mode d’imperfection qui cause la plus grande réduction de la capacité portante
est liée souvent au premier mode de flambement. Les déplacements nodaux d’un mode de
flambement sont normalisés en utilisant le déplacement maximal dans la structure et ce
déplacement maximal est pris égal à l’unité. En multipliant les déplacements normalisés par un
facteur approprié, qui est l’amplitude, les imperfections initiales rattachées au mode propre
considéré peuvent être calculées.
Afin de représenter le comportement réel de la colonne, les imperfections géométriques
initiales doivent être modélisées.
Selon la norme EN 1993-1-5-Annexe C [3], l'imperfection à utiliser dans un modèle
numérique est de 80% des tolérances géométriques (tolérances de fabrication).
1.3.1. Imperfection globale
Pour les colonnes des profilé soudés, EN 1090-2 [6] recommande d'envisager une tolérance
de déviation de D = L/750, comme le montre la figure 13. Ainsi, en considérant une imperfection
35

global égal à 80% de la tolérance géométrique, donc une imperfection de 0,8* L/750=L/937.5 est
introduite dans le modèle numérique.
1.3.2. Imperfection locale
Les tolérances de fabrication locale utilisée sont fournies par le fournisseur d'acier et ils sont
basés sur la norme EN 1090-2 [6]. Les tolérances de fabrication locales sont données dans les
figures 14 et 15. Par conséquent, l'amplitude des imperfections locales introduites est égale à 80%
de ces tolérances de fabrication. Les formules au-dessous donnent l'expression de ces
imperfections locales.
Figure 14 : La tolérance de l'imperfection locale –Âme de profilé soudé EN1090-2
Figure 13 : La tolérance de l'imperfection globale EN1090-2 [6]
36

Pour l’âme ∆= 0.8 ∗ �
𝑏
100
� = 0.8 ∗ �
500
100
� = 4𝑚𝑚 𝑎𝑣𝑒𝑐 |∆| ≥ 4𝑚𝑚
Pour la semelle ∆= 0.8 ∗ �
𝑏
100
� = 0.8 ∗ �
250
100
� = 2𝑚𝑚
1.4. Les contraintes résiduelles
Pour les profils reconstitués soudés: après le soudage, le cordon et les zones voisines
échauffées se refroidissent inégalement et se contractent tant dans le sens du cordon que dans le
sens transversal. Si les plaques assemblées sont libres à leurs extrémités, les contraintes
résiduelles sont importantes au voisinage du cordon. La figure 16 présente, à titre d’exemple, la
distribution des contraintes résiduelles mesurées dans un profil en H reconstitué de plaques en
acier [7].
Figure 15 : La tolérance de l'imperfection locale –Semelle de profilé soudé EN1090-2
Figure 16 : Distribution des contraintes
résiduelles pour des sections en H reconstituées
soudées
37

La figure 17 présente la répartition des contraintes résiduelles pour le profilé reconstitué
soudé.
2. Comparaison des résultats ULG avec le partenaire TECNALIA
2.1. Comparaison des imperfections ULG/TECNALIA
Dans toutes les simulations qu’on a effectué, nous avons utilisé une imperfection globale de
70%*(L/937.5) pendant que TECNALIA utilisent une imperfection globale qui vaut (L/1000).
Figure 17 : Les zones des répartitions des contraintes résiduelles pour la section reconstituée soudée
38

Exemple :
Une colonne de L=8m
TECNALIA Ulg
Imperfection (mm) 8 5.977
Tableau 6 : : Les imperfections géométriques utilisées selon les deux partenaires
2.2. Comparaison de la charge de ruine ULG/TECNALIA
Pour assurer la cohérence des résultats, trois cas ont été simulées par les deux partenaires en
utilisant deux logiciels différents : SAFIR à l’Université de Liège et ABAQUS à TECNALIA.
Les données des 3 cas étudiés :
• Nuance d’acier : S355
• Température : 350°C – 550°C – 700°C
• Avec contraintes résiduelles
• Longueur de la colonne : L=8m
• Le flambement selon l’axe faible
• Section :
o hw = 500 mm
o b = 250 mm
o tw = 6mm
o tf = 10mm
Ceci représente un tableau récapitulatif des résultats trouvés par TECNALIA qui utilise le
logiciel ABAQUS et des résultats trouvés par SAFIR
Charge (KN) Rapport relative
ABAQUS SAFIR 100*((SAFIR-ABAQUS)/SAFIR)
471.91 476.4 0.94
265.02 273 2.92
76.86 83.2 7.62
Tableau 7 : Charges de ruine calculées par les deux logiciels ABAQUS/SAFIR
On remarque qu’il y a une petite différence entre la charge de ruine calculée par
ABAQUS(TECNALIA) et celle calculée par SAFIR(ULG). Cette légère différence est
probablement due aux différences dans les imperfections utilisées par les deux logiciels. En
39

effet, la charge de ruine obtenue avec SAFIR est plus élevée que celle obtenue avec ABAQUS, et
ceci s’expliquera certainement par le fait que l’amplitude des imperfections géométriques est plus
petite dans SAFIR que dans ABAQUS.
On peut donc conclure qu’il existe une certaine cohérence entre les résultats obtenus via les
deux logiciels.
3. Amélioration des applications utilisées
3.1. Modification des Contraintes résiduelles(CR)
Après un millier de simulations réalisées, on a remarqué qu’il y avait une anomalie dans les
contraintes résiduelles. Quelques cas ont été simulé avec et sans contraintes résiduelles, afin de
vérifier que ces dernières étaient bien auto équilibrées.
Figure 18 : La distribution et la répartition des contraintes résiduelles
40

Figure 19 : Charges de ruine sans et avec CR pour différentes longueurs de colonne
La figure 19 représente la charge de ruine avec et sans contraintes résiduelles avant la
correction des contraintes résiduelles. On remarque que lorsqu’on applique les contraintes
résiduelles, les charges de ruine sont supérieures à celles obtenues sans contraintes résiduelles.
Or en tante logique, nous devrions observer l’effet inversé étant donné que les contraintes
résiduelles sont supposées avoir un effet défavorable sur la capacité portante.
Les contraintes résiduelles ont été corrigées et modifiées dans l’application MAILLEUR, les
figures 16 et 17 précédentes représentent la distribution et la répartition des contraintes
résiduelles corrigées.
La figure 20 représente la charge de ruine avec et sans contraintes résiduelles, après la
correction des contraintes résiduelles. On voit clairement que les contraintes résiduelles réduit la
charge de ruine.
0
100
200
300
400
500
600
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
Chragederuine(KN)
Longueur (mm)
CR appliqué
sans CR
41

Figure 20 : Charges de ruine sans et avec CR corrigées pour différentes longueurs de colonne
3.2. Exécution du logiciel SAFIR
Un souci a été rencontré du fait que le logiciel SAFIR ne tourne pas pour certains
simulations dont l’épaisseur de l’âme égale à 4mm pour fy=275 MPa, fy= 355MPa, et
fy=460MPa. Pour résoudre ce problème, un pourcentage d’effort de Traction décroissant
(Npl=A*Fy) a été appliqué sur la colonne d’acier durant les 100 premières secondes. Ensuite la
fonction d’effort de compression (Nc=-1000t) fut appliquée à son tour (voir figure ci-dessous).
Figure 21 : Evolution de la charge appliquée sur les colonnes d’acier en fonction du temps
0
100
200
300
400
500
600
0 1000 2000 3000 4000 5000 6000 7000 8000 9000
Chargederuine(KN)
Longueur (mm)
CR corrigée
sans CR
-600
-500
-400
-300
-200
-100
0
100
200
300
400
0 100 200 300 400 500 600
Lacharge(KN)
Temps (s)
traction
compression
42

L’effort de traction appliqué diffère d’un cas à l’autre de 5% jusqu’à 100% et dépend même
de la température. Et pour vérifier la validité de cette méthode, la comparaison a été faite entre la
charge de ruine obtenue pour un modèle tournant sans ajouter d’effort de traction initialement et
la charge de ruine obtenue pour le même modèle en ajoutant un effort de traction initial.
Le tableau suivant présente la comparaison des charges de ruine.
fy=235 (Npl=734375) fy=275 (Npl=859375)
Npl/2 Npl/10 Npl/12 Npl/15 Npl/2 Npl/10 Npl/12 Npl/15
La charge de ruine on appliquant
un effort de traction (KN)
278.5 266.1 265.6 265.4 317.2 306.1 305.5 305.8
La charge de ruine sans
application d'un effort de traction
(KN)
264.9 304.2
Différence relative (%) 0.188394876 0.523217789
Tableau 8 : Comparaison des charges de ruine avec et sans application d’effort de traction
On voit très clairement que le fait d’appliquer un effort de traction a pour conséquence
d’augmenter la charge de ruine, et ceci d’autant plus que l’effort de traction appliqué est grand.
Cependant, cette différence de résultat reste acceptable.
3.3. Modes propres dans RUBY
Figure 22 : Paramètres de la colonne
43

Dans tous les cas étudiés, on remarque toujours un saut dans les courbes (charge-longueur) pour
une longueur de 4m pour la courbe de flambement selon l’axe fort.
Le tableau 9 présent les imperfections géométriques des colonnes d’acier de différentes longueurs
concernant la courbe de flambement selon l’axe fort et l’axe faible.
Figure 23 : Exemple d’une courbe (Charge-Longueur) représentant le saut à 4m
44

Axe fort Axe faible
Imperfection (mm) Imperfection (mm)
Nœuds 332
(L/4)
657
(L/2)
982
(3L/4)
Nœuds 332
(L/4)
657
(L/2)
982
(3L/4)
L=1 0.062 0 -0.062 L=1 0 0 0
L=2 0.011 0.009 -0.003 L=2 1.056 1.494 1.056
L=3 -0.22 0 0.22 L=3 1.585 2.241 1.585
L=3.1 -0.142 0.485 -0.362 L=3.1 1.638 2.316 1.638
L=3.2 0.349 -0.206 -0.094 L=3.2 -1.69 -2.391 -1.69
L=3.3 0.138 -0.813 0.235 L=3.3 -1.743 -2.465 -1.743
L=3.4 0.038 0.847 0.258 L=3.4 -1.796 -2.54 -1.796
L=3.5 -0.423 -0.818 -0.305 L=3.5 -1.849 -2.615 -1.849
L=3.6 0.534 -0.019 -0.356 L=3.6 -1.902 -2.689 -1.902
L=3.7 -0.05 -0.83 -0.679 L=3.7 -1.954 -2.764 -1.954
L=3.8 -0.02 -0.984 -0.246 L=3.8 -2.007 -2.839 -2.007
L=3.9 0.583 -0.994 -0.105 L=3.9 -2.06 -2.914 -2.06
L=4 -2.103 -2.975 -2.103 L=4 -2.113 -2.988 -2.113
L=4.1 -2.157 -3.05 -2.157 L=4.1 -2.166 -3.063 -2.166
L=5 -2.633 -3.724 -2.633 L=5 -2.641 -3.735 -2.641
L=6 -3.162 -4.472 -3.162 L=6 -3.169 -4.482 -3.169
L=7 -3.691 -5.22 -3.691 L=7 -3.698 -5.229 -3.698
L=8 -4.22 -5.968 -4.22 L=8 -4.226 -5.977 -4.226
L=9 -4.749 -6.716 -4.749 L=9 -4.754 -6.724 -4.754
L=10 -5.278 -7.464 -5.278 L=10 -7.547 -10.672 -7.547
Tableau 9 : les imperfections géométriques des colonnes d’acier de différentes longueurs
On remarque que les modes propres de l’axe fort pour L<4m diffèrent des modes propres
pour L>=4m (premier mode). Par conséquent, on peut supposer que le saut est dû aux calculs des
modes propres effectués par l’application RUBY.
Figure 24 : Différents types de déformés observées
45

Chapitre IV : Nouvelles propositions
Des calculs numériques par éléments finis ont été effectués par le logiciel SAFIR afin de
calculer les charges de ruine des colonnes en acier carbone. Ensuite ces charges de ruine seront
comparées avec les charges de ruine calculées par les méthodes analytiques (EUROCODE3,
Aveiro1, et Aveiro2).
Dans la partie suivante, après avoir tracé les courbes des rapports des charges, nous avons
constaté que les 3 méthodes sont trop sécuritaires. Cela nous a amené à améliorer ces modèles
pour développer deux nouveaux modèles s’appelant UlgEC3 et UlgAv.
1. Première proposition : méthode UlgEC3
La méthode UlgEC3 a été basée sur celle de l’EUROCODE3. En se basant sur les figures des
rapports des charges qui se trouvent dans la partie suivante, des modifications ont été appliquées
au niveau du calcul des sections efficaces (voilement local) et sur le flambement global. Pour ce
faire, on a tout d'abord essayé d'augmenter la charge de ruine par le biais de l'augmentation du
coefficient réducteur de flambement. Ensuite on a augmenté la charge plastique et ce en
accroissant la section efficace.
ℎ 𝑛𝑢𝑢𝑚 = ℎ + 𝑡𝑓 La valeur de h dans le modèle numérique
• Classification de la section
𝜀𝜀 𝜃 = 0.85 ∗ �235
𝑓𝑓𝑦𝑦
�
𝐶
𝑡 𝑓
=
𝑏
2�
𝑡𝑓
𝐶
𝑡 𝑤
=
𝑡 𝑤
Classe de la semelle 𝑪
𝒕 𝒇
�
1 ≤ 9 ∗ 𝜀𝜀 𝜃
2 ≤ 10 ∗ 𝜀𝜀 𝜃
3 ≤ 14 ∗ 𝜀𝜀 𝜃
4 > 14 ∗ 𝜀𝜀 𝜃
Tableau 10 : Classification de la section pour la semelle
Classe de l’âme 𝑪
𝒕 𝒘
�
1 ≤ 33 ∗ 𝜀𝜀 𝜃
2 ≤ 38 ∗ 𝜀𝜀 𝜃
3 ≤ 42 ∗ 𝜀𝜀 𝜃
4 > 42 ∗ 𝜀𝜀 𝜃
Tableau 11 : Classification de la section pour l’âme
Classe de la section = max (Classe de la semelle ; Classe de l’âme)
46

• Section efficace
Si Classe de la section = 4
 Semelle
λ� 𝑝𝑝 =
𝐶
𝑡𝑓
�
28.4 ∗ 𝜀𝜀 ∗ � 𝐾σ
Si λ𝑝𝑝
�� ≤ 0.748 =>𝜌 = 1
Sinon
𝝆 =
𝝀� 𝒑 − (𝟎. 𝟏𝟖𝟖 ∗ 𝜺)
𝝀� 𝒑
𝟐
≤ 𝟏
𝑏 𝑒𝑓𝑓 = 𝑏 ∗ 𝑡𝑓
 Âme
𝜆̅𝑝𝑝 =
𝐶
𝑡 𝑤
�
28.4 ∗ 𝜀𝜀 ∗ � 𝐾σ
Si λ𝑝𝑝
�� ≤ 0.673 =>𝜌 = 1
Sinon
𝝆 =
𝝀� 𝒑 − (𝟎. 𝟎𝟓𝟓(𝟏 + 𝛙) ∗ 𝜺)
𝝀� 𝒑
𝟐
≤ 𝟏
ℎ 𝑒𝑓𝑓 = ℎ 𝑛𝑢𝑢𝑚 ∗ 𝑡 𝑤
Un paramètre 𝜺 = �
𝟐𝟑𝟓
𝒇 𝒚
été introduit dans la formule du coefficient réducteur pour le
voilement de la plaque afin d’augmenter la section efficace.
Sinon Classe de la section = 1, 2 ou 3
La surface efficace ∶ 𝐴 𝑒𝑓𝑓 = �ℎ 𝑒𝑓𝑓 ∗ 𝑡 𝑤� + 2 ∗ (𝑏 𝑒𝑓𝑓 ∗ 𝑡𝑓)
• Coefficient réducteur de la limite élastique
Si Classe de la section = 4
𝑓𝑓𝑦𝑦 𝜃
= 𝑘02 ∗ 𝑓𝑓𝑦𝑦
Sinon 𝑓𝑓 𝑦𝜃𝜃
= 𝑘 𝑦 ∗ 𝑓𝑓 𝑦
• La charge plastique: 𝑁𝑝𝑝𝑙𝑎𝑎𝑠𝑡𝑡𝑖𝑐 = 𝐴 𝑒𝑓𝑓 ∗ 𝑓𝑓𝑦𝑦 𝜃
47

• Courbe de flambement
• L’axe fort
𝐼 =
3
12
+ 2 ∗ (
𝑏 ∗ 𝑡𝑓
3
12
+ 𝑏 ∗ 𝑡𝑓 ∗
2
4
𝑁𝑐𝑟 =
𝜋2
∗ 𝐸𝐸 ∗ 𝐼
𝑁𝑐𝑟
�
• L’axe faible
𝐼 = �2 ∗
𝑡𝑓 ∗ 𝑏3
12
� + (
3
12
)
𝑁𝑐𝑟 =
𝜋2
∗ 𝐸𝐸 ∗ 𝐼
λ 𝑤𝑒𝑎𝑎𝑘 = �
𝑁𝑐𝑟
�
λ = max(λ 𝑠𝑡𝑡𝑟𝑜𝑛𝑔; λ 𝑤𝑒𝑎𝑎𝑘)
Si λstrong > λ 𝑤𝑒𝑎𝑎𝑘 Axe = « Axe fort »
Sinon Axe= « Axe faible »
L’axe de flambement est l’axe où l’élancement λ est supérieur. Ce paramètre dépend de la charge
critique et le moment d’inertie qui est calculé à partir des relations ci-dessus.
Si la classe de la section = 4
L’élancement réduit 𝛌� 𝜽 = 𝛌 𝟎.𝟖𝟓
∗ �
𝒌 𝟎𝟐
𝒌 𝑬
�
Sinon 𝛌� 𝜽 = 𝛌 𝟎.𝟖𝟓
∗ �
𝒌 𝒚
𝒌 𝑬
�
Nous avons introduit une puissance pour modifier l’évolution de la charges en fonction de la
longueur.
Coefficient réducteur du flambement global χ 𝑓𝑖 =
1
𝜑𝜃𝜃+� 𝜑𝜃𝜃
2−λ̅𝜃𝜃
2
Où :
 Axe faible
𝝋 𝜽 =
𝟏
𝟐
(𝟏 + �𝟎. 𝟒𝟓 ∗ 𝜶 ∗ 𝛌� 𝜽� + 𝛌� 𝜽
𝟐
)
 Axe fort
𝝋 𝜽 =
𝟏
𝟐
(𝟏 + �𝟎. 𝟓𝟓 ∗ 𝜶 ∗ 𝛌� 𝜽� + 𝛌� 𝜽
𝟐
)
𝑂ù ∶ 𝛼 = 0.65 ∗ �235
𝑓𝑓𝑦𝑦
�
48

D’où la charge de ruine :
𝑁 𝑚𝑜𝑑𝑒𝑙 = χ𝑓𝑓𝑖 ∗ 𝑁𝑝𝑝𝑙𝑎𝑎𝑠𝑡𝑡𝑖𝑐
2. Deuxième proposition : méthode UlgAv
La méthode UlgAv a été basée sur la méthode d’Aveiro. D'après les figures abordées dans la
partie qui suit, nous avons été amenés à modifier la partie du flambement global en changeant le
coefficient réducteur de flambement ainsi que l’élancement réduit. Cette deuxième méthode a été
proposée pour qu’on puisse utiliser le même coefficient réducteur de la limité d’élasticité 𝑘𝑦𝑦 pour
toutes les classes, notamment la classe 4 à la place de 𝑘0.2, et ceci afin d’éviter la discontinuité
des résultats entre des colonnes de classe 3 et de classe 4.
ℎ 𝑛𝑢𝑢𝑚 = ℎ + 𝑡𝑓 La valeur de h dans le modèle numérique
• Classification de la section
𝜀𝜀 𝜃 = 0.85 ∗ �235
𝑓𝑓𝑦𝑦
�
𝐶
𝑡 𝑓
=
𝑏
2�
𝑡𝑓
𝐶
𝑡 𝑤
=
𝑡 𝑤
Classe de la semelle 𝑪
𝒕 𝒇
�
1 ≤ 9 ∗ 𝜀𝜀 𝑇
2 ≤ 10 ∗ 𝜀𝜀 𝑇
3 ≤ 14 ∗ 𝜀𝜀 𝑇
4 > 14 ∗ 𝜀𝜀 𝑇
Tableau 12 : Classification de la section pour la semelle
Classe de l’âme 𝑪
𝒕 𝒘
�
1 ≤ 33 ∗ 𝜀𝜀 𝑇
2 ≤ 38 ∗ 𝜀𝜀 𝑇
3 ≤ 42 ∗ 𝜀𝜀 𝑇
4 > 42 ∗ 𝜀𝜀 𝑇
Tableau 13 : Classification de la section pour l’âme
Classe de la section = max (Classe de la semelle ; Classe de l’âme)
• Section efficace
Si Classe de la section >=3
𝜀𝜀 = �235
𝑓𝑓𝑦𝑦
�
𝑟𝑙𝑜𝑐 = 𝜃𝜃
𝑘02𝐴𝑣𝑒𝑖𝑟𝑜 = 𝑘02−𝐴𝑣𝑒𝑖𝑟𝑜𝜃(𝑟𝑙𝑜𝑐)
𝑘𝑦𝑦𝐴𝑣𝑒𝑖𝑟𝑜 = 𝑘𝑦𝑦𝜃(𝑟𝑙𝑜𝑐)
49

𝑟𝑙𝑜𝑐 =
𝑘02𝐴𝑣𝑒𝑖𝑟𝑜
𝑘𝑦𝑦𝐴𝑣𝑒𝑖𝑟𝑜
�
 Semelle
λ� 𝑝𝑝 =
𝐶
𝑡𝑓
�
28.4 ∗ 𝜀𝜀 ∗ � 𝐾σ
𝜌 =
(𝜆̅𝑝𝑝 + 𝛼 𝜃) 𝛽 𝑇 − 0.188
𝛼 𝜃 = 1.1 − (0.63 ∗ 𝑟𝑙𝑜𝑐
𝜀𝜀 𝜃
� )
𝛽 𝜃 = 2 − (1.1 ∗ 𝑟𝑙𝑜𝑐)
𝑏 𝑒𝑓𝑓 = 𝑏 ∗ 𝑡𝑓
 Âme
𝜆̅𝑝𝑝 =
𝐶
𝑡 𝑤
�
28.4 ∗ 𝜀𝜀 ∗ � 𝐾σ
𝜌 =
(𝜆̅𝑝𝑝 + 𝛼 𝜃) 𝛽 𝜃 − (3 + ψ)
𝛼 𝜃 = 0.9 − (0.315 ∗ 𝑟𝑙𝑜𝑐
𝜀𝜀 𝜃
� )
𝛽 𝜃 = 2.3 − (1.1 ∗ 𝑟𝑙𝑜𝑐)
ℎ 𝑒𝑓𝑓 = ℎ 𝑛𝑢𝑢𝑚 ∗ 𝑡 𝑤
Sinon Classe de la section = 1, 2
La surface efficace ∶ 𝐴 𝑒𝑓𝑓 = �ℎ 𝑒𝑓𝑓 ∗ 𝑡 𝑤� + 2 ∗ (𝑏 𝑒𝑓𝑓 ∗ 𝑡𝑓)
Nuance d′
acier dépend de la température ∶ 𝑓𝑓𝑦𝑦 𝜃
= 𝑘𝑦𝑦 ∗ 𝑓𝑓𝑦𝑦
La charge plastique ∶ 𝑁𝑝𝑝𝑙𝑎𝑎𝑠𝑡𝑡𝑖𝑐 = 𝐴 𝑒𝑓𝑓 ∗ 𝑓𝑓𝑦𝑦 𝜃
• Courbe de flambement
• L’axe fort
𝐼 =
3
12
+ 2 ∗ (
𝑏 ∗ 𝑡𝑓
3
12
+ 𝑏 ∗ 𝑡𝑓 ∗
2
4
)
𝑁𝑐𝑟 =
𝜋2
∗ 𝐸𝐸 ∗ 𝐼
𝑁𝑐𝑟
�
• L’axe faible
𝐼 = �2 ∗
𝑡𝑓 ∗ 𝑏3
12
� + (
3
12
)
𝑁𝑐𝑟 =
𝜋2
∗ 𝐸𝐸 ∗ 𝐼
λ 𝑤𝑒𝑎𝑎𝑘 = �
𝑁𝑐𝑟
�
λ = max(λ 𝑠𝑡𝑡𝑟𝑜𝑛𝑔; λ 𝑤𝑒𝑎𝑎𝑘)
Si λstrong > λ 𝑤𝑒𝑎𝑎𝑘 Axe = « Axe fort »
Sinon Axe= « Axe faible »
L’axe de flambement est l’axe où l’élancement λ est supérieur, il est calculé à partir des relations
ci-dessus.
50

Elancement réduite : 𝛌� 𝜽 = 𝛌 𝟎.𝟖𝟓
∗ �
𝒌 𝒚
𝒌 𝑬
�
Coefficient réducteur du flambement global : : χ 𝑓𝑖 =
1
𝜑𝜃𝜃+� 𝜑𝜃𝜃
2−λ�𝜃𝜃
2
𝑂ù ∶ 𝝋 𝜽 =
𝟏
𝟐
(𝟏 + �𝟎. 𝟑𝟓 ∗ 𝜶 ∗ 𝛌� 𝜽� + 𝛌� 𝜽
𝟐
)
Un coefficient de 0.35 a été modifié afin d’augmenter le coefficient réducteur de flambement.
𝑂ù ∶ 𝛼 = 0.65 ∗ �235
𝑓𝑓𝑦𝑦
�
D’où la charge de ruine :
𝑁 𝑚𝑜𝑑𝑒𝑙 = χ𝑓𝑓𝑖 ∗ 𝑁𝑝𝑝𝑙𝑎𝑎𝑠𝑡𝑡𝑖𝑐
3. Résultats
3.1. Flambement selon l’axe fort
La figure 25 représente la moyenne des rapports des charges de ruine calculées par les
méthodes analytiques et la méthode numérique en fonction de la nuance d’acier.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 100 200 300 400 500
ratio[-]
fy (MPa)
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/N_Safir
Figure 25 : Moyennes des rapports des charges de ruine des méthodes analytiques et numérique en fonction de la nuance d’acier
51

Interprétation :
D’après le graphe ci-dessus, On constate que la courbe de la méthode de l’EC3, ainsi que
d’Aveiro sont trop sécuritaires. Et on remarque ainsi que la courbe de l’EC est un peu
décroissante.
Quant à la méthode UlgEC3, on est amené à augmenter la charge de ruine par l’augmentation
de l’aire efficace et du facteur de flambement, ceci est réalisé via l’introduction du paramètre 𝜺
dans la relation de coefficient réducteur du voilement de la plaque. C’est pour cette raison, que la
courbe UlgEC3 est horizontale et assez proche de l’unité.
Même remarque pour la seconde nouvelle méthode UlgAv : Sa courbe est horizontale et
s’approche de l’unité.
On n’en déduit que les deux nouvelles méthodes sont mieux adaptées que les autres, et
qu’elles donnent des résultats plus exacte.
La figure 26 présente l’évolution de la moyenne des ratio des charges de ruine calculées par
les 5 méthodes par rapport aux charges calculées par le logiciel SAFIR en fonction de la
température de l’acier.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 100 200 300 400 500 600 700 800
ratio[-]
Température (°C)
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/N_Safir
Figure 26 : Moyennes des rapports des charges de ruine des méthodes analytiques et numérique en fonction de la température
52

Interprétation :
D’après le rapport des méthodes analytique et numérique. On constate que les deux
méthodes UlgEC3 et UlgAv sont toujours assez proche de l’unité.
Quant à la courbe Aveiro 2, on se rend compte qu’elle a une forme différente des autres. En
effet ceci s’explique par le fait que la méthode utilise une température fixe =700°C pour le calcul
de la section efficace. En revanche, Aveiro 1 dépend toujours de la température réelle.
La figure 27 présente l’évolution de la moyenne des ratios des charges de ruine calculées par
les 5 méthodes par rapport aux charges calculées par le logiciel SAFIR en fonction de la
longueur.
Interprétation :
A partir d’une longueur de 4 m, on constate que les courbes (UlgEC3 et UlgAv) deviennent
horizontales et s’approchent de l’unité.
Par contre, lorsque L<=4m, on observe qu’une petite non-linéarité. On explique cette non-
linéarité par les problèmes des modes propres calculées par RUBY (déjà expliqué dans le
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 11000
ratio[-]
Longueur (mm)
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/Nsafir
Figure 27 : Moyennes des rapports des charges de ruine des méthodes analytiques et numérique en fonction de la longueur
53

chapitre précédent). On remarque aussi que de par la modification de l’élancement réduit dans les
modèles UlgEC3 et UlgAv, la courbe a été redressé et est désormais horizontale.
Les deux figures suivantes montrent la moyenne des ratios des charges de ruine calculées par
les 5 méthodes par rapports aux charges calculées par SAFIR en fonction des rapports (hnum/tw)
et (b/tf).
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
1,2
0 10 20 30 40 50
ratio[-]
b/tf
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/N_Safir
Figure 29 : Moyennes des rapports des charges de ruine des méthodes analytiques et numérique en fonction de b/tf
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 20 40 60 80 100 120 140
ratio[-]
hnum/tw
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_Ulg2014/N_Safir
N_UlgAv/Nsafir
Figure 28 : Moyennes des rapports des charges de ruine des méthodes analytiques et numérique en fonction de hnum/tw
54

Interprétation :
Il est de nouveau clair que les deux nouvelles méthodes sont bien meilleures que les
anciennes, puisqu’elles s’approchent d’avantage de l’unité.
On se rend bien que les courbes des moyennes des rapports ne sont pas suffisantes pour
prouver que les deux nouvelles méthodes sont correctes. Par conséquent, nous avons été amenés
à tracer des courbes de densités de probabilité de loi normale à partir de la moyenne générale des
charges de ruine ainsi que leurs écarts type.
Le tableau suivant énumère les moyennes générales de tous les rapports et l’écart type aussi.
N_EC3/N_Safir N_Aveiro1/N_Safir N_Aveiro2/N_Safir N_Ulg2014/N_Safir N_UlgAv/N_Safir
Moyenne 0.831 0.866 0.801 0.938 0.977
Ecart type 0.072 0.043 0.128 0.072 0.045
Tableau 14 : la moyenne générale de tous les rapports des charges de ruine et leurs écarts type
La figure suivante représente la probabilité de la loi de Normal(Gauss) pour les rapports des
charges de ruine.
0
1
2
3
4
5
6
7
8
9
10
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 1,1 1,2
Probabilitéd'apparitiondechaquevaleur
ratio [-]
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/Nsafir
Figure 30 : Densité de probabilité de la loi normale(Gauss) pour les rapports des charges de ruine
55

Interprétation :
En comparant les deux méthodes d’Aveiro et d’EC, on se rend compte que les courbes des
deux nouvelles méthodes sont presque centrées autour de l’unité. En plus, celle de la méthode
UlgAv beaucoup plus compacté par rapport aux méthodes d’Aveiro.
Cependant, il faut aussi noter que pour les deux nouvelles méthodes il y a une quantité des
cas qui sont non sécuritaires.
Les figures (31, 32, 33, 34, et 35) ci-dessous représentent la comparaison entre les calculs
numériques effectués par le logiciel SAFIR et les calculs analytiques pour chaque méthode.
Interprétation :
D’après la comparaison des résultats numériques SAFIR et analytiques de la méthode EC3,
On remarque que la majorité des valeurs sont situés au-dessous de la courbe X=Y et non pas dans
les deux côtés de la courbe.
0
500
1000
1500
2000
2500
3000
3500
4000
0 500 1000 1500 2000 2500 3000 3500 4000
Chargeanalytique(KN)
Charge numérique (KN)
Figure 31 : Comparaison des résultats numériques SAFIR et analytiques de la méthode EC3
56

La figure 32 représente la comparaison entre les charges de ruine calculées par SAFIR et la
méthode d’Aveiro1.
Interprétation :
Sur le graphe ci-dessus, nous constatons que la plupart des valeurs sont situés au-dessous de
la courbe X=Y et non pas dans les deux côtés de la courbe.
Aveiro 1 est toujours sécuritaire.
0
500
1000
1500
2000
2500
3000
3500
4000
0 500 1000 1500 2000 2500 3000 3500 4000
Figure 32 : Comparaison des résultats numériques SAFIR et analytiques de la méthode d'Aveiro1
57

La figure suivante représente la comparaison entre les charges de ruine calculées par SAFIR
et la méthode d’Aveiro2.
Interprétation :
D’après le graphe ci-dessus, On remarque qu’il y a une dispersion de la majorité des valeurs
au-dessous de la courbe X=Y. On remarque aussi une discontinuité qui est certainement due à la
température qui était fixé à 700°C dans le modèle.
0
500
1000
1500
2000
2500
3000
3500
4000
0 500 1000 1500 2000 2500 3000 3500 4000
Figure 33 : Comparaison des résultats numériques SAFIR et analytiques de la méthode d'Aveiro2
58

La figure 34 représente la comparaison entre les charges de ruine calculées par SAFIR et la
méthode d’UlgEC3.
Figure 34 : Comparaison des résultats numériques SAFIR et analytiques de la méthode d'UlgEC3
Interprétation :
A travers la comparaison des résultats numériques SAFIR aux résultats analytiques de la
méthode d'UlgEC3, il apparaît de manière évidente que les points sont situés de part et d’autre de
la droite X=Y mais qu’ils en sont très proches.
0
500
1000
1500
2000
2500
3000
3500
4000
0 500 1000 1500 2000 2500 3000 3500 4000
+10%
-10%
59

La figure suivante représente la comparaison entre les charges de ruine calculées par SAFIR
et la méthode d’UlgAv.
Interprétation :
A l’issue de la comparaison des résultats numériques SAFIR aux résultats analytiques de la
méthode UlgAv, on constate que les points sont concentrés autour de la droite X=Y. Ceci montre
que cette méthode est plus efficace que les précédentes.
Ces dernières figures ont révélé que plusieurs cas sont non sécuritaires, surtout pour les deux
nouvelles méthodes. Nous avons donc tracé les courbes des probabilités cumulatives, afin de
mettre en évidence le pourcentage de points se trouvant au-delà de l’unité (insécuritaires).
0
500
1000
1500
2000
2500
3000
3500
4000
0 500 1000 1500 2000 2500 3000 3500 4000
+10%
-10%
Figure 35 : Comparaison des résultats numériques SAFIR et analytiques de la méthode d'UlgAv
60

La figure suivante le pourcentage des cas qui sont sécuritaires dans toutes les simulations
ayant effectuées pour différentes méthodes.
Interprétation :
On constate que pour la méthode UlgEC3, environ 80% des cas sont sécuritaires et pour la
méthode UlgAv on trouve environ 70% des cas sont sécuritaires. De plus, on remarque que le
ratio est compris entre 0.9 et 1 pour la majorité des cas, alors qu’il est inférieur à 0.9 pour les
anciennes méthodes.
3.2. Flambement selon l’axe faible
Tous les résultats et graphes concernant le flambement selon l’axe faible seront intégrés au
niveau de l’annexe 2, Vu que tous les courbes sont similaires. De plus, an a obtenus à peu près les
mêmes résultats que pour l’axe de flambement selon l’axe fort.
3.3. Points suspects
Après avoir effectué les calculs et créé la base de données on a remarqué que le rapport de
certains points obtenus par simulation numérique avec les autres méthodes était très grand. On
devait donc les analyser. On en est venu à la conclusion que ces points étaient suspects, et ils
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
110%
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 1,1 1,2
Probablitécumulative
ratio[-]
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/Nsafir
Figure 36 : Fonction de répartition de la loi normale pour les rapports des charges de ruine
61

n’ont donc pas été pris en considération afin de ne pas influencer les calibrations des modèles
simples.
Les figures ci-dessous montrent deux exemples de ces points :
0
100
200
300
400
500
600
700
800
900
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 11000
ChargeSAFIR(KN)
Longueur (mm)
Figure 37 : Charge de ruine calculée par SAFIR en fonction de la longueur pour une colonne de fy=460 Mpa, T=650°C, tw=4mm,
et tf= 14mm où le flambement selon l’axe faible
0
20
40
60
80
100
120
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 11000
ChargeSAFIR(KN)
Longueur (mm)
Figure 38 : Charge de ruine calculée par SAFIR en fonction de la longueur pour une colonne de fy=355 Mpa, T=750°C, tw=4mm,
et tf= 6mm où le flambement selon l’axe fort
62

Conclusion
La valeur ajoutée de mon sujet est sa capacité à travers cette étude de créer un point de
départ pour développer un modèle de calcul simple de dimensionnement applicable en bureau
d’études. Ce modèle qui a été calibré sur les résultats numériques, a pour objectif de remplacer le
modèle actuel de l’EUROCODE3, jugé trop sécuritaire.
Mon travail a consisté principalement à établir une base de données en générant près de
5000 calculs numérique à l’aide de logiciel SAFIR et à élaborer deux modèles de calcul. Ces
deux propositions sont des adaptations de formulations analytiques existantes (EC3 et proposition
d’Aveiro).
Par la réalisation de la base de données. 25 types de section ont été étudiés, pour 10 longueur
de colonnes variant de 1000 à 10000 mm, à 5 températures (350, 450, 550,650, et 750°C), et pour
4 limite d’élasticité (235, 275, 355, et 460Mpa).
L’acceptation des deux modèles élaborés a été faite par le responsable sur ce projet, qui a lui-
même validé le travail réalisé. De plus ces deux modèles seront transférés aux autres partenaires
membre du projet européen qui sont les mieux placés pour décider quel est le modèle le plus
approprié.
63

Bibliographies
[1] http://www-cast3m.cea.fr/
[2] J.M.Franssen. User’s manual for Safir 2011: A computer program for analysis of structures
subjected to fire 2011.
[3] EN 1993-1-1. EUROCODE3 3 : Calcul des structures en acier – Partie 1.1 : Règles générales
et règles pour les bâtiments.
[4] EN 1993-1-2. EUROCODE3 3 : Calcul des structures en acier – Partie 1.3 : Règles générales
– Calcul du comportement au feu.
[5] EN 1993-1-5. EUROCODE3 3 : Calcul des structures en acier – Partie 1.5 : Plaques plans.
[6] EN1090-2 : Exécution des structures en acier et des structures en aluminium – Partie 2 :
Exigences pour les structures en acier
[7] Bui hung cuong « Analyse statique du comportement des structures a parois minces par la
méthode des éléments finis et des bandes finies de type plaque et coque surbaissée déformables
en cisaillement »
[8] J.M.Franssen, B.Cowez, T.Gernay « Efective stress method to be used in beam finite
elements to take local instabilities into account »
[9] Carlos Couto, Bin Zhao «Verification and Numerical Validation of Benchmark Studies»
[10] N. Lopes, P.M.M.VilaReal, «Class 4 stainless steel I-beams subjected to fire»
[11] J.-M. Franssen and B. Cowez « Consideration of local instabilities in beam finite elements
by means of effective constitutive laws »
[12] P.M.M. Vila Real, R. Cazeli, L. Simoes da Silva, A. Santiago, P. Piloto «The effect of
residual stresses in the lateral torsional buckling of steel I-beams at elevated temperature»
64

Annexes
65

Annexe 1 : Logiciels et applications utilisés
1. Mailleur VB
Nous avons effectué toutes les simulations sur un élément poteau, donc au lieu de créer le
fichier.IN à chaque fois sur GID, un ingénieur du service SE de l’université de Liège a développé
une application Visual Basic « MAILLEUR VB » pour créer les fichiers.IN et faire le maillage
des éléments. Les images en dessous montrent les différentes fenêtres de l’application.
General Data : Dans cette fenêtre on fait le maillage de la colonne et on choisit la fonction de
charge.
66

Output Results : Pour celle-là on fixe tout qui concerne le temps et la précision et le comeback de
la convergence.
Materials : La fenêtre ci- dessus montre la modification des paramètres de matériau et la Tmax.
67

ParametricStudy : Cet écran permet de faire entrer les dimensions de la colonne, la température,
la nuance d’acier, et choisir l’axe de flambement.
2. Le logiciel RUBY
C'est un outil simple qui permet à l'utilisateur d'effectuer une analyse linéaire de flambement
d'un modèle de SAFIR en éléments de coque, de surmonter cette limitation du code de SAFIR,
permettant ainsi le calcul des facteurs de charges critiques et les modes propres. RUBY a
également la capacité de modifier ces modèles afin d'appliquer les imperfections géométriques
sur la base des modes propres calculés comme suggéré dans l’EN1993-1-5 (CEN, 2012). RUBY
utilise le logiciel d’élément finis CAST3M (Cast3M, 2012) pour effectuer l'analyse de
flambement linéaire du modèle, mais l'avantage de l’utilisation de RUBY est que l'utilisateur peut
faire cette opération sans aucune connaissance de Cast3M et d'une manière très simple.
Le logiciel RUBY a été développé en utilisant le langage de programmation VB.NET et le
logiciel d'éléments finis Cast3M afin d'effectuer une analyse du flambement linéaire (LBA) d'un
modèle de SAFIR. RUBY fonctionne d'une manière très simple, l'utilisateur a seulement besoin
de sélectionner un fichier de données de SAFIR, cliquer sur le bouton "Go" (voir Fig. 1) et
attendre les résultats. RUBY traduit automatiquement le modèle SAFIR dans un modèle de
68

Cast3M qui effectue la LBA dans les coulisses. A la fin, les résultats de Cast3M sont convertis à
nouveau dans le fichier de sens SAFIR pour que l'utilisateur puisse utiliser les mêmes outils pour
le poste traitement des résultats comme il le faisait avant.
La fenêtre principale du logiciel RUBY.
A l’aide de ce logiciel il est possible de choisir le nombre des modes propres à obtenir et
aussi d’appliquer les imperfections géométriques du modèle SAFIR initial basé sur la forme d'un
mode propre spécifique et avec une amplitude définie par l'utilisateur.
Certaines options avancées sont également inclues dans le logiciel tel que : forcer
uniquement des modes locaux ou globaux, l'application d'une imperfection global d'amplitude =
69

L / x où x est une valeur définie par l'utilisateur et L est la longueur de l’élément, et l'application
d'une imperfection qui a une forme basée sur une combinaison des deux modes globaux et
locaux.
RUBY peut aussi fonctionner sur un mode batch qui signifie que l'utilisateur peut
sélectionner plusieurs fichiers d'entrée, cliquer sur "Go" et attendre les résultats de tous les
fichiers d'entrée sans la nécessité de l'interaction de l'utilisateur pendant le processus.
Pour effectuer l'analyse linéaire de flambement dans Cast3M, la procédure « flambement »
est utilisée. Comme il a été mentionné dans la question précédente, RUBY traduit le modèle
SAFIR dans un modèle de Cast3M afin de calculer les résultats.
3. OUTPUT READER VB
On introduit dans cette application les fichiers.OUT pour lire tous les paramètres de la
colonne et la charge de ruine calculée à partir de SAFIR et qui sont organisés dans un fichier
result.txt (base de données).
70

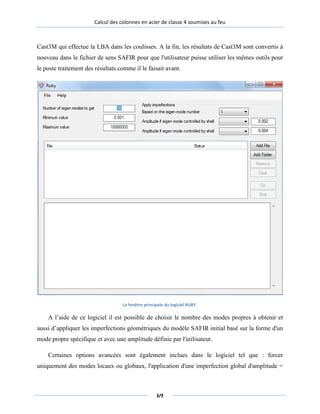
La fenêtre principale de l’application OUTPUT READER.
4. DIAMOND
Une fois que le fichierRUBY.IN est généré par RUBY, et le calcul de SAFIR s’effectue. Il
est nécessaire d’avoir recourt à un autre logiciel tiers pour lire le fichier ainsi généré, dénommé
fichier OUT. Lors de cette partie c’est le logiciel DIAMOND [47] qui a été utilisé. Il permet de
lire les fichiers OUT thermiques comme structurels pour avoir une vision claire des résultats.
71

Annexe 2 : Résultats : Flambement selon l’axe
faible
Tous les résultats des graphes concernant l’axe de flambement selon l’axe faible seront
intégrés au niveau de l’annexe n°, Vu que tous les courbes présentent une similitude, de plus, On
a obtenus à peu près les mêmes résultats pour l’axe de flambement selon l’axe fort.
Moyennes des rapports des charges de ruine des méthodes analytiques et numérique en fonction de la nuance d’acier
Moyennes des rapports des charges de ruine des méthodes analytiques et numérique en fonction de la température.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 50 100 150 200 250 300 350 400 450 500
ration[-]
fy (MPa)
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/N_Safir
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 100 200 300 400 500 600 700 800
ratio[-]
Température (°C)
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/N_safir
72

Moyennes des rapports des charges de ruine des méthodes analytiques et numérique en fonction de la longueur.
Moyennes des rapports des charges de ruine des méthodes analytiques et numérique en fonction en fonction de hnum/tw.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000 11000
ration[-]
Longueur (mm)
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/Nsafir
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 20 40 60 80 100 120 140
ratio[-]
hnum/tw
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/Nsafir
73

Moyennes des rapports des charges de ruine des méthodes analytiques et numérique en fonction en fonction de b/tf.
Le tableau suivant énumère la moyenne générale de tous les rapports et l’écart type aussi.
N_EC3/N_Safir N_Aveiro1/N_Safir N_Aveiro2/N_Safir N_Ulg2014/N_Safir N_UlgAv/N_Safir
Moyenne 0.780 0.728 0.698 0.953 0.946
Ecart type 0.042 0.075 0.091 0.052 0.067
La moyenne générale de tous les rapports des charges de ruine et leurs écarts type.
Densité de probabilité de la loi normale(Gauss) pour les rapports des charges de ruine
0
1
2
3
4
5
6
7
8
9
10
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 1,1 1,2
Probabilitéd'apparitiondechaquevaleur
ratio [-]
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/Nsafir
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 10 20 30 40 50
ration[-]
b/tf
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/Nsafir
74

Comparaison des résultats numériques SAFIR et analytiques de la méthode EC3
Comparaison des résultats numériques SAFIR et analytiques de la méthode d'Aveiro1
0
500
1000
1500
2000
2500
3000
3500
4000
0 500 1000 1500 2000 2500 3000 3500 4000
0
500
1000
1500
2000
2500
3000
3500
4000
0 500 1000 1500 2000 2500 3000 3500 4000
75

Comparaison des résultats numériques SAFIR et analytiques de la méthode d'Aveiro2
Comparaison des résultats numériques SAFIR et analytiques de la méthode d’UlgEC3
0
500
1000
1500
2000
2500
3000
3500
4000
0 500 1000 1500 2000 2500 3000 3500 4000
0
500
1000
1500
2000
2500
3000
3500
4000
0 500 1000 1500 2000 2500 3000 3500 4000
+10%
-10%
76

Comparaison des résultats numériques SAFIR et analytiques de la méthode d'UlgAv
Fonction de répartition de la loi normale pour les rapports des charges de ruine
0
500
1000
1500
2000
2500
3000
3500
4000
0 500 1000 1500 2000 2500 3000 3500 4000
+10%
-10%
0%
10%
20%
30%
40%
50%
60%
70%
80%
90%
100%
110%
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 1,1 1,2
probablitécumulative
ratio[-]
N_EC3/N_Safir
N_Aveiro1/N_Safir
N_Aveiro2/N_Safir
N_UlgEC3/N_Safir
N_UlgAv/Nsafir
77

Annexe 3 : Application des méthodes sur la base
données de TECNALIA
1. Flambement selon l’axe faible
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 100 200 300 400 500 600 700 800
ratio[-]
Température (°C)
N_EC3/N_Abaqus
N_Aveiro1/N_Abaqus
N_Aveiro2/N_Abaqus
N_UlgEC3/N_Abaqus
NUlgAv/N_Abaqus
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 1000011000
ratio[-]
Longueur (mm)
N_EC3/N_Abaqus
N_Aveiro1/N_Abaqus
N_Aveiro2/N_Abaqus
N_UlgEC3/N_Abaqus
N_UlgAv/N_Abaqus
78

2. Flambement selon l’axe fort
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 100 200 300 400 500 600 700 800
ratio[-]
Température (°C)
N_EC3/N_Abaqus
N_Aveiro1/N_Abaqus
N_Aveiro2/N_Abaqus
N_UlgEC3/N_Abaqus
N_UlgAv/N_Abaqus
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 1000011000
ratio[-]
Longueur (mm)
N_EC3/N_Abaqus
N_Aveiro1/N_Abaqus
N_Aveiro2/N_Abaqus
N_UlgEC3/N_Abaqus
N_UlgAv/N_Abaqus
79

Annexe 4 : Extrait de la Base de données (SAFIR)
Name h (mm) t,w(mm) b(mm) t,fl(mm) L(mm) fy(Mpa) T(°C) N_Safir(KN)
514x8 250x14 500 8 250 14 8000 235 350 1495.1
514x10 250x14 500 10 250 14 9000 235 350 1650.8
514x12 250x14 500 12 250 14 9000 235 350 1807
510x4 250x10 500 4 250 10 9000 235 350 867.1
512x4 250x12 500 4 250 12 9000 235 350 1036.5
514x4 250x14 500 4 250 14 9000 235 350 1192.4
506x4 250x6 500 4 250 6 9000 235 350 420.8
508x4 250x8 500 4 250 8 9000 235 350 627.8
510x6 250x10 500 6 250 10 9000 235 350 947.8
512x6 250x12 500 6 250 12 9000 235 350 1153.9
514x6 250x14 500 6 250 14 9000 235 350 1324.6
508x6 250x8 500 6 250 8 9000 235 350 710.3
510x8 250x10 500 8 250 10 9000 235 350 1057.8
512x8 250x12 500 8 250 12 9000 235 350 1290.1
514x8 250x14 500 8 250 14 9000 235 350 1462
512x8 250x12 500 8 250 12 8000 235 450 1083.5
514x8 250x14 500 8 250 14 8000 235 450 1257
512x10 250x12 500 10 250 12 9000 235 450 1192.9
514x10 250x14 500 10 250 14 9000 235 450 1380
514x12 250x14 500 12 250 14 9000 235 450 1510.6
510x4 250x10 500 4 250 10 9000 235 450 721.7
512x4 250x12 500 4 250 12 9000 235 450 868
514x4 250x14 500 4 250 14 9000 235 450 1001.3
506x4 250x6 500 4 250 6 9000 235 450 351.1
508x4 250x8 500 4 250 8 9000 235 450 528.1
510x6 250x10 500 6 250 10 9000 235 450 788.9
512x6 250x12 500 6 250 12 9000 235 450 963.1
514x6 250x14 500 6 250 14 9000 235 450 1110.8
508x6 250x8 500 6 250 8 9000 235 450 592.7
510x8 250x10 500 8 250 10 9000 235 450 881.1
512x8 250x12 500 8 250 12 9000 235 450 1078.1
514x8 250x14 500 8 250 14 9000 235 450 1222.8
512x8 250x12 500 8 250 12 8000 235 550 756.8
514x8 250x14 500 8 250 14 8000 235 550 878.6
512x10 250x12 500 10 250 12 9000 235 550 833.2
514x10 250x14 500 10 250 14 9000 235 550 964
514x12 250x14 500 12 250 14 9000 235 550 1055.4
80

510x4 250x10 500 4 250 10 9000 235 550 503.9
512x4 250x12 500 4 250 12 9000 235 550 606.6
514x4 250x14 500 4 250 14 9000 235 550 700
506x4 250x6 500 4 250 6 9000 235 550 244.9
508x4 250x8 500 4 250 8 9000 235 550 368.4
510x6 250x10 500 6 250 10 9000 235 550 550.8
512x6 250x12 500 6 250 12 9000 235 550 672.8
514x6 250x14 500 6 250 14 9000 235 550 776.4
508x6 250x8 500 6 250 8 9000 235 550 413.6
510x8 250x10 500 8 250 10 9000 235 550 615.1
512x8 250x12 500 8 250 12 9000 235 550 753
514x8 250x14 500 8 250 14 9000 235 550 854.2
510x4 250x10 500 4 250 10 1000 235 650 304.6
514x12 250x14 500 12 250 14 9000 235 650 553
510x4 250x10 500 4 250 10 9000 235 650 261.9
512x4 250x12 500 4 250 12 9000 235 650 320.6
514x4 250x14 500 4 250 14 9000 235 650 372.2
506x4 250x6 500 4 250 6 9000 235 650 125
508x4 250x8 500 4 250 8 9000 235 650 186.9
510x6 250x10 500 6 250 10 9000 235 650 283.9
512x6 250x12 500 6 250 12 9000 235 650 352.8
514x6 250x14 500 6 250 14 9000 235 650 411.8
508x6 250x8 500 6 250 8 9000 235 650 211.3
510x8 250x10 500 8 250 10 9000 235 650 316.8
512x8 250x12 500 8 250 12 9000 235 650 392.5
514x8 250x14 500 8 250 14 9000 235 650 450
508x6 250x8 500 6 250 8 8000 235 750 104.9
510x8 250x10 500 8 250 10 8000 235 750 157.5
512x8 250x12 500 8 250 12 8000 235 750 193.3
514x8 250x14 500 8 250 14 8000 235 750 227
512x10 250x12 500 10 250 12 9000 235 750 211.7
514x10 250x14 500 10 250 14 9000 235 750 246.7
514x12 250x14 500 12 250 14 9000 235 750 269.8
510x4 250x10 500 4 250 10 9000 235 750 127.9
512x4 250x12 500 4 250 12 9000 235 750 156.1
514x4 250x14 500 4 250 14 9000 235 750 181.3
506x4 250x6 500 4 250 6 9000 235 750 61
508x4 250x8 500 4 250 8 9000 235 750 91.3
510x6 250x10 500 6 250 10 9000 235 750 138.7
512x6 250x12 500 6 250 12 9000 235 750 172.1
514x6 250x14 500 6 250 14 9000 235 750 200.6
81

508x6 250x8 500 6 250 8 9000 235 750 103.2
510x8 250x10 500 8 250 10 9000 235 750 154.8
512x8 250x12 500 8 250 12 9000 235 750 191.8
514x8 250x14 500 8 250 14 9000 235 750 219.4
512x6 250x12 500 6 250 12 9000 275 350 1334.4
514x6 250x14 500 6 250 14 9000 275 350 1540.8
508x6 250x8 500 6 250 8 9000 275 350 793.6
510x8 250x10 500 8 250 10 9000 275 350 1195.7
512x8 250x12 500 8 250 12 9000 275 350 1478.4
514x8 250x14 500 8 250 14 9000 275 350 1692.4
510x4 250x10 500 4 250 10 1000 275 450 943.2
506x4 250x6 500 4 250 6 1000 275 450 489.4
508x4 250x8 500 4 250 8 1000 275 450 662.6
508x6 250x8 500 6 250 8 1000 275 450 795.8
512x10 250x12 500 10 250 12 10000 275 450 1336.3
514x10 250x14 500 10 250 14 10000 275 450 1525
514x12 250x14 500 12 250 14 10000 275 450 1695.8
510x4 250x10 500 4 250 10 10000 275 450 809.9
512x4 250x12 500 4 250 12 10000 275 450 979.6
514x4 250x14 500 4 250 14 10000 275 450 1128.2
510x6 250x10 500 6 250 10 4000 275 550 671
512x6 250x12 500 6 250 12 4000 275 550 876.5
508x6 250x8 500 6 250 8 4000 275 550 508.2
510x8 250x10 500 8 250 10 4000 275 550 746.7
512x10 250x12 500 10 250 12 5000 275 550 1015.2
514x10 250x14 500 10 250 14 5000 275 550 1205.2
514x12 250x14 500 12 250 14 5000 275 550 1340
510x4 250x10 500 4 250 10 5000 275 550 622.5
512x4 250x12 500 4 250 12 5000 275 550 806.2
514x4 250x14 500 4 250 14 5000 275 550 977.3
506x4 250x6 500 4 250 6 5000 275 550 304.2
508x4 250x8 500 4 250 8 5000 275 550 432.5
510x6 250x10 500 6 250 10 5000 275 550 666.2
512x6 250x12 500 6 250 12 5000 275 550 859.2
514x6 250x14 500 6 250 14 5000 275 550 1047.1
508x6 250x8 500 6 250 8 8000 275 650 243
510x8 250x10 500 8 250 10 8000 275 650 366.6
512x8 250x12 500 8 250 12 8000 275 650 455
514x8 250x14 500 8 250 14 8000 275 650 539.8
512x10 250x12 500 10 250 12 9000 275 650 495.2
514x10 250x14 500 10 250 14 9000 275 650 582.8
82

514x12 250x14 500 12 250 14 9000 275 650 637.2
510x4 250x10 500 4 250 10 9000 275 650 300.5
512x4 250x12 500 4 250 12 9000 275 650 372.2
514x4 250x14 500 4 250 14 9000 275 650 433.7
508x4 250x8 500 4 250 8 9000 275 650 205.8
510x6 250x10 500 6 250 10 9000 275 650 322.6
512x6 250x12 500 6 250 12 9000 275 650 407.8
514x6 250x14 500 6 250 14 9000 275 650 479.1
508x6 250x8 500 6 250 8 9000 275 650 237.6
510x8 250x10 500 8 250 10 9000 275 650 359.5
512x8 250x12 500 8 250 12 9000 275 650 450
514x8 250x14 500 8 250 14 9000 275 650 521.4
510x4 250x10 500 4 250 10 1000 275 750 169
506x4 250x6 500 4 250 6 1000 275 750 90.7
508x4 250x8 500 4 250 8 1000 275 750 116.7
508x6 250x8 500 6 250 8 1000 275 750 148.3
512x10 250x12 500 10 250 12 10000 275 750 236
514x10 250x14 500 10 250 14 10000 275 750 270.8
514x12 250x14 500 12 250 14 10000 275 750 301.2
510x4 250x10 500 4 250 10 10000 275 750 142.7
512x4 250x12 500 4 250 12 10000 275 750 175
514x4 250x14 500 4 250 14 10000 275 750 202.5
510x6 250x10 500 6 250 10 10000 275 750 156.4
512x6 250x12 500 6 250 12 10000 275 750 193.2
514x6 250x14 500 6 250 14 10000 275 750 224.6
508x6 250x8 500 6 250 8 10000 275 750 113.5
510x8 250x10 500 8 250 10 10000 275 750 172.1
512x8 250x12 500 8 250 12 10000 275 750 211
514x8 250x14 500 8 250 14 10000 275 750 245.8
514x10 250x14 500 10 250 14 7000 355 350 2434.4
514x12 250x14 500 12 250 14 7000 355 350 2697.8
510x6 250x10 500 6 250 10 7000 355 350 1332.7
512x6 250x12 500 6 250 12 7000 355 350 1745.1
514x6 250x14 500 6 250 14 7000 355 350 2077
508x6 250x8 500 6 250 8 7000 355 350 997.4
510x8 250x10 500 8 250 10 7000 355 350 1494.8
512x8 250x12 500 8 250 12 7000 355 350 1873.2
514x8 250x14 500 8 250 14 7000 355 350 2245.3
512x10 250x12 500 10 250 12 8000 355 350 2038.6
514x10 250x14 500 10 250 14 8000 355 350 2383.4
514x12 250x14 500 12 250 14 8000 355 350 2643.6
83

510x6 250x10 500 6 250 10 8000 355 350 1306.4
512x6 250x12 500 6 250 12 8000 355 350 1708.9
514x6 250x14 500 6 250 14 8000 355 350 2019.8
508x6 250x8 500 6 250 8 8000 355 350 973.2
510x8 250x10 500 8 250 10 8000 355 350 1467.9
512x8 250x12 500 8 250 12 8000 355 350 1837.3
514x8 250x14 500 8 250 14 8000 355 350 2191.3
510x6 250x10 500 6 250 10 9000 355 450 1080.8
512x6 250x12 500 6 250 12 9000 355 450 1402
514x6 250x14 500 6 250 14 9000 355 450 1651.1
508x6 250x8 500 6 250 8 9000 355 450 798.5
510x8 250x10 500 8 250 10 9000 355 450 1212.6
512x8 250x12 500 8 250 12 9000 355 450 1532.7
514x8 250x14 500 8 250 14 9000 355 450 1794
510x4 250x10 500 4 250 10 1000 355 550 807.8
506x4 250x6 500 4 250 6 1000 355 550 433.8
508x4 250x8 500 4 250 8 1000 355 550 596.8
508x6 250x8 500 6 250 8 1000 355 550 707.8
512x10 250x12 500 10 250 12 10000 355 550 1143.9
514x10 250x14 500 10 250 14 10000 355 550 1327.1
514x12 250x14 500 12 250 14 10000 355 550 1473.2
510x6 250x10 500 6 250 10 10000 355 550 745.9
512x6 250x12 500 6 250 12 10000 355 550 949.4
514x6 250x14 500 6 250 14 10000 355 550 1111.4
508x6 250x8 500 6 250 8 10000 355 550 539.6
510x8 250x10 500 8 250 10 10000 355 550 824.7
512x8 250x12 500 8 250 12 10000 355 550 1027.1
514x8 250x14 500 8 250 14 10000 355 550 1212
508x6 250x8 500 6 250 8 2000 355 550 669.8
508x6 250x8 500 6 250 8 3000 355 550 643.3
510x6 250x10 500 6 250 10 4000 355 550 820.7
512x6 250x12 500 6 250 12 4000 355 550 1090.1
508x6 250x8 500 6 250 8 4000 355 550 638
514x12 250x14 500 12 250 14 6000 355 650 866.4
510x6 250x10 500 6 250 10 6000 355 650 414.8
512x6 250x12 500 6 250 12 6000 355 650 551.5
514x6 250x14 500 6 250 14 6000 355 650 686.9
508x6 250x8 500 6 250 8 6000 355 650 315.6
510x8 250x10 500 8 250 10 6000 355 650 467.9
512x8 250x12 500 8 250 12 6000 355 650 590.1
514x8 250x14 500 8 250 14 6000 355 650 728
84

512x10 250x12 500 10 250 12 7000 355 650 639.5
514x10 250x14 500 10 250 14 7000 355 650 760.3
514x12 250x14 500 12 250 14 7000 355 650 843
510x6 250x10 500 6 250 10 7000 355 650 406.9
512x6 250x12 500 6 250 12 7000 355 650 538.7
514x6 250x14 500 6 250 14 7000 355 650 659.4
508x6 250x8 500 6 250 8 7000 355 650 305.8
510x8 250x10 500 8 250 10 7000 355 650 457.6
512x8 250x12 500 8 250 12 7000 355 650 577.2
514x8 250x14 500 8 250 14 7000 355 650 704.9
512x10 250x12 500 10 250 12 8000 355 650 625.6
514x12 250x14 500 12 250 14 9000 355 750 387.8
510x6 250x10 500 6 250 10 9000 355 750 189.8
512x6 250x12 500 6 250 12 9000 355 750 249.5
514x6 250x14 500 6 250 14 9000 355 750 297.3
508x6 250x8 500 6 250 8 9000 355 750 140.4
510x8 250x10 500 8 250 10 9000 355 750 213.6
512x8 250x12 500 8 250 12 9000 355 750 272
514x8 250x14 500 8 250 14 9000 355 750 321.4
506x4 250x6 500 4 250 6 10000 355 350 551.2
510x4 250x10 500 4 250 10 10000 355 350 1170.7
512x4 250x12 500 4 250 12 10000 355 350 1477.6
514x4 250x14 500 4 250 14 10000 355 350 1704.2
508x4 250x8 500 4 250 8 10000 355 350 785.3
506x4 250x6 500 4 250 6 4000 355 350 670.5
506x4 250x6 500 4 250 6 5000 355 350 643.9
506x4 250x6 500 4 250 6 6000 355 350 628.1
514x4 250x14 500 4 250 14 7000 355 350 1897.4
506x4 250x6 500 4 250 6 7000 355 350 611.5
508x4 250x8 500 4 250 8 7000 355 350 846.8
510x4 250x10 500 4 250 10 8000 355 350 1237
512x4 250x12 500 4 250 12 8000 355 350 1583.8
514x4 250x14 500 4 250 14 8000 355 350 1833.8
506x4 250x6 500 4 250 6 8000 355 350 593.7
508x4 250x8 500 4 250 8 8000 355 350 824.6
510x4 250x10 500 4 250 10 9000 355 350 1207.6
512x4 250x12 500 4 250 12 9000 355 350 1525.6
514x4 250x14 500 4 250 14 9000 355 350 1767.4
506x4 250x6 500 4 250 6 9000 355 350 576.1
508x4 250x8 500 4 250 8 9000 355 350 800.5
510x4 250x10 500 4 250 10 2000 355 350 1290.7
85

514x4 250x14 500 4 250 14 2000 355 350 1931.2
506x4 250x6 500 4 250 6 2000 355 350 670.2
508x4 250x8 500 4 250 8 2000 355 350 912.4
510x4 250x10 500 4 250 10 3000 355 350 1240.1
506x4 250x6 500 4 250 6 3000 355 350 630.6
508x4 250x8 500 4 250 8 3000 355 350 896.8
510x4 250x10 500 4 250 10 4000 355 350 1309.8
512x4 250x12 500 4 250 12 4000 355 350 1723.8
514x4 250x14 500 4 250 14 4000 355 350 2115.2
508x4 250x8 500 4 250 8 4000 355 350 901.8
510x4 250x10 500 4 250 10 5000 355 350 1296.2
512x4 250x12 500 4 250 12 5000 355 350 1691
510x4 250x10 500 4 250 10 10000 355 650 361
512x4 250x12 500 4 250 12 10000 355 650 456.5
506x4 250x6 500 4 250 6 10000 355 650 168.4
508x4 250x8 500 4 250 8 10000 355 650 242.7
506x4 250x6 500 4 250 6 6000 355 650 196.5
510x4 250x10 500 4 250 10 7000 355 650 388.4
506x4 250x6 500 4 250 6 7000 355 650 189.2
512x4 250x12 500 4 250 12 8000 355 650 495.2
514x4 250x14 500 4 250 14 8000 355 650 582.2
506x4 250x6 500 4 250 6 8000 355 650 182.3
512x4 250x12 500 4 250 12 9000 355 650 473.7
508x4 250x8 500 4 250 8 9000 355 650 247.6
506x4 250x6 500 4 250 6 3000 355 750 100.4
512x4 250x12 500 4 250 12 5000 355 750 263.1
514x4 250x14 500 4 250 14 5000 355 750 329.8
508x4 250x8 500 4 250 8 5000 355 750 135.3
510x4 250x10 500 4 250 10 2000 355 750 197.5
508x4 250x8 500 4 250 8 2000 355 750 147.4
510x4 250x10 500 4 250 10 4000 355 750 196.7
512x4 250x12 500 4 250 12 4000 355 750 268.7
514x4 250x14 500 4 250 14 4000 355 750 342.4
508x4 250x8 500 4 250 8 4000 355 750 143.2
510x4 250x10 500 4 250 10 5000 355 750 194.7
506x4 250x6 500 4 250 6 5000 355 750 100.6
510x4 250x10 500 4 250 10 7000 355 750 191.7
508x4 250x8 500 4 250 8 7000 355 750 130.1
510x6 250x10 500 6 250 10 9000 460 350 1472.8
512x6 250x12 500 6 250 12 9000 460 350 1997.2
514x6 250x14 500 6 250 14 9000 460 350 2448.9
86

508x6 250x8 500 6 250 8 9000 460 350 1121.8
510x8 250x10 500 8 250 10 9000 460 350 1693.5
512x8 250x12 500 8 250 12 9000 460 350 2173.8
514x8 250x14 500 8 250 14 9000 460 350 2630.9
508x6 250x8 500 6 250 8 1000 460 450 1281.3
512x10 250x12 500 10 250 12 10000 460 450 1960.2
514x10 250x14 500 10 250 14 10000 460 450 2321
514x12 250x14 500 12 250 14 10000 460 450 2566.2
510x6 250x10 500 6 250 10 10000 460 450 1234
512x6 250x12 500 6 250 12 10000 460 450 1642.4
514x6 250x14 500 6 250 14 10000 460 450 1989.2
508x6 250x8 500 6 250 8 10000 460 450 909.9
510x8 250x10 500 8 250 10 10000 460 450 1388.2
512x8 250x12 500 8 250 12 10000 460 450 1760.2
514x12 250x14 500 12 250 14 5000 460 550 2082.7
510x6 250x10 500 6 250 10 5000 460 550 986.8
512x6 250x12 500 6 250 12 5000 460 550 1317.5
514x6 250x14 500 6 250 14 5000 460 550 1660.6
508x6 250x8 500 6 250 8 5000 460 550 769.3
510x8 250x10 500 8 250 10 5000 460 550 1119.8
512x8 250x12 500 8 250 12 5000 460 550 1410.3
514x8 250x14 500 8 250 14 5000 460 550 1753.4
512x10 250x12 500 10 250 12 6000 460 550 1532.5
514x12 250x14 500 12 250 14 6000 460 550 2028.1
510x6 250x10 500 6 250 10 6000 460 550 965.3
508x6 250x8 500 6 250 8 7000 460 650 377.3
510x8 250x10 500 8 250 10 7000 460 650 558
512x8 250x12 500 8 250 12 7000 460 650 704.6
514x8 250x14 500 8 250 14 7000 460 650 880.7
512x10 250x12 500 10 250 12 8000 460 650 761.8
514x10 250x14 500 10 250 14 8000 460 650 912.9
514x12 250x14 500 12 250 14 8000 460 650 1007.5
510x6 250x10 500 6 250 10 8000 460 650 470.6
512x6 250x12 500 6 250 12 8000 460 650 639.9
514x6 250x14 500 6 250 14 8000 460 650 801
510x6 250x10 500 6 250 10 8000 460 750 230.7
512x6 250x12 500 6 250 12 8000 460 750 313.7
514x6 250x14 500 6 250 14 8000 460 750 391.3
508x6 250x8 500 6 250 8 8000 460 750 176.9
510x8 250x10 500 8 250 10 8000 460 750 264.6
512x8 250x12 500 8 250 12 8000 460 750 335.1
87

514x8 250x14 500 8 250 14 8000 460 750 416.4
512x10 250x12 500 10 250 12 9000 460 750 360.6
514x10 250x14 500 10 250 14 9000 460 750 438.2
514x12 250x14 500 12 250 14 9000 460 750 475.8
510x6 250x10 500 6 250 10 9000 460 750 222.3
512x6 250x12 500 6 250 12 9000 460 750 302.5
514x6 250x14 500 6 250 14 9000 460 750 374.6
508x6 250x8 500 6 250 8 9000 460 750 168.7
510x8 250x10 500 8 250 10 9000 460 750 255.1
512x8 250x12 500 8 250 12 9000 460 750 328.5
514x8 250x14 500 8 250 14 9000 460 750 400
506x4 250x6 500 4 250 6 1000 460 350 900.9
508x4 250x8 500 4 250 8 1000 460 350 1232.5
88

Annexe 5 : Extrait de la Base de données (ABAQUS)
Name
h (mm) t,w(mm) b(mm) t,fl(mm) L(mm) fy(Mpa) T(°C)
N_Abaqus
(KN)
HE1000AA 928 16 300 21 10000 355 20 1728.3
HE1000AA 928 16 300 21 8000 355 20 2566.3
HE1000AA 928 16 300 21 6000 355 20 4026.4
HE1000AA 928 16 300 21 4000 355 20 7564.7
HE1000AA 928 16 300 21 2000 355 20 7685.2
IPE753x173 718.8 14.4 267 21.6 10000 355 20 1274.6
IPE753x173 718.8 14.4 267 21.6 8000 355 20 1906.3
IPE753x173 718.8 14.4 267 21.6 6000 355 20 3060.1
IPE753x173 718.8 14.4 267 21.6 4000 355 20 4818
IPE753x173 718.8 14.4 267 21.6 2000 355 20 6544.8
HE700B 636 17 300 32 10000 355 20 2604
HE700B 636 17 300 32 8000 355 20 3813.6
HE700B 636 17 300 32 6000 355 20 5698.5
HE700B 636 17 300 32 4000 355 20 7891.1
HE700B 636 17 300 32 2000 355 20 10028
IPE600A 562 9.8 220 17.5 10000 355 20 591.02
IPE600A 562 9.8 220 17.5 8000 355 20 893.6
IPE600A 562 9.8 220 17.5 6000 355 20 1479.6
IPE600A 562 9.8 220 17.5 4000 355 20 2549.3
IPE600A 562 9.8 220 17.5 2000 355 20 3993.3
HE600AA 540 12 300 15.5 10000 355 20 1262.1
HE600AA 540 12 300 15.5 8000 355 20 1857.8
HE600AA 540 12 300 15.5 6000 355 20 2820
HE600AA 540 12 300 15.5 4000 355 20 4894.5
HE600AA 540 12 300 15.5 2000 355 20 4901.4
IPE550 515.6 11.1 210 17.2 10000 355 20 507.97
IPE550 515.6 11.1 210 17.2 8000 355 20 772.31
IPE550 515.6 11.1 210 17.2 6000 355 20 1292.6
IPE550 515.6 11.1 210 17.2 4000 355 20 2343.7
IPE550 515.6 11.1 210 17.2 2000 355 20 4046.9
HE450AA 398 10 300 13.5 10000 355 20 1089.3
HE450AA 398 10 300 13.5 8000 355 20 1588.5
HE450AA 398 10 300 13.5 6000 355 20 2354
HE450AA 398 10 300 13.5 4000 355 20 3235.9
HE450AA 398 10 300 13.5 2000 355 20 3905.6
IPE400A 373 7 180 12 10000 355 20 225.99
89

IPE400A 373 7 180 12 8000 355 20 345.13
IPE400A 373 7 180 12 6000 355 20 584.77
IPE400A 373 7 180 12 4000 355 20 1117.3
IPE400A 373 7 180 12 2000 355 20 1996.8
IPE330 307 7.5 160 11.5 10000 355 20 153.96
IPE330 307 7.5 160 11.5 8000 355 20 235.46
IPE330 307 7.5 160 11.5 6000 355 20 402.42
IPE330 307 7.5 160 11.5 4000 355 20 810.03
IPE330 307 7.5 160 11.5 2000 355 20 1612.1
HE340AA 297 8.5 300 11.5 10000 355 20 889.72
HE340AA 297 8.5 300 11.5 8000 355 20 1253.4
HE340AA 297 8.5 300 11.5 6000 355 20 1743.9
HE340AA 297 8.5 300 11.5 4000 355 20 2460.8
HE340AA 297 8.5 300 11.5 2000 355 20 3021.9
IPE200A 183 4.5 100 7 10000 355 20 23.673
IPE200A 183 4.5 100 7 8000 355 20 36.423
IPE200A 183 4.5 100 7 6000 355 20 63.293
IPE200A 183 4.5 100 7 4000 355 20 136.19
IPE200A 183 4.5 100 7 2000 355 20 406.63
HE200AA 170 5.5 200 8 10000 355 20 199.55
HE200AA 170 5.5 200 8 8000 355 20 299.68
HE200AA 170 5.5 200 8 6000 355 20 484.16
HE200AA 170 5.5 200 8 4000 355 20 784.62
HE200AA 170 5.5 200 8 2000 355 20 1388.6
HE1000AA 928 16 300 21 10000 355 350 1204.1
HE1000AA 928 16 300 21 8000 355 350 1720.7
HE1000AA 928 16 300 21 6000 355 350 2557.1
HE1000AA 928 16 300 21 4000 355 350 5532.1
HE1000AA 928 16 300 21 2000 355 350 5662.4
IPE753x173 718.8 14.4 267 21.6 10000 355 350 895.79
IPE753x173 718.8 14.4 267 21.6 8000 355 350 1294.1
IPE753x173 718.8 14.4 267 21.6 6000 355 350 1932.4
IPE753x173 718.8 14.4 267 21.6 4000 355 350 3168.5
IPE753x173 718.8 14.4 267 21.6 2000 355 350 4690.4
HE700B 636 17 300 32 10000 355 350 1777.4
HE700B 636 17 300 32 8000 355 350 2452.2
HE700B 636 17 300 32 6000 355 350 3567.5
HE700B 636 17 300 32 4000 355 350 5213.8
HE700B 636 17 300 32 2000 355 350 8563.4
IPE600A 562 9.8 220 17.5 10000 355 350 421.52
IPE600A 562 9.8 220 17.5 8000 355 350 622.02
90

IPE600A 562 9.8 220 17.5 6000 355 350 969.36
IPE600A 562 9.8 220 17.5 4000 355 350 1627.3
IPE600A 562 9.8 220 17.5 2000 355 350 3156.9
HE600AA 540 12 300 15.5 10000 355 350 866.83
HE600AA 540 12 300 15.5 8000 355 350 1211.3
HE600AA 540 12 300 15.5 6000 355 350 1774.8
HE600AA 540 12 300 15.5 4000 355 350 3399.2
HE600AA 540 12 300 15.5 2000 355 350 3436.7
IPE550 515.6 11.1 210 17.2 10000 355 350 362.99
IPE550 515.6 11.1 210 17.2 8000 355 350 542.46
IPE550 515.6 11.1 210 17.2 6000 355 350 863.38
IPE550 515.6 11.1 210 17.2 4000 355 350 1491.6
IPE550 515.6 11.1 210 17.2 2000 355 350 3136
HE450AA 398 10 300 13.5 10000 355 350 735.75
HE450AA 398 10 300 13.5 8000 355 350 1004.5
HE450AA 398 10 300 13.5 6000 355 350 1477.5
HE450AA 398 10 300 13.5 4000 355 350 2126
HE450AA 398 10 300 13.5 2000 355 350 2664.3
IPE400A 373 7 180 12 10000 355 350 162.8
IPE400A 373 7 180 12 8000 355 350 245.19
IPE400A 373 7 180 12 6000 355 350 399.29
IPE400A 373 7 180 12 4000 355 350 698.71
IPE400A 373 7 180 12 2000 355 350 1365.3
IPE330 307 7.5 160 11.5 10000 355 350 111.67
IPE330 307 7.5 160 11.5 8000 355 350 168.49
IPE330 307 7.5 160 11.5 6000 355 350 279.36
IPE330 307 7.5 160 11.5 4000 355 350 515.03
IPE330 307 7.5 160 11.5 2000 355 350 1068.1
HE340AA 297 8.5 300 11.5 10000 355 350 545.11
HE340AA 297 8.5 300 11.5 8000 355 350 745.85
HE340AA 297 8.5 300 11.5 6000 355 350 1121.5
HE340AA 297 8.5 300 11.5 4000 355 350 1684.4
HE340AA 297 8.5 300 11.5 2000 355 350 2072
IPE200A 183 4.5 100 7 10000 355 350 17.495
IPE200A 183 4.5 100 7 8000 355 350 26.704
IPE200A 183 4.5 100 7 6000 355 350 45.794
IPE200A 183 4.5 100 7 4000 355 350 95.705
IPE200A 183 4.5 100 7 2000 355 350 261.27
HE200AA 170 5.5 200 8 10000 355 350 136.17
HE200AA 170 5.5 200 8 8000 355 350 194.35
HE200AA 170 5.5 200 8 6000 355 350 286.8
91

HE200AA 170 5.5 200 8 4000 355 350 505.68
HE200AA 170 5.5 200 8 2000 355 350 941.31
HE1000AA 928 16 300 21 10000 355 450 998.78
HE1000AA 928 16 300 21 8000 355 450 1398.7
HE1000AA 928 16 300 21 6000 355 450 2123.4
HE1000AA 928 16 300 21 4000 355 450 4758.5
HE1000AA 928 16 300 21 2000 355 450 4924
IPE753x173 718.8 14.4 267 21.6 10000 355 450 746.38
IPE753x173 718.8 14.4 267 21.6 8000 355 450 1057.2
IPE753x173 718.8 14.4 267 21.6 6000 355 450 1599.3
IPE753x173 718.8 14.4 267 21.6 4000 355 450 2601.9
IPE753x173 718.8 14.4 267 21.6 2000 355 450 4062.7
HE700B 636 17 300 32 10000 355 450 1453.7
HE700B 636 17 300 32 8000 355 450 1977.6
HE700B 636 17 300 32 6000 355 450 2946.8
HE700B 636 17 300 32 4000 355 450 4320.8
HE700B 636 17 300 32 2000 355 450 7604.2
IPE600A 562 9.8 220 17.5 10000 355 450 354.4
IPE600A 562 9.8 220 17.5 8000 355 450 515.11
IPE600A 562 9.8 220 17.5 6000 355 450 779.42
IPE600A 562 9.8 220 17.5 4000 355 450 1342.3
IPE600A 562 9.8 220 17.5 2000 355 450 2773.9
HE600AA 540 12 300 15.5 10000 355 450 712.44
HE600AA 540 12 300 15.5 8000 355 450 974.28
HE600AA 540 12 300 15.5 6000 355 450 1469
HE600AA 540 12 300 15.5 4000 355 450 2920.4
HE600AA 540 12 300 15.5 2000 355 450 2954.4
IPE550 515.6 11.1 210 17.2 10000 355 450 305.4
IPE550 515.6 11.1 210 17.2 8000 355 450 451.71
IPE550 515.6 11.1 210 17.2 6000 355 450 699.11
IPE550 515.6 11.1 210 17.2 4000 355 450 1235
IPE550 515.6 11.1 210 17.2 2000 355 450 2759.6
HE450AA 398 10 300 13.5 10000 355 450 597.14
HE450AA 398 10 300 13.5 8000 355 450 815.96
HE450AA 398 10 300 13.5 6000 355 450 1218.6
HE450AA 398 10 300 13.5 4000 355 450 1763.7
HE450AA 398 10 300 13.5 2000 355 450 2278.8
IPE400A 373 7 180 12 10000 355 450 137.76
IPE400A 373 7 180 12 8000 355 450 205.62
IPE400A 373 7 180 12 6000 355 450 326.5
IPE400A 373 7 180 12 4000 355 450 577.96
92

IPE400A 373 7 180 12 2000 355 450 1166.3
IPE330 307 7.5 160 11.5 10000 355 450 94.927
IPE330 307 7.5 160 11.5 8000 355 450 141.89
IPE330 307 7.5 160 11.5 6000 355 450 230.58
IPE330 307 7.5 160 11.5 4000 355 450 421.19
IPE330 307 7.5 160 11.5 2000 355 450 888.48
HE340AA 297 8.5 300 11.5 10000 355 450 436.73
HE340AA 297 8.5 300 11.5 8000 355 450 617.03
HE340AA 297 8.5 300 11.5 6000 355 450 931.11
HE340AA 297 8.5 300 11.5 4000 355 450 1420.4
HE340AA 297 8.5 300 11.5 2000 355 450 1768.7
IPE200A 183 4.5 100 7 10000 355 450 15.027
IPE200A 183 4.5 100 7 8000 355 450 22.833
IPE200A 183 4.5 100 7 6000 355 450 38.853
IPE200A 183 4.5 100 7 4000 355 450 79.622
IPE200A 183 4.5 100 7 2000 355 450 215.69
HE200AA 170 5.5 200 8 10000 355 450 109.62
HE200AA 170 5.5 200 8 8000 355 450 151.07
HE200AA 170 5.5 200 8 6000 355 450 235.94
HE200AA 170 5.5 200 8 4000 355 450 419.48
HE200AA 170 5.5 200 8 2000 355 450 800.04
HE1000AA 928 16 300 21 10000 355 550 696.97
HE1000AA 928 16 300 21 8000 355 550 975.24
HE1000AA 928 16 300 21 6000 355 550 1486.2
HE1000AA 928 16 300 21 4000 355 550 3343.5
HE1000AA 928 16 300 21 2000 355 550 3465.2
IPE753x173 718.8 14.4 267 21.6 10000 355 550 521.28
IPE753x173 718.8 14.4 267 21.6 8000 355 550 736.88
IPE753x173 718.8 14.4 267 21.6 6000 355 550 1119.7
IPE753x173 718.8 14.4 267 21.6 4000 355 550 1819.4
IPE753x173 718.8 14.4 267 21.6 2000 355 550 2849.7
HE700B 636 17 300 32 10000 355 550 1013.8
HE700B 636 17 300 32 8000 355 550 1385.8
HE700B 636 17 300 32 6000 355 550 2062.8
HE700B 636 17 300 32 4000 355 550 3025.9
HE700B 636 17 300 32 2000 355 550 5349.1
IPE600A 562 9.8 220 17.5 10000 355 550 247.88
IPE600A 562 9.8 220 17.5 8000 355 550 359.56
IPE600A 562 9.8 220 17.5 6000 355 550 543.94
IPE600A 562 9.8 220 17.5 4000 355 550 939.25
IPE600A 562 9.8 220 17.5 2000 355 550 1955.5
93

HE600AA 540 12 300 15.5 10000 355 550 496.55
HE600AA 540 12 300 15.5 8000 355 550 680.65
HE600AA 540 12 300 15.5 6000 355 550 1028
HE600AA 540 12 300 15.5 4000 355 550 2053.2
HE600AA 540 12 300 15.5 2000 355 550 2075.9
IPE550 515.6 11.1 210 17.2 10000 355 550 213.69
IPE550 515.6 11.1 210 17.2 8000 355 550 315.5
IPE550 515.6 11.1 210 17.2 6000 355 550 487.24
IPE550 515.6 11.1 210 17.2 4000 355 550 864.35
IPE550 515.6 11.1 210 17.2 2000 355 550 1946
HE450AA 398 10 300 13.5 10000 355 550 415.79
HE450AA 398 10 300 13.5 8000 355 550 571.26
HE450AA 398 10 300 13.5 6000 355 550 852.66
HE450AA 398 10 300 13.5 4000 355 550 1235.3
HE450AA 398 10 300 13.5 2000 355 550 1599.8
IPE400A 373 7 180 12 10000 355 550 96.451
IPE400A 373 7 180 12 8000 355 550 143.7
IPE400A 373 7 180 12 6000 355 550 227.62
IPE400A 373 7 180 12 4000 355 550 404.65
IPE400A 373 7 180 12 2000 355 550 819.27
IPE330 307 7.5 160 11.5 10000 355 550 66.581
IPE330 307 7.5 160 11.5 8000 355 550 99.294
IPE330 307 7.5 160 11.5 6000 355 550 160.89
IPE330 307 7.5 160 11.5 4000 355 550 294.97
IPE330 307 7.5 160 11.5 2000 355 550 622.37
HE340AA 297 8.5 300 11.5 10000 355 550 305.96
HE340AA 297 8.5 300 11.5 8000 355 550 432.14
HE340AA 297 8.5 300 11.5 6000 355 550 651.43
HE340AA 297 8.5 300 11.5 4000 355 550 997.04
HE340AA 297 8.5 300 11.5 2000 355 550 1241.1
IPE200A 183 4.5 100 7 10000 355 550 10.608
IPE200A 183 4.5 100 7 8000 355 550 16.062
IPE200A 183 4.5 100 7 6000 355 550 27.241
IPE200A 183 4.5 100 7 4000 355 550 55.603
IPE200A 183 4.5 100 7 2000 355 550 150.96
HE200AA 170 5.5 200 8 10000 355 550 76.296
HE200AA 170 5.5 200 8 8000 355 550 105.09
HE200AA 170 5.5 200 8 6000 355 550 165.31
HE200AA 170 5.5 200 8 4000 355 550 293.51
HE200AA 170 5.5 200 8 2000 355 550 570.49
HE1000AA 928 16 300 21 10000 355 700 203.06
94

HE1000AA 928 16 300 21 8000 355 700 290.77
HE1000AA 928 16 300 21 6000 355 700 454.95
HE1000AA 928 16 300 21 4000 355 700 1172.2
HE1000AA 928 16 300 21 2000 355 700 1246.8
IPE753x173 718.8 14.4 267 21.6 10000 355 700 152.54
IPE753x173 718.8 14.4 267 21.6 8000 355 700 216.83
IPE753x173 718.8 14.4 267 21.6 6000 355 700 342.79
IPE753x173 718.8 14.4 267 21.6 4000 355 700 570.35
IPE753x173 718.8 14.4 267 21.6 2000 355 700 1033.9
HE700B 636 17 300 32 10000 355 700 297.56
HE700B 636 17 300 32 8000 355 700 425.68
HE700B 636 17 300 32 6000 355 700 639.97
HE700B 636 17 300 32 4000 355 700 994.11
HE700B 636 17 300 32 2000 355 700 1971.5
IPE600A 562 9.8 220 17.5 10000 355 700 73.116
IPE600A 562 9.8 220 17.5 8000 355 700 105.03
IPE600A 562 9.8 220 17.5 6000 355 700 165.8
IPE600A 562 9.8 220 17.5 4000 355 700 291.47
IPE600A 562 9.8 220 17.5 2000 355 700 715.64
HE600AA 540 12 300 15.5 10000 355 700 144.25
HE600AA 540 12 300 15.5 8000 355 700 207.18
HE600AA 540 12 300 15.5 6000 355 700 316.83
HE600AA 540 12 300 15.5 4000 355 700 739.77
HE600AA 540 12 300 15.5 2000 355 700 738.95
IPE550 515.6 11.1 210 17.2 10000 355 700 63.23
IPE550 515.6 11.1 210 17.2 8000 355 700 92.392
IPE550 515.6 11.1 210 17.2 6000 355 700 146
IPE550 515.6 11.1 210 17.2 4000 355 700 267.08
IPE550 515.6 11.1 210 17.2 2000 355 700 715.17
HE450AA 398 10 300 13.5 10000 355 700 121.48
HE450AA 398 10 300 13.5 8000 355 700 174.68
HE450AA 398 10 300 13.5 6000 355 700 263.95
HE450AA 398 10 300 13.5 4000 355 700 406.09
HE450AA 398 10 300 13.5 2000 355 700 555.67
IPE400A 373 7 180 12 10000 355 700 28.608
IPE400A 373 7 180 12 8000 355 700 42.147
IPE400A 373 7 180 12 6000 355 700 66.494
IPE400A 373 7 180 12 4000 355 700 124.77
IPE400A 373 7 180 12 2000 355 700 275.88
IPE330 307 7.5 160 11.5 10000 355 700 19.977
IPE330 307 7.5 160 11.5 8000 355 700 29.342
95

IPE330 307 7.5 160 11.5 6000 355 700 47
IPE330 307 7.5 160 11.5 4000 355 700 90.377
IPE330 307 7.5 160 11.5 2000 355 700 205.79
HE340AA 297 8.5 300 11.5 10000 355 700 95.084
HE340AA 297 8.5 300 11.5 8000 355 700 135.56
HE340AA 297 8.5 300 11.5 6000 355 700 205.83
HE340AA 297 8.5 300 11.5 4000 355 700 332.47
HE340AA 297 8.5 300 11.5 2000 355 700 429.86
IPE200A 183 4.5 100 7 10000 355 700 3.3326
IPE200A 183 4.5 100 7 8000 355 700 4.9217
IPE200A 183 4.5 100 7 6000 355 700 8.1373
IPE200A 183 4.5 100 7 4000 355 700 16.27
IPE200A 183 4.5 100 7 2000 355 700 46.764
HE200AA 170 5.5 200 8 10000 355 700 22.114
HE200AA 170 5.5 200 8 8000 355 700 32.224
HE200AA 170 5.5 200 8 6000 355 700 51.801
HE200AA 170 5.5 200 8 4000 355 700 93.23
HE200AA 170 5.5 200 8 2000 355 700 192.8
96

Calcul des colonnes en acier de classe 4 soumises au feu - Rapport PFE

Contenu connexe

En vedette

Calcul des colonnes en acier de classe 4 soumises au feu - Rapport PFE