Découverte de l'apprentissage par réseaux de neurones à travers une application concrète : la reconnaissance vocale. Les données d'entraînement sont des enregistrements vocaux de personnes dans différents états émotionnels. Elles sont traitées par Transformée de Fourier et le réseau est entraîné à renvoyer l'état émotionnel de la personne enregistrée pour un échantillon donné. Ce projet a été codé sous MatLab.

1. UFR Sciences et Techniques
Université de Toulon
M2 Robotique et Objets Connectés
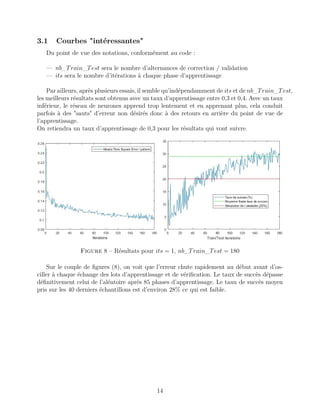
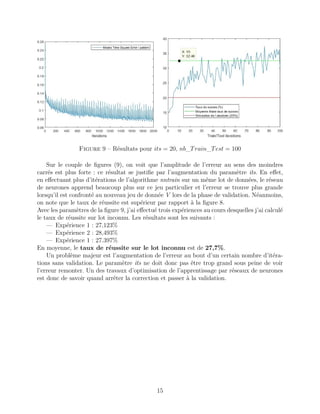
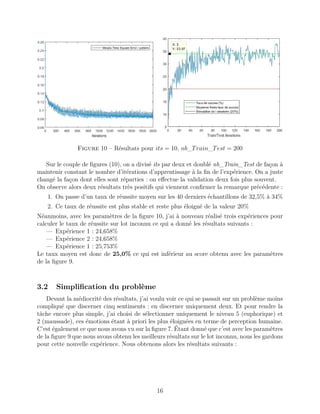
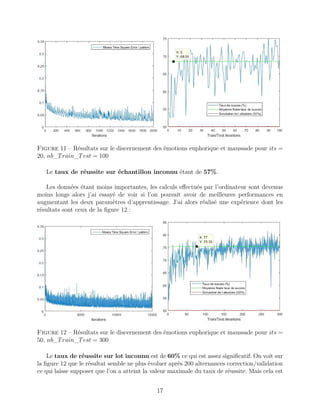
Rapport de projet Comportement - Décision
Reconnaissance vocale :
Approche par réseau de neurones
Yanis Marchand
Décembre 2018

2. Sommaire
Position du problème 1
1 Présentation de l’approche par réseau de neurones 2
1.1 Les neurones en biologie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Réseau de neurones artificiels . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.2.1 Transmission du message . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.2.2 Apprentissage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2 Préparation des données 8
2.1 Analyse du signal . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.2 Entrées du réseau de neurones . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.3 Pertinence du modèle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.4 Structure des données . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
3 Résultats 13
3.1 Courbes "intéressantes" . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
3.2 Simplification du problème . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
4 Changement d’architecture du réseau 18
4.1 Résultats avec 5 neurones de sortie . . . . . . . . . . . . . . . . . . . . . . . 19
4.2 Tentative d’explication . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
Réflexion 22
Bilan personnel 23
Annexes 24

3. Position du problème :
Ce projet invite à découvrir l’apprentissage par réseau de neurones à travers une applica-
tion concrète : la reconnaissance vocale. Plus précisément, nous voudrions rendre possible la
reconnaissance des émotions (joie, colère...) par un robot. Ainsi, on pourrait le programmer
pour ajuster son comportement à l’état émotionnel d’un utilisateur. Par exemple, reculer si
l’utilisateur est énervé ou se rapprocher s’il est triste. Pour cela, nous avons défini cinq classes
de sentiments :
— 1 : En colère
— 2 : Maussade
— 3 : Neutre
— 4 : Heureux
— 5 : Euphorique
Chacun des membres du groupe s’est enregistré en parlant dans ces différents états émo-
tionnels et nous avons concaténé tous les fichiers appartenant à une même classe dans un
seul fichier dont le nom est le numéro associé à chaque classe. Nous avons donc cinq fichiers
numérotés de 1 à 5 au format .wav à la fréquence d’échantillonnage de 44,1 kHz.
1

4. 1 Présentation de l’approche par réseau de neurones
Les réseaux de neurones artificiels ont été développés grâce aux avancées sur la com-
préhension du fonctionnement du cerveau. Par conséquent, avant d’introduire les principes
généraux de cette méthode, nous commençons par présenter les bases du fonctionnement des
neurones dans le vivant.
1.1 Les neurones en biologie
En biologie, un neurone (ou cellule nerveuse) est une cellule électrique excitable caracté-
ristique des animaux. Les neurones forment le système nerveux central (l’encéphale avec 100
milliards de neurones, et la moëlle épinière) et le système nerveux périphérique (ensemble des
neurones dans le reste du corps, dont 500 millions de neurones liés à l’intestin). Les neurones
sont présents partout dans le corps et remplissent de nombreuses fonctions fondamentales
pour l’organisme : sensations, pensées, mémoire, activation des muscles...
On peut distinguer :
— Les cellules sensorielles à l’origine d’un signal nerveux, telles que les cellules de la
rétine de l’oeil captant la lumière. Même si ce ne sont pas des neurones à proprement
parler, leurs caractéristiques sont très proches.
— Les interneurones qui font le lien entre au moins deux neurones.
— Les motoneurones qui provoquent la contraction de cellules musculaires.
Chez la plupart des animaux, les neurones présentent une organisation caractéristique :
Figure 1 – Schéma d’un réseau de neurones : La cellule sensorielle est une cellule photorécep-
trice. Trois neurones sont représentés en noir. Une cellule musculaire se trouve en sortie du réseau.
Les neurones sont constitués de plusieurs dendrites, d’un corps cellulaire, d’un axone et d’une sy-
napse. Le signal est figuré en bleu. Les différentes nuances de bleu représentent différentes natures
du signal.
2

5. Les multiples dendrites d’un neurone reçoivent un signal issu d’un neurone antérieur.
Plusieurs neurones peuvent être connectés en amont, aux dendrites d’un neurone. C’est au
sein de ces dendrites que le premier signal électrique se forme. Ce signal se propage le long
de l’axone jusqu’à la synapse. Au niveau de la synapse, des molécules permettent le passage
du signal à un autre neurone ou à une autre cellule.
Au repos, la concentration en ions n’est pas la même à l’intérieur et à l’extérieur d’une
cellule. Il existe donc une tension électrique de part et d’autre de la membrane délimitant la
cellule, appelée Potentiel de Repos. Un signal électrique est dû au passage d’ions de part et
d’autre de la membrane cellulaire.
Les dendrites et le corps cellulaire constituent une zone de sommation spatiale et
temporelle du signal. Les signaux électriques parcourant les dendrites peuvent s’addition-
ner. Ainsi, un neurone recevant au même instant deux signaux de même intensité issus de
deux neurones antérieurs renverra un signal d’une intensité deux fois plus importante. Les
signaux électriques des dendrites pouvant être excitateurs ou inhibiteurs, les signaux peuvent
également être retranchés.
Au niveau de l’axone, le signal électrique des dendrites et du corps cellulaire est trans-
formé en un signal électrique légèrement différent : les Potentiels d’Action. Cependant, il
existe un seuil d’excitabilité du neurone. Si la somme des signaux afférents dendritiques
ne dépasse pas une certaine tension seuil, aucun Potentiel d’Action ne se formera et aucun
signal ne sera transmis le long de l’axone.
Les Potentiels d’Action sont des signaux électriques ayant une amplitude et une durée (3 ms)
très précises. Durant les quelques millisecondes suivantes, aucun autre Potentiel d’Action ne
peut se former. Cette période dite période réfractaire implique que le signal ne peut ni s’ad-
ditionner en amplitude, ni être saturé. Une forte excitation de la cellule nerveuse se traduira
alors par une fréquence élevée de Potentiels d’Action le long de l’axone.
Les réseaux de neurones biologiques sont donc des structures complexes, transmettant
des signaux de différentes intensités. De plus, ces réseaux sont plastiques et peuvent se
modifier au cours de la vie de l’organisme. Par exemple, des liens entre neurones souvent
stimulés peuvent se renforcer, c’est le mécanisme à l’origine de la mémorisation. Le neurone
en aval devient alors plus sensible aux signaux émis par le neurone précédent. Certains
réseaux peuvent s’atrophier ou se développer selon qu’ils servent souvent ou non. Ainsi les
zones du cerveau liées aux mouvements des doigts sont plus développées chez les violonistes
professionnels du fait de leur activité. Certaines maladies comme la maladie d’Alzheimer
trouvent leur origine dans la mort de neurones impliqués dans la mémoire.
1.2 Réseau de neurones artificiels
Un réseau de neurones artificiels est une structure, inspirée des réseaux neuronaux naturels
présentés dans la section 1.1, au sein de laquelle sont exécutés des algorithmes de machine
learning. Ces structures permettent d’exécuter des tâches en se basant exclusivement sur
des exemples qui lui ont été donnés, et pas sur le résultat d’équations implémentées au
3

6. préalable. La figure 2 propose une schématisation d’une telle structure. Son fonctionnement
est uniquement défini par des opérations mathématiques simples et basées sur le vivant. Par
conséquent, on définit de la même manière trois types de neurones :
— Les neurones d’entrée (input layer)
— Les neurones intermédiaires (hidden layer)
— Les neurones de sortie (output layer)
Ces catégories sont représentées sur la figure 2. Dans notre étude, nous utiliserons une ar-
chitecture tout à fait similaire (une seule couche de neurones intermédiaires) mais un réseau
peut comporter un nombre quelconque de couches de ce type. L’appellation deep learning
désigne d’ailleurs les réseaux dits "profonds", comportant plusieurs couches intermédiaires.
Figure 2 – Architecture simple d’un réseau de neurones artificiels
En entrée, l’utilisateur présente les exemples qu’il a à proposer pour entraîner le réseau de
neurones. Ces exemples peuvent être des données de plusieurs types. Un exemple d’utilisation
de ces techniques est celui de la détection de chemin dans une image. Dans ce cas, les entrées
seront des images contenant effectivement des sentiers (ou pas) et les neurones d’entrée
recevront donc directement la valeur de l’intensité lumineuse d’un pixel particulier de la
photo, ou alors d’un groupe de pixels de celle-ci. Ces intensités seront alors les input 1, 2...5
du réseau présenté sur la figure 2.
En sortie, si l’on suit notre exemple, on peut choisir de placer un neurone dont la valeur
retournée indiquera si oui ou non, il y a un chemin sur la photo correspondante. Par exemple,
0 indiquera qu’il n’y a pas de chemin, et 1 qu’il y en a un.
Pour arriver à ce résultat, l’information captée par les neurones d’entrée va se transmettre
aux neurones des couches intermédiaires, pour finalement arriver à la sortie.
4

7. 1.2.1 Transmission du message
Figure 3 – Neurone artificiel
Sur la figure 3, on a zoomé sur un neurone de réseau pour voir les opérations mathé-
matiques qui y sont effectuées. Tout d’abord, une règle de base est qu’un neurone reçoit le
message émergent de tous les neurones de la couche précédente, qui sont les x1 x2 · · · xn
avec n le nombre de signaux afférents (donc le nombre de neurones de la couche précédente).
Ces messages se voient attribués une pondération analogue au renforcement des liens entre
neurones naturels souvent stimulés. Chaque poids ωi multiplie le signal afférent xi et tous ces
produits sont alors sommés et un biais b est ajouté. Cette somme est donc égale au produit
matriciel :
Sk = ω1 · · · ωn b






x1
...
xn
1






(1)
Cette opération est réalisée dans chaque neurone d’une couche donnée et prend en compte
les mêmes signaux afférents : ceux de tous les neurones de la couche précédente. On peut
généraliser l’équation (1) pour calculer et stocker le résultat de cette somme pour tous les
neurones de la couche courante dans un vecteur. Pour cela, on rassemble (en lignes) les poids
associés à un neurone particulier de cette couche et on calcule le produit matriciel suivant :






S1
S2
...
SnbN






=






ω1,1 · · · ω1,n b1
ω2,1 · · · ω2,n b2
...
...
ωnbN,1 · · · ωnbN,n bnbN






ωL12






x1
...
xn
1






(2)
avec nbN le nombre de neurones de la couche courante dont un élément est représenté sur la
figure 3.
5

8. Encore une fois, l’équation (2) peut se généraliser en utilisant tous les exemples d’entrées.
En effet, les messages afférents rassemblés dans le vecteur x1 · · · xn
T
sont différents à
chaque exemple et on peut donc stocker l’ensemble de ces messages dans les colonnes d’une
matrice : 



x1,1 · · · x1,nE
...
...
xn,1 · · · xn,nE




De fait, l’équation (2) devient :




S1,1 · · · S1,nE
...
...
SnbN,1 · · · SnbN,nE




SL2
= ωL12






x1,1 · · · x1,nE
...
...
xn,1 · · · xn,nE
1 · · · 1






XL1
(3)
L’équation (3) traduit se qui se passe pour chaque exemple dans une couche (layer) de
neurones : les signaux afférents xL1 (du layer 1) sont traités par les poids ωL12 (layer 1 vers
2) pour donner les sommes SL2 (du layer 2). Elle est codée dans l’algorithme nntest, par
exemple, pour calculer hidsum et outsum.
Une fois la somme pondérée des signaux et du biais calculée, on a simulé ce qui s’est passé
dans la dendrite. On doit désormais modéliser l’action du neurone sur ce signal entrant. On
introduit une non-linéarité en appliquant sur celui-ci une fonction d’activation. Elle résulte
d’un choix mais doit vérifier une condition : sa courbe doit comporter trois "phases".
1. En-dessous d’un certain seuil, sa sortie doit être très faible pour simuler un neurone
inactif.
2. Pour un seuil intermédiaire, sa sortie doit être un nombre strictement compris entre
0 et 1.
3. A partir d’un certain seuil, la valeur renvoyée est constante égale à 1.
La fonction sigmoïde est une candidate idéale puisqu’elle remplit ces trois conditions. Sa
courbe est tracée sur la figure 4. La valeur renvoyée constituera le message renvoyé par le
neurone en question. Il sera alors capté par tous les neurones de la couche suivante et le
processus recommencera.
6

9. Figure 4 – Tracé de la fonction sigmoïde sur l’intervalle [-10 ; 10]
1.2.2 Apprentissage
Nous avons présenté comment était modélisée, mathématiquement, la transmission d’un
message d’entrée à travers toutes les couches d’un réseau de neurones. Décrivons à présent
le processus qui permet au réseau de réellement apprendre.
La méthode consiste à envoyer en entrée les exemples que nous avons choisi et de fournir
la sortie que nous voudrions que le réseau renvoie. Dans l’exemple de la détection de sentier
sur une photo, il suffit de fournir une image de chemin et l’entier "1". Il existe alors des
algorithmes permettant de faire évoluer les poids au fil des exemples traités, de simuler le
comportement du réseau et de calculer l’erreur commise par le réseau, c’est à dire la différence
entre la sortie voulue et celle proposée par le réseau avec les poids actuels. La méthode de
la descente de gradient permet d’optimiser la convergence des poids vers ceux minimisant
l’erreur. C’est l’algorithme train qui fera ce travail dans notre étude.
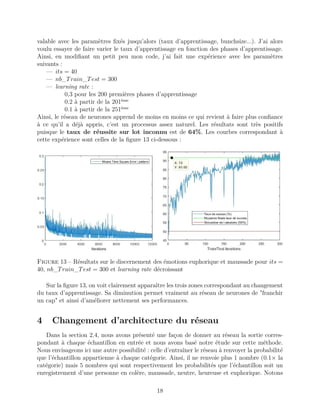
A chaque itération de cet algorithme, l’erreur est calculée et elle décroit généralement
exponentiellement avant de remonter si on a réalisé un sur-entraînement, ce qui est contre-
productif. A la fin d’une phase d’apprentissage (dite de correction), il est judicieux de tester
le jeu de poids trouvé sur de nouveaux exemples pour en analyser les performances : c’est la
phase de validation. Ensuite, dans le but de ne pas perdre le potentiel d’apprentissage de ces
nouveaux échantillons, on permute les exemples ayant servi à la correction et à la validation
et on recommence une phase d’entraînement. Au bout d’un certain nombre d’alternances
correction/validation, on réalise un test final sur des exemples non encore traités par le
réseau et on calcule le taux de réussite. Ainsi, on obtient une valeur objective de la capacité
du réseau à traiter des cas qu’il n’a encore jamais rencontrés.
7

10. 2 Préparation des données
On l’a vu dans la section 1.2, le réseau de neurones que l’on va créer apprendra à discerner
les sentiments à partir des données que nous choisissons de lui proposer en entrée. Par consé-
quent, la pertinence de celles-ci est très importante. Il est donc important de savoir, à partir
d’un fichier son, quelles transformations appliquer dans le but de donner des informations
"intéressantes" au réseau de neurones. Ceci constitue une grande partie du travail à effectuer
lorsqu’on veut implanter de l’intelligence artificielle. Les données, aussi nombreuses soit-elles,
ne permettront pas d’avoir de bonnes performances après apprentissage si elles ne sont pas
pertinentes. Plus encore que les algorithmes de machine learning, la connaissance du domaine
d’utilisation (le son dans notre cas) est absolument fondamentale.
Nous allons donc essayer de comprendre quels opérateurs mathématiques appliquer au
signal sonore brut pour obtenir ce qui sera les entrées du réseau de neurones. Pour cela, nous
avons utilisé le logiciel OCTAVE.
2.1 Analyse du signal
Chaque fichier .wav est une discrétisation de l’onde sonore enregistrée par notre micro-
phone à raison de 44100 valeurs par secondes. La commande wavread permet de lire cette
suite de nombres et de les stocker dans un vecteur colonne. La variable file peut donc se
représenter ainsi :
file =




x1
...
xF




De ce vecteur, nous aimerions extraire un certain nombre d’échantillons d’une durée fixée
pour en analyser le contenu. Étant donné la fréquence d’échantillonnage, 1 seconde de fichier
son est transformée en 44100 points. Il est donc aisé de transformer une durée que l’on choisit
en nombre de points. Nous prendrons tailleEchant = 44100. Chaque fichier n’étant pas un
multiple de cette valeur, on commence par sélectionner un nombre entier de paquets de 44100
valeurs (nos échantillons) et grâce à la fonction reshape, on place ces échantillons dans les
colonnes d’une matrice. Le fichier se présente donc sous la forme suivante :
file =




x1,1 · · · x1,nE
...
...
xtE,1 · · · xtE,nE




avec nE le nombre d’échantillons et tE la taille de ces échantillons (ici, nE = 44100).
On applique ensuite la commande fft qui permet de calculer la transformée de Fourier
discrète (TFD) d’un signal échantillonné. Appliquée à une matrice, cette fonction s’applique
sur chaque colonne, d’où l’intérêt d’avoir placé nos échantillons en colonnes. On calcule donc
pour chaque colonne :
X(k) =
tE
n=1
xke−2iπ nk
tE (4)
8

11. Figure 5 – Transformée de Fourier Discrète du fichier 1
On se retrouve avec une matrice contenant, dans chaque colonne, tous les termes de la TFD
de chaque échantillon. Après l’application de la commande abs pour obtenir le spectre dis-
cret en module, son tracé est illisible. L’application de la fonction logarithme permet alors
de "contracter" les données et de voir apparaître des zones aux valeurs distinctes (figure 5).
Sur la figure 5, on voit apparaître les échantillons en abscisse, les fréquences en ordonnée et
l’amplitude de chaque fréquence en couleur. Elle a été réalisée en prenant tE = 10000 pour
des raisons purement esthétiques. En effet, les représentations graphiques sous Octave ont
souvent posé des problèmes d’affichage. Cependant, nous pouvons analyser cette figure car
celle obtenue pour tE = 44100 est tout à fait similaire.
On remarque une symétrie haut/bas qui correspond à la symétrie hermitienne dû au fait
que le signal traité est réel. On peut donc ne conserver que la première moitié.
Une deuxième remarque que l’on peut faire est que du fait de l’équation (4), les hautes
fréquences reçoivent un indice k plus grand donc elles se retrouvent en bas de la matrice
calculée. La commande flipud permet de remédier à cela en inversant le sens des lignes. On
obtient alors le spectre de la figure 6. On y voit que l’amplitude des basses fréquences est
largement supérieure aux hautes fréquences. L’amplitude étant liée à la puissance, l’éner-
gie peut être calculée en sommant les amplitudes d’un signal. C’est l’information que nous
retiendrons comme entrée du réseau de neurones : nous calculerons l’énergie associée à des
bandes de fréquence.
9

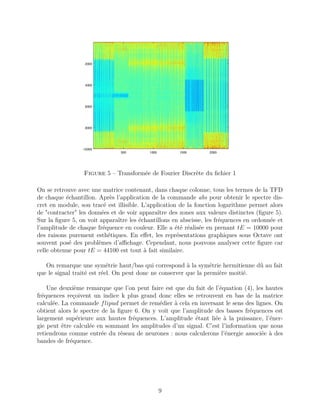
12. Figure 6 – Transformée de Fourier Discrète traitée du fichier 1
2.2 Entrées du réseau de neurones
Combien de bandes de fréquences faut-il définir et quelles limites donner à chacune d’elle ?
Pour répondre à cette question, basons-nous sur la remarque que nous avons faite au sujet
de la figure 5 : le tracé est devenu lisible en appliquant la fonction logarithme qui "contracte"
les données en transformant les puissances en facteurs multiplicatifs. Ceci laisse supposer
que l’énergie contenue dans le signal diminue exponentiellement quand la fréquence associée
augmente. Nous choisirons donc de sommer les amplitudes du signal de la manière suivante :
— BF1 = [X(1), X(2)]
— BF2 = [X(3), X(4)]
— ...
— BFi = [X(2i−1
+ 1), X(2i
)]
— ...
jusqu’à ce que la taille d’un échantillon ne soit pas un multiple de 2n+2
. Ainsi la taille de la
bande de fréquence augmente exponentiellement pour compenser la décroissance exponen-
tielle d’énergie. Notons que dans notre cas, cela définit 14 classes.
2.3 Pertinence du modèle
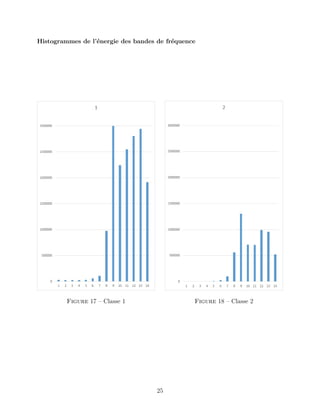
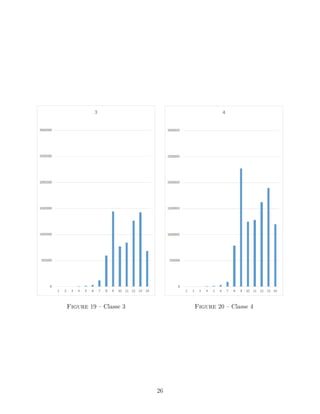
Un tel choix est-il pertinent ? En annexe, on trouvera cinq histogrammes sur lesquels on
a représenté l’énergie des bandes de fréquences ainsi définies pour les cinq classes d’émotion.
On a sommé l’énergie de tous les échantillons afin d’avoir un résultat unique pour chaque
classe. Attardons-nous sur l’énergie associée à la bande de fréquence la plus haute. Sur la
figure 7, on a tracé l’énergie associée à cette bande de fréquence. On peut voir qu’elle est
10

13. maximale pour la catégorie 1 (en colère) et 5 (euphorique) qui sont deux sentiments "ex-
trêmes". De plus, elle est minimale pour la classe 2 (maussade), plus grande pour la classe
3 (neutre) et encore plus grande pour la classe 4 (heureux). Tous ces résultats sont parfai-
tement logiques étant donné le type de voix que nous avons dans ces différentes circonstances.
Par ailleurs, les écarts de valeur entre les cinq énergies sont assez significatifs, il y a donc
peu de risque d’en confondre deux. Par conséquent, ce critère parait, à priori, être une très
bonne solution pour discriminer les émotions. En voyant ce graphique, on serait même tenté
de penser que l’énergie liée à cette unique bande de fréquence suffirait à constituer l’entrée
du réseau de neurones. Je précise tout de suite ici que j’ai évidemment essayé et cela conduit
à des résultats désastreux, donc je ne m’étendrai pas sur cette option.
Figure 7 – Énergie de la bande de fréquence la plus haute pour chaque émotion
2.4 Structure des données
Le travail décrit dans la section (2.2) est réalisé dans le programme par une boucle for
qui parcourt les cinq fichiers son et calcule les énergies des 14 bandes de fréquence. La va-
riable donnees contient nE colonnes (le nombre d’échantillons) et 14 lignes dans lesquelles
se trouvent les valeurs des énergies correspondantes.
Durant l’apprentissage, il faudra donner au réseau la sortie correspondante de chaque échan-
tillon (le numéro de classe) donc il est judicieux de le rajouter. Mais rappelons-nous qu’une
fois entraîné, la dernière opération que réalise le réseau de neurones est l’application de la
fonction sigmoïde dont la valeur est strictement comprise entre 0 et 1. Par conséquent, l’en-
semble des valeurs de sortie possibles doit également appartenir à cet intervalle. J’ai alors
décidé de changer l’appellation des catégories en multipliant par 0.1. Ainsi :
11

14. — 0.1 correspond à "en colère"
— 0.2 correspond à "maussade"
— 0.3 correspond à "neutre"
— 0.4 correspond à "heureux"
— 0.5 correspond à "euphorique"
En ajoutant une 15eme
ligne avec la catégorie de chaque fichier audio, la variable donnees
pour le fichier 1 est donc du type :
donnees =






EBF1,1 · · · EBF1,nE
...
...
EBF14,1 · · · EBF14,nE
0.1 · · · 0.1






Il subsiste un problème : tous les fichiers audio ne faisant pas la même taille, certains pro-
duiront plus d’échantillons que d’autres. Or, cela entraînerait que le réseau apprenne "plus"
certaines émotions que d’autres. Pour y remédier, j’ai écrit le script caracteristiques_donnees
qui permet de trouver le fichier de plus petite taille et renvoie le nombre d’échantillons
nb_echant_min de celui-ci. Ainsi, pour tous les autres, on choisit au hasard nb_echant_min
échantillons parmi tous ceux créés.
A la fin de chaque itération de la boucle for, on concatène en ligne les matrices donnees
dans une matrice qui les contiendra toutes : InOut. Cette matrice contient toutes les données
nécessaires au problème (entrées et sorties) et se présente sous la forme :
InOut =






E1,1 · · · E1,m E1,m+1 · · · E1,2×m · · · · · · E1,5×m
...
...
...
...
...
E14,1 · · · E14,m E14,m+1 · · · E14,2×m · · · · · · E14,5×m
0.1 · · · 0.1 0.2 · · · 0.2 · · · · · · 0.5






avec m = nb_echant_min
Il reste à séparer ces données en trois groupes :
— L contiendra la moitié de ces valeurs pour l’entraînement (la modification des poids)
— V contiendra un quart de ces valeurs pour la phase de validation (l’exécution sur des
exemples non encore connus)
— U contiendra le dernier quart de ces valeurs pour effectuer le test final
Il est absolument nécessaire que ces trois groupes aient une proportion d’échantillons de
chaque classe à peu près égale. C’est pourquoi, avant de répartir les colonnes de InOut dans
L, V et U, on les mélange de façon aléatoire grâce à la commande randperm. On notera par
ailleurs que les algorithmes nntrain et nntest ont été écrits de manière à ce que la matrice i
contenant les données présente les exemples (patterns) en lignes plutôt qu’en colonnes. Par
conséquent, on extrait les lignes de la transposée de InOut pour les mettre dans L, V et U.
12

15. De fait, L soit de la forme :
L =









E1,1 · · · E1,14 c1
...
...
...
Ei,1 · · · Ei,14 ci
...
...
...
En,1 · · · Ei,14 cn









où :
∀i ∈ [|1, n|], ci ∈ {0.1, 0.2, 0.3, 0.4, 0.5}
et :
n =
5
2
× nb_echant_min
3 Résultats
Dans le but d’analyser les résultats produits par le réseau de neurones, je me suis basé
sur deux indicateurs :
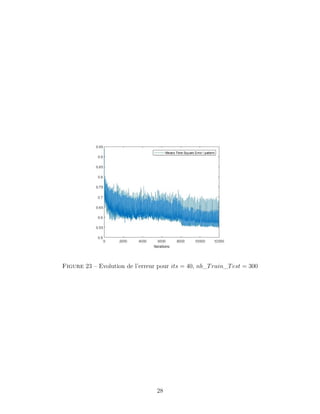
Means Square Error per pattern
L’algorithme nntrain renvoie une variable es : l’erreur au sens des moindres carrés ramenée
au nombre d’exemples. Elle est calculée à chaque itération donc on peut tracer son évolution
au cours du temps.
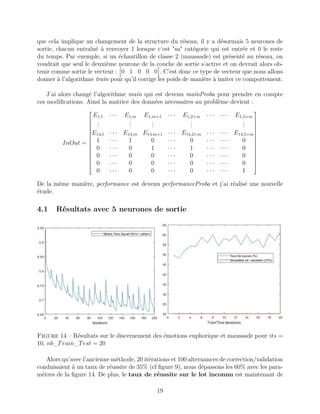
Success rate
J’ai écrit un petit algorithme (performance) qui, à l’issu de la validation (nntest), récupère
la sortie du réseau pour chaque échantillon qui y est entré (censé être proche d’un nombre
parmi {0.1, 0.2, 0.3, 0.4, 0.5}, le multiplie par 10 et l’arrondi à l’entier le plus proche. De
cette manière, le nombre obtenu devrait appartenir au multiplet {1, 2, 3, 4, 5}. Le programme
récupère également la classe de l’échantillon correspondant (contenu dans la dernière colonne
de V ) et il compte le nombre de fois que le réseau de neurones avait prédit le bon résultat.
On obtient un taux de réussite par phase de validation : on peut alors tracer son évolution
au fil des alternances correction/validation.
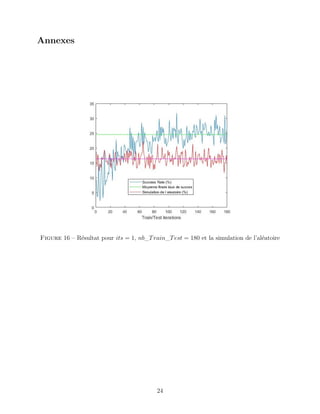
En parallèle, algorithme performance simule l’effet d’un tirage aléatoire d’un nombre
appartenant à {1, 2, 3, 4, 5} autant de fois qu’il y a d’échantillons. Son taux de succès est
calculé de la même manière ainsi on pourrait voir si le réseau fait une prédiction meilleure
qu’une personne proposant au hasard une prédiction du résultat. Cependant, contrairement
à mon attente, la valeur moyenne du taux de succès de cet algorithme n’est pas de 20% mais
plutôt de 16% et cette valeur est régulière. La figure 16 montrant ce phénomène se trouve en
annexe.
13

16. 3.1 Courbes "intéressantes"
Du point de vue des notations, conformément au code :
— nb_Train_Test sera le nombre d’alternances de correction / validation
— its sera le nombre d’itérations à chaque phase d’apprentissage
Par ailleurs, après plusieurs essais, il semble qu’indépendamment de its et de nb_Train_Test,
les meilleurs résultats sont obtenus avec un taux d’apprentissage entre 0,3 et 0,4. Avec un taux
inférieur, le réseau de neurones apprend trop lentement et en apprenant plus, cela conduit
parfois à des "sauts" d’erreur non désirés donc à des retours en arrière du point de vue de
l’apprentissage.
On retiendra un taux d’apprentissage de 0,3 pour les résultats qui vont suivre.
Figure 8 – Résultats pour its = 1, nb_Train_Test = 180
Sur le couple de figures (8), on voit que l’erreur chute rapidement au début avant d’os-
ciller à chaque échange des lots d’apprentissage et de vérification. Le taux de succès dépasse
définitivement celui de l’aléatoire après 85 phases d’apprentissage. Le taux de succès moyen
pris sur les 40 derniers échantillons est d’environ 28% ce qui est faible.
14

17. Figure 9 – Résultats pour its = 20, nb_Train_Test = 100
Sur le couple de figures (9), on voit que l’amplitude de l’erreur au sens des moindres
carrés est plus forte : ce résultat se justifie par l’augmentation du paramètre its. En effet,
en effectuant plus d’itérations de l’algorithme nntrain sur un même lot de données, le réseau
de neurones apprend beaucoup plus sur ce jeu particulier et l’erreur se trouve plus grande
lorsqu’il est confronté au nouveau jeu de donnée V lors de la phase de validation. Néanmoins,
on note que le taux de réussite est supérieur par rapport à la figure 8.
Avec les paramètres de la figure 9, j’ai effectué trois expériences au cours desquelles j’ai calculé
le taux de réussite sur lot inconnu. Les résultats sont les suivants :
— Expérience 1 : 27,123%
— Expérience 2 : 28,493%
— Expérience 1 : 27.397%
En moyenne, le taux de réussite sur le lot inconnu est de 27,7%.
Un problème majeur est l’augmentation de l’erreur au bout d’un certain nombre d’itéra-
tions sans validation. Le paramètre its ne doit donc pas être trop grand sous peine de voir
l’erreur remonter. Un des travaux d’optimisation de l’apprentissage par réseaux de neurones
est donc de savoir quand arrêter la correction et passer à la validation.
15

18. Figure 10 – Résultats pour its = 10, nb_Train_Test = 200
Sur le couple de figures (10), on a divisé its par deux et doublé nb_Train_Test de façon à
maintenir constant le nombre d’itérations d’apprentissage à la fin de l’expérience. On a juste
changé la façon dont elles sont réparties : on effectue la validation deux fois plus souvent.
On observe alors deux résultats très positifs qui viennent confirmer la remarque précédente :
1. On passe d’un taux de réussite moyen sur les 40 derniers échantillons de 32,5% à 34%
2. Ce taux de réussite est plus stable et reste plus éloigné de la valeur 20%
Néanmoins, avec les paramètres de la figure 10, j’ai à nouveau réalisé trois expériences pour
calculer le taux de réussite sur lot inconnu ce qui a donné les résultats suivants :
— Expérience 1 : 24,658%
— Expérience 2 : 24,658%
— Expérience 1 : 25,753%
Le taux moyen est donc de 25,0% ce qui est inférieur au score obtenu avec les paramètres
de la figure 9.
3.2 Simplification du problème
Devant la médiocrité des résultats, j’ai voulu voir ce qui se passait sur un problème moins
compliqué que discerner cinq sentiments : en discerner uniquement deux. Et pour rendre la
tâche encore plus simple, j’ai choisi de sélectionner uniquement le niveau 5 (euphorique) et
2 (maussade), ces émotions étant à priori les plus éloignées en terme de perception humaine.
C’est également ce que nous avons vu sur la figure 7. Étant donné que c’est avec les paramètres
de la figure 9 que nous avons obtenu les meilleurs résultats sur le lot inconnu, nous les gardons
pour cette nouvelle expérience. Nous obtenons alors les résultats suivants :
16

19. Figure 11 – Résultats sur le discernement des émotions euphorique et maussade pour its =
20, nb_Train_Test = 100
Le taux de réussite sur échantillon inconnu étant de 57%.
Les données étant moins importantes, les calculs effectués par l’ordinateur sont devenus
moins longs alors j’ai essayé de voir si l’on pouvait avoir de meilleures performances en
augmentant les deux paramètres d’apprentissage. J’ai alors réalisé une expérience dont les
résultats sont ceux de la figure 12 :
Figure 12 – Résultats sur le discernement des émotions euphorique et maussade pour its =
50, nb_Train_Test = 300
Le taux de réussite sur lot inconnu est de 60% ce qui est assez significatif. On voit sur
la figure 12 que le résultat semble ne plus évoluer après 200 alternances correction/validation
ce qui laisse supposer que l’on a atteint la valeur maximale du taux de réussite. Mais cela est
17

20. valable avec les paramètres fixés jusqu’alors (taux d’apprentissage, bunchsize...). J’ai alors
voulu essayer de faire varier le taux d’apprentissage en fonction des phases d’apprentissage.
Ainsi, en modifiant un petit peu mon code, j’ai fait une expérience avec les paramètres
suivants :
— its = 40
— nb_Train_Test = 300
— learning rate :
0,3 pour les 200 premières phases d’apprentissage
0.2 à partir de la 201ème
0.1 à partir de la 251ème
Ainsi, le réseau de neurones apprend de moins en moins ce qui revient à faire plus confiance
à ce qu’il a déjà appris, c’est un processus assez naturel. Les résultats sont très positifs
puisque le taux de réussite sur lot inconnu est de 64%. Les courbes correspondant à
cette expérience sont celles de la figure 13 ci-dessous :
Figure 13 – Résultats sur le discernement des émotions euphorique et maussade pour its =
40, nb_Train_Test = 300 et learning rate décroissant
Sur la figure 13, on voit clairement apparaître les trois zones correspondant au changement
du taux d’apprentissage. Sa diminution permet vraiment au réseau de neurones de "franchir
un cap" et ainsi d’améliorer nettement ses performances.
4 Changement d’architecture du réseau
Dans la section 2.4, nous avons présenté une façon de donner au réseau la sortie corres-
pondant à chaque échantillon en entrée et nous avons basé notre étude sur cette méthode.
Nous envisageons ici une autre possibilité : celle d’entraîner le réseau à renvoyer la probabilité
que l’échantillon appartienne à chaque catégorie. Ainsi, il ne renvoie plus 1 nombre (0.1× la
catégorie) mais 5 nombres qui sont respectivement les probabilités que l’échantillon soit un
enregistrement d’une personne en colère, maussade, neutre, heureuse et euphorique. Notons
18

21. que cela implique un changement de la structure du réseau, il y a désormais 5 neurones de
sortie, chacun entraîné à renvoyer 1 lorsque c’est "sa" catégorie qui est entrée et 0 le reste
du temps. Par exemple, si un échantillon de classe 2 (maussade) est présenté au réseau, on
voudrait que seul le deuxième neurone de la couche de sortie s’active et on devrait alors ob-
tenir comme sortie le vecteur : 0 1 0 0 0 . C’est donc ce type de vecteur que nous allons
donner à l’algorithme train pour qu’il corrige les poids de manière à imiter ce comportement.
J’ai alors changé l’algorithme main qui est devenu mainProba pour prendre en compte
ces modifications. Ainsi la matrice des données nécessaires au problème devient :
InOut =
















E1,1 · · · E1,m E1,m+1 · · · E1,2×m · · · · · · E1,5×m
...
...
...
...
...
E14,1 · · · E14,m E14,m+1 · · · E14,2×m · · · · · · E14,5×m
1 · · · 1 0 · · · 0 · · · · · · 0
0 · · · 0 1 · · · 1 · · · · · · 0
0 · · · 0 0 · · · 0 · · · · · · 0
0 · · · 0 0 · · · 0 · · · · · · 0
0 · · · 0 0 · · · 0 · · · · · · 1
















De la même manière, performance est devenu performanceProba et j’ai réalisé une nouvelle
étude.
4.1 Résultats avec 5 neurones de sortie
Figure 14 – Résultats sur le discernement des émotions euphorique et maussade pour its =
10, nb_Train_Test = 20
Alors qu’avec l’ancienne méthode, 20 itérations et 100 alternances de correction/validation
conduisaient à un taux de réussite de 35% (cf figure 9), nous dépassons les 60% avec les para-
mètres de la figure 14. De plus, le taux de réussite sur le lot inconnu est maintenant de
19

22. 58% contre 27.7% auparavant. On en déduit que les performances sont largement meilleures
avec 5 neurones de sortie, même avec un apprentissage sur moins d’exemples.
Les résultats de la simulation pour des paramètres identiques à ceux de la figure 13
(taux d’apprentissage décroissant) sont présents en annexe sur les figures 22 et 23 mais le
fait le plus intéressant est que le taux de réussite sur le lot inconnu est toujours de 58%.
Je propose ici un dernier résultat, celui d’une analyse réalisée avec les seules émotions 2
et 5 (comme dans la partie 3.2). Avec 20 itérations et 40 alternances de correction/validation,
le taux de réussite sur le lot inconnu est de 97%.
4.2 Tentative d’explication
Sans contestation possible, les résultats sont largement meilleurs en attribuant à chaque
neurone de sortie une émotion et en lui donnant le rôle de s’activer uniquement lorsque
l’échantillon correspond à cette catégorie. Comment l’expliquer ?
Tout d’abord, il est judicieux de s’intéresser à la courbe de l’erreur quadratique que nous
avons souvent laissé de côté pour l’instant. En effet, au cours des analyses présentées dans la
section 3, cette grandeur a toujours diminué de manière à passer sous la barre des 0.12 dès les
premières itérations. En changeant de modèle, on se rend compte que cette même grandeur
reste supérieure à 0.5 en fin de simulation. Cela laisse supposer que dans ce cas, le réseau a
encore une "marge de progrès". Au contraire, avec une erreur très faible, les poids n’évoluent
plus beaucoup car le modèle est déjà considéré comme parfait.
Une deuxième raison, plus qualitative, me paraît cohérente. Lorsqu’on apprend à un neu-
rone de sortie à sortir un nombre parmi 0 1 0 0 0 , il a peu de "marge de manoeuvre" en
ce sens que pour déterminer la catégorie qu’il propose, j’ai été obligé de multiplier le nombre
par 10 avant de l’arrondir à l’entier le plus proche. En revanche, avec 5 valeurs de sortie,
indiquant chacune la probabilité que la catégorie correspondante soit celle de l’exemple, je
n’ai eu qu’à chercher la place de la valeur maximale dans le vecteur de sortie. De plus, cette
valeur est censée avoir uniquement 2 états possibles (0 ou 1) dans l’intervalle qui lui est
donné. La "marge de manoeuvre" est donc beaucoup plus grande.
Enfin, rappelons nous que la forme de la fonction sigmoïde (représentée sur la figure 4),
est censée imiter le comportement d’un neurone, à savoir comporter une phase inactive, une
courte transition et une phase d’activité. Ceci laisse supposer que cette fonction est pré-
disposée à être égale à 0 ou 1 l’immense majorité du temps (0 pour x ∈ −∞, −4 et 1 pour
x ∈ 4, ∞ ). Dans ce contexte, lui imposer ce type de comportement semble convenir tout
à fait. D’ailleurs, lorsqu’on observe les valeurs de la variable similarites (sortie du réseau de
neurones), les valeurs sont souvent de ce type. La figure 15 illustre bien ce propos : trois ou
quatre des cinq valeurs de chaque colonne sont quasiment nulles alors qu’une ou deux sont
plus proches de 1. Ceci ne suffit pas à prouver que la sortie est bonne mais cela montre que
le réseau de neurones n’hésite la plupart du temps qu’entre deux catégories.
20

23. Figure 15 – Valeurs de sortie du réseau de neurones pour 6 échantillons en entrée
Ces trois arguments semblent bien converger vers une remarque de bon sens : le réseau
de neurones se comporte d’autant mieux qu’on lui apprend un comportement proche de celui
qui a fondé son émergence.
J’ai voulu mettre en place une méthode personnelle et en déterminer les performances.
Même si elles sont très basses, cela m’a permis de mener une investigation poussée sur l’in-
fluence des paramètres ; j’ai aussi pu réfléchir à la pertinence des deux modèles.
21

24. Réflexion
On voit qu’il est difficile de définir quel critère est le meilleur et le nombre de paramètres
à régler est grand. Les espaces mathématiques dont il faut trouver des valeurs optimales
sont immenses. Rien que dans notre réseau d’une seule couche intermédiaire de 20 neurones
agissant sur 14 entrées et ayant 5 neurones de sortie, la matrice des coefficients d’entrée -
couche intermédiaire ωih optimale est à chercher dans un espace vectoriel de dimension 300 et
la matrice ωho des coefficients pour passer de la couche intermédiaire aux neurones de sortie
est de dimension 105.
Trouver des optimums, ne serait-ce que locaux, dans ces espaces est un problème compli-
qué et la technique de descente de gradient peut rapidement échouer si elle converge vers un
minimum local non pertinent mais dont elle n’arrive pas à ressortir.
Enfin, comme souligné dans la section 2, la connaissance du domaine d’application des
algorithmes est absolument fondamentale. La qualité des données l’est tout autant et cela
peut permettre d’expliquer les résultats pas toujours convaincants de notre étude.
Les améliorations sont donc à rechercher à de nombreux niveaux : architecture du réseau
de neurones, qualité et type de données fournies en entrée, temps et taux d’apprentissage...
22

25. Bilan personnel
D’un point de vue personnel, j’ai trouvé difficile la recherche d’erreurs dans mon code. Ceci
est principalement dû au fait que la programmation informatique sur d’importants volumes
de données était nouvelle pour moi. Débugguer un code manipulant de faibles quantités de
données peut se faire en regardant toutes les sorties produites par un panel d’entrée choisi.
En revanche, lorsque j’ai dû comprendre la source d’un problème sur mon algorithme, j’ai
complètement changé ma manière de procéder. L’exemple le plus représentatif a été mon
utilisation intensive des outils statistiques tels que la moyenne et l’écart-type. Ce type de
méthode n’est évidemment pas utile lorsqu’on travaille sur des signaux déterministes, obéis-
sant à des équations comme j’ai pu en traiter en automatique par exemple.
Pour conclure, ce projet m’a offert la possibilité de découvrir un aspect de la programma-
tion qui m’était inconnu donc il a été très bénéfique. J’ai pu mieux saisir les problématiques
liées au traitement de données et à l’intelligence artificielle en général.
23

26. Annexes
Figure 16 – Résultat pour its = 1, nb_Train_Test = 180 et la simulation de l’aléatoire
24

27. Histogrammes de l’énergie des bandes de fréquence
Figure 17 – Classe 1 Figure 18 – Classe 2
25

28. Figure 19 – Classe 3 Figure 20 – Classe 4
26

29. Figure 21 – Classe 5
Figure 22 – Evolution du taux de réussite pour its = 40, nb_Train_Test = 300
27

30. Figure 23 – Evolution de l’erreur pour its = 40, nb_Train_Test = 300
28