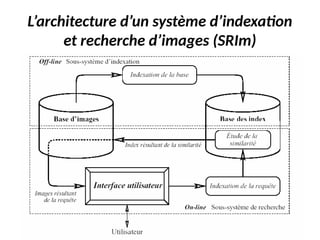
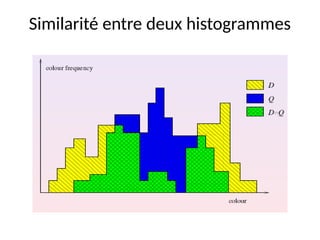
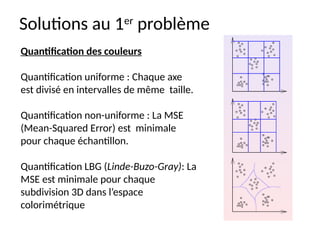
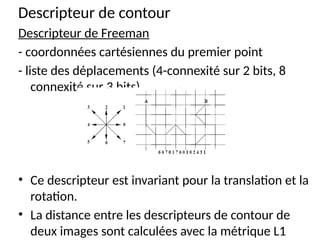
Le chapitre présente plusieurs approches pour la recherche et l'indexation d'images, allant des attributs de base aux techniques avancées utilisant la reconnaissance d'images et l'annotation manuelle. Il explore des descripteurs tels que les histogrammes de couleur, les descripteurs de forme et de texture, en abordant leurs avantages et limitations ainsi que des solutions aux problèmes rencontrés dans l'indexation. Finalement, il souligne l'importance de rendre ces techniques applicables aux images comprimées pour une meilleure efficacité de recherche.

1. CHAPITRE V
Recherche et Indexation
d’Image

2. Introduction
• Plusieurs approches pour la recherche et
l’indexation des images :
1ère
approche :
Les contenus d’une image sont organisés
autour d’attributs gérables par un SGBD
classique. Exemples de ces attributs : nom de
l’image, date de création, auteur, catégorie de
l’image, etc.

3. 2ème
approche :
Les objets de l’image sont reconnus par les
outils de reconnaissance d’image. Cette
approche n’est pas arrivée à maturité.
3ème
approche :
Elle repose sur l’annotation manuelle des
images. L’indexation et la recherche utilise les
techniques des SRIs textuelle (étudiées dans le
chapitre III).

4. 4ème
approche :
Elle utilise, pour rechercher et indexer les
images, les caractéristiques de bas niveau tel
que : la couleur, les textures et les formes
• La 2ème
et 4ème
approche sont appelées «
Recherche et indexation par le contenu »

5. L’architecture d’un système d’indexation
et recherche d’images (SRIm)

6. • Dans l’étape d’indexation, des caractéristiques
sont automatiquement extraites à partir de
l’image et stockées dans un vecteur
numérique appelé descripteur visuel.
• Dans l’étape de recherche, le système reçoit
une requête utilisateur et renvoi comme
résultat correspondant, une liste d’images
ordonnées en fonction de la similarité entre
leurs descripteurs visuels et la requête en
utilisant une mesure de distance.

7. Descripteurs de Couleur
• La recherche et l’indexation basée sur la
couleur est la plus utilisée.
• La recherche repose sur l’idée de retrouver les
images qui ont des couleurs d’apparence
similaires à l’image ou à la description de la
requête utilisateur.

8. L’histogramme :
• Chaque couleur primaire est discrétisé en m intervalles.
Ainsi, le nombre total des combinaisons de couleurs
discrètes n (appelé bin ) est égal à m3
.
• L’histogramme de l’image M peut être défini comme suit :
H (M) = (h1, h2, ..,hi,.., hn)
- H(M) est un vecteur
- hi représente le nombre de pixels de l'image M de
couleur bin i
Cet histogramme est le descripteur de l’image M, il est
stocké en tant qu’index de l'image M

9. Similarité entre deux histogrammes

10. Métriques de similarité :
• Plusieurs mesures de distance entre deux
histogrammes ont été proposées. Les plus simples
sont les métriques L1 et L2 (distance euclidienne).
• où il et hl sont le nombres de pixels ayant la
couleur du bin l.

11. Métriques de similarité :
• Intersection d’histogrammes :
• L’intersection d’histogrammes donne de
meilleurs résultats que les métriques L1 et L2.
• Les histogrammes sont faciles et rapides à
calculer, et robustes à la rotation et à la
translation.

12. Exemple d’histogrammes:
• Soient 3 images de 8x8 pixels. Les histogrammes
de ces 3 images sont :
H1 = (8, 8, 8, 8, 8, 8, 8, 8)
H2= (7, 7, 7, 7, 9, 9, 9, 9)
H3= (2, 2, 10, 10, 10, 10, 10, 10)
• Les distances entre ces trois images sont :
d(H1,H2) = 1 +1 +1 +1 +1 +1 +1 +1 = 8
d(H1,H3) = 6+6+2+2+2+2+2+2 = 24
d(H2,H3) = 5 +5 +3 +3 +3 +1 +1 +1 +1 = 23
• Les images 1 et 2 sont les plus similaires

13. Amélioration de la technique :
• L’utilisation d’histogrammes pour l'indexation et la recherche
d’images pose quatre problèmes.
- 1er
problème : ils sont de grandes tailles, donc il est difficile de
créer une indexation rapide et efficace en les utilisant tels qu'ils
sont.
- 2ème
problème : ils ne possèdent pas d’informations spatiales
sur les positions des couleurs.
- 3ème
problème : ils sont sensibles à de petits changements de
luminosité, ce qui est problématique pour comparer des images
similaires, mais acquises dans des conditions différentes.
- 4ème
problème : ils sont inutilisables pour la comparaison
partielle des images (objet particulier dans une image), puisque
calculés globalement sur toute l’image.

14. Solutions au 1er
problème
Quantification des couleurs
Quantification uniforme : Chaque axe
est divisé en intervalles de même taille.
Quantification non-uniforme : La MSE
(Mean-Squared Error) est minimale
pour chaque échantillon.
Quantification LBG (Linde-Buzo-Gray): La
MSE est minimale pour chaque
subdivision 3D dans l’espace
colorimétrique

15. Solutions au 3ème
problème
• Selon la technique de base, deux images semblables mais
sans couleurs communes ont une distance maximale.
• De nombreuses approches ont été proposées pour
résoudre ce problème.
• 1ère
approche: Elle prend compte des contributions des
couleurs d’apparence similaires (perceptually similar) dans
le calcul de similarité.
- La mesure de similarité utilisée par Niblack est la
suivante. Soient X l'histogramme de la requête et Y celui
d'une image dans la base de données. X e Y sont
normalisés.

16. • 2ème
approche : Elle utilise l’histogramme
cumulatif. L’histogramme cumulatif
• CH(M) = (ch1, ch2, . . ,chn) de l’image M est
définie en termes de l’histogramme de M H(M)
comme :
• Le calcul de distance utilise soit la métrique L1
soit la distance euclidienne. Cette approche
évite le calcul des distances entre les bins.

17. Solutions au 2ème
problème :
• Le deuxième problème est que l’histogramme de couleur de
base ne tient pas des relations spatiales entre les pixels
• Exemple : Deux images différentes qui ont le même
histogramme de couleur de base
• Pour remédier à ce problème, chaque image est segmentée
en un nombre fixe de régions et un histogramme est calculé
pour chaque région. Durant la recherche, les histogrammes
des régions correspondantes sont comparés.

18. • Un autre problème, c’est l'effet de masquage de l'arrière-
plan.
- Une image peut être composée d’arrière-plan
(backgraound) et d’avant-plan (foreground).
- L’arrière-plan contient généralement des couleurs
régulières et un grand nombre de pixels.
- Deux objets différents pris dans un même arrière-plan
sont considérés comme similaires.
- Pour résoudre le problème ci-dessus, Lu et Phillips ont
proposé d’extraire deux histogrammes distincts, l’un
pour l’arrière-plan et l’autre pour l’avant-plan. La
recherche peut alors s’intéresser soit à l’arrière-plan, soit
aux objets de l’avant-plan, soit à l’arrière et l’avant-plan en
même temps.

19. Descripteurs de Forme
• La forme est un descripteur très important dans l'indexation des
images. La forme désigne l’aspect général d’un objet, son contour.
• Il s’agit de reconnaître une forme donnée dans une image ou une
région d’une image segmentée.
• Une bonne représentation d’une forme doit satisfaire les
propriétés suivantes :
- Chaque forme doit avoir une unique représentation invariante
pour la translation, la rotation et le changement d’échelle.
- Des formes similaires doivent avoir des représentations similaires
de façon à ce que la recherche soit basée sur les distances entre
les représentations des formes.
• La 1ère
propriété permet de reconnaitre des objets de différentes
tailles, différentes positions et orientations.

20. • Axe principal : la ligne droite qui lie les deux
points les plus éloignés dans une forme.
• Axe secondaire : Une ligne droite
perpendiculaire à l’axe principale. Le rectangle
formé de l’axe principal et secondaire contient
la forme. Ce rectangle s’appelle rectangle de
base.
• Excentricité d’une forme est le rapport entre
l’axe principal et l’axe secondaire.

21. Exemples de formes

22. Descripteur de contour
Descripteur de Freeman
- coordonnées cartésiennes du premier point
- liste des déplacements (4-connexité sur 2 bits, 8
connexité sur 3 bits)
• Ce descripteur est invariant pour la translation et la
rotation.
• La distance entre les descripteurs de contour de
deux images sont calculées avec la métrique L1

23. Exemple :

24. Descripteur de forme basé sur les régions
• Soit une forme, on la divise en utilisant une grille et les
caractéristiques de chaque bloc sont calculées pour chaque
case de cette grille.
Exemple : La forme suivante peut être représentée par cette
séquence de bit :
11100000 11111000 01111110 01111111
Cette représentation est facile à obtenir et invariante à la
translation mais non à la rotation et au changement
d’échelle.

25. Description local d’une image en utilisant, par
exemple, une grille de 8 cases (régions).
Pour chaque case est appliqué une extraction des
contours. On obtient une forme pour chaque région.
Un descripteur de forme est calculé pour chaque
région.

26. Normalisation à la rotation
• Il s’agit de mettre la forme dans un rectangle de
base. L’axe principal relie les deux points les plus
éloignés de la forme. Dans ce cas il y a deux
possibilités :
• Deux représentations
sont nécessaires pour
cette forme. Mais une
seule est utilisée comme
descripteur. L’une peut
être retrouvée de l’autre

27. Normalisation au changement d’échelle
• Toutes les formes ont la même longueur de l’axe principal.
Représentation unique des formes
Après les normalisations et le choix d’une grille, on obtient
une unique représentation pour chaque forme.
Mesure de similarité
Deux formes sont à comparer, en comparant bit-à-bit leurs
représentations respectives.
La distance entre elles est égales au nombre de bits
différents.
Exemple : Soient deux formes A et B, ayant respectivement
(11111111 11100000) et (111111111111100) comme
représentations.
d(A,B)=3

28. Descripteurs de texture :
Quelques définitions :
-«La texture et un arrangement
spatial des pixels que l’intensité ou
la couleur seules ne suffisent pas à
décrire. Elle consiste en un
placement structuré d’éléments
mais peuvent aussi n’avoir aucun
élément répétitif »
-« La texture est présentée comme
une structure disposant de certaines
propriétés spatiales homogènes et
invariantes par translation »

29. • La notion de texture est liée à trois concepts
principaux:
1- un certain ordre local qui se répète dans une région de
taille assez grande,
2- cet ordre est défini par un arrangement structuré de
ses constituants élémentaires,
3- ces constituants élémentaires représentent des entités
uniformes qui se caractérisent par des dimensions
semblables dans toute la région considérée.
• Il existe un grand nombre de textures. On peut les
séparer en deux classes: les textures structurées
(macrotextures) et les textures aléatoires
(microtextures).

30. Les matrices de co-occurrences :
• En 1973, Haralick a proposé une méthode en se
basant sur les matrices de co-occurrences de niveaux
de gris.
• La texture d’une image peut être interprétée comme
la régularité d’apparition de couples de niveaux de gris
selon une distance donnée dans l’image.
• La matrice de co-occurrences contient les fréquences
spatiales relatives d’apparition des niveaux de gris
selon quatre directions (ө= 0, ө=π/4, ө=π/2, ө =3π/4).
• La matrice de co-occurrences Pd, ө (i, j) est carrée et de
dimension Δ*Δ, où Δ est le nombre de niveaux de gris
présents dans I.

31. • On définit la matrice de co-occurrences Pd, ө par :
Pd, ө=( Pd, ө(i, j))
où Pd, ө(i, j) représente le nombre de fois où un
couple de points séparés par la distance d dans l la
direction ө a présenté les niveaux de gris Ii et Ij

32. Exemple : Soit l'image suivante comportant D =4
niveau de gris {0, 1, 2, 3}:
- P1,0° (i, j)={(x1,y1), (x2, y2) I / y
∈ 1 =y2 , |x2 -x1|=d,
I(x1,y1)=i et I (x2,y2)=j}
-Les matrices P1,0° et P1,90° sont donc de
dimension 4 et valent

33. Attributs texturaux :
• Afin d'estimer la similarité entre les matrices de co-
occurrences, Haralick a proposé 14 caractéristiques
statistiques extraites à partir de cette matrice.
• Les quatre caractéristiques les plus utilisées sont :
- L’homogénéité h :
- L’entropie e :
- Le contraste c :
:

34. - Moment des différences inverses m :
• Si l’on n’utilise que ces quatre attributs
texturaux, le descripteur de texture de Haralick
sera le vecteur (h, e, c, m)

35. • Pour des images qui présentent moins de variance
l’une à l’autre, ces descripteurs ne sont pas suffisant,
notamment la reconnaissance de visages et la
reconnaissance d’empreintes digitales. D’autres
descripteurs (descripteurs spécifiques, biométriques)
sont utilisés
• Les techniques d’indexation et de recherche d’image
présentées jusqu’à maintenant permettent l’extraction
de descripteurs à partir d’images non compactées.
Comme la plupart des images sont stockées dans des
formes compactées, il serait pratique d’extraire ces
descripteurs directement à partir d’images
compactées.
Conclusion