La thèse présente une recherche sur la détection multivariée des épisodes d'apnée-bradycardie chez les prématurés en utilisant des modèles semi-markoviens cachés. Réalisée par Miguel Altuve à l'université de Rennes 1 et à la Universidad Simón Bolívar, elle a été soutenue le 8 juillet 2011 devant un jury d'experts. Le document aborde des sujets allant du contexte clinique aux méthodologies de détection, en passant par une analyse approfondie des signaux ECG.














![Table des figures
1.1 Image d’un prématuré. On peut y voir certains dispositifs de mesure (Reportés
sur la figure). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
1.2 Système de monitoring utilisé dans l’USIN de Rennes. . . . . . . . . . . . . 13
1.3 Cycle de surveillance d’un prématuré dans une USIN . . . . . . . . . . . . . 14
1.4 Structure anatomique du cœur. Image d’après [Guyton and Hall, 1956]. . . 16
1.5 Potentiel d’action des cellules cardiaques ventriculaires. . . . . . . . . . . . . 17
1.6 Système spécialisé de conduction du cœur. Image d’après [Guyton and Hall,
1956]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18
1.7 Ondes, intervalles et segments dans l’ECG. . . . . . . . . . . . . . . . . . . 20
1.8 Exemples des ECG. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
2.1 Utilisation d’un seuil d’amplitude fixe pour détecter les bradycardies à partir
des séries RR. Dans cet exemple, la détection se fait lorsque RR(k) ≥ 600
ms, où k est l’indice temporel. . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.2 Utilisation d’un seuil d’amplitude et durée fixes pour détecter les bradycardies
à partir des séries RR. Dans cet exemple, la détection est réalisée lorsque
RR(k) ≥ 600 ms pendant 4 secondes, où k est l’indice temporel. . . . . . . . 32
2.3 Utilisation d’un seuil relatif pour détecter les bradycardies à partir des séries
RR. Dans cet exemple, la détection est réalisée lorsque RR(k) ≥ 1, 33RRbase
pendant 4 s, où k est l’indice temporel et RRbase est la valeur moyenne de
la série RR calculée dans une fenêtre glissante de 20 secondes qui précède
l’intervalle RR actuel. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
2.4 Dispositifs utilisés dans le système INTEM. . . . . . . . . . . . . . . . . . . 36
2.5 Étapes du processus de détection des apnées-bradycardies proposées dans
cette thèse. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
2.6 Étape d’extraction des caractéristiques de la démarche proposée. . . . . . . 39
2.7 Étape de prise de décision de la démarche proposée. . . . . . . . . . . . . . 40
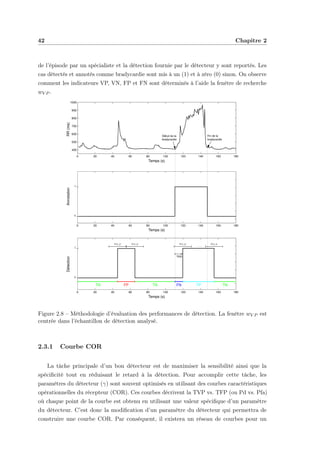
2.8 Méthodologie d’évaluation des performances de détection. La fenêtre wV P
est centrée dans l’échantillon de détection analysé. . . . . . . . . . . . . . . 42
2.9 Exemples de courbes COR. Le cercle représente le point de détection parfaite,
les étoiles représentent une détection avec une TFP = 0, 05 (5 %) et les
carrés correspondent à la distance la plus courte au point (0,1). . . . . . . . 43
3.1 Étapes de la segmentation du signal ECG . . . . . . . . . . . . . . . . . . . 51
3.2 Représentation en bloc du processus de détection des battements. . . . . . . 53
ix](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-15-320.jpg)
![x Table des figures
3.3 Banc de filtres de la décomposition en ondelettes (sans décimation). G(z) et
H(z) sont respectivement les filtres passe-haute et passe-bas. Wk
2 x[n] sont
les sorties des filtres aux échelles 2k (k = 1, 2, . . . , 5) pour le battement x[n]. 56
3.4 Indicateurs à repérer pour l’algorithme de segmentation. . . . . . . . . . . . 58
3.5 Le problème d’optimisation. . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
3.6 Optimisation par application des AE de manière séquentielle. . . . . . . . . 60
3.7 Méthodologie d’optimisation des paramètres des méthodes. Les annotations
et les détections dépendent de la méthode à optimiser. La méthode est le
détecteur des battements dans un premier essai et la segmentation du QRS
après. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
3.8 Construction des différentes bases de données utilisées pour effectuer les
processus d’adaptation et la phase d’évaluation. . . . . . . . . . . . . . . . . 63
3.9 Amplitude de l’onde R (Ramp) et durée du complexe QRS (QRSd) pour un
battement synthétique. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
3.10 De haut en bas respectivement, intervalles d’analyses de séries temporelles
RR, QRSd et Ramp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
3.11 Boîtes à moustaches de la moyenne des séries par intervalle et de la différence
de la moyenne des séries entre l’intervalle T1 et les autres intervalles, pour
les séries temporelles : (a) RR, (b) Ramp et (c) QRSd. . . . . . . . . . . . . 72
3.12 Segment typique présentant de petites différences entre l’intervalle T1 et les
autres intervalles. En (a)-(c), les lignes verticales en pointillé délimitent les
intervalles, alors que dans (d), les lignes verticales en pointillé représentent
la segmentation automatique du QRS (QRSon, pic de l’onde R et QRSoff). 73
3.13 Segment typique présentant de différences significatives entre l’intervalle T1
et les autres intervalles. En (a)-(c), les lignes verticales en pointillé délimitent
les intervalles, alors que dans (d), les lignes verticales en pointillé représentent
la segmentation automatique du QRS (QRSon, pic de l’onde R et QRSoff). 74
4.1 Exemples des séries temporelles extraites de l’ECG sur trois instants différents.
Dans (a), (b) et (c) on observe les séries RR, RAMP et QRSd respectivement
dans une période de repos. Dans (d) la série RR pressente un ralentissement
du cœur qui produit des variations dans les séries RAMP (e) et QRSd (f).
Dans (g), (h) et (i) on observe les séries RR, RAMP et QRSd respectivement
en présence d’un épisode d’apnée-bradycardie dont le cercle correspond à la
détection effectuée par la méthode classique (RR ≥ 600 ms pendant 4 s) et
le losange représente le début de la bradycardie. . . . . . . . . . . . . . . . . 84
4.2 Étapes du processus de fouille de données et leur correspondance dans cette
thèse. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
4.3 Structure de base d’un modèle de Markov caché. . . . . . . . . . . . . . . . 88
4.4 Structure de base d’un modèle de semi-Markov caché. . . . . . . . . . . . . 89
4.5 Principe de fonctionnement d’un modèle Markovien caché. . . . . . . . . . . 92
4.6 Principe de fonctionnement d’un modèle semi-Markovien caché. . . . . . . . 92
4.7 Procédure utilisée pour l’apprentissage des MSMC à partir d’une base de
données, d’après DUMONT [Dumont, 2008]. . . . . . . . . . . . . . . . . . . 97](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-16-320.jpg)


![Liste des tableaux
1.1 Valeurs normales de l’ECG pédiatrique par âge. . . . . . . . . . . . . . . . . 23
3.1 Paramètres de la méthode de détection des battements à optimiser. . . . . . 54
3.2 Paramètres de la méthode de segmentation des QRS à optimiser. . . . . . . 58
3.3 Valeurs des paramètres de la méthode de détection des battements avant
(pour les adultes) et après (pour les nouveaux-nés prématurés) le processus
d’optimisation. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
3.4 Performances du détecteur des battements avant et après le processus d’opti-
misation. Avant : paramètres réglés pour l’ECG d’adulte, Après : paramètres
réglés pour l’ECG du prématuré. . . . . . . . . . . . . . . . . . . . . . . . . 65
3.5 Valeurs optimales des paramètres de la méthode de segmentation des QRS. 66
3.6 Exemple des fenêtres de recherche et des seuils utilisés dans la méthode de
segmentation des QRS. Les paramètres de notre approche ont été déterminés
en utilisant les paramètres optimaux (Tableau 3.5) pour un intervalle RR
typique de 400 ms. Les autres approches correspondent aux paramètres
utilisés par [Dumont et al., 2010] et [Smrdel and Jager, 2004]. . . . . . . . . 66
3.7 Performances de la segmentation des QRS, avant et après le processus
d’optimisation. Avant : paramètres réglés pour l’ECG d’adulte, Après :
paramètres réglés pour l’ECG du prématuré. . . . . . . . . . . . . . . . . . . 67
3.8 wµ et wσ des séries temporelles RR, Ramp et QRSd, pour tous les intervalles
analysés. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
3.9 µDA et σDA entre l’intervalle T1 et les autres intervalles, pour les séries
temporelles RR, Ramp et QRSd. . . . . . . . . . . . . . . . . . . . . . . . . 71
3.10 tests d’hypothèse de Mann–Whitney U pour la moyenne des séries RR, Ramp
et QRSd. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
4.1 Résumé des principaux paramètres et caractéristiques des MMC et MSMC. 92
4.2 Tableau de contingence. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103
5.1 Estimation du nombre d’états par MSMC pour différentes valeurs de RSB,
pour modéliser la dynamique de la variable r. . . . . . . . . . . . . . . . . . 125
5.2 Tableau de contingence en utilisant les MSMC pour classer trois dynamiques
observées dans la variable r à 5 dB. Chaque élément du tableau représente
la somme des éléments correspondants sur les 10 répétitions. . . . . . . . . . 125
xiii](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-19-320.jpg)











![Introduction
Ce travail de thèse a été élaboré dans le cadre d’une co-tutelle entre deux laboratoires :
– Le Groupe de Bioingénierie et Biophysique Appliquée (GBBA) de l’Université Simón
Bolívar. Les activités de recherche de ce laboratoire sont centrées sur l’instrumentation
biomédicale, le traitement des signaux biomédicaux, la visualisation et le traitement
d’images médicales.
– Le Laboratoire de Traitement du Signal et de l’Image (LTSI) de l’Université de Rennes
1, composé de quatre équipes. L’équipe SEPIA (Surveillance Explication et Prévention
des Ischémies et des Arythmies) est celle qui a encadré cette thèse. L’activité de cette
équipe est basée sur une approche multidisciplinaire qui combine le traitement du
signal, la physiologie et la modélisation intégrative appliquée à l’étude du système
cardiovasculaire.
Le monitoring des signaux physiologiques est le centre de la coopération entre ces deux
laboratoires et a été abordé dans le cadre du projet KISS (Knowledge-based Interactive Signal
monitoring System) [Siregar et al., 1989], où des problèmes d’acquisition et de traitement des
signaux [Passariello, 1991; Hernández et al., 1999], de caractérisation d’arythmies [Schleich,
1993; Thoraval, 1995], d’extraction et de représentation de connaissances profondes [Siregar
et al., 1995; Hernández, 2000], d’architecture des systèmes liés au concept de monitoring
intelligent dans les Unités de Soins Intensifs Coronarien (USIC) [Mora, 1991; Mabo et al.,
1991], et plus récemment d’analyse de la dynamique des séries temporelles par fouille de
données [Dumont, 2008] ont aussi été traités.
Ce travail représente le prolongement de ces contributions. Son objectif principal est
de prédire la survenue des apnée-bradycardies chez le nouveau-né prématuré en utilisant
une méthodologie cherchant à exploiter la dynamique des séries temporelles multivariées,
extraites de l’électrocardiogramme.
La naissance prématurée de l’enfant arrive avant 37 semaines de gestation. Cette
problématique est en augmentation constante dans la plupart des pays [Martin et al., 2009;
Zeitlin, 2009]. Elle peut entraîner de nombreuses complications aux enfants en raison des
dysfonctionnements des organes, qui ne sont pas complètement développés et aptes pour la
vie extra-utérine. L’un des problèmes le plus fréquent est l’épisode d’apnée-bradycardie,
1](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-31-320.jpg)
![2 Introduction
dont la répétition influence de manière négative le développement de l’enfant [Pichler et al.,
2003; Urlesberger et al., 1999; Janvier et al., 2004]. Par conséquent, les enfants prématurés
sont surveillés en continu par un système de monitoring installé dans les unités des soins
intensifs néonatals (USIN). Ce système permet de déterminer l’évolution de l’état de santé
de l’enfant et, depuis sa mise en marche, la qualité, l’espérance de vie et le pronostic de vie
des prématurés ont été considérablement améliorés et la mortalité a été réduite.
En effet, les avancées technologiques en électronique, informatique et télécommunications
ont conduit à l’élaboration de systèmes multivoies de monitoring néonatal de plus en plus
performants. La plupart sont constitués de modules d’acquisition des données et d’une
station centrale pour visualiser les signaux acquis en temps réel. Des alarmes sont produites
lorsqu’une situation à risque est détectée, comme par exemple, une apnée-bradycardie. L’un
des principaux signaux exploités dans ces systèmes est l’électrocardiogramme (ECG). L’ECG
est un outil diagnostique qui mesure et enregistre l’activité électrique du cœur. Il reste
aujourd’hui comme la technique la plus largement utilisée pour l’exploration de l’activité
électrique cardiaque, puisqu’il s’agit d’une technique non invasive, simple, économique et
sûre.
Même si l’analyse de l’ECG a évolué au fil des années et que le développement des
méthodes de traitement des signaux électrocardiographiques a amélioré la caractérisation
et le diagnostic des maladies cardiovasculaires, l’ensemble des informations fournies par
l’ECG ne sont pas encore totalement exploitées dans les processus de décision, notamment
en monitoring en USIN. Deux points particuliers sont à nos yeux sous exploités dans les
stations de monitoring néonatal : i) l’exploration multivariée des ondes et intervalles de
l’ECG, afin de détecter précocement les épisodes d’apnée-bradycardie et ii) les méthodes
d’analyse restent des méthodes de détection et sont très peu anticipatives (prédiction de
l’évènement).
Dans ce travail, une nouvelle méthodologie pour répondre aux deux problématiques
précédentes est proposée. Elle est basée sur l’exploitation de la dynamique des séries
temporelles multivariées extraites de l’ECG. Cette dynamique est analysée par l’usage des
modèles semi-Markovien cachés (MSMC). Les MSMC sont des modèles stochastiques à
nombre d’états M fini et dont l’émission d’observations (bi) de l’état i et la durée (pi)
de l’état i sont représentées par une densité de probabilité. Un MSMC est similaire à un
modèle de Markov caché (MMC) classique, mais la principale différence est que le processus
non observé est semi-Markovien, dans le sens où un changement dans un état futur dépend
à la fois de l’état caché actuel et du temps passé sur cet état.
Les MMC et MSMC ont été appliqués dans le domaine du traitement du signal pendant
plus de deux décennies, en particulier dans le contexte de la reconnaissance automatique
de la parole. Toutefois, ils constituent également des outils souples, flexibles et robustes
pour le traitement des séries temporelles univariées et multivariées, y compris dans les cas](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-32-320.jpg)





![8 Chapitre 1
(plus de 500000) des bébés nés aux États-Unis chaque année sont prématurés [Martin et al.,
2009] et près de 6 % (près de 55000) des naissances sont prématurées en France.
Suivant le terme de la naissance, quatre niveaux de prématurité existent actuellement
dans le contexte clinique :
– la faible prématurité, caractérisée par une naissance entre 33 et 37 semaines
d’aménorrhée (SA) ;
– la grande prématurité, entre 28 et 32 SA ;
– la très grande prématurité, de 25 à 27 SA ;
– l’extrême prématurité, de moins de 24 SA.
Les facteurs les plus déterminants dans la survie du nouveau-né prématuré sont sa
maturité, exprimée par l’âge gestationnel et son poids de naissance. L’enfant né à 35 semaines
reste, dans la majorité des cas, auprès de sa mère en maternité, alors que la survie de
l’enfant de 24 semaines reste encore et toujours très difficile [Bloch et al., 2003].
La prématurité est la principale cause de morbidité et de mortalité néonatale. Elle est
responsable d’environ 35 % des décès néonataux aux États-Unis [Mathews and MacDorman,
2008]. Le risque de décès est accru dans la première année de vie et la plupart se produisent
dans le premier mois de vie. Près de 30 % des prématurés nés à 23 SA survivent ; on passe à
50 % pour des prématurés nés à 24 SA, à 75 % pour des prématurés nés à 25 SA, et à plus
de 90 % pour des prématurés nés entre 27 et 28 SA. Il importe de souligner que ce taux de
mortalité a diminué depuis la mise en place d’unités de soins intensifs néonatals (USIN)
au début des années 1970. Ainsi, les avancées en médecine et en soins des prématurés ont
amélioré leurs chances de survie en mettant le seuil de viabilité à 22 SA mais sans réduire la
prédominance des naissances prématurées. En effet, le nombre d’enfants nés prématurément
est en augmentation en France et dans le monde. Par exemple, en Ile-de-France, une étude
récente a montré que le nombre de naissances prématurées a augmenté de 5,7 % à 6,3 %
entre 2002 et 2007 [Zeitlin, 2009].
Les causes de l’augmentation des naissances prématurées ne sont pas toutes connues,
même si l’on sait qu’environ 60 % des naissances prématurées sont provoqués pour des
raisons médicales et les cas restant sont spontanés. Un âge plus tardif (plus de 35 ans) ou
précoce (moins de 18 ans) et les grossesses multiples conduisent souvent à des accouchements
prématurés. Des problèmes obstétriques tels que le col ouvert ou le décollement du placenta ;
une maladie de la mère comme la listériose, le diabète ou l’hypertension, et un milieu social
défavorisé contribuent également aux naissances prématurées [Bloch et al., 2003; Rosenberg
et al., 2005; Goldenberg et al., 2008].
Plus l’enfant est prématuré, plus graves et fréquents sont les problèmes d’adaptation et
son traitement est d’autant plus complexe. Les problèmes couramment rencontrés sont :
– Respiratoires : syndrome de détresse respiratoire, maladie des membranes hyalines
et dysplasie bronchopulmonaire,](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-38-320.jpg)
![1.1. Le nouveau-né prématuré 9
– Neurologiques : apnée du prématuré, rétinopathie, infirmité motrice cérébrale et
hémorragie cérébrale intraventriculaire,
– Cardiovasculaires : persistance du canal artériel,
– Infectieux : septicémie, pneumonie et infection urinaire,
– Hématologiques : anémie, ictère et thrombopénie,
– Métaboliques : hypoglycémie, hypocalcémie et hypothermie,
– Digestifs : entérocolite nécrosante et résidus gastriques.
L’une des complications les plus importantes est l’apnée du prématuré. Celle-ci est
un thème d’investigation en vigueur et de nombreuses recherches ont été effectuées ces
dernières années pour essayer d’expliquer les causes, les conséquences et identifier les
meilleurs traitements [Poets et al., 1993; Perlman, 2001; Janvier et al., 2004; Finer et al.,
2006; Naulaers et al., 2007; Abu-Shaweesh and Martin, 2008; Poets, 2010; Zhao et al., 2011].
S’y ajoutent des recherches technologiques en vue de détecter efficacement les épisodes
d’apnées, tout en réduisant le nombre d’appareils mis au chevet du bébé [Pichardo et al.,
2003; Pravisani et al., 2003; Cruz et al., 2006; Beuchée et al., 2007; Portet et al., 2007; Belal
et al., 2011].
Certains problèmes liés à une naissance prématurée compromettent le pronostic à court
terme et d’autres pèsent lourdement sur le pronostic à moyen et long terme comme le
développement physique, psychologique ou comportemental. Les conséquences à long terme
de la prématurité ne deviennent évidentes que lorsque l’enfant est d’âge scolaire : à l’âge de
5 ans, 12 % des grands prématurés présentent des déficiences intellectuelles (de modérées à
sévères), 36 % présentent des troubles moteurs, sensoriels ou cognitifs (5 % sévères, 9 %
modérés et 25 % mineurs) et 34 % ont besoin des soins spéciaux [Larroque et al., 2008].
À l’âge adulte, les risques de déficience médicale et sociale semblent augmenter avec la
diminution de l’âge gestationnel à la naissance et, en absence de problèmes médicaux,
le niveau scolaire atteint, les revenus et le succès familial diminuent avec le degré de
prématurité [Moster et al., 2008].
Les prématurés sont pris en charge dans une USIN où ils sont maintenus dans une
couveuse ou incubateur, qui reproduit les conditions de développement fœtal en contrôlant
sa température, l’hygrométrie et en limitant l’exposition du nouveau-né à l’environnement
extérieur (virus, bactéries, . . . ). Plus la naissance est prématurée, plus longue est la
durée d’hospitalisation [Naulaers et al., 2007]. Un monitoring continu est effectué sur des
paramètres vitaux comme la température, la respiration, la fonction cardiaque, l’oxygénation
et l’activité cérébrale. Les thérapies peuvent inclure la nutrition par cathéters intraveineux,
la supplémentation d’oxygène, la ventilation mécanique et les médicaments. Cependant, les
USIN impliquent des coûts de santé importants et l’exposition du nouveau-né à différentes
sources de stress environnemental (alarmes des moniteurs dans l’USIN, bruit ambiant, . . . )
[Perlman, 2001]. De plus, diverses études montrent l’importance de l’intégration dans le
milieu familial pour le développement du nouveau-né. Généralement sont autorisés à quitter](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-39-320.jpg)
![10 Chapitre 1
l’hôpital les prématurés qui présentent une bonne thermorégulation, une alimentation orale
parfaite et qui ne présentent pas d’apnée-bradycardies dans une période de 3 à 7 jours [Baird,
2004]. La persistance d’événements cardio-respiratoires peuvent retarder la sortie de l’enfant
de l’hôpital [Eichenwald et al., 1997]. Dans ce cas, un monitoring cardio-respiratoire à
domicile, jusqu’à 43-44 semaines d’âge postnatal, peut offrir une alternative à un séjour
prolongé à l’hôpital [Darnall et al., 1997].
1.2 Les apnées-bradycardies du nouveau-né prématuré
L’apnée du prématuré se définit par une interruption prolongée du flux ventilatoire
pendant plus de 15 à 20 secondes et témoigne d’une instabilité de la régulation du rythme
respiratoire. Elle entraîne alors un ralentissement du rythme cardiaque (bradycardie), une
cyanose, témoin de l’hypoxémie, hypoxie et acidose [Bloch et al., 2003]. La bradycardie est
définie par une chute de la fréquence cardiaque (FC), au dessous de 100 battements par
minute (bpm) ou d’au moins 33 % par rapport à une valeur moyenne, pendant 4 secondes
ou plus [Poets et al., 1993]. La bradycardie se produit généralement dans les sept premières
secondes de l’apnée et atteint la FC minimale autour de 13 secondes [Di Fiore et al., 2001;
Dorostkar et al., 2005]. Les apnées doivent être différenciées de la respiration périodique
du prématuré, où des bouffées ventilatoires, d’amplitude progressivement croissante puis
décroissante, alternent avec de brèves interruptions qui ne présentent aucun caractère
pathologique [Laugel et al., 2000].
La majorité des grands prématurés ont des apnées-bradycardies durant les premières
semaines. Cependant, elles disparaissent progressivement au cours de la maturation et ont
généralement disparu après 40 SA. D’après HOFSTETTER et al. [Hofstetter et al., 2008],
98 % des prématurés de 25 à 28 SA présentent des épisodes d’apnée et 90 % des épisodes
de bradycardie ; à 36 SA, 67 % présentent toujours des épisodes d’apnée et seulement 17 %
ont des épisodes de bradycardie. Ces constats laissent suggérer par certains auteurs que le
système cardiovasculaire mûrit plus rapidement que le système respiratoire chez les très
grands prématurés [Hofstetter et al., 2008]. De plus, 83 % des épisodes de bradycardies
sont associés aux épisodes d’apnées [Poets et al., 1993]. Concernant la durée des apnées,
73 % ont une durée de 10-14 secondes, 17 % de 15-19 secondes et 10 % supérieure à
20 secondes [Hofstetter et al., 2008].
L’apnée peut être du type symptomatique si elle provient d’une pathologie (infection,
anémie, hypoxie, hypoglycémie, hypothermie, etc.) ou idiopathique si elle est uniquement
due à l’immaturité des mécanismes de contrôle de la respiration. En outre, basées sur la
présence ou l’absence de mouvements respiratoires, l’apnée est classée dans trois catégories :
– Centrale : se produisant en l’absence des mouvements respiratoires ;
– Obstructive : se produisant en présence des mouvements respiratoires ;](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-40-320.jpg)
![1.2. Les apnées-bradycardies du nouveau-né prématuré 11
– Mixte : contenant des éléments d’apnée centrale et obstructive.
L’observation clinique de l’enfant ou le monitoring cardio-respiratoire continu permettent
de détecter uniquement l’apnée centrale, contrairement à l’apnée obstructive, où seule la
détection des phénomènes associés, comme la bradycardie et l’hypoxémie, permet de
soupçonner sa survenue. Les apnées les plus longues et les plus fréquentes sont souvent
mixtes (de 50 à 70 % des cas), les apnées courtes (moins de dix secondes) sont surtout de
type central (de 10 à 25 % des cas) et les obstructives sont peu fréquentes (de 12 à 20 % des
cas) [Laugel et al., 2000]. Les apnées courtes sont considérées comme non pathologiques car
elles ne s’accompagnent habituellement pas de bradycardies ni d’hypoxémie. En revanche,
celles qui dépassent les 20 secondes sont considérées comme graves car elles sont suivies
par une chute de la saturation, puis de la bradycardie, résultant de l’hypoxémie et dont la
profondeur est proportionnelle à la durée de l’apnée.
Les apnées-bradycardies du prématuré sont des phénomènes qui reflètent une forme
d’inadaptation à la vie extra-utérine. Elles sont liées à l’immaturité physiologique de
plusieurs éléments du système respiratoire : centres neuronaux, chémorécepteurs centraux
et périphériques, afférences et efférénces réflexes. Elles peuvent aussi être provoquées ou
aggravées par l’association d’une infection, hypoxie ou pathologie intracrânienne. D’ailleurs,
elles sont plus fréquentes lorsque la température de l’environnement est plus élevée [Tourneux
et al., 2008] et lors de sommeils agités (majoritaire chez le prématuré).
Même s’il n’existe pas de risque accru de mort subite du nourrisson par la persistance
des apnées-bradycardies [Abu-Shaweesh and Martin, 2008], les apnées longues suivies
des bradycardies profondes (inférieure à 80 bpm) produisent une chute du débit sanguin
cérébrale, une baisse de la pression artérielle, une diminution de l’oxygénation cérébrale
et une dépression de l’amplitude de l’électroencéphalogramme (EEG) [Pichler et al., 2003;
Urlesberger et al., 1999]. De plus, elles entraînent des modifications de l’oxygénation
tissulaire et de l’équilibre hémodynamique. La répétition de ces épisodes est associée à un
moins bon devenir neuromoteur à trois ans [Janvier et al., 2004].
Les apnées-bradycardies demeurent un problème clinique préoccupant en néonatalogie,
qui impose de nombreux défis dans les stratégies thérapeutiques à suivre. Les thérapies
appropriées sont données en raison des mécanismes qui provoquent l’apparition de ces
épisodes. Une stimulation cutanée permet, dans la plupart des cas, la rupture des épisodes
d’apnée-bradycardie. Des médicaments (comme la théophylline ou la caféine), l’augmentation
d’oxygène à l’aide d’une canule nasale, la respiration assistée par pression positive continue
(CPAP, Continuous Positive Airway Pressure) et la ventilation mécanique peuvent aussi
être employés pour traiter l’apnée-bradycardie, selon sa sévérité. La répétition d’épisodes
d’apnée-bradycardie et les risques associés justifient le monitoring continu des fréquences
respiratoires et cardiaques et le traitement pharmacologique. Cette surveillance cardio-
respiratoire continue permet également d’évaluer l’efficacité de traitements mis en place et
de détecter une éventuelle récidive des apnées-bradycardies après l’arrêt des traitements.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-41-320.jpg)
![12 Chapitre 1
1.3 Les systèmes de monitoring automatisés
La fragilité initiale des nouveaux-nés prématurés réclame, en plus d’une attention
médicale et l’emploi de techniques adéquates pour maintenir et réguler leurs fonctions de
bases, une surveillance continue dans une USIN pendant plusieurs semaines. Peu gênant
pour l’enfant, les dispositifs automatisés de surveillance permettent au personnel soignant,
d’un seul regard sur un écran, de vérifier les principales fonctions vitales du prématuré
(température, fréquences cardiaque et respiratoire, pression artérielle, saturation en oxygène
du sang, . . . ) et de prendre rapidement les mesures adaptées à tout instant : stimulation
manuelle pour arrêter une apnée-bradycardie, oxygénation, ventilation au masque, voire
intubation.
Le système de monitoring fait partie de la routine dans les USIN et a contribué
énormément à ce qu’un prématuré puisse survivre à un âge gestationnel de plus en plus
jeune. Même si ces dispositifs ont progressé énormément en qualité et en fiabilité au cours
de ces dernières années et représentent un progrès considérable en matière de sécurité, ils
ne remplacent pas l’observation directe sur l’enfant. En effet, ces dispositifs ne sont pas
dotés « d’intelligence » (interprétation d’une mesure parasitée qui déclenche une alarme) et
présentent des limites (l’alarme ne se déclenchera pas en apnée obstructive si le nourrisson
continue de faire l’effort respiratoire). Pour les alarmes, les moniteurs actuellement utilisables
pour la surveillance des nouveaux-nés dans les USIN utilisent uniquement des seuils fixes
basés sur des a priori, alors que des seuils adaptatifs et relatifs aux variables analysées ont
montré des améliorations sur la détection [Cruz et al., 2006; Beuchée et al., 2007].
1.3.1 L’équipement dans l’USIN
Dans une USIN, l’enfant est raccordé à un moniteur qui comprend plusieurs modules
d’acquisition des données physiologiques spécifiques et indépendants (i.e. température,
électrocardiogramme, respiration, pressions artérielle, saturation d’oxygène (SpO2), acidité
gastrique (pH), etc.). Ainsi, le système de monitoring est en général composé de différents
éléments (voir figure 1.1 et figure 1.2) :
– Un thermomètre qui mesure la température corporelle de l’enfant afin de la maintenir
autour de 36,8 oC. Ce thermomètre est appliqué sur la peau du nouveau-né et est
relié à un thermostat qui produit de l’air chaud dans la couveuse ;
– Trois petites électrodes adhésives collées sur le thorax, abdomen, bras ou jambe qui
mesurent la FC et la fréquence respiratoire. 100 et 180 bpm et 25 et 80 cycles par
minutes correspondent en général aux valeurs minimales et maximales pour déclencher
l’alarme ;
– Un brassard gonflé à intervalles réguliers et enroulé autour du bras ou de la jambe,
qui permet d’estimer la pression artérielle lorsque le brassard se dégonfle ;](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-42-320.jpg)
![1.3. Les systèmes de monitoring automatisés 13
– Un capteur fixé à la main ou au pied qui surveille la saturation en oxygène dans le
sang dont les seuils inférieur et supérieur d’alarme sont fixés autour de 8 % et 95 %
de la valeur nominale ;
– Un capteur chauffant attaché sur la peau qui détermine la pression du gaz carbo-
nique dissout dans le sang. Les limites inférieure et supérieure sont 35 mmHg et
55 mmHg [Dageville, 2007].
Canule nasale
Cathéter artériel
Cathéter central
périphérique
Figure 1.1 – Image d’un prématuré. On peut y voir certains dispositifs de mesure (Reportés
sur la figure).
Infirmière
Moniteur
Couveuse
Figure 1.2 – Système de monitoring utilisé dans l’USIN de Rennes.
De plus, des échantillons de sang peuvent être prélevés à partir d’une veine ou d’une
artère. L’imagerie par ultrasons ou par rayons X peut être utilisée pour examiner le cœur,
les poumons et d’autres organes internes. D’autres dispositifs de monitoring fournissent
des mesures complémentaires mais sont généralement limités à la recherche, telles que la
pneumographie d’impédance, la pléthysmographie d’inductance respiratoire et le dioxyde
de carbone de fin d’expiration [Atkinson and Fenton, 2009].
Après l’initialisation du système de monitoring, un processus itératif et continu d’ac-
quisition des données, d’estimation de l’état de l’enfant, de détection et de validation des](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-43-320.jpg)
![14 Chapitre 1
événements à risque et d’application des actions thérapeutiques est mis en place (voir
figure 1.3). Ainsi lorsqu’une apnée-bradycardie survient, un membre de l’équipe soignante
averti par les alarmes se dirige à la chambre appropriée, se lave les mains et applique une
stimulation tactile suffisamment douce pour ne pas être agressive pour l’enfant, telle que
frictionner la peau au niveau de la plante du pied ou du thorax, jusqu’à arrêter l’épisode
d’apnée-bradycardie. D’ailleurs, plusieurs alarmes peuvent s’activer au moment d’une apnée-
bradycardie : l’alarme de respiration si les mouvements respiratoires s’arrêtent, l’alarme
d’oxygénation si la quantité d’oxygène dans le sang diminue, ou l’alarme de FC en cas de
bradycardie.
Détection/
Validation
Diagnostic
Thérapie Acquisition
Figure 1.3 – Cycle de surveillance d’un prématuré dans une USIN
1.3.2 Délais dans le cycle de surveillance
Comme nous l’avons relevé, les apnées-bradycardies sont des événements très fréquents
qui peuvent mettre l’enfant en danger vital immédiat en absence d’une intervention rapide
et adaptée. Par conséquent, le temps entre le début et la fin de l’épisode joue un rôle
important. Ce temps peut être décomposé en plusieurs états de duré différentes : i) le
début de l’apnée, ii) le début de la bradycardie, iii) le temps nécessaire au diagnostic de
l’apnée-bradycardie par le système de monitoring et l’émission de l’alarme sonore, iv) le
temps pris par l’équipe soignante pour cesser son activité en cours (les soins d’un autre
enfant, se laver les mains afin d’éviter tout risque de contamination, se rendre au chevet du
bébé souffrant qui peut être situé dans une autre chambre), et enfin v) l’application de la
thérapie (stimulation tactile douce parmi d’autres) jusqu’à l’arrêt l’épisode.
Les délais actuellement observés en clinique restent longs pour les bébés en détresse. Plus
le temps d’intervention est long plus il est difficile d’arrêter l’épisode d’apnée-bradycardie
conduisant ainsi à des problèmes importants et à des conséquences qui peuvent être
irréversibles. Le retard d’intervention moyen, mesuré depuis l’activation de l’alarme jusqu’à
l’application de la thérapie a été estimé autour de 33 secondes, avec une durée moyenne
de stimulation tactile de 13 secondes pour obtenir la résolution de l’événement d’apnée-
bradycardie [Pichardo et al., 2003].](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-44-320.jpg)

![16 Chapitre 1
Atrium droit
Atrium gauche
Veine cave
supérieure
Aorte
Artère pulmonaire
Veine
pulmonaire
Valve mitrale
Valve aortique
Ventricule
gauche
Ventricule droit
Veine cave
inférieure
Valve
tricuspide
Valve sigmoïde
Poumons
Figure 1.4 – Structure anatomique du cœur. Image d’après [Guyton and Hall, 1956].
2. Le myocarde est la couche intermédiaire et se compose majoritairement de fibres
contractiles ;
3. L’endocarde se trouve à l’intérieur et se compose d’une couche additionnelle de
cellules épithéliales et de tissu conjonctif.
Pour accomplir la fonction de pompe, le myocarde est constitué principalement de deux
types de tissus :
1. Le tissu de conduction ou tissu nodal : Ce tissu est constitué de cellules présentant
des propriétés spécialisées d’excitabilité, de conductibilité et d’automaticité. Ces
propriétés permettent la génération régulière et spontanée des impulsions électriques
et la conduction de ces impulsions d’une manière organisée au travers du myocarde,
afin d’assurer une contraction adéquate et un pompage efficace ;
2. Le tissu myocardique contractile : Ce type de tissu est largement majoritaire et
présente aussi des propriétés d’excitabilité et de conductibilité cellulaire. Cependant,
à la différence du tissu nodal, il est constitué de cellules pourvues d’un grand nombre
de fibres musculaires capables de se contracter.
Chaque cellule cardiaque (nodale ou myocardique) est entourée et remplie avec une
solution qui contient des ions. Les trois plus importants sont : le sodium (Na+), le potassium
(K+) et le calcium (Ca2+). Au repos, l’intérieur de la membrane cellulaire est chargé
négativement par rapport à l’extérieur, qui est pris comme référence. Cette différence
de potentiel, ou potentiel de repos cellulaire, est voisin de −85 mV pour les cellules
ventriculaires et dépend des concentrations ioniques dans les milieux intracellulaire et
extracellulaire. Les processus actifs et passifs de mouvements des ions au travers des canaux
ioniques, qui traversent la membrane cellulaire, et la propagation de ces ions, cellule à
cellule, constituent les fondements de l’activité électrique cellulaire. Quand une impulsion](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-46-320.jpg)

![18 Chapitre 1
les phases 0, 1, 2 et la première partie de la phase 3 (usuellement jusqu’aux alentours
de −50 mV), une stimulation externe sera incapable de provoquer un nouveau PA. Cette
période est appelée la période réfractaire absolue (PRA). La durée de la PRA dépend de
la fréquence à laquelle la cellule est stimulée, plus longue pour des fréquences cardiaques
plus basses et inversement pour des fréquences de stimulation plus importantes. La période
réfractaire relative (PRR) est associée à la dernière partie de la phase 3 (souvent pour des
potentiels inférieurs à −50 mV ). Pendant la PRR, une stimulation d’amplitude supérieure
à la normale (supra-stimulus) peut provoquer un nouveau PA qui présentera une durée de
la phase 0 rallongée en fonction de la prématurité de la stimulation. Ces deux processus
d’adaptation de la durée de la PRA et de la phase 0 correspondent aux propriétés d’hystérésis
de la fonction cellulaire.
1.4.2 Le système spécialisé d’excitation-conduction du cœur
Le système spécialisé d’excitation-conduction comprend : le nœud sinusal, les voies
spécialisées internodales, le nœud auriculo-ventriculaire (A-V), le faisceau de His, les branches
droite et gauche et les fibres de Purkinje (voir figure 1.6). Les cellules associées à chacune
de ces parties du système d’excitation-conduction présentent une pente de dépolarisation
diastolique lente (phase 4) différente. Dans le cas physiologique normal, cette pente est plus
prononcée sur le nœud sinusal. Ainsi, le nœud sinusal est appelé le pacemaker dominant du
cœur.
Nœud
sinusal
Voies spécialisées
internodales
Nœud A-V
Branche droite
Faisceau de His
Branche gauche
Fibres de Purkinje
Figure 1.6 – Système spécialisé de conduction du cœur. Image d’après [Guyton and Hall,
1956].
L’activité électrique normale du cœur suit la séquence d’activation suivante :
1. Le nœud sinusal : L’activité électrique est générée spontanément dans le nœud
sinusal. Il est situé dans la partie haute de la paroi intérieure de l’oreillette droite,
au niveau où débouche la veine cave supérieure. L’impulsion cardiaque initiée dans](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-48-320.jpg)


![1.5. L’électrocardiogramme du nouveau-né prématuré 21
et le début du complexe QRS. Il représente le temps de transmission du front de
dépolarisation par le nœud auriculo-ventriculaire ;
– Le segment ST : Il est compris entre la fin du complexe QRS (ou point J) et le
début de la phase ascendante de l’onde T. Ce segment correspond au temps pendant
lequel l’ensemble des cellules myocardiques sont dépolarisées (phase de plateau) et
donc, dans le cas normal, doit être isoélectrique ;
– L’intervalle QT : Il représente le temps entre le début du complexe QRS et la fin
de l’onde T. Il donne une indication de la longueur des phases de dépolarisation et de
repolarisation ventriculaire (longueur moyenne d’un PA ventriculaire).
L’intervalle QT varie en fonction de la FC. Par conséquent il est généralement corrigé
(QTc), le plus souvent en utilisant la formule de BAZETT [Bazett, 1920] :
QTc = QT/
√
RR (1.1)
Une naissance prématurée est un bouleversement pour le système cardiovasculaire. En
effet, chez le prématuré, les fermetures des shunts foramen ovale et du canal artériel peuvent
ne pas être complètes, laissant une communication entre les circuits droit et gauche du cœur.
Dans ce cas, une partie du débit sanguin dans l’aorte va retourner vers l’artère pulmonaire
et, pour assumer la surcharge de débit engendrée par cette fuite, une augmentation du débit
cardiaque doit se produire [Dageville, 2007]. Cependant, le myocarde du prématuré contient
moins d’éléments contractiles et est plus compliant que celui de l’adulte. La réponse aux
changements de précharge (mécanisme de Frank-Starling) reste donc fonctionnelle seulement
dans une plage étroite de pression de fin de diastole du ventricule gauche [Kirkpatrick et al.,
1976]. Pour satisfaire l’augmentation de la demande d’oxygène du corps du prématuré, la
FC est doublée, mais les dépenses cardiaques engendrées sont deux fois supérieures à celles
de l’adulte, dû en partie à cette contractilité réduite. Ainsi, la FC d’un prématuré est aux
alentours de 150 bpm.
Si l’électrocardiogramme de l’adulte a été très étudié tant sur l’analyse de la morphologie
des ondes (P, QRS, T), des intervalles temporels (PR, QT) que des durées (P, QRS, T), ce
qui a permis d’établir des normes avec l’âge, l’ECG du prématuré est moins connu.
La FC très élevée, le faible épaisseur de la cage thoracique et le processus de dévelop-
pement du système cardio-respiratoire et du myocarde chez les nouveaux-nés prématurés
produisent des ECG très différents de ceux des adultes normaux. Les différences les plus
remarquables sont :
– Les intervalles (RR, PR et QT) et les durées des ondes (P, T et complexe QRS) sont
plus courts ;
– La taille du ventricule droit est plus épaisse que le ventricule gauche chez les nouveaux-
nés tandis que le ventricule gauche est beaucoup plus épais chez les adultes. Cette
prédominance du ventricule droit s’exprime dans l’ECG par une déviation axiale du](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-51-320.jpg)
![22 Chapitre 1
complexe QRS vers la droite (entre 65o et 174o) [Costa et al., 1964; Park, 2007] ;
– Les ondes R sont de plus grande amplitude dans la dérivation frontale aVR (voltage
unipolaire augmentée sur le bras droit) et dans les dérivations précordiales V4 (5e
espace intercostal gauche, sur la ligne médioclaviculaire), V1 (4e
espace intercostal
droit, bord droit du sternum) et V2 (4e
espace intercostal gauche, bord gauche du
sternum).
– Les ondes S sont plus profondes dans la dérivation frontale I (mesure bipolaire entre
bras droit et bras gauche) et dans les dérivations précordiales V5 (même horizontale
que V4, ligne axillaire antérieure) et V6 (même horizontale que V4, ligne axillaire
moyenne).
– L’intervalle QTc est prolongé chez les prématurés [Costa et al., 1964]. Au cours des
6 premiers mois de vie, l’intervalle QTc est considéré comme normal à moins de
0,49 secondes. Après l’enfance, ce seuil est généralement de 0,44 secondes [Sharieff
and Rao, 2006].
– Les modifications de l’onde T sur l’ECG ont tendance à être non spécifiques et sont
souvent une source de controverses. On convient que les ondes T plates ou inversées
sont normales. En fait, les ondes T dans les dérivations V1 à V3 sont généralement
inversées après la première semaine de vie jusqu’à l’âge de 8 ans [Sharieff and Rao,
2006].
– L’onde P est de plus grande amplitude et plus pointue dans la dérivation frontale
II (mesure bipolaire entre bras droit et jambe gauche) et la dérivation précordiale
V1 [Costa et al., 1964].
La figure 1.8a présente un exemple d’ECG d’un adulte. Cet ECG correspond à une
personne sédentaire, sans complication cardiaque, de sexe masculin et âgé de 20 ans. Sa FC
est d’environ 82 bpm. De même, un exemple d’ECG d’un nouveau-né prématuré est montré
figure 1.8b. Cet ECG correspond à celui d’un bébé de sexe masculin, de 32 semaines d’âge
gestationnel et de 1575 grammes de poids. Il présentait plus d’une bradycardie par heure,
n’avait pas d’infection systémique, pas de traitement médicamentaux à la caféine et n’avait
pas besoin de respiration assistée par CPAP.
L’examen de ces deux ECG montre explicitement ces différences, qui sont quantifiées et
résumées dans le tableau 1.1 qui reporte les valeurs des ECG normaux pédiatriques observés
chez les nouveaux-nés, nourrissons, enfants et adolescents [Sharieff and Rao, 2006]. Ce
tableau présente la gamme des valeurs normales de la FC, l’axe du complexe QRS, la durée
de l’intervalle PR et la durée du complexe QRS. Des changements rapides se produisent
dans la première année de vie en raison de l’évolution de la circulation et de la physiologie
cardiaque. Après l’enfance, les changements ultérieurs sont moins rapides jusqu’à la fin de
l’adolescence et à l’âge adulte.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-52-320.jpg)

![24 Chapitre 1
L’impossibilité de ne prévenir ni les apnées-bradycardies, ni leurs conséquences, impose
une surveillance cardio-respiratoire rigoureuse et continue qui permet une intervention
rapide et adaptée à tout instant. La détection précoce de ces épisodes permettrait de réduire
les risques associés, de favoriser le développement des nouveaux-nés prématurés, d’améliorer
leur qualité de vie et de diminuer la durée d’hospitalisation. En effet, le traitement médical
de première intention consiste en la stimulation douce et manuelle du bébé. Même si cette
stimulation du nouveau-né au moment de l’apnée-bradycardie reste la méthode la plus
efficace, l’expérience montre que pour les bébés en détresse, les délais d’interventions restent
longs avec un retard d’intervention moyen (mesuré depuis l’activation de l’alarme jusqu’à
l’application de la thérapie) autour de 33 secondes, et un temps de stimulation manuelle de
13 secondes pour terminer l’épisode apnéique [Pichardo et al., 2003].
Pour répondre à ce problème, des systèmes de stimulation vibrotactile, aussi sûrs et
efficaces que la stimulation manuelle, ont été développés récemment [Pichardo et al., 2003;
Beuchée et al., 2007]. Cependant, les délais d’interventions sont finalement peu réduits
car le temps nécessaire au diagnostic de la bradycardie (10 secondes en moyenne après le
début de l’apnée) n’est pas pris en compte. Une manière de réduire encore ce temps est de
proposer un méthode de détection précoce des événements de bradycardie voire de prédire
l’apparition de la bradycardie. Ces objectifs constituent le thème principal de recherche de
ce mémoire de thèse et des solutions à base de modèles de Markov cachés seront proposées
au chapitres 4 et 5.
On a vu également que la compréhension des changements physiologiques cardiaques
associés à l’âge et à la maturation ainsi que la capacité d’interpréter l’ECG (durée des
segments et intervalles, déviations d’axes et morphologies des ondes) et sa relation avec
l’âge, sont des outils très importants au moment de différencier les ECG normaux des ECG
pathologiques. Le chapitre 3 permettra de répondre à cette problématique difficile.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-54-320.jpg)





![30 Chapitre 2
entre sensibilité, spécificité et retard à la détection. Dans la première section, une analyse
des travaux antérieurs sur ce problème et, en particulier, ceux développés au sein de nos
laboratoires : GBBA (Université Simón Bolívar, Caracas) et LTSI (Université de Rennes 1,
Rennes) est présentée. Ensuite, la méthodologie proposée pour la détection d’événements et
pour l’évaluation clinique des traitements proposés dans ce travail est détaillée et justifiée.
Finalement, la méthodologie d’évaluation des performances de détection est exposée.
2.1 Travaux antérieurs
L’équipe SEPIA (Surveillance, Explication et Prévention des Ischémies et des Arythmies
cardiaques) du LTSI (Laboratoire de Traitement du Signal et de l’Image), travaille sur cette
problématique depuis plusieurs années. Les travaux de l’équipe se concentrent principalement
sur la modélisation du système nerveux autonome (SNA) et le monitoring des apnées-
bradycardies du prématuré. Plus spécifiquement, l’équipe s’intéresse à étudier :
– L’influence du SNA du nouveau-né prématuré sur la FC [Pladys et al., 2008; Beuchée,
2005]. Cette influence est déterminée en évaluant la variabilité de la fréquence cardiaque
(VFC) par deux types de mesure : l’une dans le domaine temporel et l’autre dans le
domaine spectral.
– Le système cardio-respiratoire de l’agneau fœtal ou nouveau-né [Gaillot et al., 2005;
Pladys et al., 2008; Patural et al., 2010] en collaboration avec le Québec (Sherbrooke et
Montréal). En effet, en menant des études sur l’agneau fœtal, les chercheurs ont réussi
à mieux comprendre le phénomène d’apnée-bradycardie des nouveaux-nés prématurés.
– La relation entre les apnées-bradycardies et les infections [Beuchée et al., 2009], ainsi
que sa relation avec les vaccins.
– Le traitement de la bradycardie par stimulation kinesthésique après la détection des
épisodes de bradycardies [Beuchée et al., 2007].
– La modélisation et la validation de modèles sur des données animales, pour mieux
comprendre les mécanismes complexes du couplage cardio-respiratoire du nouveau-
né [Le Rolle et al., 2008]. Une thèse est également en cours actuellement au laboratoire
sur ce sujet.
– L’EEG du prématuré de façon à quantifier les temps de sommeil calme, les effets des
médicaments.
– Un système de monitoring intégrant tous ces modules basés sur une architecture multi-
agents [Cruz, 2007; Hernández et al., 2007a,b]. La partie détection de bradycardie
est actuellement en évaluation dans le cadre d’un projet PHRC sur trois centres
hospitaliers : Rennes, Nantes et Tours.
Concernant la détection des apnées-bradycardies chez les nouveaux-nés prématurés,
de nombreuses études ont été réalisées et sont sommairement présentées dans la section
suivante.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-60-320.jpg)

![32 Chapitre 2
le paramètre temporel a plusieurs effets sur la détection. Un effet positif, puisqu’il
permet la diminution du nombre de fausses détections comme par exemple celles dues
aux faux négatifs du détecteur des battements, tout en gardant la même quantité de
non détection de la méthode précédente. Cependant, cette méthode induit des retards
plus importants à la détection. La figure 2.2 montre un exemple en utilisant cette
méthode et permet d’apprécier (figure 2.1) l’augmentation du retard de la détection.
0 20 40 60 80 100 120
200
300
400
500
600
700
800
900
1000
Bradycardie
Seuil
RR(ms)
Temps (s)
Détection
Retard
4 s
Figure 2.2 – Utilisation d’un seuil d’amplitude et durée fixes pour détecter les bradycardies
à partir des séries RR. Dans cet exemple, la détection est réalisée lorsque RR(k) ≥ 600 ms
pendant 4 secondes, où k est l’indice temporel.
3. Détection par seuil d’amplitude relatif : Du fait que la durée du cycle cardiaque
dépend en grande partie de l’âge gestationnel et que cette durée évolue au cours du
temps, même pendant la journée, une nouvelle méthode a été proposée de manière
à prendre en compte des changements dans l’intervalle RR par rapport au seuil qui
change au cours du temps [Poets et al., 1993]. Dans cette méthode, une bradycardie
est détectée lorsque l’intervalle RR instantané (RR(k)) dépasse le seuil relatif : un
pourcentage de l’intervalle RR moyenné dans une fenêtre glissante (RRbase) et qui
précède l’intervalle RR actuel. De plus, un paramètre temporel est utilisé afin de
réduire la quantité de fausses détections. Le nombre des fausses détections et d’épisodes
manqués ainsi que le retard de la détection sont ajustés en changeant : le pourcentage
du seuil, la taille de la fenêtre pour déterminer la moyenne de l’intervalle RR et le
temps passé au-dessus du seuil. Cette méthode est plus avantageuse que les méthodes
précédentes. En effet, puisque le seuil est adaptatif, la détection est moins sensible aux
changements de rythme basal du prématuré. En revanche, la taille de la fenêtre pour
déterminer la moyenne modifie la dynamique du seuil (son taux de changement) et en
conséquence : i) en cas de changement rapide de l’intervalle RR, la détection peut être
réalisée plus précocement qu’en utilisant un seuil fixe mais, ii) en cas de changement
lent, la détection peut être réalisée plus tardivement ou l’épisode peut être manqué.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-62-320.jpg)
![2.1. Travaux antérieurs 33
La figure 2.3 montre un exemple de détection d’un épisode de bradycardie en utilisant
un seuil relatif. Le seuil est fixé à 33 % de la moyenne des intervalles RR dans une
fenêtre glissante de 20 secondes qui précèdent l’intervalle RR actuel. La détection est
réalisée lorsque l’intervalle RR instantané dépasse le seuil relatif pendant au moins
4 secondes : RR(k) ≥ 1, 33RRbase. Les changements du seuil au cours du temps sont
clairement observés. On constate aussi que l’instant de détection est plus précoce que
ceux de l’exemple reporté sur la figure 2.2.
0 20 40 60 80 100 120
200
300
400
500
600
700
800
900
1000
1100
Temps (s)
Seuil
RR(ms)
Détection
4 s
Retard
Bradycardie
Figure 2.3 – Utilisation d’un seuil relatif pour détecter les bradycardies à partir des séries
RR. Dans cet exemple, la détection est réalisée lorsque RR(k) ≥ 1, 33RRbase pendant 4 s,
où k est l’indice temporel et RRbase est la valeur moyenne de la série RR calculée dans une
fenêtre glissante de 20 secondes qui précède l’intervalle RR actuel.
La simplicité de ces trois détecteurs et la diminution du nombre de fausses alarmes
(spécificité élevée) ont permis de les voir acceptées facilement par les spécialistes. Cependant,
ces méthodes sont peu robustes. Plusieurs bradycardies ne sont pas détectées ou que
tardivement. Des améliorations ont donc été apportées.
Une première approche sur la prédiction à court terme de l’épisode de bradycardie
chez les nouveaux-nés prématurés, en utilisant la fouille de données, a été introduite par
PRAVISANI et al. [Pravisani et al., 2003]. Des mesures linéaires et non linéaires de la VFC
ont été extraites sur des périodes de 3 minutes précédant le début de la bradycardie jusqu’au
début de l’épisode, en utilisant une fenêtre glissante de 20 secondes et un recouvrement
de 15 secondes. Les mesures linéaires analysées correspondent à l’énergie dans les bandes
de basse fréquence (LF, Low Frequency) et haute fréquence (HF, High Frequency) et le
coefficient LF/HF [Task Force, 1996]. Les mesures non linéaires explorées correspondent
aux mesures de l’entropie approximée et l’entropie spectrale [Rezek and Roberts, 1998].
L’évolution de ces paramètres a été étudiée par analyse en composante principale (ACP) et
analyse hiérarchique ascendante [Ward, 1963]. Sur un ensemble de 13 épisodes appartenant
à 5 nouveaux-nés prématurés, ils ont constaté une diminution du coefficient LF/HF avant le](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-63-320.jpg)
![34 Chapitre 2
début de la bradycardie et une diminution simultanée du composant LF, montrant ainsi une
réduction de la modulation sympathique et une augmentation du tonus vagal. De plus, une
diminution progressive de l’entropie approximée et de l’entropie spectrale a été observée,
montrant ainsi que le système est de plus en plus régulier et prévisible avant la bradycardie.
En outre, des profils d’évolution de la VFC en utilisant l’ACP ont été mis en évidence pour
10 épisodes mais il n’a pas été possible d’identifier une description unique des classes. Ces
résultats montrent qu’aucun des paramètres étudiés étaient capables à lui seul de prédire
la survenue d’une bradycardie. Cependant il semblait que chaque variable contribue à la
prédiction de l’événement.
Une autre étude consiste à utiliser la théorie des changements abrupts de valeur
moyenne [Basseville and Nikiforov, 1993] pour proposer une nouvelle méthode de dé-
tection des bradycardies [Beuchée et al., 2007]. La détection de changement de valeur
moyenne est faite à partir du Cusum test [Basseville and Nikiforov, 1993] et consiste à
confronter deux hypothèses composites : présence et absence de bradycardie à chaque
instant. Cette méthode détecte avec une sensibilité de 96,84 %, une spécificité de 96,60 %
et un retard à la détection de -2,85 battements (autour de 1,2 secondes) par rapport aux
annotations manuelles d’un expert (test réalisé sur 1188 battements en bradycardie chez 40
nouveaux-nés prématurés) [Cruz et al., 2006]. La valeur négative du retard à la détection
obtenue s’explique par le fait que l’annotation a été définie à l’instant de croisement du
seuil de 600 ms et non pas au tout début de l’événement d’apnée-bradycardie.
Une autre méthode, basée sur la fusion optimale de détecteurs, a permis d’améliorer la
performance de la détection des bradycardies [Cruz et al., 2006]. Les algorithmes fusionnés
correspondent aux méthodes de seuil et de durée fixe (RR(k) ≥ 600 ms pendant 4 s ou plus),
de seuil relatif (RR(k) ≥ 1, 33RRbase pendant 4 s ou plus) et de détection par changements
abrupts. La fusion optimale consiste à effectuer la somme pondérée des résultats de chaque
détecteur. Les coefficients de pondération sont trouvés en utilisant un critère d’optimisation
proposé par [Chair and Varshney, 1986]. Cet algorithme a obtenu une sensibilité de 97,67 %,
une spécificité de 97,00 % et un retard à la détection de -2,22 battements (autour de 1
seconde) sur la même base de données.
D’autres algorithmes ont été proposés dans la littérature. L’un d’entre eux utilise la
méthode présentée par YU et al. [Yu et al., 2002] qui cherche un changement abrupt dans
la valeur moyenne dans une fenêtre mobile pour détecter la bradycardie [Portet et al.,
2007]. Une sensibilité de 90,20 %, une valeur prédictive positive de 61,30 % ainsi qu’un
temps de retard médian de 8 secondes et d’écart-type de 35,3 secondes pour le début
de la bradycardie, ont été reportés sur une base de données annotée. Une autre façon
de détecter les bradycardies est d’appliquer une technique d’apprentissage automatique
par arbre de décision. Dans [Portet et al., 2007], la méthode C4.5 [Quinlan, 1993] est
utilisée pour apprendre l’arbre de décision dont les attributs sont : la valeur brute, la
superficie, la pente linéaire, l’écart-type, l’amplitude minimale, l’amplitude maximale, la](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-64-320.jpg)
![2.1. Travaux antérieurs 35
dérivée maximale, la moyenne et la médiane de la série RR. Une fois appris, la sortie de
l’arbre de décision est lissée par une fenêtre Blackman de 31 échantillons et les début et fin
des épisodes sont cherchés par comparaison à un seuil. Une sensibilité de 78,20 %, une valeur
prédictive positive de 68,70 %, un temps de retard médian de 7 secondes et un écart-type
de 8,5 secondes, ont été obtenus.
Récemment, une approche fondée sur l’intervalle RR, la fréquence respiratoire et la SpO2,
extraites de 2426 heures d’enregistrement de 54 nouveaux-nés (44±7 heures) a été proposée
pour la détection d’apnée du prématuré sur des segments préalablement choisis [Belal
et al., 2011]. Trois approches, combinant détection et classification, ont été reportées et
comparées. Les auteurs montrent alors qu’en exploitant les dérivées de l’intervalle RR, de la
fréquence respiratoire et de la SpO2, initialement pré-traitées (un filtre médian et un filtre
passe-bas sont appliqués sur les données) et une règle de fusion à base d’un ET logique,
des performances très satisfaisantes (100 % de sensibilité et 96,19 % de spécificité) sont
enregistrées sur une base de données pré-sélectionnées. Les résultats reportés ici, établis en
parallèle à l’étude reportée dans ce mémoire de thèse, sont donc intéressants, confirment le
bien-fondé de notre démarche mais appellent à quelques remarques :
– la classification de l’évènement « présence » ou « absence » d’apnée du prématuré
a été déterminée sur des segments prédéfinis et non pas en proposant d’effectuer la
détection en ligne,
– le temps de retard de la détection n’a pas été évalué, et comme précisé auparavant,
est crucial pour notre étude,
– la fréquence d’échantillonnage de 1 Hz apparaît à nos yeux trop basse pour l’analyse
de la série RR, car il a été montré des composantes spectrales liées à la régulation du
SNA dans les bandes LF de 0,02 à 0,2 Hz et HF de 0,2 à 1,5 Hz [Chatow et al., 1995;
Beuchée, 2005],
– une fusion de type ET augmente la sensibilité en détriment de la spécificité alors
que des études antérieures ont montré que la fusion optimale pourrait être plus
pertinente [Cruz et al., 2006].
2.1.2 Système multi-agents de monitoring appliqué aux soins néonatals
La thèse de CRUZ [Cruz, 2007], développée entre le Groupe de Bio-ingénierie et
Biophysique appliquée (GBBA, en espagnol Grupo de Bioingeniería y Biofísica Aplicada) à
Caracas au Vénézuela et le LTSI à Rennes, a proposé un système de monitoring intelligent
(INTEM) basé sur une architecture de systèmes multi-agents. Ce système est composé de
plusieurs agents intelligents qui interagissent selon certaines relations et avec un objectif.
Ainsi, dans ces travaux, quatre agents sont utilisés pour accomplir les tâches classiques du
processus de monitoring : acquisition, traitement, diagnostic et thérapie. Un agent différent
est associé à chacune de ces étapes.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-65-320.jpg)
![36 Chapitre 2
Le système de monitoring est composé de plusieurs dispositifs (c.f. figure 2.4) :
– Un dispositif d’acquisition de données qui acquiert un ECG de deux voies à une
fréquence d’échantillonnage de 1 kHz. Ce dispositif est lié par signal radio-fréquence
au dispositif qui délivre la stimulation et à celui qui capte la lumière du moniteur. De
plus, il est aussi connecté par bluetooth à la station de monitoring.
– Un dispositif qui délivre une stimulation vibrotactile au bébé. Il est composé d’un
vibreur, tel que recommandé par [Lovell et al., 1999], développé par la société Audio-
logical Engineering. Le vibreur est placé sur l’abdomen du prématuré et est activé
chaque fois qu’une bradycardie survient. L’intensité de la stimulation vibrotactile
peut être réglée manuellement, à l’aide des boutons, ou à partir de la station de
monitoring.
– Un ordinateur portable qui sert de station de monitoring et qui permet d’enregistrer
l’ECG du prématuré et d’appliquer les traitements du signal en temps-réel. Sur l’écran
sont affichés l’ECG, un battement moyen, la courbe de VFC, la FC, etc.
– Un dispositif qui capte la lumière du moniteur installé dans l’USIN. Il est composé
d’une diode photosensible collée devant l’écran du moniteur et qui capte la lumière
lorsque ce moniteur détecte une apnée-bradycardie. La fonction de ce dispositif est de
comparer les instants de détection des bradycardies du moniteur installé dans l’USIN
et le système de monitoring développé au LTSI.
Dispositif
d'acquisition d'ECG
Électrodes
Dispositif qui délivre
la stimulation vibrotactile
Vibreur
Station de monitorage
Antenne
Figure 2.4 – Dispositifs utilisés dans le système INTEM.
Cette station de monitoring accueille l’ensemble d’algorithmes qui ont été développés, no-
tamment des approches de fusion de données pour la détection multivoie des QRS [Hernández
et al., 1999] et pour la détection d’épisodes d’apnée-bradycardies. L’architecture proposée
et les méthodes d’activation du vibreur ont fait l’objet d’un dépôt de brevet [Hernández
et al., 2007a,b].](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-66-320.jpg)

![38 Chapitre 2
ECG
Personnel soignant
Intervention
Extraction de
caractéristiques
Base de données
Prise de
décision
Figure 2.5 – Étapes du processus de détection des apnées-bradycardies proposées dans cette
thèse.
les suivants : médicaments connus pour influencer le SNA à l’exception de la caféine,
l’assistance respiratoire intra-trachéale, une lésion intra-cérébrale ou une malformation.
Au moment de l’enregistrement, le poids de naissance médian était de 1235 g (1065, 1360),
l’âge médian était de 31,2 semaines (29,7, 31,9) et l’âge post-natal était de 12,1 jours (6,7,
19,5). Six enfants présentaient une infection systémique, seize avaient une aide respiratoire
de pression nasale avec ventilation spontanée en pression positive continue et dix-sept
étaient traités avec de la caféine.
Tous les enregistrements ont été acquis en utilisant le système Powerlab/Graphique v4.2
installé sur un ordinateur Pentium III. Ils se composaient d’un ECG acquis sur une voie
pendant 1 heure à une fréquence d’échantillonnage de 400 Hz. Les enfants ont été placés
dans des couveuses, positionnés sur le côté, enroulés dans un cocon. La lumière a été éteinte,
les volets extérieurs baissés et la porte fermée afin d’obtenir une pièce calme et sans lumière
vive [Beuchée, 2005].
2.2.2 Extraction de caractéristiques
L’objectif de cette étape est d’extraire les caractéristiques les plus importantes de l’ECG
et de générer les séries temporelles utiles pour la détection des épisodes de bradycardie. Elle
comporte plusieurs étapes, représentées dans la figure 2.6 :
– Le pré-traitement de l’ECG : Cette étape de débruitage du signal ECG est
composé d’un ensemble de filtres.
– La détection des battements : Elle permet de repérer les battements cardiaques.
Nous avons repris une version améliorée de l’algorithme de PAN et TOMPKINS [Pan
and Tompkins, 1985; Cruz, 2007].
– La segmentation des battements : Elle permet d’identifier les instants de début](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-68-320.jpg)
![2.2. Méthodologie proposée 39
et de fin des ondes qui composent l’ECG. Nous avons utilisé l’algorithme développé
dans notre laboratoire [Dumont, 2008] et qui emploie une approche temps-échelles
par décomposition en ondelettes du signal ECG issue de la littérature [Martínez et al.,
2004; Li et al., 1995].
– L’optimisation des méthodes par algorithmes évolutionnaires : Les méthodes
reportées dans la littérature de détection et de segmentation des battements ne sont pas
adaptées à l’ECG des prématurés. Une procédure d’optimisation des paramètres, basée
sur des algorithmes évolutionnaires, permettra de résoudre ce problème multi-objectif
et d’ajuster automatiquement les paramètres de ces méthodes.
– L’extraction des séries temporelles : Une fois les méthodes de la chaîne de seg-
mentation d’ECG adaptées aux ECG des prématurés, la prochaine étape comporte
l’extraction des indicateurs les plus pertinents pour caractériser les épisodes d’apnée-
bradycardie. Cette information correspond aux indicateurs utilisés par les cardiologues
pour caractériser le cycle cardiaque comme les intervalles et amplitudes des ondes
présentées (voir figure 1.7), ainsi que le rythme cardiaque. Cette étape permet de
réduire la dimension des données et de conserver une information interprétable par les
spécialistes. L’automatisation de cette étape permet un gain de temps ainsi qu’une
meilleure répétabilité des analyses effectuées. Les séries temporelles retenues corres-
pondent aux variables suivantes : intervalle RR, amplitudes de l’onde R et durées des
QRS.
Pré-traitement
de l'ECG
Segmentation
des battements
Détection
des battements
Oui
NoOptimisation des
méthodes par
algorithmes
évolutionnaires
Paramètres
des méthodes
optimisés ?
Extractions des
séries temporelles
Figure 2.6 – Étape d’extraction des caractéristiques de la démarche proposée.
2.2.3 Prise de décision
L’objectif est ici d’émettre une décision sur la présence ou absence d’un épisode d’apnée-
bradycardie, en exploitant les dynamiques des variables étudiées et non seulement leurs
valeurs instantanées. Nous avons retenu une approche à base de modèles semi-Markoviens
cachés (MSMC). Ce choix sera justifié plus en détail au chapitre 4 mais il nous apparaissaient
évident que les MSMC étaient adaptés à la fois pour traiter la dynamique, prendre en
compte plusieurs variables simultanément, et proposer un processus de décision entièrement
basé sur la vraisemblance des modèles. Cette étape comporte les phases montrées figure 2.7 :
– L’apprentissage des modèles MSMC : une fois les séries temporelles obtenues,](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-69-320.jpg)






![Chapitre 3
Analyse multi-variée de l’ECG pour
la détection et la caractérisation de
l’apnée-bradycardie des
nouveaux-nés prématurés
L’objectif de ce chapitre est d’étudier le contenu d’information des caractéristiques
extraites de l’ECG avant, pendant et après les épisodes d’apnée-bradycardie, avec le but
de les intégrer dans une approche de détection précoce d’épisodes d’apnée-bradycardie.
Afin d’atteindre cet objectif et d’extraire les caractéristiques d’intérêt, deux grandes étapes
doivent être suivies ; d’une part, la détection précise de chaque battement et d’autre part,
la segmentation de chaque complexe QRS. Pour la première étape, plusieurs algorithmes
de détection des complexes QRS ont été proposés dans la littérature [Pan and Tompkins,
1985; Köhler et al., 2002; Chen et al., 2006; Arzeno et al., 2008]. Cependant, ces méthodes
ont été développées pour l’ECG de l’adulte et, à notre connaissance, aucune d’entre elles
n’ont été adaptées aux caractéristiques spécifiques de l’ECG du nouveau-né prématuré
(FC supérieure à celles des adultes, durée du complexe QRS plus courte . . .). En ce qui
concerne la deuxième étape, les méthodes basées sur une transformée en ondelettes pour
la décomposition de l’ECG, suivie d’un ensemble de règles heuristiques pour segmenter
les principales caractéristiques de chaque battement ont également été proposées dans
la littérature [Li et al., 1995; Martínez et al., 2004; Dumont et al., 2010]. Encore une
fois, à notre connaissance, ces méthodes sont spécifiques aux caractéristiques de l’ECG
adulte. Par conséquent, les méthodes pour les deux étapes doivent être tout d’abord
adaptées aux propriétés spécifiques de l’ECG du nouveau-né prématuré. Ces adaptations
sont généralement effectuées manuellement, en modifiant les paramètres de chaque méthode.
Toutefois, en raison du nombre important de paramètres utilisés dans les deux méthodes,
47](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-77-320.jpg)
![48 Chapitre 3
cette démarche n’est pas aisée.
Dans ce chapitre, un processus d’optimisation proposé initialement dans [Hernández
et al., 2002; Dumont et al., 2010] est adapté. Synthétiquement, on cherche à minimiser la
probabilité d’erreur de détection et la moyenne et l’écart-type du jitter de détection, sur
une base de données annotées, en optimisant les paramètres de la chaîne de traitement par
un algorithme évolutionnaire.
Une brève étude bibliographique des techniques de segmentation de l’ECG est présentée
au début du chapitre suivi de la présentation en détail des techniques de détection et de
segmentation utilisées dans ce mémoire. Cependant, comme les méthodes de détection des
battements et de segmentation de l’ECG ne sont pas aptes à travailler sur les ECG des
prématurés, une procédure d’optimisation est proposée et ensuite présentée. Enfin, une
analyse du complexe QRS sous différentes conditions physiopathologiques est conduite,
afin de caractériser les épisodes d’apnée-bradycardie chez les nouveaux-nés prématurés.
Les résultats du chapitre sont divisés en trois parties : la performance du détecteur des
battements optimisé, la performance de la segmentation du QRS optimisé et l’analyse
statistique des séries temporelles extraites de l’ECG des prématurés. L’information extraite
de ces détecteurs optimisés est analysée dans le chapitre suivant au moyen des modèles
semi-Markovien cachés.
3.1 Segmentation des ondes : position du problème et biblio-
graphie
L’étape de segmentation de l’ECG consiste à identifier les instants de début, de fin
et les extrema des ondes P, Q, R, S et T de chaque battement du signal. Les outils de
segmentation automatique (ou semi-automatique) de l’ECG intègrent différentes étapes
de transformation ou de modélisation de l’ECG. Les fondements des différentes méthodes
issues de la littérature sont brièvement commentées dans cette section.
3.1.1 Algorithme basé sur la dérivée filtrée
Cette méthode consiste à générer le signal dérivé filtré passe-bas du signal ECG [Laguna
et al., 1994]. L’algorithme détecte les extrema du signal filtré à l’aide d’un seuil adaptatif et
définit le pic de l’onde R comme le passage à zéro entre le maximum et le minimum du
signal filtré dans une fenêtre temporelle prédéfinie. Ce principe est également utilisé pour
définir les pics des ondes Q et S. Pour les ondes P et T, un deuxième filtrage passe-bas
est employé et des fenêtres temporelles sont fixées afin de repérer les pentes significatives
(une fenêtre relative à la FC est utilisée pour l’onde T). Les points de croisements par](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-78-320.jpg)
![3.1. Segmentation des ondes : position du problème et bibliographie 49
zéro des signaux dérivés-filtrés et des seuils relatifs aux amplitudes des pentes significatives
sont employés pour définir les pics et les limites des ondes P et T. Cette méthode est une
solution envisageable mais des remarques s’imposent : d’une part, l’algorithme comporte
de nombreuses approches subjectives (les recherches des points fiduciaux sont basées sur
des seuils plus ou moins approximatifs) et d’autre part, le filtre passe-bas utilisé coupe des
fréquences significatives de l’onde T.
3.1.2 Algorithme basé sur le filtrage adaptatif
Dans cette méthode, l’ECG est filtré par un filtre classique puis par un filtre adap-
tatif [Soria-Olivas et al., 1998]. La méthode inclut une étape d’apprentissage qui permet
l’estimation d’une constante d’adaptation introduite dans le filtre adaptatif. Les résultats
obtenus sont satisfaisants mais la méthode ne peut être employée sans une pré-détection par
un cardiologue. De plus, il est difficile de préciser les différences de performance avec une
approche totalement automatique car les auteurs n’ont pas réalisé de tests sur des bases de
données.
3.1.3 Algorithme basé sur la modélisation physiologique
Cette méthode modélise des potentiels d’action à partir d’un modèle physiologique
de la phase de repolarisation ventriculaire afin d’ajuster, puis de segmenter l’onde T de
l’ECG [Vila et al., 2000]. Le modèle physiologique est constitué d’une somme de deux
potentiels d’action. Les paramètres du modèle sont estimés par optimisation non linéaire
de l’erreur quadratique moyenne entre le modèle et le signal (algorithme du type Gauss-
Newton). L’onde T est segmentée en analysant les dérivées première et seconde de l’équation
obtenue. Des améliorations de segmentation en comparaison avec l’algorithme basé sur
la dérivée filtrée [Laguna et al., 1994] ont été reportées. Ainsi, cette approche devient
intéressante en présence de bruit [Wong, 2004]. Une limitation de la méthode est qu’elle ne
permet que la segmentation de l’onde T.
3.1.4 Algorithme basé sur le réalignement temporel
Dans cette méthode, le battement à segmenter est comparé et ré-aligné avec une
base de données de battements préalablement segmentés. Un réalignement temporel par
programmation dynamique (DTW, Dynamic Time Warping) est utilisé et consiste à réaligner
les points d’une série temporelle un à un, sur une autre série prise comme référence, de
manière à minimiser une distance cumulée sur l’ensemble des points. La méthodologie à
base de DTW peut être soit une approximation linéaire par morceaux [Vullings et al., 1997]](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-79-320.jpg)
![50 Chapitre 3
ou soit une approximation constante adaptative par morceaux [Zifan et al., 2006]. Cette
méthode est dépendante de l’ensemble des battements de référence et il est difficile de
comparer tous les battements annotés au battement à traiter en temps réel.
3.1.5 Algorithme basé sur la modélisation Markovienne
Les modèles Markoviens ont été d’abord appliqués pour la segmentation des complexes
QRS en 1993 [Coast, 1993], puis pour la segmentation de l’ensemble des ondes [Thora-
val, 1995]. Les premiers modèles ont intégré dans les états des informations de pentes,
d’amplitudes ou de durées des ondes [Koski, 1996; Clavier and Boucher, 1996]. De plus,
en exploitant les coefficients d’une décomposition en ondelettes, de bons résultats ont été
obtenus [Hughes et al., 2003]. Les modèles de Markov sont particulièrement adaptés pour
la décomposition de la séquence ECG. Cependant, leur application sur de grandes bases de
données est peu fréquente. En effet, le choix des caractéristiques dont la dynamique doit
être modélisée demeure un problème, ainsi que le grand nombre de données nécessaires à
l’apprentissage.
3.1.6 Algorithme basé sur la transformée en ondelettes
La transformée en ondelettes fait partie des méthodes d’analyse de signaux, dites
temps-échelle, qui ont suppléé la transformée de Fourier pour l’analyse des signaux non
stationnaires. La transformée en ondelettes décompose un signal f(t) en une somme pondérée
de fonctions de bases qui sont des versions dilatées et translatées d’une fonction ψ appelée
ondelette mère :
f(t) =
a∈Z k∈Z
cakψ(sa
t − k) (3.1)
Pour un scalaire s fixé, tel que |s| < 1, le coefficient a contrôle l’échelle à laquelle le
signal est analysé : si a est grand, les caractéristiques temporelles longues (i.e. les basses
fréquences) sont analysées ; si a est faible les caractéristiques courtes (les hautes fréquences)
sont analysées.
Les ondes P et T ont des durées statistiquement similaires et occupent de ce fait, dans
l’espace transformé, le même ensemble d’échelles d’analyse car les composantes fréquentielles
de ces ondes se recouvrent totalement. Cependant, la durée des ondes P et T est très différent
à la durée du complexe QRS et en conséquence l’ensemble d’échelles d’analyse du complexe
QRS est différent. Une portion des composantes fréquentielles de ce dernier recouvre la
totalité des composantes fréquentielles des ondes P et T.
Les extrema locaux de la décomposition d’un niveau de résolution correspondent aux](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-80-320.jpg)
![3.2. Détection et segmentation automatique du QRS 51
plus fortes pentes présentes dans le signal ECG et aux passages par zéro des extrema
locaux du signal ECG. La recherche des minima et maxima passe par la définition des
fenêtres temporelles, limitant la zone de recherche, et par la définition de seuils, permettant
uniquement la conservation des minima et maxima significatifs.
La principale difficulté de cette méthode est liée à la définition de nombreux paramètres,
les fenêtres temporelles et les seuils, qui sont ajustés empiriquement. Pour résoudre ce
problème, une solution a été proposée [Dumont et al., 2010]. Il s’agit d’une chaîne de
segmentation d’ECG dont les paramètres de la méthode de segmentation ont été optimisés
par algorithmes évolutionnaires.
3.2 Détection et segmentation automatique du QRS
Les paragraphes qui suivent ont pour volonté de présenter la chaine de traitement
que nous avons développée. De manière générale, la segmentation automatique de l’ECG
peut être décomposée en trois grandes étapes (montrées figure 3.1) et expliquées dans les
sous-sections suivantes.
Segmentation des
battements
Détection des
battements
Pré-traitement
de l'ECG
Extraction des
battements
Figure 3.1 – Étapes de la segmentation du signal ECG
3.2.1 Pré-traitement de l’ECG
Cette étape consiste principalement à éliminer certains bruits qui perturbent le signal
ECG tels que :
– Les déviations de la ligne de base : Elles correspondent aux déviations de basses-
fréquences de l’amplitude de l’ECG liées principalement aux mouvements du patient
et à sa respiration. Plusieurs techniques ont été développées afin de soustraire la ligne
de base de l’ECG : le filtrage adaptatif et les approximations par splines [Meyer and
Keiser, 1977; Sörnmo, 1993; Jane et al., 1992]. Toutefois, pour résoudre ce problème
particulier, nous avons choisi d’appliquer un algorithme à base de bancs de filtres multi-
cadences [Shusterman et al., 2000]. Les étapes de filtrage et de sous-échantillonnage
de cet algorithme permettent de réaliser un filtre dont la fréquence de coupure est
bien maîtrisée, tout en évitant les déphasages et les temps de calcul plus longs qui
seraient introduits par un filtre unique (mais d’ordre plus élevé).
– L’interférence à 50/60 Hz : C’est un bruit qui provient de l’alimentation des
appareils de mesure. Pour éliminer cette interférence, des méthodes basées sur des](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-81-320.jpg)
![52 Chapitre 3
filtres passe-bande ou des filtres adaptatifs sont utilisées [Levkov et al., 2005]. Dans
ce mémoire, le filtrage adaptatif a été retenu car il permet de suivre les changements
de phases et d’amplitudes de l’interférence [Ziarani and Konrad, 2002].
3.2.2 Détection des battements
La seconde étape est associée à la détection des complexes QRS de l’ECG. La dé-
tection automatique des battements a connu depuis de nombreuses années de multiples
développements. Une bibliographie est reportée dans [Köhler et al., 2002].
Nos avons utilisé un algorithme de détection des QRS en temps réel développé dans
notre laboratoire [Cruz, 2007]. Cet algorithme est inspiré du travail de PAN et TOMP-
KINS [Pan and Tompkins, 1985]. Il calcule la position d’un point, appelé point fiducial
(PF), correspondant à la pente maximale, pour chaque complexe QRS détecté. Ce point se
situe où la version filtrée passe-bande du signal ECG présente l’énergie la plus élevée.
L’algorithme de détection des QRS adapté peut être représenté de façon synthétique
comme l’illustre la figure 3.2. Les quatre premières étapes sont analogues à celles proposées
par PAN et TOMPKINS [Pan and Tompkins, 1985], où premièrement le signal ECG (x[n])
est traité par un filtre passe-bande (cascade des filtres passe-bas et passe-haut) avec des
fréquences de coupure fcLow et fcHigh pour produire xPB[n]. Deuxièmement, la sortie
(xPB[n]) est dérivée (xD[n]) et troisièmement une quadration est appliquée au signal dérivé
pour produire xQ[n] qui est ensuite intégré sur une fenêtre glissante de taille TMWI afin de
produire xI[n]. Le signal ECG à traiter par le détecteur des battements est gardé dans un
tampon circulaire de taille HISTO et le processus commence lorsque le tampon est rempli.
La dernière étape de la chaîne de détection des QRS est basée sur des seuils qui
sont continuellement ajustés par un ensemble de règles heuristiques, afin de suivre les
changements du signal ECG. Cependant, au lieu d’utiliser deux ensembles de seuils, comme
dans le travail de PAN et TOMPKINS [Pan and Tompkins, 1985], un seuil référé aux
maxima du signal transformé xI[n], est utilisé.
Le seuil adaptatif (THR) est calculé en utilisant l’équation 3.2, où δ est une constante,
Speak est la moyenne des NP pics du signal supérieur à THR (Speak) et Npeak est la
moyenne des NP pics du signal inférieur THR (Npeak). Speak et Npeak sont déterminés
en utilisant les équations 3.3 et 3.4, respectivement. Les pics supérieurs à THR sont classés
comme des complexes QRS (y[n]).
THR = Npeak + δ(Speak − Npeak) (3.2)](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-82-320.jpg)
![3.2. Détection et segmentation automatique du QRS 53
Filtre
passe-bande
ECG
Pics du QRS
Filtre
différenciateur
Quadration
Intégrateur
Règles de décision
Figure 3.2 – Représentation en bloc du processus de détection des battements.
Speak =
1
NP
NP
i=1
Speaki (3.3)
Npeak =
1
NP
NP
i=1
Npeaki (3.4)
L’algorithme applique une période de suppression réfractaire (TRefr) et une fenêtre
de recherche (TPeak) dans le signal filtré passe-bande (xPB[n]) pour la détection de crête
maximale (PF). Si un QRS n’est pas trouvé pendant TRRlim, le seuil THR est réinitialisé et
un nouveau processus de détection des QRS commence à partir du dernier QRS correctement
détecté.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-83-320.jpg)
![54 Chapitre 3
Le tableau 3.1 récapitule les paramètres du détecteur des battements à optimiser. Le
pseudo-code de la méthode de détection des battements utilisée est montré dans l’algo-
rithme 1.
Tableau 3.1 – Paramètres de la méthode de détection des battements à optimiser.
Paramètre Description
fcLow Fréquence de coupure du filtre passe-bas
fcHigh Fréquence de coupure du filtre passe-haut
TMWI Taille de la fenêtre glissante de l’intégrateur
NP Nombre de pics pour déterminer sa valeur moyenne
δ Constante pour la détermination du seuil adaptatif
TRefr Période de suppression réfractaire
TPeak Taille de la fenêtre pour détecter la crête maximale QRS
TRRlim Temps limite pour réinitialiser la détection des QRS
Algorithme 1 Pseudo-code de la méthode de détection des battements.
// Filtrage passe-bande
Réaliser le filtrage passe-bande de x pour obtenir xP B
// Différenciateur
Calculer la dérivée de xP B pour obtenir xD
// Quadration
xQ[n] = xD[n]2
// Intégrateur
Réaliser l’intégration de xQ dans une fenêtre glissante de taille TMW I afin d’obtenir xI
// Initialisation de THR
Pendant une période de TINI secondes (usuellement initialisé à 6 secondes), estimer
xImax = max(xI)
Détecter les pics > xImax/2
Utiliser ces pics comme les premiers QRS
Initialiser les premiers NP Npeak pics à 0
Calculer THR selon l’équation 3.2
// Règles de décision
Ignorer les pics qui sont détectés TRefr secondes après le dernier QRS
Classifier le pic comme Speak s’il est plus grand que THR ou Npeak en cas contraire
Actualiser la valeur de THR selon l’équation 3.2
Chercher la crête maximale du QRS dans xP B, TPeak seconds avant Speak
Réinitialiser THR s’il n’y a pas eu de détection pendant TRRlim
3.2.3 Extraction des battements
Chaque battement détecté est extrait de l’ECG et délimité dans une fenêtre temporelle
autour du complexe QRS. Il est ensuite recalé sur des battements prototypes qui représentent
des types de morphologies différentes. Les battements prototypes sont créés par la moyenne
des battements les plus récents détectés dans un historique de 10 secondes. Seuls les
battements qui présentent une corrélation croisée normalisée supérieure à 0,96 sont utilisés](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-84-320.jpg)
![3.2. Détection et segmentation automatique du QRS 55
pour mettre à jour les battements prototypes. Dans le cas contraire, le battement courant
devient alors lui-même un prototype.
3.2.4 Segmentation des battements par ondelettes
L’étape de segmentation automatique est la plus complexe. En effet, effectuer une
délimitation précise des ondes est une tâche difficile pour plusieurs raisons : i) le signal ECG
est non-stationnaire, ii) les battements peuvent présenter un rapport signal sur bruit (RSB)
faible, iii) une grande variété de morphologies d’ondes existe, même parmi les sujets sains,
iv) il n’y a pas de définition universelle sur les positions des bornes des ondes (en particulier
pour les ondes Q et T), la variabilité portant sur la segmentation peut être élevée même
entre cardiologues [Party, 1985] et v) les composantes spectrales des ondes se chevauchent.
Compte-tenu de ces difficultés, une approche temps-fréquence a été retenue dans cette
thèse pour segmenter les battements telle que l’algorithme basé sur la transformée en
ondelettes initialement proposé par LI et al. [Li et al., 1995] et modifié récemment par
DUMONT et al. [Dumont et al., 2010].
Dans l’algorithme de segmentation par ondelettes, chaque battement prototype actualisé
est décomposé en cinq niveaux de détail, W1
2 à W5
2 , par une cascade de filtres (en octave) :
des filtres de détail G(z) (passe-haut) et des filtres d’approximation H(z) (passe-bas).
La délimitation précise des ondes est faite en utilisant des règles de décision basées sur
l’amplitude du signal décomposé. Afin de favoriser la résolution temporelle dans les différentes
échelles et l’invariance temporelle, la cascade de filtres est implémentée sans décimation
(même fréquence d’échantillonnage dans toutes les échelles de décomposition) [Martínez
et al., 2004]. La figure 3.3 montre les différentes étapes de la segmentation des battements
par transformée en ondelettes. Pour ne pas alourdir la présentation, nous avons reporté la
présentation de la transformée en ondelettes annexe B.
En raison du contenu à haute fréquence des complexes QRS, seules la première et la
deuxième échelle ont été analysées dans cette thèse. Dans la version initiale de l’algorithme,
les échelles 3 à 5 sont utilisées pour la segmentation des ondes P et T [Dumont et al., 2010].
Dans ce travail les ECG de la base de données ne montrent pas ces ondes de façon claire et
cette possibilité n’a donc pas été explorée.
Plusieurs paramètres temporels et de seuils sont utilisés afin de trouver les limites des
ondes. Les paramètres temporels sont :
– TR1 et TR2, utilisés pour la recherche des ondes R avant et après le PF,
– TQlim utilisé pour trouver l’onde Q,
– TSlim utilisé pour rechercher les ondes S.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-85-320.jpg)
![56 Chapitre 3
Corrélation et
Moyennage
Règles de
décision
Règles de
décision
Détection:
QRSon,
Q, R, S
et QRSoff
Détection:
Pon, P et Poff
Ton, T et Toff
Banc de filtres de la décomposition en ondelettes
Battements
templates
Battements
Figure 3.3 – Banc de filtres de la décomposition en ondelettes (sans décimation). G(z) et
H(z) sont respectivement les filtres passe-haute et passe-bas. Wk
2 x[n] sont les sorties des
filtres aux échelles 2k (k = 1, 2, . . . , 5) pour le battement x[n].
Pour faire face aux variations importantes de la FC observées chez les nouveaux-nés
prématurés, une approche, proposée ici, est de définir les différents paramètres temporels
comme des versions proportionnelles à l’intervalle RR :
Ti = miRR (3.5)
où i ∈ {R1, R2, Qlim, Slim}, et mi est le facteur d’échelle devant être optimisé.
Les seuils liés aux amplitudes sur la deuxième échelle de la transformation en ondelettes
(W2
2 ) sont également exprimés en tant que facteurs proportionnels comme suit :
– Le seuil γQRSpre est utilisé pour trouver des pentes significatives de l’onde Q. Il est
proportionnel à l’amplitude maximale de l’échelle 2 dans la fenêtre de recherche
TQlim et est donné par :
γQRSpre = mγQRSpre max(|W2
2 x[n]|) (3.6)
où mγQRSpre est le facteur d’échelle à être optimisé et n ∈ TQlim
– Le seuil γQRSpost est utilisé pour trouver des pentes importantes de l’onde S. Il est
proportionnel à l’amplitude maximale de l’échelle 2 dans la fenêtre de recherche
TSlim. Il est calculé en utilisant l’équation 3.7, où mγQRSpost est le facteur d’échelle](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-86-320.jpg)
![3.2. Détection et segmentation automatique du QRS 57
à être optimisé et n ∈ TSlim.
γQRSpost = mγQRSpost max(|W2
2 x[n]|) (3.7)
– Le seuil ξQRSon est utilisé pour la recherche du début du complexe QRS (QRSon). Il
est lié à l’amplitude de la première pente importante dans W2
2 , et est calculé comme
suit :
ξQRSon =
mξQRSonp
W2
2 x[nfirst] ∀ W2
2 x[nfirst] > 0
mξQRSonn
W2
2 x[nfirst] ∀ W2
2 x[nfirst] < 0
(3.8)
où mξQRSonp
et mξQRSonn
sont les facteurs d’échelle à être optimisés et W2
2 x[nfirst]
correspond à l’échelle 2 de la décomposition en ondelettes du signal x à la première
pente significative (nfirst).
– Le seuil ξQRSoff est utilisé pour la recherche de la fin du complexe QRS (QRSoff). Il
est lié à l’amplitude de la dernière pente significative dans W2
2 , et est donné par :
ξQRSoff =
mξQRSoffp
W2
2 x[nlast] ∀ W2
2 x[nlast] > 0
mξQRSoffn
W2
2 x[nlast] ∀ W2
2 x[nlast] < 0
(3.9)
où mξQRSoffp
et mξQRSoffn
sont les facteurs d’échelle à être optimisés et W2
2 x[nlast]
correspond à l’échelle 2 de la décomposition en ondelettes du signal x à la dernière
pente significative (nlast).
Un test pour vérifier si les pics trouvés sont plus éloignés du niveau iso-électrique que
le début ou la fin du complexe QRS a été effectué comme dans les travaux de DUMONT
et al. [Dumont et al., 2010]. Par conséquent, la détection du niveau iso-électrique (ISOp)
est une contrainte importante. SMRDEL et JAGER [Smrdel and Jager, 2004] définissent
le ISOp comme la partie la plus plate dans l’intervalle PQ. Ce niveau iso-électrique est
segmenté en définissant les paramètres temporels suivants :
– TPQ : fenêtre de recherche temporelle pour le ISOp.
– TIso : taille de la fenêtre où la forme d’onde est la plus plate.
TPQ et TIso peuvent aussi être représentés comme une fonction de l’intervalle RR en
utilisant l’équation 3.5.
Le tableau 3.2 récapitule les paramètres de la méthode de segmentation des QRS
à optimiser. Le pseudo-code de la méthode de segmentation des QRS est montré dans
l’algorithme 2. La figure 3.4 résume les indicateurs temporels qui seront déterminés dans la
segmentation. Pour plus de détails concernant l’algorithme de segmentation, nous invitons
le lecteur à consulter les références [Martínez et al., 2004; Dumont et al., 2010].](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-87-320.jpg)
![58 Chapitre 3
Tableau 3.2 – Paramètres de la méthode de segmentation des QRS à optimiser.
Paramètre Description Utilisation
mR1 Constante de proportionnalité TR1 = mR1RR
mR2 Constante de proportionnalité TR2 = mR2RR
mQlim Constante de proportionnalité TQlim = mQlimRR
mSlim Constante de proportionnalité TSlim = mSlimRR
mγQRSpre Constante de proportionnalité γQRSpre = mγQRSpre max(|W2
2 x[n]|)
mγQRSpost Constante de proportionnalité γQRSpost = mγQRSpost max(|W2
2 x[n]|)
mξQRSonp
Constante de proportionnalité ξQRSon = mξQRSonp
W2
2 x[nfirst]
mξQRSonn
Constante de proportionnalité ξQRSon = mξQRSonn
W2
2 x[nfirst]
mξQRSoffp
Constante de proportionnalité ξQRSoff = mξQRSoffp
W2
2 x[nlast]
mξQRSfofn
Constante de proportionnalité ξQRSoff = mξQRSoffn
W2
2 x[nlast]
mPQ Constante de proportionnalité TPQ = mPQRR
mISO Constante de proportionnalité TIso = mISORR
Q
R
S
QRSoffQRSon
ISOp
Figure 3.4 – Indicateurs à repérer pour l’algorithme de segmentation.
3.3 Optimisation de la chaîne de segmentation d’ECG
Comme indiqué précédemment, les paramètres du processus de détection des battements
et les paramètres de la méthode de segmentation des complexes QRS doivent être adaptés
au traitement des signaux ECG acquis des nouveaux-nés prématurés, caractérisé par un
faible RSB, une FC plus élevée et de fréquents épisodes de bradycardie.
Dans le problème d’optimisation, le modèle est connu, ainsi que la réponse souhaitée
(sortie). La tâche consiste à trouver les entrées qui conduisent à cette sortie [Eiben and Smith,
2003], comme l’illustre simplement la figure 3.5. Ainsi, dans le problème d’optimisation
posé, l’objectif est de trouver une solution globalement satisfaisante de l’ensemble des
paramètres (entrées) des méthodes de la chaîne de segmentation (modèle), afin que la
segmentation automatique (sortie) ressemble aux annotations manuelles des cardiologues
des ondes enregistrées dans une base de données (spécifiées).
Cependant, des contraintes doivent être prises en compte dans le choix de la procédure](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-88-320.jpg)
![3.3. Optimisation de la chaîne de segmentation d’ECG 59
Algorithme 2 Pseudo-code de la méthode de segmentation des QRS.
Calculer les niveaux de décompositions W1
2 x[n] et W2
2 x[n]
// Détection de l’onde R
Calculer TR1 et TR2 selon l’équation 3.5
Définir une fenêtre de recherche sur W2
2 x[n] de TR1 secondes avant et TR2 secondes après le PF
Calculer les deux plus grandes extrémités de signes opposés de cette fenêtre (npre et npost) centrés
dans le PF
L’onde R correspond au croisement par zéro entre ces deux extrémités sur W1
2 x[n]
En cas de plusieurs croisements par zéro, utiliser celui associé à la plus grande amplitude de x[n]
// Détection du ISOp
Calculer TP Q et TIso selon l’équation 3.5
Définir une fenêtre de recherche sur x[n] de TP Q secondes avant l’onde R
Le ISOp correspond à la partie la plus plate de taille TIso de cette fenêtre
// Détection de l’onde Q
Calculer TQlim selon l’équation 3.5
Calculer mγQRSpre
selon l’équation 3.6
Définir une fenêtre de recherche sur W2
2 x[n] de TQlim secondes avant npre
Calculer les maxima locaux de cette fenêtre supérieure à mγQRSpre
Calculer les croisements par zéro entre ces maxima locaux sur W1
2 x[n].
L’onde Q est sélectionnée selon le signe et la séquence des maxima locaux
// Détection du QRSon
Calculer ξQRSon selon l’équation 3.8
Définir une fenêtre de recherche sur W2
2 x[n] de TQlim secondes avant npre
Chercher le premier maximum local (nfirst) dans cette fenêtre
Chercher le point où W2
2 x[n] est inférieur à ξQRSon : QRSon1
Calculer les minima locaux avant nfirst
QRSon est le point le plus proche du complexe QRS entre QRSon1 et les minima trouvés
// Détection de l’onde S
Calculer TSlim selon l’équation 3.5
Définir une fenêtre de recherche sur W2
2 x[n] de TSlim secondes après npost
Calculer les maxima locaux de cette fenêtre supérieure à mγQRSpost
Calculer les croisements par zéro entre ces maxima locaux sur W1
2 x[n].
L’onde S est sélectionnée selon le signe et la séquence des maxima locaux
// Détection du QRSoff
Calculer ξQRSoff selon l’équation 3.9
Définir une fenêtre de recherche sur W2
2 x[n] de TSlim secondes après npost
Chercher le dernier maximum local (nlast) dans cette fenêtre
Chercher le point où W2
2 x[n] est inférieur à ξQRSoff : QRSoff1
Calculer les minima locaux après nlast
QRSoff est le point le plus proche du complexe QRS entre QRSoff1 et les minima trouvés
Modèle
connu
Entrée
?
Sortie
spécifié
Figure 3.5 – Le problème d’optimisation.
d’optimisation. Par exemple, la présence des multiples optima locaux de la fonction de coût
peuvent conduire à des mauvais choix de paramètres. En outre, les algorithmes de la méthode
de segmentation sont composés de différents paramètres (seuils, fenêtres temporelles, . . . ) et
de fait, le critère évaluant les performances sera très certainement une fonction discontinue
dans l’espace des paramètres. Ces contraintes ne sont pas compatibles avec l’utilisation](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-89-320.jpg)
![60 Chapitre 3
des méthodes d’optimisation multivariées basées sur les gradients (méthodes de Gauss-
Newton) ou des méthodes du simplex [Nelder and Mead, 1965], qui risquent de s’arrêter
dans des minima locaux. D’un autre côté, les méthodes d’optimisation stochastique, telles
que les algorithmes évolutionnaires (AE) [Eiben and Smith, 2003], dont la continuité de
la fonction de coût ainsi que sa dérivée ne sont pas exigées, sont particulièrement bien
adaptés pour ce type problème. Les AE, méthodes d’optimisation inspirées sur les théories de
l’évolution et la sélection naturelle, ont d’ailleurs déjà été utilisés avec succès dans différentes
applications biomédicales, pour estimer de larges ensembles de paramètres [Hernández et al.,
2002; Herrero et al., 2008; Dumont et al., 2010]. Les fondements sur les AE sont reportés
annexe C.
3.3.1 Méthode proposée
Le problème d’adaptation peut être considéré comme la minimisation d’une fonction
de coût en comparant les événements observés (annotations des ondes) et la sortie de
l’algorithme (détection des ondes).
Deux AE indépendants ont été appliqués de manière séquentielle : le premier, nommé
AE1, permet d’optimiser les paramètres du détecteur des battements alors que le second,
AE2, permet d’optimiser les paramètres de la méthode de segmentation des QRS. Un
schéma explicatif est montré dans la figure 3.6. Un tel fractionnement est possible car la
segmentation des QRS ne sera optimale que si le détecteur de battements est déjà optimisé.
Détection de batements
AE1
Base de données
Segmentation des QRS
AE2
Paramètres
optimisés
Base de données
Figure 3.6 – Optimisation par application des AE de manière séquentielle.
La figure 3.7 montre la méthodologie à suivre pour optimiser les paramètres à partir d’une
base de données annotée appropriée et un AE. Les types d’annotations sont différents dans
chaque méthodologie : des annotations du PF pour optimiser le détecteur des battements
(AE1) et des annotations du ISOp et de la position du pic de l’onde R, du QRSon et du
QRSoff pour optimiser la segmentation des QRS (AE2).
L’AE minimise une fonction de coût qu’il convient de définir. Comme proposé par
DUMONT et al. [Dumont et al., 2010], la fonction coût devant être minimisée par l’AE
combine trois critères :
1. La probabilité d’erreur de détection (Perr) : Il s’agit d’une estimation quan-
titative de la performance de la méthode. Elle est déterminée par l’équation 3.10,](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-90-320.jpg)

![62 Chapitre 3
Les fonctions de coût (CF1 et CF2 pour AE1 et AE2) sont alors calculées comme suit :
CF1 = PerrPF + µDJPF + σDJPF (3.13)
CF2 =
I
i=1
Perri + µDJi + σDJi (3.14)
où PF est le point fiducial et i ∈ {onde R, QRSon, QRSoff, ISOp}.
3.3.2 Optimisation des paramètres
Dans AE1, servant à optimiser le détecteur des battements, les paramètres à optimiser
ont été largement modifiés par rapport aux paramètres originaux montrés dans [Pan and
Tompkins, 1985] pour créer la population initiale. Dans AE2, utilisé pour optimiser la
méthode de segmentation des complexes QRS, les paramètres d’échelle liés à la fenêtre
de recherche temporelle ont été définis à partir des positions extrêmes possibles et des
connaissances physiologiques sur la durée de chaque onde, alors que les paramètres liés à
l’échelle des seuils ont été largement modifiés par rapport à ceux proposés dans [Martínez
et al., 2004; Dumont et al., 2010], pour créer la population initiale. La sélection par
classement et les opérateurs génétiques standards des chromosomes à valeurs réelles (cross-
over simple, arithmétique et heuristique, mutation multi-non uniforme et non uniforme)
ont été utilisés dans les deux AE [Michalewicz, 1996].
Vingt paramètres ont été employés dans la méthodologie d’optimisation : huit à partir
du détecteur des battements (tableau 3.1) et douze à partir de la méthode de segmentation
automatique des complexes QRS (tableau 3.2). Les AE ont été appliqués pour 80 générations
de 200 individus, avec une probabilité de croisement de 0,7 et une probabilité de mutation
élevée pendant les premières générations et faible à la fin [Bäck and Schütz, 1996]. Une
comparaison des performances avant et après optimisation des paramètres dans les deux
méthodes a été réalisée par l’évaluation de SEN (équation 2.1), VPP (équation 2.4), µDJ
(équation 3.11) et σDJ (équation 3.12) sur des ensembles de test.
Pour résoudre ce problème d’optimisation, deux sous-ensembles de données (DB1 et
DB2), constitués à partir de la base de données détaillée dans la section 2.2 page 37 ont été
formés (c.f. figure 3.8) :
1. Le sous-ensemble DB1, appliqué pour adapter la méthode de détection des batte-
ments de l’ECG du nouveau-né prématuré, est composé de 50 segments d’ECG, définis
sur un support temporel de cinq minutes avant le début d’un épisode de bradycardie
jusqu’à deux minutes après la fin, et ne contenant qu’un seul épisode de bradycardie
pendant toute cette période. Ce sous-ensemble est composé de segments d’ECG d’un
ou plusieurs patients. Seulement 27 patients de la base de données ont présenté au
moins un épisode tel que décrit ci-dessus. DB1 est caractérisée par 51655 battements](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-92-320.jpg)
![3.3. Optimisation de la chaîne de segmentation d’ECG 63
(autour de 1000 battements par segment ECG). Les positions de l’onde R ont été
annotées pour chaque battement par un expert.
2. Le sous-ensemble DB2, appliqué pour adapter la méthode de segmentation des
QRS de l’ECG du nouveau-né prématuré, est composé de 93 segments d’ECG, choisis
au hasard à partir de la base de données complète et avec au moins un segment
ECG par patient. Chaque segment d’ECG est composé d’une phase de repos, suivie
d’un ou plusieurs épisodes de bradycardie. Ce fichier est composé de 4464 battements
(48 battements par segment). Les positions de l’onde R, du QRSon, du QRSoff et du
ISOp ont été annotées pour chaque battement par un expert. Obtenir ces annotations
battement à battement est une tâche difficile, particulièrement en présence de bruit.
Des annotations précises ont pu être obtenues uniquement pour les 93 segments d’ECG
sélectionnés.
Dans tous les cas, les événements de bradycardie ont été détectés et annotés par
l’analyse de l’intervalle RR. Un épisode de bradycardie est défini comme une augmentation
de l’intervalle RR sur un seuil fixé à 600 ms, pendant une durée de quatre secondes ou
plus [Poets et al., 1993]. Les moniteurs néonataux sont en général basés sur cette méthode
de détection simple.
Enregistrements d'ECG
- 32 nouveau-nés prématurés
- Apnée-bradycardie récurrent
DB1L
- 25 segments d'ECG
- 50 battements par segment
DB2:
- Permet d'adapter la méthode de segmentation
du QRS
- 93 segments d'ECG contenant episodes
de repos et de bradycardie
- 48 battements par segment
- Annotation: position du ISOp, QRSon, QRSoff
et onde R.
DB1:
- Permet d'adapter la méthode de détection
des battements
- 50 segments d'ECG
- 1 bradycardie par segment
- segments d'ECG > 7 minutes
- Annotation: position des ondes R
DB2L
- 47 segments d'ECG
DB2T
- 46 segments d'ECG
DB1T
- La totalité du DB1
Figure 3.8 – Construction des différentes bases de données utilisées pour effectuer les
processus d’adaptation et la phase d’évaluation.
Deux ensembles d’apprentissage et deux ensembles de test ont été construits pour réaliser
l’optimisation (voir Figure 3.8) :
– Le premier ensemble d’apprentissage (DB1L) est composé de 25 segments
d’ECG à partir de DB1 (la moitié des segments d’ECG de DB1). Cette base de
données est utilisée pour AE1.
– Le deuxième ensemble d’apprentissage (DB2L) constitué à partir de DB2,
contient 47 segments d’ECG choisis au hasard. Cette base de données est utilisée
pour AE2.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-93-320.jpg)
![64 Chapitre 3
– Le premier ensemble de test (DB1T), utilisé pour tester les paramètres optimaux
trouvés pour le détecteur de battement, est composé de l’ensemble DB1.
– Le deuxième ensemble de test (DB2T) basé sur DB2 contient les 46 autres
segments d’ECG. Cette base de données est utilisée pour tester les paramètres
optimaux du processus de segmentation des QRS.
Plusieurs morphologies de complexes QRS sont présentes dans ces quatre ensembles
de données. La comparaison entre les annotations et les détections a été réalisée dans une
fenêtre temporelle de 10 ms.
3.4 Résultats de détection et de segmentation
Les résultats sont présentés en deux parties : i) l’évaluation de la détection des battements
avec les paramètres optimaux obtenus par AE1 et ii) l’évaluation de la méthode de
segmentation des complexes QRS avec les paramètres optimaux obtenus par AE2. Par
simplicité, le signal ECG a été sur-échantillonné à 500 Hz, afin de s’accorder avec la fréquence
d’échantillonnage du détecteur des battements et la méthode de segmentation des QRS.
3.4.1 Performances du détecteur des battements
Les valeurs des paramètres du détecteur de battements avant et après la méthode
d’optimisation sont présentées dans le tableau 3.3. Ces valeurs ont été déterminées en
utilisant AE1 sur DB1L et ont été choisis comme les valeurs moyennes, pour cinq réalisations
différentes de l’AE, des meilleurs individus de la dernière génération. Comparativement à
ceux utilisés chez les adultes [Pan and Tompkins, 1985], les paramètres optimaux montrent
une augmentation des fréquences de coupure du filtre passe-bas et du filtre passe-haut, qui
indiquent évidemment que le complexe QRS des nouveaux-nés prématurés est généralement
plus fin, avec un contenu fréquentiel plus élevé que les QRS des adultes. En outre, on
observe une diminution de la taille de la fenêtre glissante de l’intégrateur, qui peut aussi
s’expliquer par la teneur plus élevée en fréquence du complexe QRS des prématurés. Ces
paramètres ont été utilisés pour évaluer la performance de la méthode de détection des
QRS sur DB1T.
Le tableau 3.4 montre les performances de la méthode de détection en utilisant DB1T,
avant (avec les paramètres réglés pour l’ECG d’adulte) et après (avec les paramètres
réglés pour l’ECG du prématuré) le processus d’optimisation. La SEN et la VPP ont été
obtenues en utilisant une fenêtre de recherche de 10 ms. Ce tableau montre clairement une
amélioration dans la détection du PF.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-94-320.jpg)
![3.4. Résultats de détection et de segmentation 65
Tableau 3.3 – Valeurs des paramètres de la méthode de détection des battements avant
(pour les adultes) et après (pour les nouveaux-nés prématurés) le processus d’optimisation.
Paramètre Avant Après Unité
fcLow 15 20,71 Hz
fcHigh 5 9,49 Hz
TMWI 150 78,41 ms
NP 5 7 Battements
δ 0,31 0,1485
TRefr 200 233,54 ms
TPeak 20 30,75 ms
TRRlim 1500 1959,46 ms
Tableau 3.4 – Performances du détecteur des battements avant et après le processus
d’optimisation. Avant : paramètres réglés pour l’ECG d’adulte, Après : paramètres réglés
pour l’ECG du prématuré.
Indicateur SEN (%) VPP (%) µDJ (ms) σDJ (ms)
Avant Après Avant Après Avant Après Avant Après
PF 91,20 97,74 92,22 98,03 3,51 1,18 15,60 10,23
3.4.2 Performances de la méthode de segmentation des QRS
Le tableau 3.5 montre les paramètres optimaux de la méthode de segmentation des QRS
par ondelettes, en utilisant AE2 sur DB2L. Un exemple des valeurs de paramètres optimaux,
déterminé pour un intervalle RR typique de 400 ms, est illustré dans le tableau 3.6. Une
comparaison entre notre approche et les travaux de DUMONT et al. [Dumont et al., 2010],
ainsi que ceux de SMRDEL et JAGER [Smrdel and Jager, 2004] est également reportée dans
ce tableau. On observe une réduction de toutes les fenêtres de recherche et une augmentation
du seuil utilisé pour trouver les ondes Q (γQRSpre), du seuil lié à l’amplitude de la première
pente négative significative pour trouver le QRSon (ξQRSonn) et du seuil lié à l’amplitude
de la dernière pente négative significative pour trouver le QRSoff (ξQRSoffn). On peut
également observer une diminution du seuil de détection des ondes S (γQRSpost), du seuil lié
à l’amplitude de la première pente positive significative pour trouver le QRSon (ξQRSonp) et
du seuil lié à l’amplitude de la dernière pente positive significative pour trouver le QRSoff
(ξQRSoffp).
Le tableau 3.7 montre les performances de la méthode de segmentation des QRS basée
sur les ondelettes, en utilisant les paramètres optimaux sur DB2T, avant et après le processus
d’optimisation. Ce tableau montre une amélioration dans la détection du QRSon, QRSoff](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-95-320.jpg)
![66 Chapitre 3
Tableau 3.5 – Valeurs optimales des paramètres de la méthode de segmentation des QRS.
Paramètre Valeur
mR1 0,1211
mR2 0,0990
mQlim 0,1030
mSlim 0,1170
mγQRSpre 0,1241
mγQRSpost 0,0909
mξQRSonp
0,0486
mξQRSonn
0,0800
mξQRSoffp
0,1635
mξQRSoffn
0,6995
mPQ 0,1192
mISO 0,0149
Tableau 3.6 – Exemple des fenêtres de recherche et des seuils utilisés dans la méthode de
segmentation des QRS. Les paramètres de notre approche ont été déterminés en utilisant
les paramètres optimaux (Tableau 3.5) pour un intervalle RR typique de 400 ms. Les autres
approches correspondent aux paramètres utilisés par [Dumont et al., 2010] et [Smrdel and
Jager, 2004].
Paramètre Approche proposée Autres approches
TR1 48,44 ms 118† ms
TR2 39,60 ms 111† ms
TQlim 40,12 ms 88† ms
TSlim 46,80 ms 154† ms
mγQRSpre 0,1241 0,09†
mγQRSpost 0,0909 0,11†
mξQRSonp
0,0486 0,07†
mξQRSonn
0,0800 0,07†
mξQRSoffp
0,1635 0,21†
mξQRSoffn
0,6995 0,23†
TPQ 47,68 ms 108‡ ms
TISO 5,96 ms 20‡ ms
† [Dumont et al., 2010]
‡ [Smrdel and Jager, 2004]
et du ISOp. Cependant, pour trouver l’onde R, la SEN reste identique avant et après le
processus d’optimisation. Concernant le calcul de la VPP pour ces indicateurs, FP serait
toujours égal à 0 dans la fenêtre de recherche car ces indicateurs sont toujours présents.
Ceci conduirait à une VPP = 100 %.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-96-320.jpg)
![3.5. Analyse du QRS pour la caractérisation de l’apnée-bradycardie 67
Tableau 3.7 – Performances de la segmentation des QRS, avant et après le processus
d’optimisation. Avant : paramètres réglés pour l’ECG d’adulte, Après : paramètres réglés
pour l’ECG du prématuré.
Indicateur SEN (%) µDJ (ms) σDJ (ms)
Avant Après Avant Après Avant Après
Onde R 98,46 98,46 1,39 1,69 1,44 0,66
QRSon 40,33 90,21 43,48 3,07 11,61 1,27
QRSoff 77,07 80,24 7,81 4,49 5,64 2,64
ISOp 0 80,61 48,88 4,29 2,61 2,29
Les performances obtenues après le processus d’optimisation sont comparables à celles
rapportées par ailleurs dans la littérature en utilisant des paramètres et des bases de données
d’ECG standard d’adultes [Dumont et al., 2010; Martínez et al., 2004; Pan and Tompkins,
1985].
3.5 Analyse du QRS pour la caractérisation de l’apnée-bradycardie
3.5.1 Principe et objectif de l’étude
Une fois le complexe QRS détecté et segmenté, des nouvelles séries temporelles peuvent
être construites à partir des indicateurs tels que les amplitudes des ondes et la durée des
intervalles et segments de l’ECG. Dans ce travail les séries temporelles de la durée du cycle
cardiaque (RR), l’amplitude de l’onde R (Ramp) et la durée du complexe QRS (QRSd)
ont été déterminées et analysées pour chaque segment d’ECG de DB1. La série RR est
déterminée classiquement comme la différence successive des instants de détection des ondes
R de l’ECG. L’amplitude de l’onde R est déterminée comme la différence entre le pic de
l’onde R et le ISOp. La durée du complexe QRS est calculée comme la différence entre la
fin et le début du QRS (QRSoff − QRSon). La figure 3.9 montre la façon de déterminer
Ramp et QRSd pour un battement synthétique. Les séries correspondantes aux amplitudes
des ondes Q et S peuvent être analysées que dans certains cas. Ces ondes sont en effet de
très faible amplitude et parfois absentes de l’ECG acquis.
Quatre intervalles ont été utilisés pour analyser chaque série, comme illustré dans la
figure 3.10 :
– L’intervalle T1 défini dès le début de chaque segment d’ECG de DB1 (5 minutes
avant la bradycardie) jusqu’à la deuxième minute. Cet intervalle contient les FC au
repos (sans aucune perturbation liée à un événement d’apnée-bradycardie).](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-97-320.jpg)

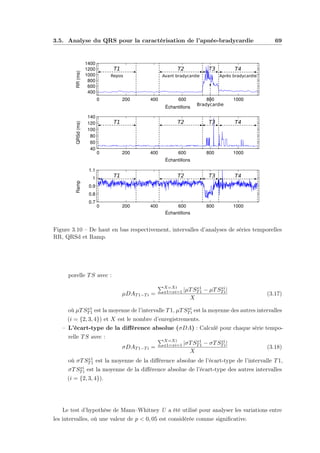
![70 Chapitre 3
3.5.2 Résultats
Les séries temporelles représentant RR, Ramp et QRSd ont été extraites des 50 segments
d’ECG de vingt-sept nouveaux-nés prématurés avec un épisode de bradycardie par segment.
Ces caractéristiques sont particulièrement intéressantes car une étude récente réalisée chez
l’adulte souffrant d’apnée obstructive du sommeil indique que les changements de la pression
intra-thoracique lors de l’épisode apnée obstructive du sommeil peuvent se traduire par des
changements dans les ondes de l’ECG [Penzel et al., 2006]. Une augmentation de la durée
du cycle cardiaque en présence de bradycardie peut élargir la durée de la dépolarisation des
ventricules correspondant à la durée du complexe QRS.
Le tableau 3.8 montre les valeurs de wµ et de wσ des séries temporelles RR, Ramp et
QRSd pour tous les intervalles analysés. Les résultats pour les séries RR et QRSd montrent
les valeurs les plus élevées pour l’intervalle T3 (cas de bradycardie), suivie par l’intervalle
T2 et les valeurs les plus faibles pour le T1. En ce qui concerne Ramp, la valeur le plus basse
de wµ est obtenue pour T3 (ainsi que la valeur la plus élevée pour wσ). Une diminution est
observée dans wµ de T1 à T3 ainsi qu’une augmentation de wσ de T1 à T3. La valeur le
plus grande de wµ est obtenue dans le dernier intervalle.
Tableau 3.8 – wµ et wσ des séries temporelles RR, Ramp et QRSd, pour tous les intervalles
analysés.
Série temporelle T1 T2 T3 T4
wµ wσ wµ wσ wµ wσ wµ wσ
RR (ms) 407,90 14,60 414,58 28,43 712,01 147,94 413,89 19,72
Ramp 0,8233 0,0605 0,8187 0,0638 0,8155 0,0754 0,8293 0,0661
QRSd (ms) 61,03 5,887 61,58 6,22 66,35 15,06 61,43 7,08
Les valeurs de µDA et de σDA sont indiquées dans le tableau 3.9. Ces valeurs sont
calculées entre l’intervalle T1 et les autres intervalles, pour les séries temporelles RR, Ramp
et QRSd. Pour toutes les séries temporelles, des valeurs élevées de µDA et de σDA sont
obtenues entre T1 et T3.
Les résultats des tests d’hypothèse de Mann–Whitney U sont présentés dans le ta-
bleau 3.10, calculé pour la moyenne des séries RR, Ramp et QRSd, entre les intervalles
analysés. Comme prévu, des différences significatives entre les intervalles T1 et T3 sont
observées pour les séries temporelles RR. En ce qui concerne la différence moyenne entre
l’intervalle T1 et les autres intervalles, des différences significatives ont été observées pour
toutes les séries temporelles lors de la comparaison T1 − T2 vs. T1 − T3 et T1 − T3 vs.
T1 − T4.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-100-320.jpg)





![76 Chapitre 3
d’ECG de 27 nouveaux-nés prématurés. Lorsque les valeurs de repos sont utilisés comme
référence (pendant T1), les tests d’hypothèse de Mann–Whitney U pour la moyenne
de chaque série temporelle ont montré des variations significatives (p < 0, 05) entre les
intervalles précédant la bradycardie et au cours de la bradycardie (T1−T2 vs. T1−T3). Des
variations significatives ont été aussi obtenus entre l’épisode de bradycardie et la période de
repos qui le suit (T1 − T3 vs T1 − T4). Ces résultats ont été obtenus pour toutes les séries
temporelles analysées.
Les principales contributions des travaux présentés dans ce chapitre ont été : i) la
proposition de méthodes de détection et de segmentation de l’activité électrique ventriculaire,
spécifiques au nouveau-né prématuré et ii) l’observation des modifications de l’amplitude
de l’onde R et de la durée du complexe QRS, associée à la survenue des épisodes d’apnée-
bradycardie.
Ces travaux ont été publiés dans un article de journal international [Altuve et al., 2011]
et dans une conférence internationale [Altuve et al., 2009]. Les résultats de ce chapitre
montrent les bénéfices potentiels d’une approche multidimensionnelle pour la détection
précoce et la caractérisation des apnée-bradycardies. D’autre part, l’analyse de différences
montre explicitement des distinctions entre la phase stable du bébé et la phase d’apnée-
bradycardie. Ceci suggère non pas d’analyser les valeurs instantanées mais plutôt de prendre
en compte les dynamiques de ces séries. L’objet du prochain chapitre est de proposer une
méthodologie adaptée à cette problématique.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-106-320.jpg)





![82 Chapitre 4
présentées. Ces modifications, qui constituent les principales contributions de ce chapitre,
concernent notamment l’utilisation des lois uniforme et non uniforme pour quantifier
les séries temporelles et la prise en compte des versions retardées de la série temporelle.
La première cherche à augmenter le rapport signal sur bruit et à optimiser le vecteur
d’observation par état. La deuxième cherche à incrémenter l’observabilité du système tout
en conservant le même nombre de sources. Une méthodologie empirique est enfin proposée
pour rechercher les valeurs optimales des paramètres des modèles.
4.1 Position du problème et état de l’art
4.1.1 Positionnement du problème
La détection des épisodes d’apnée-bradycardie est basée sur le fait que l’apnée du
prématuré entraîne souvent, quelques secondes après, un ralentissement de la FC et une
chute de la SpO2. Si l’apnée est souvent observée chez les nouveaux-nés prématurés, elle
n’est considérée pathologique que lorsqu’elle s’accompagne d’une bradycardie ou d’une
désaturation d’oxygène. La détection de l’apnée-bradycardie du prématuré a été largement
étudiée depuis quelques années. Cependant, la plupart ces travaux exploitent une seule
caractéristique extraite de l’ECG : la durée du cycle cardiaque sous forme d’une série
temporelle appelée RR. Parmi les travaux dédiés à détecter les épisodes d’apnée-bradycardie
on peut citer notamment ceux de :
– POETS [Poets et al., 1993] qui suggère l’utilisation d’un seuil relatif à l’amplitude de
la série RR,
– PRAVISANI et al [Pravisani et al., 2003] qui analysent les mesures linéaires et non
linéaires de la VFC par ACP et par analyse hiérarchique ascendante,
– CRUZ et al [Cruz et al., 2006], PORTET et al [Portet et al., 2007], et BELAL et
al [Belal et al., 2011] qui utilisent la technique des changements abrupts de valeur
moyenne,
– CRUZ et al [Cruz et al., 2006] qui réalisent une fusion optimale des détecteurs
d’apnée-bradycardie reportés dans la littérature,
– PORTET et al [Portet et al., 2007] qui exploitent diverses caractéristiques de la série
RR (superficie, pente, amplitudes minimale et maximale, dérivée, moyenne, etc.) par
arbres de décision,
– BELAL et al [Belal et al., 2011] qui utilisent les séries RR, fréquence respiratoire
et SpO2 pour détecter l’apnée du prématuré par des techniques comme la somme
cumulée, la corrélation et la dérivée.
Tel qu’il a été montré dans le chapitre précèdent, certaines caractéristiques extraites de
l’ECG, comme par exemple l’amplitude de l’onde R, la durée du complexe QRS et l’intervalle
RR, contiennent des informations pertinentes qui peuvent être prises en compte dans une](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-112-320.jpg)
![4.1. Position du problème et état de l’art 83
démarche de détection précoce de l’apnée-bradycardie. De plus, l’examen de ces séries
renseigne sur les différents systèmes physiologiques impliqués dans cette pathologie (système
nerveux autonome, respiratoire, circulatoire, etc.) et leur interaction avec l’environnement.
Comme déjà mentionné, l’intérêt principal de ce travail de thèse est de développer une
technique de détection des épisodes d’apnée-bradycardie robuste, efficace et applicable en
temps-réel, basée exclusivement sur des indicateurs extraits du signal ECG. Cette approche
pourrait, à terme, être intégrée dans un dispositif communicant, facile à appliquer sur les
nouveaux-nés, avec un encombrement minimal (seul l’ECG serait acquis). Ce travail se
place donc dans le domaine de la détection précoce d’événements dans un contexte bruité et
non-stationnaire, où l’extraction des connaissances nécessaires pour optimiser la détection
doit être réalisée à partir de bases de données cliniques multivariées.
4.1.2 Fouille de données temporelles multivariées
La fouille de données désigne le processus d’extraction de nouvelles informations non-
triviales et utiles (connaissances) à partir de grandes quantités de données, par l’utilisation
des méthodes issues de la statistique et de l’intelligence artificielle. Les méthodes de
fouille de données ont été appliquées sur des contextes variés, comme la prédiction, la
classification, le clustering, la recherche par contenu ou encore la visualisation et la détection
d’anomalies [Witten and Frank, 2005]. Quelques travaux ont été plus précisément consacrés
à l’analyse de séries temporelles [Povinelli, 2001; Kantardzic and Press, 2003; Mörchen, 2006;
Laxman and Sastry, 2006]. Ces méthodes de fouille de données peuvent être appliquées,
dans le domaine biomédical, pour identifier l’information utile contenue dans des larges
bases de données cliniques ou biologiques, afin d’en extraire des connaissances qui pourront
être exploitées dans une finalité diagnostique ou thérapeutique.
Dans ce travail de thèse, des méthodes de fouille de données temporelles et multivariées
sont proposées et appliquées dans le contexte de la détection d’événements physiopatho-
logiques. La figure 4.1 illustre ce problème d’extraction des connaissances à partir des
caractéristiques extraites de l’ECG. Trois exemples des séries RR, RAMP et QRSd y sont
reportés dans différents états physiopathologiques du nouveau-né prématuré : au repos
(en haut), en présence d’un ralentissement de la FC non pathologique (au milieu) et en
présence d’une bradycardie profonde (en bas). Sur les figures 4.1g, 4.1h et 4.1i, le début
de la bradycardie est indiqué par un losange et la détection effectuée par le système de
monitoring installé dans l’USIN est représentée par un cercle. Il apparaît clairement qu’une
analyse classique (basée uniquement sur les amplitudes instantanées de ces séries) ne serait
pas efficace. On observe également la complexité des séries à traiter. Les tendances cachées à
repérer peuvent être observées dans une ou plusieurs variables à la fois (cas uni et multivarié
respectivement), en même temps ou avec des différences significatives de phase. L’analyse
de l’évolution temporelle (dynamique) de ces variables n’est pas souvent prise en compte,](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-113-320.jpg)



![4.1. Position du problème et état de l’art 87
relève notamment des applications en traitement du signal, comme par exemple dans le
domaine de reconnaissance de la parole [Chibelushi et al., 2002; Beritelli et al., 2006; Dufour
et al., 2009], la bioinformatique [Mittag et al., 2010; Csizmok et al., 2008; Givaty and Levy,
2009], la climatologie [Maseng and Bakken, 1981; Kusiak et al., 2009; Fan et al., 2009],
etc. Cette caractérisation de dynamiques est fréquemment décomposée en deux problèmes
distincts [Mörchen, 2006] :
1. L’estimation de mesures de similarité, basée sur la forme ou sur les caractéristiques in-
trinsèques du signal. Les méthodes basées sur la forme nécessitent peu de connaissances
a priori et sont bien adaptées aux problèmes de classification, mais la résolution de
problèmes de prédiction et de prise en compte de données multivariées à dynamiques
hétérogènes n’est pas directe. Les méthodes basées sur les caractéristiques nécessitent
plus de connaissances a priori sur les données (sélection des caractéristiques infor-
matives). La définition d’une distance dans l’espace des caractéristiques n’est pas
évidente, qui plus est, dans le cas de données temporelles multivariées.
2. Les approches à base de modèles. Elles permettent, pour la plupart, la prise en compte
de séries temporelles multidimensionnelles et de différentes tailles. L’introduction de
connaissances a priori peut être réalisée à plusieurs niveaux de détail, en fonction de
l’application visée. Cette approche permet également de mesurer l’adéquation d’un
individu à un modèle donné (tâche de classification) ou de réaliser des prédictions,
par simulation. Cependant, elle est, en général, plus difficile à mettre en œuvre et est
particulièrement dépendante de la quantité et de la qualité des données utilisées dans
la période d’apprentissage ou de validation du modèle.
L’analyse des paragraphes précédents a orienté notre choix vers les approches à base de
modèles de type « boîte noire ». Ce choix se justifie par le fait que, dans notre problème de
caractérisation des dynamiques des séries temporelles extraites de l’ECG, i) les connaissances
a priori directement exploitables sont limitées, ii) plusieurs variables peuvent contenir de
l’information utile et ces variables doivent être traitées de manière conjointe (multivariée)
et iii) les dynamiques des différentes variables étudiées sont hétérogènes, car elles sont
la conséquence de processus physiologiques fonctionnant avec des constantes de temps
très différentes. De plus, les approches à base de modèles permettent d’aborder l’étape de
prédiction et les paramètres identifiés (même dans le cas des modèles à « boîte noire »),
peuvent être utilisés pour mieux comprendre les phénomènes physiologiques observés.
Plusieurs méthodes ont été proposées dans la littérature pour la modélisation des
dynamiques des séries temporelles multivariées :
– les modèles dans les espaces de phases reconstruits [Suzuki et al., 2003; Kong et al.,
2009; Garcia and Almeida, 2006],
– les filtres de Kalman [Kalman et al., 1960; Houtekamer and Mitchell, 2001; Fahrmeir,
1992],
– les réseaux bayésiens dynamiques [Murphy, 2002; Zweig and Russell, 1998],
– les réseaux de neurones artificiels [Raman and Sunilkumar, 1995; Bishop, 1995],](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-117-320.jpg)
![88 Chapitre 4
– les modèles de Markov cachés [Rabiner, 1989],
– les modèles semi-Markovien cachés [Ferguson, 1980; Yu, 2010].
Des travaux de doctorat récents effectués dans notre laboratoire (thèse de DUMONT J.
[Dumont, 2008]) ont été dédiés à l’étude et à la comparaison de ces principales méthodes de
modélisation des dynamiques sur des séries temporelles issues du domaine biomédical, dans
un cadre d’analyse de données physiologiques temporelles et multivariées. Les résultats de ce
travail ont montré que les modèles Markoviens cachés (MMC) et les modèles semi-Markoviens
cachés (MSMC) présentent un certain nombre de propriétés qui les rendent particulièrement
adaptés à la modélisation des dynamiques de séries temporelles en cardiologie.
Dans les sections suivantes, un rappel de la théorie des modèles de Markov et semi-
Markov cachés est présenté. L’approche méthodologique proposée dans les travaux de
DUMONT [Dumont, 2008; Dumont et al., 2008, 2009b,a] est ensuite décrite brièvement.
Enfin, des améliorations proposées dans le présent travail aux méthodes existantes sont
détaillées.
4.2 Les modèles de Markov et semi-Markov cachés
Dans cette section, une brève introduction aux MMC et MSMC et leurs propriétés de
base est présentée. Pour en savoir plus, on invite le lecteur à se reporter aux travaux de
EPHRAIM et MERHAV [Ephraim and Merhav, 2002] ou MACDONALD et ZUCCHINI
[MacDonald and Zucchini, 1997] pour les MMC et KULKARNI [Kulkarni, 2010] ou YU
[Yu, 2010] pour les MSMC.
Un MMC est un processus doublement stochastique où le processus stochastique sous-
jacent est une chaîne de Markov d’états finis et à temps discret. La séquence d’états n’est
pas observable (d’où le terme « caché ») et influence un autre processus stochastique qui
produit une séquence d’observations. La structure de base des MMC est illustrée dans la
figure 4.3.
S2S1 S3
O1 O2 O3
Observations
Chaîne de Markov (non observée)
Figure 4.3 – Structure de base d’un modèle de Markov caché.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-118-320.jpg)
![4.2. Les modèles de Markov et semi-Markov cachés 89
Introduits par BAUM et PETRIE [Baum and Petrie, 1966], les MMC ont été appliqués
dans un grand nombre de domaines comme :
– la biologie [Churchill, 1992; Pedersen and Hein, 2003; Munshaw and Kepler, 2010],
– la reconnaissance de la parole [Rabiner, 1989],
– le traitement de l’image [Yamato et al., 1992],
– la reconnaissance de texte [Chen et al., 1994].
Cependant, en raison d’une probabilité non nulle d’auto-transition d’un état, la durée d’un
état MMC suit une distribution géométrique. Cela rend les MMC inadaptés dans certaines
applications, telles que la reconnaissance des gènes humains dans l’ADN [Burge and Karlin,
1997] ou la modélisation des séries chronologiques financières [Bulla and Bulla, 2006].
Pour résoudre ce problème, FERGUSON [Ferguson, 1980] a proposé un modèle qui
permet des distributions de temps de séjours arbitraires pour le processus caché. Comme le
processus caché devient semi-Markovien, ce modèle est appelé un modèle semi-Markovien 1
caché (également connu sous le nom de MMC de durée variable ou MMC de durée explicite).
FERGUSON a considéré les MSMC comme une approche alternative aux MMC pour
la modélisation de la parole, car ces derniers n’étaient pas assez souples pour décrire le
temps passé dans un état donné. Après ce travail pionnier, plusieurs problèmes liés aux
MSMC ont été étudiés par différents auteurs, par exemple, LEVINSON [Levinson, 1986],
GUEDON [Guédon, 2003], SANSOM et THOMSON [Sansom and Thomson, 2001], YU et
KOBAYASHI [Yu and Kobayashi, 2003], BULLA [Bulla, 2006]. La structure de base des
MSMC est illustrée figure 4.4.
Différentes hypothèses ont été considérées dans la littérature pour la distribution
des observations, ainsi que pour la représentation du temps passé dans un état. Pour
cette dernière, trois types de modélisation sont principalement utilisés : par une famille
paramétrique de distributions continues [Levinson, 1986], par une famille des distributions
exponentielles [Mitchell and Jamieson, 1993] ou par la loi binomiale négative [Durbin, 1998].
S2S1 S3
Observations
Chaîne de Markov (non observée)
O1 On On+1 On+m On+m+1 On+m+h
Figure 4.4 – Structure de base d’un modèle de semi-Markov caché.
1. Un processus semi-Markovien a la propriété suivante : la probabilité de passer d’un état caché i vers
un autre j dépend uniquement du temps passé depuis l’entrée en l’état actuel i. Au contraire, la propriété
d’un processus Markovien suppose que la probabilité de changer d’état dépend uniquement de l’état actuel.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-119-320.jpg)
![90 Chapitre 4
Même si le domaine d’application le plus commun des MSMC est la reconnaissance de
la parole [Ferguson, 1980], ces modèles ont été appliqués avec succès dans des nombreux
autres domaines :
– l’électrocardiographie [Thoraval, 1995; Dumont, 2008],
– la reconnaissance de textes [Kundu et al., 1997; Weinman et al., 2009],
– la reconnaissance des gènes humains dans l’ADN [Burge and Karlin, 1997; Aydin
et al., 2006],
– l’analyse des modes de ramification et de floraison des plantes [Guédon et al., 2001],
– l’analyse des données pluviométriques [Sansom and Thomson, 2001],
– la modélisation des séries chronologiques financières [Bulla and Bulla, 2006].
L’application des MMC et des MSMC dans ces différents domaines est principalement
due à leur polyvalence et leur résolubilité mathématique, car ils sont caractérisés par les
propriétés suivantes [MacDonald and Zucchini, 1997] :
– Disponibilité de tous les moments : moyenne, variance, autocorrélations.
– L’évaluation d’une séquence d’observation est facile à calculer, son calcul est linéaire
dans le nombre d’observations et de nombreux algorithmes existent.
– Les distributions marginales, souvent représentées par des lois des probabilités géo-
métriques, gaussiennes, etc., peuvent être déterminées aisémment et les observations
manquantes peuvent être manipulés avec un effort mineur, du fait des lois des proba-
bilités utilisées.
– Les distributions conditionnelles P(Y = y|X = x) sont disponibles, grâce au processus
doublement stochastique et à l’architecture des modèles, l’identification des valeurs
aberrantes est possible car des probabilités très faibles seront obtenues pour ces valeurs
et les distributions prévues peuvent être calculées.
4.2.1 Architecture des modèles
Soit S = {1, . . . , M} l’ensemble d’états d’une chaîne de Markov. La séquence d’états est
désignée par S1:T S1, . . . , ST , où St ∈ S est l’état à l’instant t. Une réalisation de S1:T
est dénotée comme s1:T .
La séquence d’observation est souvent notée par O1:T O1, . . . , OT , où Ot ∈ V est
l’observation à l’instant t et V = {ν1, ν2, . . . , νK} est l’ensemble de valeurs observables.
Dans les MMC, une observation est produite dans chaque état i car les états n’ont pas
une durée. Par exemple, pour la séquence d’observation o1:T , la séquence d’états Markoviens
sous-jacente est s1:T = i1, i1, i1, i2, . . . , in où n
m=1 sm = T et i1, i2, . . . , in ∈ S.
Par opposition, dans les MSMC, chaque état i a une durée d variable, qui est associée
au nombre d’observations produites lorsqu’on reste dans l’état. La durée des états est
une variable aléatoire et prend une valeur entière dans l’ensemble D = {1, 2, . . . , D}. Par](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-120-320.jpg)

![92 Chapitre 4
Tableau 4.1 – Résumé des principaux paramètres et caractéristiques des MMC et MSMC.
Paramètre Symbole MMC MSMC
Élément de la matrice de transition aij j∈S{i} aij = 1 aii = 0
Probabilité d’observation bi(νk) νk
bi(νk) = 1 νk
bi(νk) = 1
Probabilité de durée pi(d) Non définie Explicite†
Probabilité de l’état initial πi i πi = 1 i πi = 1
† Détaillée section 4.3.1
transition a11 et produit l’observation o2 selon la probabilité bi1 (o2). Ensuite, il transite
vers i2 d’après a12 et produit o3 selon bi2 (o3). Ensuite, il transite vers i2, . . . , in jusqu’à ce
que la dernière observation soit produite.
Figure 4.5 – Principe de fonctionnement d’un modèle Markovien caché.
Un exemple d’un MSMC, inspiré de YU [Yu, 2010], est représenté dans la figure 4.6.
Le premier état i1 est choisi selon la probabilité π1. Le processus reste pendant une du-
rée d1 = 2 dans l’état i1 et deux observations sont donc produites dans cet intervalle
de temps o1, o2 , suivant les probabilités d’émission d’observations bi1 (o1), bi1 (o2) . Il
transite vers l’état i2 d’après la probabilité de transition a12 où il va rester d = 3 unités de
temps et produire trois observations o3, o4, o5 selon les probabilités d’émission d’observa-
tions bi2 (o3), bi2 (o4), bi2 (o5) . Ensuite, il transite vers i3, . . . , in jusqu’à ce que la dernière
observation soit produite.
Figure 4.6 – Principe de fonctionnement d’un modèle semi-Markovien caché.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-122-320.jpg)
![4.2. Les modèles de Markov et semi-Markov cachés 93
Dans notre problème de modélisation de la dynamique des séries temporelles extraites
de l’ECG, le temps passé dans un état peut être d’une importance capitale, ou du moins,
tout aussi important que les transitions entre états : il est notamment possible que certains
états se distinguent par des temps de passage très courts et d’autres par des temps de
passage beaucoup plus élevés. À partir des figures 4.5 et 4.6, on peut constater plusieurs
avantages des MSMC par rapport aux MMC, qui les rendent particulièrement adaptés à
notre application :
– Dans les MMC la probabilité de rester dans un même état n’est pas explicite et elle
suit une loi géométrique pi(d) = ad
ii(1 − aii) qui est une représentation irréaliste de
la durée des séquences d’observations analysées, car elle suppose que les temps de
passage courts sont plus probables que les temps de passage longs.
– Les MSMC re-définissent de manière plus explicite le temps passé dans chaque
état par des distributions paramétriques qui leur sont spécialement affectées. Cette
représentation est plus adaptée à notre application où des lois Gaussiennes sont
souvent observées.
– Le temps passé dans un état dans les MSMC est un paramètre appris comme les
autres paramètres.
– Dans les MMC le temps passé dans un état est une variable discrète tandis que dans
les MSMC le temps passé dans un état peut être représenté par une variable continue
avec des valeurs µ ± σ.
4.2.2 Estimation des paramètres des modèles
Les paramètres des MMC et MSMC sont généralement estimés en utilisant la méthode
du maximum de vraisemblance (MV). L’ensemble des paramètres λ (λMSMC et λMMC)
sont obtenus à partir des observations O1:T . λ est estimé, puis re-estimé de sorte que la
fonction de vraisemblance
L(λ; O1:T ) = P(O1:T |λ) (4.9)
augmente et converge vers sa valeur maximale, où P(O1:T |λ) est la probabilité que la
séquence observée O1:T soit générée par le modèle avec l’ensemble de paramètres λ.
Les deux approches les plus courantes pour estimer les paramètres d’un MMC sont
l’algorithme espérance-maximisation (EM) [Dempster et al., 1977] et la maximisation directe
numérique de la vraisemblance [Campillo and Le Gland, 1989]. Cependant, l’algorithme
EM est la méthode préférée en raison de sa plus grande stabilité [Bulla and Bulla, 2006].
L’algorithme EM cherche à trouver le MV par l’application itérative de deux étapes :
– Étape 1 « Espérance » (E) : détermine l’espérance de la log-vraisemblance selon les
données observées O1:T et les paramètres courants λ(t) :
Q(λ|λ(t)
) = E [log L(λ; O1:T )] (4.10)](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-123-320.jpg)
![94 Chapitre 4
– Étape 2 « Maximisation » (M) : trouve les paramètres qui maximisent cette quantité :
λ(t+1)
= arg max
λ
Q(λ|λ(t)
) (4.11)
Pour l’estimation des paramètres λ, l’algorithme forward-backward [Levinson, 1986] et
l’algorithme de Viterbi [Forney Jr, 1973] sont souvent employés. Ces deux algorithmes sont
issus d’une approche itérative EM. L’algorithme forward-backward considère l’ensemble des
observations pour déterminer L(λ; O1:T ) tandis que la méthode de Viterbi ne prend en
compte que le chemin optimal.
Évidemment, les résultats obtenus de ces algorithmes de type EM dépendent fortement
du choix des valeurs initiales. Une solution possible, proposée par DUMONT [Dumont, 2008]
permet l’initialisation des paramètres à partir d’un enchaînement des modèles constitués
par : i) un partitionnement de données par l’algorithme K-means, ii) un modèle de mélanges
de gaussiennes, iii) un MMC et finalement iv) un MSMC. Cette méthode d’initialisation,
ainsi que l’approche méthodologique globale proposée par DUMONT, seront détaillées dans
la section suivante.
4.3 Rappel de la méthode proposée par DUMONT J.
La thèse de DUMONT J. [Dumont, 2008] s’est concentrée sur la modélisation des
dynamiques des séries temporelles en cardiologie par MSMC. Pendant ces travaux, une
méthode basée sur des MSMC à densité d’observation continue a été proposée pour la
classification, le clustering et la représentation des données physiologiques temporelles
et multivariées. Cette méthode a été évaluée sur des données réelles dans la détection
d’événements ischémiques et la caractérisation de la réponse autonomique des patients
souffrant d’un syndrome de Brugada. D’un point de vue clinique, l’ensemble des résultats
obtenus montre l’importance de l’analyse de la dynamique des séries temporelles dans la
distinction d’états physiopathologiques de l’individu.
Dans cette section, les principales contributions des travaux de DUMONT sont présentées
brièvement, car ils sont à la base des propositions réalisées dans le présent travail de thèse.
4.3.1 Les distributions des durées et d’observation
La distribution des durées des états des MSMC (pi(d)) peut être paramétrique ou
non paramétrique. De même, la distribution des observations des MSMC et des MMC
(bi(νk)) peut être paramétrique ou non paramétrique, discrète ou continue et dépendante
ou indépendante des durées de l’état, selon le cas. La distribution des observations peut
également être définie par un mélange de distributions. Une discussion plus approfondie sur](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-124-320.jpg)
![4.3. Rappel de la méthode proposée par DUMONT J. 95
les différentes distributions de durées et des observations peut être trouvée dans YU [Yu,
2010]. Dans l’approche proposée par DUMONT, la distribution des durées des états pi(d) et
la distribution d’observation bi(νk) sont modélisées par une densité de probabilité gaussienne
de type :
f(x; µ, σ2
) =
1
σ
√
2π
e−1
2 (x−µ
σ )
2
(4.12)
pour le cas univarié où x correspond aux données associées aux durées des états et aux
données associées aux observations et µ et σ2 définissent respectivement la moyenne et la
variance de x. Pour le cas multivarié, elle est définie comme :
f(x; µ, Σ) =
1
(2π)n/2|Σ|1/2
e−
1
2(x−µ)TΣ−1(x−µ)
(4.13)
où x correspond aux données associées aux observations multivariées, n est le nombre de
dimensions, µ est le vecteur de moyennes de x (µ ∈ Rn), Σ est la matrice de covariance semi-
définie positive de x (Σ ∈ Rn×n), l’exposant T est la transposée et |Σ| est le déterminant de
Σ. Cette expression se réduit à la densité de probabilité gaussienne univariée (équation 4.12)
si Σ est un scalaire (matrice 1 × 1).
On utilise la nomenclature f(x) ∼ N(µ, σ2) (où f(x) ∼ N(µ, Σ)) pour représenter cette
densité de probabilité gaussienne. Ainsi, d’une part, pour représenter les temps de passage
pi(d) ∼ N(µd
i , σd
i
2
), où les scalaires µd
i et σd
i
2
définissent respectivement la moyenne et
la variance des gaussiennes assignées à chaque état i, et d’autre part, pour représenter
la probabilité d’observation bi(νk) ∼ N(µνk
i , σνk
i
2
), où les scalaires µνk
i et σνk
i
2
définissent
respectivement la moyenne et la variance des gaussiennes assignées à chaque état i. Dans le
cas multivarié, la distribution d’observation est représentée par une densité de probabilité
gaussienne multidimensionnelle bi(νk) ∼ N(µνk
i , Σνk
i ), où µνk
i est le vecteur des centres des
gaussiennes multivariées de chaque état et Σνk
i sa matrice de covariance.
4.3.2 Méthodologie utilisée pour l’estimation des paramètres des MSMC
L’algorithme de Viterbi [Forney Jr, 1973] a été choisi pour l’estimation des paramètres
car i) c’est l’algorithme le plus populaire de programmation dynamique pour l’estimation du
MV de la séquence des états d’un MMC, ii) il converge plus rapidement vers un maximum
local, iii) il est moins sensible aux problèmes de stabilité numérique (par exemple lorsque les
vraisemblances observées bj(νk) deviennent très petites) et iv) il est aisément transposable
aux MSMC. Par ailleurs, les paramètres du modèle seront estimés avec le plus grand nombre
de séries temporelles possibles, limitant ainsi le risque de tomber dans des minima locaux
erronés. Pour ne pas alourdir la présentation, nous avons reporté Annexe D la présentation
de l’algorithme de Viterbi.
Au cours de l’étape de rétropropagation de l’algorithme de Viterbi, plusieurs variables](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-125-320.jpg)

![4.3. Rappel de la méthode proposée par DUMONT J. 97
– Un algorithme k-means pour initialiser les centres des gaussiennes (ˇµi) d’un modèle
de mélanges de gaussiennes (MMG). Le centre de chaque gaussienne correspond au
barycentre de chaque état dans l’espace d’observation.
– Une procédure EM permet d’estimer les centres (˜µi) et covariances (˜Σi) du MMG.
– Un algorithme de Viterbi pour l’estimation des paramètres d’un MMC équivalent :
probabilité de transition (ˆaij), probabilité d’état initial (ˆπi) et les centres (ˆµi) et
covariances (ˆΣi) de la probabilité d’émission des observations. Les paramètres ˆaij
et ˆπi sont initialisés avec une probabilité uniforme et ˜µi et ˜Σi sont utilisées comme
valeurs initiaux de ˆµi et de ˆΣi.
– Un MMC équivalent pour initialiser les paramètres du MSMC. Les chemins le plus plau-
sibles (déterminées sur les séquences d’observations) et le temps passé dans chaque état
du MMC sont utilisés pour l’initialisation des moyennes (µd
i ) et variances (σd
i
2
) des pro-
babilités de temps de séjour des états. Finalement, l’algorithme de Viterbi, étendu aux
MSMC, est utilisé pour l’estimation de λMSMC = {aij, bi(µνk
i , Σνk
i ), πi, pi(µd
i , σd
i
2
)}.
Base de données
d'apprentissage
k-means
Modèle de
mélanges gaussiens
Espérance-Maximisation
Modèle de
Markov caché
Algorithme
de Viterbi
Modèle de
semi-Markov caché
Algorithme
de Viterbi modifié
Figure 4.7 – Procédure utilisée pour l’apprentissage des MSMC à partir d’une base de
données, d’après DUMONT [Dumont, 2008].
4.3.3 Estimation du nombre d’états
Le nombre d’états cachés M est généralement supposé connu dans le cadre de certaines
applications. Toutefois, dans notre contexte, le nombre d’états est inconnu dans la pratique
et doit être estimé. Créer des modèles avec un nombre approprié d’états n’est pas un
problème trivial : un modèle avec trop d’états va sur-apprendre les observations, tandis
qu’un modèle avec trop peu d’états va décrire mal les observations qui lui sont affectées.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-127-320.jpg)
![98 Chapitre 4
Le critère d’information bayésien (BIC) [Schwarz, 1978], largement utilisé pour estimer
M dans le contexte de fouille de données [Katz, 1981; Li et al., 2002; Dumont et al., 2009b],
a été retenu dans ces travaux. Le BIC ne nécessite pas de connaissances a priori et favorise
les modèles plus simples par rapport aux modèles plus complexes [Schwarz, 1978].
Le nombre d’états est donc estimé en utilisant :
ˆM = arg max
M
log L λ(M); O1:T − f(M)
log I
2
(4.16)
où I est le nombre de séquences d’observations et f(M) est le nombre de paramètres du mo-
dèle en fonction du nombre d’états M. En utilisant des distributions des durées et d’observa-
tions gaussiennes, f(M) = M(1+2M +M2) pour le cas MMC et f(M) = M(3 + 2M + M2)
pour le cas MSMC.
4.3.4 Évaluation d’une séquence observée
Notre objectif pour les applications ciblées sera de reconnaître plusieurs dynamiques
différentes. Ce problème n’est rien d’autre qu’un problème de classification. L’intérêt est que
les MMC et MSMC offrent un cadre théorique direct pour répondre à cette problématique.
Cette tâche consiste à déterminer la probabilité d’une séquence de sortie particulière, compte
tenu des paramètres du modèle. Ce problème peut être traité efficacement en utilisant
l’algorithme de Viterbi (Annexe D). Pour le cas MMC, ceci revient à choisir :
P(O1:T |λMMC
) = max
j∈S
δT (j)
= max
j∈S
max
i∈S
δT−1(i)aij bj(oT )
(4.17)
où δt(i), définie par l’équation 4.18, représente le maximum de vraisemblance d’une trajec-
toire unique jusqu’au temps t, qui prend en compte les premières t observations et s’arrête
à l’état i.
δt(i) max
s1:t−1
P(s1, s2, . . . , st = i, o1:t|λ) (4.18)
Pour le cas de MSMC, on utilise :
P(O1:T |λMSMC
) = max
j∈S,d∈D
δT (j, d)
= max
j∈S,d∈D
max
i∈S{j},d ∈D
δT−d(i, d )aij pj(d)bj(oT−d+1:T )
(4.19)
où δt(i, d), définie par l’équation 4.20, représente le maximum de vraisemblance d’une
trajectoire unique jusqu’au temps t, qui prend en compte les premières t observations et](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-128-320.jpg)
![4.3. Rappel de la méthode proposée par DUMONT J. 99
s’arrête à l’état i de durée d.
δt(i, d) max
s1:t−d
P(s1:t−d, St−d+1:t = i, o1:t|λ) (4.20)
4.3.5 Un exemple de modélisation d’observations bivariées par MSMC
Un exemple de modélisation d’observations bivariées est présenté dans cette section
en utilisant les MSMC. L’objectif est de montrer leur aptitude à prendre en compte des
dynamiques complexes. Le système de Rössler (équation 4.21) a été utilisé pour générer des
séries bivariées : x&y = [ x
y ], x&z = [ x
z ] et y&z = [ y
z ]. Un bruit blanc gaussien a été ajouté
aux séries afin d’obtenir un rapport signal sur bruit (RSB) de 15 dB. L’équation 4.16 a été
utilisée pour déterminer le nombre d’états optimal de chaque MSMC.
dx
dt
= −y − z
dy
dt
= x + ay
dz
dt
= b + z(x − c)
(4.21)
La figure 4.8 montre les caractéristiques des MSMC chargés de modéliser les observations.
Dans ces figures, les ellipses noires décrivent chaque état (centre) et leurs matrices de
covariance (axes de l’ellipse), les chiffres correspondent au temps moyen passé dans chaque
état et les flèches d’épaisseurs variables représentent les coefficients de la matrice de
transition.
−6 −4 −2 0 2 4 6 8
−8
−6
−4
−2
0
2
4
6
4.25
3.8583
8.8667
3.38
2.745
3.1733
8.1667
7.325
4.5333
2.8649
6.425
7.5667
5.2167
2.9267
(a)
−6 −4 −2 0 2 4 6 8
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5833
3.0056
5
5
25.2167
3.8662
5.51365.5136 4.0111
3
5.0067
(b)
−6 −4 −2 0 2 4 6
−1
−0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
3.8114
8.5944
7
3
2.98612.9861
11.0056
4
8.2533
3
3.0133
86
(c)
Figure 4.8 – Modélisation des séries bivariées issues d’un attracteur de Rössler par des
MSMC. On observe dans (a) la projection dans le plan x&y d’un MSMC avec 14 états,
dans (b) la projection dans le plan x&z d’un MSMC avec 10 états et dans (c) la projection
dans le plan y&z d’un MSMC avec 12 états.
L’invariance des paramètres des MSMC à la multiplication et à l’addition d’une des](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-129-320.jpg)
![100 Chapitre 4
variables par une quantité fixe a été aussi testée. L’objectif de ce test est d’étudier le
comportement des paramètres lorsque i) une des variables montre des variations d’amplitude
importantes (cas de la multiplication) et ii) une des variables présente une composante
continue et est de fait translatée par rapport à la variable d’origine (cas de l’addition). Ce
test est important car, dans notre application réelle, les variables ne se trouvent pas dans le
même niveau d’amplitude.
Les séquences d’observations bivariées x&z à 15 dB ont été donc modifiées afin de
produire les séquences d’observation 1000x&z = [ 1000x
z ] et (1000 + x)&z = [ 1000+x
z ]. Trois
MSMC sont chargés de modéliser les observations x&z, 1000x&z et (1000+x)&z. Le nombre
d’états des MSMC a été fixé à 10 états. On observe figure 4.9 que les caractéristiques des
trois MSMC sont quasi identiques. On a constaté que le fait de multiplier une variable a
plus d’effets sur les paramètres du MSMC que le fait d’ajouter une composante continue
aux séries. Cependant, ces petites différences sont minimes et sont dues à une initialisation
différente de chaque MSMC. Cet exemple montre clairement l’aptitude des MSMC à
prendre en compte seulement les dynamiques des séries analysées et non pas leurs valeurs
instantanées.
−8 −6 −4 −2 0 2 4 6 8
−2
−1
0
1
2
3
4
5
6
7
8
666666666
12.2612.2612.2612.2612.2612.2612.2612.2612.26
19.2219.2219.2219.2219.2219.2219.2219.2219.22 999999999
5.20375.20375.20375.20375.20375.20375.20375.20375.2037
5.00675.00675.00675.00675.00675.00675.00675.00675.0067
9.93339.93339.93339.93339.93339.93339.93339.93339.9333
4.99334.99334.99334.99334.99334.99334.99334.99334.9933444444444
4.00674.00674.00674.00674.00674.00674.00674.00674.0067
(a)
−8000 −6000 −4000 −2000 0 2000 4000 6000 8000
−2
−1
0
1
2
3
4
5
6
7
8
4.44674.44674.44674.44674.44674.44674.44674.44674.4467
555555555
8.73038.73038.73038.73038.73038.73038.73038.73038.7303
3.99333.99333.99333.99333.99333.99333.99333.99333.9933
5.52595.52595.52595.52595.52595.52595.52595.52595.5259
19.844619.844619.844619.844619.844619.844619.844619.844619.8446
333333333
8.89868.89868.89868.89868.89868.89868.89868.89868.8986
6.00676.00676.00676.00676.00676.00676.00676.00676.0067
131313131313131313
(b)
992 994 996 998 1000 1002 1004 1006 1008
−2
−1
0
1
2
3
4
5
6
7
8
19.013319.013319.013319.013319.013319.013319.013319.013319.0133
666666666
10.653310.653310.653310.653310.653310.653310.653310.653310.6533
10.683310.683310.683310.683310.683310.683310.683310.683310.6833
5.99335.99335.99335.99335.99335.99335.99335.99335.9933
4.77044.77044.77044.77044.77044.77044.77044.77044.7704
666666666
444444444
999999999
4.00674.00674.00674.00674.00674.00674.00674.00674.0067
(c)
Figure 4.9 – Comparaison des MSMC chargés de modéliser des séries bivariées : Projection
dans le plan x&z dans (a) pour les séries originaux, dans (b) pour 1000x&z et dans (c)
pour (1000 + x)&z.
4.3.6 Classification/détection par MMC et par MSMC
Les MMC et MSMC peuvent être utilisés pour classer/détecter des évènements d’intérêt
en analysant la vraisemblance. Pour cette approche, K modèles sont utilisés pour représenter
K dynamiques différentes de l’ensemble d’observations analysé (univarié ou multivarié).
L’hypothèse sous-jacente étant que ces différentes dynamiques sont associées à des états
ou événements physiopathologiques distincts, qui doivent être discriminés. Les séquences
d’observations contenant les K dynamiques sont extraites des séries temporelles. Ces
dernières sont réduites par rapport à l’écart type mesuré sur des enregistrements de
référence, afin d’analyser les différents indicateurs extraits avec le même poids. De plus,](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-130-320.jpg)


![4.3. Rappel de la méthode proposée par DUMONT J. 103
TEG = 1 −
K
i=1
xii
K
i=1
K
j=1
xij
(4.26)
TECk = 1 −
xkk
K
i=1
xki
(4.27)
Tableau 4.2 – Tableau de contingence.
Classification
Classe 1 . . . Classe K
Référence
Classe 1 x11 . . . x1K
...
...
...
...
Classe K xK1 . . . xKK
Lorsqu’on se restreint à deux classes et on s’intéresse à détecter, par exemple, la classe 1 :
SEN = 1 − TEC1 (4.28)
et
SPC = 1 − TEC2 (4.29)
Résultats sur des signaux réels
Cette méthode a été évaluée dans des situations cliniques réelles [Dumont, 2008].
Un clustering hiérarchique de type descendant avec une augmentation progressive du
nombre de MSMC a été proposé pour : i) la classification d’épisodes ischémiques à partir
d’enregistrements Holter, extraits de la base de données LTST [Jager et al., 2003] et ii) la
classification de patients atteints du syndrome de Brugada, à partir d’ECG acquis lors
d’une épreuve d’effort. Les taux d’erreur global (équation 4.26) sont respectivement de 29 %
et de 24,5 % alors que les approches ne prenant pas en compte les dynamiques présentent
des TEG de 46,7 % et 29,6 %, respectivement.
L’approche a été aussi appliquée à la détection de l’ischémie myocardique sur la base
de données STAFF3 [García et al., 1999], qui regroupe des enregistrements d’angioplastie
coronaire transluminale percutanée (PTCA) où l’instant de début du processus ischémique
est très précisément annoté. L’originalité de cette démarche repose sur l’analyse de la](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-133-320.jpg)
![104 Chapitre 4
dynamique des séries temporelles extraites de l’ECG, alors que les méthodes traditionnelles
sont fondées sur des règles de décision statique. Après l’extraction d’un vecteur de caracté-
ristiques, à partir de signaux ECG de la base de données, la dynamique est caractérisée par
un MSMC. Le détecteur utilise un « MSMC de référence » et un « MSMC ischémique » et
puis compare la log-vraisemblance des séries temporelles aux MSMC. Les valeurs optimales
de L et T ont été de 20 et 140 secondes respectivement. Les résultats obtenus montrent
de très bonnes performances de détection : une sensibilité de 96 % et une spécificité de
80 % lorsque la série RT est utilisée (cas univarié) et une sensibilité de 94,7 % et une
spécificité de 71,9 % lorsque les séries RT et Ramp sont analysées de manière conjointe (cas
multivarié) [Dumont et al., 2009b,a].
4.3.7 Synthèse sur les MSMC
Cette approche basée sur des MSMC présente plusieurs avantages par rapport à d’autres
méthodes de modélisation des dynamiques des séries temporelles :
– Les MSMC représentent les dynamiques de manière simple et peuvent être comparés
entre eux.
– Ils sont bien adaptés au traitement multivarié et des versions rapides des algorithmes
d’apprentissage des paramètres existent.
– Ils offrent une représentation graphique de la dynamique grâce aux états.
– Ils peuvent représenter l’évolution temporelle d’une série grâce aux paramètres pi(d).
– Ils ne nécessitent pas de connaissances a priori sur les données à traiter.
– M est le seul hyper-paramètre à régler.
– Il est possible de donner une interprétation physiologique raisonnable aux états
(« cachés ») de la chaîne de Markov.
Une approche basée sur des réseaux neuronaux artificiels (RNA) pourrait être également
capable de caractériser la dynamique de ces séries temporelles. Cependant, une interprétation
physiologique du phénomène étudié et un contrôle de différents étapes du RNA serait plus
difficile. D’ailleurs, les RNA ont été récemment appliqués par BELAL [Belal et al., 2011] et
curieusement n’ont pas montré une amélioration de performance de détection/classification
des épisodes d’apnée du prématuré par rapport à d’autres méthodes (somme pondérée,
corrélation, dérivée).
4.4 Contributions de ce travail de thèse
Même si les résultats obtenus dans les travaux de DUMONT [Dumont, 2008; Dumont
et al., 2009a] ont été très satisfaisants sur les données cardiaques utilisées, plusieurs améliora-
tions peuvent être envisagées dans la méthode de détection proposée. Dans notre application
de détection précoce des épisodes d’apnée-bradycardie des nouveaux-nés prématurés, ces](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-134-320.jpg)
![4.4. Contributions de ce travail de thèse 105
améliorations visent à incrémenter les performances détection et à diminuer le temps de
retard à la détection, en utilisant une approche multivariée des séries temporelles extraites
de l’ECG.
L’un des objectifs du présent travail de thèse a été donc de poursuivre les développe-
ments de cette approche en s’intéressant plus particulièrement aux aspects décrits dans les
paragraphes suivants.
4.4.1 Évaluation du temps de retard à la détection (TRD)
L’évaluation du retard à la détection, défini comme le temps écoulé entre l’instant
d’annotation et la détection de l’épisode, n’a pas été considérée dans les travaux précédents.
Ce paramètre est fondamental pour évaluer la performance du détecteur en particulier dans
le cadre d’une détection précoce en temps réel. En cas de détection, le TRD est déterminé
dans la fenêtre de recherche des vrais positifs, centrée dans l’annotation donnée, tel que
détaillé dans la section 2.3.
4.4.2 Exploration de l’hétérogénéité des modèles
Dans la méthode de détection proposée par DUMONT [Dumont et al., 2009b,a], les K
modèles utilisés pour caractériser les K dynamiques de la séquence d’observation partagent
le même nombre d’états (M1 = M2 = . . . = MK), même si il a été déterminé à l’aide du
critère BIC (équation 4.16). Toutefois, l’hétérogénéité des modèles pourrait aussi améliorer
les performances car, chaque modèle explore des dynamiques différentes et, par conséquent,
peut nécessiter un nombre d’états différent.
4.4.3 Adaptation au traitement en ligne
Afin de pouvoir l’appliquer sur un système de monitoring des nouveaux-nés prématurés,
la méthode de détection développée doit être adaptée au traitement en ligne. En effet,
l’implémentation proposée dans DUMONT [Dumont et al., 2009b,a] est restreinte au
traitement par blocs et n’est pas adaptée à notre cas. Les pré-traitements des observations
exposés dans la section précédente (section 4.3.6), tels que la normalisation des séries et
la soustraction de la médiane dans les L premiers secondes de chaque série, ne sont pas
retenus.
En effet, la méthode de normalisation des séquences d’observations proposée par DU-
MONT [Dumont et al., 2009a] risque de produire de valeurs trop faibles de Σνk
i , conduisant
à des problèmes numériques lors de l’étape d’apprentissage. Dans le présent travail, et vu](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-135-320.jpg)



![4.4. Contributions de ce travail de thèse 109
Algorithme 5 Pseudo-code pour déterminer ∆QNU optimal.
1: Initialiser δQNU
2: Estimer Mk
en utilisant l’équation 4.16
3: Estimer λk
4: Réaliser la détection
5: Déterminer DCDP selon l’équation2.5
6: Modifier la valeur de δQNU
7: Répéter 2-6 jusqu’à obtenir la valeur de DCDP plus petite
intégrant la version retardée de la série univariée. En ce sens, une matrice d’observation
est construite, en intégrant la version originale de la séquence observée à l’instant t et la
version retardée de la séquence observée à l’instant t − τ, où τ est un délai prédéfini. Cette
matrice d’observation peut être représentée comme suit :
O =
Ot−T+1:t
Ot−τ−T+1:t−τ
(4.32)
Dans le cas de la série RR, l’application d’un tel retard présente également une résonance
physiologique puisque l’on sait que l’intervalle RR à un instant t dépend des précédents
par des mécanismes de régulation autonomique qui ont, principalement, deux dynamiques
différentes pour les systèmes sympathique (plus lent) et parasympathique (plus rapide). Ces
matrices d’observation seront représentées en gras dans le présent document, tel que RR.
Recherche du retard τ optimal
Pour la série RR, la recherche d’une valeur a priori de τ nous conduit à l’analyse
spectrale de la VFC. À partir d’études expérimentales, le spectre de fréquences de la
VFC est divisée principalement en quatre bandes de fréquence choisies pour sa pertinence
physiologique [Task Force, 1996]. Dans le cas des nouveaux-nés prématurés, deux bandes de
fréquence nous intéressent :
– L’énergie du signal dans les basses fréquences (LF) de 0,02 à 0,2 Hz est expliquée
à la fois par un phénomène de résonance dans la boucle liée au délai de la réponse
vasculaire à la modulation adrénergique, par une rythmicité endogène centrale de
l’activité sympathique et par l’activité du tonus parasympathique [Chatow et al.,
1995; Beuchée, 2005].
– L’énergie du signal dans les hautes fréquence (HF) de 0,2 à 1,5 Hz est associée à
l’arythmie sinusale respiratoire (oscillation de la durée de l’intervalle RR corrélée à la
fréquence respiratoire), mais aussi à l’activité parasympathique (action du nerf vague
sur le cœur) [Chatow et al., 1995; Beuchée, 2005].
La différence entre les deux pics (LF et HF) est d’environ 0,9 Hz, ce qui correspond à
une demi-période de 0,556 secondes. Par conséquent, la valeur optimale de τ sera recherchée](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-139-320.jpg)









![Chapitre 5
Application des MSMC sur des
signaux simulés et réels
Nous avons déjà justifié et expliqué tout au long de ce mémoire l’intérêt de prendre en
compte les dynamiques des séries temporelles dans le cadre de la détection d’événements
physiopathologiques. C’est ainsi que finalement dans ce chapitre, les résultats de classification
et de détection, exploitant les dynamiques temporelles des observations multivariées par
des MMC et par des MSMC, sont présentés. Dans ce chapitre, la classification correspond à
l’identification de séquences d’observations qui contiennent ou pas un événement d’intérêt.
Une procédure hors-ligne (en batch) est utilisée pour cette tâche de classification et l’instant
précis de l’arrivée de l’événement n’est pas estimé. La détection est réalisée à partir d’une
procédure récursive spécifique et a comme but l’estimation de l’instant précis des événements
d’intérêt. Les améliorations proposées dans le chapitre 4, comme la quantification des
observations et la prise en compte de versions retardées des observations, sont ici appliquées
sur des signaux simulés et sur des signaux réels.
Les travaux sur signal simulé sont présentés dans la section 5.1 et ont comme objectif
de montrer la faisabilité de notre approche et d’optimiser la structure des MMC ou MSMC
pour l’analyse de la dynamique de variables. Le modèle de FitzHugh-Nagumo [Fitzhugh,
1961] a été utilisé pour générer des signaux simulés bivariés, qui ont été ensuite contaminés
avec plusieurs niveaux de bruit. Ce modèle est particulièrement adapté à notre problème
car ses deux variables d’état présentent des dynamiques hétérogènes (variables d’état lente
et rapide du modèle) et ces dynamiques peuvent être modifiées par l’ajustement d’un
paramètre.
La section 5.2 présente l’application des méthodes proposées sur des séries temporelles
multivariées réelles. Elles correspondent aux caractéristiques extraites de l’ECG de nouveaux-
nés prématurés (RR, Ramp et QRSd), tel que décrit dans le chapitre 3 de ce manuscrit.
119](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-149-320.jpg)

![5.1. Évaluation de la faisabilité des MSMC sur signal simulé 121
le chapitre 4 (quantification et prise en compte de la version retardée des séries
temporelles) sont appliquées. L’objectif est ici de mesurer l’impact de la quantification,
uniforme et non uniforme, des observations et l’influence de la prise en compte des
données précédentes dans le processus de décision.
4. Détection d’un évènement d’intérêt basée uniquement sur la dynamique des observables
(section 5.1.5). L’intérêt est ici d’évaluer l’impact des modifications proposées dans les
valeurs de sensibilité, spécificité et retard à la détection, sur des signaux simulés dont
la dynamique est finement modifiée à partir des paramètres du modèle FitzHugh-
Nagumo.
5.1.1 Le modèle de FitzHugh-Nagumo pour la génération des séries syn-
thétiques
Les expériences d’évaluation de l’approche proposée ont été conduites sur des séries
temporelles générées par un modèle de FitzHugh-Nagumo [Fitzhugh, 1961]. Le modèle de
FitzHugh-Nagumo (MFN) est un modèle générique, constitué de deux variables, qui est
utilisé pour décrire un système excitable (comme par exemple une cellule myocardique) à
partir des équations suivantes :
dv
dt
= 3(v −
1
3
v3
+ r + I)
dr
dt
= −
1
3
(v − a + 0.8r)
(5.1)
où v est le potentiel de membrane (variable rapide), r est la variable de récupération
(variable lente), I est la valeur du courant d’excitation externe et a est un paramètre qui
peut changer l’état de repos et la dynamique du système.
Dans le MFN, les variables v et r sont fréquemment initialisées à une valeur de « repos »
(point fixe) et une perturbation est appliquée au moyen de la variable I pour déclencher
une excursion dans l’espace des phases des variables v et r, avant de retourner à leurs
valeurs de repos. L’algorithme de Runge-Kutta d’ordre 4 [Jameson et al., 1981], avec un
pas d’intégration variable, a été utilisé pour simuler des séries temporelles r et v, avec deux
dynamiques différentes, en fonction de la valeur du paramètre a, qui a été modifié selon
une distribution uniforme dans l’intervalle :
a1 ∼ U(0,58, 0,62)
a2 ∼ U(0,78, 0,82)
(5.2)
La figure 5.1a illustre un diagramme de phases (r en abscisses et v en ordonnées) et les
figures 5.1b et 5.1c montrent des exemples des séries temporelles v et r respectivement, pour](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-151-320.jpg)


![124 Chapitre 5
Base de données synthétiques pour la détection
Dans le cas de détection, l’apprentissage des K modèles est effectué en utilisant 20 %
des séquences d’observation de chaque sous-ensemble LSMFNk, k in{1, 2, 3}, présentés
dans la section précédente. Le sous-ensemble de test est constitué par 400 séries temporelles
r, v et v&r, de taille 400 secondes chacune, générées avec le MFN (équation 5.1). Une
perturbation de valeur constante (I = −0.2) est introduite dans l’intervalle [300,305] (5
secondes de durée). Deux dynamiques différentes ont été générées en modifiant le paramètre
a selon l’équation 5.2 : a1 et a2. Parmi les 400 séries temporelles, 200 ont été générées avec
a1 et 200 avec a2. L’amplitude des séries temporelles a été réduite en la divisant par sa
valeur absolue maximale. Ensuite, les séries temporelles ont été multipliées par 1000 pour
éviter que σνk
2
i → 0 et un bruit blanc gaussien a été ajouté aux séries temporelles afin
d’obtenir différentes valeurs de RSB : 5, 10, 15, 20 dB. La figure 5.3 montre un exemple de
la dynamique de la série temporelle r (sans contamination) pour une valeur de a = 0, 58.
0 50 100 150 200 250 300 350 400
−200
0
200
400
600
800
1000
Temps (s)
Début de la stimulation
10 s
Figure 5.3 – Exemple d’une réalisation de la variable r, générée avec a1 = 0, 58.
5.1.2 Étude comparative de classification par MMC et MSMC
L’objectif de cette étude est de comparer les performances des MMC et des MSMC dans
la classification de séquences d’observations univariées présentant des valeurs d’amplitudes
égales, mais des dynamiques légèrement différentes.
Apprentissage des modèles
Des séries temporelles univariées r des sous-ensembles LSMFNk, k ∈ {1, 2, 3}, ont été
utilisées. K = 3 MMC et K = 3 MSMC ont été crées pour apprendre la dynamique de](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-154-320.jpg)


























![152 Chapitre 5
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
0.9
0.95
1
Seuil fixe
Seuil relatif
TFP
TVP
(a)
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5
−2
−1
0
1
2
3
4
5
6
7
8
TFPTRD(s)
Seuil fixe
Seuil relatif
(b)
Figure 5.20 – Performance de détection de l’apnée-bradycardie par MSMC. Dans (a) courbes
COR et dans (b) courbes TRD moyen en fonction de TFP. Le caractère « x » représente le
point correspondant à la DCDP.
D’autres travaux au laboratoire se sont intéressés à réduire le temps de retard à la
détection. C’est le cas de l’approche proposée par CRUZ [Cruz et al., 2006] qui effectue
la fusion optimale de trois détecteurs (détecteur fixe, détecteur relatif et détecteur par
changements abrupts sur la moyenne), par une méthode de fusion décentralisée [Hernández
et al., 1999]. Cette approche montre des valeurs de sensibilité et de spécificité de 97,67 %
et 97,00 % respectivement et une réduction de la détection à 2,22 battements (autour de
1 seconde) sur une base de données de 1188 épisodes de bradycardie de 40 individus. Il
faut signaler que le début de l’annotation des évènements dans ce travail correspond au
croisement de la série RR par 600 ms et dans notre cas le début de l’annotation a été placée
au point où la dérivée de la fonction sigmoïde qu’approche la série RR est supérieure à
1. De plus, la base de données et les procédures d’annotations ne sont pas identiques. Il
n’en reste pas moins, que cette étape de fusion a démontré son utilité, en particulier pour
améliorer la spécificité de la méthode de détection des ruptures [Cruz et al., 2006]. Dans
ce sens, l’étape finale d’évaluation de notre détecteur a été donc d’adapter la méthode de
fusion utilisée dans [Hernández et al., 1999; Cruz et al., 2006] et d’évaluer son intégration
avec la méthode par MSMC proposée dans cette thèse.
5.2.4 Fusion des détecteurs
Deux architectures de fusion de données sont souvent employées dans la littérature dans
le cadre de la détection d’événements : une architecture centralisée, où un modèle est
utilisé pour apprendre la dynamique de plusieurs variables de manière conjointe, et une
architecture décentralisée, où différents modèles sont utilisés pour analyser la dynamique
de chaque variable et chaque modèle produit une décision locale qui est combinée avec les](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-182-320.jpg)
![5.2. Évaluation des MSMC sur signaux réels 153
décisions des autres détecteurs. Dans cette thèse, lorsque les MSMC ont été appliqués pour
modéliser la dynamique de plusieurs variables physiologiques de manière conjointe, on a
réalisé une fusion centralisée. Ce type de fusion a montré, dans les sections précédentes,
la possibilité d’améliorer les performances de détection par rapport au cas univariée : les
valeurs SEN = 74, 20% et SPC = 92, 77% pour RR et SEN = 63, 64% et SPC = 76, 28%
pour Ramp passent à SEN = 80, 46% et SPC = 91, 28% pour RR&Ramp. Cependant,
la performance de détection obtenue par ce moyen n’a pas été la meilleure performance
reportée.
L’objectif de cette section est donc de combiner, d’une manière décentralisée, la décision
de chaque détecteur afin d’améliorer les performances de détection, tout en minimisant
le temps de retard à la détection. En effet, les détecteurs de bradycardie basés sur des
MSMC, montrés dans la section précédente, analysent différentes variables et différentes
dynamiques temporelles et, en conséquence, ils sont basés sur des hypothèses des réponses
physiologiques différentes. Ces détecteurs peuvent être considérés comme complémentaires
entre eux, ce qui nous motive à réaliser une fusion des décisions.
Différentes règles de fusion peuvent être utilisées pour combiner les décisions locales
de chaque détecteur. Les règles de fusion les plus simples consistent en l’application
d’opérateurs logiques ET (fusion ET) ou OU (fusion OU) aux décisions des détecteurs
locaux. Il y a aussi des règles plus complexes comme la fusion VOTE où la décision finale
est basée sur la décision des k des n détecteurs individuels. Des règles de fusion optimale
(fusion OPTIMALE), ont également été proposées, souvent basées sur la moyenne pondérée
des décisions individuelles en offrant un poids plus important aux détecteurs les plus
performants [Chair and Varshney, 1986]. Dans la méthode de fusion proposée par CHAIR
et VARSHNEY [Chair and Varshney, 1986], les coefficients de pondération peuvent être
optimisés à partir de courbes COR [Hernández et al., 1999].
Fusion des détections obtenues pour RR, Ramp et QRSd
Premièrement, la fusion décentralisée OU, ET, VOTE et OPTIMALE est réalisée pour
les trois variables : RR, RAMP et QRSd. Les résultats sont montrés tableau 5.24 et la
figure 5.21 montre les courbes COR. On peut constater une amélioration des performances
de détection en utilisant la fusion OPTIMALE, cependant, celle-ci reste en dessous des
meilleurs résultats reportés dans la section précédente.
Fusion des trois détecteurs par MSMC
Les règles de fusion OU, ET, VOTE et OPTIMALE vont maintenant être appliquées à
trois détecteurs de la section précédente : RRQNU, RRQNU et RR&QRSdQU. Les résultats](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-183-320.jpg)





![Conclusions et perspectives
La détection précoce de l’apnée-bradycardie chez les prématurés est un sujet de recherche
majeure dans notre laboratoire depuis 10 ans. De nombreux travaux ont été développés au
cours de ces derniers années dans le but de caractériser ces épisodes [Beuchée, 2005; Cruz
et al., 2006; Beuchée et al., 2007; Cruz, 2007; Pladys et al., 2008b,a; Beuchée et al., 2009;
Altuve et al., 2009, 2011].
Les épisodes d’apnée-bradycardie chez les nouveaux-nés prématurés mettent en danger
sa vie et son avenir. Ces épisodes sont en partie la conséquence du développement partiel des
organes et des mécanismes de régulation cardio-respiratoires chez le nouveau-né prématuré
et justifient le monitoring continu en USIN avec des finalités diagnostiques et thérapeutiques.
Actuellement, dans les unités des soins intensifs néonatals, la détection des épisodes
d’apnée-bradycardie est réalisée en exploitant une seule variable extraite de l’électro-
cardiogramme : la durée du cycle cardiaque. Cependant, d’autres variables extraites de
l’électrocardiogramme peuvent être prises en compte dans une démarche de détection
multi-variable. Cette démarche est compatible avec les exigences imposées dans ces unités
des soins, où on limite au minimum nécessaire les instruments de mesure afin de favoriser le
développement de l’enfant et de le préserver dans un milieu aussi tranquille que possible
(approche de la NIDCAP [Als and Gibes, 1986]). L’objet de ce mémoire était donc de
proposer des solutions pour répondre à ces exigences.
Nous nous sommes en tout premier lieu intéressés à la segmentation de l’électrocar-
diogramme du nouveau-né prématuré. Ceci consiste à délimiter les ondes qui composent
chaque battement cardiaque. Plusieurs étapes sont nécessaires pour accomplir cette tâche :
l’élimination des interférences du signal électrocardiographique, la détection, le moyen-
nage et l’alignement des battements et, enfin, la segmentation des ondes proprement dite.
Dans le passé, ces méthodes ont été développées pour l’électrocardiogramme d’adultes.
Cependant, des différences remarquables entre l’électrocardiogramme de l’adulte et du
prématuré existent. Par exemple, la fréquence cardiaque de base du prématuré est trois
fois plus élevée, les ondes et intervalles sont plus courts et le complexe QRS est plus fin,
donnant ainsi des contenus spectraux de plus hautes fréquences. Par conséquent, notre
première contribution a été d’adapter les algorithmes de détection et de segmentation des
159](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-189-320.jpg)

![Conclusions et perspectives 161
étudiées.
– l’analyse multi-variée à base MSMC adaptée à la détection en temps réel.
Une comparaison avec les méthodes de détections classiques utilisées dans les unités de
soins intensifs néonataux a été également effectuée. Les valeurs de sensibilité, de spécificité
et du temps du retard à la détection, étudiées par des courbes opérationnelles du récepteur,
ont démontré que l’approche basée sur les modèles semi-Markovien est plus intéressante
que les méthodes classiques. La quantification des séries a amélioré les performances, tant
sur signaux simulés que sur signaux réels. En exploitant la dynamique des séries extraites
de l’électrocardiogramme, la détection d’épisodes d’apnée-bradycardie a été améliorée et le
temps de détection a été réduit par rapport aux détecteurs classiques, laissant espérer des
temps d’intervention des personnels soignants plus brefs.
Les perspectives de ce travail sont multiples et dirigées vers l’étude d’autres carac-
téristiques provenant de l’ECG du nouveau-né prématuré, telles que l’intervalle PR, la
morphologie de l’onde P et l’intervalle QT. Un travail antérieur développé dans notre labo-
ratoire a montré une amélioration de la détection de l’onde P de l’ECG adulte [Hernández
et al., 2000]. La méthodologie d’optimisation proposée dans ce document pourrait être
appliquée afin d’adapter l’algorithme de détection des ondes P à l’ECG des nouveaux-nés
prématurés. Nous pourrions alors focaliser notre étude sur la segmentation précise des
ondes P en analysant l’activité auriculaire du nouveau-né prématuré en présence ou non
d’apnée-bradycardie.
Afin d’améliorer la segmentation de l’électrocardiogramme, réalisée ici en exploitant
une seule voie, une approche de détection multi-voies pourrait être considérée. Deux
approches sont à retenir : i) la centralisée qui produit une segmentation unique en exploitant
l’information contenue dans chacune des voies et ii) la décentralisée dont la segmentation
correspond à la meilleure segmentation (ou à la moyenne, la médiane) réalisée sur chaque
voie.
La détection multi-variée analysée dans ce mémoire peut être vue comme une approche
par fusion centralisée, où les dynamiques sont exploitées de manière conjointe pour produire
une détection unique. Une fusion décentralisée a été également mise en œuvre et évaluée.
Même si théoriquement cette dernière approche doit produire des performances compa-
rables ou inférieures à l’approche centralisée, elle a produit une légère augmentation des
performances, tout en minimisant le retard à la détection. Ces résultats impliquent que
l’approche centralisée par MSMC, telle que présentée dans ce travail de thèse, doit être
encore améliorée. Nous pensons, en particulier, à la proposition d’architectures de MSMC
couplés, plus complexes à mettre en œuvre, mais qui permettront de mieux reproduire
les dynamiques de chaque variable indépendamment, tout en gardant une représentation
multivariée par couplage entre les états de chaque modèle [Pieczynski, 2003; Derrode and
Pieczynski, 2004].](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-191-320.jpg)
![162 Conclusion
Dans ce mémoire, nous n’avons pas prêté d’attention à l’origine de l’apnée. Succinctement,
les épisodes peuvent être classés en obstructifs, centraux et mixtes. En exploitant la théorie
semi-Markovienne préconisée ici, trois modèles, pour explorer la dynamique de chaque
classe d’apnée-bradycardie, pourraient être exploités pour identifier l’origine de l’apnée et
ainsi délivrer une thérapie optimale. D’autres variables pourraient être aussi analysées par
l’approche semi-markovienne. Par exemple, en analysant le temps passé entre les épisodes
d’apnée-bradycardie on peut supposer que, lorsque un certain temps sans détection s’est
écoulé, l’apparition d’un épisode devient plus probable. Cette approche pourrait permettre
aussi de modéliser le temps entre épisodes à partir des types d’apnée-bradycardie possibles
(centrale, obstructive ou mixte).
Enfin, nous n’avons pas pris en compte dans ce travail les autres modalités monitorées
telles que le flux respiratoire, les mouvements abdominaux, l’électromyogramme ou élec-
troencéphalogramme, car nous souhaitions développer un système de détection qui exploite
uniquement le signal électrocardiographique afin de réduire les appareils de mesures. Ces
mesures pourraient très bien être exploitées dans une approche multi-variable de détection
par modèles semi-Markovien. Enfin, l’approche par modèles de Markov cachés s’est enrichi
aussi d’extensions apparues récemment dans la littérature et qui pourraient être envisagées
dans un cadre de détection/classification des apnée-bradycardies. On peut citer :
– L’utilisation des modèles de Markov couplés [Pieczynski, 2003; Derrode and Pieczynski,
2004]. Dans cette approche, les modèles de Markov cachés sont utilisés pour chaque
variable et les états cachés au temps t pour chaque MMC sont conditionnés par les
états au temps t−1 de tous les MMC connexes. Dans les modèles de modèles de Markov
couplés, la markovianité du couple (processus caché, processus observé)=(X, Y ) est
considérée directement.
– L’usage des modèles de Markov triplet [Pieczynski and Desbouvries, 2005; Pieczynski,
2007]. Ces modèles permettent de traiter des observations non stationnaires, de
généraliser les modèles semi-markoviens cachés, d’effectuer la fusion de Dempster-
Shafer dans un cadre markovien et de mettre en place un filtrage optimal en présence
de sauts. Dans les modèles de Markov triplets, on introduit un processus U auxiliaire
qui sert d’outil de calcul du processus triplet markovien (processus caché, processus
auxiliaire, processus observé)=(X, U, Y ).
– L’emploi des arbres de Markov cachés [Crouse et al., 1998; He et al., 2008; Du-
rand et al., 2004]. Ces modèles permettent d’intégrer l’information multi-résolutions
temps/fréquence d’une décomposition en ondelettes. Ces modèles ont été conçus pour
la modélisation de la loi des coefficients d’une transformée en ondelettes, lorsque
ceux-ci sont non-gaussiens et non-indépendants.
– L’utilisation des modèles hybrides MMC/réseaux de neurones artificiels (RNA) [Tren-
tin and Gori, 2001; Hagen and Morris, 2005; Tóth and Kocsor, 2007; Garcia-Moral
et al., 2011]. L’estimation des probabilités d’émission des états des MMC, habituelle-
ment effectuée en utilisant des modèles de mélange gaussien, est substituée par des](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-192-320.jpg)
![Conclusions et perspectives 163
RNA. Toutefois, les exigences de calcul sont fortement augmentées en raison de la
nécessité d’entraîner la RNA.
– L’emploi des modèles de Markov cachés à effets mixtes [Altman, 2007; Delattre,
2010]. Ces modèles permettent la modélisation des multiples processus à la fois et
l’incorporation de covariables et des effets aléatoires dans les modèles. Ils sont adaptés
à l’analyse de données longitudinales recueillies lors d’essais cliniques.
– L’usage des chaînes de Markov évidentielles [Fouque et al., 2000; Lanchantin and
Pieczynski, 2005]. Ces modèles exploitent la théorie de l’évidence de Dempster-Shafer
pour l’analyse de données temporelles.
Comme on peut le voir, les perspectives tracées, sont autant de challenges à mener et
s’inscrivent finalement dans un cadre théorique unique où les approches semi-Markoviennes
jouent un rôle primordial étant donné leurs avantages : i) un hyper-paramètre à ajuster,
ii) aucune connaissance a priori, iii) une capacité à modéliser des observations multi-variées
et continues et iv) une représentation compacte de dynamiques.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-193-320.jpg)





![Annexe B
La transformée en ondelettes pour la
segmentation des battements
Les filtres passe-haut (G(z)) et passe-bas (H(z)) de la figure 3.3 sont dérivés à partir
d’une ondelette mère ψ(t) de type spline quadratique, dont la transformée de Fourier est :
Ψ(Ω) = jΩ
sin Ω
4
Ω
4
4
(B.1)
Les réponses fréquentielles des filtres G(z) et H(z) sont données par l’équation B.2
tandis que ses réponses impulsionnelles sont données par l’équation B.3.
G(ejω
) = 4jejω/2
sin
ω
2
H(ejω
) = ejω/2
cos
ω
2
3 (B.2)
g[n] =
1
8
{δ[n + 2] + 3δ[n + 1] + 3δ[n] + δ[n − 1]}
h[n] = 2{δ[n + 1] − δ[n]}
(B.3)
La réponse en fréquence du filtre équivalent Qk(ejω) pour l’échelle de décomposition k est
donnée par B.4. Les réponses en fréquence d’amplitude des cinq premières échelles du filtre
équivalent Qk(ejω) sont représentées dans la figure B.1 pour une fréquence d’échantillonnage
de 250 Hz. Il est à noter que les fonctions de transfert montrent une caractéristique passe-bas
dérivée. La bande passante à 3 dB pour chaque échelle est montrée dans le tableau B.1 [Li
et al., 1995]
169](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-199-320.jpg)
![170 Annexe B
Tableau B.1 – Bande passante à 3 dB pour chaque échelle du filtre équivalente Qk(ejω)
Échelle Bande passante (Hz)
k = 21 62.5 ∼ 125.0
k = 22 18 ∼ 58.5
k = 23 8 ∼ 27
k = 24 4 ∼ 13.5
k = 25 2 ∼ 6.5
Qk(ejω
) =
G(ejω) k = 1
G(ej2k−1ω) k−2
l=0 H(ej2lω) k ≥ 2
(B.4)
0 20 40 60 80 100 120
0
0.5
1
1.5
2
2.5
3
3.5
4
Fréquence (Hz)
|Q |
k = 2
k = 3
k = 4
k = 5
k = 1
k
Figure B.1 – Réponse en fréquence d’amplitude du filtre équivalente Qk(ejω) pour les
échelles 1 à 5 pour une fréquence d’échantillonnage de 250 Hz.
De plus, pour obtenir les filtres à d’autres fréquences d’échantillonnage, les réponses
impulsionnelles du filtre équivalent à 250 Hz sont ré-échantillonnées [Martínez et al., 2004].
Les réponses en fréquence des filtres à 500 Hz et 1 kHz sont montrées figure B.2. Il peut
être observé que les réponses en fréquence du banc de filtres adaptés constituent une bonne
approximation des filtres d’origine.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-200-320.jpg)


![Annexe C
Les algorithmes évolutionnaires
Les AE sont des méthodes de recherche stochastique qui s’inspirent des principes de
la sélection naturelle Darwiniens du XIXe
siècle et imitant la métaphore de l’évolution
biologique naturelle.
Le principe derrière les AE est le suivant [Eiben and Smith, 2003] : étant donnée une
population d’individus dans un certain environnement qui a des ressources limitées, les
rivalités entraînent une sélection naturelle (survie du plus fort) et donc, une augmentation
de l’aptitude de la population. Un ensemble de candidats (des individus de la population)
est choisi aléatoirement. Ensuite, une fonction de coût à maximiser est appliquée aux
candidats comme une mesure d’aptitude et, sur les bases de ces valeurs, certains meilleurs
candidats sont choisis pour semer la prochaine génération. Ceci est fait par l’application de
la recombinaison et/ou de la mutation. D’un coté, la recombinaison est un opérateur qui est
appliqué à deux ou plusieurs candidats sélectionnés (les soi-disant parents) produisant un
ou plusieurs nouveaux candidats (les enfants), et de l’autre, la mutation est appliquée à un
candidat et résulte en la création d’un nouveau. En résumé, l’exécution des opérations de
recombinaison et de mutation des parents conduit à la création d’un ensemble de nouveaux
candidats (la descendance) qui rivalisent ensuite avec les anciens, en fonction de leurs
aptitudes et probablement en fonction de l’âge, pour une place dans la prochaine génération.
Ce processus est réitéré jusqu’à ce qu’un candidat avec une qualité suffisante (une solution)
soit trouvé ou qu’une limite de calcul précédemment fixée soit atteinte.
La base des AE repose fondamentalement sur deux qualités : d’une part, les opérateurs
de variation (recombinaison et mutation) qui créent la diversité dans la population et
facilitant ainsi la nouveauté, et d’autre part, la sélection qui augmente la qualité moyenne
des solutions dans la population. Un diagramme général d’un algorithme évolutionnaire,
d’après EIBEN et SMITH [Eiben and Smith, 2003], est montré figure C.1.
Les éléments les plus importants d’un AE sont donc :
173](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-203-320.jpg)

![C.3. Population 175
C.3 Population
L’objectif de la population est de garder des solutions possibles. Une population est
constituée par un ensemble fini de génotypes, où de multiples copies d’un individu sont
possibles. Cependant, il faut souligner que les individus ne changent pas ; c’est la population
qui le fait.
C.4 Mécanisme de sélection des parents
Le résultat fourni par la fonction de coût va permettre de sélectionner les individus
ayant la meilleure performance. Ainsi, les individus choisis vont devenir parents de la
prochaine génération. Une génération est la population à un instant donné. Plusieurs
critères de sélection ont été rapportés dans la littérature dont les plus courants sont le
tirage à la roulette [Holland, 1975] et la sélection par rang [Baker, 1987]. Dans la première,
la probabilité de sélectionner un individu dépend de sa performance, alors que dans la
deuxième, la probabilité de sélection dépend du rang (classement) de l’individu dans la
population, triée en fonction des performances des individus, et non directement de sa
performance.
C.5 Opérateurs de variation
Les opérateurs de variation créent de nouveaux individus à partir des anciens. Ils sont
divisés en deux : l’opérateur unaire (mutation) et l’opérateur binaire (recombinaison).
C.5.1 Mutation
La mutation modifie les gènes d’un génotype afin de produire un enfant (mutant modifié).
Ces gènes sont mutés avec une probabilité pm. La mutation évite la convergence prématurée
de l’algorithme. Parmi les types de mutation pour un codage à valeurs réelles on distingue
deux types de mutation :
– Uniforme : qui remplace la valeur du gène choisi xi par une valeur aléatoire xi tiré
d’une distribution uniforme sur l’intervalle possible de ce gène [Li,Ui] où Li et Ui sont
les limites inférieure et supérieure respectivement ;
– Non-uniforme : qui ajoute au gène choisi xi, une valeur aléatoire tirée d’une
distribution non uniforme, comme une distribution Gaussienne avec moyenne nulle
et écart type spécifiés par l’utilisateur. La probabilité de mutation non-uniforme se
rapproche de 0 au fur et à mesure que le nombre de générations augmente.](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-205-320.jpg)
![176 Annexe C
C.5.2 Recombinaison
La recombinaison combine les gènes de deux (ou plusieurs) parents pour en obtenir un
(ou plusieurs) enfants. Ainsi, les enfants héritent de certaines caractéristiques de leurs parents.
La recombinaison est appliquée avec une probabilité pc. Trois types de recombinaisons
existent pour un codage à valeurs réelles :
– Arithmétique : les enfants (E1 et E2) sont créés à partir des combinaisons linéaires
des parents (x et y) :
E1 = αx + (1 − α)y
E2 = (1 − α)x + αy
(C.1)
où α est choisi uniformément dans l’intervalle [0,1].
– Simple : l’enfant 1 (E1) correspond aux premiers k gènes du parent 1 (x) et le reste
est la moyenne arithmétique des deux parents :
E1 = x1, . . . , xk, αyk+1 + (1 − α)xk+1, . . . , αyn + (1 − α)xn (C.2)
où α est choisi uniformément dans l’intervalle [0,1], n est la taille du génotype et k
est le point de recombinaison choisi et suit une loi uniforme sur l’intervalle [1,n − 1].
Pour l’enfant 2, les parents sont renversés :
E2 = y1, . . . , yk, αxk+1 + (1 − α)yk+1, . . . , αxn + (1 − α)yn . (C.3)
– Heuristique : on utilise les valeurs de performance des deux parents pour créer les
enfants :
E1 = BP + α(BP − WP)
E2 = BP
(C.4)
où α suit une distribution uniformément dans l’intervalle [0,1] et où BP est le parent
qui a une performance plus grande que le parent WP.
C.6 Mécanisme de sélection des survivants
La sélection des survivants permet de former une nouvelle population à partir des
individus (parents et enfants) de la génération courante. Elle est similaire à la sélection des
parents mais est utilisée dans une autre étape du cycle évolutionnaire, c’est-à-dire, après la
création des enfants. Ainsi, le rôle de la sélection des survivants est de réduire le nombre
d’individus de µ parents et de λ enfants à λ individus pour la prochaine génération. À la
différence de la sélection des parents, qui est stochastique, la sélection des survivants est](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-206-320.jpg)


![Annexe D
L’algorithme de Viterbi
L’algorithme de Viterbi fait sa première apparition dans la littérature de codage dans
un document écrit par AJ VITERBI en 1967 [Viterbi, 1967]. Cet algorithme choisit les
états qui sont individuellement le plus probables afin de trouver la séquence d’états la plus
probable associée à la séquence observée. L’algorithme comprend une étape de récursion
qui parcourt le signal et qui enregistre les états qui maximisent L(O1:T |λ) et une étape de
rétropropagation qui parcourt le signal en sens inverse, en partant de l’état pour laquelle la
vraisemblance à T est maximum et en tenant compte des états précédents enregistrés dans
l’étape de récursion.
Pour trouver la meilleure séquence d’état, S1:T = S1, . . . , ST , pour la séquence d’obser-
vation donnée, O1:T O1, . . . , OT , nous devons définir la quantité
δt(i) max
s1:t−1
P(s1, s2, . . . , st = i, o1:t|λ) (D.1)
qui représente le maximum de vraisemblance d’une trajectoire unique jusqu’au temps t, qui
prend en compte les premières t observations et s’arrête à l’état i. Par induction nous avons
δt+1(j) = max
i∈S
δt(i)aij bj(ot+1). (D.2)
Pour retrouver la séquence d’états, nous avons besoin de garder une trace de l’argument
qui maximise D.2, pour chaque t et j. Nous le faisons par l’intermédiaire du tableau Ψt(j).
La procédure complète pour trouver la meilleure séquence d’états peut maintenant être
déclarée comme suit :
179](https://image.slidesharecdn.com/a0e450d5-2366-4dd6-96bc-5f3cff8c416c-161115125600/85/these_altuve-209-320.jpg)














