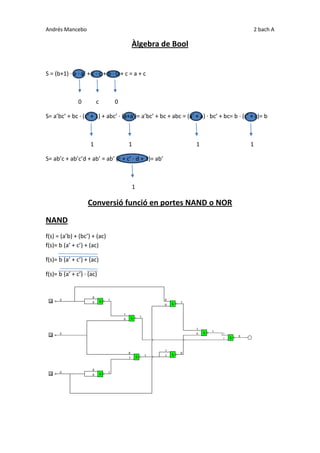
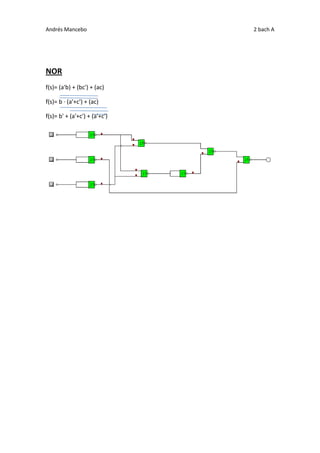
Le document traite de la logique booléenne, spécifiquement des expressions et des conversions de fonctions à l'aide de portes NAND et NOR. Il présente des équations impliquant des variables a, b et c, additionnant et multipliant les résultats pour simplifier les expressions. Enfin, des transformations de fonction en termes de portes logiques sont expliquées.

1. Andrés Mancebo
2 bach A
Àlgebra de Bool
S = (b+1) · a · a’ + c · c + b · 0 + c = a + c
0
c
0
S= a’bc’ + bc · (c’ + 1) + abc’ · (a+a’)= a’bc’ + bc + abc = (a’ + a) · bc’ + bc= b · (c’ + c)= b
1
1
1
S= ab’c + ab’c’d + ab’ = ab’ (c + c’ · d + 1)= ab’
1
Conversió funció en portes NAND o NOR
NAND
f(s) = (a’b) + (bc’) + (ac)
f(s)= b (a’ + c’) + (ac)
f(s)= b (a’ + c’) + (ac)
f(s)= b (a’ + c’) · (ac)
1

2. Andrés Mancebo
NOR
f(s)= (a'b) + (bc') + (ac)
f(s)= b · (a'+c') + (ac)
f(s)= b' + (a'+c') + (a'+c')
2 bach A