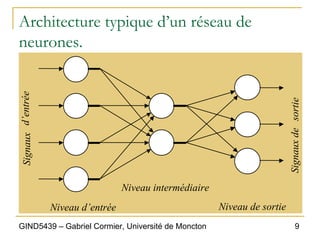
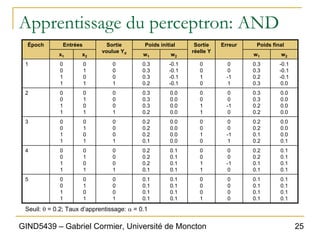
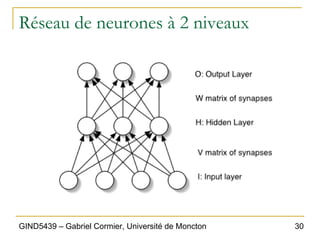
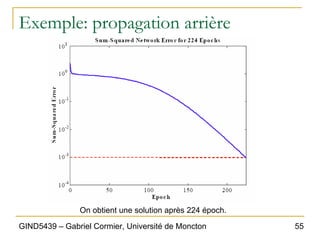
Le chapitre 6 du document présente les réseaux de neurones comme un modèle d'apprentissage machine inspiré du cerveau humain, consistant en un ensemble de neurones interconnectés. Il décrit les mécanismes de fonctionnement, y compris le calcul des sorties basées sur les poids des connexions et les fonctions d'activation, ainsi que l'apprentissage supervisé via des perceptrons. Le document aborde également les limitations des perceptrons simples et introduit l'idée des réseaux de neurones multi-niveaux, permettant une plus grande complexité dans l'apprentissage.

















![21
GIND5439 – Gabriel Cormier, Université de Moncton
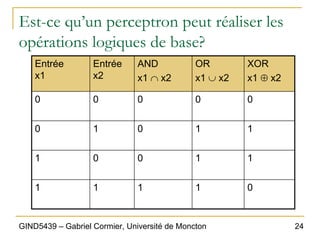
Algorithme d’apprentissage
„ Étape 1: initialisation
‰ On crée les poids initiaux w1, w2, …, wn et le seuil
θ à des valeurs aléatoires dans l’intervalle [-0.5,
0.5].
‰ Rappel: Si l’erreur e(p) est positive, il faut
augmenter la sortie Y(p) du perceptron; si l’erreur
est négative, il faut diminuer la sortie.](https://image.slidesharecdn.com/gind5439chapitre6-220528230335-6f44c96e/85/GIND5439_Chapitre6-pdf-21-320.jpg)


















![43
GIND5439 – Gabriel Cormier, Université de Moncton
Algorithme d’apprentissage, propagation
arrière
„ Étape 3: Poids
‰ On ajuste les poids dans le réseau à propagation arrière
qui propage vers l’arrière les erreurs.
‰ Calculer le gradient d’erreur pour les neurones du niveau
de sortie:
où
‰ Calculer les corrections aux poids.
‰ Ajuster les poids aux neurones de sortie.
[ ] )
(
)
(
1
)
(
)
( p
e
p
y
p
y
p k
k
k
k ⋅
−
⋅
=
δ
)
(
)
(
)
( , p
y
p
y
p
e k
k
d
k −
=
)
(
)
(
)
( p
p
y
p
w k
j
jk δ
α ⋅
⋅
=
∆
)
(
)
(
)
1
( p
w
p
w
p
w jk
jk
jk ∆
+
=
+](https://image.slidesharecdn.com/gind5439chapitre6-220528230335-6f44c96e/85/GIND5439_Chapitre6-pdf-43-320.jpg)
![44
GIND5439 – Gabriel Cormier, Université de Moncton
Algorithme d’apprentissage, propagation
arrière
„ Étape 3 (suite)
‰ Calculer le gradient d’erreur pour les neurones
dans le niveau caché:
‰ Calculer les corrections aux poids:
‰ Ajuster les poids aux neurones cachés:
)
(
)
(
)
(
1
)
(
)
(
1
]
[ p
w
p
p
y
p
y
p jk
l
k
k
j
j
j ∑
=
⋅
−
⋅
= δ
δ
)
(
)
(
)
( p
p
x
p
w j
i
ij δ
α ⋅
⋅
=
∆
)
(
)
(
)
1
( p
w
p
w
p
w ij
ij
ij ∆
+
=
+](https://image.slidesharecdn.com/gind5439chapitre6-220528230335-6f44c96e/85/GIND5439_Chapitre6-pdf-44-320.jpg)











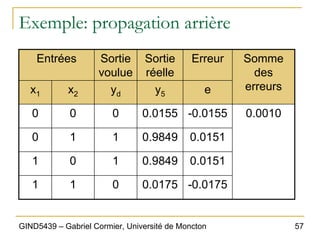




















![79
GIND5439 – Gabriel Cormier, Université de Moncton
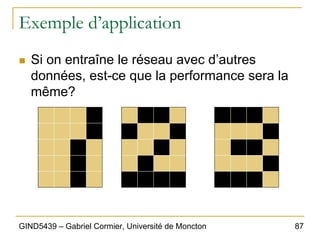
Exemple d’application
„ L’entrée sera donc composée de 20 « bits »,
de valeur 0 ou 1.
„ Exemple, entrée 1:
‰ input1 = [ 0; 0; 1; 0; 0; 0; 1; 0; 0; 0; 1; 0; 0; 0; 1; 0; 0; 0; 1; 0;];
Bit 1
1 2 3 4
5 6 7 8
9 10 11 12
13 14 15 16
17 18 19 20
Les pixels 3, 7, 11, 15
et 19 ont la valeur 1.
Les autres ont la
valeur 0.](https://image.slidesharecdn.com/gind5439chapitre6-220528230335-6f44c96e/85/GIND5439_Chapitre6-pdf-79-320.jpg)
![80
GIND5439 – Gabriel Cormier, Université de Moncton
Exemple d’application
„ On refait le processus de pixelisation pour les deux
autres entrées:
‰ input2 = [ 1; 1; 1; 1; 0; 0; 0; 1; 1; 1; 1; 1; 1; 0; 0; 0; 1; 1; 1; 1;];
‰ input3 = [ 1; 1; 1; 1; 0; 0; 0; 1; 1; 1; 1; 1; 0; 0; 0; 1; 1; 1; 1; 1;];
„ Il faut maintenant créer le réseau de neurones:
‰ net = newff([0 1; 0 1; 0 1; 0 1; 0 1; 0 1; 0 1; 0 1; 0 1; 0 1; 0 1; 0 1; 0 1; 0
1; 0 1; 0 1; 0 1; 0 1; 0 1; 0 1],[5 2],{'logsig','logsig'});
‰ On crée un réseau à deux niveaux, où les entrées varient
entre 0 et 1. Le premier niveau a 5 neurones, le deuxième
niveau en a 2 (2 sorties). La fonction d’activation utilisée
est « logsig ».](https://image.slidesharecdn.com/gind5439chapitre6-220528230335-6f44c96e/85/GIND5439_Chapitre6-pdf-80-320.jpg)

![82
GIND5439 – Gabriel Cormier, Université de Moncton
Exemple d’application
„ On spécifie quelques paramètres:
‰ net.trainParam.goal = 1e-10;
‰ net.trainParam.epochs = 200;
‰ Soit le but (somme des erreurs = 1e-10) et le
nombre maximal d’époques: 200.
„ On entraîne maintenant le réseau:
‰ input = [input1 input2 input3];
‰ target = [1 0 1; 0 1 1];
‰ net = train(net,input,target);](https://image.slidesharecdn.com/gind5439chapitre6-220528230335-6f44c96e/85/GIND5439_Chapitre6-pdf-82-320.jpg)
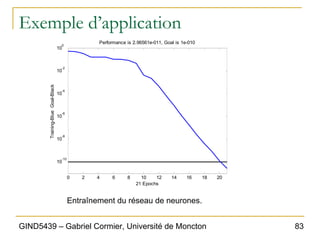


![86
GIND5439 – Gabriel Cormier, Université de Moncton
Exemple d’application
„ On obtient comme résultat:
‰ test1 = [ 0; 0; 1; 0; 0; 1; 1; 0; 0; 0; 1; 0; 0; 0; 1; 0; 0; 1; 1; 1;];
‰ output1 = sim(net,test1)
‰ test2 = [ 1; 1; 1; 0; 0; 0; 0; 1; 0; 1; 1; 0; 1; 0; 0; 0; 1; 1; 1; 1;];
‰ output2 = sim(net,test2)
‰ test3 = [ 1; 1; 1; 1; 0; 0; 0; 1; 0; 1; 1; 0; 0; 0; 0; 1; 1; 1; 1; 0;];
‰ output3 = sim(net,test3)
„ Résultats:
‰ output1 = 0.0002 1.0000 “c’est comme un 1”
‰ output2 = 1.0000 0.0001 “c’est comme un 2”
‰ output3 = 0.9999 1.0000 “c’est comme un 3”](https://image.slidesharecdn.com/gind5439chapitre6-220528230335-6f44c96e/85/GIND5439_Chapitre6-pdf-86-320.jpg)