Téléchargé 141 fois
Téléchargé parsadjida bellatreche
Réseaux neurons
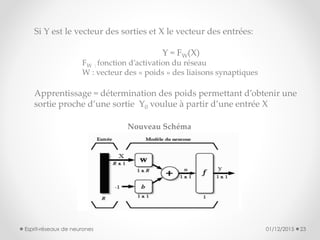
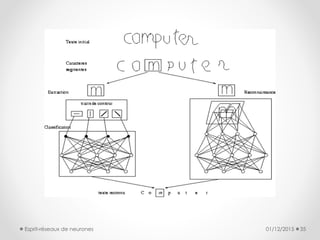
Le document présente une introduction aux réseaux de neurones, discutant de leur histoire, de leur architecture, et des paradigmes d'apprentissage. Il explique les analogies entre neurones biologiques et formels, décrit plusieurs modèles tels que le perceptron multicouche et les cartes de Kohonen, et souligne leurs applications variées. Enfin, il conclut sur le potentiel futur des réseaux de neurones dans divers domaines, en s'appuyant sur des bases mathématiques solides.
![Comprendre l’intelligence artificielle [webinaire]](https://cdn.slidesharecdn.com/ss_thumbnails/technologiawebinaireintelligenceartificielleclaudemarson01042019-190403213713-thumbnail.jpg?width=640&height=640&fit=bounds)
Réseaux neurons
- 1.
- 2. Plan ! 201/12/2015Réseaux desNeurones • Introduction Pourquoi les réseaux de neurones? Historique • Analogie neurone formel et neurone biologique Le neurone biologique Le neurone formel : - Le modèle Mc Culloch et Pitts • Architecture des réseaux de neurones Réseaux bouclés et réseaux non bouclés • Notion d’apprentissage Apprentissage supervisé et non supervisé • Quelques modèles de réseaux de neurones Le perceptron multicouche Le modèle de Hopefield Les cartes de Kohonen • Exemples d’applications • Conclusion
- 3.
- 4. Pourquoi les réseauxde neurones? Caractéristiques de l’architecture du cerveau humain: une architecture massivement parallèle un mode de calcul et une mémoire distribués une capacité d'apprentissage une capacité de généralisation une capacité d'adaptation une résistance aux pannes une faible consommation énergétique Esprit-réseaux de neurones
- 5. Définition o C’est uneapproche qui a été privilégiée par l'Intelligence Artificielle. o Les réseaux de neurones artificiels sont des réseaux fortement connectés de processeurs élémentaires fonctionnant en parallèle. Chaque processeur élémentaire calcule une sortie unique sur la base des informations qu'il reçoit. Toute structure hiérarchique de réseaux est évidemment un réseau. 501/12/2015Esprit-réseaux de neurones
- 6. Historique Quelques repères • 1943: o Modèle de McCulloch et Pitts • 1948: D. Hebb propose une règle d'apprentissage pour des réseaux de neurones . • 1960 : o Rosenblatt : perceptron et théorème de convergence o Minsky et Papert : limites du perceptron mono-couche • 1980 : o Modèle de Hopefield o Werbos : rétropropagation dans le cadre des perceptrons multi-couches (popularisé en 1986 par Rumelhart) 01/12/2015 6Esprit-réseaux de neurones
- 7. Intérêt 01/12/2015 7 Les RNAsont efficaces pour effectuer à grande vitesse des calculs et, d’une manière générale des tâches mécaniques La limitation des ordinateurs existants . La structure des réseaux de neurones étant elle-même parallèle, leur fonctionnement présente de nombreux avantages : une vitesse de calcul accrue, la résistance aux pannes locales, et enfin la régularité de la structure Ils s’inscrivent dans les mutations tech. Esprit-réseaux de neurones
- 8. 801/12/2015 Analogie neurone formel etneurone biologique Esprit-réseaux de neurones
- 9.
- 10. 01/12/2015 10 Le neuronebiologique Esprit-réseaux de neurones
- 11. 01/12/2015 11 Le neuronebiologique Dendrites : Signaux d’entrée Axone : Signal de sortie Esprit-réseaux de neurones
- 12. Description schématique deséléments d’une synapse 1201/12/2015 Transmission entre un axone et une dendrite Synapses excitatrices / synapses Esprit-réseaux de neurones
- 13. Structure d’un neurone artificiel 01/12/201513 Mise en correspondance neurone biologique / neurone artificiel Esprit-réseaux de neurones
- 14. 01/12/2015 14 Le neuroneformel Esprit-réseaux de neurones
- 15. Neurone formel: lemodèle Mc Culloch et Pitts 01/12/2015 15Esprit-réseaux de neurones
- 16. Le Neurone Formel 01/12/201516 Le neurone formel, l’unité élémentaire d’un RNA, se compose de deux parties : évaluation de la stimulation reçue (fonction E) évaluation de son activation (fonction f) Il est caractérisé par : son état X (binaire, discret, continu) le niveau d’activation reçu en entrée U (continu) le poids des connections en entrée Esprit-réseaux de neurones
- 17. Le Neurone Formel 1701/12/2015 Lafonction d’entrée : somme pondérée des signaux d’entrée Le biais d’entrée (biais input): unité fictive dont le poids permet de régler le seuil de déclenchement du neurone Esprit-réseaux de neurones
- 18. Les fonctions de transfert(d’activation) 01/12/2015 18Esprit-réseaux de neurones
- 19. 01/12/2015Esprit-réseaux de neurones19 Comparaison Biological Neuron Artificial Neuron corps cellulaire neurone Dendrites inputs Axone output Synaps poids
- 20. 01/12/2015 20 Architecture desréseaux de neurones Esprit-réseaux de neurones
- 21. 01/12/2015 21 Réseaux bouclés Lesneurones ne peuvent pas être ordonnés de sorte qu’il n’y ai pas de connexion vers l’arrière Exemple -> réseau entièrement connecté : Esprit-réseaux de neurones
- 22. 01/12/2015 22 Réseaux «non bouclés » ou réseaux à couches Les neurones peuvent être ordonnés de sorte qu’il n’y ai pas de connexion vers l’arrière Exemple -> réseau à une couche intermédiaire : Esprit-réseaux de neurones
- 23. 01/12/2015 23 Si Yest le vecteur des sorties et X le vecteur des entrées: Y = FW(X) FW : fonction d’activation du réseau W : vecteur des « poids » des liaisons synaptiques Apprentissage = détermination des poids permettant d’obtenir une sortie proche d’une sortie Y0 voulue à partir d’une entrée X Nouveau Schéma Esprit-réseaux de neurones
- 24.
- 25. 01/12/2015 25 Mise àjour des poids de connexion, en général à partir d’un ensemble de données d’entraînement Modification itérative des poids Paradigme d’apprentissage : modélisation de l’environnement dans lequel le réseau opèrera. 3 paradigmes d’apprentissage: Supervisé : on veut qu’à une entrée corresponde une sortie préalablement définie Non supervisé : on veut construire un réseau dont on ne connaît pas a priori la sortie correspondant à des entrées données Hybride Règles d’apprentissage : gouvernent la mise à jour des poids du réseau Algorithme d’apprentissage : procédure dans laquelle les règles d’apprentissage sont utilisées en vue de l’ajustement des poids Esprit-réseaux de neurones
- 26. Règles d’apprentissage 01/12/2015 26 4règles principales Par compétition Règle de Hebb Par correction d’erreur Apprentissage de Boltzmann Esprit-réseaux de neurones
- 27. Autres règles • Apprentissagepar descente de gradient : il s'agit de calculer une erreur et d'essayer de minimiser cette erreur. • Apprentissage par la règle de Widrow-Hoff (ou Adaline) : au lieu de calculer les variations des poids en sommant sur tous les exemples de S, l'idée est de modifier les poids à chaque présentation d'exemple. 01/12/2015 27Esprit-réseaux de neurones
- 28. Correction d’erreur • Sid est la sortie désirée et y la sortie obtenue, la modification des poids se fait en fonction de (d-y) • Algorithme de retro-propagation • Algorithme d’apprentissage du perceptron: o Initialisation des poids et du seuil à de petites valeurs aléatories o Présenter un vecteur d’entrées x(μ) et calculer sa sortie o Mettre à jour les poids en utilisant : wj(t+1) = wj(t) + η (d- y) xj avec d la sortie désirée, w vecteur des poids 01/12/2015 28Esprit-réseaux de neurones
- 29. 01/12/2015 29 Quelques modèlesde réseaux de neurones Esprit-réseaux de neurones
- 30. Le Perceptron multicouches 3001/12/2015 •Modèle du perceptron simple: o pas de seuil o fonction d’activation = fonction signe o Séparation de deux classes d’entiers A et B -> apprentissage supervisé o Inconvénient : A et B doivent être linéairement séparables Esprit-réseaux de neurones
- 31. 01/12/2015 31 • Mémorisationde formes et de motifs • Mémoire distribuée • Mémoire associative Le modèle de Hopefield Esprit-réseaux de neurones
- 32. 01/12/2015 32 • Nneurones binaires (1 ou -1) : 2N états possibles pour le réseau • Réseau entièrement connecté, connexion de poids Cij = Cji • État du neurone i à l’instant t: • L’état du neurone i dépend de l’état du réseau en général -> mémoire distribuée • But : trouver les Cji qui vont permettre de mémoriser un état particulier du réseau • Soient S1, S2… Sp p configuration du réseau à mémoriser : on veut, a partir d’une configuration proche de Sm, converger vers Sm -> mémoire associative • Principe de Hebb : Esprit-réseaux de neurones
- 33. 01/12/2015 33 Les cartesde Kohonen On veut un réseau ayant deux caractéristiques particulières : Apprentissage non supervisé Les réponses associées à des entrées voisines sont voisines : auto organisation Notion de voisinage entre les classes d’observation Algorithme : Initialisation : à chaque classe on associe un vecteur code dans l’espace d’observation Etape : on tire un point au hasard dans l’espace des observations (données). On déplace ensuite la classe la plus proche, ainsi que tous ses voisins les plus proches, vers ce point. Esprit-réseaux de neurones
- 34.
- 35. 01/12/2015 35Esprit-réseaux deneurones
- 36.
- 37. Conclusion • les réseauxde neurones reposent à Présent sur des bases mathématiques solides qui permettent d’envisager des applications dans presque tout les domaines y compris industriel et à grande échelle, notamment dans le domaine de la classification. 01/12/2015 37Esprit-réseaux de neurones
- 38. Perspectives Les réseaux deneurones ont une histoire relativement jeune (environ 50 ans) et les applications intéressantes des réseaux de neurones n’ont vu le jour que depuis une vingtaine d’année (développement de l’informatique), et ils ont un futur très prometteur, on entend parler (par exemple) du WEB sémantique, RFID, … etc. 01/12/2015 38Esprit-réseaux de neurones
- 39.