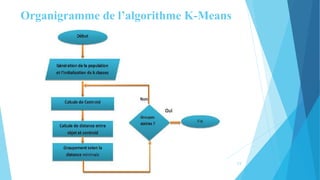
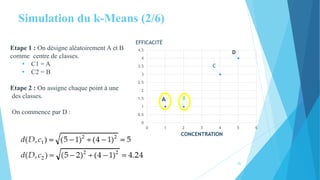
Le document traite de la segmentation par clustering, en présentant notamment l'algorithme k-means, qui permet de regrouper des objets similaires. Il aborde la définition de la segmentation, les critères d'un bon regroupement, les mesures de similarité, ainsi que les domaines d'application et les variantes de k-means. Enfin, il souligne les avantages et inconvénients de cette méthode en matière de classification non supervisée.

1. Clustering
(Segmentation)
Alya LETAIF
Donia HAMMAMI

2. Plan de la présentation
1. C’est quoi la segmentation ?
2. Qu’est ce qu’un bon regroupement ?
3. Classification des algorithmes de clustering
4. Mesure de similarité
5. Présentation de l’algorithme K-Means
6. Domaine d’application de l’algorithme K-Means
7. Variantes de K-Means
8. Organigramme de l’algorithme K-Means
9. Algorithme K-Means
10.Simulation de l’algorithme K-Means
11.Avantages et Inconvénients de l’algorithme K-means
12.Conclusion 2

3. C’est quoi la segmentation ?
 Regroupement (Clustering): construire une collection d’objets
 Similaires au sein d’un même groupe
 Dissimilaires quand ils appartiennent à des groupes différents
 Pour cette tâche, il n'y a pas de classe à expliquer ou des valeurs à prédire définies
à priori, il s'agit de créer des groupes homogènes dans la population (l'ensemble des
enregistrements).
 Le Clustering est de la classification non supervisée: Elle vise à identifier des
ensembles d’éléments qui partagent certaines similarités. Elle ne se base pas sur des
classes prédéfinies.
3

4. 4
Qu’est ce qu’un bon regroupement ?
 Une bonne méthode de regroupement permet de garantir :
 Une grande similarité intra-groupe
 Une faible similarité inter-groupe
 La qualité d’un regroupement dépend donc de la mesure de similarité utilisée
par la méthode et de son implémentation.

5. Mesure de similarité (1/3)
 Il n’y a pas de définition unique de la similarité entre objets .
 Différentes mesures de distances d (x ,y).
 La définition de la similarité entre objets dépend de :
 Le type des données considérées
 Le type de similarité recherchée
5

6. Mesure de similarité (2/3)
 Données Numériques :
 Distance de Minkowski:
 Distance euclidienne: q=2
 Distance de Manhattan : q=1
6

7. Mesure de similarité (3/3)
 Données binaires: d(0,0)=d(1,1)=0, d(0,1)=d(1,0)=1
 Donnée énumératives: Distance nulle si les valeurs sont égales et 1
sinon.
 Donnée énumératives ordonnées: idem. On peut définir une distance
utilisant la relation d’ordre.
7

8. Classification des algorithmes de Clustering (1)
 Algorithmes Hiérarchiques: Construisent les clusters en divisant de manière
récursive les instances. On a deux catégories :
 Segmentation hiérarchique des divisions: chaque objet est initialement
supposé un cluster.
 Segmentation hiérarchique ascendante: tous les objets forment un seul
cluster.
 Algorithmes basés sur la densité: Fondés sur des notions de connectivité et de
densité. Les points qui appartiennent à chaque groupe sont tirés d'une distribution de
probabilité spécifique.
 Algorithmes de grille: Basés sur une structure à multi-niveaux de granularité.
8

9. Classification des algorithmes de Clustering (2)
 Algorithmes basés sur le modèle: Un modèle est supposé pour chaque cluster ensuite
on vérifie chaque modèle sur chaque groupe pour choisir le meilleur. Les modèles les
plus utilisés sont:
 Les arbres de décision.
 Les réseaux de neurone.
 Algorithmes de Partitionnement: Consistent à relocaliser les instances en les déplaçant
d'un cluster à l'autre en partant d’un partitionnement initial. De tels procédés nécessitent
que le nombre de cluster sera prédéfinit par l'utilisateur. Parmi les algorithmes utilisés:
 L’algorithme des K-moyennes (K-Means).
9

10. Présentation de l’algorithme K-Means
 Un algorithme de classification non supervisée.
 Encore appelée méthode des centres mobiles.
 L’algorithme des K-moyennes permet de trouver des classes dans des données.
 Les classes qu’il construit n’entretiennent jamais de relations hiérarchiques: une classe
n’est jamais incluse dans une autre classe .
 L’algorithme fonctionne en précisant le nombre de classes attendues.
 L’algorithme calcule les distances Intra-Classe et Inter-Classe.
10

11. Domaines d’application
 Marketing : Segmentation du marché afin d’obtenir des groupes de clients
distincts à partir d’une base de données d’achat.
 Assurance : Identification des groupes d’assurés distincts associés à un nombre
important de déclarations.
 Planification des villes : Identification des groupes d’habitons suivant le type
d’habitation, ville, localisation géographique …
 Médecine : Localisation de tumeurs dans le cerveau
11

12. K-Means : Variantes
 Algorithme basé sur la sélection des centres initiaux .
 Algorithme basé Calcul des similarités.
 Algorithme basé Calcul des centres.
 Algorithme GMM : Variante basée sur les probabilités.
 Algorithme K-modes : Utilisé pour les données catégorielles.
 Algorithme K-prototype: Utilisé pour les données mixtes (numériques et catégorielles).
12

13. Organigramme de l’algorithme K-Means
13

14. Algorithme des k-moyennes (K-Means)
 Algorithme K-Means
Entrée : k le nombre de groupes cherchés
DEBUT
Choisir aléatoirement les centres des groupes
REPETER
i. Affecter chaque cas au groupe dont il est le plus proche à son centre
ii. Recalculer le centre de chaque groupe
JUSQU‘A (stabilisation des centres)
OU (nombre d'itérations =t)
OU (stabilisation de l’inertie totale de la population)
FIN
14

15. Simulation du k-Means (1/6)
A B
C
D
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 1 2 3 4 5 6
EFFICACITÉ
CONCENTRATION
 4 types de médicaments ayant
chacun deux modalités : La
concentration et l’efficacité, on
veut créer deux classes => K=2.
Médicaments Concentration Efficacité
A 1 1
B 2 1
C 4 3
D 5 4
15

16. Simulation du k-Means (2/6)
Etape 1 : On désigne aléatoirement A et B
comme centre de classes.
• C1 = A
• C2 = B
Etape 2 : On assigne chaque point à une
des classes.
On commence par D :
A B
C
D
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 1 2 3 4 5 6
EFFICACITÉ
CONCENTRATION
16

17. Simulation du k-Means (3/6)
A B
C
D
C2
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 1 2 3 4 5 6
EFFICACITÉ
CONCENTRATION
Etape 3 : Calcul les nouveaux centres des
classes compte tenu de la nouvelle
classification.
17

18. Simulation du k-Means (4/6)
 Nous voilà à nouveau à l’étape 1.
 On commence la deuxième
itération de l’algorithme.
 On réassigne chaque médicament à
une classe en calculant la distance
les séparant des nouveaux centres
de classe .
 On repart à l’étape 2.
A B
C
D
C2
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 1 2 3 4 5 6
EFFICACITÉ
CONCENTRATION
18

19. Simulation du k-Means (5/6)
 On répète les étapes jusqu’à
convergence.
 Connaissant les membres de chaque
classe, on recalcule les centres des
classes pour chacun de leurs nouveaux
membres.
A B
C
D
C2
C1
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 1 2 3 4 5 6
EFFICACITÉ
CONCENTRATION
19

20. Simulation du k-Means (6/6)
Le résultat final est donc:
 Classe1 = {A , B} avec centre de
classe c1 = (1.5 , 1).
 Classe2 = {C , D} avec centre de
classe c2 = (4.5 , 3.5).
A B
C
D
C2
C1
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
0 1 2 3 4 5 6
EFFICACITÉ
CONCENTRATION
20

21. K-moyennes : Avantages
 L’algorithme de k-Means est très populaire du fait qu’il est très facile à comprendre
et à mettre en œuvre,
 La méthode résolve une tâche non supervisée, donc elle ne nécessite aucune
information sur les données,
 Rapidité et faibles exigences en taille mémoire,
 La méthode est applicable à tout type de données (mêmes textuelles), en choisissant
une bonne notion de distance.
21

22.  Le nombre de classes est un paramètre de l’algorithme. Un bon choix du nombre k est
nécessaire, car un mauvais choix de k produit de mauvais résultats.
 Les points isolés sont mal gérés (doivent-ils appartenir obligatoirement à un cluster ?)
 L'algorithme du K-Means ne trouve pas nécessairement la configuration la plus optimale
correspondant à la fonction objective minimale.
 Les résultats de l'algorithme du K-Means sont sensibles à l'initialisation aléatoires des
centres.
K-moyennes : Inconvénients
22

23. Conclusion
 Le clustering groupe des objets en se en basant sur leurs similarités.
 La mesure de similarité peut être calculée pour différents types de données.
 La sélection de la de mesure de de similarité dépend des des données utilisées et le type
de similarité recherchée.
 La segmentation est utilisée dans différents domaines de recherche tels que la bio-
informatique, analyse financière, classification des séquences d'ADN, génie logiciel,
locomotion de robots, etc…
23

24. Merci pour votre
attention 