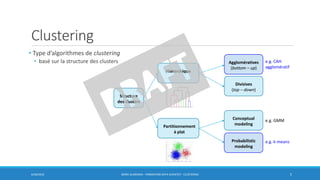
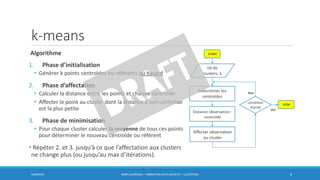
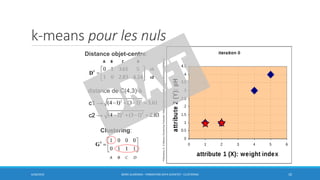
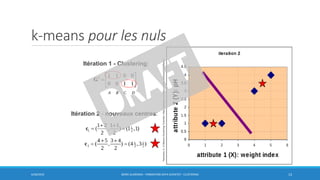
Ce document traite des méthodes de clustering, principalement le k-means et la classification ascendante hiérarchique (CAH), en détaillant leurs algorithmes, applications et mesures de performance. Il souligne la différence entre l'apprentissage supervisé et non supervisé, ainsi que l'importance de la distance et de la similarité dans le regroupement des données. Enfin, des pratiques pour déterminer le nombre optimal de clusters et des considérations sur leurs avantages et inconvénients sont également abordées.

1. Clustering: k-means et
CAH
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 1

2. Objectifs
 Comprendre les objectifs des méthodes de clustering
 Connaître les types des méthodes de clustering basés sur la structure de données
 Comprendre les notions de distance et similarité
 Comprendre l’algorithme k-means
 Connaître les mesures de performance de k-means
 Comprendre l’algorithme CAH (bottom - up)
 Comprendre les avantages et limites de CAH et k-means
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 2

3. Sommaire
• Introduction au clustering
• Algorithme k-means et application avec R
• Classification Ascendante Hiérarchique (CAH) et application avec R
• k-means vs. CAH
• Bibliographie
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 3

4. Clustering
• Apprentissage non supervisé
• pas de réponse Y, pas de libellé
• Faire émerger des groupes homogènes (ayant des caractéristiques communes) des données
• observations similaires dans le clusters
• observations dissimilaires entre les clusters
• Cas d’usage
• exploration de données: détection de schémas, détection de points aberrants, prétraitement
• marketing: segmentation clients,
• segmentation d’image,
• séquençage de l’ADN,
• analyse des réseaux sociaux,
• données hospitalières
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 4

5. Clustering
• Type d’algorithmes de clustering
• basé sur la structure des clusters
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 5
Structure
des clusters
Hiérarchique
Partitionnement
à plat
Agglomératives
(bottom – up)
Divisives
(top – down)
Conceptual
modeling
Probabilistic
modeling
e.g. GMM
e.g. k-means
e.g. CAH
agglomératif

6. k-means
• Partitionnement à plat en k clusters Ck
• méthode de réallocation
• Les nuées dynamiques sont une généralisation du
principe de cet algorithme
• k = nombre de clusters, définie par avance
• Groupes homogènes: notion de similarité
• distance euclidienne, cosinus, Manhattan, …
• Mesure de compacité:
• within-cluster sum of squares (WSS) à minimiser
• Mesure de séparation
• between-cluster sum of squares (BSS) à maximiser
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 6

7. k-means
• Mesure de compacité:
• within-cluster sum of squares (WSS) à minimiser
• Mesure de séparation
• between-cluster sum of squares (BSS) à maximiser
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 7
centroïde
du cluster Ci
observation
nb de
clusters
moyenne de
l’échantillon
d’observations
nb
d’observations
dans le cluster Ci
total sum
of squares
TSS =
WSS + BSS
distance

8. k-means
Algorithme
1. Phase d’initialisation
• Générer k points centroïdes ou référents au hasard
2. Phase d’affectation
• Calculer la distance entre les points et chaque centroïde
• Affecter le point au cluster dont la distance à son centroïde
est la plus petite
3. Phase de minimisation
• Pour chaque cluster calculer la moyenne de tous ces points
pour déterminer le nouveau centroïde ou référent
• Répéter 2. et 3. jusqu’à ce que l’affectation aux clusters
ne change plus (ou jusqu’au max d’itérations).
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 8
nb de
clusters: k
Déterminer les
centroïdes
Distance observation -
centroïde
Affecter observation
au cluster
condition
d’arrêt
Non
Oui
START
STOP

9. k-means pour les nuls
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 9
Valeurs initiales des centres :
c1 = (1,1) et c2 = (2,1)
K = 2
•Teknomo,K.,K-MeansClusteringTutorials.http://people.revoledu.com/kardi/tutorial/kMean/

10. k-means pour les nuls
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 10
Distance objet-centre:
Clustering:
distance de C(4,3) à
c1 →
c2 →
A B C D
c1
c2
•Teknomo,K.,K-MeansClusteringTutorials.http://people.revoledu.com/kardi/tutorial/kMean/

11. k-means pour les nuls
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 11
Clustering:
Itération 1 - nouveaux centres:
•Teknomo,K.,K-MeansClusteringTutorials.http://people.revoledu.com/kardi/tutorial/kMean/

12. k-means pour les nuls
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 12
Itération 1 - Distance objet-
centre:
Itération 1 - Clustering:
2 clusters
A B C D
c1
c2
•Teknomo,K.,K-MeansClusteringTutorials.http://people.revoledu.com/kardi/tutorial/kMean/

13. k-means pour les nuls
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 13
Itération 1 - Clustering:
Itération 2 - nouveaux centres:
Teknomo,K.,K-MeansClusteringTutorials.http://people.revoledu.com/kardi/tutorial/kMean/

14. k-means pour les nuls
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 14
Itération 2 - Distance objet-
centre:
Itération 2 - Clustering:
G2 = G1 ==> STOP !
2 clusters
A B C D
c1
c2
•Teknomo,K.,K-MeansClusteringTutorials.http://people.revoledu.com/kardi/tutorial/kMean/

15. k-means
• La solution finale dépend des représentants initiaux
choisis
• un choix aléatoire rend l'algorithme non déterministe
• Pas de minimum global de la distance intra-classe, seul
le minimum local est atteint.
• Il est fortement conseillé de centrer et réduire les
données: soustraire la moyenne et diviser par l’écart-
type
• scale(data)
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 15
« Quelles deux variables sont les plus
similaire ?
• X1 = (28, 72000, 120)
• X2 = (56, 73000, 80)
• X3 = (29, 74500, 118)
Intuition  X1, X3
Distance euclidienne  X1, X2 »

16. k-means
• Comment choisir k ?
• Le ratio des WSS / TSS décroit lorsque l’on augmente k
• … jusqu’à avoir un cluster par observation !
• Meilleur k avec méthode heuristique: « la règle du coude »
• point où WSS/TSS décroit lentement, WWS/TSS < 0.2
• point à partir duquel une augmentation de k n’a plus d’influence ni sur la
compacité ni sur la séparation
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 16
meilleure k: 3 ou 4

17. k-means
• Performances
• Apprentissage non supervisé: pas de « précision »,
« rappel », etc. car on a pas de réponse ou libellé
• Il n’y a pas de vérité !
• L’objectif n’est pas de libeller les observations mais de
mieux comprendre (gain insight) la structure des données
• Nous souhaitons alors une meilleure compacité (WSS) et
une meilleure séparation (BSS)
• Alternative à WSS et BSS:
• Mesure de compacité: Diameter
• Mesure de séparation: Intercluster Distance
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 17
DataCamp,Machine Learning MOOC, Chapter Clustering

18. k-means
• Performances
• L’indexe de Dunn
• plus il est grand plus compact ou plus séparés seront es
clusters
• attention:
• calcul intensif
• si un cluster possède un diamètre important alors que les autres sont
bien compacts, l’indexe sera petit; par conséquent, il faut considérer
comme un indicateur du « pire des cas »
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 18
DataCamp,Machine Learning MOOC, Chapter Clustering

19. k-means
kmeans(x = data, centers = 3, nstart = 20)
• centers = k, le nombre de clusters, affectation aléatoire initiale de k observations en tant que
centroïdes
• nstart le nombre d’affectations aléatoires initiales, kmeans retournera le meilleur résultat
my_km <- kmeans(x = data, centers = 3, nstart = 20)
>my_km$tot.withinss
>my_km$betweenss
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 19

20. Classification Ascendante Hiérarchique
• Quelles observations se regroupent en premier ?
• Quels clusters fusionnent en premier ? et quand ?
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 20
A
C
B
D
E
A
C
B
D
E
A
C
B
D
E
A
C
B
D
E

21. Classification Ascendante Hiérarchique
• Avantage par rapport à k-means: pas besoin de définir k an avance
• comme pour k-means, il n’y a pas de solution (scientifique, analytique, ...) pour déterminer le meilleur k
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 21
1 cluster 2 clusters 5 clusters
heuristique: on coupe là où il y a des
« long bras »

22. Classification Ascendante Hiérarchique
• Algorithme: CAH (bottom – up)
1. Calculer la matrice de similarité (de distance) entre
toutes les observations (n x n)
2. Une observation = un cluster
3. Trouve les 2 observations les plus proches et les
fusionner en un cluster
4. Nouvelle matrice des distance (avec un cluster en moins)
5. Répéter 3. et 4. jusqu’à l’obtention d’un seul cluster
• Quelle « distance » ou « similarité » utiliser pour la
construction de la matrice ?
• Quel critère utiliser pour déterminer les 2 observations
les plus proches pour la fusion ?
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 22
distanceentreclusteravantfusion
barres horizontales = les fusions

23. Classification Ascendante Hiérarchique
• Matrice de distance
• Distance euclidienne
• Corrélation entre observations!
• Coefficient de Dice, Indice de Jaccard, Cosinus
• Méthodes d’agrégation (fusion ou linkage)
• à lien unique (single link): peut produire des classes qui sont relativement peu homogènes
(dendrogramme déséquilibré)
• à lien complet (complete link): peut produire des classes fortement homogènes (dendrogramme peu
réaliste)
• à lien moyen (average link): peut produire des dendrogrammes plus réalistes qu’avec les deux dernières
méthodes
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 23

24. Classification Ascendante Hiérarchique
• Matrice de distance
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 24
4 observations =
4 documents
vocabulaire d’indexation
avec 5 termes
AminiM.-R.,GaussierE.,Recherched’information,ISBN9782212135329,Eyrolles,2013

25. Classification Ascendante Hiérarchique
• Méthodes d’agrégation (fusion ou linkage)
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 25
Amini M.-R., Gaussier E., Recherche d’information, ISBN 9782212135329, Eyrolles, 2013
lien unique lien complet
lien moyen

26. k-means vs. CAH
• k-means
• + calcul rapide
• + on peut défaire les fusions
• - on doit fixer k en avance
• - dépendent des centroïdes initiaux
• CAH
• + pas besoin de fixer k en avance
• + meilleure analyse et compréhension
• - calcul coûteux
• - on peut pas défaire les fusions
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 26

27. Classification Ascendante Hiérarchique
Matrice de distance
• dist(x, method) ici method: distance
Méthodes d’agrégation (fusion ou linkage)
• hclust(d, method) ici d: matrice de distance, method: méthode d’agrégation
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 27

28. Bibliographie
• Amini M.-R., Gaussier E., Recherche d’information, ISBN 9782212135329, Eyrolles, 2013
• DataCamp, Machine Learning MOOC, Chapter Clustering
• Teknomo, K., K-Means Clustering Tutorials. http://people.revoledu.com/kardi/tutorial/kMean/
6/30/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - CLUSTERING 28