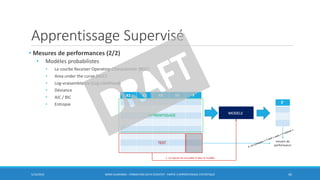
Ce document aborde l'apprentissage statistique et ses relations avec l'intelligence artificielle et le machine learning, en détaillant les méthodes supervisées et non supervisées. Il présente également l'évolution de la statistique depuis les années 40, les concepts de modélisation, ainsi que les techniques d'analyse de données et de validation des modèles. L'objectif principal est de comprendre et d'optimiser les modèles en équilibre avec la complexité et l'interprétabilité.
































![Apprentissage Supervisé
5/10/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - PARTIE 3 APPRENTISSAGE STATISTIQUE 37
• Ajouter des variables :
multicolinéarité des variables explicatives
fait croître la variance des estimateurs
fait croître la variance des prévisions:
VARIANCE IMPORTANTE
SURAJUSTEMENT (overfit)
𝐸[ መ𝑓(x) - 𝐸[ መ𝑓(x)] ]2 à savoir
expliquer!
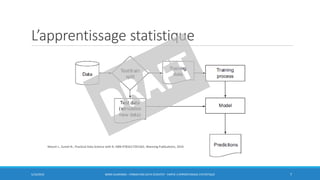
Ng A., Machine Learning MOOC, Coursera – Stanford University](https://image.slidesharecdn.com/03appstatistiquev2-160630085213/85/03-Apprentissage-statistique-37-320.jpg)
![Apprentissage Supervisé
5/10/2016 BORIS GUARISMA - FORMATION DATA SCIENTIST - PARTIE 3 APPRENTISSAGE STATISTIQUE 38
à savoir
expliquer!
• On introduit du biais:
on essaie d’approximer un problème
relativement complexe avec un modèle trop
simple
le modèle a déjà une idée préconçue de la
relation entre Y et X
BIAIS IMPORTANT
FAIBLE AJUSTEMENT (underfit)
𝐸[ መ𝑓(x)] - 𝑓(x)
Ng A., Machine Learning MOOC, Coursera – Stanford University](https://image.slidesharecdn.com/03appstatistiquev2-160630085213/85/03-Apprentissage-statistique-38-320.jpg)