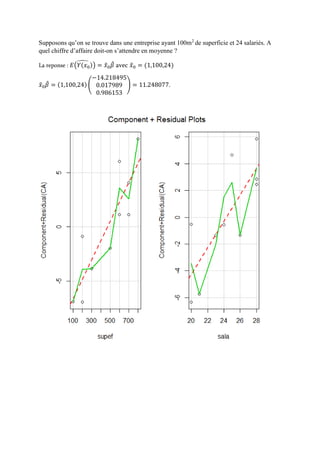
Le document traite de la régression linéaire multiple, une méthode statistique qui examine les variations d'une variable dépendante en fonction de plusieurs variables indépendantes. Il explique le modèle théorique, les hypothèses à respecter, et détaille la méthode des moindres carrés pour estimer les paramètres du modèle. Enfin, il aborde l'estimation de la variance des résidus et le testing des modèles statistiques.

1. REGRESSION LINEAIRE
MULTIPLE
Projet Statistique
yoople
robentz26@yahoo.fr
Préparé par:
Pierre Robentz CASSION
Pierre Danou PASCAL
Idatson ELYSEE
Emerson SAINT-LOUIS

2. Introduction
Le problème ?
En dehors de la magie, tous les phénomènes naturels
ont une explication. L’explication de ces phénomènes
est souvent liée à plusieurs facteurs extérieurs.
Considérons que le phénomène qu’on cherche à
expliquer est une variable (tension électrique, intensité
du courant, rendement, croissance, etc.). Soit y cette
variable et x le vecteur contenant les valeurs des divers
facteurs extérieurs influençant sur y. On appellera y la
variable expliquée et x le vecteur des variables
explicatives. Puisque y dépend de x, n’y a-t-il pas une
fonction qui la relie à x? On verra la réponse dans la
suite

3. Régression
Plus haut, nous nous avons demandé s’il y a une fonction qui relie y à x. Eh bien la réponse
est oui. C’est cette fonction de relation qui définit le terme régression.
Ainsi on peut écrire: Y=A+f(x)+ε. Y variable expliquée, x vecteur des variables
explicatives. f: fonction qui lie x à Y, εle terme d’erreur, A Valeur de Y quand rien n’agit sur
lui.
Régression linéaire
On parle de régression linéaire lorsque la fonction est linéaire.
Régression linéaire simple : C’est une régression linéaire où le vecteur x de l’équation
Y=A+f(x)+εa un seul composant. Ainsi l’équation devient : Y=A+αx+ ε.
Régression linéaire multiple: le vecteur x a plus qu’un seul composant. x(x1,x2,...,xn). On
ecrit alors 𝑌 = 𝛽0 + 𝛽1 𝑥1 + 𝛽2 𝑥2 + ⋯ 𝛽 𝑛 𝑥 𝑛 + 𝜀
Pourquoi ce terme d’erreur ?
Bah ouais! Parfois il peut avoir plus de variables explicatives que ce qu’on a pour cette raison
il est judicieux de prévoir un terme d’erreur.

4. Retour à notre sujet !
Régression linéaire
Multiple
La régression linéaire multiple est une analyse statistique qui décrit les
variations d'une variable endogène ou expliquée associée aux variations de
plusieurs variables exogènes ou explicatives.
Modèle Théorique
Considerons ce tableau:
𝒏 𝒐
𝒐𝒃𝒔. 𝒙 𝟏 𝒙 𝟐 …. 𝒙𝒋 … 𝒙 𝒑 𝒚
1 𝒙 𝟏𝟏 𝒙 𝟏𝟐 … 𝒙 𝟏𝒋 … 𝒙 𝟏𝒑 𝒚 𝟏
...
...
...
...
...
...
𝑖 𝒙𝒊𝟏 𝒙𝒊𝟐 … 𝒙𝒊𝒋 … 𝒙𝒊𝒑 𝒚𝒊
...
...
...
...
...
...
𝑛 𝒙 𝒏𝟏 𝒙 𝒏𝟐 … 𝒙 𝒏𝒋 … 𝒙 𝒏𝒑 𝒚 𝒏
Moy 𝒙̅ 𝟏 𝒙̅ 𝟐 𝒙̅𝒋 𝒙̅ 𝒑 𝑦̅
E-type 𝒔 𝟏 𝒔 𝟐 𝒔𝒋 𝒔 𝒑 𝒔 𝒚
Ce Tableau 1 contient l’information sur n observations.

5. Ecrivons les equation de tous les 𝑌𝑖:
𝑌1 = 𝛽0 + 𝛽1 𝑥11 + 𝛽2 𝑥12 + ⋯ 𝛽 𝑝 𝑥1𝑝 + 𝜀 1
⋮ ⋮ ⋮ ⋮ ⋮ ⋮
𝑌𝑖 = 𝛽0 + 𝛽1 𝑥𝑖1 + 𝛽2 𝑥𝑖2 + ⋯ 𝛽 𝑝 𝑥𝑖𝑝 + 𝜀 𝑖
⋮ ⋮ ⋮ ⋮ ⋮ ⋮
𝑌𝑛 = 𝛽0 + 𝛽1 𝑥 𝑛1 + 𝛽2 𝑥 𝑛2 + ⋯ 𝛽 𝑝 𝑥 𝑛𝑝 + 𝜀 𝑖
Cette écriture nous fait découvrir un système d’équation.
Pour mieux manipuler cet ensemble, écrivons-le sous forme matricielle:
Notation matricielle
On a:
Considérons l’unité expérimentale i. On a:
𝑌𝑖 = 𝛽0 + 𝛽1 𝑥𝑖1 + 𝛽2 𝑥𝑖2 + ⋯ 𝛽 𝑝 𝑥𝑖𝑝 + 𝜀
𝑖
𝑌𝑖 𝑒𝑠𝑡 𝑙𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑒𝑥𝑝𝑙𝑖𝑞𝑢é𝑒 𝑜𝑢 𝑒𝑛𝑑𝑜𝑔è𝑛𝑒 , 𝑐′
𝑒𝑠𝑡
𝑢𝑛𝑒 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑎𝑙é𝑎𝑡𝑜𝑖𝑟𝑒
(𝑥𝑖𝑗) 𝑎𝑣𝑒𝑐 𝑖 𝑓𝑖𝑥𝑒 𝑒𝑠𝑡 𝑙𝑒 𝑣𝑒𝑐𝑡𝑒𝑢𝑟 𝑑𝑒𝑠 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠
𝑒𝑥𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑣𝑒𝑠 𝑜𝑢 𝑒𝑥𝑜𝑔𝑒𝑛𝑒𝑠 𝑓𝑖𝑥é𝑒 𝑝𝑜𝑢𝑟 𝑙′
𝑜𝑏𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑜𝑛 𝑖
𝐿𝑒𝑠 𝛽𝑗, 𝑗 = 0, … , 𝑝 𝑠𝑜𝑛𝑡 𝑙𝑒𝑠 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑟𝑒𝑠 𝑖𝑛𝑐𝑜𝑛 nus qu’on
determinera en d’autre terme 𝛽𝑗 correspond à l’augmentation de
𝑌𝑖 lorsqu’on augmente 𝑥𝑖𝑗 d’une unite et qu’on maintient les
autres 𝑥 𝑘𝑗, avec k différent de j, constant.
𝜀
𝑖
𝑒𝑠𝑡 𝑙𝑒 𝑡𝑒𝑟𝑚𝑒 𝑑′
𝑒𝑟𝑟𝑒𝑢𝑟 𝑑𝑒 𝑌𝑖. 𝐶′
𝑒𝑠𝑡 𝑙𝑒 𝑐𝑜𝑡é 𝑎𝑙𝑒𝑎𝑡𝑜𝑖𝑟𝑒 𝑑𝑒 𝑌𝑖

6. (
𝑌1
⋮
𝑌𝑖
⋮
𝑌𝑛)
=
[
1
⋮
1
𝑥11
⋮
𝑥𝑖1
𝑥12
⋮
𝑥𝑖2
⋮ ⋮ ⋮
1 𝑥 𝑛1 𝑥 𝑛2
⋯
⋱
⋯
𝑥1𝑝
⋮
𝑥𝑖𝑝
⋮
𝑥 𝑛𝑝] (
𝛽0
𝛽1
𝛽2
⋮
𝛽 𝑝)
+ (
𝜀1
⋮
𝜀𝑖
⋮
𝜀 𝑛
)
𝑌 = 𝑋 𝛽 + 𝜀
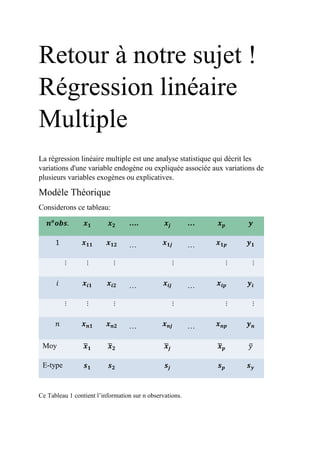
Il est facile de voir que 𝑌 est le vecteur des variables explicatives, X matrice à n lignes et
p+1 colonnes des variables prédictrices, 𝛽 vecteur des paramètres inconnus et 𝜀 celui des
termes d’erreurs.
Les hypothèses
Dans le modèle linéaire multiple , les hypothèses d'exogénéité, de non colinéarité, de non
corrélation des termes d'erreur et d'homoscédasticité doivent être respectées.
Exogeneité : Les variables explicatives ne sont pas corréler au terme d’erreur c’est-a-dire
𝑐𝑜𝑣𝑎𝑟(𝜀𝑗, 𝑥𝑖𝑘) = 0 , ∀𝑖, 𝑗, 𝑘. Avec 𝑋 constant, on a𝐸(𝜀) = 0⃗ .
Homoscédasticité : ∀𝜀𝑗 ,𝑗=1,…,𝑛, 𝑣𝑎𝑟(𝜀𝑗) = 𝜎2
, 𝑎𝑣𝑒𝑐 𝜎 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡.
Non colinearité des termes d’erreur : ∀𝑖, 𝑗, 𝑗 ≠ 𝑖, 𝑐𝑜𝑣𝑎𝑟(𝜀𝑖, 𝜀𝑗) = 0.
On peut aussi dire que les termes d’erreur doivent suivre une loi normale
centrée réduites.
Un vecteur comme variable aléatoire????????
Il n’est pas nouveau d’entendre parler de vecteur aléatoire en statistique ou
probabilité. Ce qui nous intéresse maintenant est de savoir l'espérance et la
variance d’un vecteur aléatoire.
L’espérance d’un vecteur aléatoire est le vecteur des espérances. Par exemple :
𝐸(𝜀) =
(
𝐸( 𝜀1)
⋮
𝐸( 𝜀𝑗)
⋮
𝐸( 𝜀 𝑛))

7. La variance d’un vecteur aléatoire est une matrice.
𝑉(𝜀) = (
𝑐𝑜𝑣𝑎𝑟( 𝜀1, 𝜀1) ⋯ 𝑐𝑜𝑣𝑎𝑟( 𝜀1, 𝜀 𝑛)
⋮ ⋱ ⋮
𝑐𝑜𝑣𝑎𝑟( 𝜀 𝑛, 𝜀1) ⋯ 𝑐𝑜𝑣𝑎𝑟( 𝜀 𝑛, 𝜀 𝑛)
)
Dans notre cas où les hypothèses ci-dessus sont vérifiées, 𝑉(𝜀) =
𝜎2
𝐼 𝑑 , 𝑎𝑣𝑒𝑐 𝐼 𝑑 𝑑𝑒 𝑡𝑎𝑖𝑙𝑙𝑒 𝑛 × 𝑛.
Estimation des paramètres
En statistique inférentielle, on a toujours comme but d’estimer les paramètres inconnus à partir des
données recueilli lors d’une ou plusieurs observations c’est-à-dire donner une approximation générale
des variables inconnus à partir de quelques observations.
Soit :
𝑌𝑖 = 𝛽0 + 𝛽1 𝑥𝑖1 + 𝛽2 𝑥𝑖2 + ⋯ 𝛽 𝑝 𝑥𝑖𝑝 + 𝜀 𝑖
Estimer les βi revient à les chercher de façon à ce que la combinaison linéaire des prédicteurs pour
chaque unité d’observation i approche le plus possible des 𝑦𝑖 de nos observations.
Ecriture de la combinaison :
𝑦𝑖 = 𝛽0
̂ + 𝛽1
̂ 𝑥𝑖1 + 𝛽2
̂ 𝑥𝑖2 + ⋯ 𝛽 𝑝
̂ 𝑥𝑖𝑝 + 𝑒𝑖
En prenant ensemble de ces équations, on trouve une équation de cette forme : 𝑌 = 𝑋𝛽̂ + 𝐸
Avec Y vecteurs des réponses observées, 𝛽̂ vecteur des estimations, X matrice des
prédicteurs, E vecteur des termes d’erreurs.
Cela revient à chercher ces coefficients de manière à minimiser les erreurs 𝑒 𝑖
(résidus
observés). Pour faire cela, on va utiliser la méthode des moindres carrées qui consiste à minimiser la
somme des carrées des écarts.
En prenant
𝑦𝑖̂ = 𝛽0
̂ + 𝛽1
̂ 𝑥𝑖1 + 𝛽2
̂ 𝑥𝑖2 + ⋯ 𝛽 𝑝
̂ 𝑥𝑖𝑝 valeur prédite cour l’unité expérimentale i, on 𝑒𝑖 = 𝑦𝑖 − 𝑦̂𝑖
Méthode des moindres carrées
Cette méthode consiste à chercher les coefficients qui minimisent la somme des carrées des écarts
autrement dit la somme des carrées des résidus ou termes d’erreur ∑ 𝑒𝑖
2
.
La solution de ce problème de minimisation est cette fameuse equation : 𝑋′
𝑋 𝛽̂ = 𝑋′𝑌
Avec 𝑋′ la matrice transposée de 𝑋.
Pour résoudre cette équation, 1) il est clair que 𝑋′
𝑋 soit inversible, 2) le nombre d’observation doit
être supérieure ou égale au nombre de paramètre à estimer.

8. Propriétés de l’estimateur 𝜷̂
L’estimateur 𝛽̂ dit estimateur de moindre carrée est sans biais. Sachant qu’on a par hypothèse
l’exogénéité des variables c’est-à-dire 𝐸(𝜀) = 0⃗ . Montrons que : 𝐸(𝛽̂) = 𝛽.
Preuve
𝛽̂ = ((𝑋′
𝑋)−1
𝑋′
𝑌) <=> 𝛽̂ = ((𝑋′
𝑋)−1
𝑋′
(𝑋𝛽 + 𝜀))𝛽̂ = 𝛽 + (𝑋′
𝑋)−1
𝑋′𝜀 𝐸(𝛽̂) =
𝐸(𝛽 + (𝑋′
𝑋)−1
𝑋′
𝜀) => 𝐸(𝛽̂) = 𝛽 + (𝑋′
𝑋)−1
𝑋′
𝐸(𝜀) => 𝐸(𝛽̂) = 𝛽 + (𝑋′
𝑋)−1
𝑋′
0⃗ . D’où
le resultat : 𝐸(𝛽̂) = 𝛽.
Ceci nous montre, en prenant 𝛽̂ comme estimateur, en moyenne on tombe sur la vraie valeur
de 𝛽.
Deuxième propriété 𝑉(𝛽̂) = (𝑋′
𝑋)−1
𝜎2
.
Preuve :
Afin de démontrer cette formule sous sous hypothèse, montrons que l’ième ligne et le jème
colonne de la matrice (𝑋′
𝑋)−1
est la 𝑐𝑜𝑣𝑎𝑟(𝜀𝑖, 𝜀𝑗)/𝜎2
.
Posons : 𝐶 = ( 𝑋′
𝑋)
−1
𝑋′
=> 𝛽̂ = 𝐶𝑌 => 𝛽̂ = (
𝑐11 ⋯ 𝑐1𝑛
⋮ ⋱ ⋮
𝑐 𝑝1 ⋯ 𝑐 𝑝𝑛
) × (
𝑦1
⋮
𝑦 𝑛
)
Alors 𝛽̂𝑖−1 = ∑ 𝑐𝑖𝑙
𝑛
𝑙=1 𝑦𝑙 et 𝛽̂𝑗−1 = ∑ 𝑐𝑗𝑘
𝑛
𝑘=1 𝑦 𝑘.
𝑐𝑜𝑣𝑎𝑟 ( 𝛽̂
𝑖−1, 𝛽̂
𝑗−1) = 𝑐𝑜𝑣𝑎𝑟(∑ 𝑐𝑖𝑙
𝑛
𝑙=1 𝑦𝑙, ∑ 𝑐𝑗𝑘
𝑛
𝑘=1 𝑦 𝑘)
𝑐𝑜𝑣𝑎𝑟(∑ 𝑐𝑖𝑙
𝑛
𝑙=1 𝑦𝑙, ∑ 𝑐𝑗𝑘
𝑛
𝑘=1 𝑦 𝑘) = ∑ ∑ 𝑐𝑖𝑙
𝑛
𝑘=1
𝑛
𝑙=1 𝑐𝑗𝑘 × 𝑐𝑜𝑣𝑎𝑟( 𝑦𝑙, 𝑦 𝑘) =>
Avec l’hyphothese de Non colinearité des termes d’erreur.
{
𝑐𝑜𝑣𝑎𝑟( 𝑦𝑙, 𝑦 𝑘) = 0 𝑠𝑖 𝑙 ≠ 𝑘
𝑐𝑜𝑣𝑎𝑟( 𝑦𝑙, 𝑦 𝑘) = 𝑣𝑎𝑟( 𝑦 𝑘) 𝑠𝑖 𝑙 = 𝑘
Avec 𝑣𝑎𝑟( 𝑦 𝑘) = 𝜎2
= 𝑣𝑎𝑟(𝜀)
𝑐𝑜𝑣𝑎𝑟 ( 𝛽̂
𝑖−1, 𝛽̂
𝑗−1) = ∑ ∑ 𝑐𝑖𝑘
𝑛
𝑘=1
𝑛
𝑘=1 𝑐𝑗𝑘 𝜎2
=> 𝑐𝑜𝑣𝑎𝑟 ( 𝛽̂
𝑖−1, 𝛽̂
𝑗−1) = 𝜎2
(𝐶𝐶′)𝑖𝑗 ou le (𝐶𝐶′)𝑖𝑗
est le composant du ieme ligne et jieme colonne de la matrice 𝐶𝐶′.
𝑉(𝛽̂) = (
𝑐𝑜𝑣𝑎𝑟(𝛽̂0, 𝛽̂0) ⋯ 𝑐𝑜𝑣𝑎𝑟(𝛽̂0, 𝛽̂ 𝑛)
⋮ ⋱ ⋮
𝑐𝑜𝑣𝑎𝑟(𝛽̂ 𝑛, 𝛽̂0) ⋯ 𝑐𝑜𝑣𝑎𝑟(𝛽̂ 𝑛, 𝛽̂ 𝑛)
) = 𝜎2
(
( 𝐶𝐶′
)00
⋯ ( 𝐶𝐶′
)0𝑛
⋮ ⋱ ⋮
( 𝐶𝐶′
) 𝑛0
⋯ ( 𝐶𝐶′
) 𝑛𝑛
) =>
𝐶′
= ((𝑋′
𝑋)−1
𝑋′)′
=> 𝐶′
= 𝑋((𝑋′
𝑋)−1
)′ => 𝐶′
= 𝑋(𝑋′
𝑋)−1
((𝑋′
𝑋)−1
)′ 𝑒𝑠𝑡 𝑒𝑔𝑎𝑙 (𝑋′
𝑋)−1
parce que 𝑋′
𝑋 étant symétrique implique que (𝑋′
𝑋)−1
l’est
également.

9. Donc : 𝐶𝐶′
= (𝑋′
𝑋)−1
𝑋′
𝑋(𝑋′
𝑋)−1
=> 𝐶𝐶′
= (𝑋′
𝑋)−1
.
De ce resultat, on obtient : 𝑽(𝜷̂) = 𝝈 𝟐(𝑿′
𝑿)−𝟏
.
Nous servirons par la suite avec ce résultat pour trouver des intervalles de confiance des paramètres
estimés.
Si on se sert du point moyen, le modèle est parfaitement ajusté c’est-à-dire 𝑦𝑖̅ = 𝛽0
̂ + 𝛽1
̂ 𝑥̅𝑖1 + 𝛽2
̂ 𝑥̅𝑖2 +
⋯ 𝛽 𝑝
̂ 𝑥̅𝑖𝑝.
Estimation de la variance des résidus 𝝈 𝟐
Definissons 𝑆𝐶𝐸 𝑅 comme etant la Somme des Carrés des Ecarts due aux Résidus.
𝑆𝐶𝐸 𝑅 = ∑ 𝑒𝑖
2
𝑖 .
𝜎2
peut être estimée par ∑
(𝑦 𝑖−𝑦̂ 𝑖)2
𝑛−𝑝−1
=𝑖
𝑆𝐶𝐸 𝑅
𝑛−𝑝−1
. Cet estimateur est non biaisé. En effet,
Il est évident que
𝑆𝐶𝐸 𝑅
𝜎2 ~𝜒 𝑛−(𝑝+1)
2
,et que 𝐸 (
𝑆𝐶𝐸 𝑅
𝜎2 ) = 𝑛 − 𝑝 − 1. On a alors : 𝐸 (
𝑆𝐶𝐸 𝑅
𝑛−𝑝−1
) = 𝜎2
. On
tombe en moyenne sur la vraie valeur de 𝜎2
alors on peut conclure que notre estimateur n’est pas
biaisés.
Quelques proprietes des residus
1) 𝑆𝐶𝐸 𝑅 = ∑ 𝑒𝑖
2
𝑖 <=> 𝑆𝐶𝐸 𝑅 = 𝐸′
𝐸. 𝑎𝑣𝑒𝑐 𝐸 = 𝑌 − 𝑋𝛽̂ , 𝑜𝑛 𝑎 ∶ 𝐸′ = 𝑌′ − 𝛽̂′𝑋′ . Ces
relations impliquent 𝑆𝐶𝐸 𝑅 = (𝑌′
− 𝛽̂′
𝑋′
)(𝑌 − 𝑋𝛽̂) => 𝑆𝐶𝐸 𝑅 = 𝑌′
𝑌 − 𝑌′
𝑋𝛽̂ −
𝛽̂′
𝑋′
𝑌 + 𝛽̂′
𝑋′
𝑋𝛽̂
𝑜𝑟 𝑋′
𝑋𝛽̂ = 𝑋′𝑌 alors 𝛽̂′
𝑋′
𝑋𝛽̂ = 𝛽̂′
𝑋′
𝑌 , 𝑺𝑪𝑬 𝑹 = 𝒀′
𝒀 − 𝒀′
𝑿𝜷̂ .
2) Calcule de 𝑋′
𝐸. 𝑋′
𝐸 = 𝑋′
( 𝑌 − 𝑋𝛽̂) <=> 𝑋′
𝐸 = 𝑋′ 𝑌 − 𝑋′
𝑋𝛽̂ . Avec 𝑋′
𝑋𝛽̂ = 𝑋′𝑌 , on
trouve que : 𝑋′
𝐸 = 𝑋′ 𝑌 − 𝑋′
𝑌. Au final : 𝑿′
𝑬 = 𝟎⃗⃗ .
Ceci veut dire que
[
1
𝑥11
𝑥12
⋮
𝑥1𝑝
1
𝑥21
𝑥22
⋮
𝑥1𝑝
⋯
…
⋯
…
1
𝑥 𝑛1
𝑥 𝑛2
⋮
𝑥 𝑛𝑝]
× [
𝑒1
𝑒2
⋮
𝑒 𝑛
] =
[
0
0
0
⋮
0]
C’est equivalent à dire : {
∑ 𝑒𝑖𝑖 = 0
∑ 𝒙𝒊𝒋 𝒆𝒊
𝒏
𝒊=𝟏 = 𝟎, ∀𝒋 = 𝟏 … 𝒑.
Décomposition de la variabilité
SCER : Somme des Carrées des Ecarts due aux résidus ∑ 𝑒𝑖
2
𝑖 avec 𝑒𝑖 = 𝑦𝑖 − 𝑦̂𝑖 .
SCEM : Somme des Carrées des Ecarts due au Modèle . ∑ (𝑦̂𝑖 − 𝑦̅)2
𝑖
SCET : Somme des Carrées des Ecarts Totale . ∑ (𝑦𝑖 − 𝑦̅)2
𝑖
Propriété

10. SCET =SCEM +SCER
Cette propriété vient par le fait que : 𝑦𝑖 − 𝑦̅ = (𝑦̂𝑖 − 𝑦̅) + (𝑦𝑖 − 𝑦̂𝑖).
Maintenant nous allons voir un point tres important dans notre sujet. Il s’agit de tester
notre modele.
En premier lieu , nous allons tester globalement notre modele , ensuite faire des test
particulier.
Test global
Tester globalement le système revient à regarder si tous les prédicteurs sont sans effet sur le
modèle ou au moins l’un d’entre eux a un effet sur le modèle.
Hypothèse null (H0 ): Tous les 𝛽𝑗, avec j=1…n, sont égaux à zéro.
Hypothèse non null (H1 ): Il existe au moins un 𝛽𝑗, avec j=1…n, différent de zéro .
Posons CMR (carrée moyen résiduel)=
𝐒𝐂𝐄 𝑹
𝑛−𝑃−1
= 𝜎̂2
et CMM ( carrée moyen due au modèle
)=
𝐒𝐂𝐄 𝑴
𝑃
Pour effectuer ce test, nous allons jouer sur la variabilité résiduelle et la variabilité due
modèle.
On sait que quelque soit l’hypothèse 𝐸(𝜎̂2) = 𝜎2
.
Supposons maintenant que H0 soit vrai :
On aura ∑ (𝑦̂𝑖 − 𝑦̅)2
𝑖 = ∑ (𝑦̂𝑖 −
∑ 𝑦 𝑗𝑗
𝑛
)2
𝑖 => 𝑆𝐶𝐸 𝑀 = ∑ (
∑ (𝑦̂ 𝑖−𝑦 𝑗 )𝑗
𝑛
)2
𝑖
H0 vrai=> 𝑦̂𝑖 = 𝛽̂0 => 𝑆𝐶𝐸 𝑀 = ∑ (
∑ (𝛽̂0−𝑦 𝑗 )𝑗
𝑛
)2
𝑖
Ainsi lorsque H0 vrai , E(CMM)= 𝜎2
.
Ceci nous montre que la non-influence des prédicteurs n’implique pas que 𝑆𝐶𝐸 𝑀 soit nulle.
Puisque le test repose sur la comparaison de la variabilité résiduelle et la variabilité due au
modèle.
𝐹𝑜𝑏𝑠 =
𝑆𝐶𝐸 𝑀
𝑝
𝜎̂2 =
𝑆𝐶𝐸 𝑀
𝑝
𝑆𝐶𝐸 𝑅
𝑛−𝑝−1
=
𝐶𝑀 𝑀
𝐶𝑀 𝑅
.
Avec H0 vraie , on connait la distribution de 𝐹𝑜𝑏𝑠 : 𝑙𝑜𝑖(𝐹𝑜𝑏𝑠) = 𝐹𝑣2=𝑛−𝑝−1
𝑣1=𝑝
.
Il est facile de voir lorsque H0 vraie, 𝐹𝑜𝑏𝑠 =
𝐶𝑀 𝑀
𝐶𝑀 𝑅
=
𝜎̂2
𝜎̂2
= 1.
Loi(𝐹𝑜𝑏𝑠)=𝐹𝑣2=𝑛−𝑝−1
𝑣1=𝑝
.
Nous allons élaborer la règle de décision :

11. En prenant 𝛼(choisit à l’avance) comme étant le risque de première espèce, la limite de la
zone de rejet est définie par le 1 − 𝛼 quantile de la loi 𝐹𝑣2=𝑛−𝑝−1
𝑣1=𝑝
.Si 𝐹𝑜𝑏𝑠>𝐹𝑣2=𝑛−𝑝−1
𝑣1=𝑝
(1 − 𝛼)
on rejette l’hypothèse null. Sinon , on l’accepte.
Test de signification d’un coefficient de régression (𝜷𝒋 )
Nous venons de tester si notre modèle est significatif en testant regardant si tous les
variables explicatives n’ont aucune influence sur notre variable expliquée. Maintenant la
question que l’on peut se poser est : Peut-on voir si une variable prédictrice a une influence
sur notre variable expliquée ou pas ? Eh bien la réponse est oui. Nous mettre en place une
procédure de test.
Hypothèse null (H0 ): 𝛽𝑗 est égal à zéro.
Hypothèse non null (H1 ): 𝛽𝑗 différent de zéro .
Quel que soit l’hypothèse considérée, on a : 𝑬(𝜷̂ 𝒋) = 𝜷𝒋, la variance de 𝜷̂ 𝒋 est la jeme ligne
et jeme colonne de 𝑽(𝜷̂) = 𝝈 𝟐(𝑿′
𝑿)−𝟏
c’est-a-dire (𝜷̂ 𝒋) = 𝝈 𝟐
(𝑿′
𝑿)𝒋𝒋
−𝟏
= 𝝈 𝜷̂ 𝒋
𝟐
.
Selon notre hypothese : 𝑙𝑜𝑖( 𝜀𝑗)=𝒩(0, 𝝈 𝟐). De cette hypothese on deduit que 𝑙𝑜𝑖(𝛽̂𝑗) =
𝒩( 𝜷𝒋, 𝝈 𝜷̂
𝒋
𝟐
).
Si on ne connait pas la variance 𝝈 𝟐
, on peut l’estimer par : 𝝈̂ 𝟐
= 𝑪𝑴 𝑹 . En estimant 𝝈 𝟐
, on peut
trouver l’estimateur 𝝈̂ 𝜷̂ 𝒋
𝟐
soit 𝝈̂ 𝜷̂ 𝒋
𝟐
= 𝝈̂ 𝟐
(𝑿′
𝑿)𝒋𝒋
−𝟏
.
Le remplacement de 𝝈 𝜷̂ 𝒋
𝟐
par son estimateur implique que 𝑙𝑜𝑖 (
𝛽̂ 𝑗−𝛽 𝑗
𝝈̂ 𝜷̂
𝒋
𝟐 ) = 𝑡 𝑣=𝑛−𝑝−1.
Sous Hypothèse null (H0 ): 𝑙𝑜𝑖 (
𝛽̂ 𝑗
𝝈̂ 𝜷̂
𝒋
𝟐 ) = 𝑡 𝑣=𝑛−𝑝−1
C’est l’indicateur 𝑡 𝑜𝑏𝑠 =
𝛽̂ 𝑗
𝝈̂ 𝜷̂
𝒋
𝟐 qui nous fera dire si on doit rejeter H0 ou pas.
L’hypothese nulle est acceptée si |𝑡 𝑜𝑏𝑠| ≤ 𝑡1− 𝛼
2⁄
𝑣=𝑛−𝑝−1
sinon on la rejette.
Intervalle de confiance de 𝜷𝒋.
On se sert de la loi 𝜷̂ 𝒋 standardisée : 𝑙𝑜𝑖 (
𝛽̂ 𝑗−𝛽 𝑗
𝝈̂ 𝜷̂
𝒋
𝟐 ) = 𝑡 𝑣=𝑛−𝑝−1. On choisit notre risque de premiere
espece 𝛼. Les deux bornes de l’intervalle de confiance de 𝜷̂ 𝒋 est alors : 𝛽̂𝑗 ∓ 𝑡1− 𝛼
2⁄
𝑛−𝑝−1
𝝈̂ 𝜷̂
𝒋
𝟐
.

12. Prédiction de Y en un point x0
L’une des plus grandes utilités de la régression multiple est la prévision.
Supposons qu’on ait un ensemble de variable prédicatrices, représentées par un vecteur 𝑥0 =
(𝑥01, … , 𝑥0𝑝) 𝑒𝑡 𝑥̃0 = (1, 𝑥01, … , 𝑥0𝑝) , et qu’on veut trouver la valeur de la variable
expliquée notée Y. Quelle valeur de Y peut-on s’attendre en moyenne en ce point 𝑥0 ? C’est
la quête de cette valeur qui nous fait employer le mot prédiction.
𝑌(𝑥0) = 𝑥̃0 𝛽 + 𝜀0.
Notre objectif consiste à chercher la valeur 𝑌 qu’on attend en moyenne en 𝑥0 c’est-a-dire
𝐸(𝑌( 𝑥0)). Par hypothèse 𝑙𝑜𝑖(𝜀𝑗) = 𝑁(0, 𝜎2
) ce qui implique que 𝐸(𝑌( 𝑥0)) = 𝐸(𝑥̃0 𝛽 +
𝜀0) = 𝑥̃0 𝛽 <=> (𝑌(𝑥0)) = 𝑥̃0 𝛽 . Estimer la valeur 𝑌(𝑥0) attendue en moyenne revient à
estimer 𝛽 ce qui nous fait dire que 𝐸(𝑌(𝑥0))̂ = 𝑥̃0 𝛽̂. Cet estimateur est sans biais. Effet ,
𝐸(𝑥̃0 𝛽̂) = 𝐸(𝛽̂0 + 𝛽̂1 𝑥01 + … + 𝛽̂ 𝑝 𝑥0𝑝) = 𝐸(𝛽̂0) + 𝐸(𝛽̂1) 𝑥01 + … + 𝐸(𝛽̂ 𝑝)𝑥0𝑝
𝐸(𝑥̃0 𝛽̂) = 𝛽0 + 𝛽1 𝑥01 + … + 𝛽 𝑝 𝑥0𝑝
𝐸(𝑥̃0 𝛽̂) = 𝑥̃0 𝛽 <=> 𝐸(𝑥̃0 𝛽̂) = 𝐸(𝑌(𝑥0)) Ceci exprime que l’estimateur 𝑥̃0 𝛽̂ est sans biais.
𝑉( 𝑥̃0 𝛽̂) = 𝑐𝑜𝑣𝑎𝑟(∑ 𝛽̂𝑖 𝑥0𝑖
𝑝
𝑖=0 , ∑ 𝛽̂𝑗 𝑥0𝑗
𝑝
𝑗=0 ) <=> 𝑉( 𝑥̃0 𝛽̂) = ∑ ∑ 𝑥0𝑖 𝑥0𝑗 𝑐𝑜𝑣𝑎𝑟(𝛽̂𝑖, 𝛽̂𝑗)
𝑝
𝑗=0
𝑝
𝑖=0 <=>
Or 𝑜𝑣𝑎𝑟(𝛽̂𝑖, 𝛽̂𝑗) = (( 𝑋′
𝑋)
−1
)
𝑖𝑗
𝜎2 . on a alors : 𝑉( 𝑥̃0 𝛽̂) = 𝜎2 ∑ ∑ 𝑥0𝑖 (( 𝑋′
𝑋)
−1
)
𝑖𝑗
𝑥0𝑗
𝑝
𝑗=0
𝑝
𝑖=0 <=>
𝑉( 𝑥̃0 𝛽̂) = 𝜎2 𝑥̃′0 ( 𝑋′
𝑋)
−1
𝑥̃0 = 𝜎 𝑥̃0 𝛽̂
2
.
En fin : 𝑙𝑜𝑖(𝑥̃0 𝛽̂) = 𝑁(𝑥̃0 𝛽, 𝜎𝑥̃0 𝛽̂
2
)
En générale, on ignore 𝜎2
, on l’estime par 𝝈̂ 𝟐
= 𝑪𝑴 𝑹=> 𝜎̂ 𝑥̃0 𝛽̂
2
= 𝜎̂2
𝑥̃′0(𝑋′
𝑋)−1
𝑥̃0.
Déterminons les bornes de l’intervalle de confiance , comme d’habitude , a partir de la loi
student :
𝑥̃0 𝛽̂ ∓ 𝑡1− 𝛼
2⁄
𝑛−𝑝−1
𝜎̂ 𝑥̃0 𝛽̂
2

13. Exemple de manipulation de données
Nous nous trouvons dans une situation où l’on cherche à expliquer le chiffre d’affaire d’une
entreprise en fonction de la superficie et le nombre de salariés.
Sachant que la régression linéaire multiple nous permet d’expliquer une variable endogène
quantitative en fonction de plusieurs variables exogènes, nous allons utiliser ce modele pour
effectuer cette étude.
Tableau des variables
Variable à expliquer Variables explicatives
Y 𝑥1 𝑥2
Chiffre d’affaire Superficie Nombre de salariés
Le modèle s’écrit alors : 𝑌 = 𝛽0 + 𝛽1 𝑥1 + 𝛽2 𝑥2 + 𝜀.
Le problème qui se pose maintenant est d’estimer les paramètres𝛽0, 𝛽1 et 𝛽2.
Pour ce faire on a relevée 10 échantillons de données :
Les échantillons Superficie x1(m2
) Nbre de salariés x2 Chiffre d’affaire y
1 100 24 11
2 600 28 23
3 600 20 20
4 700 23 21
5 700 26 21
6 500 21 13
7 800 28 30
8 300 28 18
9 200 20 7
10 200 25 18
Maintenant nous allons manipuler ces données sur R afin de trouver une estimation de nos
paramètres 𝛽0, 𝛽1 et 𝛽2.
On entre les données :
> supef<-c(100,600,600,700,700,500,800,300,200,200)
> sala<-c(24,28,20,23,26,21,28,28,20,25)
> CA<-c(11,23,20,21,21,13,30,18,7,18)
Superf : pour superficie. Sala : pour nbre de salariés. CA : chiffre d’affaire.
Ensuite on utilise la fonction lm de R pour mettre en place notre modèle linéaire.
> reg.multiple<-lm(CA~supef+sala)
Voici les resultats founis dans R :
> summary(reg.multiple)

14. Call:
lm(formula = CA ~ supef + sala)
Residuals:
Min 1Q Median 3Q Max
-3.0140 -1.8737 -0.5193 1.6472 3.9668
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -14.218495 7.153199 -1.988 0.08718 .
supef 0.017989 0.003874 4.643 0.00236 **
sala 0.986153 0.299152 3.296 0.01318 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.832 on 7 degrees of freedom
Multiple R-squared: 0.8544, Adjusted R-squared: 0.8129
F-statistic: 20.55 on 2 and 7 DF, p-value: 0.001176
Les données présentés ci-dessus nous permet d’affirmer que l’estimation de :
𝑦̂ = −14.218495 + 0.017989 𝑥1 + 0.986153 𝑥2.
SCER=2.832 avec 7ddl.
Ces données qu’on vient de recolter suffisent largement pour faire plus d’etude sur notre
modèle.
Voyons si notre modele est significatif :
On choisit 𝛼 =5% notre risque de premiere espece : le p-value associé à l’intercept est :
0.08718 est supérieur à 𝛼 ce qui veut dire l’intercept 𝛽0 peut etre omis du modèle.
Le p-value associé à la superficie est 0.00236< 𝛼 ce qui veut dire 𝛽1 est significatif.
Le p-value associé au nombre de salariés est 0.01318< 𝛼 ce qui veut dire 𝛽2 est significatif.
Le p-value globale du modèle est 0.001176< 𝛼 ce qui nous fait dire que le modele est
globalement significatif.
Prevision du model :

15. Supposons qu’on se trouve dans une entreprise ayant 100m2
de superficie et 24 salariés. A
quel chiffre d’affaire doit-on s’attendre en moyenne ?
La reponse : 𝐸(𝑌(𝑥0))̂ = 𝑥̃0 𝛽̂ avec 𝑥̃0 = (1,100,24)
𝑥̃0 𝛽̂ = (1,100,24) (
−14.218495
0.017989
0.986153
) = 11.248077.