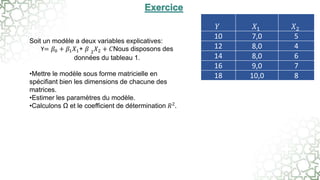
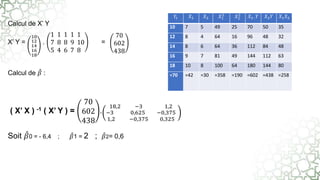
Ce document traite de la régression linéaire multiple, une méthode d'analyse statistique qui explore la relation entre une variable dépendante et plusieurs variables indépendantes. Il décrit comment estimer les paramètres du modèle à l'aide de la méthode des moindres carrés et introduit des concepts tels que les résidus, la variabilité totale et le coefficient de détermination pour évaluer la qualité de l'ajustement du modèle. Le texte aborde également des aspects techniques liés à la manipulation des données et à l'interprétation des résultats.

1. En analyse explicative simple, nous avons essayé de définir la relation qui existe entre deux variables
statistiques.
nous avons considéré qu’une variable endogène est expliquée à l’aide d’une seule variable exogène.
Exemples :
- Le Revenu hebdomadaire de famille et les dépenses en consommation hebdomadaire;
Cependant, il est extrêmement rare qu’un phénomène économique ou social puisse être appréhendé par une
seule variable.
Le modèle linéaire Multiple est une généralisation du modèle de régression simple dans lequel figurent
plusieurs variables explicatives
Donc, L'analyse de régression linéaire multiple permet d'examiner le lien entre une variable dépendante et
plusieurs variables indépendantes pour faire des prédictions.

3. M
. odèle
Etudier la liaison entre une "variable à expliquer" quantitative Y et une suite de
"variables explicatives" quantitatives X1 ... Xk
Terme d’Erreur
composante aléatoire
ε quantifie les écarts entre les valeurs réellement
observées et les valeurs prédites par le modèle
Donc (𝜷0 , 𝜷1 ,… , 𝜷k ) Sont les paramètres du modèle que l’on veut estimer à l’aide des données
Paramètres
Terme constant
Variables explicatives
(composante déterministe)
Variable Endogène
Yi   0   1x i1  .. .  k x ik  i

4. Y
Variable à expliquer
Variable dépendante
Variable endogène
X1 X2 ... Xk
Variables explicatives
Variables indépendantes
Variables exogènes

5. Expliquer En fonction
de
Prix d'un
appartement
■ superficie
■ standing
■ quartier
■ sécurité
■ proximité de commerce
■ investissements
■ publicité
■ prix de vente
Prévoir des
ventes

7. Afin d’en alléger l’écriture et de faciliter l’expression de certains résultats, on a habituellement recours
aux notations matricielles. En écrivant le modèle, observation par observation, nous obtenons :
Soit, sous forme matricielle :
Nous remarquons la première colonne de la matrice X, composée de 1, qui correspond au coefficient
𝜷𝟎 (coefficient du terme constant).
L’écriture sous forme matricielle rend plus aisée la manipulation du modèle linéaire général, c’est pourquoi
nous l’adoptons par la suite.
𝒀(𝒏,𝟏)=𝑿(𝒏,𝒌+𝟏)𝜷(𝒌+𝟏,𝟏)+𝜺(𝒏,𝟏)
Y1   0   1x 11  .. .  k x 1k  1
Y2   0   1x 21  .. .  k x 2k  2
.
.
Yi   0   1x i1  .. .  k x ik  i
Yn   0   1x n1  .. .  k x nk  n

9. Y = X  + ε
Soit le modèle sous forme matricielle à k variables explicatives et n observations :
Avec:
et:
A fin d’estimer le vecteur a nous appliquons la méthode des MCO qui consiste à
minimiser la somme des carrés des erreurs. Soit:
Pour minimiser cette fonction par rapports à 𝜷, nous allons différencier S par rapport à 𝜷
Donc:
𝑴𝒊𝒏 𝒊=𝟏
𝒏
𝜺𝒊
𝟐
= 𝑴𝒊𝒏 𝜺′
𝜺 = Min (𝒀 − 𝑿𝜷)′ (𝒀 − 𝑿𝜷) = 𝑴𝒊𝒏𝑺
𝐒 = 𝐘 − 𝐗𝛃 ′ 𝐘 − 𝐗𝛃 = 𝐘′𝐘 − 𝐘′𝐗𝛃 − 𝛃′𝐗′𝐘 + 𝛃′𝐗′𝐗𝛃
= 𝐘′𝐘 − 𝟐𝛃′𝐗′𝐘 + 𝛃′𝐗′𝐗𝛃
𝛛𝐒
𝛛𝛃
= −𝟐𝐗′𝐘 + 𝟐𝐗′𝐗𝜷 = 𝟎 𝜷=(𝑿′𝑿)−𝟏X’Y

10. Soit, sous forme matricielle :
Le modèle estimé s’écrit :
avec où et est le résidu, c’est-à-dire l’écart entre la valeur observée de la
variable à expliquer et sa valeur estimée (ajustée).
Il convient de bien distinguer entre l’erreur de spécification du modèle (noté 𝛆𝐢) qui
est et restera inconnue et le résidu (𝒆𝒊) qui, lui, est connu.
𝒆𝒊= 𝒚𝒊 − 𝒚𝒊
𝒚𝒊=𝜷𝟎+𝜷𝟏𝒙𝟏𝒊+𝜷𝟐𝒙𝟐𝒊+…+𝜷𝑲𝒙𝑲𝒊+𝒆𝒊
𝒏 𝒙𝟏𝒊 𝒙𝟐𝒊 ⋯ 𝒙𝒌𝒊
𝒙𝟏𝒊 𝒙²𝟏𝒊 𝒙𝟏𝒊 𝒙𝟐𝒊 ⋯ 𝒙𝟏𝒊 𝒙𝒌𝒊
𝒙𝟐𝒊 𝒙𝟐𝒊 𝒙𝟏𝒊 𝒙²𝟐𝒊 ⋯ 𝒙𝟐𝒊 𝒙𝒌𝒊
⋮ ⋯ ⋯ ⋯ ⋯
𝒙𝒌𝒊 𝒙𝒌𝒊 𝒙𝟏𝒊 𝒙𝒌𝒊 𝒙𝟐𝒊 ⋯ 𝒙²𝒌𝒊
𝜷𝟎
𝜷𝟏
𝜷𝟐
⋮
𝜷𝒌
=
𝒚𝒊
𝒙𝟏𝒊 𝒚𝒊
𝒙𝟐𝒊 𝒚𝒊
⋮
𝒙𝒌𝒊 𝒚𝒊

11. Si nous raisonnons sur des données centrées, l’estimateur de 𝜷 peut s’écrire en
fonction des matrices des variances et covariances empiriques :
Avec 𝜷𝟎 = 𝒚 − 𝜷𝟏𝒙𝟏 − 𝜷𝟐𝒙𝟐 − ⋯ − 𝜷𝑲𝒙𝑲
𝜷𝟎
𝜷𝟏
𝜷𝟐
⋮
𝜷𝒌
=
𝑽𝒂𝒓(𝒙𝟏) 𝑪𝒐𝒗(𝒙𝟏𝒙𝟐) 𝑪𝒐𝒗(𝒙𝟏𝒙𝟑) ⋯ 𝑪𝒐𝒗(𝒙𝟏𝒙𝒌)
𝑪𝒐𝒗(𝒙𝟐𝒙𝟏) 𝑽𝒂𝒓(𝒙𝟐) 𝑪𝒐𝒗(𝒙𝟐𝒙𝟑) ⋯ 𝑪𝒐𝒗(𝒙𝟐𝒙𝒌)
𝑪𝒐𝒗(𝒙𝟑𝒙𝟏) 𝑪𝒐𝒗(𝒙𝟑𝒙𝟐) 𝑽𝒂𝒓(𝒙𝟑) ⋯ 𝑪𝒐𝒗(𝒙𝟑𝒙𝒌)
⋮ ⋮ ⋮ ⋯ ⋯
𝑪𝒐𝒗(𝒙𝒌𝒙𝟏) 𝑪𝒐𝒗(𝒙𝒌𝒙𝟐) 𝑪𝒐𝒗(𝒙𝒌𝒙𝟑) ⋯ 𝑽𝒂𝒓(𝒙𝒌)
×
𝑪𝒐𝒗 𝒙𝟏𝒚
𝑪𝒐𝒗 𝒙𝟐𝒚
𝑪𝒐𝒗 𝒙𝟑𝒚
⋮
𝑪𝒐𝒗 𝒙𝒌𝒚
-1

12. Que sont des données centrées sur la moyenne ?
Soit 𝒙𝒊 une variable connue sur n observations et 𝒙 sa moyenne, nous
pouvons calculer une nouvelle variable (𝑿 = 𝒙𝒊–x) dont la somme est par
construction nulle :
𝒙𝒊 − 𝒙 = 𝒙𝒊 = 𝟎
Nous avons donc 𝑿= 0.

13. Yi  𝜷𝟎 𝜷𝟏x 1i .. . 𝜷𝒌x ki 𝒆𝒊
Soit le modèle estimé :
Si la variable 𝐱𝟐 passe de la valeur 𝐱𝟐𝐢 à ( 𝐱𝟐𝐢+ ∆ 𝐱𝟐𝐢), toutes choses étant
égales par ailleurs (les k − 1 autres variables restant constantes), alors la
variable à expliquer varie de :
𝛃𝟐 × ∆𝐱𝟐: ∆𝐲𝐢 = 𝛃𝟐𝐱𝟐𝐢
Les coefficients s’interprètent donc directement en terme de propension marginale.

15. Considérons les propriétés de l’estimateur.
Le modèle sous forme matricielle peut s'écrire de différentes manières.
Y = Xa + ε
Y = Xa + e
𝑌 = Xa
=> 𝑒 = 𝑌 + 𝑌 (e = résidu).
Nous obtenons que:
𝑎 = (𝑋′𝑋)−1X′Y
𝑎 = (𝑋′𝑋)−1X′(Xa + ε)
𝑎 = (𝑋′
𝑋)−1
𝑋′
𝑋𝑎 + (𝑋′
𝑋)−1
𝑋′ε
D’où 𝐸(𝑎) = a+(𝑋′𝑋)−1𝐸(ε) = a car 𝐸(ε) = 0
L’estimateur est donc sans biais : 𝐸(𝑎) = a
𝑎 = a + (𝑋′
𝑋)−1
𝑋′ε

16. Calculons maintenant la matrice des variances et covariances des
coefficients de régression 𝑎.
𝑎 = 𝐸{ 𝑎 − 𝑎 𝑎 − 𝑎 ′}
D’apres l’equation précédente:
(𝑎 − 𝑎) = 𝑋′𝑋 −1𝑋′𝜀
Et puisque 𝑋′𝑋 −1est symétrique , donc 𝑎 − 𝑎 ′=𝜀′X 𝑋′𝑋 −1
 𝑎 − 𝑎 𝑎 − 𝑎 ′ = 𝑋′𝑋 −1𝑋′𝜀 𝜀′ X 𝑋′𝑋 −1
D’où 𝑎= 𝑋′𝑋 −1X′E(𝜀 𝜀′ )X 𝑋′𝑋 −1
Avec E(𝜀 𝜀′ )= 𝜀= 𝜎𝜀
2
I= matrice des variances et des covariances
de l’erreur 𝜀.
𝜀 = 𝐸 𝜀𝜀′ =
𝐸(𝜀1𝜀1) 𝐸(𝜀1𝜀2) … 𝐸(𝜀1𝜀𝑛)
𝐸(𝜀2𝜀1) 𝐸(𝜀2𝜀2) … 𝐸(𝜀2𝜀𝑛)
…
𝐸(𝜀𝑛𝜀1) 𝐸(𝜀𝑛𝜀2) … 𝐸(𝜀𝑛𝜀𝑛)

17. =
𝜎𝜀
2
0 0 … 0
0 𝜎𝜀
2
0 … 0
. .
0 0 0 … 𝜎𝜀
2
Soit 𝑎= 𝜎𝜀
2 𝑋′𝑋 −1X′X 𝑋′𝑋 −1
Donc 𝑎= 𝜎𝜀
2 𝑋′𝑋 −1
𝑎 =
𝜎𝜀
2
𝑛
𝑋′𝑋
−1
𝑛
, lim 𝑎 = 0 si n
(D’après les hypothèses H3 et H7). L’estimateur est donc convergent.
∞

18. Comme pour le modèle de régression simple, nous avons :
a) 𝑖 𝑦𝑖 = 𝑖 𝑦𝑖 → 𝑦𝑖 = 𝑦
b) 𝑖 𝑒𝑖 = 0
De ces deux relations , nous en déduisons l’équation fondamentale d’analyser de la variance :
𝑖
𝑦𝑖 − 𝑦 2
=
𝑖
𝑦𝑖 − 𝑦
2
+
𝑖
𝑒𝑖
2
SCT = SCE + SCR
La variabilité totale (SCT) est égale à la variabilité expliquée (SCE) + la variabilité des résidus (SCR).

19. Cette équation va nous permettre de juger de la qualité de l’ajustement d’un modèle ; en effet, plus la
variance expliquée est « proche » de la variance totale , meilleur est l’ajustement global du modèle.
C’est pourquoi nous calculons le rapport SCE sur SCT :
𝑅2 est appelé le coefficient de détermination, et R le coefficient de corrélation multiple. 𝑅2 mesure la
proportion de la variance de Y expliquée par la régression de Y sur X.
Dans le cas de données centrées (moyenne nulle) et seulement dans ce cas, le coefficient de
détermination est égal à :
𝑅2
= 𝑖
𝑦𝑖 − 𝑦 2
𝑖 𝑦𝑖 − 𝑦 2
= 1 − 𝑖
𝑒𝑖
2
𝑖 𝑦𝑖 − 𝑦 2
𝑅2 =
𝑌′ 𝑌
𝑌′ 𝑌
= 1 −
𝑒′ 𝑒
𝑌′ 𝑌

20. Cette qualité de l’ajustement et l’appréciation que l’on a du 𝑅2 doivent être tempérées par le degré de
liberté de l’estimation. En effet, lorsque le degré de liberté est faible1, il convient de corriger le
𝑅2 afin de tenir compte du relativement faible nombre d’observations comparé au nombre de facteurs
explicatifs par le calcul d’un 𝑅2« corrigé » noté 𝑅2 :
On a 𝑅2 < 𝑅2 et si n est grand 𝑅2 ≃ 𝑅2 .
Nous verrons au chapitre 4 section IV deux critères (Akaike et Schwarz) permettant d’arbitrer, lors de
l’introduction d’une ou plusieurs variables explicatives, entre la perte de degrés de liberté et l’apport
d’information.
𝑅² = 1 −
𝑛−1
𝑛−𝑘−1
(1 − R²)

21. 𝑌 𝑋1 𝑋2
10 7,0 5
12 8,0 4
14 8,0 6
16 9,0 7
18 10,0 8
Soit un modèle a deux variables explicatives:
Y= 𝛽0 + 𝛽1𝑋1+ 𝛽 2𝑋2 + 𝐶Nous disposons des
données du tableau 1.
•Mettre le modèle sous forme matricielle en
spécifiant bien les dimensions de chacune des
matrices.
•Estimer les paramètres du modèle.
•Calculons Ω et le coefficient de détermination 𝑅2.

22. Y   0   1x i  2x 2  𝜺
Y  - 6, 4 2x 1  0,6x 2  𝜺
Sorti Eviews

23. 1) Forme matricielle :
Nous disposons de 5 observation et 2 variables explicatives , le modèle peut donc s’écrire :
Y =
𝟏𝟎
𝟏𝟐
𝟏𝟒
𝟏𝟔
𝟏𝟖
; X =
𝟏 𝟕 𝟓
𝟏 𝟖 𝟒
𝟏 𝟖 𝟔
𝟏 𝟗 𝟕
𝟏 𝟏𝟎 𝟖
; 𝜷 =
𝜷0
𝜷1
𝜷2

24. 2) Estimation des paramètres
Nous avons :
𝛽0
𝛽1 = ( X’.X )-1. ( X’.Y )
𝛽2
Calcul de (X’.X) et de ( X’.Y )
(X’.X ) =
5 42 30
42 358 258
30 258 190
: (X’.X)-1 =
18,2 −3 1,2
−3 0,625 −0,375
1,2 −0,375 0,325

25. Calcul de X’ Y
X’ Y =
10
12
14
16
18
.
1 1 1 1 1
7 8 8 9 10
5 4 6 7 8
=
Calcul de 𝛽 :
( X’ X ) -1 ( X’ Y ) =
70
602
438
.
18,2 −3 1,2
−3 0,625 −0,375
1,2 −0,375 0,325
Soit 𝛽0 = - 6,4 ; 𝛽1 = 2 ; 𝛽2= 0,6
70
602
438
𝑌𝑡 𝑋1 𝑋2 𝑋1
2
𝑋2
2
𝑋1. 𝑌 𝑋2𝑌 𝑋1𝑋2
10 7 5 49 25 70 50 35
12 8 4 64 16 96 48 32
14 8 6 64 36 112 84 48
16 9 7 81 49 144 112 63
18 10 8 100 64 180 144 80
=70 =42 =30 =358 =190 =602 =438 =258

26. 3-1) Calcul Ω
on a Ω = 𝜎𝜀 .
(X’.X)-1
𝜎2 =
𝑆𝐶𝑅
𝑛−3
=
1,2
5−3
= 0,6
la matrice des variances et covariances estimées des coefficients
Ω = 0,6 .
18,2 −3 1,2
−3 0,625 −0,375
1,2 −0,375 0,325
Ω =
10,92 −1,8 0,72
−1,8 0,375 −0,225
0,72 −0,225 0,195
𝑌 y- 𝑦 ( 𝑦 − 𝑦 )2 ( 𝑦 − 𝑦)2
10,6 -0,6 0, 36 16
12 0 0 4
13,2 0,8 0,64 0
15,8 0,2 0,04 4
18,4 -0,4 0,16 16

27. 3-2) Le calcul du R2
R2 = 1-
𝑆𝐶𝑅
𝑆𝐶𝑇
= 1 -
1,2
40
= 0,97
donc
Le R2 corrigé
𝑅 = 1-
𝑛−1
𝑛−𝑘−1
(1- R2) = 1-
5−1
5−4
( 1- 0,97) = 0,88
Nous observons la bais du coefficient de détermination lorsque nous le corrigeons par le degré
de liberté

28. MERCI POUR VOTRE
ATTENTION