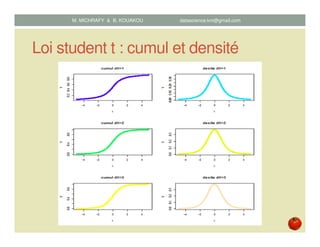
Le document traite de la régression simple, une méthode statistique pour analyser la relation entre une variable dépendante y et une variable indépendante x. Il décrit les concepts fondamentaux tels que l'estimation des paramètres, la validation du modèle, et les erreurs associées ainsi que les méthodes pour évaluer ces modèles via des hypothèses statistiques et des calculs. Des outils en langage R pour la régression simple sont également mentionnés, ainsi que les méthodes pour calculer les estimateurs et vérifier les conditions sous-jacentes au modèle.


























![Commande R : analyse du modèle
• model <- lm(formula=y~x) data=donnee.csv) :
établir un modèle de régression linéaire simple, x est le prédicteur et y
est la variable à expliquer.
• Names(model)
[1] "coefficients" "residuals" "effects" "rank“
[5] "fitted.values" "assign" "qr" "df.residual"
[9] "xlevels" "call" "terms" "model"
• model$coef : le vecteur ߚመ ሺ ߚ, ߚଵሻ
• model$res : le vecteur résidus ܧ ൌ ܻ െ ܻ
• model$fitted : le vecteur estimé ܻ
• model$df.residual : le nombre des dll des résidus
M. MICHRAFY & B. KOUAKOU datascience.km@gmail.com](https://image.slidesharecdn.com/regressionsimplepublicationweb-150816090859-lva1-app6892/85/Regression-simple-27-320.jpg)









![Commande R : analyse de la variance
• anVar <- anova(model)
Donne l’analyse de la variance
• names(anVar) :
[1] "Df" "Sum Sq" "Mean Sq" "F value" "Pr(>F)"
• anVar$Df : vecteur de dll
• anVar$ "Sum Sq" : vecteur ܯܥெ , ܯܥோ
• anVar$”F value” : donne ܨ௦
• anvar$"Pr(>F)" : donne la probabilité critique (p-value)
M. MICHRAFY & B. KOUAKOU datascience.km@gmail.com](https://image.slidesharecdn.com/regressionsimplepublicationweb-150816090859-lva1-app6892/85/Regression-simple-37-320.jpg)
![Commande R : Vérification des
hypothèses
• rstudent(model) : résidus studentarisée
• acf(model) : graphe d’autocorrelation des résidus
• qqnorm(model$res) : normal Q-Q plot
• plot(model$fitted,rstudent(model)) : graphe pour
identifier les points qui sont hors l’intervalle [-2,2]
• hist(resid(model)) : histogramme des résidus
M. MICHRAFY & B. KOUAKOU datascience.km@gmail.com](https://image.slidesharecdn.com/regressionsimplepublicationweb-150816090859-lva1-app6892/85/Regression-simple-38-320.jpg)