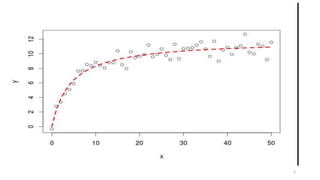
Le document traite de la régression non linéaire, soulignant la nécessité d'utiliser des modèles non linéaires lorsque l'effet d'une variable dépend de ses niveaux. Il présente des exemples de modèles quadratiques et polynomiaux, ainsi que des modèles logarithmiques, et discute des tests d'hypothèses pour évaluer la pertinence des modèles. Enfin, il indique que le choix du modèle dépend des spécificités des données et du contexte de l'analyse.

1. Régression non linéaire
1

2. Jusqu’à présent, nous avons supposé que la fonction de
régression était linéaire, c’est-à-dire que nous avons traité
le paramètre de pente de la fonction de régression comme
une constante.
Cela implique que l'effet sur un changement d'une unité
dans X ne dépend pas du niveau de X .
Toutefois, si l'effet d'un changement dans X dépend de la
valeur de X , nous devrions utiliser une fonction de
régression non linéaire.
2

3. 3

4. Exemple d’initiation:
library(AER)
library(stargazer)
data(CASchools)
str(CASchools)
4

5. la droite de régression linéaire semble surestimer la véritable
relation entre les deux variables.
lorsque le revenu est très élevé ou très faible
lesous-estimer pour le groupe à revenu intermédiaire.
On peut penser alors à un autre modèle qui pourrait capter
mieux la relation:
Modèle de régression quadratique
5

6. # Estimation du quadratic Model
quadratic_model <- lm(score ~ income + I(income^2), data =
CASchools)
6

7. La régression quadratique est un cas particulier de la
régression polynomiale
L'équation générale d'un modèle de régression polynomiale
est :
n est le degré du polynôme.
7

8. Ce test nous permettra de tester si l relation est linéaire ou
non: Si H0 est vraie c’est une simple relation linéaire sinon
c’est une relation quadratique.
8

9. Représentation graphique
9

10. 10

11. On voit que la fonction quadratique s’adapte mieux que la
fonction linéaire
11

12. Régression polynomiale
Il s’agit de généraliser la régression quadratique pour un
degré r
Pour r = 3 il suffit d’écrire: degree = 3
cubic_model <- lm(score ~ poly(income, degree = 3, raw =
TRUE), data = CASchools)
La fonction poly génère des polynomes
12

13. La question qui se pose quel degré choisir pour une régression ?
nous pouvons tester l'hypothèse nulle selon laquelle la vraie
relation est linéaire contre l'hypothèse alternative selon
laquelle la relation est un polynôme de degré r
13

14. Par exemple, nous pouvons tester la valeur nulle d'un modèle linéaire
par rapport à l'alternative d'un polynôme de degré maximal r = 3
comme suit.
# test d'hypotheses linear model vs quadratic or polynomial
R <- rbind(c(0, 0, 1, 0), c(0, 0, 0, 1)) # pour écrire b2=b3 = 0
R
linearHypothesis(cubic_model, hypothesis.matrix = R,white.adj =
"hc1") 14

15. P value = 9.043e-16 donc on refuse H0, les deux coefficients b2 et b3
sont significativement différents de 0
Le modèle cubique est acceptable, ceci dit on ne peut pas conclure que
r=3 est le meilleur modèle.
En pratique pour estimer r on peut suivre une approche séquentielle:
15

16. 1-Estimer un modèle polynomial pour une valeur
maximale r
2-Utiliser un test de student H0:βr= 0, rejeter H0 cela
veut dire que Xr fait partie du modèle.
3- L’acceptation de H0 dans 2 signie qu’on peut éliminer
Xr, continuer la procédure en 1 avec l’ordre r-1 et faire
le test de student.
4-Si le test de l’étape 3 est rejeté, poursuivez la
procédure jusqu’à ce que le coefficient de la puissance
la plus élevée soit statistiquement significatif.
16

17. La littérature économique suggère de ne pas dépasser 2 ou 2
ou 4 comme degré du polynome.
Exemple: cubic model
summary(cubic_model)
17

18. Modèle Logarithmique
Un autre type de régression non linéaire est l’usage des algorithmes.
Il existe 3 situations de passage en Log:
Transformer y sans transformer x
Transformer x sans stranformer y
Transformer les deux en Log
1er cas: y en Log uniquement:
Parfois il est intéressant de passer au Log de y pour bien capter la
relation:
# Estimer le modèle par usage du Log:
LogLinear_model <- lm(log(score) ~ income, data = CASchools)
18

19. # Résumé des coefficients estimés
coeftest(LogLinear_model,vcov = vcovHC, type = "HC1")
vcovHC:correction de covariance robuste (Heteroskedasticity-
Consistent, HC) avec la méthode HC1.
coeftest est utilisé pour effectuer des tests sur les coefficients du
modèle en tenant compte de la robustesse aux hétéroscédasticités.
Cela peut être particulièrement important lorsque l'on soupçonne
que les erreurs de votre modèle ne présentent pas une variance
constante.
19

20. Variation d’une unite de x entraine une variation de 100×β1%
de y
20

21. Cas 2: Appliquer le Log à x sans y:
LinearLog_model <- lm(score ~ log(income), data =
CASchools)
# Calcul des coefficients estimés
coeftest(LinearLog_model, vcov = vcovHC, type = "HC1")
21

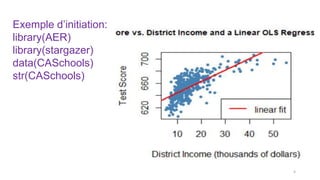
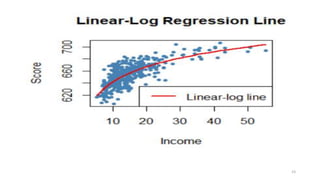
22. # Graphique de la relation:
plot(score ~ income, col = "steelblue",pch = 20, data =
CASchools,ylab="Score",xlab="Income", main = "Linear-Log
Regression Line")
order_id <- order(CASchools$income)
lines(CASchools$income[order_id],
fitted(LinearLog_model)[order_id], col = "red",
lwd = 2)
legend("bottomright",legend = "Linear-log line",lwd = 2,col
="red")
22

23. 23

24. Variation de 1 % de x entraine une variation de 0,01 β1 de
y
24

25. Cas 3: x et y transformées par la fonction Log:
LogLog_model <- lm(log(score) ~ log(income), data
= CASchools)
coeftest(LogLog_model,
vcov = vcovHC, type = "HC1")
25

26. 1% variation de x est associée à 1% * b1 de y, b1
est appelée élasticité de y par rapport à x
# graphique du modèle log-log:
plot(log(score) ~ income,
col = "steelblue",
pch = 20,
data = CASchools,
ylab="log(Score)",
xlab="Income",
main = "Log-Linear Regression Function")
26

27. 27

28. Les logarithmes peuvent être utilisés pour transformer la
variable dépendante ou la variable indépendante X,
ou les deux (la variable transformée doit être positive).
28

29. Comparons graphiquement cubic model linear-log model:
plot(score ~ income,
data = CASchools,
col = "steelblue",
pch = 20,
ylab="Score",
xlab="Income",
main = "Linear-Log and Cubic Regression Functions")
29

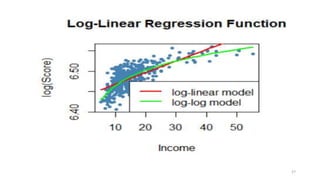
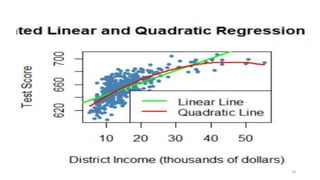
30. # Ajoutons the linear-log regression line
order_id <- order(CASchools$income)
lines(CASchools$income[order_id],
fitted(LinearLog_model)[order_id],
col = "darkgreen",
lwd = 2)
30

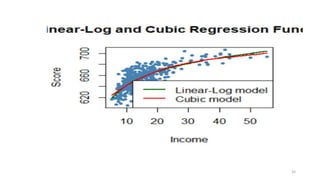
31. # Ajoutons cubic model:
#
lines(x = CASchools$income[order_id],
y = fitted(cubic_model)[order_id],
col = "red",
lwd = 2)
# add a legend
legend("bottomright",
legend = c("Linear-Log model", "Cubic model"),
lwd = 2,
col = c("darkgreen", "red"))
31

32. 32

33. Les deux droites de régression semblent presque identiques.
Dans l’ensemble, le modèle logarithmique linéaire peut être
préférable pour évaluer des accroissements par exemple,
le modèle logarithmique est adapté aux situations où les
changements relatifs sont importants, tandis que le modèle
cubique est plus flexible pour capturer des formes de courbes
complexes. Le choix entre les deux dépend du contexte
spécifique de votre problème et des caractéristiques des
données.
33

34. Exercice
x=1:15
y=c(59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10,
9.5)
Faire le plot de x et y
Proposer un modèle de régression
Résultats du modèle
34