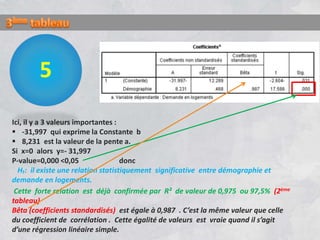
Le document explique l'analyse de régression, un outil statistique servant à établir des relations linéaires entre des variables dépendantes et indépendantes. Il décrit la différence entre régression bivariée et régression multiple, ainsi que l'importance des coefficients de corrélation (r) et de détermination (r2) pour évaluer la force de la relation. En utilisant des exemples, il démontre comment prédire des valeurs dépendantes à partir de données démographiques, tout en soulignant la nécessité d'une corrélation adéquate entre les variables.

2. .
Conditions d’utilisation de l’analyse de régression
Trois
conditions

3. La régression et la corrélation conviennent pour détecter une
relation linéaire entre variables.
Donc, la régression vise aussi à analyser l’association entre une
variable dépendante(variable prédicteur) et une ou plusieurs
variables indépendantes (variable à prédire) et à prédire la
variable dépendante si la variable indépendante est connue .

4. Pour atteindre cet objectif, on doit se référer à l’équation de régression.
a: la pente
b: la constante
x: la variable indépendante
y: la variable dépendante
En termes plus clairs, la relation entre x et y est matérialisée par
une ligne droite dont la pente est « a » .

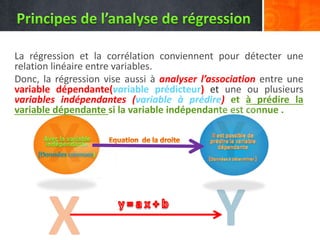
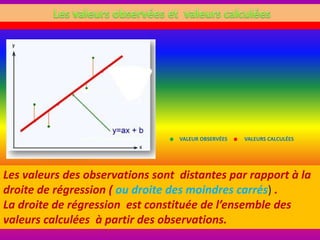
5. Cette équation de la droite exprime une relation linéaire entre x et y, la valeur de la
variable dépendante (y) est fonction de la valeur de la ou des variable(s)
indépendante(s) (x), y=f(x).
Donc, il y a 2 types de régression:
Régression bivariée /une seule variable indépendante (x)
est associée à une variable dépendante (y),
Exemple: température intérieure(ti)=f[température extérieure,(te)], ti=a(te)+b
Régression bivariée

6. Régression multiple
•Régression multiple / 2 ou plusieurs variables indépendantes (x₁, x₂)
sont associées à une seule variable dépendante (y). y= a₁x₁+a₂x₂+b
Exemple: température intérieure (ti)=f[température extérieure (te) ,
humidité relative (H%)].
i= a₁(te)+ a₂(H%)+b

7. Ici, les observations (nuage de point en verte) suivent presque une ligne droite. La ligne bleue, qui
exprime le meilleur ajustement des valeurs observées, est la régression . Cependant, cette droite de
régression n’exprime pas parfaitement la position parfaite des différentes observations, il y a toujours
une erreur (Ɛ), car il existe une certaine distance entre les valeurs observées et les valeurs calculées
qui constituent ligne bleue de régression. Pour cela qu’il faut introduire Ɛ dans l’équation y=ax+b.
y= ax + b + Ɛ constitue uniquement une prédiction. D’où x (la variable indépendante) ne dépend pas
totalement de y (la variable dépendante) et qu’il y a uniquement des preuves qui attestent de
l’existence d’une relation entre les 2 variables.

8. . VALEUR OBSERVÉES . VALEURS CALCULÉES
Les valeurs des observations sont distantes par rapport à la
droite de régression ( ou droite des moindres carrés) .
La droite de régression est constituée de l’ensemble des
valeurs calculées à partir des observations.

9. « Il n'existe aucune relation entre démographie et demande en
logements »
Variable indépendante Variable dépendante
Si H₀ est rejetée, cela signifie que la pente b=0
Si H1 est acceptée, cela signifie que la pente b≠0
Avant de procéder à l’analyse du modèle de régression, il est nécessaire que
les variables indépendante et dépendante soient bien corrélées.

10. Analysons maintenant les données des variables « démographie » et « demande »
Analyse Régression
Linéaire
1

11. A l’inverse de la corrélation, la régression
exige que la variable indépendante et la
variable dépendante soient bien spécifiées
et placées séparément dans des champs
différents : la variable dépendante dans
«Dépendant :» et la variable indépendant
dans « Variables indépendantes: »
Transférons les deux variables
dans leur champ correspondant.
Appuyez sur le bouton Ok sans toucher
aux autres.
2

12. Nous obtenons 4 tableaux dont 3 uniquement qui nous
intéressent pour l’analyse de régression « Variables
introduites/supprimées » , « Récapitulatif des modèles » et
« Coefficients »
3
indique la
variable indépendante
« Démographie »
La variable dépendante
« demande en logements »

13. 2 valeurs importantes dans le modèle de régression : R = 0,987 (coefficient de
corrélation) et R² =0,975 (R X R)
 R (r) (coefficient de corrélation) presque égal à 1 indique clairement que les 2 variables sont
significativement en relation. (Même valeur obtenue lors de l’analyse de corrélation)
 R² (coefficient de détermination ) mesure la qualité de prédiction d’une régression linéaire
R² de valeur de 0,975 (97,5%) indique que la démographie explique la demande en logements dans
un fort pourcentage de 97,5 .
0 ≤R²≤1
Ce coefficient se situe entre 0 (exprime un pouvoir de prédiction faible) et 1 (exprime un pouvoir de
prédiction fort voire parfait).
Sur le plan graphique
 Plus R² se rapproche de 0, plus le nuage de points est diffus et se disperse autour de la droite de
régression.
 Plus le R² tend vers 1, plus le nuage de points se rapproche et se resserre autour de la droite
de régression.
 Quand les points sont exactement alignés sur la droite de régression, R²=1.
4

14. Ici, il y a 3 valeurs importantes :
 -31,997 qui exprime la Constante b
 8,231 est la valeur de la pente a.
Si x=0 alors y=- 31,997
P-value=0,000 <0,05 donc
H₁: il existe une relation statistiquement significative entre démographie et
demande en logements.
Cette forte relation est déjà confirmée par R² de valeur de 0,975 ou 97,5% (2ème
tableau)
Bêta (coefficients standardisés) est égale à 0,987 . C’est la même valeur que celle
du coefficient de corrélation . Cette égalité de valeurs est vraie quand il s’agit
d’une régression linéaire simple.
5

15. H₁: il existe une relation statistiquement significative entre démographie et
demande en logements, b≠0.
Y= ax + b (l’équation de la régression)
Selon le 3ème tableau , Pente =8,23 et Constante = - 31,99
Y= 8,23 * démographie +(- 31,99)
Quelle est la demande en logements pour une démographie
de 28 millions d’habitants ?
Y= 8,23 * 28 - 31,99= 198,45
Donc, pour la valeur de démographie de 28 millions (variable
indépendante), la valeur prédite en demande en logements
(variable dépendante), est 198,45 (en milliers) environ,
En conclusion , R, R² et le coefficient non standardisés (A) sont
les plus importants nombres à chercher et à contrôler pour
effectuer l'analyse de régression.
Comme c’est déjà annoncé, on peut prédire la variable
dépendante (le résultat) avec l’analyse de régression.
6