Teste d'homogeniete

Le shéma suivant présente les différentes étapes de la chaîne
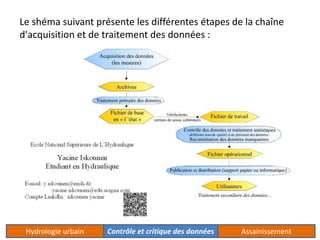
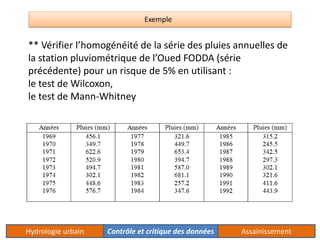
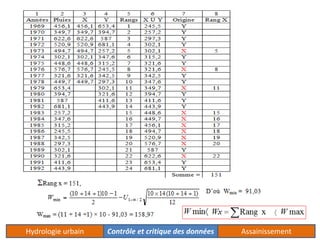
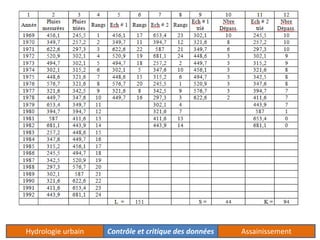
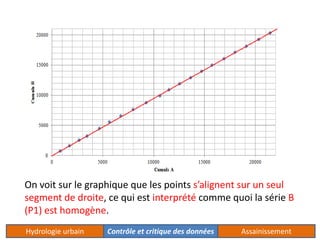
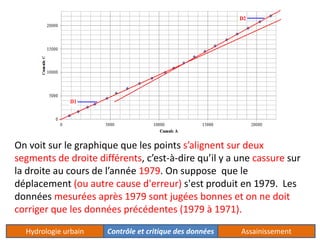
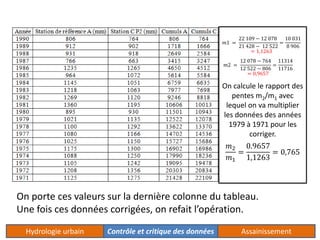
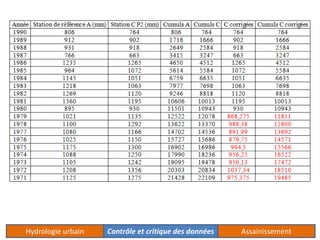
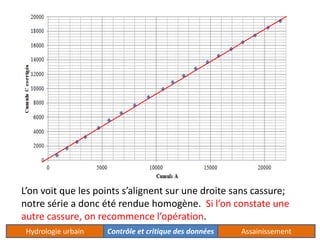
d'acquisition et de traitement des données :
Hydrologie urbain Contrôle et critique des données Assainissement

Les données sont homogènes - Une série de données est réputée
non homogène lorsque:
 elle provient de la mesure d'un phénomène dont les
caractéristiques évoluent durant la période de mesure; le
phénomène est alors dit non-stationnaire (par exemple:
variations climatiques, variations du régime des débits dues à
une déforestation ou un reboisement). Il est également possible
d'observer des signes d'une non stationnarité apparente
lorsque l'électronique intégrée à l'équipement de mesure
présente une dérive temporelle ou lors du changement de
l'observateur.
 elle reflète deux ou plusieurs phénomènes différents. Le régime
d'une rivière à l'aval de la confluence de deux sous bassins dont
le comportement hydrologique est très contrasté constitue un
bon exemple de ce défaut d'homogénéité.

le test de Wilcoxon et le test de de Mann-Whitney
non-paramétriques
Pour cela on les appel des tests :

1-Test de Wilcoxon
Nous formons le tableau suivant pour faciliter les calculs. On
commence par diviser notre série pluviométrique en deux
échantillons de longueurs respectives N1 = 10 valeurs et N2 = 14
valeurs (N = N1 + N2 = 10 + 14 = 24). Dans la première colonne
on porte les dates des mesures de pluie, dans la seconde
colonne on porte les données brutes, dans la troisième
colonne on porte le premier échantillon X, dans la quatrième
colonne on porte le deuxième échantillon Y, dans la cinquième
et la sixième colonnes on porte respectivement les rangs et les
valeurs classées de la série originale, dans la septième colonne
l’origine de la valeur de la série, c’est à dire on note si elle
provient de l’échantillon X ou de l’échantillon Y et dans la
huitième colonne on inscrit le rang de la valeur qui provient de
la série X.

On calcule ensuite les valeurs de :
- Wx = ΣRang x
- des deux bornes Wmax et Wmin, données
par les formules suivantes:
( 1) 1 1 2 1 2
( 1)
12
2
1 / 2
1 2 1
min
 

  
 
N N N N
U
N N N
W
max 1 2 1 min W  (N  N 1)N W
représente la valeur de la variable centrée réduite de la loi normale
correspondant à 1- α/ 2 (au seuil de 95 %, nous avons =1,96).
1/ 2 U
1/ 2 z
On vérifie l’inégalité:
on conclue que notre série est homogène

2- Test de Man-Whitney
on divise notre échantillon en deux sous-ensembles de tailles
respectives N1 et N2 avec: N1 < N2.
x1, x2, ........................... xi...................................xN1
y1, y2, ............................ yi...................................xN2
La taille de l'échantillon original est N = N1+ N2.
On classe ensuite nos valeurs par ordre croissant de 1 à N et l'on
note les rangs R(xi) des éléments du premier sous-ensemble et
R(yi) ceux des éléments du second sous-ensemble dans
l'échantillon original.
On définit K et S comme suit:퐾 = 퐿 −
푁1×(푁1+1)
2
et 푆 = 푁1 × 푁2 − 퐾 ;
avec ; 퐿 c'est à dire la somme des rangs des éléments de
l'échantillon 1 dans l'échantillon original.

K est la somme des nombres de dépassements de chaque
élément du second échantillon par ceux du premier échantillon.
S est la somme des nombres de dépassements des éléments du
premier sous-ensemble (ou échantillon) par ceux du second.
On montre que lorsque N > 20, N1 > 3 et N2 > 3; K et S sont
distribués selon une loi normale ayant :
- une moyenne égale à: 퐾 = 푆 =
푁1×푁2
2
- et un écart-type égal à: 푆푘= 푆푠 =
푁1×푁2
12
× (푁1 + 푁2 + 1)
On peut alors tester l’hypothèse H0 que les deux sous-ensembles
proviennent de la même population, au niveau de signification
α, en comparant la grandeur:

avec la variable normale centrée réduite ayant une probabilité
de dépassement α /2. Si T < z1-α/2 on accepte H0
On forme le tableau suivant pour faciliter la compréhension :
La colonne 1 donne les années.
La colonne 2 donne les pluies dans l’ordre où elles ont été
relevées.
La colonne 3 indique les pluies triées par ordre croissant.
La colonne 4 donne rangs des données triées.
La colonne 5 donne les N1 valeurs de l'échantillon 1
la somme des éléments de cette colonne est égale à L
La colonne 6 indique le rang de chaque valeur du sous-ensemble 1
dans l'échantillon original de N valeurs classées.
La colonne 7 donne les N2 valeurs de l'échantillon 2.
La colonne 8 donne le rang de chaque valeur du sous-ensemble 2
dans l'échantillon original de N valeurs classées.

La colonne 9 indique les valeurs du sous-ensemble 1 triées.
La colonne 10 donne le nombre de fois que chaque élément du
sous ensemble 1 est dépassé par les éléments du sous-ensemble
2, la somme des éléments de cette colonne est égale
à S .
La colonne 11 donne les valeurs du sous-ensemble 2 triées.
La colonne 12, enfin, donne le nombre de fois que chaque
élément du sous-ensemble 2 est dépassé par les éléments du
sous-ensemble 1, la somme des valeurs de cette colonne est
égale à K .
On trouve : L , K et S ; les équations et le tableau donnent
respectivement les mêmes valeurs pour K et L.

퐾 = 푆 =
푁1×푁2
2
et 푆푘 = 푆푠 =
푁1×푁2
12
× 푁1 + 푁2 + 1 et 푇 =
퐾−퐾
푠푘
Pour  = 95 % on a =1,96 > T Ce qui veut dire qu’on peut
accepter l’hypothèse H0 que les deux sous-ensembles
proviennent de la même population et que notre série
pluviométrique est homogène.

Exemple
** Vérifier l’homogénéité de la série des pluies annuelles de
la station pluviométrique de l’Oued FODDA (série
précédente) pour un risque de 5% en utilisant :
le test de Wilcoxon,
le test de Mann-Whitney

Méthode des doubles cumuls
Elle permet de détecter la non-homogénéité d'une série de
mesures et de la corriger. La méthode consiste à comparer les
pluies (ou toute autre variable) cumulées d'une station B, à
propos de laquelle on éprouve des doutes quant à son
homogénéité, avec les pluies cumulées d'une station A dont les
mesures sont jugées homogènes.

Application de la méthode à la série P1 : On commence donc
par établir le tableau ci-dessous: Dans les trois premières
colonnes on porte respectivement les années et les
précipitations mesurées aux stations A et B. Dans les
quatrième et cinquième colonnes on calcule les cumuls
respectifs des pluies aux stations A et B. Ensuite on porte ces
valeurs sur du papier millimétré, avec les valeurs de A en
abscisses et les valeurs de B en ordonnées

On voit sur le graphique que les points s’alignent sur un seul
segment de droite, ce qui est interprété comme quoi la série B
(P1) est homogène.

Application de la méthode à la série P2 : On commence donc
par établir le tableau ci-dessous: Dans les trois premières
colonnes on porte respectivement les années et les
précipitations mesurées aux stations A et C. Dans les
quatrième et cinquième colonnes on calcule les cumuls
respectifs des pluies aux stations A et C. Ensuite on porte ces
valeurs sur du papier millimétré, avec les valeurs de A en
abscisses et les valeurs de C en ordonnées.

On voit sur le graphique que les points s’alignent sur deux
segments de droite différents, c’est-à-dire qu’il y a une cassure sur
la droite au cours de l’année 1979. On suppose que le
déplacement (ou autre cause d'erreur) s'est produit en 1979. Les
données mesurées après 1979 sont jugées bonnes et on ne doit
corriger que les données précédentes (1979 à 1971).

La décision de corriger ou non les données de l’année1979 est
prise après une connaissance détaillée des circonstances de
“ l’accident ” au cours de cette année.
On calcule les pentes m1 du segment de droite qui contient les
données de 1990 à 1979 ( D1) , et m2 du segment de droite qui
contient les données de 1979 à 1971 (D2).

푚1 =
22 109 − 12 078
21 428 − 12 522
=
10 031
8 906
= 1,1263
푚2 =
12 078 − 764
12 522 − 806
=
11314
11716
= 0,9657
On calcule le rapport des
pentes m2/m1 avec
lequel on va multiplier
les données des années
1979 à 1971 pour les
corriger.
푚2
푚1
=
0.9657
1,1263
= 0,765
On porte ces valeurs sur la dernière colonne du tableau.
Une fois ces données corrigées, on refait l’opération.

L’on voit que les points s’alignent sur une droite sans cassure;
notre série a donc été rendue homogène. Si l’on constate une
autre cassure, on recommence l’opération.

Teste d'homogeniete

Contenu connexe

Tendances

En vedette

Dernier

Teste d'homogeniete

Notes de l'éditeur