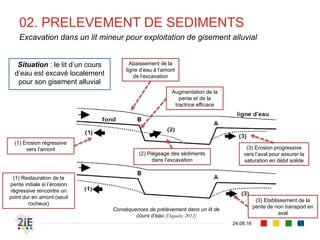
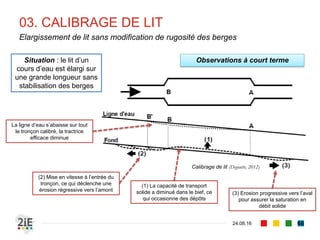
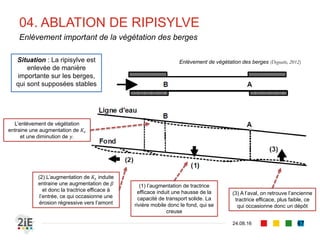
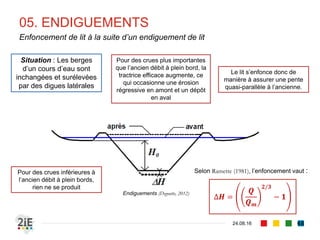
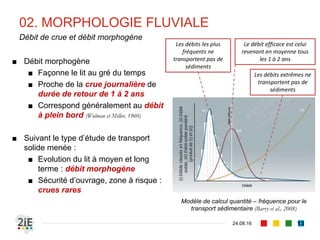
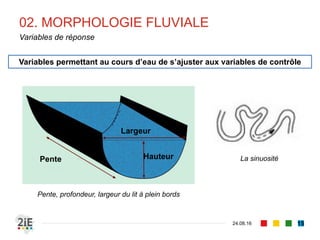
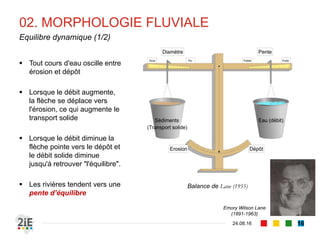
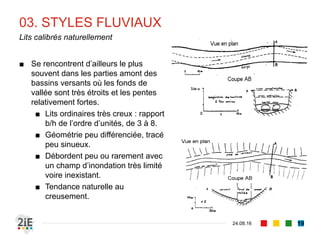
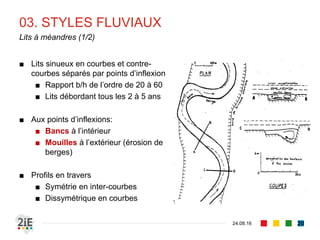
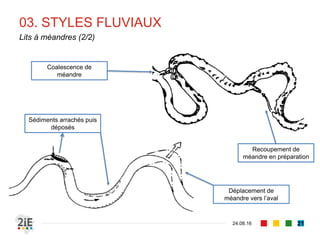
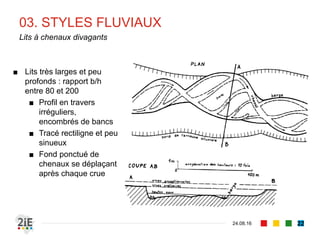
Le document explore la morphologie fluviale et le transport sédimentaire dans les cours d'eau naturels, en détaillant des concepts clés tels que l'équilibre dynamique, les modes de transport des sédiments et les conséquences morphologiques des aménagements. Il présente également des éléments bibliographiques et une terminologie spécifique aux cours d'eau, ainsi qu'une classification des rivières en fonction de leur pente. Enfin, il examine les mécanismes influençant la sédimentation et l'interaction entre le courant et les sédiments dans différents types de lits fluviaux.

1. v1.1.0
Morphologie fluviale et transport sédimentaire en cours d’eau naturel
HYDRAULIQUE FLUVIALE
Roland O. YONABA
Doctorant, Assistant d’Enseignement de Recherche
Département Génie Civil et Hydraulique (GCH)
Laboratoire Hydrologie et Ressources en Eau (LEAH)/2iE
Email: ousmane.yonaba@2ie-edu.org / roland.yonaba@gmail.com

2. OBJECTIFS DE COURS
■ Notions de morphologie fluviale
■ Mécanismes modifiant la morphologie d’un cours d’eau naturel
■ Variables de contrôle, variables de réponse
■ Equilibre dynamique, tri granulométrique, pavage
■ Transport sédimentaire
■ Modes de transport des sédiments
■ Formules empiriques associées
■ Techniques de mesures du transport solide
■ Conséquences morphologiques de quelques aménagements
■ Développements hydrodynamiques
■ Equations de Saint-Venant & Exner
■ Calcul d’évolution de fond de lit de cours d’eau
04.09.16 2

3. INDICATIONS BIBLIOGRAPHIQUES
04.09.16 3
■ Belleudy, Philippe, ‘Le Transport Solide En Rivière: Lacunes de Connaissance et Besoins
Méthodologiques’ (Institut National Polytechnique de Grenoble, 2001)
■ Degoutte, Gérard, Diagnostic, Aménagement et Gestion Des Rivières: Hydraulique et
Morphologie Fluviales Appliquées (Ed. Tec & doc, 2012)
■ Einstein, Hans Albert, The Bed-Load Function for Sediment Transportation in Open
Channel Flows, 1026 (US Department of Agriculture, 1950)
■ Engelund, Frank et Eggert Hansen, A Monograph on Sediment Transport in Alluvial
Streams (TEKNISKFORLAG Skelbrekgade 4 Copenhagen V, Denmark., 1967)
■ Garde, R. J., History of Fluvial Hydraulics (New Age International, 1995)
■ Graf, Walter Hans et Mustafa Siddik Altinakar, ‘Hydraulique Fluviale, Traité de Génie Civil,
Vol. 16’, Presses Polytechniques et Universitaires Romandes, 2000
■ Meyer-Peter, Eugen et Robert Müller, ‘Formulas for Bed-Load Transport’ (IAHR, 1948)
■ ONEMA, Eléments de Connaissance Pour La Gestion Du Transport Solide En Rivière
(ONEMA)
■ Recking, Alain, Frédéric Liébault, Christophe Peteuil, et Thomas Jolimet, ‘Testing Bedload
Transport Equations with Consideration of Time Scales’, Earth Surface Processes and
Landforms, 37 (2012), 774–89
■ Shields, Albert, Application of Similarity Principles and Turbulence Research to Bed-Load
Movement (Soil Conservation Service, 1936)

4. SOMMAIRE
04.09.16 4
I. Morphologie Fluviale
Cours d’eau, morphologie fluviale, styles fluviaux
II. Transport de sédiments
Généralités, contrainte tractrice, formules de transport solide, vitesse
de début d’entrainement, géométrie d’équilibre, mesure du transport
solide
III. Conséquences morphologiques de quelques aménagements
Excavation en lit mineur, calibrage, ablation de végétation,
endiguement, rétrécissement de section, retenues d’eau, ouvrages
obliques
IV. Développements hydrodynamiques
Equations de Saint-Venant-Exner, calcul d’évolution de fond de lit

5. MORPHOLOGIE FLUVIALE
Chapitre I

6. 01. COURS D’EAU
04.09.16
Définition et usages
6
■ Cours d’eau
■ Chemin naturel creusé par le passage habituel des eaux de
ruissellement, de manière permanente ou sporadique
■ Positionné naturellement au point bas d’une région, fond de vallée
■ Multiples usages
■ Support de transport et de navigation
■ Production électrique, force mortice,…
■ Pêche, chasse, culture, pâturage
■ Sédiments transportés et déposés
■ Ressource en eau (boisson, besoins
domestiques,…)

7. 01. COURS D’EAU
04.09.16
Fonctions d’un cours d’eau
7
■ Fonction hydrologique
■ Ecoulement des débit liquides
■ Fonction hydraulique
■ Dissipation de l’énergie potentielle par frottement
■ Fonction sédimentologique
■ Production, transport et dépôt de débit solide
■ Fonction hydrogéologique
■ Drainage ou recharge de la nappe
■ Fonction écologique
■ Entretien des milieux aquatiques et humides

8. 01. COURS D’EAU
04.09.16
Vocabulaire des cours d’eau (1/3)
8
Lit moyen : inondé pour les
crues intermédiaires de
durée de retour de 1 à 5 ans
Lit majeur : pleine
inondable occupé
par les crues
exceptionnelles
Berge : talus incliné séparant
le lit mineur du lit majeur
Rive : zone plate en crête des
berges séparant le milieu
aquatique du milieu terrestre
Lit mineur : chenal
occupé par
l’écoulement des
crues courantes,
sujet à une forte
dynamique

9. 01. COURS D’EAU
04.09.16
Vocabulaire des cours d’eau (2/3)
9
Ripisylve : formation végétale
naturelle qui borde la rive d’un cours
d’eau. Peut également être une
véritable forêt alluviale. C'est un
milieu lié à la rivière, particulièrement
riche en terme de diversité
floristique.
La ripisylve influence et entretient :
• la faune et la flore
• le paysage
• la température de l’eau
• l’écoulement des crues
• La stabilité des berges
Mais génère quelques inconvénients :
• Alimentation de la rivière en bois arrachés
par les crues, susceptibles de créer des
embâcles, d’obstruer les ponts et
d’aggraver les crues localement
• Apport de matière organique dû à la
décomposition des feuilles
• Accessibilité difficile pour les promeneurs
ou les pêcheurs ;
• Consommation d’eau pouvant diminuer les
débits d’étiage

10. 01. COURS D’EAU
04.09.16
Vocabulaire des cours d’eau (3/3)
10
Alluvions et substratum: la rivière coule sur ses alluvions (grains fins ou
grossiers alternativement déposés ou repris par le courant) qui recouvrent le
substratum rocheux formé d'une roche dure (ou plus ou moins tendre) (schistes,
grés, marnes…). Si les dépôts et la mise en suspension des alluvions s’alternent,
l’altération du substratum est quant à elle irréversible :
les alluvions assurent la protection du substratum.

11. 02. MORPHOLOGIE FLUVIALE
04.09.16
Définition
11
Morphologie : ensemble décrivant les caractéristiques, la configuration et
l'évolution des formes d’un cours d’eau
Comment la rivière évolue t’elle ?
Elle est façonnée et entretenue naturellement
Ou elle est le résultat de l’action anthropique

12. 02. MORPHOLOGIE FLUVIALE
04.09.16
Distribution des vitesses d’écoulement
12
Les vitesses maximales sont
mesurées légèrement en dessous
de la surface, en zone « libre »
proche des axes principaux
d’écoulement
Les vitesses minimales sont
mesurées près des parois
d’écoulement

13. 02. MORPHOLOGIE FLUVIALE
04.09.16
Débit de crue et débit morphogène
13
■ Débit morphogène
■ Façonne le lit au gré du temps
■ Proche de la crue journalière de
durée de retour de 1 à 2 ans
■ Correspond généralement au débit
à plein bord (Wolman et Miller, 1960)
■ Suivant le type d’étude de transport
solide menée :
■ Evolution du lit à moyen et long
terme : débit morphogène
■ Sécurité d’ouvrage, zone à risque :
crues rares
Modèle de calcul quantité – fréquence pour le
transport sédimentaire (Barry et al., 2008)
Les débits les plus
fréquents ne
transportent pas de
sédiments
Les débits extrêmes ne
transportent pas de
sédiments
Le débit efficace est celui
revenant en moyenne tous
les 1 à 2 ans

14. 02. MORPHOLOGIE FLUVIALE
04.09.16
Variables de contrôle
14
Débit liquide Débit solide
Variables s’imposant au cours d’eau et qui contrôlent son évolution physique
Variables
Principales
Variables
secondaires

15. 02. MORPHOLOGIE FLUVIALE
04.09.16
Variables de réponse
15
Variables permettant au cours d’eau de s’ajuster aux variables de contrôle
La sinuosité
Pente, profondeur, largeur du lit à plein bords
Pente
Largeur
Hauteur

16. 02. MORPHOLOGIE FLUVIALE
04.09.16
Equilibre dynamique (1/2)
16
Balance de Lane (1955)
 Tout cours d'eau oscille entre
érosion et dépôt
 Lorsque le débit augmente, la
flèche se déplace vers l'érosion, ce
qui augmente le transport solide
 Lorsque le débit diminue la flèche
pointe vers le dépôt et le débit
solide diminue jusqu'à retrouver
"l'équilibre".
 Les rivières tendent vers une pente
d’équilibre
Emory Wilson Lane
(1891-1963)

17. 02. MORPHOLOGIE FLUVIALE
04.09.16
Equilibre dynamique (2/2)
17
■ Les rivières tendent à établir une combinaison « dynamiquement stable »
■ Ajustement permanent entre variables de contrôle et de réponse
■ Ainsi, il est nécessaire d’identifier le seuil à partir duquel les oscillations et
modifications géométriques ne sont plus liées à l’équilibre mais deviennent
indicateurs de dysfonctionnement
■ Conséquences de modifications:
■ Faible ampleur : pas de changement dans le style fluvial
■ Lourde : métamorphose fluviale, évolution vers un nouvel équilibre
■ Lourde mais peu durable : évolution vers un nouveau style fluvial et
retour progressif au style antérieur

18. 03. STYLES FLUVIAUX
04.09.16
Profil en long
18
■ Le profil en long du lit ordinaire et
celui du champ d’inondation sont très
grossièrement parallèles donc
assimilables sur des grandes
longueurs
■ Le profil en long du fond du fond du lit
ordinaire est accidenté par des points
hauts et des points bas qui se
succèdent assez rapidement d’amont
en aval
Points hauts :
seuils (ou radiers)
Points bas :
mouilles (ou pools)

19. 03. STYLES FLUVIAUX
04.09.16
Lits calibrés naturellement
19
■ Se rencontrent d’ailleurs le plus
souvent dans les parties amont des
bassins versants où les fonds de
vallée sont très étroits et les pentes
relativement fortes.
■ Lits ordinaires très creux : rapport
b/h de l’ordre d’unités, de 3 à 8.
■ Géométrie peu différenciée, tracé
peu sinueux.
■ Débordent peu ou rarement avec
un champ d’inondation très limité
voire inexistant.
■ Tendance naturelle au
creusement.

20. 03. STYLES FLUVIAUX
04.09.16
Lits à méandres (1/2)
20
■ Lits sinueux en courbes et contre-
courbes séparés par points d’inflexion
■ Rapport b/h de l’ordre de 20 à 60
■ Lits débordant tous les 2 à 5 ans
■ Aux points d’inflexions:
■ Bancs à l’intérieur
■ Mouilles à l’extérieur (érosion de
berges)
■ Profils en travers
■ Symétrie en inter-courbes
■ Dissymétrique en courbes

21. 03. STYLES FLUVIAUX
04.09.16
Lits à méandres (2/2)
21
Sédiments arrachés puis
déposés
Coalescence de
méandre
Recoupement de
méandre en préparation
Déplacement de
méandre vers l’aval

22. 03. STYLES FLUVIAUX
04.09.16
Lits à chenaux divagants
22
■ Lits très larges et peu
profonds : rapport b/h
entre 80 et 200
■ Profil en travers
irréguliers,
encombrés de bancs
■ Tracé rectiligne et peu
sinueux
■ Fond ponctué de
chenaux se déplaçant
après chaque crue

23. TRANSPORT DE SEDIMENTS
Chapitre II

24. 01. GENERALITES
04.09.16
Hydraulique torrentielle et hydraulique fluviale (1/2)
24
■ Selon Bernard (1925), sur la base de la pente, nous pouvons distinguer :
■ les rivières : pente inférieure à 1% ;
■ les rivières torrentielles : pente comprise entre 1 et 6% ;
■ les torrents : pente supérieure à 6%
Rivière Rivière torrentielle Torrent

25. 01. GENERALITES
04.09.16
Hydraulique torrentielle et hydraulique fluviale (2/2)
25
■ Hydraulique torrentielle : concerne les torrents
■ Caractérisée par des événements exceptionnels tels les laves
torrentielles, mélanges de boue et de pierres
■ transports solides très spectaculaires
■ Ne sera pas traité dans le cadre de ce cours
■ Hydraulique fluviale : concerne les rivières ou les rivières torrentielles.
■ Phénomène implicitement couplé
■ Mais peut être approché de manière découplée
■ En dissociant la phase liquide et la phase solide
■ En tenant compte de l’évolution du fond de lit

26. 01. GENERALITES
04.09.16
Ecoulement d’un mélange
26
■ Pour l’écoulement gravitationnel d’un mélange eau-
sédiment, Graf et Altinakar (2000) proposent la
classification suivante :
Mélange quasi-
newtonien :
Cs < 8%
Mélange eau-sédiment
de concentration
volumique Cs
Mélange non-
newtonien :
Cs > 8%
Mélange
newtonien :
Cs << 1%
Charriage et
suspension
Courant de
turbidité
Ecoulements
Débris-lave
Mustafa Siddik Altinakar
Water Hans Graf
(1936 - )

27. 01. GENERALITES
04.09.16
Transport solide : définition et modes de transport
27
■ Le transport solide correspond au transport de matériaux granulaires
■ Les matériaux apportés à la rivière.
■ Les arbres arrachés aux berges ou au lit majeur.
Modes de transport en hydraulique fluviale (Degoutte, 2012)

28. 01. GENERALITES
04.09.16
Diagramme de Hjulström
28
Henning Filip Hjulström
(1902-1982)
Diagramme
définissant l’état d’un
grain, en fonction de
sa taille et de la
vitesse de
l’écoulement.
Diagramme de Hjuström (1935)

29. 01. GENERALITES
04.09.16
Tri granulométrique
29
■ Les pentes des rivières naturelles sont
plus fortes en amont qu’en aval
■ Caractère torrentiel à l’amont et
fluvial à l’aval
■ Les sédiments seront mobilisés en
amont puis déposés en chemin
d’écoulement :
■ Les particules les plus grosses se
déposent initialement
■ Les fines étant emportées se
déposent plus loin.
■ On assiste alors à un tri
granulométrique d’amont en aval.

30. 01. GENERALITES
04.09.16
Armure
30
■ Couche de surface
grossière, résultat de
l'exportation des
éléments fins pendant et
après chaque période de
mouvement de tout ou
d’une partie des grains
disponibles au transport
(Bray et Church, 1980)
■ La rupture de l’armure
est fréquente, au moins
1 fois/an

31. 01. GENERALITES
04.09.16
Pavage
31
■ Couche mise en place à la
suite du même processus
aboutissant aux armures,
mais elle est cependant
beaucoup plus solide et
pérenne.
■ les particules constituant la
surface des lits pavés ne sont
mises en mouvement que lors
d‘épisodes hydrologiques
exceptionnels (très fortes
crues (Bray et Church, 1980)
Vue d’un pavage (Degoutte, 2012)
Rôle protecteur de la couche de pavage

32. 01. GENERALITES
04.09.16
Rivière à sable et rivière à graviers (1/2)
32
Rivière à graviersRivière à sable
 Substrat constitué de particules
de petite taille (< 2 mm) et à
granulométrie dite uniforme
 Le fond est tapissé
d’ondulations de fond de type
rides, dunes et antidunes
 Substrat constitué d’éléments
grossiers (petits graviers à gros
graviers), la granulométrie est
dite étalée.
 Présence en général d’un
pavage observé au fond du lit,
qui reste sans ondulations.

33. 01. GENERALITES
04.09.16
Rivière à sable et rivière à graviers (2/2)
33
Caractéristiques principales des rivières à sable et à gravier

34. ■ Le débit solide 𝑄𝑠 est le volume de matériaux granulaires transportés
par le courant par unité de temps.
■ L’énergie de l’écoulement définit une capacité de transport
■ L’écoulement cherche toujours à assurer la saturation en débit solide
pour peu que le matériau à transporter soit disponible
■ À chaque instant, l'écoulement est saturé en débit solide (charriage et
suspension)
■ Le bief de rivière considéré est donc en équilibre : 𝑄𝑠,𝑖𝑛 = 𝑄𝑠,𝑜𝑢𝑡
■ Saturation en débit solide : principe fondamental de la dynamique fluviale
■ Si 𝑄𝑠 > capacité de transport : dépôt au fond du lit
■ Si 𝑄𝑠 < capacité de transport : érosion du fond du lit et/ou des berges
01. GENERALITES
04.09.16
Débit solide et capacité de transport
34

35. ■ Soit 𝑑 𝑥 le diamètre de
grain correspondant à
𝑥% en poids de tamisât
■ Le coefficient de Hazen
(1895) ou coefficient
d’uniformité 𝐶𝑈 permet
de classifier la
granulométrie
01. GENERALITES
04.09.16
Taille des grains et granulométrie
35
𝑪𝑼 =
𝒅 𝟔𝟎
𝒅 𝟏𝟎
Courbe granulométrique exprimée en % de passants
(Degoutte, 2012)
𝑪𝑼 < 𝟑 : granulométrie uniforme
𝑪𝑼 > 𝟑 : granulométrie étalée
Allen Hazen
(1869-1930)

36. 01. GENERALITES
04.09.16
Interpolation logarithmique
36
■ On souhaite interpoler un
diamètre 𝒅 au sein d’une
distribution granulométrique pour
laquelle l’on ne connait que deux
diamètres caractéristiques 𝑑 𝑥 et
𝑑 𝑦.
■ En admettant que 𝑝 correspond à un pourcentage en masse de passant
■ Cette interpolation reste en général valable entre les points d’inflexion de
la courbe granulométrique, soit le 𝑑10 et le 𝑑90
𝑝 = 𝑖 ln 𝑘𝑑 𝑝 , ∀𝑖, 𝑘 = 𝐶 𝑡𝑒 d’où :
𝒅 = 𝒂𝒆 𝒃𝒑, ∀𝑎, 𝑏 = 𝐶 𝑡𝑒
𝒃 =
𝟏
𝒙 − 𝒚
𝐥𝐧
𝒅 𝒙
𝒅 𝒚
𝒂 =
𝒅 𝒙
𝒆 𝒙𝒃
=
𝒅 𝒚
𝒆 𝒚𝒃

37. ■ La contrainte tractrice 𝜏0 est la force de frottement de l’eau contre les parois
de la section mouillée dans le sens tangentiel et par unité de surface
02. CONTRAINTE TRACTRICE
04.09.16
Définition
37
Contraintes appliquée par
l’eau sur les parois
(Degoutte, 2012)
En écoulement non uniforme, on
démontre que :
𝝉 𝟎 = 𝜸 𝒘 𝑹 𝒉 𝒋
Pour une section très large :
𝑦 ≪ 𝑏 ⇒ 𝑅ℎ ≈ 𝑦
𝝉 𝟎 = 𝜸 𝒘 𝒚𝒋
Par ailleurs, pour l’écoulement
uniforme, 𝒊 = 𝒋
Il est à remarquer que le rapport 𝜏0/𝜌 a la dimension du
carré d’une vitesse, appelée vitesse de frottement et
notée 𝒖∗
𝒖∗
𝟐 =
𝝉 𝟎
𝝆
= 𝒈𝑹 𝒉 𝒋

38. 02. CONTRAINTE TRACTRICE
04.09.16
Mise en mouvement d’un grain de diamètre d
38
Equilibre d’un grain posé au fond d’un chenal
(Degoutte, 2012)
𝑃 = 𝜋𝛾𝑠
𝑑3
6
𝑃𝑡 = 𝑃 sin 𝜂
𝑃′ = 𝜋𝛾 𝑤
𝑑3
6
𝑆 = 𝑐𝛾 𝑤 𝑑2
𝑉2
2𝑔
𝑃𝑛 = 𝑃 cos 𝜂
𝐹 = 𝑃𝑛 − 𝑃′
tan 𝜑
𝑬 = 𝑭 − 𝑷 𝒕 = 𝒃𝝉 𝟎 𝒅 𝟐

39. ■ Au seuil de la mise en mouvement :
02. CONTRAINTE TRACTRICE
04.09.16
Paramètre de Shields (1/2)
39
𝐸 = 𝑏𝜏0 𝑑2
= 𝐹 − 𝑃𝑡
𝜂 étant petit :
cos 𝜂 → 1 et sin 𝜂 → 0
⇒ 𝑃𝑡 = 𝑃 sin 𝜂 → 0
⇒ 𝑃𝑛 = 𝑃 cos 𝜂 → 𝑃
𝑏𝜏0 𝑑2 = 𝐹 = 𝑃𝑛 − 𝑃′ tan 𝜑
𝑏𝜏0 𝑑2
= 𝜋
𝑑3
6
tan 𝜑 𝛾𝑠 − 𝛾 𝑤
𝜏0
𝛾𝑠 − 𝛾 𝑤 𝑑
=
𝜋
6𝑏
tan 𝜑
 Shields (1936) définit alors le
paramètre adimensionnel :
𝝉∗
=
𝝉 𝟎
𝜸 𝒔 − 𝜸 𝒘 𝒅
=
𝜸 𝒘 𝑹 𝒉 𝑱
𝜸 𝒔 − 𝜸 𝒘 𝒅
 Le terme ( Τ𝜋
6𝑏) tan 𝜑 est un
seuil critique constant lié au
sédiment.
 La mise en mouvement du
grain de diamètre 𝑑 se produit
donc lorsque 𝜏∗ dépasse une
valeur critique

40. ■ En résumé, la contrainte tractrice sur fond plat s’écrit :
■ Le paramètre de Shields (1936), forme adimensionnelle de la contrainte
tractrice sur fond plat, est définie par :
■ Sur une pente d’angle 𝛽 (cas des berges), la contrainte tractrice s’écrira
02. CONTRAINTE TRACTRICE
04.09.16
Paramètre de Shields (2/2)
40
𝝉 𝟎 = 𝜸 𝒘 𝑹 𝒉 𝒋
Si l’écoulement est uniforme, 𝑖 = 𝑗 ⇒ 𝜏0 = 𝛾 𝑤 𝑅ℎ 𝑖
𝝉∗ =
𝝉 𝟎
𝜸 𝒔 − 𝜸 𝒘 𝒅
𝝉 𝜷 = 𝟏 −
𝐬𝐢𝐧 𝟐 𝜷
𝐬𝐢𝐧 𝟐 𝝋
𝝉 𝟎
On donne :
• 𝛾𝑠 ≈ 26 à 27 𝑘𝑁/𝑚3
• 𝛾 𝑤 ≈ 10 𝑘𝑁/𝑚3
Albert Frank Shields
(1908-1974)

41. Shields (1936) montre
expérimentalement, pour
la granulométrie uniforme,
l’existence de la relation :
02. CONTRAINTE TRACTRICE
04.09.16
Diagramme de Yalin-Shields (1972)
41
𝜏0 ≡ 𝑓(𝑅 𝑒
∗
)
avec 𝑅 𝑒 =
𝑢∗ 𝑑
𝜈
et 𝑢∗ = 𝜏0/𝜌 = 𝑔𝑅ℎ 𝐼
Yalin (1972) met en relation le paramètre de Shields 𝜏∗
à un diamètre adimensionnel 𝑑∗
:
Diagramme de Yalin-Shields (1972)
Selim M. Yalin
(1925-2007)
𝑑∗ = 𝑑
𝛾𝑠 − 𝛾 𝑤
𝛾 𝑤
𝑔
𝜈2
Τ1 3

42. ■ Ramette (1981) propose des valeurs seuils pour la granulométrie uniforme
02. CONTRAINTE TRACTRICE
04.09.16
Seuils de mise en mouvement (1/2)
42
On pourra toutefois retenir
les seuils suivants pour le
paramètre de Shields
Granulométrie Mise en
mouvement
Dépôt
Uniforme (rivière à
sable)
𝜏∗
≥ 0,047 𝜏∗
≤ 0,047
Etalée
(rivière à graviers)
𝜏 𝑑50
∗
≥ 0,138 𝜏 𝑑50
∗
≤ 0,047

43. Le mode de transport est aussi donné par le
Nombre de Rouse, en admettant la
constante de Von Karmán 𝒦 = 0,41
Ferguson et Church (2006) proposent une
relation donnant la vitesse de sédimentation
𝑉𝑠𝑠 d’un grain
02. CONTRAINTE TRACTRICE
04.09.16
Seuils de mise en mouvement (2/2)
43
𝑽 𝒔𝒔 =
𝟏𝟔, 𝟏𝟕𝒅 𝟐
𝟏, 𝟖. 𝟏𝟎−𝟓 + 𝟏𝟐, 𝟏𝟐𝟕𝟓𝒅 𝟑 𝟎,𝟓
𝑷 =
𝑽 𝒔𝒔
𝓚𝒖∗
Nombre de
Rouse
Mode de transport
P > 2,5 Charriage
1,2 < P < 2,5 Suspension à 50 %
0,8 < P < 1,2 Suspension à 100 %
P < 0,8 Charge flottante
De manière indicative, Graf (1971) propose
𝒖∗
𝑽 𝒔𝒔
> 𝟎, 𝟏: 𝒅é𝒃𝒖𝒕 𝒅𝒆 𝒄𝒉𝒂𝒓𝒓𝒊𝒂𝒈𝒆
𝒖∗
𝑽 𝒔𝒔
> 𝟎, 𝟒: 𝒅é𝒃𝒖𝒕 𝒅𝒆 𝒍𝒂 𝒔𝒖𝒔𝒑𝒆𝒏𝒔𝒊𝒐𝒏
Hunter Rouse
(1906-1996)

44. ■ La contrainte de frottement 𝜏0 résulte
de l’effet conjugué des cisaillement
générés par ondulations de fond de
lit et des grains
■ Pour une formulation de type Chézy
(1768) soit 𝜏0 = 𝜌𝑔𝑈2
/𝐶2
■ Qui peut se traduire aussi en :
02. CONTRAINTE TRACTRICE
04.09.16
Notion de contrainte tractrice efficace (1/2)
44
𝝉 𝟎 = 𝝉 𝒈𝒓𝒂𝒊𝒏𝒔 + 𝝉 𝒇𝒐𝒏𝒅
𝟏
𝑲 𝒔
𝟐
=
𝟏
𝑲 𝒈𝒓𝒂𝒊𝒏𝒔
𝟐
+
𝟏
𝑲 𝒇𝒐𝒏𝒅
𝟐
𝟏
𝑪 𝟐
=
𝟏
𝑪 𝒈𝒓𝒂𝒊𝒏𝒔
𝟐
+
𝟏
𝑪 𝒇𝒐𝒏𝒅
𝟐

45. 02. CONTRAINTE TRACTRICE
04.09.16
Notion de contrainte tractrice efficace (2/2)
45
𝜷 =
𝑲 𝒔
𝑲 𝒈𝒓𝒂𝒊𝒏𝒔
Τ𝟑 𝟐
Selon Ramette (1981):
𝜷 =
𝟎, 𝟎𝟔
𝝉∗ + 𝟎, 𝟒𝟏𝝉∗
Τ𝟏𝟓 𝟏𝟔
Notons toujours que :
𝟎, 𝟑𝟓 < 𝜷 < 𝟏
𝑲 𝒔: Rugosité d’ensemble de section, dûe au fond et aux
grains
𝑲 𝒈𝒓𝒂𝒊𝒏𝒔: Rugosité dûe au grains (rugosité de peau)
𝑲 𝒈𝒓𝒂𝒊𝒏𝒔 ≈
𝟐𝟏, 𝟏
𝒅 𝟓𝟎
Τ𝟏 𝟔
≈
𝟐𝟔
𝒅 𝟗𝟎
Τ𝟏 𝟔
𝝉 𝟎 = 𝜷𝝉 𝟎 + 𝟏 − 𝜷 𝝉 𝟎
Contrainte
tractrice totale
Contrainte tractrice dûe
aux grains, dite tractrice
efficace
Contrainte
tractrice dûe aux
dunes
En l’absence d’ondulations du fond (c’est souvent le
cas en granulométrie étalée), on prendra 𝜷 = 𝟏

46. 02. CONTRAINTE TRACTRICE
04.09.16
Rides, dunes et antidunes
46
Disparition des dunes et apparition
des antidunes pour 𝝉∗
> 𝟒, 𝟓 à 𝟓
Apparition des dunes pour 𝝉∗
= 𝟎, 𝟎𝟔𝟐,
qui deviennent maximales pour 𝜏∗
= 0,38
et disparaissent pour 𝜏∗
= 2,5
Les rides deviennent prononcées pour 𝛽
minimal, soit 𝝉∗
= 𝟎, 𝟑𝟖

47. ■ Il existe plusieurs formules ou « modèles » d’évaluation du transport solide
■ Evaluent la capacité de transport et non le transport effectif !
■ Restent valables sous des conditions bien définies
■ Il existe essentiellement 3 types de formulations de transport solide :
■ Formules de type Du Boys, liées à la tension de frottement
■ Formules de type Schoklitsch, liées au débit liquide
■ Formules de type Einstein, liées à la portance du grain
■ Aucune formule n’existe pour la suspension intrinsèque!
■ Elle est estimée en déduisant le charriage du débit solide total
03. FORMULES DE TRANSPORT SOLIDE
04.09.16
Typologie des formules de transport
47

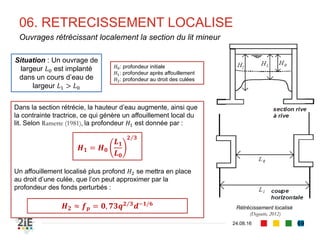
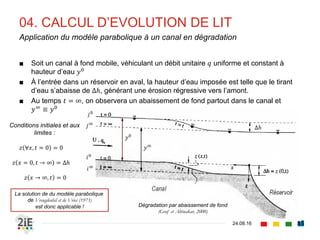
48. ■ Largeurs de bras vifs 𝐿 : dimension transversale du chenal sur laquelle les
grains sont mobilisables. On estimera pour la suite que 𝑳 ≅ 𝒃
■ Nous définissons également les termes suivants :
■ Densité spécifique : 𝒔 𝒔 = 𝜸 𝒔/𝜸 𝒘
■ Débit liquide unitaire : 𝒒 = 𝑸/𝒃
■ Aussi, nous adopterons les notations suivantes de débit en [m3.s-1.m-1] :
■ 𝒒 𝒔𝒃 : débit solide unitaire par charriage
■ 𝒒 𝒔 : débit solide total
■ Ainsi, nous définirons définira donc les débits en [m3.s-1], 𝑄𝑠 et 𝑄𝑠
■ 𝑸 𝒔 = 𝒒 𝒔 𝑳 ≈ 𝒒 𝒔 𝒃 : débit solide total vides non compris
■ 𝑸 𝒔 = Τ𝑸 𝒔 𝟏 − 𝒏 : débit solide total, vides compris
03. FORMULES DE TRANSPORT SOLIDE
04.09.16
Conventions et notations
48

49. 03. FORMULES DE TRANSPORT SOLIDE
04.09.16
Domaine de validité de quelques formules de transport
49
Domaines de validité des formules de transport (Belleudy, 2001)
Phillipe Belleudy
(1951 - )

50. 03. FORMULES DE TRANSPORT SOLIDE
04.09.16
Formules de charriage (1/4)
50
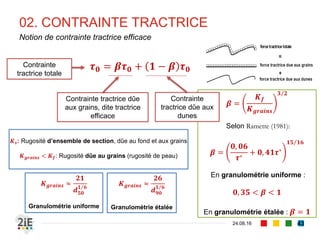
■ En granulométrie uniforme:
■ 𝝉 𝒄𝒓
∗ = 𝟎, 𝟎𝟒𝟕 et 𝑑 = 𝑑 𝑚𝑜𝑦𝑒𝑛
■ En granulométrie étalée à fond sans
ondulations (Parker, 1982):
■ 𝝉 𝒄𝒓
∗
= 𝟎, 𝟏𝟑𝟖, 𝛽 = 1 et 𝑑 = 𝑑50
𝒒 𝒔𝒃 = 𝟖 𝒈 𝒔 𝒔 − 𝟏 𝒅 𝟑 𝜷𝝉∗
− 𝝉 𝒄𝒓
∗ Τ𝟑 𝟐
Conditions de validité
• Ecoulement uniforme
• 0,01 𝑚 < 𝑦 < 1,20 [𝑚]
• 0,04 % < 𝑖 < 2 %
• 0,4 𝑚𝑚 < 𝑑 < 30 [𝑚𝑚]
• Granulométrie uniforme
• 𝜏∗
< 0,25 : charriage (Ramette, 1981)
Eugène Meyer-Peter
(1883-1969)
Robert Müller
(1908-1987)
Formule de Meyer-Peter et Müller (1948)

51. 03. FORMULES DE TRANSPORT SOLIDE
04.09.16
Formules de charriage (2/4)
51
■ Einstein (1937) introduit l’idée que le grain se déplace
sur une distance proportionnelle à taille. Il en résulte
que :
■ Cette relation complexe et nécessitant des abaques
a été lissée par Brown (1950) sous la forme :
■ Le diamètre caractéristique est donné par :
■ 𝑑 = 𝑑 𝑚𝑜𝑦𝑒𝑛 (uniforme) et 𝑑 = 𝑑50 (étalée)
𝒒 𝒔𝒃 = 𝒈 𝒔 𝒔 − 𝟏 𝒅 𝟑 𝟐
𝟑
+
𝟑𝟔𝝂 𝟐
𝒈 𝒔 𝒔−𝟏 𝒅 𝟑 −
𝟑𝟔𝝂 𝟐
𝒈 𝒔 𝒔−𝟏 𝒅 𝟑 𝒇(𝝉∗)
Conditions de validité
0,3 𝑚𝑚 < 𝑑 < 29 [𝑚𝑚]
𝑞 𝑠𝑏
𝑔 𝑠𝑠 − 1 𝑑
= 𝑓
𝛾𝑠 − 𝛾 𝑤
𝜏0
′ 𝑑
𝑓(𝜏∗
) = ൝
2,15𝑒−0,391/𝜏∗
𝑠𝑖 𝜏∗
< 0,182
40𝜏∗3
𝑠𝑖 𝜏∗
> 0,182
Formule de Brown-Einstein (1950)
Hans Albert Einstein
(1904 - 1973)

52. 03. FORMULES DE TRANSPORT SOLIDE
04.09.16
Formules de charriage (3/4)
52
■ On définit un débit critique d’érosion 𝑞 𝑐𝑟 :
■ Le charriage est alors donné par :
■ Le diamètre caractéristique est donné par :
■ Granulométrie uniforme : 𝑑 = 𝑑 𝑚𝑜𝑦𝑒𝑛
■ Granulométrie étalée : 𝑑 = 𝑑40 (Bathurst et. al, 1987)
𝒒 𝒔𝒃 =
𝟐, 𝟓
𝒔 𝒔
𝒒 − 𝒒 𝒄𝒓 𝒊 Τ𝟑 𝟐
Conditions de validité
• 0,03 % < 𝑖 < 10 %
• 0,3 𝑚𝑚 < 𝑑 < 7 [𝑚𝑚]
𝒒 𝒄𝒓 = 𝟎, 𝟐𝟔 𝒔 𝒔 − 𝟏 Τ𝟓 𝟑
𝒅 Τ𝟑 𝟐
𝒊 Τ𝟕 𝟔
Formule de Schoklitsch (1962)
Armin Karl Kult Schoklitsch
(1888-1969)

53. 03. FORMULES DE TRANSPORT SOLIDE
04.09.16
Formules de charriage (4/4)
53
■ Bathurst (1985) définit un débit critique 𝑞 𝑐 :
■ Selon Rickenmann (1990), le charriage est alors donné par :
■ Le diamètre caractéristique pour 𝑞 𝑐 est donné par :
■ 𝑑 = 𝑑 𝑚𝑜𝑦𝑒𝑛 (uniforme) et 𝑑 = 𝑑50 (étalée)
𝒒 𝒔𝒃 =
𝟑,𝟏
𝑺 𝒔−𝟏 𝟑/𝟐
𝒅 𝟗𝟎
𝒅 𝟑𝟎
𝟎,𝟐
𝒒 − 𝒒 𝒄 𝒊 𝟑/𝟐
si 𝒊 > 𝟑%
𝒒 𝒔𝒃 =
𝟏𝟐,𝟔
𝒔 𝒔−𝟏 𝟏,𝟔
𝒅 𝟗𝟎
𝒅 𝟑𝟎
𝟎,𝟐
𝒒 − 𝒒 𝒄 𝒊 𝟐
si 𝐢 < 𝟑%
Conditions de validité
• 0,3 % < 𝑖 < 20 %
• 0,4 𝑚𝑚 < 𝑑 < 10 [𝑚𝑚]
𝒒 𝒄 = 𝟎, 𝟎𝟔𝟓 𝒔 𝒔 − 𝟏 𝟏,𝟔𝟕
𝒈 𝟏/𝟐
𝒅 𝟑/𝟐
𝒊−𝟏,𝟏𝟐
Si ൗ𝑑90
𝑑30
inconnu,
prendre ൗ𝑑90
𝑑30
= 1,05
Formule de Rickenmann (1990)
Dieter Rickenmann

54. 03. FORMULES DE TRANSPORT SOLIDE
04.09.16
Formules de transport solide total (1/3)
54
■ Engelund et Hansen (1967) établissent que :
■ Le diamètre caractéristique est donné par :
■ 𝑑 = 𝑑 𝑚𝑜𝑦𝑒𝑛 (uniforme) et 𝑑 = 𝑑50 (étalée) Conditions de validité
• Pente faible (?)
• 0,15 𝑚𝑚 < 𝑑 < 1,6 [𝑚𝑚]
𝒒 𝒔 = 𝟎, 𝟎𝟓 𝒈 𝒔 𝒔 − 𝟏 𝒅 𝟑
𝑲 𝒔
𝟐 𝑹 𝒉
𝟏/𝟑
𝒈
𝝉∗ 𝟓/𝟐
Formule de Engelund et Hansen (1967)
Frank Anker Engelund
(1925 - 1983)
Karl Henry Eggert Hansen
(1914 - 1999)

55. 03. FORMULES DE TRANSPORT SOLIDE
04.09.16
Formules de transport solide total (2/3)
55
■ Graf et Acaroglu (1968) définissent un paramètre d’intensité de
frottement Ψ𝐴 comme critère de transport solide et mettent en
évidence qu’il est lié à un paramètre de transport Φ 𝐴
■ De manière expérimentale, ils établissent par suite que :
■ Le diamètre caractéristique est donné par :
■ 𝑑 = 𝑑 𝑚𝑜𝑦𝑒𝑛 (uniforme) et 𝑑 = 𝑑50 (étalée)
Conditions de validité
• 0,3 𝑚𝑚 < 𝑑 < 1,7 [𝑚𝑚]
Ψ𝐴 = 𝜏∗ −1
=
(𝑆𝑠−1)𝑑
𝑅ℎ 𝑖
Φ 𝐴 =
Τ𝑞 𝑠 𝑞 𝑈𝑅ℎ
𝑔 𝑠𝑠 − 1 𝑑3
Φ 𝐴 = 𝑓(Ψ𝐴)
Φ 𝐴 = 𝑎Ψ𝐴
−𝛽
= 10,39 Ψ𝐴
−2,52
⇒ 𝒒 𝒔 = 𝟏𝟎, 𝟑𝟗𝒈 𝟎,𝟓
𝒚𝑹 𝒉
𝟏,𝟓𝟐
𝒊 𝟐,𝟓𝟐
𝒔 𝒔 − 𝟏 𝟐,𝟎𝟐 𝒅 𝟏,𝟎𝟐
Formule de Graf et Acaroglu (1968)
Walter Hans Graf
(1936 - )

56. 03. FORMULES DE TRANSPORT SOLIDE
04.09.16
Formules de transport solide total (3/3)
56
■ On définit le terme Fgr :
■ Le charriage est alors donné par :
■ Le diamètre caractéristique est donné par :
■ 𝑑 = 𝑑 𝑚𝑜𝑦𝑒𝑛 (uniforme) et 𝑑 = 𝑑35 (étalée)
𝒒 𝒔 = 𝟎, 𝟎𝟐𝟓𝒒
𝒅
𝒚
𝑭 𝒈𝒓
𝟎, 𝟏𝟕
− 𝟏
𝟏,𝟓
Conditions de validité
• 𝐹𝑟 < 0,8 (Bathurst et al., 1987)
• 0,04 [𝑚𝑚] < 𝑑 < 4 [𝑚𝑚]
𝑭 𝒈𝒓 =
𝟏
𝒈 𝒔 𝒔 − 𝟏 𝒅
𝑼
𝟑𝟐 𝐥𝐨𝐠 𝟏𝟎
𝒚
𝒅
Formule de Ackers et White (1973)
P. Ackers

57. ■ La vitesse provoquant le début de la mise en mouvement d’un grain de
diamètre 𝑑 est appelée vitesse de début d’entrainement 𝑈0
■ Elle est établie en injectant l’expression de la pente 𝑖 donnée par l’équation
de Shields (1936) dans l’expression de Manning-Strickler pour la vitesse
04. VITESSE DE DEBUT D’ENTRAINEMENT
04.09.16
Vitesse 𝑈0 au début de la mise en mouvement
57
Or, de l’équation de Manning-Strickler (1891) :
𝑈 = 𝐾𝑠 𝑅ℎ
Τ2 3
𝑖 ⇒ 𝑈2
= 𝐾𝑠
2
𝑅ℎ
Τ4 3
𝑖
Du paramètre de Shields (1936), on tire :
𝜏 𝑐𝑟
∗ =
𝛾 𝑤 𝑅ℎ 𝑖
𝛾𝑠 − 𝛾 𝑤 𝑑
⇒ 𝑖 = (𝑠𝑠 − 1)
𝑑
𝑅ℎ
𝜏 𝑐𝑟
∗
𝑼 𝟎 = 𝒔 𝒔 − 𝟏 𝟏/𝟐 𝑲 𝒔 𝑹 𝒉
Τ𝟏 𝟔
𝒅 𝟏/𝟐 𝝉 𝒄𝒓
∗ Τ𝟏 𝟐

58. 05. STABILITE D’UN PAVAGE
04.09.16
Prédiction de la stabilité d’une couche de pavage
58
𝝉∗𝒂,𝒄𝒓 = 𝝉∗𝒄𝒓 𝟎, 𝟒
𝒅 𝟓𝟎
𝒅 𝟓𝟎 𝒂,
𝟏
𝟐
+ 𝟎, 𝟔
𝟐
𝒖∗𝒂,𝒄𝒓 = 𝒈 𝒔 𝒔 − 𝟏 𝒅 𝟓𝟎 𝒂,
𝝉∗𝒂,𝒄𝒓
𝟎,𝟓
Diagramme de Yalin-Shields (1972)
𝜏∗𝑐𝑟 est donné par le diagramme de Yalin-
Shields (1972), soit 𝝉∗𝒄𝒓 ≈ 𝟎, 𝟎𝟓
𝝉∗𝒄𝒓
Lors du développement d’un pavage, l’augmentation de la vitesse
de frottement 𝑢∗ emporte les particules les plus petites, laissant en
places les plus grosses. Le pavage devient instable et sera détruit
pour 𝑢∗ > 𝑢∗𝑎,𝑐𝑟 Arved Jaan Raudviki
Raudviki (1990) propose une relation empirique
pour la prédiction de la stabilité de la couche
de pavage de diamètre médian 𝑑50 𝑎
.

59. ■ La profondeur maximale des fonds
perturbés (ou susceptible d’être affouillée) au
voisinage des rétrécissements locaux est
donnée par Izard et Bradley (1958) :
■ Ce calcul est surtout important pour les
ouvrages (piles de pont) non fondés dans le
substratum rocheux
■ En présence de pavage, ce calcul n’a de
sens que pour les débits susceptibles de
rompre le pavage
06. GEOMETRIE D’EQUILIBRE
04.09.16
Profondeur des fonds perturbés
59
𝒇 𝒑 = 𝟎, 𝟕𝟑
𝒒 Τ𝟐 𝟑
𝒅 𝟏/𝟔
Principe d’affouillement d’une pile de pont
fp
Profondeur des fonds perturbés

60. ■ Soit un bief de rivière en aval d’un point de piégeage des sédiments
transportés (seuil, barrage par exemple). Le débit liquide reste inchangé.
Supposons que les berges ne sont pas mobilisables.
■ La saturation en débit solide n’est plus assurée : une érosion
régressive se déclenche en aval
■ Le lit du cours d’eau évoluera à long terme vers une nouvelle pente
d’équilibre 𝐼𝑒𝑞 ou de non-transport 𝐼 𝑁𝑇
■ Pour l’établir, on considère que pour le débit à plein bord, la contrainte
exercée sur le fond (équation de Manning-Strickler) coïncide avec la
contrainte critique de mise en mouvement (équation de Shields)
■ Le calcul est itératif
06. GEOMETRIE D’EQUILIBRE
04.09.16
Pente de non transport ou pente d’équilibre (1/2)
60

61. ■ L’équation de Shields (1936) donne, à l’équilibre :
■ À partir de l’équation de Manning-Strickler (1891), on peut aussi écrire :
■ Ce qui permet de déduire l’expression suivante, non implicite en 𝑦 que l’on
peut résoudre avec de manière itérative ou avec un solveur
■ Par suite, la valeur de 𝐼𝑒𝑞 sera calculée à partir de l’équation de Shields
(1936) ou de Manning-Strickler (1891)
06. GEOMETRIE D’EQUILIBRE
04.09.16
Pente de non transport ou pente d’équilibre (2/2)
61
𝑅ℎ(𝑦)
𝐼𝑒𝑞 = 𝑠𝑠 − 1 𝑑𝜏 𝑐𝑟
∗
𝑆(𝑦)
2
𝑅ℎ(𝑦)
Τ4 3
𝐼𝑒𝑞 =
𝑄2
𝐾𝑠
2 ⇒ 𝑆(𝑦)
2
𝑅ℎ(𝑦)
Τ1 3
(𝑅ℎ(𝑦)
𝐼𝑒𝑞) =
𝑄2
𝐾𝑠
2
𝑺(𝒚)
𝟐
𝑹 𝒉(𝒚)
Τ𝟏 𝟑
=
𝑸 𝟐
𝑺 𝒔 − 𝟏 𝑲 𝒔
𝟐
𝒅𝝉 𝒄𝒓
∗

62. 07. MESURE DU TRANSPORT SOLIDE
04.09.16
Mesure du charriage
62
■ Principe : mesurer les dépôts dans un secteur
qui naturellement piège les sédiments charriés
■ Mesure des volumes de dépôts effectués par
suivi bathymétrique
■ Possibilité d’utiliser les structures existantes
■ Barrages ou anciennes fosses d’extraction
■ Alternativement, construire des fosses à piégeage
dans le lit mineur.
■ Risque d’érosion progressive : à implanter
donc dans une zone sans enjeux particuliers
■ Volume équivalent à 1~2 ans d’apports
solides, prédéterminé par les équations de
transport solide
■ Après chaque mesure, effectuer des curages
Barrage envasé
Trappe à sédiment
en lit mineur de
cours d’eau

63. ■ Autres échantillonneurs :
■ Bedload Transport Meter Arnhem
(BTMA), développé aux Pays-Bas
■ Karolyi, développé en Hongrie
07. MESURE DU TRANSPORT SOLIDE
04.09.16
Equipements d’échantillonage
63
Karolyi
BTMA
■ Préleveur Helley-Smith :
■ Préleveur le plus connu et répandu
■ Modèles variant suivant la taille des
grains à échantillonner ainsi que la
vitesse de l’écoulement
Préleveur Helley-Smith
𝑞 𝑠𝑏 = 𝑘𝑠𝑠 1 − 𝑝
𝑉
𝑏𝑇

64. 07. MESURE DU TRANSPORT SOLIDE
04.09.16
Equipements d’échantillonage
64
 La bouteille de Delft sur chariot permet
la mesure de saltation et suspension à
différentes hauteurs d’eau entre 0,05 [m]
et 0,5 [m] au dessus du fond.
 Il est adapté aux cours d’eau dont les
alluvions sont composés de sables et
graviers fins.
 L’appareil est conçu de façon à ce que
l’écoulement – et le transport des
matériaux solides ne soient pas
perturbés : c’est une caractéristique
propre à cet équipement
Bouteille de Delft sur chariot

65. CONSEQUENCES MORPHOLOGIQUES DE
QUELQUES AMENAGEMENTS
Chapitre III

66. ■ Les aménagements portés sur le bassin versants sont susceptibles de modifier
les formes naturelles des cours d’eau
■ Dans la recherche de l’équilibre dynamique, le cours d’eau peut mobiliser :
■ le lit : érosion sur le profil en long
■ les berges : érosion latérale ou érosion des berges
■ Le lit d’un cours d’eau :
■ peut se creuser au fil du temps : érosion ou incision
■ Peut se surélever dans le temps : exhaussement
■ Ces modifications peuvent se propager :
■ vers l’amont : érosion ou exhaussement régressifs
■ Vers l’aval : érosion ou exhaussement progressifs
01. AMENAGEMENTS DE COURS D’EAU
04.09.16
Conséquences morphologiques
66

67. 02. PRELEVEMENT DE SEDIMENTS
04.09.16
Excavation dans un lit mineur pour exploitation de gisement alluvial
67
Conséquences de prélèvement dans un lit de
cours d’eau (Degoutte, 2012)
Situation : le lit d’un cours
d’eau est excavé localement
pour son gisement alluvial
Abaissement de la
ligne d’eau à l’amont
de l’excavation
Augmentation de la
pente et de la
tractrice efficace
(1) Erosion régressive
vers l’amont
(2) Piégeage des sédiments
dans l’excavation
(3) Erosion progressive
vers l’aval pour assurer la
saturation en débit solide
(1) Restauration de la
pente initiale si l’érosion
régressive rencontre un
point dur en amont (seuil
rocheux)
(3) Etablissement de la
pente de non transport en
aval

68. 03. CALIBRAGE DE LIT
04.09.16
Elargissement de lit sans modification des berges (1/2)
68
La ligne d’eau s’abaisse sur tout
le tronçon calibré, la tractrice
efficace diminue
(2) Mise en vitesse à l’entrée du
tronçon, ce qui déclenche une
érosion régressive vers l’amont
(3) Erosion progressive vers l’aval
pour assurer la saturation en
débit solide
(1) La capacité de transport
solide a diminué dans le bief, ce
qui occasionne des dépôts
Situation : le lit d’un
cours d’eau est élargi sur
une grande longueur sans
stabilisation des berges
Observations à court terme
Calibrage de lit (Degoutte, 2012)

69. 03. CALIBRAGE DE LIT
04.09.16
Elargissement de lit sans modification des berges (2/2)
69
Sur le long termeSur le long terme, le bief élargi modifie sa pente et
subséquemment, le tirant d’eau, de sorte à ajuster
sa capacité de transport solide à celui du bief
amont.
Du terme 𝑞 𝑠2
nous pouvons extraire la valeur
d’une contrainte tractrice 𝜏2
∗
qui permettra de
disposer d’une relation fonctionnelle entre les
connues 𝑦2 et 𝑖2
En outre, l’élargissement ne modifie pas le débit
liquide écoulé.
𝑞 𝑠1
𝑏1 = 𝑞 𝑠2
𝑏2 ⇒ 𝑞 𝑠2
=
𝑏1
𝑏2
𝑞 𝑠1
Le tirant d’eau 𝑦2 est alors donné par :
Et si une approximation de type 𝑅ℎ ≈ 𝑦 est possible :
La pente 𝑖2 sera alors déduite de l’équation de
Manning-Strickler (1981) ou de Shields (1936)
𝑅ℎ 𝑦2
𝑖2 = 𝑠𝑠 − 1 𝑑𝜏2
∗
𝑆(𝑦2) 𝑅ℎ(𝑦2)
Τ2 3
𝑖2 =
𝐾𝑠1
𝐾𝑠2
𝑆(𝑦1) 𝑅ℎ(𝑦1)
Τ2 3
𝑖1
𝑺(𝒚 𝟐)
𝟐
𝑹 𝒉 𝒚 𝟐
Τ𝟏 𝟑
=
𝑲 𝒔 𝟏
𝟐
𝑲 𝒔 𝟐
𝟐
𝑺(𝒚 𝟏)
𝟐
𝑹 𝒉(𝒚 𝟏)
Τ𝟒 𝟑
𝒊 𝟏
𝒔 𝒔 − 𝟏 𝒅𝝉 𝟐
∗
𝒚 𝟐 =
𝑲 𝒔
𝟐
𝟐
𝑲 𝒔
𝟐
𝟏
𝒔 𝒔 − 𝟏 𝒅𝝉 𝟐
∗
𝒚 𝟏
Τ𝟏𝟎 𝟑
𝒊 𝟏
−
𝟑
𝟕

70. 04. ABLATION DE RIPISYLVE
04.09.16
Enlèvement important de la végétation des berges
70
L’enlèvement de végétation
entraine une augmentation de 𝐾𝑠
et une diminution de 𝑦.
(2) L’augmentation de 𝐾𝑠 induite
entraine une augmentation de 𝛽
et donc la tractrice efficace à
l’entrée, ce qui occasionne une
érosion régressive vers l’amont
(3) A l’aval, on retrouve l’ancienne
tractrice efficace, plus faible, ce
qui occasionne donc un dépôt
(1) l’augmentation de tractrice
efficace induit une hausse de la
capacité de transport solide. La
rivière mobile donc le fond, qui se
creuse
Situation : La ripisylve est
enlevée de manière
importante sur les berges,
qui sont supposées stables
Enlèvement de végétation des berges (Degoutte, 2012)

71. 05. ENDIGUEMENTS
04.09.16
Enfoncement de lit à la suite d’un endiguement de lit
71
Pour des crues inférieures à
l’ancien débit à plein bords,
rien ne se produit
Situation : Les berges
d’un cours d’eau sont
inchangées et surélevées
par des digues latérales
Endiguements (Degoutte, 2012)
Pour des crues plus importantes
que l’ancien débit à plein bord, la
tractrice efficace augmente, ce
qui occasionne une érosion
régressive en amont et un dépôt
en aval
Le lit s’enfonce donc de
manière à assurer une pente
quasi-parallèle à l’ancienne.
Selon Ramette (1981), l’enfoncement vaut :
∆𝑯 =
𝑸
𝑸 𝒎
𝟐/𝟑
− 𝟏

72. 06. RETRECISSEMENT LOCALISE
04.09.16
Ouvrages rétrécissant localement la section du lit mineur
72
Situation : Un ouvrage de
largeur 𝐿0 est implanté
dans un cours d’eau de
largeur 𝐿1 > 𝐿0
𝐻0: profondeur initiale
𝐻1: profondeur après affouillement
𝐻2: profondeur au droit des culées
Dans la section rétrécie, la hauteur d’eau augmente, ainsi que
la contrainte tractrice, ce qui génère un affouillement local du
lit. Selon Ramette (1981), la profondeur 𝐻1 est donnée par :
Un affouillement localisé plus profond 𝐻2 se mettra en place
au droit d’une culée, que l’on peut approximer par la
profondeur des fonds perturbés :
Rétrécissement localisé
(Degoutte, 2012)
𝑯 𝟏 = 𝑯 𝟎
𝑳 𝟏
𝑳 𝟎
Τ𝟐 𝟑
𝑯 𝟐 ≈ 𝒇 𝒑 = 𝟎, 𝟕𝟑𝒒 Τ𝟐 𝟑 𝒅−𝟏/𝟔

73. 07. RETENUES D’EAU
04.09.16
Influence des barrages (1/2)
73
La retenue d’un barrage joue un rôle
décanteur : la charge solide est déposée
du fait du ralentissement de la vitesse,
suivant un tri granulométrique de l’entrée
de la retenue vers l’aval. Le comblement
progressif est irréversible
Influence d’un barrage sur la charge solide
(Degoutte, 2012)
À l’aval, le lâcher d’eau claire crée un défit
en charge solide. Pour assurer la
saturation, l’écoulement prélève dans le
matériau en place, ce qui déclenche une
érosion progressive pouvant déchausser le
pied de la digue

74. 07. RETENUES D’EAU
04.09.16
Influence des barrages (2/2)
74
Vörösmarty, Charles J, Michel Meybeck, Balázs Fekete, Keshav Sharma, Pamela Green,
and James PM Syvitski. 2003. “Anthropogenic Sediment Retention: Major Global Impact
from Registered River Impoundments.” Global and Planetary Change 39 (1): 169–90.
Efficience de piégeage de sédiments transportés à
l’échelle des grands bassins versants
(Vörösmarty et al., 2003)

75. 08. OUVRAGES OBLIQUES
04.09.16
Influence de l’implantation d’ouvrages obliques
75
L’implantation d’ouvrages obliques (épis, quais) peut avoir
divers types de conséquences
■ Tout ouvrage oblique vers l’aval provoque un rejet du
courant vers la berge, qui peut en aggraver les risques
d’affouillement et d’érosion
■ Tout ouvrage orienté vers l’amont favorisera le rejet du
courant vers l’axe de la rivière, avec un déplacement en
conséquent des risques d’affouillement si la tête fait
obstacle
Epis en rochers
Ouvrage orienté vers l’amontOuvrage orienté vers l’aval
Quai

76. DEVELOPPEMENTS
HYDRODYNAMIQUES
Chapitre IV

77. ■ Nous présenterons ici les développements
hydrodynamiques caractérisant l’écoulement à surface libre
sur un lit à fond mobile
■ Pour la simplification des expressions, nous supposerons
une section d’écoulement rectangulaire, de largeur au
radier 𝑏
■ Les équations régissant les écoulements à surface libre
sur fond fixe sont les équations de Saint-Venant (1871)
■ L’équation de continuité
■ L’équation de l’énergie
■ À ces relations s’ajoute l’équation d’Exner (1920) qui prend
en compte le caractère mobile du fond du lit
01. EQUATIONS HYDRODYNAMIQUES
04.09.16
Equations fondamentales de l’écoulement à surface libre sur fond mobile
77
Adhémar Jean Claude Barré de
Saint-Venant (1797-1886)
Felix Maria Exner von Ewarten
(1876-1930)

78. Volume entrant par la section (1) :
𝑄 𝑥 𝑑𝑡
02. EQUATIONS DE SAINT-VENANT
04.09.16
Principe de conservation de masse
78
Volume sortant par la section (2) :
𝑄 𝑥+𝑑𝑥 𝑑𝑡 = 𝑄 𝑥 𝑑𝑡 +
𝜕𝑄
𝜕𝑥
𝑑𝑥𝑑𝑡
Variation de volume liée à l’élévation de la
surface libre (3) :
∆𝑆𝑑𝑥 =
𝜕𝑆
𝜕𝑡
𝑑𝑡 𝑑𝑥
On obtient l’équation de continuité en posant (3) = (1) - (2) :
𝜕𝑆
𝜕𝑡
+
𝜕𝑄
𝜕𝑥
= 0 ⇒
𝜕𝑆
𝜕𝑡
+ 𝑈
𝜕𝑆
𝜕𝑥
+ 𝑆
𝜕𝑈
𝜕𝑥
= 0
Pour un canal rectangulaire, en posant 𝑆 = 𝑆(𝑦) = 𝑏𝑦 et en
simplifiant par 𝑏, on obtient :
𝝏𝒚
𝝏𝒕
+ 𝒚
𝝏𝑼
𝝏𝒙
+ 𝑼
𝝏𝒚
𝝏𝒙
= 𝟎

79. 02. EQUATIONS DE SAINT-VENANT
04.09.16
Principe de conservation de l’énergie
79
La pente d’énergie 𝑗 est liée à 𝐻 par :
𝑗 = −
𝑑𝐻
𝑑𝑥
⇒ 𝑑𝐻 = −𝑗𝑑𝑥 ⇒ 𝑑
𝑈2
2𝑔
+ 𝑧 + 𝑦 = −𝑗𝑑𝑥
Or :
𝑑𝑧 =
𝜕𝑧
𝜕𝑥
𝑑𝑥
𝑑𝑦 =
𝜕𝑦
𝜕𝑥
𝑑𝑥
Et :
𝑑
𝑈2
2𝑔
=
1
2𝑔
𝑑𝑈𝑡,𝑥
2
=
1
2𝑔
𝜕𝑈2
𝜕𝑡
𝑑𝑡 +
𝜕𝑈2
𝜕𝑥
𝑑𝑥
𝑑
𝑈2
2𝑔
=
𝑈
𝑔
𝜕𝑈
𝜕𝑡
𝑑𝑡 +
𝜕𝑈
𝜕𝑥
𝑑𝑥
En simplifiant par 𝑑𝑥, sachant que Τ𝑑𝑡 𝑑𝑥 = 𝑈, il
vient que :
La pente 𝑗 est alors donnée par une loi de frottement:
𝝏𝑼
𝝏𝒕
+ 𝑼
𝝏𝑼
𝝏𝒙
+ 𝒈
𝝏𝒚
𝝏𝒙
+ 𝒈
𝝏𝒛
𝝏𝒙
= −𝒈𝒋
𝒋 = 𝒇(𝒚, 𝑼, ƒ)

80. Pour exprimer la continuité de la
phase solide (à l’image de l’équation
de continuité pour la phase liquide),
Krishnappan (1981) propose :
𝜕𝑧
𝜕𝑡
+
1
1 − 𝑝
𝜕𝑞 𝑠
𝜕𝑥
= 0
où le débit solide 𝑞 𝑠 est une fonction
(à déterminer) du débit liquide et des
sédiments charriés :
𝑞 𝑠 = 𝑓(𝑦, 𝑈, 𝑠é𝑑𝑖𝑚𝑒𝑛𝑡𝑠)
03. EQUATIONS DE SAINT-VENANT-EXNER
04.09.16
Equations couplées de l’écoulement des phases liquide et solide
80
𝜕𝑦
𝜕𝑡
+ 𝑦
𝜕𝑈
𝜕𝑥
+ 𝑈
𝜕𝑦
𝜕𝑥
= 0
𝜕𝑈
𝜕𝑡
+ 𝑈
𝜕𝑈
𝜕𝑥
+ 𝑔
𝜕𝑦
𝜕𝑥
+ 𝑔
𝜕𝑧
𝜕𝑥
= −𝑔𝑗
𝑗 = 𝑓(𝑦, 𝑈, 𝑘)
𝜕𝑧
𝜕𝑡
+
1
1 − 𝑝
𝜕𝑞 𝑠
𝜕𝑥
= 0
𝑞 𝑠 = 𝑓(𝑦, 𝑈, 𝑠é𝑑𝑖𝑚𝑒𝑛𝑡𝑠)
Equations de Saint -
Venant, exprimant
l’écoulement de la phase
liquide sur fond mobile
Equations exprimant le
transport de la phase
solide
Equations de Saint-Venant-Exner
Bommanna
Krishnappan

81. 03. EQUATIONS DE SAINT-VENANT-EXNER
04.09.16
Effort de résolution (1/3)
81
■ Les équations de Saint-Venant-Exner sont implicitement couplées. En
pratique, pour les résoudre il faudrait :
■ chercher une solution pour la phase liquide
■ puis une solution pour la phase solide, afin d’obtenir la variation 𝑧(𝑥,𝑡)
■ Pour les coupler de manière explicite, Krishnappan (1981) propose d’exprimer
la continuité pour la phase liquide :
■ Dès lors, les équations de Saint-Venant-Exner peuvent être résolues
■ De manière analytique pour des cas simples
■ De manière numérique pour des cas plus complexes
𝜕𝑦
𝜕𝑡
+
𝜕𝑧
𝜕𝑡
+
𝜕𝑞
𝜕𝑥
= 0

82. 03. EQUATIONS DE SAINT-VENANT-EXNER
04.09.16
Effort de résolution (2/3)
82
■ Les équations de Saint-Venant-Exner sont non linéaires et hyperboliques
■ Trouver des solutions analytiques est très complexe
■ Mais des approximations peuvent être faites
■ Hypothèse : écoulement à faible nombre de Froude : 𝑭 𝒓 < 𝟎, 𝟔
■ Ecoulement quasi-stationnaire : Τ𝜕 𝜕𝑡 ≈ 0
■ Hypothèse valable car en pratique, 𝜕𝑞/𝜕𝑡 se produit sur un court terme
tandis que 𝜕𝑧/𝜕𝑡 se produit sur un long terme, lorsque 𝜕𝑞/𝜕𝑡 a déjà
disparu
■ Si l’on étudie donc 𝑧(𝑥, 𝑡) sur le long terme, alors 𝑞 = 𝐶 𝑡𝑒
et Τ𝜕 𝜕𝑡 ≈ 0
■ On écrira donc pour équations de continuité et d’énergie :
𝒚
𝝏𝑼
𝝏𝒙
+ 𝑼
𝝏𝒚
𝝏𝒙
= 𝟎 𝑼
𝝏𝑼
𝝏𝒙
+ 𝒈
𝝏𝒚
𝝏𝒙
+ 𝒈
𝝏𝒛
𝝏𝒙
= −𝒈𝒋

83. 03. EQUATIONS DE SAINT-VENANT-EXNER
04.09.16
Effort de résolution (3/3)
83
■ On peut coupler les équations de Saint-Venant en une seule équation en
multipliant l’équation de continuité par 𝑔/𝑈 et en l’éliminant avec l’équation
de l’énergie. Il vient alors que :
■ Associons à cette nouvelle équation celle de la continuité de la phase solide
(Krishnappan, 1981) en réécrivant toutefois le terme 𝜕𝑞 𝑠/𝜕𝑥
■ Ces équations étant non linéaires, seules des solutions numériques sont
envisageables.
𝜕𝑧
𝜕𝑡
+
1
1 − 𝑝
𝜕𝑞 𝑠
𝜕𝑥
= 0 ⇒
𝝏𝑼
𝝏𝒙
𝑼 − 𝒈
𝒚
𝑼
+ 𝒈
𝝏𝒛
𝝏𝒙
= −𝒈𝒋
(𝟏 − 𝒑)
𝝏𝒛
𝝏𝒕
+
𝝏𝒒 𝒔
𝝏𝑼
𝝏𝑼
𝝏𝒙
= 𝟎

84. 03. EQUATIONS DE SAINT-VENANT-EXNER
04.09.16
Modèle parabolique (1/4)
84
Selon Vreugdenhil et de Vries (1973), la quasi-
stationnarité implique une quasi-uniformité
de l’écoulement, donc Τ𝜕𝑈 𝜕𝑥 ≈ 0. Il vient
alors que, pour l ’équation de l’énergie, en
supposant une loi de frottement de Chézy :
𝜕𝑧
𝜕𝑥
= −𝑗 = −
𝑈2
𝐶2ℎ
= −
𝑈3
𝐶2 𝑞
⇒
𝜕2
𝑧
𝜕𝑥2
= −
3𝑈2
𝐶2 𝑞
𝜕𝑈
𝜕𝑥
D’où :
Dans l’équation de Krishnappan (1981), nous
pouvons réintroduire la nouvelle écriture du
terme 𝜕𝑈/𝜕𝑥. Il vient donc :
En définissant donc un coefficient de
diffusion 𝐾(𝑡):
Nous déduisons donc le modèle parabolique:
𝜕𝑧
𝜕𝑡
−
1
3
𝜕𝑞 𝑠
𝜕𝑈
1
1 − 𝑝
𝐶2
ℎ
𝑈
𝜕2
𝑧
𝜕𝑥2
= 0
𝐾(𝑡) =
1
3
𝜕𝑞 𝑠
𝜕𝑈
1
1 − 𝑝
𝐶2
ℎ
𝑈
𝝏𝒛
𝝏𝒕
− 𝑲
𝝏 𝟐 𝒛
𝝏𝒙 𝟐
= 𝟎
𝝏𝑼
𝝏𝒙
= −
𝟏
𝟑
𝑪 𝟐 𝒉
𝑼
𝝏 𝟐 𝒛
𝝏𝒙 𝟐
M. J. de Vries
C. B. Vreugdenhil

85. 03. EQUATIONS DE SAINT-VENANT-EXNER
04.09.16
Modèle parabolique (2/4)
85
■ Le modèle parabolique reste valable pour les cas applicatifs suivants :
■ Ecoulement à faible nombre de Froude : 𝑭 𝒓 < 𝟎, 𝟔
■ Calcul sur le long terme : 𝑥, 𝑡 assez grands et 𝑥 > 3𝑦/𝑗 (de Vries,
1973)
■ En outre, de Vries (1973) propose que la constante 𝐾 soit linéarisée en :
𝑲 =
𝟏
𝟑
𝒒 𝒔 𝒃 𝒔
𝟏
𝟏 − 𝒑
𝟏
𝒋 𝟎
𝝏𝒛
𝝏𝒕
− 𝑲
𝝏 𝟐 𝒛
𝝏𝒙 𝟐
= 𝟎
𝒃 𝒔 = 𝟐𝜷 = 𝟐 𝟐, 𝟓𝟐 ≈ 𝟓
cf. formule de Graf et Acaroglu (1968)
William Henry Froude
(1810-1879)

86. 03. EQUATIONS DE SAINT-VENANT-EXNER
04.09.16
Modèle parabolique (3/4)
86
■ Posons des conditions aux limites et initiales pour le modèle parabolique
■ Vreugdenhil et de Vries (1973), en utilisant les transformées de Laplace,
définissent alors une solution analytique au modèle parabolique :
■ Où erfc fait référence à la fonction complémentaire d’erreur, définie par :
𝒛 𝒙, 𝒕 = ∆𝒉 𝐞𝐫𝐟𝐜
𝑿
𝟐 𝑲𝒕
𝑧 ∀𝑥, 𝑡 = 0 = 0 𝑧 𝑥 = 0, 𝑡 → ∞ = ∆ℎ 𝑧 𝑥 → ∞, 𝑡 = 0
𝐞𝐫𝐟𝐜 𝒀 =
𝟐
𝝅
න
𝒀
∞
𝒆−𝝃 𝟐
𝒅𝝃
𝜕𝑧
𝜕𝑡
− 𝐾
𝜕2
𝑧
𝜕𝑥2
= 0

87. 03. EQUATIONS DE SAINT-VENANT-EXNER
04.09.16
Modèle parabolique (4/4)
87
Les valeurs de la fonction complémentaire
d’erreur :
■ sont disponibles dans les tables
mathématiques
■ Fournies par Microsoft Excel, en standard,
via la fonction ERFC
■ Implémentées en librairies/packages
standards pour divers langages et/ou
environnements de programmation
Abramowitz and Stegun (1964) proposent une
approximation polynomiale :
Table de la fonction complémentaire d’erreur
- tiré de Graf et Altinakar (2000)
𝐞𝐫𝐟𝐜(𝒀) ≈ 𝟏 + ෍
𝒊=𝟏
𝟔
𝒂𝒊 𝒀𝒊
−𝟏𝟔
+ 𝝐(𝒀)
Où 𝝐 𝒀 ≤ 𝟑. 𝟏𝟎−𝟕
a1 = 0,0705230784
a2 = 0,0422820123
a3 = 0,0092705272
a4 = 0,0001520143
a5 = 0,0002765672
a6 = 0,0000430638
Milton Abramowitz
(1912-1958)
Irene Ann Stegun
(1912-2008)

88. 04. CALCUL D’EVOLUTION DE LIT
04.09.16
Cas simples d’application du modèle parabolique
88
Schémas de dégradation ou d’aggradation
(Graf et Altinakar, 2000)
Le modèle parabolique reste pratique
pour décrire l’évolution du fond de lit
pour des simples de dégradation ou
d’aggradation
■ Cas de dégradation :
■ Débit solide interrompu en
amont
■ Augmentation de débit liquide
■ Baisse d’un point fixe en aval
■ Cas d’aggradation :
■ Augmentation de débit solide en
amont
■ Diminution de débit liquide
■ Montée d’un point fixe en aval

89. 04. CALCUL D’EVOLUTION DE LIT
04.09.16
Application du modèle parabolique à un canal en dégradation
89
■ Soit un canal à fond mobile, véhiculant un débit unitaire 𝑞 uniforme et constant à
hauteur d’eau 𝑦0
■ À l’entrée dans un réservoir en aval, la hauteur d’eau imposée est telle que le tirant
d’eau s’abaisse de ∆ℎ, générant une érosion régressive vers l’amont.
■ Au temps 𝑡 = ∞, on observera un abaissement de fond partout dans le canal et
𝑦∞
≡ 𝑦0
Dégradation par abaissement de fond
(Graf et Altinakar, 2000)
Conditions initiales et aux
limites :
𝑧 ∀𝑥, 𝑡 = 0 = 0
𝑧 𝑥 = 0, 𝑡 → ∞ = ∆ℎ
𝑧 𝑥 → ∞, 𝑡 = 0
La solution de du modèle parabolique
de Vreugdenhil et de Vries (1973)
est donc applicable !

90. 04. CALCUL D’EVOLUTION DE LIT
04.09.16
Application du modèle parabolique à un canal en aggradation
90
■ Soit un canal à fond mobile, en équilibre, véhiculant un débit unitaire 𝑞 uniforme et
constant à hauteur d’eau 𝑦0
■ À une section particulière, il y a surcharge en débit solide (apport localisé). Une
aggradation du fond de lit commence et la côte du fond augmente de ∆ℎ ainsi que
celle de la surface libre
Aggradation par surcharge en débit solide
(Graf et Altinakar, 2000)
Conditions initiales et aux
limites :
𝑧 ∀𝑥, 𝑡 = 0 = 0
𝑧 𝑥 = 0, 𝑡 → ∞ = ∆ℎ(𝑡)
𝑧 𝑥 → ∞, 𝑡 = 0
La solution de du modèle parabolique
de Vreugdenhil et de Vries (1973)
est donc applicable !

91. 04. CALCUL D’EVOLUTION DE LIT
04.09.16
Quelques problèmes typiques (1/2)
91
■ Problème : Après combien de temps, à une position 𝒙∆𝒑, la côte de fond aura-
t-elle baissé de ∆𝒑 ?
■ On pose alors que 𝑧 𝑥, 𝑡 = ∆𝑝. Il vient alors que :
■ Problème : Quelle est l’allure du fond du canal après une durée ∆𝒕 ?
■ On définit en premier lieu la profondeur affouillée ∆ℎ(𝑡) = 𝑧 0, 𝑡 = ∆𝑡 donnée
par Soni et al. (1980)
■ On calcule alors à diverses abscisses 𝑥𝑖 sur la longueur souhaitée les
profondeurs 𝑧(𝑥𝑖, 𝑡 = ∆𝑡) par la solution au modèle parabolique
∆𝑝
∆ℎ
= erfc
𝑥∆𝑝
2 𝐾𝑡∆𝑝
⇒
∆𝒉(𝒕) =
𝒒 𝒔∆𝒕
𝟏, 𝟏𝟑 𝟏 − 𝒑 𝑲𝒕
= ∆𝒉
𝒕∆𝒑 =
𝒙∆𝒑
𝟐𝑲 𝒆𝒓𝒇𝒄−𝟏 ∆𝒑
∆𝒉
𝟐

92. 04. CALCUL D’EVOLUTION DE LIT
04.09.16
Quelques problèmes typiques (2/2)
92
■ Problème : Quelle est la longueur 𝑳 𝒂 d’aggradation après un temps ∆𝒕?
■ On pose alors qu’il s’agit de la longueur à partir de laquelle le ratio 𝑧/∆ℎ
devient très faible. Il vient alors que :
■ En définitive, il l’emploi du modèle parabolique pour les calcul de dégradation et
d’aggradation ne convient que lorsque :
■ L’écoulement est quasi-stationnaire (variation du fond sur le long terme)
■ L’écoulement est quasi-uniforme et fluvial: 𝑭 𝒓 < 𝟎, 𝟔
■ Le calcul est effectué sur de grandes longueurs : 𝒙 > 𝟑𝒚/𝒋
■ Dans le cas où ces conditions ne sont pas remplies, il convient de faire la
résolution des équations de Saint-Venant et Exner de façon numérique.
𝑧
∆ℎ
≈ 0,01 ⇒ 𝒙 = 𝟐 𝑲∆𝒕 ≅ 𝟑, 𝟔𝟓 𝑲∆𝒕

93. 05. MODELES HYDROSEDIMENTAIRES
04.09.16 93
Quelques modèles numériques de simulation du transport hydrosédimentaire