Cours hydraulique 2_annee_6

Hydraulique

INTRODUCTION.....................................................................5
GÉNÉRALITÉS ET PROPRIÉTÉS DES FLUIDES ......................................... 5
HISTORIQUE .............................................................................. 5
SYSTÈME D'UNITÉ ........................................................................ 6
PROPRIÉTÉ DES FLUIDES ............................................................... 6
Définition : solides - fluides........................................................................................................6
Masse volumique, poids volumique et densité ...........................................................................6
Pression......................................................................................................................................7
Compressibilité ...........................................................................................................................7
Viscosité .....................................................................................................................................8
Tension superficielle : capillarité.................................................................................................9
La pression de vapeur saturante ................................................................................................9

HYDROSTATIQUE ................................................................10
Définition...................................................................................................................................10
Pression en un point.................................................................................................................10
Equilibre d'un prisme ................................................................................................................10
Equation fondamentale de l'hydrostatique................................................................................11
Utilisation ..................................................................................................................................11
Différence de pression entre 2 points.......................................................................................12
Pression absolue ou relative ....................................................................................................12
Changement de référentiel de pression ...................................................................................13
Application ................................................................................................................................13
Tube en U.................................................................................................................................14
Différence de pression entre 2 réservoir ..................................................................................14
Changement de référentielle ....................................................................................................15

FORCE DE PRESSION .................................................................. 15
Poussée sur une surface plane ................................................................................................15
Crève tonneau de Pascal .........................................................................................................19
Ecole d’ingénieurs du Canton de Vaud
Environnement construit et Géoinformation

Page 1

WILDBOLZ Antoine, FORRE Fabien
06.01.2004

Hydraulique

Vérin hydraulique......................................................................................................................19
Poussée sur une surface gauche (non plane)..........................................................................20

FORCE D'ARCHIMÈDE .................................................................. 22
Principe d'un corps immergé de forme cylindrique...................................................................22
Application ................................................................................................................................23
Un iceberg flottant dans l'océan ...............................................................................................23
Equilibre des corps immergés ..................................................................................................24
Equilibre des corps flottants .....................................................................................................24

EQUATION DE BERNOUILLI ........................................................... 25
Rappel des hypothèses fondamentales ...................................................................................25
Application de l'équation de bernouilli ......................................................................................26
Généralisation de l'équation de Bernouilli avec machine hydraulique......................................28

THÉORÈME DES QUANTITÉS DE MOUVEMENT ...................................... 29
Cas de l'hydraulique .................................................................................................................29
Effort exercé par un coude de canalisation (coude horizontal d'où Poids = 0).........................30
Force d'un jet sur un aubage mobile ........................................................................................30
Cas d'embouchement...............................................................................................................31

EQUATION FLUIDE PARFAIT GÉNÉRALISÉ ........................................... 32
Equation de conservation d'énergie (intégrée par une ligne de courant) .................................32
Equation de quantité de mouvement........................................................................................32

HYDRODYNAMIQUE DES FLUIDES RÉELS .............................32
GÉNÉRALITÉ SUR LA VISCOSITÉ ..................................................... 32
Expérience de couette (viscosité dynamique et cinématique)..................................................32
Fluide Newtoniens en non-Newtoniens ....................................................................................33
Variation de la viscosité............................................................................................................33

EQUATION DE NAVIER-STOKES ...................................................... 34


Page 2

06.01.2004

Hydraulique

LES DIFFÉRENTS RÉGIMES D'ÉCOULEMENT......................................... 34
Expérience de Reynolds...........................................................................................................34
Le nombre de Reynolds ...........................................................................................................34

ECOULEMENT LAMINAIRE ............................................................. 35
ECOULEMENT TURBULENT ........................................................... 35
Généralité .................................................................................................................................35
Equations de Reynolds.............................................................................................................35

HYDRAULIQUE DES CONDUITES (ÉCOULEMENT EN CHARGE) .35
Généralité .................................................................................................................................35
Equation de conservation d'énergie .........................................................................................35
Formule de pente de charges linéaires (de Chézy)..................................................................36

EQUATION DE DARCY-WEISSBACH (HR) ............................................ 37
En écoulement laminaire ..........................................................................................................37
En écoulement turbulent lisse .................................................................................................37
En écoulement turbulent rugueux.............................................................................................37
Régime turbulent de transition..................................................................................................37
Diagramme de Moody ..............................................................................................................37
Formule de Strickler .................................................................................................................38
Rayon hydraulique....................................................................................................................38
Perte de charges singulières ....................................................................................................38

CALCUL DE RÉSEAUX (PRINCIPE ET TECHNIQUE).................................. 39
Conduite entre 2 réservoirs ......................................................................................................39
Conduite crachant " à gueule bée " ..........................................................................................39
Conduite en série .....................................................................................................................40

TECHNIQUE DE RÉSOLUTION PAR RÉITÉRATION ................................... 40
Recherche de hR.......................................................................................................................40
Recherche de Q .......................................................................................................................40
Recherche de D........................................................................................................................41

Page 3

06.01.2004

Hydraulique

CALCUL DE RÉSEAUX MAILLÉ ........................................................ 41
Conduite en parallèle................................................................................................................41
Les deux lois fondamentales de Kirchhoff................................................................................41
Calcul d'une maille ...................................................................................................................42
Cas de plusieurs mailles...........................................................................................................43

HYDRAULIQUE DES CANAUX (ÉC. EN NAPPE LIBRE) ..............43
GÉNÉRALITÉ ............................................................................ 43
Définitions.................................................................................................................................43
But de l’étude............................................................................................................................43
Classification des fluides ..........................................................................................................43

EQUATIONS FONDAMENTALES (TJS LES MÊMES, MAIS ADAPTÉES)............. 44
Equation de continuité ..............................................................................................................44
Equation de conservation d’énergie .........................................................................................44
Equation de quantité de mouvement (tjs valable) ....................................................................45
Nombre de Froude : FR............................................................................................................45

ECOULEMENT UNIFORME.............................................................. 46
Lois des pertes de charges : ....................................................................................................46
Profondeur normale..................................................................................................................47
Différents problèmes rencontrés ..............................................................................................48

ECOULEMENT GRADUELLEMENT VARIÉ .............................................. 49
Définition...................................................................................................................................49
Courbe d’égal débit « étude de la fonction Hs ».......................................................................49
Valeur de tCR en canal rectiligne ...............................................................................................50

COURBES DE REMOUS ................................................................ 51
Équations fondamentales .........................................................................................................51
Equations différentielles dans un canal prismatique ................................................................51
Etude qualitative et classification des lignes d’eau...................................................................52
Illustrations en rivière................................................................................................................52
Illustrations en torrent ...............................................................................................................53

Page 4

06.01.2004

Hydraulique

Introduction
Hydraulique

Mécanique des fluides

Mécanique

Physique

Hydrostatique
Cinématique
Dynamique

Fluide parfait (viscosité nulle)

Ecoulement en charge
Ecoulement en nappe libre

Fluide réel (écoulement permanent = indép. du temps)

Généralités et propriétés des fluides
Bibliographie :

Hydraulique générale et appliquée

(Carlier, éd. Eyrolles)

Manuel d’hydraulique générale

(Lencastre, éd. Eyrolle)

Mécanique des fluides et hydraulique

(R.V Gile)

Fluid mechanics

(V. Streeter anglais)

Traité de génie civil

(Gref et Altinater)

Historique
Haute antiquité dès 4’000 ans avant J.C en Mésopotamie en Egypte avec un barrage sur le nil. Le puits de
Joseph au Caire de 90m de profondeur.
Civilisation grecque :

Ecole d’Alexandrie

Archimède :

287 – 212 avant J.C

Ctésibios :

Pompe aspirante – refoulante
Hydraule (orgue)

Moyen âge :

Rien

Renaissance :

1452 – 1519 Léonard de Vinci : Equation de continuité

Siècle des lumières :


Vis d’Archimède
Le principe d’Archimède
Théorie des corps flottants

Stevin (Hollande)
Paradoxe de l’hydrostatique
Louis 14
Torricelli
Pascal (traité des liqueurs)
Newton (liquide Newtoniens viscosité)
Page 5

06.01.2004

Hydraulique
18ème siècles :

Théorie :

Bernoulli :
Euler :

Hydraulique appliquée :

Equation de conservation de l’énergie
Equation de quantité de mouvement
Chézy (perte de charge)

19ème siècles :

machine hydro :
essai sur modèle :

Temps moderne :

école de Götting, Prandtl
essai sur modèle

Francis (turbine)
Froude, Reynolds

Système d'unité
Cours de M. Métroz + brochure UBS
Système légal : Système I international S.I.
Unité encore tolérée :
(pas dans le SI)

-

litre = 1 dcm3
Km/h
Car heure au lieu de secondes
KW h
bar (pression)
grade
mm de mercure (Hg)

Propriété des fluides
Définition : solides - fluides
Un fluide : milieu matériel continu déformable (sans rigidité)
Liquide : occupe un volume déterminé, peu modifiable par la température et la pression
séparation par "la surface libre" d'avec le gaz qui le surmonte
Gaz

: occupe tout l'espace à disposition, pas forcément uniforme, et le volume est
fortement modifiable par la température et la pression

Masse volumique, poids volumique et densité

La masse volumique est la masse d'un corps par unité de volume et noté
S.I. : masse
Volume

kg
m3

Poids volumique : poids par unité de volume
S.I. : Poids
Volume


ρ [rhô]

γ [gamma]

N
m3

Page 6

06.01.2004

Hydraulique
Relation :

Poids = Masse X Accélération

Champs terrestre :

Poids = Masse X g
Poids = Masse X g
Volume
Volume

Par unité de volume :

ce qui donne :

γ = ρ x g

Densité : rapport entre le poids d'un corps et le poids d'un corps de référence ayant le même volume

- eau (4°) :

ρ = 1000 kg/m3
γ = 9807 N/ m3

- air (20°):

Quelques valeurs:

ρ=

1.20 kg/m3

ρ diminue avec la température (portance des avions pays chaud)
- mercure (0°) :
- mercure (20°) :

ρ=
ρ=

13595 kg/m3
13546 kg/m3

Pression
L'ensemble des phénomènes liés aux forces de contacts transmises d'un élément à un élément
Pression :

p = force de surface
Surface

[Pa]

Contrainte :

p = force
Surface

résistance des matériaux

Unité tolérée : le bar

[N]
[m2]

1 bar = 105 Pa

Compressibilité
C'est la possibilité de se déformer, en présence de forces extérieures
∆ pression
∆ volume
volume init.

Module de compressibilité :

E

=

Quelques valeurs :

- eau (15°) :
- air (15°) :

E à une unité de pression
(Pa, N/m2)

E = 2.16 * 109 N/m2
E = 1.13 * 105 N/m2
E = 1.58 * 105 N/m2

(isotherme)
(adiabatique)

sans échange de chaleur

Page 7

06.01.2004

Hydraulique

Vitesse de propagation d'une onde de pression
c=

E (isotherme)
ρ

ceau = 1470 m/s
cair = 300 m/s

Viscosité

Existence d'efforts tangentiels dans un fluide
Viscosité dynamique :

F = ∂v ⋅ ∂s ⋅ µ
∂x
µ : coefficient de viscosité dynamique [Pa*s]
si µ = 0 fluide parfait
si µ = cste fluide newtonien (ex: l'eau)

µ
ρ

Viscosité cinématique :

υ=

Quelques valeurs:

- eau (15°) :

µ = 1.14*10-3 Pa*s
ν = 1.14*10-6 m2/s

- air (15°):

µ=
ν=

µeau
νeau


>
<

ν [nû] = m2/s

1.78*10-5 Pa*s
1.55*10-5 m2/s

µair
νair

Page 8

06.01.2004

Hydraulique
Tension superficielle : capillarité
A la surface d'un liquide, pas d'équilibre de la particule (dissymétrie des fores)

σ=

travail = force ⋅ déplacement [j]
surface
surface [m2]

σ [sigma] = travail nécessaire pour rester à la surface

Utilisation capillarité :

h = 2 ⋅σ cos θ
ρ ⋅g⋅r

Loi de Jurin :

h=k
r

Quelques valeurs:

- mercure :

- eau :

k = cste en fonction du liquide
r = diamètre du tube

σ=
θ=
σ=
θ=

0.514 N/m
140°

k ≅ -14 mm2

0.0736 N/m
0°

k ≅ 30 mm2

La pression de vapeur saturante
Si la pression augmente, la température d'ébullition augmente. (stérilisation)
Si la pression diminue, la transformation du liquide se fait à une chaleur inférieure.
(ébullition à température ambiante)
Cavitation :

Si la vitesse augmente cela diminue la pression et on a une ébullition à une température
ambiante.
Lorsque que la vitesse diminue la pression ré augmente et il y a une implosion des bulles de
vapeur, ce qui provoque une usure.


Page 9

06.01.2004

Hydraulique

Hydrostatique
Définition
Science qui étudie les conditions des fluides au repos :

- pression
- force de pression
- principe d'Archimède

Pression en un point
Les différentes forces agissantes sur un élément :
Forces intérieur : elles forment un système équivalent à zéro (aucune action)
Forces extérieurs : - pour qu'elle soit significative, il faut que les éléments soient très proche
l'un de l'autre (force de surface)
- Force de volume, lié au champ :

-pesanteur
- magnétique
- électromagnétique

Equilibre d'un prisme
Relation géométrique

Dx = dl * cosα
Dz = dl * sinα

Poids : P = ½ * (dx * dy * dz) * g * ρ

Condition d'équilibre :

∑F

=0

Projection sur l'axe X .
0 + dF2 – dF3 * sinα + 0 = 0
p2 *(dz * dy) – p3 *sinα *(dz/sinα) = 0
p2 = p 3
Projection sur l'axe Y :
DF1 + 0 – dF3 * cosα - P = 0
p1 *(dx * dy) – p3 *cosα *(dx/cosα) –(½ * (dx * dy * dz) * g * ρ) = 0
p1 = p 3
Infiniment petit donc négligé

Conclusion : elles sont donc (dFi) toutes perpendiculaires à la surface, sinon la composante tangentielle
entraînerait un glissement des particules. (donc mouvement d'où pas d'hydrostatique)
les coefficients p (pression) sont les mêmes dans toutes les directions
Forces de pression :


dF = p * ds

Page 10

06.01.2004

Hydraulique
Equation fondamentale de l'hydrostatique
Equilibre d'un cylindre à axe vertical :
équilibre des forces et projection sur l'axe Oz
dF2 = p ⋅ ds
dF1 = (p +

∂p
⋅ dz) ⋅ ds
∂z

dF2 – dF1 – P = 0
( p ⋅ ds ) – ( (p +

(

P = g ⋅ ρ ⋅ dz ⋅ ds

∂p
⋅ dz) ⋅ ds ) – ( z ⋅ ρ ⋅ dz ⋅ ds ) = 0
∂z

∂p
⋅ dz) - (z ⋅ρ ) = 0
∂z

Forme différentielle

∂p
)- ρ ⋅x =0
∂z
∂p
( )-ρ ⋅y =0
∂z
∂p
( )- ρ ⋅z =0
∂z
(

Donc pression en point

p 2 - p1 =

ρ ⋅ g (z1 - z2)

Utilisation
Plan de charge = indication de la pression

H=

p

ρ ⋅g

H


Page 11

06.01.2004

Hydraulique
Différence de pression entre 2 points
pA + ρ ⋅ g ⋅ zA = pB + ρ ⋅ g ⋅ zB
pB - pA = ρ ⋅ g ⋅ (zA - zB)
d'où pB > pA

Principe de Pascal
pB - p A =

ρ ⋅ g (zA - zB)

On modifie la pression en A de ∆ pA sans modifier l'équilibre du système donc la pression en B est modifiée
de ∆ pB
(pB + ∆ pB ) – (pA + ∆ pA )=

ρ ⋅ g (zA - zB)

∆ pB = ∆ pA

Dans un fluide incompressible au repos les va rations de pression se transmette intégralement en tout
point de la masse du fluide.

Pression absolue ou relative
Expérience de Torricelli
zA +

p

ρ

A
Hg

= zB +

p

ρ

pA = pATM

pATM =

ρ

B
Hg

pB = vide = 0

Hg

⋅ g (zB - zA)
A Yverdon : zB - zA = 0.72 m de Hg
donc pATM = 0.72*9.81*13'600 = 96'000 Pa

ρ

Hg

= 13'600 Kg/m3

Au niveau de la mer, latitude moyenne (45°) avec
du mercure à 0° : zB - zA = 0.76 m de Hg
donc pATM = 0.76*9.806*13'595 = 101'324 Pa
= 1.013 bar
101'324 Pa =

ρ eau ⋅ g ⋅


∆z

∆z = 10.33 m. correspond à la hauteur du tube remplis d'eau.

Page 12

06.01.2004

Hydraulique
Changement de référentiel de pression
pression absolue : pression avec le vide comme référence

vide = 0

pression relative : pression avec pATM comme référence

pATM = 0

Application
Liquides superposé (non miscible : pas mélangeable)

ρ1

<

ρ2

<

ρ3

ρ1
ρ
ρ

en pression relative : pATM = 0

2

3

ρ 1 ⋅ g ( zA - zB)
pB +

ρ

2

⋅ g ( zB - zC)

p B + pC +

ρ

3

⋅ g ( zC - zD)

Pression au point D :
avec pA = 0

pB - p A =
pC - p B =
pD - p C =

pD =

ρ 1 ⋅ g (zA - zB)
ρ 2 ⋅ g (zB - zC)
ρ 3 ⋅ g (zC - zD)

ρ 1 ⋅ g (zA - zB) + ρ


ρ 1 ⋅ g (zA - zB)
pC = pB + ρ 2 ⋅ g (zB - zC)
pD = pB + pC + ρ 3 ⋅ g (zC - zD)
pB =

2

⋅ g (zB - zC) + ρ

3

⋅ g (zC - zD)

Page 13

06.01.2004

Hydraulique
Tube en U

Egalité de pression : 1 pB = pA
(on peut passer de A à B sans changer de pression)

pA = pATM +

ρ 1⋅g⋅

pB = pATM +

ρ 2 ⋅ g ⋅ zB

1

ρ 1⋅g⋅
ρ 1⋅

zA =

zA =

zA

ρ 2 ⋅ g ⋅ zB
ρ 2 ⋅ zB

Différence de pression entre 2 réservoir

px - p y = ?
1 p 4 = p5
2 p 4 = px +
3 p 5 = py +

1 px +

ρ x ⋅g⋅
ρ y ⋅g⋅

ρ x ⋅g⋅

px - p y = +

pour des gaz,

Lx
Ly +

Lx = p y +

ρ y ⋅g⋅

Ly

ρ

ρ

x

et

ρ ⋅ g ⋅ ∆h

ρ y ⋅ g ⋅ Ly + ρ ⋅ g ⋅ ∆ h
ρ x ⋅ g ⋅ L + ρ ⋅ g ⋅ ∆h
x

x

sont petit face à

px - p y =


ρ

mercure

ρ ⋅ g ⋅ ∆h

Page 14

06.01.2004

Hydraulique
Changement de référentielle
- surface de référence : la surface libre du liquide
- pression de référence : pATM = 0
- axe vertical 'h' : positif vers le bas

Relation fondamentale
p + ρ ⋅ g ⋅ z = cste , mais avec z = - h
p - ρ ⋅ g ⋅ h = cste

Entre A et B
pA - ρ ⋅ g ⋅ hA = pB - ρ ⋅ g ⋅ hB
pA - pB = ρ ⋅ g ⋅ (hA – hB)

Entre A et C
pA - ρ ⋅ g ⋅ hA = pC - ρ ⋅ g ⋅ hC

hc = 0
pC = pATM = 0

pA = ρ ⋅ g ⋅ hA

p = ρ ⋅g⋅ h

h=

p

ρ ⋅g

Force de pression
Poussée sur une surface plane
Paroi plane horizontale
dF = p ⋅ ds = ( ρ ⋅ g ⋅ h) ⋅ ds

∫ dF = F
∫ ( ρ ⋅g⋅

h) ⋅ ds =

ρ ⋅ g ⋅ h ∫ ds = ρ ⋅ g ⋅ h ⋅ S

D'où
F=


ρ ⋅g⋅ h ⋅ S

Page 15

06.01.2004

Hydraulique
Paroi plane verticale, de profondeur B = cste

F=

=

∫ dF = ∫ ( ρ ⋅ g ⋅
ρ ⋅g⋅ B

h2

∫

h) ⋅ ds

ds = (B ⋅ dh)

h ⋅ dh

h1

=

=

ρ ⋅ g ⋅ B ⋅ 1 h2
2

h2
h1

ρ ⋅ g ⋅ ( h1+h2 ) ⋅ B ⋅ (h2 - h1)
2
pression moyenne

surface

F = pmoyenne ⋅ S

Paroi plane inclinée

a) intensité de la force
F=
=

∫ dF = ∫ ( ρ ⋅ g ⋅

h) ⋅ ds =

∫ ρ ⋅ g ⋅ L ⋅ sinα ⋅ ds

ρ ⋅ g ⋅ sinα ∫ L ⋅ ds
définit la position du centre de gravité

=

ρ ⋅ g ⋅ sinα ⋅ LG ⋅ S = ρ ⋅ g ⋅ hG ⋅ S = pG ⋅ S
F = pG ⋅ S


pression au centre de gravité de la surface S

Page 16

06.01.2004

Hydraulique
b) direction de la force
- toutes les dF sont perpendiculaire au plan de la surface
- donc elles sont parallèles entre elles
- et donc F est perpendiculaire au plan de la surface

c) point d'application de la force (F) : centre de poussée "c"

∫ dM

= F ⋅ LC

calcul de

d'où

∫ dM

=

∫ dF ⋅

L=
=

Donc

LC =

LC =

∫ ρ ⋅g⋅

∫dM
F

L2 ⋅ sinα ⋅ ds

ρ ⋅ g ⋅ sinα ⋅ ∫ L2 ⋅ ds

ρ ⋅ g ⋅ sinα ⋅ ∫ L2 ⋅ ds

=

ρ ⋅ g ⋅ sinα ∫ L ⋅ ds

IOO'

IOO'
S ⋅ LG

= inertie de la surface par rapport à l'axe OO'

IOO'

=

IGG

+ S ⋅ L2G

LC =

On montre que :

IOO' = IGG + LG
S ⋅ LG S ⋅ LG

LC - L G =

LC = L G +

inertie par rapport à un axe passant par G et // à OO'

IGG
S ⋅ LG

IGG
S ⋅ LG

LC - L G ≥ 0

La figure à un axe de symétrie // à l'axe 'L' et 'C' est sur une // à l'axe 'L' passant par 'G'


Page 17

06.01.2004

Hydraulique

Paroi rectangulaire : hauteur h, largeur B

ρ ⋅ g ⋅ h ⋅ (B ⋅ h)
2
1 ρ ⋅ g ⋅ B ⋅ h2
=
2

Force :

F = pG ⋅ S =

Position :

LC - L G =

IGG
S ⋅ LG

B ⋅ h3
12
=
(B ⋅ h) ⋅ h
2
= h

6

d'où C – A = h - h - h =

2

6

h
3

Vanne circulaire : Rayon R, centre O à la hauteur h de la surface, point O = G

Force : F = pG ⋅ S =

ρ ⋅ g ⋅ h ⋅ π ⋅ R2

Position : LC - LG = hC - hG =

IGG
S ⋅ LG

=

π ⋅ R4 ⋅
1
4
π ⋅ R 2 ⋅ hG

=

R
4 ⋅ hG


2

Page 18

06.01.2004

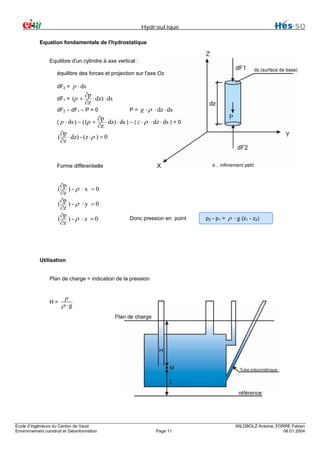
Hydraulique
Crève tonneau de Pascal
Liquide :
10-2 [dm2] ⋅ 100 = 1 [dm3] = 1 litre
Augmentation de pression :

ρ ⋅ g ⋅ ∆h ≅ 104 ⋅ 10 = 105 Pa
Augmentation de force
∆p ⋅ S = 105 ⋅ 1 ⋅ 0.1 = 104 N
Charge normale :

ρ ⋅ g ⋅ h ⋅ S = 104 ⋅ 0.5 ⋅ 0.1 = 250 KN

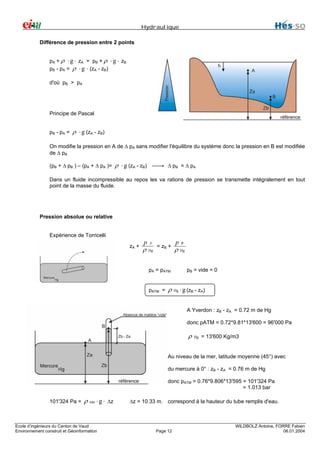
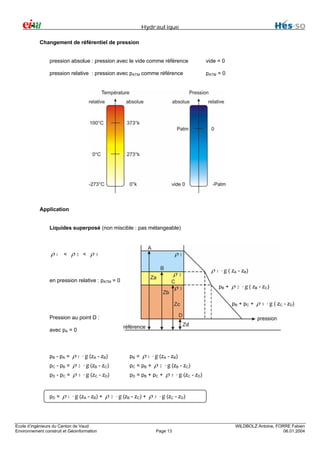
Paradoxe de l'hydraulique (by Stevin)

Vérin hydraulique

2 portions dans le même plan horizontal
avec la pression p

p=

f = F
s S

d'où : F =

S ⋅f
s

volume du fluide : s ⋅ l = S ⋅ L
travail à gauche :

f⋅ l = p⋅ s⋅ l
conservation du travail

travail à droite : F ⋅ L = p ⋅ s ⋅ S ⋅ L = p ⋅ s ⋅ l
s


Page 19

06.01.2004

Hydraulique
Poussée sur une surface gauche (non plane)
Les dF ne sont plus // entre elles.
La somme des dF ne donne pas (en générale) une force unique.
On définit une force dans une direction donnée

Intensité de ces forces (composante horizontale et verticale)

dFX = dF ⋅ cosα =

dF =

dFX
dFZ

ρ ⋅ g ⋅ h ⋅ ds ⋅ cosα
ds projeté sur le plan verticale = dSV

FX =

∫

∫ ρ ⋅ g ⋅ h ⋅ dSV

dFX =

FX =

=

ρ ⋅ g ∫ hGV ⋅ dSV = ρ ⋅ g ⋅ hGV ⋅ SV

ρ ⋅ g ⋅ hGV ⋅ SV = pGV ⋅ SV

hGV : distance du centre de gravité de la projection de la hauteur sur un plan vertical jusqu'au plan de pression nul
SV : surface projetée sur le plan vertical
FX : passe par le centre de poussée de SV

dFZ =

ρ ⋅ g ⋅ h ⋅ ds ⋅ sinα
ds projeté sur le plan horizontale = dSH

FZ =

∫

dFZ =

∫ ρ ⋅ g ⋅ h ⋅ dSH

=

ρ ⋅ g ∫ h ⋅ dSH = ρ ⋅ g ⋅ V

FZ =

ρ ⋅g ⋅ V = P

V : volume compris entre la surface et le plan de pression nulle
FX passe par le centre de poussée de SV

Cas particuliers
Si la surface S possède un centre de courbure fixe (cylindre ou sphère), toutes les forces (F)
passent par ce centre et donc la résultante passe aussi par ce point.


Page 20

06.01.2004

Hydraulique
Paroi de ¼ de cylindre (profondeur B = 1m.)
2

FX =

ρ ⋅ g ⋅ hGV ⋅ SV = ρ ⋅ g ⋅ R ⋅ (R ⋅ B) = ρ ⋅ g ⋅ R ⋅ B
2
2

FZ =

ρ ⋅g⋅π ⋅R ⋅B

F=

2

4

ρ ⋅ g ⋅ R2 ⋅ B ⋅ 1 + π

tgα =

4

2

16

FZ = π
FX
2

Vanne hydraulique, liquide à gauche (B =1m.)

FX =

2

ρ ⋅ g ⋅ hGV ⋅ SV = ρ ⋅ g ⋅ R ⋅ B
2

FZ = ρ ⋅ g ⋅ B (R 2−

π ⋅ R 2) = ρ ⋅ g ⋅ B ⋅ 2 (1 − π )
R
4

4

1 ⎛ π
+ ⎜1 −
F = ρ ⋅g⋅R ⋅B⋅
4 ⎜
4
⎝
2

tgα =

⎞
⎟
⎟
⎠

2

FZ = 2(1 − π )
FX
4

Vanne hydraulique, liquide à droite (B = 1m.)

2

FX =

ρ ⋅ g ⋅ hGV ⋅ SV = ρ ⋅ g ⋅ R ⋅ (R ⋅ B) = ρ ⋅ g ⋅ R ⋅ B
2
2

FZ =

ρ ⋅ g ⋅ B (R 2− π ⋅ R )
2

4

=

ρ ⋅ g ⋅ B ⋅ R 2 (1 − π )
4

La force FZ passe par le centre de poussée de SV
et est dirigée vers le haut.


Page 21

06.01.2004

Hydraulique

Force d'Archimède
Principe d'un corps immergé de forme cylindrique

On circonscrit au corps immergé un cylindre d'axe vertical de hauteur H
A : volume compris entre le solide et le cylindre, en bas : poids P1
B : volume compris entre le solide et le cylindre, en haut : poids P2

Forces agissant sur les volume A et B
1 - F1 - P1 + p1 ⋅ S = 0
2 F2 - P2 - p2 ⋅ S = 0

PAR DEFINITION : on appelle force d'Archimède FA, la différence entre les forces F1 et F2

FA = F1 – F2
Volume de FA = (- P1 + p1 ⋅ S) - (P2 + p2 ⋅ S)
= S⋅

ρ ⋅ g ⋅ H - (P1 + P2)

FA =

ρ ⋅g ⋅ V

V : volume immergé du solide

Tout corps solide plongé dans un fluide subit une poussée égale et directement opposée au poids du
volume de fluide déplacé.

ATTENTION
1. pour un corps flottant, prendre le volume qui est immergé
2. la force d'Archimède passe par le centre de gravité du volume de fluide déplacé et dirigée vers le haut


Page 22

06.01.2004

Hydraulique
Application
Masse volumique d'un corps
Un objet pèse :

dans l'eau, 540N
dans l'air, 240N

Volume ?
P = FA + T
FA = 540 – 240 = 300N
FA =

ρ ⋅g ⋅ V

D'où V =

FA =

ρ ⋅g

300
= 0.031 m3 = 31 dm3 = 31 litres
1000 ⋅ 9.81

Masse volumique ?

ρeau ⋅ g
= 1800 kg/m3
ρ = masse = P ⋅
volume g
FA

Un iceberg flottant dans l'océan

ρ glace : 912 kg/m3
ρ eau salée : 1025 kg/m3
partie visible : 600 m3 : V1
volume total de l'iceberg ?
Condition :

P = FA

poids total
(V1 + V2) ⋅
V2 = V1 ⋅

volume immergé

ρ glace ⋅ g = V2 ⋅ ρ eau salée ⋅ g

ρ glace
= 4843 m3
ρ eau salée ⋅ ρ glace

Volume iceberg = 4843 + 600 = 5443 m3


Page 23

06.01.2004

Hydraulique
Equilibre des corps immergés

Equilibre : FA = P

et colinéaire

P : passe par le centre de gravité du solide
FA : passe par le centre de gravité du volume du fluide déplacé

C et G sur une même verticale = équilibre stable

C et G sur une même verticale = équilibre instable

C et G confondu = équilibre indifférent

Equilibre stable

Equilibre des corps flottants
Ex : une balle de ping pong.
La position relative de C et G ne suffit
pas pour déterminer l'équilibre.
C'est le métacentre.
Equilibre stable


Page 24

06.01.2004

Hydraulique

Equation de Bernouilli
Rappel des hypothèses fondamentales

Fluide compressible :

ρ = cste
∂V = 0
∂t

Ecoulement permanent :

Force de volume due à l'apesanteur

x=0
y=0
z=0

F

hypothèse supplémentaire : intégrale de l'équation intrinsèque le long de la ligne de courant
2

ρ ⋅ g ⋅ z + P + ρ ⋅ V = cste
2

Autre forme de l'équation :
2ème équation fondamentale de l'hydraulique

Divisant par

2

z + P + V = cste
ρ ⋅g 2⋅g

ρ ⋅g :

équation de Bernouilli ou équation
de conservation d'énergie (E.E.)

2

2

= z2 + P2 + V 2
ρ ⋅g 2⋅g
2⋅g

E.E.1-2 : z1 + P1 + V 1

ρ ⋅g

charge H2

charge H1

2

Plan de charge : z +

2

P +V
ρ ⋅g 2⋅g

La ligne piézométrique : z +
c'est aussi :


V1
2⋅g
P1

ρ ⋅g

2

V2
2⋅g
P2

ρ ⋅g

P

ρ ⋅g
2
H- V
2⋅g

Page 25

06.01.2004

Hydraulique
Interprétation énergétique
Energie de vitesse
(cinétique)

Résultat d'intégration :

2

ρ ⋅ g ⋅ z + P + ρ ⋅ V = cste
2

Energie potentielle
Energie de pression

(de hauteur)

! ! ! conservation de l'énergie totale ! ! ! par unité de volume
Energie : Le Joule = Newton * mètres
Alors que : P= Pa = Newton
Mètre2

Application de l'équation de bernouilli
Ecoulement par un orifice
2

2

= z2 + P2 + V 2
ρ ⋅g 2⋅g
2⋅g

E.E.1-2 : z1 + P1 + V 1

ρ ⋅g

pATM

pATM
V1 très petit
V1/2g = 0

E.E.1-2 : (z1 - z2) 2g = V22

V2 =

∆H

2g ⋅ ∆H

formule de torriceli

Débit :

Q = V2 ⋅ S2

Equation de continuité (E.C.)


Page 26

06.01.2004

Hydraulique

Tube de Pilot (vue en plan)

ρ ⋅ g ⋅ ∆H

1. réaction hydrostatique : p1 – p2 =

2

2

= z2 + P2 + V 2
ρ ⋅g 2⋅g
2⋅g

2. E.E.1-2 : z1 + P1 + V 1

ρ ⋅g

∆H

z1 = z2 = 0 car même altitude
V1 = déviation à 90° = 0
(ATTENTION : uniquement plan horizontal)
E.E.1-2 : P1 - P2 = V 2

ρ ⋅g

donc :

V2 =

2

d'où : ∆H = V 2

2⋅g

2

2⋅g

2 ⋅ g ⋅ ∆H

Tube de Venturi

1. réaction hydrostatique : p1 – p2 =
2

2. E.E.1-2 : z1 + P1 + V 1

ρ ⋅g

E.E.1-2 : P1 - P2 =

ρ ⋅g

2⋅g

ρ ⋅ g ⋅ ∆H

= z2 + P2 + V 2
ρ ⋅g 2⋅g

1 ( 2 − 2)
2 ⋅ g V2 V1

ou encore :

(ATTENTION : uniquement plan horizontal)

2 ⋅ g ⋅ ∆H =V 22 −V 12

3. E.C. : Q = cste = V1 ⋅ S1 = V2 ⋅ S2

Q 2 Q 2
) −( )
S2
S1

Si on cherche le débit : 2 ⋅ g ⋅ ∆H = (

2
2 ⋅ g ⋅ ∆H = Q ( 1 2 − 1 2 )
S2 S1

2

V1
2⋅g

2

∆H

V2
2⋅g

Q = ...

P1

ρ ⋅g

P2

ρ ⋅g


Page 27

06.01.2004

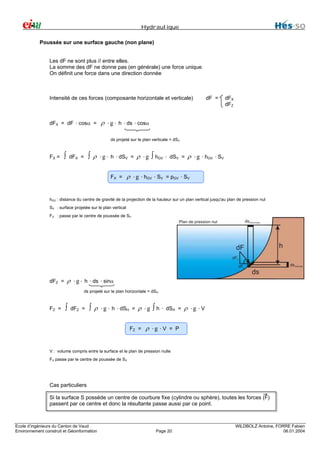
Hydraulique

Généralisation de l'équation de Bernouilli avec machine hydraulique

2

Rappel : EE sans machine : z1 + P1 + V 1

ρ ⋅g

2⋅g

= z2 + P2 + V 2
ρ ⋅g 2⋅g
=

charge H1

charge H2

Avec machine

∆HP
∆HT

2

V1
2⋅g
pompe : H1
turbine : H1

=
=

H3 - ∆HP
H2 + ∆HT

P1

ρ ⋅g

2

z1 + P1 + V 1 = z2 + P2 + V 2 ± ∆HT / P
ρ ⋅g 2⋅g
ρ ⋅g 2⋅g

Puissance d'une turbomachine (pas de démo.)
Relier la "puissance" de la machine aux grandeurs usuelles de l'hydraulique
Puissance = Energie *

1
Temps

= Déplacement * Force *

1
Temps

Déplacement * accélération * masse *
m.


P=

m/s2

* kg/m3

∆H

puissance :

*
*

g

*

ρ

1
Temps

* 1/s * m3
*

Q

ρ ⋅ g ⋅ Q ⋅ ∆ HT / P [watts]

Page 28

06.01.2004

Hydraulique

Théorème des quantités de mouvement
Rappel mécanique : Théorème d'Euler = 2ème loi de Newton

∑F

ext

= m⋅a =

∂(m ⋅ V)
∂t

m ⋅ V : impulsion ou quantité de mouvement

Cas de l'hydraulique
Hypothèse :

- mouvement permanent
- fluide incompressible
- filet liquide sur la section droite
- pas d'écoulement à travers
le "tube" de courant

Ø = cste

V = cste

Démonstration :
Volume initial ABCD ( à l'instant t)
Volume devient A'B'C'D' ( à l'instant t + ∆t)

- par continuité : ABB'A' = CC'DD' = Q * dt
- pour écoulement permanent, quantité de mvt de A'B'CD reste le même
- la variation de quantité de mvt sera :

m1 = Q ⋅ ∂t ⋅ρ
m2 = Q ⋅ ∂t ⋅ρ

∂(m ⋅ V) = m2 ⋅ V2 - m1 ⋅ V1

mais :

∂(m ⋅ V) = ρ ⋅ Q ⋅ ∂t ⋅ (V2 - V1)

et comme

∑F

ext

= ρ ⋅ Q ⋅ (V2 - V1)

∑F

ext

=

∂(m ⋅ V)
∂t

équation de quantité de mouvement
(théorème d'Euler)

forces de pesanteur

F ext =

P

K (= force nécessaire pour maintenir le liquide à l'intérieur)
force de réaction des parois sur le fluide R

force de pression

Rem. : c'est une équation vectorielle, donc pour l'utiliser, il faut faire les projections sur les axes.

Page 29

06.01.2004

Hydraulique
Effort exercé par un coude de canalisation (coude horizontal d'où Poids = 0)
k2
Donnée :

- déviation α
- débit Q
- section S1 et S2
k1

α

Projection sur X :

0 + k1 - k2 ⋅ cosα - RX = ρ ⋅ Q(V2 ⋅ cosα- V1)
0 + (p1 ⋅ S1) - (p2 ⋅ S2) ⋅ cosα - RX = ρ ⋅ Q(V2 ⋅ cosα- V1)

Projection sur Y :

0 + 0 - k2 ⋅ sinα + RY = ρ ⋅ Q(V2 ⋅ sinα - 0)
0 + 0 - (p2 ⋅ S2) ⋅ sinα + RY = ρ ⋅ Q(V2 ⋅ sinα )
2 équations à 6 inconnues ( p1, p2, V1, V2, RX, RY)

E.C. :

Q = V1 ⋅ S1

Q = V2 ⋅ S2

E.E. :

z1 + P1 + V 1 = z2 + P2 + V 2
ρ ⋅g 2⋅g
ρ ⋅g 2⋅g

et

+ 2 équations

2

+ 1 équation

5 équations à 6 inconnues !!! pour résoudre, il faut une donnée en plus.

Force d'un jet sur un aubage mobile
Principe :

- vitesse absolue du jet V
- vitesse absolue périphérique de l'aubage u
- vitesse relative du jet par rapport à l'aubage ( V - u )
- débit reçu par l'aubage Q = S ( V - u )
- puissance de la turbine P = RX ⋅ u


Page 30

06.01.2004

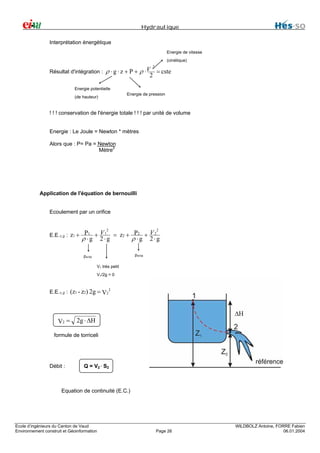
Hydraulique
Exemple : trouver la puissance d'une turbine Pelton

S = 10 cm2
direction = 150 °

u = 20 m/s
V = 45 m/s

vitesse relative : 45 – 20 = 25 m/s

α

25 ⋅ 0.0010 = 0.025 m /s
3

débit relatif :

pression = pATM = 0
E.E. : ( V - u ) = cste le long de l'aubage

- RX = ρ ⋅ Q(Vsortie - Ventrée )

E.M. :

(V -

u ) ⋅ cosα

(V -

u)

- RX = ρ ⋅ Q(V - u ) ( cosα - 1)
puissance :

= 1167 KN

P = 1167 ⋅ 20 = 23.3 KW

Cas d'embouchement

E.M. :

∑F

ext

= ρ ⋅ Q(Vsortie - Ventrée )

Il faut reprendre l'équation de base avec:

∑F

ext


c'est faux d'utiliser cette équation

∂(m ⋅ V)

= ρ [ ∑(Q ⋅ Vsortie) -

∑(Q ⋅ V

Page 31

entrée

)]

06.01.2004

Hydraulique

Equation fluide parfait généralisé
Equation de conservation d'énergie (intégrée par une ligne de courant)

2
2
z1 + P1 + α1 ⋅ U1 = z2 + P2 + α2 ⋅ U2
2⋅g
2⋅g
ρ ⋅g
ρ ⋅g

U = vitesse moyenne = Q/S

α = coefficient de Coriolis

1 < α < 2

Domaine usuel du G.C. :

1.05 < α < 1.10

Equation de quantité de mouvement

∑F

ext

= ρ ⋅ Q ⋅ (β2 ⋅ U2 - β1 ⋅ U1)

U = vitesse moyenne = Q/S

α = coefficient de Boussinesq
Domaine usuel du G.C. :

1 < β < 1.35

β = 1.05

Hydrodynamique des fluides réels
Généralité sur la viscosité
Expérience de couette (viscosité dynamique et cinématique)

Le cylindre extérieur tourne
Le cylindre intérieur fixe grâce à une force
F : force qui empêche le cylindre intérieur de tourner
F : proportionnelle à la vitesse
F : proportionnelle à la surface (2*π*R*H)
F : inversement proportionnelle à "e"
F : lié à la nature du fluide (K)


Page 32

06.01.2004

Hydraulique

F = V ⋅S ⋅ K
e

mais

avec les dérivées : ∂F = ∂V ⋅ ∂S ⋅ K

∂y

∂F c'est aussi la contrainte tangentielle :
∂S

τ = ∂V ⋅ K
∂y

ou encore

∂F = ∂V ⋅ K
∂S ∂y

K = coefficient de viscosité
dynamique noté aussi µ

τ = ∂V ⋅ µ
∂y

aussi

τ = grad. V ⋅ µ

Viscosité cinématique :
Par définition la viscosité cinématique : ν =

µ
ρ

Unité de viscosité dans le S.I.:

µ=

Dynamique :

τ

∂V
∂y
µ
ν=
ρ

Cinématique :

[Pa*sec.]

[m2/sec.]

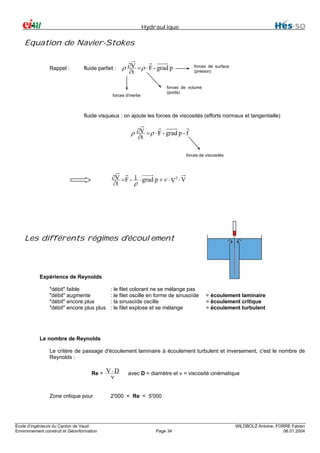
Fluide Newtoniens en non-Newtoniens
(répartition de

τ

fonction de ∂V )

∂y

τ

-µ=0

axe ∂V = fluide parfait

- µ = cste

droite passant par l'origine = fluide Newtonien (eau..)

- µ ≠ cste

courbe passant par l'origine (sang, encre, lait..)

-µ= ∞

solide élastique = axe

∂y

τ

∂V
∂y

Variation de la viscosité
Influence de la pression
Influence de la température


:
:

très faible pour les liquides
très importante
température augmente
viscosité diminue
ex. : l'huile dans une poêle

Page 33

06.01.2004

Hydraulique

Equation de Navier-Stokes
Rappel :

fluide parfait :

ρ ∂V = ρ ⋅ F - grad p

forces de surface
(presion)

∂t

forces de volume
(poids)

forces d'inertie

fluide visqueux : on ajoute les forces de viscosités (efforts normaux et tangentielle)

ρ ∂V = ρ ⋅ F - grad p - f
∂t

forces de viscosités

∂V =F - 1 ⋅ grad p + ν ⋅ ∇2 ⋅ V
ρ
∂t

Les différents régimes d'écoulement

Expérience de Reynolds
"débit" faible
"débit" augmente
"débit" encore plus
"débit" encore plus plus

: le filet colorant ne se mélange pas
: le filet oscille en forme de sinusoïde
: la sinusoïde oscille
: le filet explose et se mélange

= écoulement laminaire
= écoulement critique
= écoulement turbulent

Le nombre de Reynolds
Le critère de passage d'écoulement laminaire à écoulement turbulent et inversement, c'est le nombre de
Reynolds :
Re =

Zone critique pour


V⋅D
ν

avec D = diamètre et ν = viscosité cinématique

2'000 < Re < 5'000

Page 34

06.01.2004

Hydraulique

Ecoulement laminaire
Intégration de Navier-Stokes

Ecoulement turbulent
Généralité
La vitesse près de la paroi change de répartition

Equations de Reynolds
On ajoute aux équations de Navier-Stokes les forces de turbulence

f ':

ρ ∂V = ρ ⋅ F - grad p - f - f '
∂t

Comme ce sont des vecteurs, on effectue ensuite la projection sur les axes.

Hydraulique des conduites (écoulement en charge)
Généralité
Domaine d'étude : conduite entièrement remplie d'un seul fluide
Hypothèse

:

fluide incompressible ρ = cste
écoulement permanent
champs d'apesanteur (X = 0; Y = 0; Z = -g)

Equation de conservation d'énergie
2
2
z1 + P1 + α1 ⋅ U1 = z2 + P2 + α2 ⋅ U2 ± ∆HT / P + hR
2⋅g
2⋅g
ρ ⋅g
ρ ⋅g

Perte d'énergie le long de la conduite

Page 35

06.01.2004

Hydraulique

Formule de pente de charges linéaires (de Chézy)

Hypothèse :

α

2

V1
2⋅g

P1
ρ ⋅g

2

V2
2⋅g

- α et θ sont petit d'ou cosα = 1 et cosθ =1
- sinα = tgα = J
- sinθ = tgθ

τ0

P2
ρ ⋅g

V12 = z2 + P2 + V22 + h
E.E.1-2 : z1 + P1 +
R

ρ ⋅g

ρ ⋅g

2⋅g

=0

1)

θ

2⋅g
=0

hR = (z1 - z2) + P1 - P2
ρ ⋅g

E.M. projection l'axe du tuyau
périmètre du tuyau

(p1 ⋅ S1) - (p2 ⋅ S2) + G ⋅ sinθ - τ0 ⋅ P ⋅ ∆L = 0

avec

∆L = z1 - z2
sinθ

ρ ⋅ g ⋅ ∆L ⋅ S

en divisant ensuite par

ρ ⋅g :

2) (z1 - z2) + P1 - P2 =

ρ ⋅g

d'où :

2

τ

⋅ P ⋅ ∆L = hR
ρ ⋅g S
0

hR = V ⋅ ∆L
g ⋅ K RH

Formule de Chézy :


mais

τ

J= V ⋅ 1
g ⋅ K RH

c=

Page 36

0

2

hR = J
∆L

V = c ⋅ J ⋅ RH

2

=V
ρ K
S = rayon hydraulique RH
p

En hydro :

K ⋅ g = coefficient de Chézy

06.01.2004

Hydraulique

Equation de Darcy-Weissbach (hR)

2

2

hR = λ ⋅ L ⋅ V
D 2⋅g

λ

ou

Q
hR = λ ⋅ L ⋅
D 2 ⋅ g ⋅ S2

est sans dimension et fn(Re et rugosité relative)

En écoulement laminaire

λ

Equation de Naver-Stockes :

En écoulement turbulent lisse

=

64
Re

avec Re = V ⋅ D

ν

K=0

Equation de von Karman:

1 = - 2,0 ⋅ log ⎛ 2,51 ⎞
⎟
⎜
λ
⎝ Re ⋅ λ ⎠

En écoulement turbulent rugueux K ≠ 0
Equation de Nikuradge :

1 = - 2,0 ⋅ log ⎛ K ⎞
⎜ 3,7 ⋅ D ⎟
⎝
⎠
λ

Régime turbulent de transition

⎛ 2,51
Equation de Colebrook et White : 1 = - 2,0 ⋅ log ⎜
+

λ

⎝ Re ⋅ λ

K ⎞
⎟
3 ,7 ⋅ D ⎠

Diagramme de Moody
Attention, question d'examen final
Voir feuille annexe

harpe de Nikuradge


Page 37

06.01.2004

Hydraulique
Formule de Strickler

V = KS ⋅ RH2/3 ⋅ J1/2

pente de la ligne de charge
Rayon hydraulique

hR = J
L

section
périmètre mouille

Coefficient de Strickler [m1/3 / s]

30 < KS < 120

Vitesse moyenne de l'écoulement

ATTENTION : pour le calcul de conduite en nappe libre !!!

Rayon hydraulique

RH =

section
périmètre mouillé

Pour une conduite circulaire :

RH =

π ⋅ D2 ⋅ 1 = D
4
π⋅D 4

On peut toujours trouver RH pour une conduite quelconque. On remplace D par le diamètre équivalent = 4*
RH.
Ceci est satisfaisant quand la forme de la conduite s'approche d'un cercle.

Perte de charges singulières

Outre les pertes de charges linéaires, on trouve des particularité (singulières) dues :
changement de section brusque
changement de direction brusque ou de pente
vannes, grille, crépine
problème de joints : environ 2 à 5% de hR

hS =

2
ζ V

2⋅g

ζ est en fn de la géométrie et éventuellement du nombre Re

Réf. Bibliographique : Mémento des pertes de charges, éd. Eyrolles


Page 38

06.01.2004

Hydraulique

Calcul de réseaux (principe et technique)

Conduite entre 2 réservoirs

E.E.1-2 :

2
2
z1 + P1 + V1 = z2 + P2 + V2 + hR
ρ ⋅g 2⋅g
ρ ⋅g 2⋅g

=0

=0

=0

=0

hR = z1 - z2 = ∆H

D-W :

2

hR = λ ⋅ L ⋅ V
D 2⋅g

ATTENTION : la ligne de charge est indépendante de la pente du tuyau !!!

Conduite crachant " à gueule bée "

E.E.1-2 :

2
2
z1 + P1 + V1 = z2 + P2 + V2 + hR
ρ ⋅g 2⋅g
ρ ⋅g 2⋅g

=0

=0

=0

2
hR = V2 + ∆H
2⋅g

2

D-W :

V2
2⋅g

2

hR = λ ⋅ L ⋅ V
D 2⋅g


Page 39

06.01.2004

Hydraulique

Conduite en série

E.C.

: Qi = cste

E.E.1-2 : z1 - z2 = ∆H = hR1 + hR2 + hR3 + hS1 + hS2

∆H = ∑ hRi + ∑ hSi
i

hS = ζ ⋅

i

2

V
2⋅g

Technique de résolution par réitération
Recherche de hR

Q, L, D, K et ν connus
Rugosité rel. =

K
D

Re =

V⋅D
ν

diagramme Moody :

λ

D – W : hR

Recherche de Q

hR, L, D, K et ν connus

calcul de la rugosité rel. =

Choix de λ

Re =

Vitesse V

V⋅D
ν

K
D

diagramme Moody :

avec λ '

λ'

λ'

=

λ

?

si oui : stop
si non
2

calcul de Q avec D – W :


Q
hR = λ ⋅ L ⋅
D 2 ⋅ g ⋅ S2

Page 40

06.01.2004

Hydraulique
Recherche de D

K = ? et Re = V ⋅ D = ?
D
ν

hR, L, K et ν connus

1

D – W + E.C. = D 5

2

Technique :

Re + E.C

= Re et K'
D

2

1

Q
hR = λ ⋅ L ⋅
D 2 ⋅ g ⋅ S2

2

Re =

Choix de λ

5
D =λ⋅

8 ⋅ L ⋅ Q2
g ⋅ π 2⋅ hR

V⋅D = 4⋅Q ⋅ 1
ν
π ⋅ν D
2 calcul Re et K'
D

1 calcul D

Moody :

λ'

λ'

avec λ '

=

λ

?

si oui : stop
si non

Calcul de réseaux maillé
Conduite en parallèle
Q = Q1 + Q2
A et B = noeuds

Les deux lois fondamentales de Kirchhoff

1. pour un nœud :

∑Q

entrant

=

∑Q

sortant

convention de signe : les débits entrants et sortants sont de signe contraire.
d'où :

2. pour une maille :

∑Q=0

la perte de charge est la même quel que soit l'itinéraire : hR (A-B)
convention de signe pour un itinéraire complet (A

a)

= hR (A-B)

b)

A) :

Q est > 0 s'il est choisi dans le sens positif et hR a le signe de Q
d'où :

∑Q=0

Page 41

06.01.2004

Hydraulique
Calcul d'une maille
But : trouver la répartition des débits dans les différents itinéraires
2

Q
2
hR = λ ⋅ L ⋅
= m⋅Q
D 2 ⋅ g ⋅ S2

(1)

(2)

hR = m ⋅ Q
Q

Hyp. : Choix arbitraire des répartitions Qa et Qb
Répartition exacte :

Qa' = Qa + ∆q

Avec cette répartion :

Qb' = Qb - ∆q

∑ h '=0
R

ma (Qa + ∆q) - mb (Qb - ∆q) = 0
2

Alors :

2

2 ⋅ ∆q (ma ⋅ Qa + mb ⋅ Qb) + ∆q 2 ( . . . ) = - ma ⋅ Qa + mb ⋅ Qb
2

2

2

= 0 car au carré devient très petit

2

Avec (1) :

La formule

2

ma ⋅ Qa - mb ⋅ Qb 1
∆q = ⋅
ma ⋅ Qa + mb ⋅ Qb 2

∆q = -

:

Avec (2) :

∆q = - hRa - hRb ⋅ 1
hRa + hRb 2
Qa Qb

∑h
2⋅∑ h
Q
Ri

Ri
i

Exemple :

Q = 200 l/s

K = 0.1 mm

L1 = 500 m
D = 30 cm

ν = 1.3*10-6 m3/s

L2 = 600 m
D = 20 cm

Tronçon
AB
BA

Q choisis [l/s]
+ 140
- 60

hR [m]
+ 5.54
- 10.17
- 4.63

hR/Q
0.0396
0.1695
0.2091

∆q [l/s]
+ 11.1
+ 11.1

Q corrigé [l/s]
+ 151.1
- 48.9
200.0

AB
BA

+ 151.1
- 48.9

+ 6.37
- 6.82
- 0.45

0.0421
0.1395
0.1816

+ 1.2
+ 1.2

+ 152.3
- 47.7
200.0

Contrôle : on calcule avec les nouveaux débits les hR jusqu'à ce qu'il soit identique.

Page 42

06.01.2004

Hydraulique

Cas de plusieurs mailles
Pour la maille 1 : terme correcteur de ∆q1
Pour la maille 2 : terme correcteur de ∆q2
ATTENTION tronçon commun AB
affecte la maille 1 de - ∆q2
affecte la maille 2 de - ∆q1

Voir exemple sur feuille annexe

Hydraulique des canaux (éc. En nappe libre)
Généralité
Définitions
Il y a une surface de liquide avec un gaz (l’air à la pATM)

But de l’étude
-

relation entre forme des frontières, débit, ligne d’eau
transformation d’énergie potentiel / cinétique
particularités d’écoulement dues à des obstacles

Classification des fluides
Ecoulement permanent :
- écoulement uniforme : section transversalle (y.c. ligne d’eau) = cste
- écoulement varié : - ec. graduellement varié : courbe de remous
- ec. brusquement varié : ressaut hydraulique

Ecoulement non permanent :
- onde de transition
- houle


Page 43

06.01.2004

Hydraulique

Equations fondamentales (tjs les mêmes, mais adaptées)
Equation de continuité
Q = V⋅ S

où S n’est plus donné par le profil entier mais par la section d’eau

Equation de conservation d’énergie

Particule à la surface :
2

(z+t)
hauteur

+

0

V
2⋅g

+

pression

+

cinétique

hR

= cste

perte de charge

Hyp : V = cste dans une section transversale (α = coefficient de Coriolis = 1)

Particule dans le liquide :
( z + t’ )

+

2

P
ρ ⋅g

V +
+
2⋅g

= t’’ (idem, si R est très grand)

hR

= cste

or t’ + t’’ = t

2

(z+t)

+

V
2⋅g


+

hR

= cste = H

Page 44

où H est la charge hydraulique
06.01.2004

Hydraulique

Equation de quantité de mouvement (tjs valable)

∑F

ext

= ρ ⋅ Q ⋅ (V2 - V1)

équation de quantité de mouvement
(théorème d'Euler)

P (poids)
force de pression K (= force nécessaire pour maintenir le liquide à l'intérieur)
force de réaction des parois sur le fluide R
force de pesanteur

F ext =

Rem. : c'est une équation vectorielle, donc pour l'utiliser, il faut faire les projections sur les axes.

Ec. en charge

Ec. en nappe libre

ρ ⋅g ⋅H

p = cste

p=

Force de pression = p ⋅ S

Force de pression = pG ⋅ S

Nombre de Froude :

FR

V2 1
Force d' inertie
masse ⋅ accél. vitesse 2 1
⋅ =
⋅ =
=
=
L g
Force de gravité
masse ⋅ g
longêur g
Q2 1
Q 2 ⋅ L' 1
Q 2 ⋅ L' 1
⋅ = 2
⋅
⋅
=
S2 ⋅ L g
S3
g
S ⋅ L ⋅ L' g

FR =


Q2 ⋅ B 1
⋅
S3
g

Page 45

06.01.2004

Hydraulique

Ecoulement uniforme
Dans un lit prismatique (profil en travers constant)
V = cste d’une section à l’autre
E.C.

S = cste

t = cste

∂H
=0
∂x

E.E. : charge H = cste

2

H= z + t +

V + h
R
2⋅g

V2
∂(
)
∂H
∂z
∂t
∂hR
2⋅g
=
+
+
+
= 0
∂x
∂x
∂x ∂x
∂x
J = pente de la ligne de charge
-Jo = pente du lit du canal
= -Jo + 0 + 0 + J = 0
D’où

Jo = J

Conclusion :

les 3 lignes

lit du canal
ligne d’eau
ligne de charge

sont parallèles.

Lois des pertes de charges :
1. Formule de Chézy :

V = c ⋅ J ⋅ RH

RH =


c = coefficient de Chézy [m1/2/s]
V = vitesse moyenne de l’écoulement
RH = rayon hydraulique
J = pente de la ligne de charge

13 (rugueux) < c < 120 (lisse)

Surface
périmètre mouillé

Page 46

06.01.2004

Hydraulique

2. Formule de Bazin
Formule de Chezy + explication de « c »

87

c=

1+

γ

où γ dépend de la nature de la paroi (0.06 (lisse) à 1.75 (rugeux))

RH

3. Formule de Strickler
RH : rayon hydraulique
J : pente de la ligne de charge

V = KS ⋅ RH2/3 ⋅ J1/2

Ks : coefficient de Strickler [m1/3 / s]

Q = KS ⋅ S ⋅ RH 2/3 ⋅ J1/2
rivière :
béton :

23
75

<
<

Ks
Ks

<
<

50
85

Profondeur normale

Profondeur en écoulement uniforme : t0

Loi de Strickler : Q = KS ⋅ S ⋅ RH

2/3

⋅ J1/2

en éc. uniforme J = J0 = cste

S ⋅ RH2/3 en fonction de la profondeur


Page 47

06.01.2004

Hydraulique
Cas particulier :

a) canal rectangulaire, infiniment large

RH =

Q = KS ⋅ S ⋅ RH 2/3 ⋅ J1/2

B⋅t
=t
B+ 2⋅t

où

2 ⋅ t est négligé

Q = KS ⋅ (B ⋅ t) ⋅ t 2/3 ⋅ J1/2

⎛
⎞
Q
t =⎜
⎜ KS ⋅ (B ⋅ t) ⋅ 1/2 ⎟
⎟
J ⎠
⎝

3/5

b) canaux circulaire ou ovoïde (égouts)

Q max

= 1.6 * Q plein

Différents problèmes rencontrés

- rugosité non uniforme

⎡
⎢ P
Formule d’Einstein : K pondéré = ⎢
Pi
⎢ ∑ 3/2
⎣ Ki

⎤
⎥
⎥
⎥
⎦

- lit mineur / majeur

Q =

∑

Q partiels

- lit avec méandres
mais


J0 Majeur ≠ J0 Mineur

Page 48

06.01.2004

Hydraulique

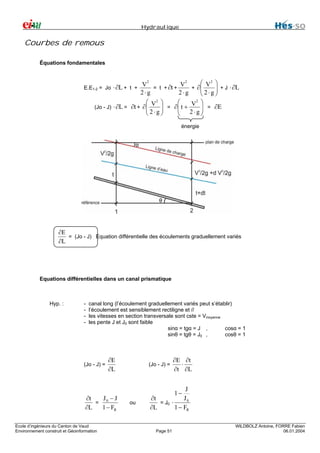
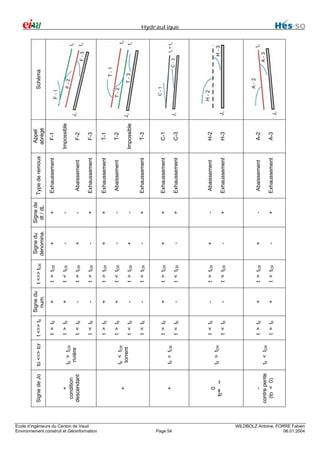
Ecoulement graduellement varié
Définition

- graduellement

∂t
est petit, donc perte de charge faible
∂L

- brusquement

∂t
est grand, donc perte de charge importante
∂L

Charge spécifique Hs

2

2
V = t + Q
Hs = t +
2⋅g
2 ⋅ g ⋅ S2

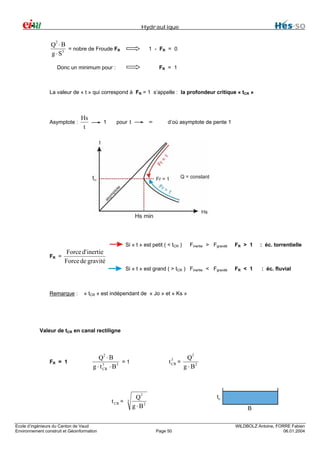
Courbe d’égal débit « étude de la fonction Hs »

En fonction de t (Q = cste)
ED(f) : [ 0 , ∞ ]

0

alors

Hs

∞

t

Minimum lorsque

t

∞

alors

Hs

∞

∂Hs
=0
∂t

1+

2
Q ⋅B
=0
1g ⋅ S3

B : largeur libre du canal


2
Q ⎛ 2 ⎞ ∂s
⋅⎜− ⎟⋅ = 0
2 ⋅ g ⎝ S3 ⎠ ∂t

Page 49

06.01.2004

Hydraulique
2
Q ⋅B
= nobre de Froude FR
g ⋅ S3

1 - FR = 0
FR = 1

Donc un minimum pour :

La valeur de « t » qui correspond à FR = 1 s’appelle : la profondeur critique « tCR »

Asymptote :

Hs
t

1

pour t

∞

d’où asymptote de pente 1

Si « t » est petit ( < tCR )

FR > 1

: éc. torrentielle

Si « t » est grand ( > tCR ) Finertie < Fgravité

FR =

Finertie > Fgravité

FR < 1

: éc. fluvial

Force d' inertie
Force de gravité

Remarque :

« tCR » est indépendant de « Jo » et « Ks »

Valeur de tCR en canal rectiligne

FR = 1

2

2
Q ⋅B
=1
g ⋅ t 3 ⋅ B3
CR

t3 =
CR

Q
g ⋅ B2

2

t CR =


3

Q
g ⋅ B2

Page 50

06.01.2004

Hydraulique

Courbes de remous
Équations fondamentales
2
2
⎛ 2 ⎞
⋅ ∂L + t + V = t + ∂t + V + ∂⎜ V ⎟ + J ⋅ ∂L
⎜ 2⋅g ⎟
2⋅g
2⋅g
⎝
⎠
2
2
⎛ V ⎞
⎛
V ⎞
(Jo - J) ⋅ ∂L = ∂t + ∂⎜
⎜ 2 ⋅ g ⎟ = ∂⎜ t + 2 ⋅ g ⎟ = ∂E
⎜
⎟
⎟
⎝
⎝
⎠
⎠

E.E1-2 = Jo

énergie
α

θ

∂E
= (Jo - J) Equation différentielle des écoulements graduellement variés
∂L

Equations différentielles dans un canal prismatique

Hyp. :

-

canal long (l’écoulement graduellement variés peut s’établir)
l’écoulement est sensiblement rectiligne et //
les vitesses en section transversale sont cste = Vmoyenne
les pente J et J0 sont faible
sinα = tgα = J ,
cosα = 1
sinθ = tgθ = J0 ,
cosθ = 1

(Jo - J) =

∂E
∂L

J −J
∂t
= 0
∂L
1 − FR

(Jo - J) =

∂E ∂t
⋅
∂t ∂L

J
J0
∂t
= J0 ⋅
1 − FR
∂L
1−

ou

Page 51

06.01.2004

Hydraulique

Etude qualitative et classification des lignes d’eau

a) rappel :

Si FR > 1
Si FR < 1

t < tCR
t > tCR

b)

Si t > t0
Si t < t0

J < J0
J > J0

t0 > tCR
t0 < tCR

c) définitions :

éc. torrentielle
éc. fluvial

le canal est une rivière
le canal est un torrent

d) convention de signe
J0 > 0 (positif)

pour un canal descendant

e) conditions aux limites
t

t0 , J

t

tCR , FR

t

∞ , FR

t = tCR

J0
1

0, J
alors :

∂t
∂L
∂t
alors :
∂L
∂t
alors :
∂L

alors :

0

0

profondeur normal est 1 asymptote

∞

tangente verticale pour la profondeur critique

J0

∂t
= J0
∂L

Illustrations en rivière


Page 52

06.01.2004

Hydraulique

Illustrations en torrent


Page 53

06.01.2004

to <=> tcr


Page 54

0

∞

contre pente
(to < 0)

t0

+

t0 < tCR

t0 > tCR

t0 = tCR

t0 < tCR
torrent

+
condition
descendant

+

t0 > tCR
rivière

Signe de Jo

t <=> tCR

t < tCR
t > tCR
t < tCR
t > tCR
t < tCR

+
+
-

t < t0

t < t0

t > t0

t > t0

t < t0

t < t0

t > tCR

t > tCR

+

t > t0

t > t0

t > t0

t > tCR
t < tCR

+

t < tCR

-

t < t0
-

t > tCR

-

t < t0

t < t0

t < tCR

+

t < tCR

+

t > t0

t > t0

t > tCR

Signe du
num.

t <=> t0

+

-

+

-

+

-

+

-

+

-

+

-

+

-

+

Signe du
dénomina.

+

-

+

-

+

+

+

-

-

+

+

-

-

+

Signe de
dt / dL

Exhaussement

Abaissement

Exhaussement

Abaissement

Exhaussement

Exhaussement

Exhaussement

Abaissement

Exhaussement

Exhaussement

Abaissement

Exhaussement

Type de remous

A-3

A-2

H-3

H-2

C-3

C-1

T-3

Impossible

T-2

T-1

F-3

F-2

Impossible

F-1

Appel
abrégé
Schéma

Hydraulique

06.01.2004

Cours hydraulique 2_annee_6

Contenu connexe

Tendances

En vedette

Similaire à Cours hydraulique 2_annee_6

Cours hydraulique 2_annee_6