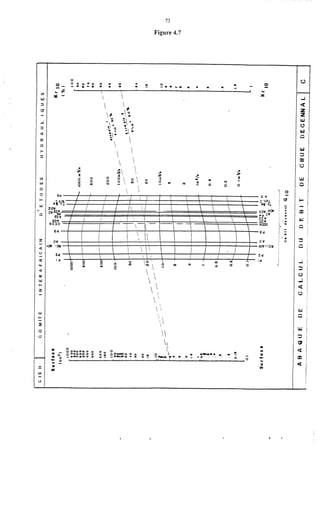
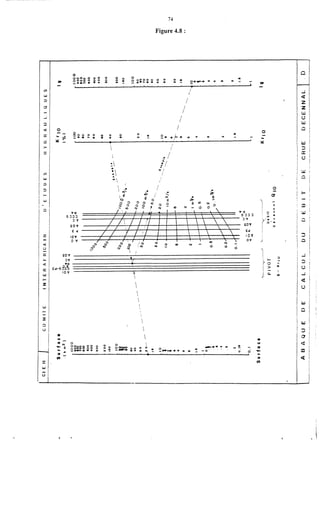
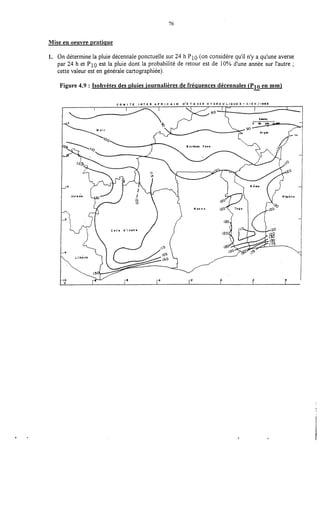
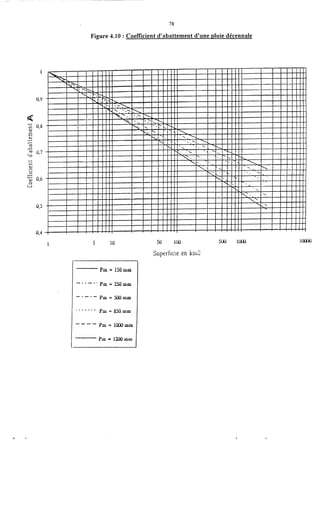
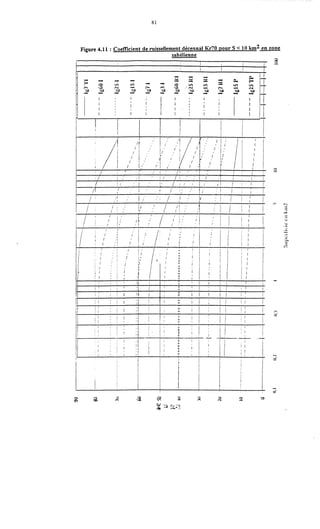
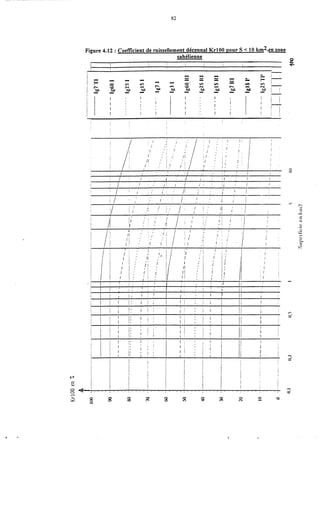
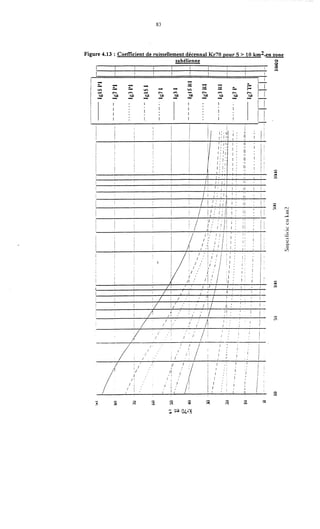
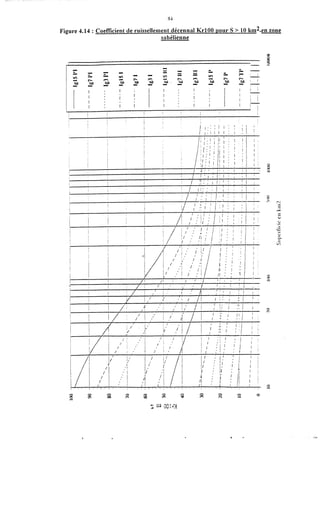
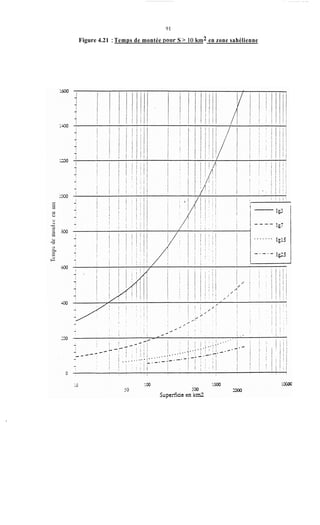
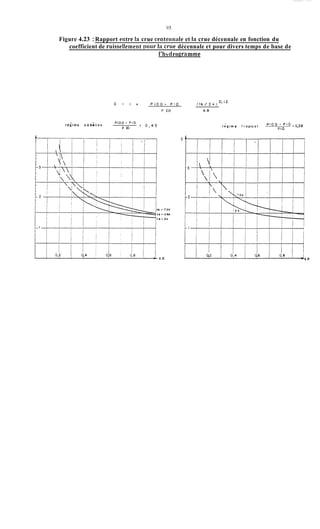
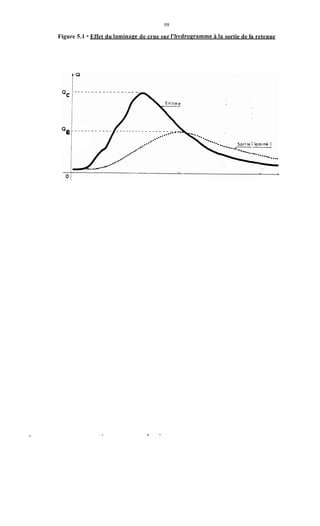
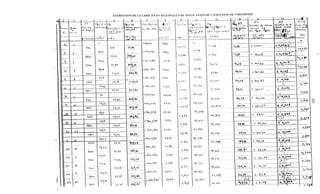
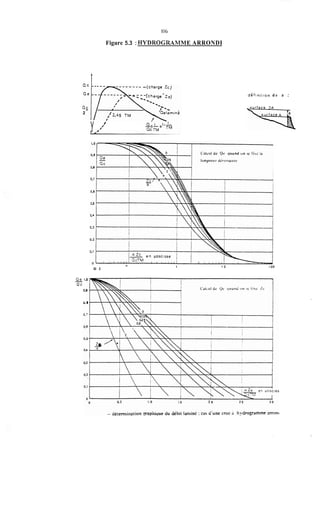
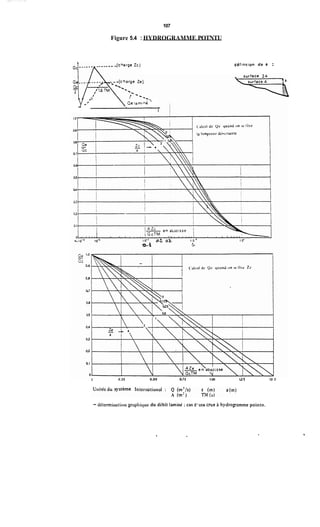
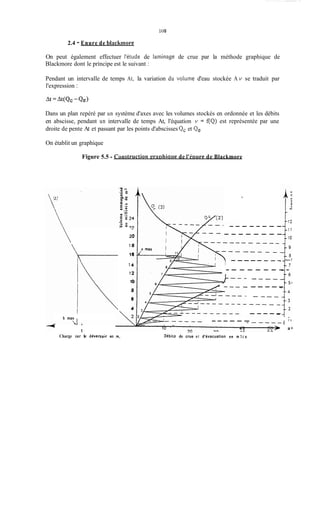
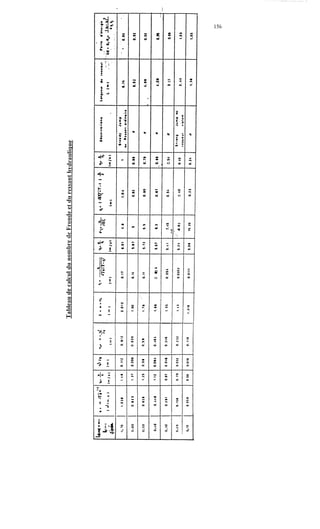
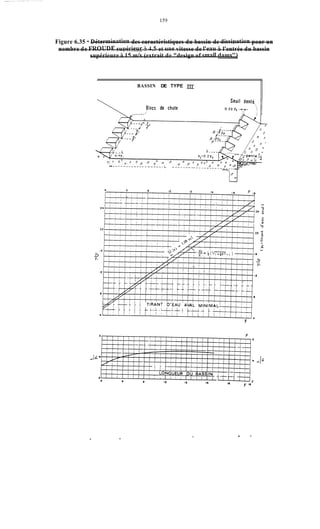
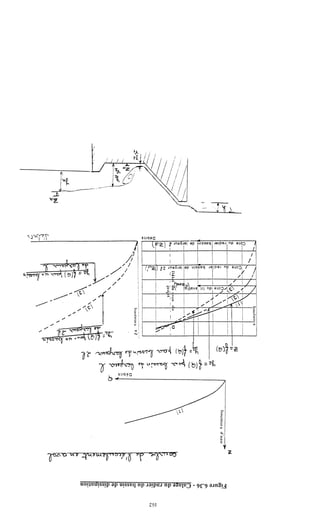
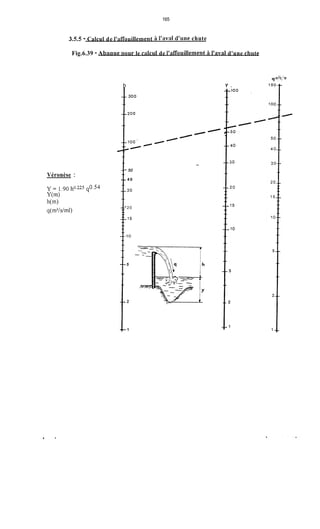
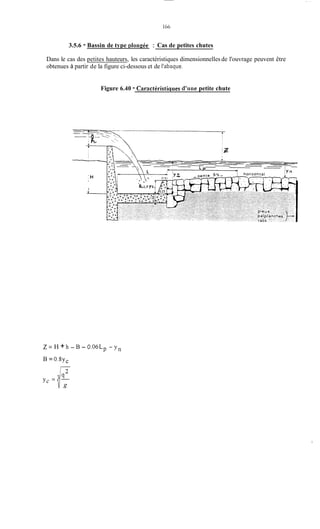
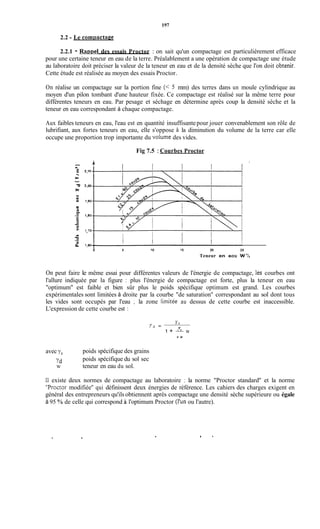
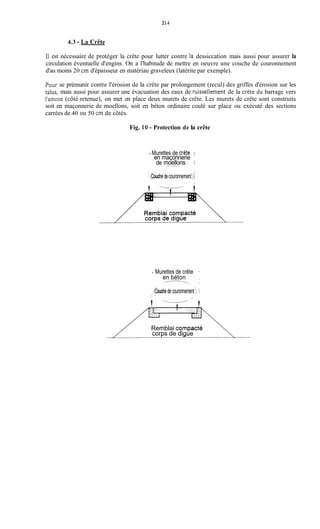
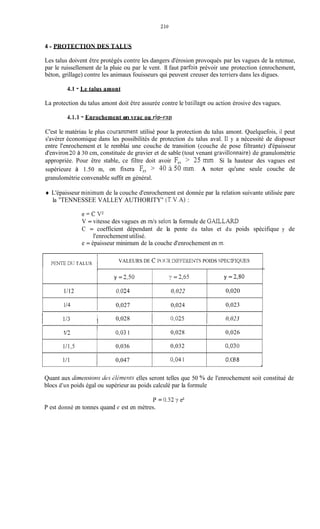
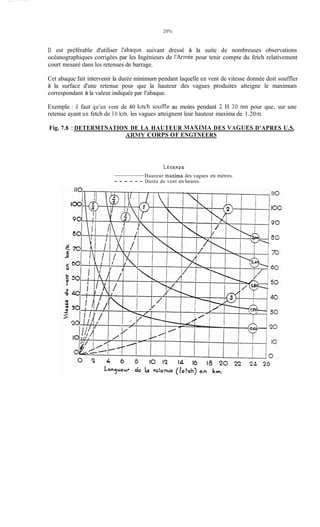
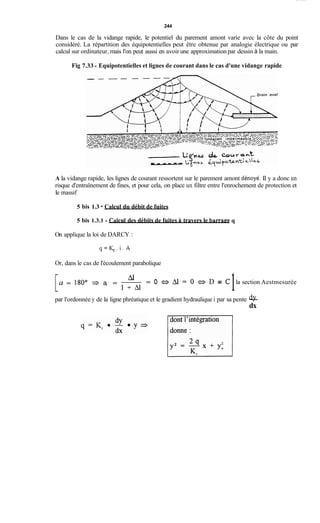
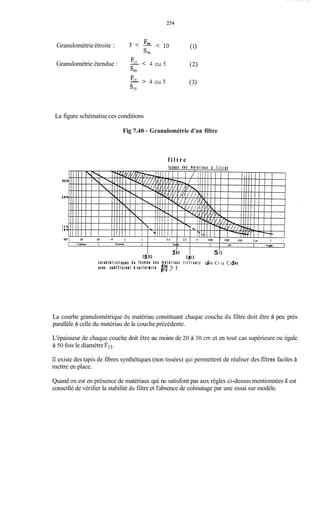
Le document traite de la modélisation des crues dans des bassins versants, en utilisant divers paramètres tels que l'altitude, le temps de montée, et la surfraction des bassins. Il explique les méthodes d'estimation des crues décennales et centennales, ainsi que l'importance du coefficient de ruissellement dans l'évaluation des débits de pointe des crues. L'étude inclut également des techniques de laminage pour réduire les effets des crues, avec des équations pour modéliser ces dynamiques.









































































![101
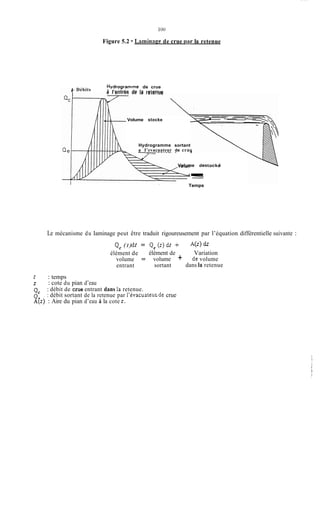
- EQUATION DE CONTUINITE
Nous écrivonsle bilan en volume des différents apports pendant le temps dt :
- volume entrant Qc(t)dt
-volume sortant Qe( W
- variation de stock : A ( Z W
ce qui permet d'écrire :
2 - RESOLUTTON
Il existe de nombreuses méthodes pour résoudre cette équation.
2.1 - Calcui numériclue
La résolution de l'équation peut aussi être faite numériquement par exemple avec la méthode
de Runge-Kutta.
L'équation est de type :
dz
dt
-= f(t,z)
Les différentielles totales sont apptoximées par des différences finies :
Azdz
dt At
Y --
La valeur de la fonction f(t,z) est estimée dans l'intervelle [t ;t +At] par une fonction <b(t,z,At).
La valeur de 4 est une moyenne de valeurs de f dans l'intervalle [t ;t +At].
Quatrevaleurs de f sont calculées :
f* =f(t,z)
fi =f(t +-,,+for>At At
2
f2 = f(t +-,z+f,Z>At At
2
f3 =f(t +-,z+fzAt)At
2
dont nous faisons une moyenne
+(t,z,At) =z[fo +2fi +2f2 +f3]
La vaieur de la cote du plan d'eau au temps t + At es ainsi :
Z =Zt +&t,z,At).At
Le calcul est poursuivijusqu'à obtention de l'hydrograrmne laminé complet.
1
t-At](https://image.slidesharecdn.com/polybarrage-180504183807/85/cours-de-barrage-2eme-edition-M-L-COMPAORE-112-320.jpg)





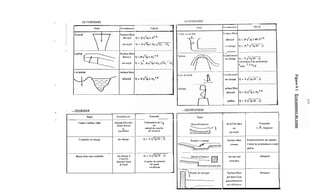






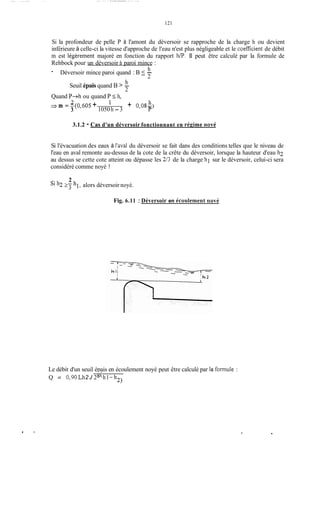
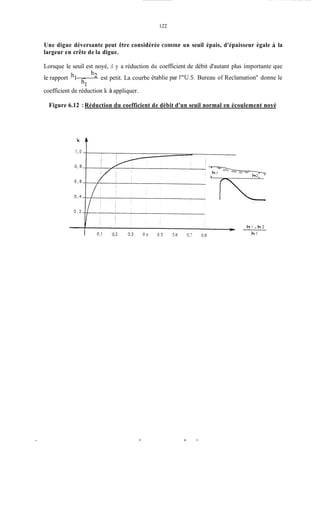































![171
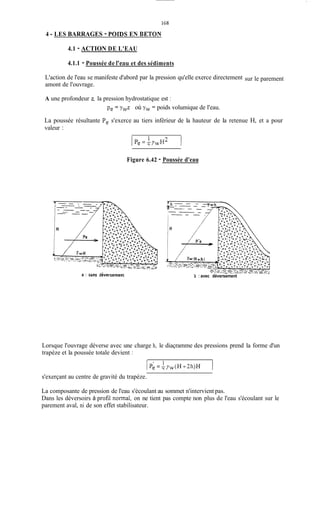
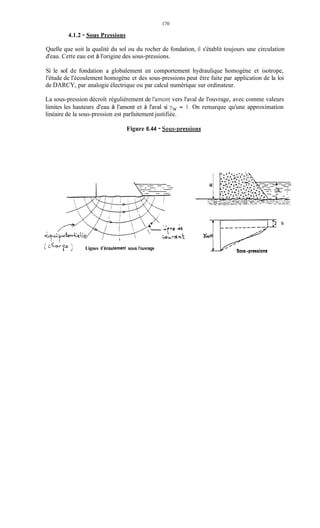
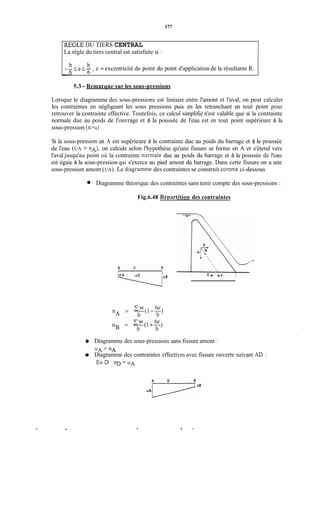
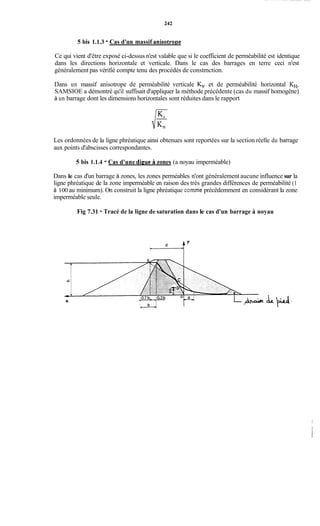
La prise en compte des sous -pressions se fera en choisissant l'un des diagrammes ci-dessous
correspondant à l'une des hypothèses suivantes :
- Diagramme a : les fondations hétérogènes et anisotropes ne sont pas traitées. II peut
exister des fissures en communication avec l'amont du barrage qui ne débouchent pas à
l'aval. La sous-pression s'établit alors sous tout l'ouvrage avec une valeur constante
correspondant à la charge amont.
- Diagramme b : les fondations homogènes et isotropes ne sont pas traités. On admet qu'il y
a circulation d'eau d'amont en aval avec perte de charge linéaire. La sous-pression décroît
linéairement de la valeur yw H, charge aval.
- Diagramme c : les fondations homogènes sont étanchées par un rideau d'injection ou tout
autre coupure étanche en amont, qui entraîne une perte de charge amont importante. Les
sous-pressions décroissent linéairement d'une valeur amont yw[h +/i(H- h)] à une valeur
aval yw h. On admet en général h = X .
- Diagramme d : les fondations homogènes et étanches sont drainées à l'aval de l'organe
d'étanchéité. On admet en général que le drainage est efficace à 50?6 et que, au niveau du
drain, la sous-pression tombe à la valeur ;yw - h) =-yw(H + h)
1 :
Les diagrammes correspondant aux cas a et b sont rarement observés en fait. Les cas c et d
sont ceux qui correspondent le mieux aux mesures qui ont pu être faites. Il faut noter toutefois
que ces mesures ont été réalisées sur des ouvrages bien conçus et bien réalisés.](https://image.slidesharecdn.com/polybarrage-180504183807/85/cours-de-barrage-2eme-edition-M-L-COMPAORE-182-320.jpg)










































![. ... ,
226
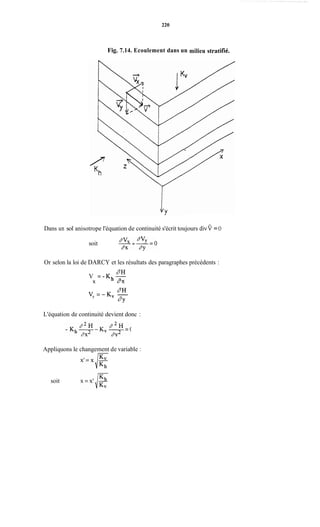
. Y est la vitesse d'écoulement tangente à la nappe y1en A,. Comme les deux nappes sont
. La surface d s est égale a Al A2 x 1 m=Al A2
. fiest le vecteur unitaire perpendiculaire à la surface dS. Ïi .dS est donc le vecteur surface.
infiniment proches, c'est aussi la vitesse tangente à y2 en A,.
donc dS=A,A,
fi a pour coordonnées : [i:ns:]
. A x = x ~- x2 ; AY=Y,-Y2 ; (Xi.Y1) e t ( x 2 4
étant les coordonnées respectivement de A, et A,
Ecrivons le débit qui s'écoule entre ces deux nappes de courant :
dq = V.dS ou encore vectoriellement dq = V.fi dS
- -
Or iï = cos a i + sin aj
(le signe - s'explique par le fait que Ax = x1 - x2 > O et que a
-Ax -Axsina =-- --
A1A2 d S
Ax< O ;donc sin a < O et comme Ax > O, sin a = - -
Al A2 )
donc E-dS = cosa-dSi f sin m d S j
or V = - 1 - -- "wl
dY dX
donc dq = v . fi dS = -w - Ay + - Ax
dY dX
Donc entre deux lignes de courant, il s'écoule par unité d'épaisseur un débit égal à la variation
de la fonction de courant entre les deux lignes
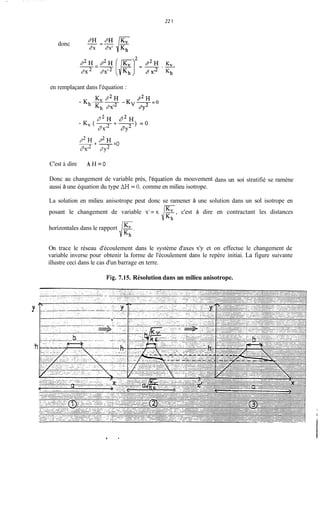
5.2.2.3. Troisième conséquence : définition des éaui~otentielleset forme du réseau
de lignes
Considérons la fonction <p = - KH. Elle est telle que :
Y = - K gradH = gr5d - KH = gitad p
soit V=gradg>J
(0 est la fonction de potentiel](https://image.slidesharecdn.com/polybarrage-180504183807/85/cours-de-barrage-2eme-edition-M-L-COMPAORE-237-320.jpg)



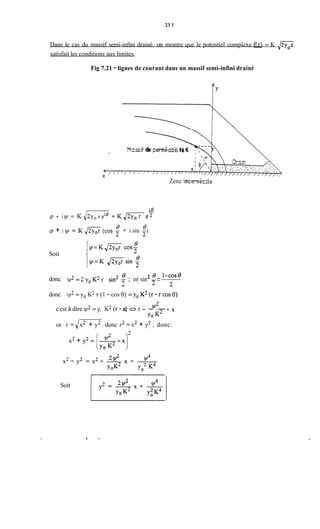

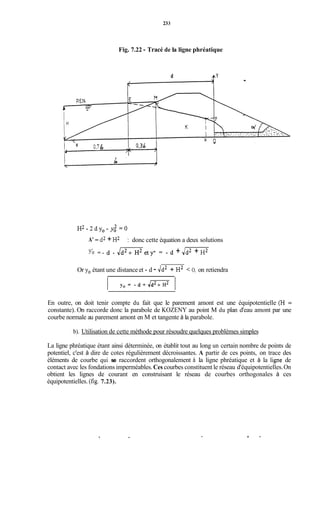


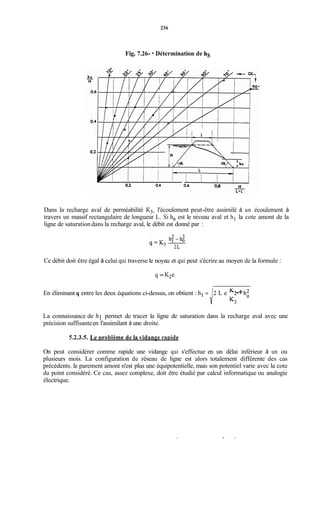

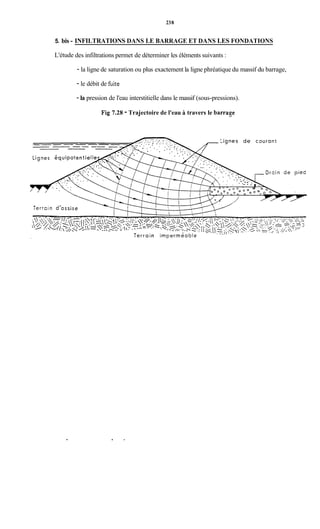
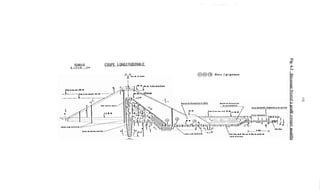
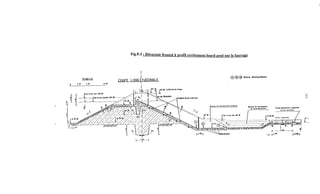
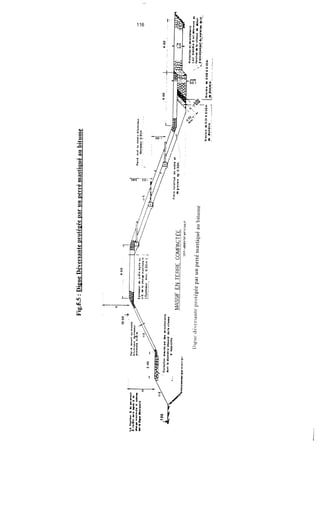
![239
5. bis.1 -Détermination des éauipotentielleset des lignes de courant
5 bis 1.1 - Tracé de la lime phréatique
5 bis. 1.1.1 - Cas d'un massif homoPéne non drainé
Fig 7.29 - Détermination de la ligne phréatique
Définitions
h = charge d'eau = tirant d'eau
d = largeur en base du barrage diminuée de 0.7b [et de la largeur du filtre s'il y a lieu]
b = projection horizontale de la partie mouillée du parement amont.
K, = coefficient de perméabilité du remblai de la digue (remblai compacté)
E = hauteur de l'endiguement
a = angle du talus aval.
En partant du cas théorique simple d'un écoulement plan a travers un massif Dermeable reposant
sur une fondation plane imperméable à l'amont jusqu'au point O et de même perméabilité que Ie
massif vers l'aval à partir du point O, KOZENY a montré que, dans un barrage en terre homogène
non drainé, la ligne phréatique peut être assimilée dans sa partie médiane à une parabole d'axe
horizontal dont le foyer O est situé au pied du parement aval du barrage.
Etant donné que la parabole admet le point O comme foyer, son équation serait :
. # *](https://image.slidesharecdn.com/polybarrage-180504183807/85/cours-de-barrage-2eme-edition-M-L-COMPAORE-250-320.jpg)


















![262
Moment des forces résistantes :
C(N - udl) tg$ R + C(c.dl)R = R [C(N - udl) t& + CI]
Moment des forces motrices : CTR = U T
Le coefficient de sécurité :
C(N- udl)tg4 + clF =A
CT
7.2.2.3 - Méthode de Bishon
Elle est plus générale car si l'on conserve zn+, - zn= 0 . On admet que Xn+,# X,
D'autre part on tient compte systématiquement de la pression interstitielle, comme dans la 2ème
variante de la méthode de Fellenius.
Le coefficient de sécurité a la même définition que ci-dessus, mais son expression est plus
complexe :
cdl + tg$ (N - üdl)
mx = coefficient différent pour chaque tranche et lui- même fonction de F
(a= angle entre l'élément dl et l'horizontale)
Le calcul s'opère par itérations successives. On évalue par la méthode le Fellenius une première
valeur de F qui est introduite dans le calcul, ce qui donne une deuxième évaluation plus fine etc.
La méthode de Bishop est plus précise que celle de Fellenius mais elle nécessite 3 à 4 fois plus de
calculs (obligation d'opérer 3 à 4 itérations). Les coefficients de sécurité obtenus sont en général
un peu plus élevés.
Le plus souvent, pour alléger les calculs, on détermine d'abord le cercle le plus critique par la
méthode de Fellenius et on vérifie que la valeur du coefficient de sécurité calculé par la méthode
de Bishop est supérieure à celle calculée par la méthode Fellenius. Si ce n'est pas le cas, il faut
reprendre la recherche du cercle critique selon la méthode de Bishop.](https://image.slidesharecdn.com/polybarrage-180504183807/85/cours-de-barrage-2eme-edition-M-L-COMPAORE-273-320.jpg)