Ce polycopié de cours est destiné aux étudiants de M1 en géotechnique et traite de l'hydraulique, abordant des concepts fondamentaux tels que l'hydrostatique, l'hydrodynamique et l'assainissement routier. Organisé en six chapitres, il fournit des explications claires sur les propriétés des fluides et les méthodes de calcul applicables dans divers domaines d'ingénierie. Cet ouvrage est conçu pour être accessible et utile également aux étudiants en génie civil et travaux publics.

1. 1
.
Polycopié de Cours déstiné aux étudiants
M1 Géotechnique
Mr. BOUDERBALA Abdelkader
Maître de conférences classe « B »
Septembre 2017
Université de Khemis Miliana ‫مليـانـــــة‬ ‫خميــــس‬ ‫جامعـــــة‬
Faculté des Sciences de la Nature et de la Vie
et des Sciences de la Terre
‫الطبيـعـــــة‬ ‫علـــوم‬ ‫كليـــــة‬
‫األرض‬ ‫و‬ ‫الحيـــاة‬ ‫و‬
Département des Sciences de la Terre ‫قســـم‬
‫علـــوم‬
‫األرض‬

2. 2
Avant-propos
L’hydraulique occupe une place prépondérante dans notre vie quotidienne et dans
l’environnement naturel. Ses applications couvrent plusieurs domaines d’ingénierie tel que :
le domaine des sciences de l’eau (hydraulique urbaine, hydraulique à surface libre,
hydraulique souterraine, hydraulique agricole, hydrotechnique,…), le domaine des sciences
industrieles des fluides sous pression (hydroénergitique, moteur et pompe hydraulique,
l’energie hydraulique, machine hydrailique…), il y a même certains principes de
l’hydraulique sont utilisés en biologie dans le corps humain (système cardiovasculaire).
Le présent polycopie de cours que je présente dans le cadre de mon habilitation universitaire,
est destiné essentiellement aux étudiants de géotechnique, de deuxième cycle universitaire
(Master). Il peut être aussi utile pour d’autre spécialités : de génie civil ou travaux publics. Il
est surtout focalisé sur les lois d’hydrostatique et d’hydrodynamique des liquides et établit
des modes d’application de ces lois à la résolution des problèmes pratiques. Les principes sont
expliqués d’une façon claire avec une langue et vocabilaire assez accessibles.
Ce polycopié est arrangé en six chapitres. Le premier chapitre aborde les diffirentes unités
utilisées dans le système internationales ainsi que propriétés principales physiques des fluides.
Le deuxième chapitre est conscacré à l’hydrostatique, à la branche de l’hydraulique qui
s’occupe de l’équilibre du liquide et son intéraction avec les corps solides. Il examine la
variation horizonale et verticale de la pression, ainsi que les forces de preesion qui se
manifestent sur les parois planes et courbes.
Le chapitre troisième traite la dynamique des fluides, où il s’occupe des lois du mouvement
des particules fluides soumises à un système de force. Le chapitre traite le principe de
conservation de masse, et les équations d’Euler et de Bernoulli d’un fluide parfait.
Le quatermième chapitre est consacré aux régimes d’écouelemnt des liquides réels, c’est la
partie la plus importante de l’hydraulique, il traite surtout les régimes d’écoulement des
liquides, le mouvement de l’eau dans les conduites qui conduit à la perte d’énergie, et les
méthodes de détermination des pertes de charge linéaire et sigulière.
Le cinquième chapitre a été consacré aux écoulements à surface libre. Ces écoulements ont
une importance majeure, par ce que l’évacuation des eaux superfielles s’effectue par gravité.
Nous avons présenté les lois fondamentales de l’écoulement à surface libre pour un
écoulement parmanent uniforme et non-uniforme. L’objectif principal de ce chapitre est
d’arriver à dimensionner les canaux artificiels pour différentes formes, ainsi que de
déterminer ses hauteurs minimales.
Le troisième chapitre traite les problèmes posés par l’évacuation des eaux pluviales, c’est
l’assainissement routier. Il concerne surtout la configuration du réseau d’évacuation des eaux
superficielles dans les cas des talus en déblai ou en remblai, les formes des fossés utilisés, et
les ouvrages hydrauliques de franchissement des cours d’eau.
L’auteur
Mr. Bouderbala Abdelkader

3. 3
SOMMAIRE
INTRODUCTION GENERALE.......................................................................................................... 1
CHAPITRE 1: PROPRIETES PHYSIQUES DES FLUIDES.......................................................... 2
1.1 Définition d’un fluide.................................................................................................................... 2
1.2 Système d’unité............................................................................................................................. 2
1.3 Propriétés des liquides................................................................................................................... 2
1.3.1 La masse volumique (ρ, Rou) ................................................................................................ 2
1.3.2 Le poids volumique (γ, gamma)............................................................................................. 3
1.3.3 La densité ............................................................................................................................... 3
1.3.4 La viscosité............................................................................................................................. 3
1.3.5 La tension superficielle .......................................................................................................... 5
1.3.5 La capillarité........................................................................................................................... 6
CHAPITRE 2: HYDROSTATIQUE................................................................................................... 8
2.1 Introduction................................................................................................................................... 8
2.2 Pression en un point d’un fluide.................................................................................................... 8
2.3 Lois fondamentales........................................................................................................................ 8
2.3.1. Surfaces isobares................................................................................................................... 8
2.3.2. Variation de la pression sur un plan vertical......................................................................... 9
2.4 Quelques principes d’hydrostatique .............................................................................................. 9
2.4.1 Pression d’un point en différent forme d’un réservoir ........................................................... 9
2.4.2 Additivité des pressions ....................................................................................................... 10
2.4.3 Vases communicants............................................................................................................ 10
2.5 Pression absolue (totale) et pression relative (effective)............................................................. 11
2.6 Transmission des pressions (principe de Pascal)......................................................................... 11
2.7 Dispositifs de mesure de la pression ........................................................................................... 12
2.8 Les forces de pression sur les surfaces de la paroi ...................................................................... 13
2.8.1 Force de pression sur une surface plane............................................................................... 13
2.8.2 Force de pression sur une surface verticale ou inclinée ....................................................... 13
2.8.3 Force de pression sur une surface courbe............................................................................. 14

4. 4
CHAPITRE 3: DYNAMIQUE DES FLUIDES................................................................................ 19
3.1 Introduction................................................................................................................................. 19
3.2 Notion de base............................................................................................................................. 19
3.2.1 Fluide parfait et fluide réel................................................................................................... 19
3.2.2 Ecoulement parmanent et non-parmanent............................................................................ 19
3.2.3 Ecoulement en charge et à surface libre............................................................................... 19
3.2.4 Fluide compressible et incompressible ................................................................................ 19
3.2.5 Ecoulement uniforme et non-uniforme ................................................................................ 19
3.2 Ligne de courant, tube de courant ............................................................................................... 20
3.3 Débit volumique, débit massique ................................................................................................ 20
3.4. Principe de conservation de la masse......................................................................................... 20
3.5 Equation d’Euler.......................................................................................................................... 21
3.6 Relation de Bernoulli................................................................................................................... 21
3.7 Tube de Pitot ............................................................................................................................... 23
3.8 Tube de Venturi........................................................................................................................... 23
CHAPITRE 4: REGIME D’ECOULEMENT DES LIQUIDES REELS...................................... 27
4.1 Introduction................................................................................................................................. 27
4.2 Experience de Reynolds .............................................................................................................. 27
4.3 Répartition de profils de vitesses................................................................................................. 28
4.4 Théorème de Bernoulli appliqué à un fluide réel avec pertes de charge..................................... 29
4.5 Pertes de charges ......................................................................................................................... 29
4.5.1 Pertes de charge linéaire....................................................................................................... 29
4.5.2 Pertes de charges singulières................................................................................................ 33
4.5.3 Perte totale de charges.......................................................................................................... 34
4.6 Equation de Bernoulli généralisée............................................................................................... 34
CHAPITRE 5: ECOULEMENT A SURFACE LIBRE................................................................... 37
5.1 Introduction................................................................................................................................. 37
5.2 Classification des écoulements.................................................................................................... 37
5.2.1 Variation temporelle............................................................................................................. 37
5.2.2 Variation spatiale ................................................................................................................. 37
5.3 Paramètres essentiels................................................................................................................... 38
5.3.1 Paramètres géométriques...................................................................................................... 38
5.3.2 Paramètres hydrauliques ..................................................................................................... 40
5.4 Equation de continuité................................................................................................................. 42

5. 5
5.4.1 Vitesse d’écoulement ........................................................................................................... 42
5.4.2 Régimes d’écoulement......................................................................................................... 44
5.5 Ecoulement en régime permanent uniforme................................................................................ 45
5.6 Forme de section la plus avantageuse ......................................................................................... 48
5.7 Ecoulement parmanent non-uniforme......................................................................................... 49
5.7.1 Ecoulement graduellement varie.......................................................................................... 49
5.7.2 Ecoulement rapidement varié............................................................................................... 51
5.8 Section de contôle ....................................................................................................................... 53
CHAPITRE 6: ASSAINISSEMENT ROUTIER.............................................................................. 57
6.1. Rappels sur l’hydrologie de surface........................................................................................ 57
6.1.1 Notion d’un bassin versant................................................................................................... 57
6.1.2 Notion sur les précipitations................................................................................................. 57
6.1.3 Notion d'une averse et d'une intensité .................................................................................. 58
6.1.4 Notion de la période de retour.............................................................................................. 59
6.1.5 Courbes IDF (intensité-durée-fréquence)............................................................................. 59
6.1.6 Evaluation régionale des précipitations................................................................................ 60
6.1.7 Ecoulements superficiels...................................................................................................... 60
6.2. Assainissement routier............................................................................................................. 66
6.2.1 Introduction.......................................................................................................................... 66
6.2.2 Etapes à suivre pour une étude d’assainissement routier ..................................................... 66
6.2.3 Réseaux de collecte longitudinaux....................................................................................... 67
6.2.4 Ouvrages transversaux et de raccordement.......................................................................... 73
6.2.5 Ouvrages de contenance et de dépollution........................................................................... 73
6.2.6 Exutoires ............................................................................................................................. 73
6.2.7 Types et formes des fossés................................................................................................... 74
6.2.8 Autres ouvrages d’assainissement........................................................................................ 76
6.2.9 Les ouvrages de concentration des eaux .............................................................................. 79
6.2.10 Ouvrages de franchissement............................................................................................... 80

6. 1
INTRODUCTION GENERALE
L’hydraulique est la science qui traite des problèmes posés par l’eau en mouvement ou en repos.
Généralement on la trouve dans plusieurs domaines de l’ingénieur à savoir :
- L’hydraulique urbaine traite essentiellement les problèmes de conception des réseaux de
distribution d'eau potable et d'évacuation des eaux usées et pluviales en milieu urbain.
- L’hydraulique agricole traite essentiellement les problèmes liés à la conception du réseau
d’irrigation, son stockage et sa distribution, et le drainage des eaux en surplus dans le sol.
- L’hydraulique fluviale traite essentiellement l'écoulement à surface libre dans les cours d'eau
naturels ou artificiels
- L’hydraulique maritime doit envisager la protection des ports contre la houle, l’étude de la
stabilité des digues et des jetées, la lutte contre l’érosion des plages, l’ensablement des entrées
de ports, etc.
- L’hydraulique souterraine constituée par l’étude générale des fluides dans les milieux poreux :
les écoulements de nappes souterraines, les bilans hydrologiques, l’étude des puits et des
forages, l’infiltration sous les ouvrages, la stabilité des digues en terre, l’irrigation et le
drainage, la diffusion de la pollution.
- L’hydraulique routière ou encore l’assainissement routier est l’ensemble des moyens
techniques utilisés pour résoudre les problèmes de collecte et d’évacuation des eaux
superficielles provenant des précipitations atmosphériques, et l’évacuation des eaux
souterraines internes. L’accumulation de ces eaux est privilégiée par les talwegs et dépressions
du relief. L’assainissement routier sera développé dans le dernier chapitre de ce polycopie vu
son importance pour les géotechnicien.
Nous mettons l’organigramme suivant pour les branches de l’hydraulique :
Physique
Mécanique
Mécanique des fluides
Hydraulique
Statique des fluides Dynamique des fluides
Dynamique des fluides parfaits Dynamique des fluides réels
Ecouelement en charge
Ecouelement à surface libre
Cinématique des fluides

7. 2
CHAPITRE 1: PROPRIETES PHYSIQUES DES FLUIDES
1.1 Définition d’un fluide
Un fluide est un milieu continu, même si l'on choisit un très petit élément de volume, il sera toujours
beaucoup plus grand que la dimension des molécules qui le constitue. Une gouttelette de brouillard,
aussi petite soit-elle à notre échelle, est toujours immense à l'échelle moléculaire. Elle sera toujours
considérée comme un milieu continu. Un fluide peut s'écouler librement par suite du peu d'adhérence
entre elles des molécules qui le composent. Cette propriété que l’on appelle fluidité est due à une
grande mobilité des particules fluides. On distingue les liquides et les gaz.
Les liquides sont : considérés comme incompressible, occupent un volume déterminé et adoptent la
forme du récipient où ils sont versés, produisent une surface libre en contact avec l’air,
Les gaz sont : très compressibles, n’ont pas de forme et occupe le volume maximum qui lui est offert,
et ne produisent aucune surface libre,
1.2 Système d’unité
Les unités de mesure de base du système internationale sont :
Grandeur physique symbole dimension unité
La longueur L ou l L m : mètre
Le temps t T s: seconde
La masse m M Kg : kilogramme
La température T t °C : degré celcius
La vitesse v LT-1
m/s
L’accélération a LT-2
m/s²
La force F M LT-2
N
La masse volumique ρ M T-3
Kg/m3
Le poids volumique γ M L-2
T-2
N/ m3
La pression P M L-1
T-2
N/ m2
= Pa
La viscosité cinématique υ L² T-1
m²/s
La viscosité dynamique µ ML-1
T-1
Kg/m.s = Pa.s
1.3 Propriétés des liquides
1.3.1 La masse volumique (ρ, Rou)
La masse volumique (ou masse spécifique) d’un corps, quelque soit son état est le quotient de sa
masse par son volume.
ρ = M/V [kg/m3
]
Les liquides comme les huiles et les alcools ont une masse volumique inférieure à celle de l’eau, alors
que la masse volumique du mercure est supérieure à celle de l’eau.
ρeau à 20 °C = 998.16 kg/m3
, ρmercure à 20 °C = 13546 kg/m3
les gaz ont une masse volumique très faible : ρair = 1.225 kg/m3
à 15°C au niveau de la mer (Z = 0m).

8. 3
La masse volumique de l’air est variable, en fonction de l’altitude.
Z = 0 m ρair = 1.225 kg/m3
Z = 2000 m ρair = 1.007 kg/m3
Z = 8000 m ρair = 0.525 kg/m3
Z = 12000 m ρair = 0.320 kg/m3
La masse volumique des liquides est une fonction inverse avec la tepérature. Donc si la température
augmente, la masse volumique de fluide diminue légèrement.
On donne ici quelques valeurs de la masse volumique de l’eau en fonction de la température
Tableau 1.1 Masse volumique de l’eau en fonction de la température
Température
(°C)
Masse volumique
de l’eau (kg/m3
)
Température
(°C)
Masse volumique
de l’eau (kg/m3
)
0 999.79 50 988.04
4 999.97 60 983.13
10 999.65 70 977.70
20 998.16 80 971.81
30 995.59 90 965.34
40 992.17 100 958.40
1.3.2 Le poids volumique (γ, gamma)
Le poids volumique est notion très utile, on le définit par le rapport du poids sur le volume de la
masse, ou la masse volumique multiplié par la gravité.
γ = ρ . g = (m . g)/V [N/m3
]
1.3.3 La densité
La densité d’une substance est égale à la masse volumique de la substance par la masse volumique du
corps de référence. Pour les liquides, la densité de l’eau est utilsée comme référence
(à 4 °C ρeau ≈ 1000 kg/m3
). Pour les gaz, les mesures s’effectué par rapport à l’air. La densité est un
grandeur physique sans dimension.
à
[Sans unité]
1.3.4 La viscosité
La viscosité d’un fluide est sa propriété de resister aux efforts tangentiels qui tendent à faire déplacer
les couches liquides les unes par rapport aux autres. C’est une grandeur qui caracterise les frottements
internes des fluides, elle est due à l’interaction entre les molecules des fluides. Elle caracterise la
resistance d’un fluide à son ecoulement.
Les fluides de faible viscosité s’ecoulant facilement comme l’eau, alors d’autres liquides coulent
difficilement comme les huiles de véhicules qui sont très visqueux.

9. 4
a./ Viscosité dynamique
La définition du coefficient de viscosité découle de la formule de Newton, fondée sur le modèle de
plusieurs plans superposés de surface « S », distants d’un espace « dy » et dont le plan supérieur est
animé d’une vitesse « V ».
Les plans successifs étant retenus entre eux par les forces de frottement, il s’établit entre eux une force
de cisaillement « F » responsables de la diminution de la vitesse de déplacement des plans successifs
d’une valeur « dv ».
Fig. 1.1 : Comportement d'un fluide dans un écoulement laminaire entre deux plaques parallèles
lorsque la plaque supérieure se déplace avec une vitesse constante.
La formule de Newton définit la viscosité dynamique « µ » comme étant le rapport entre la contrainte
de cisaillement (Force sur Surface) et le gradient de vitesse (taux de déformation).
[Pa.s]
une autre unité est utilisé pour la viscosité dynamique, c’est le « poise », avec 1 Pa.s = 10 Poise
Fig. 1.2 : Contrainte de cisaillement en fonction de taux de déformation pour les fluides Newtonien

10. 5
Remarque :
- Les fluides Newtoniens, sont des fluides qu’ont une viscosité constante, comme l’air, l’eau, l’huile
Alors que les fluides non-newtoniens ont une viscosité variable, comme les boues, les pates, …
- Nous pouvons dire aussi, que les fluides parfaits ont une viscosité nulle (c’est un fluide qui n’existe
pas dans la nature).
- La viscosité existe dès qu’il y a mouvement relatif entre particules, que ce soit en régime laminaire
ou turbulent.
- La viscosité dynamique de l’eau diminue avec l’augmentation de la température.
b./ Viscosité cinématique
La viscosité cinématique υ (nu) s’obtient en divisant la viscosité dynamique par la masse volumique ρ
Soit :
[m²/s]
Elle peut être exprimée aussi en Stockes (St) , avec 1St = 10-4
m²/s
Tableau 1.1 Quelques valeurs des viscosités dynamique et cinématiques pour différents fluides.
D’après ce tableau nous constatons :
µmercure > µeau > µair et υmercure < υeau < υair
1.3.5 La tension superficielle
Les molécules de fluides sont attirées mutuellement par des forces d’attraction appelées forces
cohésives. Les forces d’attraction des molécules de deux différents liquides non-miscibles sont
appelées adhésives.
Imagénons, deux plaques de verre entre lesquelles on
met un mince film d’eau. La plaque inférieure peut
supporter une masse de plusieurs centaines de
grammes avant de tomber. Les deux plaques semblent
être collées l’une à l’autre.
Certains insects sont capables de
se déplacer sur l’eau
Une piece de monnie flotte à la
surface de l’eau
Une épingle d’acier flotte à la
surface de l’eau
Fig. 1.3 : Quelques phénomènes de la tension superficielle

11. 6
Les phénomènes observés dans ces images sont dûs à l’existance des forces à la surface libre du
liquide, c’est la tension de surface. La tension superficielle est un phénomène physico-chimique lié
aux interactions moléculaires d'un fluide. La surface libre du liquide se comporte comme une
membrane élastique tendue.
La tension superficielle est une propriété des liquides
qui permet de maintenir en équilibre leur surface libre.
Elle caractérise le contact entre deux fluides,
généralement un liquide et un gaz. Une molécule dans
un liquide immobile est soumise aux forces
d'attraction de ses proches voisines.
Si cette molécule est située au sein du liquide, la
résultante de ces forces est nulle. Mais si cette
molécule est située en surface du liquide, la résultante
est une force dirigée vers l'intérieur du liquide.
Fig. 1.4 : Schéma de la tension superficielle
1.3.5 La capillarité
Le phénomène de capillarité est un phénomène d'interaction qui regroupe l'ensemble des phénomènes
qui ont lieu à la surface d'un liquide au contact d'une paroi solide. Donc les molécules d’une surface
solide attirent les molécules du liquide avec une force plus grande que celle qui existe entre les
molécules du liquide (à l’exeption du mercure). Le liquide s’élève au-dessus du niveau de l’eau ou
descend en-dessous du niveau en fonction des caractéristiques du liquide (masse volumique), en
fonction du diamètre de tube capillaire, et en fonction de la tension superficielle de ce liquide.
La surélévation d’eau dans le tube est appelée montée capillaire, et l’abaissement de mercure est
appelée la descente capillaire.
Fig. 1.5 : Phénomène de capillarité
La hauteur de capillarité « h » est déterminé par la formule de Jurin (en mètres) :
Avec, ϴ : angle de contact entre le liquide et la surface solide en degré
σ : tension superficielle du liquide (N/m²)
d : diamètre interne de tube capillaire (m)
Adhésion > Cohésion Adhésion < Cohésion

12. 7
Exercice 1 :
Un cylindre de 12.2 cm de rayon tourne à l’intérieur d’un cylindre fixe de même axe et de 12.8 cm de
rayon. Les deux cylindres ont 30 cm de long.
- Déterminer la viscosité du liquide qui remplit l’espace entre les deux cylindres s’il est nécessaire
d’appliquer un couple de 0.881 N.m pour maintenir la vitesse angulaire à 2π rad/s.
Solution :
La vitesse tangentielle du cylindre intérieur est : V = ω . r = 2 π x 0.122 = 0.766 m/s
Vu que l’intervalle entre les deux cylindre est petit, on peut admettre que le gradient est rectiligne et
on peut utiliser le rayon moyen.
Le couple de rotation : C = F x R
La force de cisaillement : F = τ x A (A : surface de contact du liquide avec le cylindre)
τ = 29.93 Pa
, µ = 29.93/128 = 0.234 Pa.s µ = 0.234 Pa.s
Exercice 2 :
Un tube en glace de diamètre 0,6 mm est inséré dans l’eau à 20 C.
- Déterminer l’ascension capillaire de l’eau dans le tube
Si : La tension superficielle de l'eau à 20 ° C est de 0,073 N/m.
L'angle de contact de l'eau avec le verre est de 0 °
Solution :
Selon la formule du Jurin
h = (4 x 0.073 x Cos 0°)/(1000x9.81x0.6 x 10-3
)
h = 0.05 m = 5 cm
L'eau monte dans le tube de 5 cm au-dessus du niveau de la surface du liquide.
Si le diamètre du tube était de 1 cm, la remontée capillaire serait de 0,3 mm, ce qui est à peine
perceptible à l'oeil. En fait, l'effet capillaire peut être ignoré pour les tubes de grand diamètre.

13. 8
CHAPITRE 2: HYDROSTATIQUE
2.1 Introduction
L’hydrostatique ou la statique de fluide est la branche de l’hydraulique qui s’occupe des fluides au
repos (équilibre absolu) ou accélérés en bloc (équilibre relatif) et son interaction avec les surfaces et
les corps solides immergés.
2.2 Pression en un point d’un fluide
Dans un fluide au repos, la pression désigne la force par unité de surface qui s’exerce
perpendiculairement à un élément de surface dS. La pression est indépendante de l'orientation de la
surface sur laquelle elle agit.
P = F/A
La pression hydrostatique en un point est égale dans toutes les directions
2.3 Lois fondamentales
Il existe deux lois fondamentales en hydrostatiques, et la connaissance de ces lois est absolument
nécessaire.
2.3.1. Surfaces isobares
Comment s’exerce la pression en différents points d’un plan horizontal dans un fluide d’une façon
générale ?
Imaginons, à l’intérieur d’un fluide un parallélépipède de faible hauteur allongé sur un plan horizontal
dont chacun des petits côtés est un élément de surface dS.
Pour une profondeur constante h1 = h2
La poussée vers la droite est : dF1 = P1 . dS
La poussée vers la gauche est : dF2 = P2 . dS
Et puisque le volume est à équilibre : ∑F = 0
Ce qui donne P1 = P2
Cette première loi fondamentale s’énonce ainsi :
La pression est identique en tous les points d’un plan horizontal dans un fluide en équilibre.
Fig. 2.2 : Variation de la pression sur un plan
horizontal
Fig. 2.1 : Direction d’une force sur un plan

14. 9
2.3.2. Variation de la pression sur un plan vertical
Comment s’exerce la pression en différents points d’un plan vertical dans un fluide ?
Imaginons, à l’intérieur d’un fluide un cube dont chacune des dimensions est un élément de longueur
dx, dy, et dz
Les forces sur les surfaces (forces de pression)
dF1= - P dx.dy = - P. dS
dF2 = + (P + dP) dx.dy = + (P + dP). dS
Les forces de volume (poids)
dw = - ρ.g. dx.dy.dz = - ρ.g. dS. dz
Puisque le volume est à l’équilibre ∑F = 0
– dF1 + dF2 - dw = 0 , avec dz = –Z2 – (–Z1)
ce qui donne + dP = – ρ.g. dZ
Cette équation peut s’écrire sous la forme : [m]
Cette équation peut s’écrire sous la forme c’est la loi de la statique de fluide.
Cette deuxième loi fondamentale s’énonce de la façon suivante :
Dans un plan vertical, la variation de pression entre deux points est égale au poids volumique du
fluide multiplie par la variation de la profondeur et la pression s’accroit avec la profondeur.
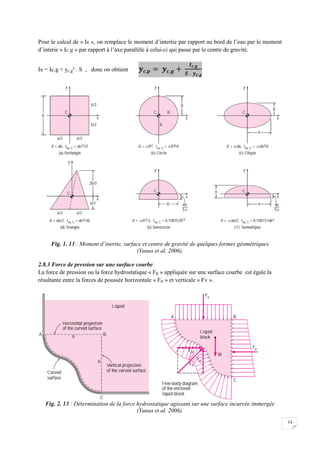
2.4 Quelques principes d’hydrostatique
A partir des lois fondamentales précédemment démontrées, on peut déduire trois principes de base
applicables au cas des liquides.
2.4.1 Pression d’un point en différent forme d’un réservoir
Démontrer que pour la même hauteur en différents volumes d’un réservoir, la pression est la même ?
Pour établir une équation qui permet de calculer directement la pression à une profondeur précise on
différents volumes d’un même liquide.
Fig. 2.3 : Variation de la pression sur un plan
vertical

15. 10
On a , avec h2-h1 = h
Si on considère que la pression en surface est P1 = 0, ce qui donne
On voit que peu importe la forme du volume, s’il s’agisse du même liquide, on arrive à la même
pression.
Le premier principe de l’hydrostatique s’énonce :
La pression exercée par un liquide à une profondeur donnée est totalement indépendante de la forme
et du volume de liquide au-dessus de ce niveau.
2.4.2 Additivité des pressions
Quand des liquides non miscibles de masse volumique différente se superposent,
le calcul de la pression présente un cas particulier.
Ce deuxième principe de l’hydrostatique se formule de la manière suivante :
La pression en un point donné, dans les liquides hétérogènes, est égale à la somme des pressions
exercées par chacun des liquides au-dessus de ce point.
2.4.3 Vases communicants
Prenons le cas d’un réservoir avec différents
embranchement. Toutes les surfaces libres du
même liquide, supportant la même pression
sont dans le même plan horizontal.
Fig. 2.6 : Vases communicants
Fig. 2.5 : Additivité des pressions
Fig. 2.4 : Differentes formes de réservoirs

16. 11
Le troisième principe de l’hydrostatique s’énonce comme suit :
Dans le cas d’un liquide à l’équilibre, la surface du liquide est en tout point à niveau égal quelle que
soit la forme du contenant.
2.5 Pression absolue (totale) et pression relative (effective)
La pression relative est référée à la pression atmosphérique. Dans de nombreux cas les effets de la
pression atmosphérique se compensent quand elle agit sur toutes les parois : seuls sont alors
intéressants les effets de la pression due au liquide (pression uniquement due au fluide). cette pression
peut donc prendre une valeur positive si la pression est supérieure à la pression atmosphérique ou une
valeur négative si la pression est inférieure à la pression atmosphérique.
La pression absolue est la pression mesurée par rapport au vide absolu (c'est-à-dire l'absence totale de
matière). Elle est toujours positive.
Les deux types de pressions correspondent physiquement à la même pression, elles sont simplement
exprimées sur des échelles ayant des "zéros" différents. La relation suivante permet de passer de l'une
à l'autre:
Pabsolue = Prelative + Patmosphérique
On parle parfois de pression différentielle: il s'agit de la différence de pression mesurée entre deux
points. Cette différence a évidemment la même valeur pour des pressions exprimées en pression
absolue ou en pression relative.
On parle de dépression quand la pression absolue est inférieure à la pression atmosphérique:
la pression relative est négative dans le cas d'une dépression.
2.6 Transmission des pressions (principe de Pascal)
un liquide en équilibre transmet intégralement et en tous ses
points toutes variations de pression produites en un point
quelconque de ce liquide.
Ce principe est connu sous le nom de principe de pascal.
Ce phenomene de transmission de pression permet le
developpement du fonctionnement de la presse hydraulique, le
cric, piston hydraulique.
Fig. 2.8: Transmission de pression
Fig. 2.7 : Le référence zéro des
pressions absolue et relative

17. 12
La transmission de pression conduit au rapport suivant dans
une presse hydraulique :
P1 = P2 , donc F1/S1 = F2/S2
Donc on appliquant une faible force F1 dans la S1, on obtient
une très grande force F2 qui depent directement de la surface S2
dans un cric hydraulique par exemple, les pressions en A
et B sont égales , ce qui donne :
FB = FA x SB /SA , donc la force FB est multiplie
Si on applique une force Fo sur le levier du cric, soit à
une distance « a » par raport au point de rotation, et à une
distance « b » du centre de piston au point de rotation, et
appliquant le pricipe des moments on obtient :
Fo x a = FA x b , cela donne FA = Fo . a / b
Et donne finalement FB = Fo . (a / b) . (SB /SA)
On tenant compte des pertes d’energie dans les parties frottantes, nous introduisons un facteur de
randement qui varie généralement entre η = 0.8 à 0.9
Ce qui donne FB = η . Fo . (a / b) . (SB /SA)
2.7 Dispositifs de mesure de la pression
La mesure de la pression se fait par divers types de manometres pour les pressions relatives
(manometriques) positives, et par le vacuometre pour les pressions relatives negatives (pressions
vacuometriques). Il y’a entre autre divers types d’instrument de mesures de la pression, dont :
 Les tubes manometriques : utilises pour la mesure de pressions relativement faibles, comme les
tubes piézometriques, tubes à liquide manométriques, manomètres différentiels, les anciens
baromètres,…
 Les manometres mecaniques : utilises pour la mesure de pressions relativement plus elevées,
comme les manometres mecaniques à aiguille ou numérique, nouveaux baromètres,
vacuomètres,…
Fig. 2.10 : Cric hydraulique
Fig. 2.9: Principe de Pascal

18. 13
2.8 Les forces de pression sur les surfaces de la paroi
2.8.1 Force de pression sur une surface plane
Sur un plan horizontal dans un liquide au repos la pression
est la même.
F = ρ . g . h . S (S : est la surface)
Fig. 2.11: force de pression sur une surface plane.
La force de pression du liquide correspond au poids de la colonne du liquide à une hauteur « h »
au-dessus de lui. Donc la force dépend de la hauteur « h » et de la surface du fond, et ne dépend ni du
volume, ni du fond du réservoir (pour différentes formes de réservoir, la force de pression est la
même).
2.8.2 Force de pression sur une surface verticale ou inclinée
Chaque point d’une surface inclinée en contact avec le liquide est soumis à une pression différente en
fonction de la profondeur d’immersion.
avec, hc.g : hauteur du centre de gravité de la surface « S »
Donc pour calculer la valeur de la force de pression « F » sur un paroi, on doit connaitre la position de
son centre de gravité.
Fig. 2.12: Force de pression et centre de poussée d’un liquide sur un plan incliné (Ghernaout 2010).
Pour déterminer le point d’application de la force « F », on doit déterminer la hauteur du centre de
poussée « hc.p ». pour cela on utilise un principe de la mécanique, soit :
Avec, S : surface de la paroi ;
yc.g : la distance entre le bord de l’eau et le centre de gravité ;
Ix : le moment d’inertie de la surface de la paroi par rapport au bord de l’eau.

19. 14
Pour le calcul de « Ix », on remplace le moment d’intertie par rapport au bord de l’eau par le moment
d’interie « Ic.g » par rapport à l’axe parallèle à celui-ci qui passe par le centre de gravité.
Ix = Ic.g + yc.g² . S , donc on obtient
Fig. 1. 13 : Moment d’inertie, surface et centre de gravité de quelques formes géométriques
(Yunus et al. 2006).
2.8.3 Force de pression sur une surface courbe
La force de pression ou la force hydrostatique « FR » appliquée sur une surface courbe est égale la
résultante entre la forces de poussée horizontale « FH » et verticale « Fv ».
Fig. 2. 13 : Détermination de la force hydrostatique agissant sur une surface incurvée immergée
(Yunus et al. 2006).

20. 15
La composante horizontale de poussée est égale au produit de cette pression « P » et de la projection
verticale de cette surface.
FH = Fx = ρ . g . hc.g . Sv avec Sv : surface sur la projection verticale
Fv = Fy + W = Fy + ρ . g . V avec V: volume du liquide de la surface ABC.
β = Arctg (Fv / FH)
Fig. 2. 14 : Exemples de détermination du poids « W » dans le cas d’une surface courbe

21. 16
Exercice 1 :
La figure ci-dessous représente un réservoir ouvert, équipé de deux tubes piézométriques et rempli
avec deux liquides non miscibles :
L'huile a masse volumique ρ1=720 kg/m3
, avec une hauteur h1 = 1.7 m,
L’eau salée a masse volumique ρ2=1025 kg/m3
, une hauteur h2 =0.3 m.
- Déterminer la hauteur de l’huile au point E ;
- Déterminer la pression relative au point B ;
- Déterminer la pression relative au point C ;
- Déduire le niveau piézométrique au point D.
Solution :
- Le point E s’élèvera dans le piézomètre à la même
hauteur que le liquide A dans le réservoir, par ce
le piézomètre et le réservoir sont soumis les deux
à la pression atmosphérique
- La pression relative au point B :
PB = ρhuile x g x h1 = 720 x 9.81 x 1.7 = 12007 Pa
- La pression relative au point C :
PC = ρhuile x g x h1 + ρeau x g x h2 = 12007 + 1025 x 9.81 x 0.3 = 15024 Pa
- Le niveau piézométrique au point D
Exercice 2 :
De l’huile de densité 0.75 coule à travers la conduite
représentée dans la figure ci-dessous, et fait monter le
mercure dans le manomètre en U.
Calculer la valeur de h si la pression en A est de 1.38
bar.
Solution :
Pression en B = Pression en C
PB = PA + ρhuile.g. (0.8 + h)
Pc = PD + ρmercure.g. (h)
PA + ρhuile.g. (0.8 + h) = PD + ρmercure.g. (h)
1.38 105
+ 750 x 9.81 x (0.8+h) = 0 + 13570 x 9.81 x h ce qui donne h = 1.14 m

22. 17
Exercice 3 :
Calculer la grandeur de la force due à l’action de l’eau sur une surface rectangulaire de 6m x 3 m pour
une paroi verticale (A-B) et une paroi inclinée de forme triangulaire (C-D) de 6m x 4m avec un
sommet au point C, comme représentée dans la figure ci-dessous.
Déterminer la position du centre de poussée de l’eau
Solution :
1) grandeur de la force et position de la force de
poussée de la surface verticale AB:
FpAB : force s’exerçant sur la paroi verticale
AB = ρghc.g SAB
FpAB = 1000 x 9.81 x (4+3) x (6 x 3) = 1236.06 KN
La force résultante s’applique au centre de pression qui est situé à une profondeur par rapport à la
surface de :
2) La grandeur de la force et position de la force de poussée de la surface inclinée CD:
FpCD : force s’exerçant sur la paroi inclinée CD = ρghc.g SCD
FpAB = 1000 x 9.81 x (4+ x Sin 45°) x ( ) = 1071.72 KN
La force résultante s’applique au centre de pression qui est situé à une profondeur par rapport à la
surface de :
Exercice 4 :
Déterminer les composantes de la force due à l’action de l’eau par
mètre de longueur sur la surface courbe AB.
Solution :
Fx : force s’exerçant sur la projection verticale CB = ρghc.g SCB
Fx = 1000 x 9.81 x (1) x (2x1) = 19620 N
Qui agit à (2/3) x (2) = 1.33 m de C
Fy : poids de l’eau au-dessus de la surface AB = 9810 (π 2²/4 x 1) = 30820 N

23. 18
Exercice 5 :
AB est un arc circulaire de 2m de rayon et de 1m de largeur.
- Calculez la magnitude et la direction de la force hydrostatique exercée sur la surface AB
Solution :
Fx = FAC = 1000 x 9.81 x (4+1) x (2 x 1) = 98.1 KN
Fy = W + FCB ;
W = 1000 x 9.81 x 3.14 = 30.8 KN
FCB = 1000 x 9.81 x 4 x (2 x 1) = 78.5 KN
Fy = 109.3 KN
Les coordonnées du centre de la pression
yc.p : est la composante horizontale
xc.p : est la composante verticale (∑MC = 0)
xc.p x Fy = FBC x 1m + W x , avec
ce qui donne xc.p = 0.957 m
avec une direction ϴ = Arctag (Fy/Fx) = 48.1°

24. 19
CHAPITRE 3: DYNAMIQUE DES FLUIDES
3.1 Introduction
L’hydrodynamique c’est la partie de l’hydraulique qui s’intéresse surtout aux mouvements des fluides.
L’étude des principes de conservation de la masse, l’écoulement tubulaire (laminaire/turbulent), les
mesures du débit,…
L’hydrodynamique étudie un grand nombre de problème d’ordre pratique lié au mouvement du liquide
tel que : le mouvement de l’eau dans les conduites et dans les canaux, les turbomachines,…
3.2 Notion de base
3.2.1 Fluide parfait et fluide réel
Un fluide parfait est un fluide dépourvu de la viscosité. Ses particules glissent les unes sur les autres
sans frottement, sans tourner sur elles-même et sans tourbilloner, donc sans perte de charge.
En mécanique des fluides, un fluide est dit parfait s'il est possible de décrire son mouvement sans
prendre en compte les effets de frottement.
Contrairement à un fluide parfait, qui n’est qu’un modèle pour simplifier les calculs, pratiquement
inexistant dans la nature, un fluide réel se caractérise par sa viscosité ce qui conduit à une perte
d’energie à cause des frottement le long du mouvement du fluide.
3.2.2 Ecoulement parmanent et non-parmanent
Un régime est dit parmanent quand en un point ou dans une section, la vitesse moyenne, le débit, la
pression, et tous autre paramètres restent constante dans le temps. Alors qu’on régime non-parmanent
(variable) se caractérise par la variation de ces paramètres dans le temps du même point ou de la même
section.
3.2.3 Ecoulement en charge et à surface libre
L’écoulement en charge c’est un écoulement sous-pression qu’on le trouve dans les conduites à
section pleine. Alors que l’écouelemnt à surface libre qui a lieu dans les cours d’eau et les canaux
artificiels, son plan d’eau supérieur étant libre et il est en contact direct avec l’atmosphère, et
l’écoulement se fait par gravité.
3.2.4 Fluide compressible et incompressible
On sait que la compressibilité des gaz est très élevée et influe beaucoup sur leur comportement.
Par contre les liquides sont très peu compressibles. En pratique on les considèrent comme
incompressibles. Un fluide est dit incompressible lorsque le volume occupé par une masse donnée ne
varie pas on appliquant une pression extérieure.
3.2.5 Ecoulement uniforme et non-uniforme
L’écouelement uniforme est subdivisé en un écoulement uniforme et un autre non-uniforme (varie).
D’une section à une autre section, si rien ne varie (vitesse moyenne, débit) le long d’une distance,
l’écoulement est dit uniforme. C’est le cas de l’écoulement dans les tuyaux rectilignes, loin des
singularités.
L’écoulement non-uniforme diffère par la variabilité des paramètres. On le rencontre dans les cas où la
vitesse moyenne change avec la présence d’un changement de section, même si le débit reste le même.

25. 20
3.2 Ligne de courant, tube de courant
On appelle lignes de courant, des lignes tangentes en chacun de
leur point à la direction des vecteurs de vitesses d'écoulement à
l'instant « t ». Cette ligne est tracée par une série de points dans le
liquide en mouvement. On peut dire que la ligne de courant
représente le parcours d’une masse élémentaire de fluide.
L’ensemble des filets d’écoulement traversant une section
quelconque perpendiculaire aux flux général détermine un tube
d’écoulement de courant.
3.3 Débit volumique, débit massique
En hydraulique, en utilise souvent la notion de débit et la vitesse moyenne d’écoulement.
Le débit du liquide est la quantité du liquide passant par unité de temps par une section d’écoulement
donnée du courant, on distingue :
- Le débit volumique « Q » mésuré en m3
/s ou en l/s : étant le volume de liquide qui traverse une
section par unité de temps
Q = volume /temps = vitesse x section (Q = volume/temps = V x S)
- Le débit massique « » mesuré en Kg/s : étant la masse de liquide qui traverse une section par unité
de temps
= masse volumique / temps ( = m/t = ρ x volume/temps = ρ x Q)
avec
V : vitesse moyenne en m/s ;
S : section transversale de la conduite en m² ;
ρ : masse volumique du liquide en m3
/s
3.4. Principe de conservation de la masse
Soient S1 et S2 deux sections normales d’un petit tube de courant, ρ1 et ρ2 les masses spécifiques, V1
et V2 les vitesses scalaires moyennes du fluide qui traverse ces sections. Selon le principe de
conservation de la masse, les débits de masse à travers S1 et S2 sont égaux en régime stationnaire:
ρ1 S1 V1 = ρ2 S2 V2
Dans le cas d’un liquide incompressible : ρ1 = ρ2 ,
Ce qui donne S1 V1 = S2 V2 c’est le débit volumique
Ce résultat s’applique notamment à l’écoulement d’un liquide
dans un tuyau de section variable. C’est l’équation de continuité
d’un filet liquide incompressible.
Fig. 3.1 : Ligne et tube de
courant pour un écoulement
Fig. 3.2 : Principe de
conservation de masse

26. 21
3.5 Equation d’Euler
Prenons un tube de courant ayant à l’intérieur un volume infinitésimal de fluide dont l’aire de section
est « S », la longueur « ds » et de masse « m ». à cet endroit le tube de courant fait un angle « α » avec
l’horizontale. A la section 1, la pression est « P » et à la section 2, la pression est « P+ dP ». de la
section 1 à la section 2, il y a un changement de vitesse « dv » et une hausse de niveau « dx ».
A la section (1) la force F1 = P.S
A la section (2) la force F2 = -(P + dP).S (sens inverse de l’écoulement)
La projection de la masse dans le sens d’écoulement : - m.g.Sin(α)
Selon la deuxième loi de Newton, la poussée nette est égale à Qm.dv, donc :
-dP.S – m.g. Sin(α) = Qm.dv = (ρ. V. S ). dv
On a : m = ρ. S.dx et Sin(α) = dz / dx
-dP.S – (S.dx . ρ.g). dz / dx = ρ.V.S. dv
En simplifiant, on obtient une relation très importante en mécanique des fluides, l’équation d’Euler.
3.6 Relation de Bernoulli
Appliquons l’équation d’Euler à l’écoulement du liquide parfait ; la masse volumique étant invariable,
il devient facile d’intégrer chaque terme de cette équation entre deux sections quelconques, 1 et 2 :
Ce qui donne :
Cette relation peut s’écrit sous la forme :
C’est l’équation de Bernoulli (1700-1782)
Fig. 3.3 : Principe de
conservation de masse

27. 22
Expression dans laquelle
P : désigne la pression,
z : la hauteur par raport à un niveau de repère,
v : la vitesse du courant.
L’unité pour les trois termes est le joule par newton, c'est-à-dire d’énergie par unité de poids :
a. L’équation de Bernoulli peut s’interpréter en terme de hauteur
z : hauteur géométrique / altitude
: hauteur due à la pression / hauteur manométrique , : hauteur piézométrique
: hauteur due à la vitesse / hauteur capable
Les trois hauteurs donnent la hauteur de la charge totale
b. L’équation de Bernoulli peut s’interpréter en terme de pression
P : pression statique
: pression hydrostatique
: pression cinétique ou pression dynamique (elle résulte du mouvement)
Les trois termes donnent la pression totale (ou la charge)
c. L’équation de Bernoulli peut s’interpréter en terme d’énergie
multiplions tous les termes de l’équation par un volume « V »
Epr = P.V : Energie de pression ;
Ep = z.ρ.g.V = m.g.z : Energie potentielle ;
Ec = = : Energie cinétique
Em = Cte
.V : Energie totale / energie mécanique
d. Représentation graphique de l’équation de Bernoulli
Nous pouvons représenter les trois hauteurs de l’équation de Bernoulli pour différentes sections d’une
conduite. Il devient facile, et parfois très utile, d’en faire une représentation graphique.
Vu qu’il s’agit d’un fluide parfait, l’energie totale par unité de poids demeure constante ;
elle détermine une droite parallèle au plan de référence, la ligne de charge énergitique ou plus
simplement ligne de charge. La somme des deux premiers termes (z + P/ρg) détermine une ligne qu’on
appelle la ligne piézométrique.

28. 23
Fig. 3.4 : Représentation de l’équation de Bernoulli d’un d’un fluide parfait
(Beaudy et Rolland 1995)
3.7 Tube de Pitot
Le tube de pitot est largement utilisé comme une sonde portative pour mesurer la vitesse d’un
écoulement. Il s’agit d’un tube de faible diamètre ≈ 5 mm.
La formule utilisée pour le cas d’un tube de Pitot, qui donne la vitesse en fonction de la différence de
hauteur.
Avec :
Cv : coefficient de vitesse dont la valeur est fournie par le fabricant de l’instrument ou obtenue
par étalonnage. Dans le cas des appareils bien conçus Cv = 0.98
3.8 Tube de Venturi
Considérons l’écoulement d’un fluide incompressible dans un Venturi dont l’entrée est « S1 », la
section de la gorge « S2» et la section de sortie « S3». Les tubes piézométriques placés au niveau des
sections 1, 2 et 3 indiquent des hauteurs h1, h2 et h3.
En supposant qu’il n’y a aucune perte de charge dans ce tronçon de conduite, et l’écoulement est
permanent, l’équation de Bernoulli s’écrit :
Fig. 3.5 : Tube de Pitot

29. 24
V1, V2 et V3 sont les vitesses moyennes dans les sections 1, 2 et 3
en appliquant l’équation de continuité, on a :
V1 S1 = V2 S2 = V3 S3 = Q………………….(2)
Q : étant le débit volumique passant dans le Venturi
On va chercher la valeur de la vitesse « V2 » en fonction de « V1 ». En remplaçant dans la formule (1)
la valeur V1 , on trouve finalement la relation suivante :
En réalité le débit déterminé par cette relation est inférieur à la valeur réelle mesurée
exprimentalement. Cette différence est décrite par le coefficient de débit « Cq », ce coefficient peut
être déterminé exprimentalement, il est généralement compris entre 0.9 à 0.99
Fig. 3.6 : Tube de Vernturi (Gaaloul 2013)

30. 25
Exercice 1 :
L’eau s’écoule de point A vers B à un débit de 0,37 m3
/s et une hauteur de pression en A de 6,6 m.
Considérant qu’il n’y a aucune perte d’énergie entre A et B.
Calculer la pression en B et tracer la ligne de charge.
On donne : diamètres en A = 30 cm et en B = 60 cm
Côtes en A=3,0 m et en B=7,5 m
Solution :
On applique l’équation de Bernoulli en les points A et B
VA = Q / SA = 5.24 m/s et VB = 1.31 m/s
Exercice 2 :
On considère le siphon schématisé dans la
figure, de diamètre 10 mm.
- Calculer la vitesse au point 4 et le débit
volumique;
- Calculer la pression au point 3 ;

31. 26
Solution :
On applique l’équation de Bernoulli en les points 2 et 4
On a P1 = P2 = P4 = Patm , V2 ≈ 0 m/s , Z2 = 0.5 m et Z4 = 0 m
= 3.13 m/s
Le debit volumique Q = V4. S → Q = 0.246 l/s
La pression au point 3 : (On applique l’équation de Bernoulli en les points 3 et 4)
On a P4 = Patm , Z3 = 1.0 m et Z4 = 0 m
Pression relative P3rel = -1 m CE (P3rel = -10 KPa) et pression absolue P3abs ≈ + 9 mCE (P3 abs ≈ 90 KPa)
Exercice 3 :
Un tube Venturi, avec un diamètre d’entré de 30 cm et la gorge à un
diamètre de 15 cm, utilisé pour la mesure de débit. La dénivellation du
mercure du manomètre différentiel est de 35.8 cm.
Déterminer le débit traversant le Venturi, si le coefficient de débit
Cq=0.99 (on néglige les pertes de charge)
Solution :
On applique l’équation de Bernoulli en les points A et B
QA = QB → VA . SA = VB . SB ce qui donne VA = 0.25 VB
On a la pression au point L = à la pression au point R
PA + ρeau g (z + 0.358) = PB + ρeau g (0.75 + z) + ρmercure g (0.358 )
PA – PB = 3845.52 + 47657.57 = 51503.1 Pa
Donc 51503.1 = 7357.5 + 468.75 VB² , soit VB = 9.7 m/s
et
Le débit réel qui traverse le Venturi = Q x Cq = 0.172 x 0.99 = 0.17 m3
/s

32. 27
CHAPITRE 4: REGIME D’ECOULEMENT DES LIQUIDES REELS
4.1 Introduction
Lorsque on considère le fluide comme étant parfait, c’est comme s’il se comportait de façon idéale
dans son écoulement, sans perte de charge causée par les frottements entre les molécules du fluide et
les parois, alors que ce n’est pas la réalité, par ce que il y a effectivement des pertes d’energie le long
d’un écoulement dans les conduites. Donc il faut une méthode pour calculer ces pertes de charge.
Plusieurs scientifique s’intéressent à la perte d’energie dans les conduites, mais c’est à l’ingénieur
anglais Reynolds (1842-1912) que revient le mérite d’avoir défini clairement ce qu’est un liquide réel.
4.2 Experience de Reynolds
Un liquide est dit réel lorsqu’on tient compte de sa viscosité qui est le paramètre représentant sa
résistance à l’écoulement.
On dit qu’un liquide est visqueux
lorsqu’il s’écoule avec difficulté.
C’est donc la viscosité qui
engendre les forces de frottements
ou de cisaillement entre le liquide
et les parois de la conduite.
Reynolds a réalisé une étude systématique du régime d’écouelement en fonction de différents
paramètres intervenant dans le régime d’écoulement : vitesse d’écoulement, viscosité, diamètre.
Il a mis en évidence deux catégories d’écoulemnt pour un liquide réel : un régime laminaire et un autre
turbulent, avec un régime de transition entre les deux régimes.
Reynolds a constaté à partir de ses travaux sur le liquide réel, qu’il existe deux forces :
- La force d’inertie, qui dépend de la vitesse moyenne du liquide, du diamètre de la conduite et
de la masse volumique du liquide.
- La force de viscosité, qui est la viscosité dynamique du liquide.
Reynolds a donné son nom a ce nombre sans dimension appelé nombre de Reynolds « Re » donné par
la relation :
V : vitesse moyenne d’écoulement (m/s) ;
µ : viscosité dynamique du liquide (Pa.s) ;
D : diamètre intérieur de la conduite (m) ;
υ : viscosité cinématique du liquide (m²/s).
ρ : masse volumique du liquide (Kg/m3
)
Fig. 4.1 : Montage de l’experience Reynolds

33. 28
l’experience montre que :
Si Re < 2000 le régime est Laminaire : la force viscosité domine le mouvement du liquide
Fig. 4.2 : Ecoulement laminaire, en minces filets parallèles
Si 2000 < Re < 3000 le régime est intermédiaire (transition)
Fig. 4.3 : Ecoulement de transition,avec des filets de courant sinueux
Si Re > 3000 le régime est Turbulent : la force viscosité ne contrôle plus le mouvement des
molécules de liquide.
Fig. 4.4 : Ecoulement turbulent,apparition de turbulence
4.3 Répartition de profils de vitesses
En régime Laminaire: en écoulement laminaire la vitesse des particules est faible et que les lignes de
courant sont régulières, parallèles aux parois du contenant. Le profil de vitesse se répartit de manière
hyperbolique dans la section du conduit. Dans cette configuration, les forces visqueuses de
cisaillement sont supérieures aux forces de frottement.
En régime Turbulent : dans un écoulement turbulent les directions des particules se déplacent en
tourbillons, dont la taille, la localisation et l'orientation varient constamment, de manière désordonnée.
Ils apparaissent lorsque la vitesse est importante par rapport aux forces de viscosité. La dissipation des
énergies génère finalement un profil des vitesses plutôt régulier. Dans cette configuration, la vitesse
décroit de manière brutale au plus près des parois.
Fig. 4.5 : Profil de vitesse en régime laminaire
Fig. 4.6 : Profil de vitesse en régime turbulent

34. 29
4.4 Théorème de Bernoulli appliqué à un fluide réel avec pertes de charge
Lors d'un écoulement d'un fluide réel, il peut y avoir des pertes de charge entre deux sections (1) et
(2): dans le cas d’une installation ne comportant pas de machine hydraulique (pompe ou turbine) on
écrira la relation de Bernoulli sous la forme :
ΔH1-2 : les pertes de charge totale (en m)
4.5 Pertes de charges
Nous avons vu qu'il existe des freins au bon écoulement d’un liquide, à l'origine de chutes de pression
autrement appelées pertes de charge. Ces dernières dépendent :
 Des frictions intermoléculaires en relation avec la viscosité du liquide ;
 des frottements superficiels contre les parois de la canalisation ;
 des obstacles qui créent des variations géométriques.
 de la forme, des dimensions et de la rugosité de la canalisation
 de la vitesse d'écoulement
Ces pertes de charges totales « ΔHt = ΔHL + ΔHS » sont divisées en deux catégories :
- Pertes de charge primaires / linéaires «ΔHL » : elles sont dues aux frottements du liquide sur
la paroi interne de la tuyauterie. Les frictions visqueuses et les frottements sont liés à la
longueur de la canalisation. On les appelle aussi pertes de charge régulières ou systématiques.
- Pertes de charge secondaires / singulières «ΔHS »: elles sont provoquées par les accidents de
parcours (coudes, élargissements ou rétrécissement de la section, organes de réglage, etc.). On les
appelle aussi pertes de charge accidentelles ou locales.
4.5.1 Pertes de charge linéaire
Ce genre de perte est causé par le frottement intérieur qui se produit dans les liquides ; il se rencontre
dans les tuyaux lisses aussi bien que dans les tuyaux rugueux. Entre deux points séparés par une
longueur L, dans un tuyau de diamètre D apparaît une perte de charge ΔH1-2.
Fig. 4.7 : Perte de charge linéaire ΔH1-2 entre les sections 1 et 2

35. 30
Les pertes de charges linéaires, sont des pertes de charge réparties régulièrement le long des conduites.
En chaque point d’un écoulement permanent, les caractéristiques de l’écoulement sont bien définies et
ne dépendent pas du temps. La vitesse étant constante, la ligne piézométrique et la ligne de charge sont
parallèles.
Les chercheurs Weisbach et Darcy qui poursuivaient des recherches sur les écoulements, ont démonté
que pour un écoulement donnée les pertes de charge linéaires :
 Sont proportionnelles à la longueur L de la conduite, inversement proportionnelles à son
diamètre D, proportionnelle au carré de la vitesse débitante V du fluide.
 Dépendent de la rugosité de la paroi ε, de la viscosité µ et de la masse volumique ρ du
liquide.
Ils donnent la relation suivante :
ΔHL : perte de charge linéaire (m)
λ : représente le coefficient de frottement (coefficient de perte de charge)
L : longueur de la conduite (m)
D : diamètre hydraulique (m) (diamètre hydraulique = 4 x Section / Périmètre)
V : vitesse moyenne d’écoulement (m/s)
Les nombreuses formules de calcul mettent en jeu l'effet de la viscosité (au travers du nombre de
Reynolds Re) et celui de la rugosité (au travers de l'indice de rugosité absolue ε) et ce, plus ou moins
selon le régime d'écoulement. Les formules sont adaptées selon le régime d'écoulement : laminaire
Re ≤ 2000, transitoire, ou bien turbulent lisse ou rugueux avec Re > 2000. Face à la difficulté des
calculs, une représentation graphique par le diagramme de Moody, permet d'approximer le coefficient
de frottement λ.
a./ Formule de calcul du coefficent de frottement
 Pour un écoulement laminaire dans un tube circulaire Re < 2000, on utilise la corrélation de
Hagen-Poiseuille.
 Pour un écoulement turbulent dans un tube circulaire Re > 3000, il existe un grand nombre de
corrélations, certaines simples mais imprécises, d’autres plus lourdes mais plus proches de la
réalité.
 Formule de Blasius 1911-1913, pour 3000 < Re < 100 000
 Formule de Van Karman et Prandtl 1930, Re jusqu’à 3000 000

36. 31
 Formule de Colebrook-White 1939, pour des rugosités 0.1 mm < ε < 10 mm
 Formule de Stuart W. Chrchill, utilisée pour les deux régimes (laminaire et turbulent)
Tableau 4.1 : Rugosité moyenne de conduites commerciales
b./ Diagramme de Moody
En 1944, Moody a établi un diagramme à partir de l’équation de Colebrook-White. Cet abaque permet
de déterminer graphiquement la valeur de « λ » en fonction du nombre de Reynolds « Re » et la
rugosité relative « ε/D », ce qui simplifie beaucoup la détermination du coefficient de frottement « λ ».
Le diagramme montre bien qu’il existe :
- Une zone à écoulement laminaire (Re < 2000), le coefficient de frottement « λ » ne dépend
que de « Re » ;
- Une zone à écoulement transitoire (2000 < Re < 4000) le coefficient de frottement « λ »
dépend à la fois de « ε/D » et « Re »,
- Une zone de turbulence lisse (Re > 4000), le coefficient de frottement « λ » ne dépend que de
« Re », et toutes les iso ε/D sont confondues, cette zone correspond aux cas où l’épaisseur de
la couche visqueuse est nettement supérieure à la taille moyenne des rugosité de paroi. ;
- Une zone de turbulence transitoire, le coefficient de frottement « λ » dépend à la fois de
« ε/D » et « Re »,

37. 32
- Une plage de variation des paramètres dans laquelle le coefficient de perte de charge linéaire
ne dépend pas du nombre de Reynolds , c’est la partie droite de l’abaque, dans laquelle des
courbes iso ε/D sont presque horizontales.
c./ Formule empirique
Plusieurs formules empiriques ont été developpées pour l’estimation des pertes de charge linéaire,
nous citons à titre d’exemple la formule de Hazen-Williams (1902) :
Avec :
Chw : coefficeint de Hazen-Williams donnée sous forme de table
Coefficient de rugosité Valeur de Chw
Acier 120
Béton, brique 100
Bois 120
Cuivre 150
Étain 130
Fonte 100
Matière plastique, PVC 150
Plomb 130
Verre 140
Fig. 4.8 : Diagramme de Moody

38. 33
4.5.2 Pertes de charges singulières
Les pertes de charge singulières (ou locales) se produisent en présence d'obstacles, lorsque au moins
une partie des lignes de courant s’écartent de la direction principale de l’écoulement. Il y a alors
décollement de la paroi ou formation de zones de recirculation, par exemple au niveau des changement
de direction (coudes, raccords en Y ou en T, grilles...), ou de sections (jonctions, clapets, vannes, à
l'entrée ou en sortie de conduite...). Ces accessoires produisent une chute d'énergie rapide ; vitesse et
pression diminuent sur une distance plus ou moins importante.
Chaque accessoire est affecté d'un coefficient de perte de charge singulière «K » , déterminé
éxpriméntalement; sa valeur peut varier selon le constructeur. Le coefficient « K » est destiné à
soustraire une partie de l'énergie cinétique, il est donc toujours compris entre 0 et 1.
La perte de charge singulière est le produit du coefficient de perte de charge « K » de l'obstacle par la
représentation de l'énergie cinétique.
Avec :
ΔHs : perte de charge singulière ;
K : coefficient de perte de charge singulière de l’accessoire (de la singularité)
V : vitesse moyenne dans la section (m/s)
g : accélération de pesanteur = 9.81 m/s²
Fig. 4.9 : Valeurs de coefficient de perte de charge singuliètre de quelques singularités

39. 34
4.5.3 Perte totale de charges
Dans un circuit en ligne, la perte de charge totale « ΔHt » du circuit est, la somme des pertes de
charges linéaires et singulières.
ΔHt = ΔHL + ∑ ΔHS (m)
ΔHL : perte de charge linéaire (m) ;
∑ΔHS : la somme des pertes de charges singulières (m) ;
Dans la pratique, la perte de charge linéaire est majorée de 10 à 15 % pour compenser les
approximations liées à la détermination des coefficients de pertes de charges singulières « K ».
4.6 Equation de Bernoulli généralisée
D'autre part, la canalisation dispose parfois de moyen d'élévation de la charge (pompes), comme elle
peut disposer des appareils de consommation d’energie (Turbines). Tout ceci s'équilibre dans ce que
l'on nomme l'équation de Bernouilli généralisée dont l’expression utilisée en hydraulique est :
Avec :
HP : charge délivrée par la pompe
HT : charge délivrée à la turbine
ΔH1-2 : perte de charge totale entre les sections (1) et (2)
Fig. 4.10 : Théorème de Bernoulli généralisé
aux machines hydrauliques

40. 35
Exercice 1 :
On pompe du l’huile vers le réservoir C, par 1829 m de tuyau d’acier neuf de 406 mm de diamètre
intérieur. La pression en A est de 13.8 KPa, quand le débit est de 198 l/s, et la viscosité cinématique du
liquide est 5.16 10-6
m²/s, la densité du liquide d= 0.861, et la rugosité absolue de la conduite est
1.83 mm
a) Quelle est la puissance fournie par la pompe ?
b) Quelle doit être la pression en B ?
c) Tacer la ligne piézométrique
Solution :
a) détermination de la puissance fournie par la pompe :
On a rugosité relative
A partir du diagramme de Moody → f =0.03
Appliquons l’équation de Bernoulli entre A et C, avec plan de référence A, ce qui donne :
Ce qui donne Hp = 38.9 m,
donc la puissance fournie par la pompe = ρ.g.Q.Hp = 861 x 9.81 x 0.198 x 38.9 = 65040 w
b) détermination de la pression au point « B »
On applique l’équation de Bernoulli entre les points A et B
PB = 40.5 m et PB = 342333 Pa
c) La ligne piézométrique
La ligne piézométrique est représenté dans la figure ci-dessus, avec :
PA = 100+1.63 =101.6 m, PB = 100 + 40.5 = 140.5 m, et PC ≈ 124.4 m

41. 36
Exercice 2 :
La pompe BC fournit de l’eau au réservoir F. On a représenté la ligne piézométrique dans la figure ci-
dessous. Calculer :
a) La puissance fournie à l’eau par la pompe BC ;
b) La puissance consommée par la turbine DE ;
c) Le niveau d’eau du réservoir F.
Solution :
a) La puissance fournie à l’eau par la pompe :
on applique l’équation de Bernoulli entre le point B et C
On a VB = VC (même diamètre de la conduite, et même débit)
On néglige les pertes de charge au niveau de la pompe
Donc
on applique l’équation de Bernoulli entre le point C et D (même diamètre de la conduite VC = VD)
ce qui donne V= 2.97 m/s , soit Q = 0.84 m3
/s
La puissance fournie par la pompe = ρ . g . HP . Q = 1000 x 9.81 x 85 x 0.84 = 700.4 KW
b) La puissance consommée par la turbine = ρ . g . HT . Q = 1000 x 9.81 x (105-99)x0.84 = 49.4 KW
c) le niveau du réservoir F
on applique l’équation de Bernoulli entre le point E et F
Ce qui donne ZF = 99 – 9 = 90 m

42. 37
CHAPITRE 5: ECOULEMENT A SURFACE LIBRE
5.1 Introduction
L’écoulement est dit à surface libre, si la surface du liquide est partout soumise à la pression
atmosphirique, donc la surface est en contact direct avec l’atmosphère (l’air libre). C’est un
écoulement gravitaire.
Il est rencontré généralement dans les canaux naturels (cours d’eau, rivières) ou dans les canaux
artificiels découverts ou couverts réalisés par l’homme.
Fig 5.1. Types de canaux (Graf et Altinakar 1993).
5.2 Classification des écoulements
Un écoulement en surface libre peut être classé et décrit de diverses manières en fonction de la
variation de la profondeur d'eau par rapport au temps et à l'espace.
5.2.1 Variation temporelle
- Ecoulement permanent – les paramètres caractérisant l’écoulement ne changent pas au cours du
temps ou sont constants pendant l'intervalle de temps considéré.
- Ecoulement instationnaire (ou non permanent) - La profondeur de l'écoulement varie avec le
temps.
5.2.2 Variation spatiale
- L’écoulement est dit uniforme si les paramètres caractérisant l’écoulement restent invariables
dans les diverses sections du canal. La ligne de la pente du fond est donc parallèle à la ligne de la
surface libre dans chaque section du canal.
-L’écoulement non uniforme (ou varié) - les paramètres caractérisant l’écoulement varient le
long du canal. Un écoulement non uniforme peut être soit permanent soit instationnaire.

43. 38
Fig 5.2. Schéma des écoulements parmanents, uniformes et variés (Graf et Altinakar 1993).
5.3 Paramètres essentiels
5.3.1 Paramètres géométriques
Les paramètres géométriques sont relatifs à une section du canal dans un plan perpendiculaire à son
axe. Les paramètres essentiels sont :
b: Largeur du canal ;
y : Le tirant d’eau
B : La largeur au miroir ou largeur de la section mouillée : est la largeur du canal au niveau de la
surface libre.
m : Fruit des berges
Fig 5.3. Eléments géométriques de la section (Yonaba 2015).

44. 39
On peut définir certains paramètres hydrauliques :
- La section transversale d’un canal est la section plane normale à la direction de l’écoulement.
- La section mouillée (Sm) : est la portion de la section occupée par le liquide dans la section du canal.
- Le périmètre mouillé (Pm) : est formé par la longueur de la ligne de contact entre la surface mouillée
et les parois de la section du canal (la largeur de la surface libre n’entre pas en compte).
- Le rayon hydraulique est donné par le quotient Rh = Sm/Pm
- La profondeur moyenne ou la profondeur hydraulique est donnée par hm = Dh = Sm/B
Un canal dont la section, la pente et la rugosité restent constantes est appelé : canal prismatique.
Type de cours d'eau : il existe plusieurs classications. Une distinction des cours d'eau peut se faire en
fonction de la pente « I »:
I < 3 % on parle de rivière,
3 < I < 6 % on parle de rivière torrentielle,
I > 6 % on parle de torrent,
La pente du canal, notée « I » est la pente de son fond (radier), mesurée tout le long de son axe, et
comptée positivement si le chenal est descendant.
I = - dz/dx = sin α
Tous les paramètres B, y, Sm, Pm, Rh dépendent du débit et ne sont donc pas des constantes
géométriques. Seule la pente (i) qui est indépendante du débit, mais certes, mais elle peut varier dans
l’espace.
Tableau 5.1 : Eléments géométriques pour différentses sections de canaux
(Graf et Altinakar 1993).

45. 40
5.3.2 Paramètres hydrauliques
- La masse volumique de l'eau est notée ρw et vaut 1000 kg/m3
dans le cas de l’eau sans matières en
suspension.
- Le poids volumique de l'eau est noté γw= g. ρw = et vaut 9,81 kN/m3
pour de l’eau sans matières en
suspension. « g » désigne l'accélération de la pesanteur et vaut 9,81 m/s2
.
- Le débit « Q » est le volume d’eau qui traverse une section perpendiculaire à l’axe du canal par
unité de temps.
- La vitesse moyenne d’écoulement est V= Q/S
a./ Pression hydrostatique en un point
Dans un liquide au repos, ZA + P/ρw est constant au point « A » de masse liquide. ZA désigne la côte
du point. Dans ce suit, P désignera la pression relative, donc à une profondeur « h » sous la surface
libre P = γw . h
b./ Charge hydraulique en un point d’un liquide en mouvement
La charge hydraulique en un point « p » d’une ligne de courant est la valeur
HA = ZA + PA/ρw + VA
2
/2g
Où :
ZA : est la côte du point A
PA : est la pression en ce point A
VA : est la vitesse au point « A »
Si ΔZ désigne la différence d’altitude entre le point « A » et la surface libre,
La pression relative en point « A » est γw . ΔZ, avec ΔZ = yA . Cos (α) (puisque la pente est faible de
quelques ‰ à quelques %, donc Cos (α) ≈ 1)
Donc, en hydraulique à surface libre et pour une pente faible, la charge hydraulique en un point est :
HA = ZA + yA + VA
2
/2g
Fig 5.4. Charge hydraulique en un point (Degoutte 2006).

46. 41
c./ Ligne piézométrique
Dans un écoulement à surface libre, la hauteur piézométrique coïncide avec la surface libre pour les
faibles pentes du radier.
Fig 5.5. Ligne piézométrique (Degoutte 2006).
d./ Ligne de charge moyenne
La ligne de charge moyenne (ou ligne d’energie) est obtenue en reportant graphiquement Vp
2
/2g
au-dessus de la ligne piézométrique.
Fig 5.6. Ligne de charge moyenne (Degoutte 2006).
e./ Charge spécifique
La charge spécifique est la charge moyenne mesurée par rapport au fond du canal.
Hs = Hp – Zf = y + V2
/2g
Dans un écoulement à surface libre en régime uniforme, la perte de charge unitaire (ΔH1-2/L) ou pente
hydraulique de l’écoulement ou pente de la ligne d’énergie « j » est donc égale à la pente géométrique
« I » du fond du canal

47. 42
Fig 5.7. Diagramme d’energie pour un écoulement parment uniforme.
5.4 Equation de continuité
L’équation de continuité c’est l’équation fondamentale de la mécanique des fluides.
« La variation de la masse fluide contenue dans un volume donné pendant un certain temps est égale à
la somme des masses fluides qui y entrent, diminuée de celles qui en sortent » c’est le principe de
conservation de masse.
en faisant l’hypothèse d’un régime permanent Q = V.S
5.4.1 Vitesse d’écoulement
Dans les canaux en générale, les vitesses ponctuelles/locales sont nulles contre les parois (juste au
niveau des parois), et s’accroît très vite quand on s’éloigne. Sa valeur maximale est atteinte
approximativement entre 10 à 15 % en dessous de la surface libre.
Fig 5.8. Répartition de la vitesse ponctuelle dans quelque formes de canaux
(Graf et Altinakar 1993.)
Z1
Z2
h1 = P1/ρg
V1/2g
V2/2g
ΔH1-2
L
h2 = P2/ρg

48. 43
La vitesse moyenne en canal est V= Q/S
Quelques relations empiriques existent :
Vmoy = 0.82 Vmax (Prony 1839)
Vmoy = 0.5 (V0.2 + V0.8) (USGS)
Vmoy ≈ V0.4 (Grag 1996)
La vitesse moyenne d’écoulement Vmoy ne doit être ni trop faible, ni trop élevée. Cette vitesse doit être
supérieure à la vitesse d’auto-curage (0.4 m/s) et inférieure à la vitesse de cisaillement du matériau
afin d’éviter sa dégradation (érosion, abrasion…), cette dernière dépend de la résistance du matériau,
elle est de 4 m/s pour le béton et atteint 6 m/s pour les matériaux polyéthylènes.
Tableau 5.2 : quelques valeurs de la vitesse maximale en fonction de la nature de paroi du canal
(Degoutte 2006).
Nature de paroi du canal Vitesse maximum en m/s
Sables fins argileux ou limons argileux 0.75
Limons ou argiles sableux, bois 0.9
Argiles compactes 1.1
Mélanges de graviers, sables et limons, pierre cassées 1.2 - 1.5
Graviers, cailloux moyens, briques, blocs en béton 1.5 - 1.8
Paroi en métal, béton coulé sur place, béton préfabrique 2.0 - 2.5
Zone rocheuses ou béton 3.5 – 4.0
Béton armé dosé à 450 kg/m3
ou amiante de ciment 4.5
Matériau en polyéthylène 6.0
Si le matériau en place qui forme le canal a une granulométrie connue (diamètre du granulat est
connu), les Vmin et Vmax peuvent être choisies sur la base du diagramme de Hjulström.
Diagramme définissant l’état d’un grain, en fonction de sa taille et de la vitesse de d’écoulement.
Fig 5.9. Vitesses d’érosion et de sédimentation selon diagramme de Hjulström
(Graf et Altinakar 1993).

49. 44
5.4.2 Régimes d’écoulement
Les régimes d’écoulements sont caractérisés par le nombre de Reynolds et/ou nombre de froude.
Nombre de Reynolds
Il est déterminer en utilisant comme longueur caractéristique, le diamètre hydraulique Dh
é
Avec :
V : vitesse d’écoulement moyenne en m/s
Dh : diamètre hydraulique m
ν : viscosité cinématique en m²/s
Le nombre de Reynolds, c’est un rapport entre la force d’inertie par rapport à la force de viscosité
(résistance visqueuse). Ce nombre permet de classifier l’écoulement en trois régimes d’écoulements :
 L'écoulement laminaire (Re < 500): écoulement laminaire (rectiligne), le fluide s'écoule en
filets parallèles à l'axe de la conduite, sans mélange.
 L'écoulement intermédiaire/transitoire (500 < Re <2000): l'écoulement est plus ou moins
rectiligne, avec un peu de mélange (petits tourbillons).
 L'écoulement turbulent (Re > 2000): l'écoulement se fait avec de grands tourbillons, avec un
mélange important.
N.B : cette classification a peu d’importance en hydraulique à surface libre, les écoulements sont
rarement laminaires.
Nombre de Froude
Ce nombre apparaît essentiellement dans les écoulements à surface libre. Il s’exprime par le rapport
entre la vitesse moyenne (force d’inertie) et la force de pesenteur qui s’exerce sur celle-ci (vitesse de
propagation des petites ondes gravitaires).
é
Avec :
V : vitesse moyenne d’écoulement en m/s ;
g : accélération de la pesanteur (9,81 m/s2
) ;
hm : hauteur d’eau moyenne dans le canal en m
La détermination du régime d’écoulement permet de distinguer trois régimes d’écoulement :
F r > 1 : régime torrentiel, avec une faible hauteur d'eau et une forte vitesse.
F r < 1 : régime fluvial, avec une forte hauteur d'eau et une faible vitesse.
Fr = 1 : régime critique, c’est le cas limite de passage d’un régime à un autre.

50. 45
5.5 Ecoulement en régime permanent uniforme
Par définition, le régime d’écoulement est dit permenent uniforme, si le débit Q, la vitesse moyenne V,
la hauteur d’eau h restent constants tout le long du tronçon considéré. On paut dire aussi que les
pentes : du radier du canal, de la ligne d’eau et de la ligne piézometrque sont parallèles.
Fig 5.10. Ecoulement uniforme et non-uniforme dans un canal (Graf et Altinakar 1993).
Si on considère un élément de fluide de forme rectangulaire, et on applique la deuxième loi de Newton
en état d’équilibre.
 La force de frottement sur les parois est :
 La force de gravité :
Pour un état d’équilibre, la somme des forces = 0
= , après simplification
Vu que la pente est faible,
Donc la force tractrice au fond devient égale ……..(1)
Fig 5.11. Equilibre des forces appliquées sur une portion d'écoulement permanent uniforme
(Yonaba 2015).

51. 46
Le coefficient de frottement est donné par la formule Darcy-Weisbach.
La force tractrice égale aussi :
………….(2)
Nous faisons l’égalité entre les équations (1) = (2)
Donc la vitesse moyenne égale :
c’set l’équation de Chezy (1768)
C : coefficient de Chézy (en m1/2
/s) qui dépend de la forme de la section du canal, de la rugosité des
parois et des conditions d’écoulements.
Plusieurs formules sont utilisées pour déterminer le coefficient de Chézy « C »
a. Formule de Kutter (Allemagne 1869)
Avec :
Rh : rayon hydraulique, γK : coefficient de rugosité de Kutter en m1/2
b. Formule de Manning (Irlandais 1889) et Strickler (Américain 1891)
Avec :
Rh : rayon hydraulique ;
n : coefficient de rugosité de Manning en m-1/3
. s ;
Ks : coefficient de rugosité de Strickler en m1/3
/ s ;
c. Formule de Bazin (France 1897)
Avec :
Rh : rayon hydraulique, γB : coefficient de rugosité de Bazin en m1/2
d. Formule de Pavlovski (Russé 1940)
Pour Rh ≤ 1 m et pour Rh > 1 m
Avec :
n : coefficient de rugosité de Pavlovski

52. 47
e. Formule de Powell (Américain 1950)
Avec :
ε : rugosité absolue des parois du canal
Re : Nombre de Reynolds
f. Formule d’Agroskine (Russé)
Avec :
n : coefficient de rugosité d’Agroskine
N.B :
1) la formule de Manning-Strickler est la plus utilisée grâce à sa simplicité, comme il a indiqué Chow
dans son livre (Chow 1959) ;
2) Les coefficients de rugosité (de Bazin, de Manning,…) sont donnés se forme des tableaux ;
3) Pour une section à périmètre mouillé non-homogène (lit du fond et les berges du canal ont des
rugosités différentes), il faut alors calculer un coefficient de rugosité équivalente.
Ou
Formule d’Agroskine
Tableau 5.3 : valeurs de coefficient de rugosité de Strickler appropriés à la nature des parois du canal
(Degoutte 2006)
Nature de paroi du canal Coefficient de Strickler « Ks »
Rivière à berges étroites, végétation très dense 10 - 15
Rivière de plaine, large, végétation peu dense 30
Rivière de plaine, sans végétation arbustive 35 – 40
Canal en pierres, roches 30 - 40
Canal en terre, enherbé 50
Canal en terre, non enherbé 60
Canal en béton/béton lisse 70 – 75
Canal en matériau polyéthylène 80 - 100
Dans le cas d’un chenal dont le fond et les berges sont en graviers, des formules empiriques ont pu être
établies :
Formule de Strickler : Ks = 21 / d50
1/6
Formule de Meyer-Peter et Müller : Ks = 26 / d90
1/6
d: désigne le diamètre (en mètres) des grains du lit

53. 48
5.6 Forme de section la plus avantageuse
La section d’un canal la plus avantageuse, pour une pente donnée, est celle qui évacue le débit
maximal dans un périmètre mouillé minimal, donc maximisé le rayon hydraulique. Cette section
avantageuse coûtera d’autant moins cher, et c’est la section la plus économique.
 C’est la section semi-circulaire est la forme idéale pour faire passer le plus grand débit dans la
section ayant le plus petit périmètre. Cependant cette forme n'est réalisable que pour des canaux
artificiels en béton préfabriqués (petits canaux d'irrigation par exemple). Les grands canaux seront
eux de forme trapézoïdale ou rectangulaire.
Sm = π r²/2 , Pm = π r
Rh = r/2 = h/2
 Dans le cas d’une forme trapézoïdale, la section la plus avantageuse est celle qui vérifie les dérivés
de section et de périmètre mouillés égales à zéro.
dSm = 0 et dPm = 0
ona :
et
ce qui se traduit par les deux équations :
On tire de chaque équation dl/dh, ensuite nous faisons l’égalité entre les deux équations
Ce qui donne
…………(3)
On remplace la valeur de l de l’équation (3) dans les équations de Sm et Pm, ce qui donne :
Nous remarquons que la valeur de R est indépendante de la pente de talus « m ». De plus, notons que
l'on retrouve le même rayon hydraulique que pour la section semi-circulaire inscrite dans le trapèze.
 La détermination de la section la plus avantageuse de la forme rectangulaire, nous déterminons dS
= 0 et dP = 0, ensuite nous faisons l’égalité entre les équations.
et
Donc
et
Ce qui donne
donc
Donc nous retrouvons le même rayon hydraulique que pour la section semi-circulaire et pour la
section trapézoïdale.

54. 49
Remarque importante
La surélévation de la hauteur « H » de la section transversale du canal ouvert par rapport à la
profondeur d’eau est fonction du débit selon certains auteurs ou en fonction de la hauteur « h » pour
certains d’autre chercheurs.
Tableau 5.4 : valeurs de la revanche en fonction de débit
Q (m3
/s) <1 1-5 5-10 10-20 20-30 30-40 40-50 > 50
Revanche (m) 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Pour le cas des ouvrages de franchissements (ouvrages sous-chaussés), la revanche est couramment
appelée le tirant d’air (Ta), elle est prise égale Ta ≥ h (soit 25 % de h).
Certains auteurs recommandent un tirant d’air dans une conduite circulaire, plus de 20 %.
5.7 Ecoulement parmanent non-uniforme
Dans un écoulement non-uniforme ou varié, les paramètres caractérisant l’écoulement changent d’une
section à l’autre, et la pente de la surface libre diffère de celle du fond. Cet écoulement peut être
accéléré ou décéléré suivant que la vitesse croît ou décroît dans le sens du mouvement.
Lorsque le mouvement est graduellement varié, la profondeur ainsi que les autres paramètres varient
lentement d’une section à l’autre. Alors quand le mouvement est rapidement varié, les paramètres
caractérisant l’écoulement changent brusquement.
5.7.1 Ecoulement graduellement varie
C’est en présence d’une singularité (rétrécissement, élargissement, seuil, chute,…) le régime n’est plus
uniforme mais varié. Si les variations sont lentes donc l’écoulement est graduellement varie :
I ≠ J ≠ i , h1 ≠ h2 et V1 ≠ V2.
Avec :
I : pente du radier ;
J : pente de la ligne d’eau ;
i : pente de la ligne de charge.
Fig 5.13. Schéma d’un écoulement parment non-uniforme sur une pente fixe.
Z1
Z2
h1 = P1/ρg
h2 = P2/ρg
V1/2g
V2/2g
ΔH1-2

55. 50
L’énergie spécifique dans les sections (1) et (2) :
Es1 = h1 + V1
2
/2g
Es2 = h2 + V2
2
/2g
Si ΔH1-2 > ΔZ1-2 donc (Es1 - Es2) > 0 → la ligne d’eau décroit
Si ΔH1-2 < ΔZ1-2 donc (Es1 - Es2) < 0 → la ligne d’eau croit
Examinons la fonction Es = h + V2
/2g → Es = h + Q2
/2gS²
On a pour h → 0 l’énergie spécifique Es →
On a pour h → l’énergie spécifique Es →
On voit que, pour le même débit d’écoulement, la charge spécifique Es peut s’écouler sous deux
profondeurs différentes : l’une « h’ » correspondant au régime rapide ou torrentiel, et l’autre « h’’ »
correspondant au régime lent ou fluvial. Elles sont appelées : profondeurs conjuguées.
Le passage d’un écoulement à un autre est fait à la profondeur critique « hc », sous une charge/énergie
critique « Ec », et tous les paramètres hydrauliques prennent l’indice « c ou cr : critique » au niveau de
cette profondeur critique (hc, Smc, Pmc, Rhc, Vc, Esc, Ic…).
Conformément aux règles mathématiques, la détermination d’une valeur minimale d’une fonction est
s’effectuée après l’annulation de la première dérivée de la fonction.
Donc on va mettre , soit , avec
Ce qui donne : → →
L : largeur au miroir
On a → → →
Le nombre de Froude est posé égal à :
Fig 5.14. Variation de l’energie spécifique « Es » suivant « h » pour un débit « Q » donné
(Bniaiche 2013 modifié).
yn
yc
FLUVIAL
TORRENTIEL
yn
1
y

56. 51
Nous avons trois cas :
 h > hc → Fr < 1 : le régime est fluvial
 h = hc → Fr = 1 : le régime est critique
 h < hc → Fr > 1 le régime est torrentiel
Les expressions des profondeurs critiques hc et des charges critiques Ec pour différentes formes sont :
Ec = hc + Q2
/2gSc² et
Avec
b: largeur du canal, L : largeur au miroir, m : fruits des berges, D : diamètre de la conduite (m)
a) cas de la forme rectangulaire
b) cas de la forme triangulaire
c) cas de la forme circulaire
pour 0.1 < < 0.9
d) cas de la forme trapézoïdale
on peut utiliser une solution approximative proposée par Agroskine
Avec et
Remarque :
On peut définir le régime d’écoulement en comparant la valeur de la pente du radier « I » avec la pente
critique « Ic ». L’augmentation de la pente entraîne une diminution de « h ».
I < Ic : écoulement fluvial ;
I = Ic : écoulement critique
I > Ic : écouelemnt torrentiel
5.7.2 Ecoulement rapidement varié
Lors de présence d’une singularité hydraulique (seuil, changement de pente…) ou un changement de
section du canal, les caractéristiques hydrauliques changent, et on observe un écoulement rapidement
varie, en forme d’un ressaut hydraulique.
Le ressaut hydraulique est défini comme étant une surélévation brusque de la surface libre d’un
écoulement permanent qui se produit lors du passage du régime torrentiel au régime fluvial.
Il est accompagné d’une agitation marquée et de grandes pertes d’énergie.

57. 52
Les hauteurs y1 et y2 sont appelées « profondeurs conjuguées du ressaut ». La hauteur du ressaut est
représentée par Δh. L est longueur du ressaut.
Fig 2.15. Profondeurs conjuguées du ressaut hydraulique (Bniaiche 2013).
a./ Détermination des hauteurs conjuguées
On ne peut pas appliquer le théorème de Bernoulli entre les sections 1 et 2. La perte de charge n’est
pas connue et les formules du régime uniforme ne sont pas applicables. C’est le théorème d’Euler qui
permet de résoudre le problème. En raisonnant, suivant un tube de courant en régime permanent, les
forces qui agissent sur cet élément sont :
En écrivant le théorème de la quantité de moment sur l’axe des x:
En négligeant la force de pesanteur et la force de frottement, il reste :
Avec : yG1 et yG2 sont les hauteurs des centres de gravité dans les sections 1 et 2
Après la résolution de l’équation on trouve les hauteurs conjuguées comme suit pour un canal
rectangulaire:
et
Fig 5.16. Pertes de charge dans un ressaut hydraulique (Bniaiche 2013).
)
( 1
2 V
V
Q
F 

 
)
( 1
2
2
1 V
V
Q
F
F
F fr
p
p 


 
)
( 1
2
2
2
1
1 V
V
Q
y
gS
y
gS G
G 

 


 
2
1
1
2 8
1
1
2
y r
F
y



 








 2
2
2
1 8
1
1
2
y r
F
y

58. 53
b./ Détermination des pertes de charge
Les pertes de charge dans un ressaut sont déterminées par la formule :
Fig 5.17. Longueur d’un ressaut hydraulique (Bniaiche 2013).
Lors que la longueur du ressaut est déterminée par les formules empiriques, dont les plus utilisées
sont :
- La formule de Miami district : Lr ≈ 5 (y2 – y1) ;
- La formule Safranez : Lr ≈ 4.5 y2 ;
- La formule Smetana : Lr ≈ 6 (y2 – y1) ;
5.8 Section de contôle
Il s’agit de toute singularité permettant le passage d’un régime fluvial au régime torrentiel.
Cela suppose l’existance d’un régime critique localisé au droit de la section de contrôle, où la relation
débit-hauteur est visible.
La section de contrôle peut être utilisée pour la mesure de débit. Et au niveau de cette section on peut
tracer la courbe Q = f (h) qui appelée « courbe de tarage ». Cette courbe de tarage propre a cette
section de contrôle, est réalisé après une série de mesure du couple (h et Q), ce qui permet de tracer
une courbe de tendance la plus représentative possible pour cette section, qui permet la détermination
de débit par une simple projection de « h » sur la courbe Q = f (h).
Le contrôle d’un écoulement fluvial se fait à l’aval de cet écoulement, et le contrôle de l’écoulement
torrentiel se fait à l’amont de cet écoulement.
 
2
1
3
1
2
y
4
y
h
y
y




59. 54
Exercice 1 :
Déterminer le diamètre d’une conduite qui évacue les eaux pluviales, de débit Q = 10 m3
/s, une pente
de 1 %, le coefficient de Strickler Ks = 75 m1/3
/s.
Solution :
Nous avons l’équation de Manning-Strickler
Donc
Pour une conduite en pleine section , ,
= 4.28 → D = 1.725 m, on normalise ce diamètre, on prend D = 2 m
Pour D = 2 m, on a Sm = 3.14 m² , Pm = 6.28 m , et Rh = 0.5 m
Ce qui donne Vps = 4.725 m/s et Qps = 14.836 m3
/s
Ce qui correspond à ≈ 0.6 et correspond à ≈ 1.072 ce qui donne une vitesse d’écoulement dans la
conduite de V = 5.07 m/s
Exercice 2 :
Un canal rectangulaire de largeur b=12 m, débite 14 m3
/s sous une profondeur de 1,22 m.
- Quel est le régime d’écoulement dans ces conditions si le coefficient de Manning est pris égal
à 0,017 m-1/3
.s ?
- Calculer la pente critique de ce canal.
- Quelle pente faut-il donner à ce canal pour produire un écoulement uniforme sous une profondeur
de 1,22 m?
Solution :
- Le régime d’écoulement est déterminé par le nombre de Froude
, on a b=12 m , h = 1.22, donc S = 12 x 1.22 = 14.64 m²
Dans un canal rectangulaire, largeur au miroir B = b
Donc = 0.28 < 1, donc le régime est fluvial
- La pente critique du canal
Afin d’avoir une pente critique dans un canal, lorsque Fr = 1. Donc L et Q sont invariables dans ce
canal rectangulaire, on doit calculer hc
Cela donne Smc = 6.21 m² et Pmc = 13.04 m, donc Rhc = 0.48 m
On a l’équation de Manning-Strickler , ce qui donne Ic = 3.95 ‰

60. 55
- Pente uniforme
C’est la pente dans les conditions normales, donc on applique l’équation de Manning
Avec Ks = 1/n = 58.82 m1/3
/s, Sm = 12 x 1.22 = 14.64 m², Pm = 12 + 2x1.22 = 14.44 m
Rh = 14.64/14.44 = 1.01 m
Donc I = 2.6 10-4
Exercice 3 :
Un canal rectangulaire 10 m de large se compose de 3 tronçons. Le premier a une pente I1 ,
le deuxième a une pente I2 = 0,02 et le fond du troisième est horizontal. Le canal est en béton avec un
coefficient de rugosité de Manning de 0,0133 m-1/3
.s, et le débit est 100 m3
/s.
a. Calculer la profondeur et la pente critique de ce canal.
b. Si la profondeur uniforme dans le 1er
tronçon est 5 m, Quel est le régime d’écoulement dans
ce tronçon?
c. Quel est le régime d’écoulement dans le 2ème tronçon ? Calculer son nombre de Froude.
d. Calculer la profondeur à l’aval immédiat du ressaut qui se forme dans le tronçon horizontal.
e. Schématiser la ligne d’eau dans tout le canal.
Solution
a) La hauteur et la pente critiques du canal
Afin d’avoir une pente critique dans un canal, lorsque Fr = 1. Donc B et Q sont invariables dans ce
canal rectangulaire, on doit calculer hc
=
Nous pouvons dire ici que la pente critique et la hauteur critique sont indépendant des pentes du canal.
b) Le régime d’écoulement dans le tronçon 1
Nous avons déjà calculé hc = 2.17 m < hn1 =5m donc l’écoulement est fluvial
Nous pouvons vérifier le régime d’écoulement, on détermine le nombre de Froude
< 1 (le régime est fluvial)

61. 56
c) Le régime d’écoulement dans le tronçon 2
Ic = 2.17 10-3
et I2 = 0.02 donc I2 > Ic le régime est torrentiel
Nous pouvons vérifier le régime d’écoulement, on détermine le nombre de Froude
On doit déterminer la hauteur normale dans le tronçon 2, cela s’effectué par la formule de Manning-
Strickler
La résolution de l’équation par itération donne une hauteur normale hn2 = 1.04 m
Donc
> 1 (le régime est torrentiel)
d) La profondeur à l’aval immédiat du ressaut
On a = = 3.94 m
Si on calcule le nombre de Froude on trouve
< 1 (le régime est fluvial)
Et si on vérifié la valeur de y2 pour la formule de ressaut on trouve 1.04 m
e) Schéma de la ligne d’eau

62. 57
CHAPITRE 6: ASSAINISSEMENT ROUTIER
6.1. Rappels sur l’hydrologie de surface
6.1.1 Notion d’un bassin versant
Le bassin versant en une section droite d'un cours d'eau, est défini comme la totalité de la surface
topographique drainée par ce cours d'eau et ses affluents à l'amont de cette section. Il est entièrement
caractérisé par son exutoire, à partir duquel nous pouvons tracer le point de départ et d'arrivée de la
ligne de partage des eaux qui le délimite.
La ligne de partage des eaux correspond à la ligne de crête. On parle alors de bassin versant
topographique.
Un bassin versant est caractérisé par : une surface, un périmètre, une forme, un relief, des altitudes
maximale et minimale, une altitude moyenne et médiane, une pente moyenne, un réseau
hydrographique,…
Fig 6.1.1. Exemple d’un bassin versant, avec les limites des partages des eaux de surface.
6.1.2 Notion sur les précipitations
Les précipitations désignent tous les eaux météoriques qui tombent sur la surface de la terre, sous
forme liquide (bruine, pluie, averse) ou solide (grésil, grêle, neige). Elles sont provoquées par un
changement de température ou de pression.
Quelle que soit la forme de la précipitation, liquide ou solide, on mesure la quantité d'eau tombée
durant un certain laps de temps. On l'exprime généralement en hauteur de précipitation ou lame d'eau
précipitée par unité de surface horizontale (mm).
On définit aussi son intensité (mm/h) comme la hauteur d'eau précipitée par unité de temps.
Les différents instruments permettant la mesure des précipitations directement sont :

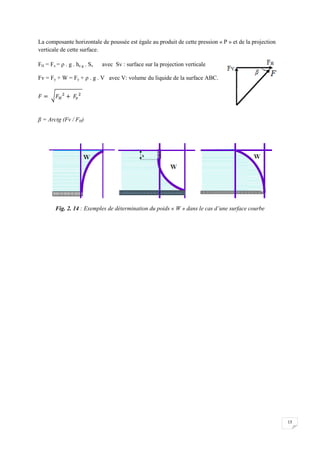
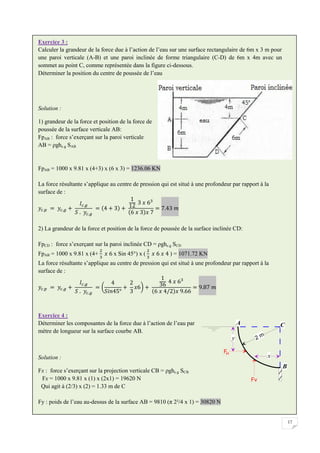
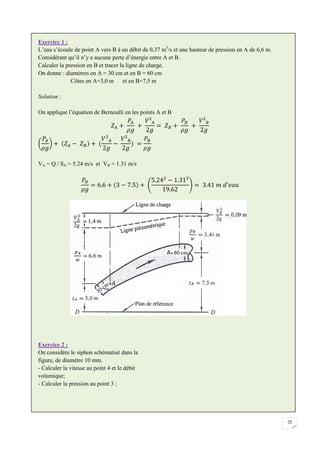
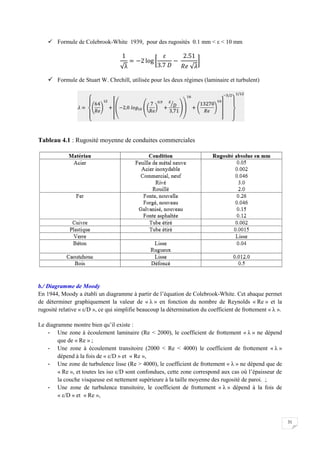
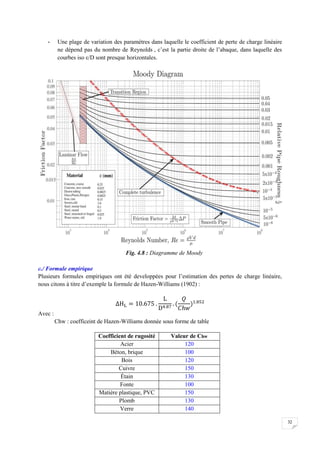
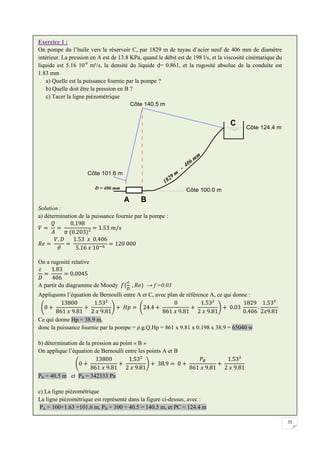
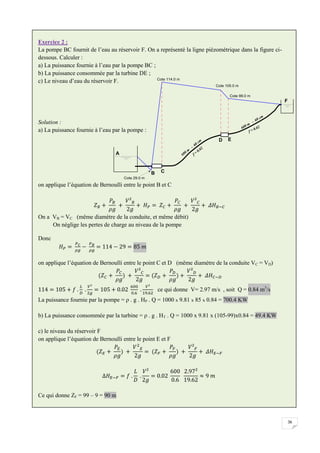
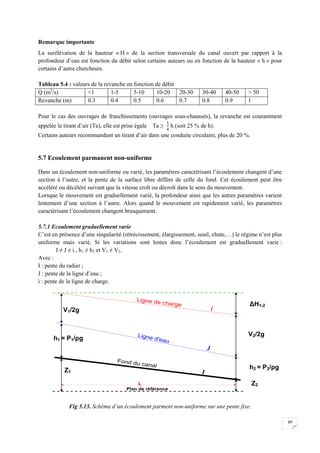
63. 58
 Le pluviomètre : instrument de base de la mesure des précipitations liquides ou solides.
Il indique la quantité d'eau totale précipitée et recueillie à l'intérieur d'une surface calibrée
dans un intervalle de temps séparant deux relevés.
 Le pluviographe : instrument captant la précipitation de la même manière que le pluviomètre
mais avec un dispositif permettant de connaître, outre la hauteur d'eau totale, leur répartition
dans le temps, autrement dit les intensités.
6.1.3 Notion d'une averse et d'une intensité
Une averse désigne un ensemble de pluies associé à une perturbation météorologique bien définie.
La durée d'une averse peut donc varier de quelques minutes à une centaine d'heures et intéresser une
superficie allant de quelques kilomètres carrés (orages) à quelques milliers (pluies cycloniques).
On définit finalement une averse comme un épisode pluvieux continu, pouvant avoir plusieurs pointes
d'intensité.
L'intensité moyenne d'une averse s'exprime par le rapport entre la quantité d’eau tombée (Δh) durant
une unité de temps « Δt » de l'averse :
Δ
Δ
Où :
im : intensité moyenne de la pluie [mm/h, mm/min] ou ramenée à la surface [l/s.ha],
Δh : hauteur de pluie de l'averse observée [mm],
Δt : durée de l'averse [h ou min].
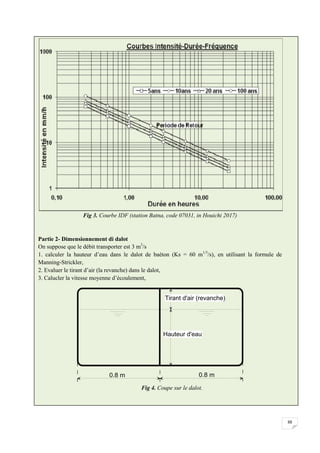
L'intensité des précipitations varie à chaque instant au cours d'une même averse suivant les
caractéristiques météorologiques de celle-ci. Plutôt que de considérer l'averse entière et son intensité
moyenne, on peut s'intéresser aux intensités observées sur des intervalles de temps au cours desquels
on aura enregistré la plus grande hauteur de pluie. On parle alors d'intensité maximale.
Deux types de courbes déduites des enregistrements d'un pluviographe permettent d'analyser les
averses d'une station : La courbe des hauteurs de pluie cumulée, et le hyétogramme.
- La courbe des hauteurs de pluie cumulées représente en ordonnée, pour chaque instant t, l'intégrale
de la hauteur de pluie tombée depuis le début de l'averse.
Fig 6.1.2. Courbe des hauteurs des pluies cumulées.

64. 59
- Le hyétogramme est une représentation sous la forme d'un histogramme, de l'intensité de la pluie
en fonction du temps. Les éléments importants d'un hyétogramme sont le pas de temps « Δt » et sa
forme. Généralement, on choisit le plus petit pas de temps possible selon la capacité des
instruments de mesure. La forme du hyétogramme, varie donc d'une averse à une autre.
Fig 6.1.3. Exemple d’un hyétogramme d’une averse.
L’étude statistique d’une série chronologique des précipitations a pour but principal est d’utiliser des
mesures d’événements passés afin d’estimer les probabilités futures d’occurrence (faire une prévision
pour le futur au moyen d’une analyse fréquentielle).
L’analyse fréquentielle est utilisée, en particulier, pour estimer l’ampleur de l’événement temporel
auquel est associé un période de retour T (quantile de période de retour T ou de probabilité au
dépassement p = 1/T). L’estimation de la valeur du quantile s’obtient en ajustant une loi de probabilité
F (x; θ) à un échantillon de « n » observations x ={ }, où θ représente le vecteur de
paramètres associé à la distribution de probabilité F.
Les lois statistiques fréquemment utilisées en analyse fréquentielle sont : loi normale, loi log-normale,
loi de Gumbel, loi GEV, loi Pearson.
6.1.4 Notion de la période de retour
La notion de temps de retour (ou période de retour) est destinée à caractériser la fréquence
d’apparition d'un phénomène. Par exemple, une crue centennale est une crue théorique calculée à
partir de l'analyse des crues passées et qui a 1 chance sur 100 de se produire chaque année. On peut
aussi dire que la crue centennale se produit en moyenne dix fois par millénaire.
6.1.5 Courbes IDF (intensité-durée-fréquence)
Les courbes IDF sont construites pour un but bien précis. Elles permettent d'une part de synthétiser
l'information pluviométrique au droit d'une station donnée et, d'autre part de calculer rapidement des
débits de projet et d'estimer des débits de crue ainsi que de déterminer des pluies de projet utilisées en
modélisation hydrologique.
Les courbes IDF sont établies sur la base de l'analyse d'averses enregistrées à une station au cours
d'une longue période. Les courbes obtenues peuvent donc être construites de manière analytique ou
statistique.
Différentes formules analytiques sont proposées pour représenter l’intensité moyenne d'une pluie en
fonction de sa durée. La formule la plus simple (avec T variable) est proposée par Montana sous la
forme suivante :

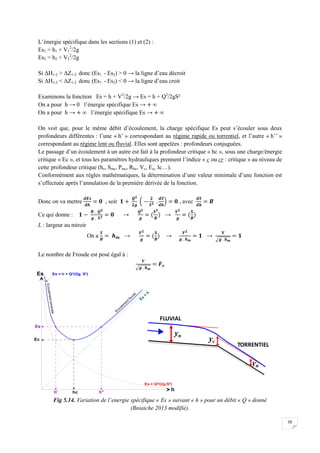
65. 60
Avec :
i: intensité moyenne de la pluie [mm/h],
t: durée de la pluie, généralement prise égale au temps de concentration [minutes ou heures],
T; intervalle de récurrence (ou temps de retour) [années],
a, b: constantes locales, dépendant généralement du lieu et de la fréquence de pluie (déterminé
statistiquement ou en fonction de l’exposant climatique de la région).
Fig 6.1.4. Les courbes IDF (Intensité-Durée-Fréquence)
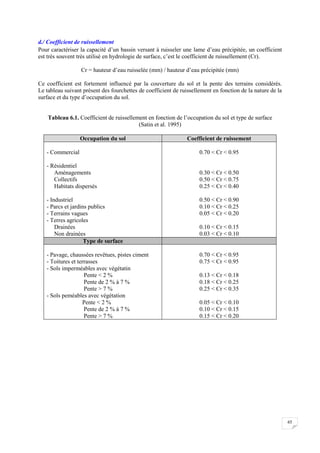
6.1.6 Evaluation régionale des précipitations
Les méthodes les plus simples et les plus couramment utilisées sont les méthodes de calcul de
moyennes ou les méthodes d'interpolation des données pluviométriques collectées localement.
Ces méthodes permettent notamment le calcul des lames d'eau moyennes à l'échelle du bassin, la
cartographie des précipitations, et le calcul de hyétogrammes moyens.
Avant de procéder au calcul de la précipitation moyenne du bassin versant, il est important de
contrôler la qualité des données pluviométriques, leur homogénéité et leur représentativité.
Parmi les méthodes généralement proposées pour calculer la pluie moyenne à partir de l'ensemble des
mesures ponctuelles obtenues à plusieurs stations pluviométriques sur le bassin ou à proximité, on
distingue : la méthode de la moyenne arithmétique, la méthode des polygones de Thiessen ou
l'utilisation d'isohyètes. Le choix de la méthode dépendra notamment de la longueur de la série de
données dont on dispose, la densité du réseau de mesure, et la variation du champ pluviométrique.
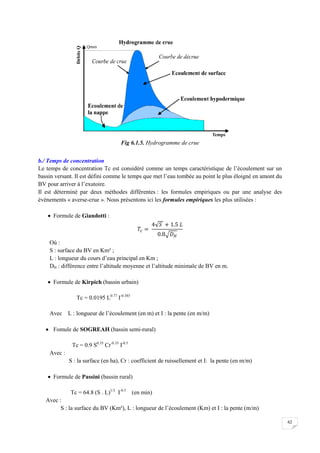
6.1.7 Ecoulements superficiels
Les précipitations une fois arrivent au sol (après l’évaporation d’une partie importante), se répartissent
en : infiltration, ruissellement, écoulement hydro-dermique.
Si l’intensité de pluie au cours de l’averse excède la capacité d’infiltration du sol, une partie de l’excès
d’eau s’accumule dans les dépressions de la surface et l’autre partie s’écoule par gravité le long des
pentes vers l’exutoire.

66. 61
Le débit à l’exutoire s’accroit avec l’arrivée successive des apports de ruissellement provenant des
zones du bassin les plus éloignées. Si l’averse dure suffisamment longtemps, le débit d’écoulement
commence à augmenter, il arrive un moment où l’ensemble du bassin versant débite à l’exutoire.
Si l’averse est de courte durée, le ruissellement de la partie la plus éloignée du bassin arrive à
l’exutoire au cours de la phase décroissante du débit, longtemps après la fin de la pluie.
On appelle "écoulement hypodermique", la partie des précipitations infiltrées et s’écoule dans la
couche superficielle pour réapparaitre à l’air libre à la rencontre d’un chenal d’écoulement.
La présence d’une couche imperméable à faible profondeur favorise se genre d’écoulement.
Les méthodes les plus utilisées pour l’estimation de débit dans un cours d’eau sont :
 La méthode volumétrique : consiste à mesurer le temps « t » nécessaire pour remplir un
volume « V » connu. Cette méthode est utilisée pour mesurer les faibles débits.
 La méthode des déversoirs : il existe plusieurs formes de déversoir qui peuvent être utilisé
pour la mesure de débit (triangulaire, rectangulaire ou trapézoïdal). Les débits sont fonction de
la hauteur « h » de l’eau, la hauteur de la pelle « p », la forme de déversoir, épaisseur de la
crête du seuil « c ». Généralement les formules de chaque type de déversoir sont déterminées
expérimentalement.
 La méthode du jaugeage par dilution :
Cette méthode est utilisée pour mesurer les petits torrents. Elle consiste à injecter dans une section
S1 un traceur à une concentration C1 avec un débit q. Ensuite, on prélève un échantillon à une
section S2, située en aval, à une distance suffisante pour un bon mélange. La concentration de cet
échantillon est C2. En régime permanent, le flux entrant du traceur est égale au flux sortant :
 Le jaugeage par exploration du champ de vitesse :
Il s’agit de mesurer la vitesse de l’eau en plusieurs points d’une section d’un cours d’eau.
La mesure est faite par une hélice qui est placée dans le sens d’écoulement, va tourner grâce à la
vitesse de l’eau. Le nombre de tours par minute que fait l’hélice est proportionnelle à la vitesse de
l’eau. Ensuite, grâce à un système de comptage du nombre de tours par unité de temps que fait
l’hélice dans le cours d’eau on détermine la vitesse de l’eau au point de mesure. On mesure la
vitesse de l’eau à des profondeurs différentes, le long de plusieurs verticales bien réparties à
travers la section d’un cours d’eau.
Pour les faibles débits, on utilise les moulinets, et pour les débits importants on utilise les
saumons.
a./ Hydrogramme de crue généré par une averse
On appelle hydrogramme la représentation graphique du débit instantané, en un point du cours d’eau,
en fonction du temps.
Sur l’hydrogramme on distingue :
- Le temps de montée, entre le début de ruissellement direct et le point de la crue ;
- Le temps de base ou durée de ruissellement, entre le début de la pluie efficace et la fin de
ruissellement direct ;
- Le temps de décrue, entre le point de la crue et la fin de ruissellement.

67. 62
Fig 6.1.5. Hydrogramme de crue
b./ Temps de concentration
Le temps de concentration Tc est considéré comme un temps caractéristique de l’écoulement sur un
bassin versant. Il est défini comme le temps que met l’eau tombée au point le plus éloigné en amont du
BV pour arriver à l’exutoire.
Il est déterminé par deux méthodes différentes : les formules empiriques ou par une analyse des
évènements « averse-crue ». Nous présentons ici les formules empiriques les plus utilisées :
 Formule de Giandotti :
Où :
S : surface du BV en Km² ;
L : longueur du cours d’eau principal en Km ;
DH : différence entre l’altitude moyenne et l’altitude minimale de BV en m.
 Formule de Kirpich (bassin urbain)
Tc = 0.0195 L0.77
I-0.385
Avec L : longueur de l’écoulement (en m) et I : la pente (en m/m)
 Fomule de SOGREAH (bassin semi-rural)
Tc = 0.9 S0.35
Cr-0.35
I-0.5
Avec :
S : la surface (en ha), Cr : coefficient de ruissellement et I: la pente (en m/m)
 Formule de Passini (bassin rural)
Tc = 64.8 (S . L)1/3
I-0.5
(en min)
Avec :
S : la surface du BV (Km²), L : longueur de l’écoulement (Km) et I : la pente (m/m)

68. 63
 Formule de Ventura
Tc = 0.763 (S/I)0.5
Avec :
S : la surface du BV (en ha), et I: la pente (en m/m)
Des comparaisons d’estimation de temps de concentration Tc pourront être faites avec ces différentes
formules.
c./ Méthodes d’estimation des débits
Le calcul d’un débit de pointe QP(T) d’un bassin versant non jaugé pour une période retour bien
déterminé est l’une des préoccupations majeures des ingénieurs hydrologues. Des très nombreuses
recherches et études ont été consacrées à ce sujet depuis un siècle, par ce qu’il n’existe pas de méthode
consensuelle qui donne donne des valeurs exactes de ces débits. Nous ne pouvons donc pas échapper à
cette constatation générale. Nous pensons cependant, qu’en dehors d’une activité de recherche qui
devrait viser à l’universalité des résultats, le choix d’une méthode ou d’une formule à des fins
concrètes doit reposer sur l’analyse de la précision avec laquelle un résultat est attendu, au regard des
diverses incertitudes qui entourent l’évaluation de ce résultat et qui, en matière d’hydrologie, sont
nombreuses et souvent mal connues.
Donc sur la base des caractéristiques géomorphologiques du bassin versant, et sur la base des analyses
statistiques des données pluviométriques des stations météorologiques les plus proches au bassin
versant de la zone d’étude, il est possible de faire une estimation approximative des débits de pointe
pour une période de retour bien déterminé qui génèrent l’écoulement des eaux superficielles dans un
BV.
Mais, il reste l’investigation sur le terrain afin de réaliser une reconnaissance sur les ouvrages
existants, les passages d’eau, dégradation/destruction des ouvrages afin d’identifier le passage d’eau et
son importance, l’une des méthodes importantes avant toute estimation des débits.
c.1./ Méthode rationnelle
La méthode la plus ancienne d’estimation du débit de pointe à partir de la pluie est appelée méthode
rationnelle. Elle remonte au milieu du 19e
siècle. Mais ce n’est qu’en 1906 qu’elle a été généralisée.
Elle est considérée valide pour les superficies de moins de 10 Km². Elle suppose que le débit
maximum est obtenu lorsque toute la superficie du bassin versant contribue au ruissellement à
l’exutoire avec la plus grande intensité moyenne de précipitation. Cette plus grande intensité
correspond à la plus grande précipitation pour la durée du temps de concentration.
L’équation s’écrit habituellement comme suit : Q = Cr. i. A / 360
Où :
Q : est le débit de pointe en m3
/s,
Cr : est le coefficient de ruissellement,
i : est l’intensité de pluie (mm/h) pour une durée égale au temps de concentration tc
A : est la superficie du bassin de drainage (versant) en hectares (ha).
La valeur de l'intensité « i » est basée sur les courbes Intensité-Durée-Fréquence (IDF).
Mais, elle peut être déterminé par la formule de Montana, après une hydrologique.

69. 64
t : durée de l’averse, égale au temps de concentration « Tc » en heure ;
T : période de retour (5, 10, 20, 25, 50 ou 100 ans) ;
b : exposant climatique de la région ;
P24,T : pluie maximale journalière pour une période de retour bien déterminée.
c.2./ Méthode superficielle ou Méthode de Caquot
Cette méthode est la plus fréquemment utilisée pour des surfaces moins de 200 ha et des pentes
moyennes comprises entre 0,002 et 0,05 m/m.. Elle est décrite dans l’instruction technique de 1977.
Elle donne le débit de pointe pour une fréquence de dépassement « F » ou de période de retour T (avec
T = 1/F)
Q(F) = k1/u
. iv/u
. Cr1/u
. Aw/u
. m
Avec :
Q(F) : est le débit de fréquence de dépassement « F » exprimé en m3
/s ;
I : est la pente moyenne du bassin versant (en m/m) ;
Cr : est le coefficient de ruissellement pondéré (ou coefficient d’imperméabilisation);
A : est la superficie du bassin de versant ou sous-bassin versant (en ha).
k : est un coefficient d’expression k = 0.5 b(F) . a(F)/6.6 ;
u : est un coefficient d’expression u = 1 + 0.287 b(F) ;
v : est un coefficient d’expression v = -0.41 b(F) ;
w : est un coefficient d’expression w = 0.95 + 0.507 b(F) ;
m : coefficient correctif d’expression
a(F) et b(F) : sont des coefficients de Montana. Ces paramètres sont fonction de la région considérée et
de la période de retour T de la pluie.
i(t,F) = a(F) . tb(F)
, c’est l’intensité de pluie de durée « t », de fréquence de dépassement F, exprimé en
mm/min.
M : est coefficient d’allongement du bassin versant, donné par l’expression
avec L : la longueur du cheminement hydraulique le plus long du BV.
c.3/ Formule de Turazza
Q = Cr. H. A / (3.6 Tc)
Avec :
Q : débit maximum de crue en m3
/s ;
Cr : coefficient de ruissellement ;
H : hauteur totale maximum des précipitations d’une durée égale au temps de concentration du
bassin (en heures) ;

70. 65
d./ Coefficient de ruissellement
Pour caractériser la capacité d’un bassin versant à ruisseler une lame d’eau précipitée, un coefficient
est très souvent très utilisé en hydrologie de surface, c’est le coefficient de ruissellement (Cr).
Cr = hauteur d’eau ruisselée (mm) / hauteur d’eau précipitée (mm)
Ce coefficient est fortement influencé par la couverture du sol et la pente des terrains considérés.
Le tableau suivant présent des fourchettes de coefficient de ruissellement en fonction de la nature de la
surface et du type d’occupation du sol.
Tableau 6.1. Coefficient de ruissellement en fonction de l’occupation du sol et type de surface
(Satin et al. 1995)
Occupation du sol Coefficient de ruissement
- Commercial
- Résidentiel
Aménagements
Collectifs
Habitats dispersés
- Industriel
- Parcs et jardins publics
- Terrains vagues
- Terres agricoles
Drainées
Non drainées
0.70 < Cr < 0.95
0.30 < Cr < 0.50
0.50 < Cr < 0.75
0.25 < Cr < 0.40
0.50 < Cr < 0.90
0.10 < Cr < 0.25
0.05 < Cr < 0.20
0.10 < Cr < 0.15
0.03 < Cr < 0.10
Type de surface
- Pavage, chaussées revêtues, pistes ciment
- Toitures et terrasses
- Sols imperméables avec végétatin
Pente < 2 %
Pente de 2 % à 7 %
Pente > 7 %
- Sols peméables avec végétation
Pente < 2 %
Pente de 2 % à 7 %
Pente > 7 %
0.70 < Cr < 0.95
0.75 < Cr < 0.95
0.13 < Cr < 0.18
0.18 < Cr < 0.25
0.25 < Cr < 0.35
0.05 < Cr < 0.10
0.10 < Cr < 0.15
0.15 < Cr < 0.20

71. 66
6.2. Assainissement routier
6.2.1 Introduction
Maintenir le corps de la route, ces accotements et ces bordures en bon état, assurer la sécurité des
usagers face à la stagnation des eaux en surface de la route, et la lutte contre la pollution routière, sont
des préoccupations des ingénieurs intervenants dans le projet.
Lors de la pluie, les eaux de pluie qui tombe sur la chaussée peuvent s’accumuler et pénétrer à
l’intérieur du corps de la chaussée et causeent ainsi des problèmes au niveau de la route.
Il est donc important de collecter et d’évacuer assez rapidement l’eau qui tombe sur la chaussée y
compris celle provenant du reste de l’emprise de la route ou du terrain naturel avoisinant.
Les problèmes d’hydraulique routière résultent en :
- La route est un ouvrage se développant linéairement sur un terrain au relief duquel elle apporte
par ses déblais et remblais des modifications sur les écoulements naturels ;
- Toute submersion de la route par les eaux a des conséquences dommageables. Elle constitue un
gène, voire un obstacle à la circulation des véhicules, comme elle entraine une dégradation et
fissuration de la couche de finition du bitume.
Lors de la réalisation des ouvrages routiers, l’un des problèmes techniques le plus important auquel
doit faire attention. Il s’agit essentiellement de la collecte et l’évacuation de ces eaux sur l’emprise de
la route, vers les petits ouvrages de franchissements (buses, dalots, …). Seulement, il est recommandé
d’assurer une surveillance et un entretien permanent de ces ouvrages d’évacuation des eaux, afin de les
maintenir en bon état.
L'assainissement de la route a pour but d'éloigner l'eau de la chaussée en vue d'assurer de bonnes
conditions de viabilité et de sauvegarder l'ouvrage routier tout en préservant les milieux récepteurs de
ces rejets. Donc on peut dire que l’assainissement routier est l’ensemble de moyennes mises en œuvre
pour collecte et l’évacuation des eaux superficielles, ainsi que pour rétablissement des écoulements
superficiels vers l’extérieur de la route.
Les ouvrages qui permettront d’assurer la collecte des eaux de ruissellement sont soit placés en
bordure, soit en terre plein central, cela dépondra du type de la route ou de son emprise. Il s’agit
essentiellement des caniveaux, des fossés, des bordures et des bourrelets. Comme il s’agit aussi des
ouvrages de concentration des eaux, tels que les avaloirs, les regards, les raccordements, les
raccordements bourrelet-descente d’eau, les buses …..
6.2.2 Etapes à suivre pour une étude d’assainissement routier
Le projet de collecte des eaux superficielles comme tout autre projet commence toujours par une étude
sommaire ou encore avant projet, qui va consister à examiner tous les facteurs relatifs à
l’assainissement qui peuvent avoir une influence sur les choix à effectuer lors de l’étude et sur
l’estimation du projet.
- Une première étape consiste au tracé du réseau d’évacuation des eaux sur les plans topographiques
de grande échelles (1/500, 1/000 ou 1/2000) et sur les profils en long et les profils en travers de la
phase d’avant projet détaillé (c’est la phase qui suit la phase d’avant projet sommaire).
- Une deuxième étape consiste à identifier les exutoires susceptibles de recevoir les eaux collectées et
faire une étude sommaire sur leurs capacités à recevoir les débits des eaux qui y seront évacuées.
Puisque la chaussée peut faire l’objet de pollutions accidentelles, les eaux collectées sont donc
susceptibles d’être polluées. Il y donc lieu de faire une étude de vulnérabilité des exutoires identifiés,
afin d’éviter toute pollution des cours d’eau ou rivières ou encore des aquifères sous-jacentes.

72. 67
- La troisième étape consiste à identifier les bassins versants naturels qui sont susceptible de diriger
leurs eaux sur l’ouvrage routier à construire. Ces bassins versants doivent être reportés sur plans et
cartes. Un problème majeur qu’il faut prendre en charge au niveau de ces bassins versants, c’est
l’érosion et le transport solide, une étude sommaire est nécessaire afin de donner les moyens de lutte
contre ce problème et minimiser son influence sur les ouvrages d’évacuation des eaux.
Une route, qu’elle soit en remblais ou en déblais, subit des risques graves d’érosion due aux eaux de
ruissellement. Les protections contre ces dégradations peuvent être :
 Directe soit par augmentation de la résistance du sol à l’érosion, par des rectifications
régulières au niveau des surfaces érodées aux moyens des aménagements spéciaux;
 Indirectes, par localisation du ruissellement dans les ouvrages étudiés spécialement pour
écouler les eaux sans dégâts : c’est un système d’assainissement constitué par un réseau de
fossés et caniveaux…. Et leurs ouvrages de décharge.
Ces fosses, caniveaux,… concentrent toutes les eaux de ruissellement ayant une action directe sur la
route (eaux qui proviennent du BV, plate forme routière, des talus…)
Le réseau d’évacuation (ou réseau d’assainissement) est constitué par des ouvrages de collecte, des
ouvrages de concentration des eaux et de leur évacuation. Il doit collecter les eaux de ruissellement
provenant des bassins versants routiers et des talus pour les évacuer vers des exutoires. Son
architecture se développe principalement tout le long de l’infrastructure suivant une logique
hydraulique gravitaire (entre un point haut et un point bas) par assemblage d’ouvrages élémentaires
(linéaires ou ponctuels, enterrés ou superficiels).
L’architecture d’un réseau d’assainissement peut être décomposée conventionnellement en
4 grandes parties : Les réseaux de collecte longitudinaux, les ouvrages transversaux et de
raccordement, les ouvrages de contenance et de dépollution, et les exutoires.
6.2.3 Réseaux de collecte longitudinaux
a./ Réseaux de crête de talus de déblai
Le rôle du réseau de crête de talus de déblai est d’éviter l’érosion du talus et d’alimenter en
écoulement le réseau de pied de talus. L’érodabilité des talus d’une telle route dépend, en plus de la
pluviosité, de la cohésion de la roche dans laquelle la route a été taillée ou des roches qui bordent cette
route, mais aussi de l’étendue de la route et des pentes du talus.
Vue l’importance économique de la route, les talus sont souvent revêtu afin de les bien stabilisés. Le
rôle de l’assainissement d’un tel type d’ouvrage se limite à un rôle de prévention et d’entretien contre
l’érosion (lente, mais certaine) des talus pour maintenir pendant longtemps leur stabilité, mais aussi
contre l’infiltration dans le talus. Ce réseau dit réseau de crête de talus en déblai, est un réseau
longitudinal constitué de façon générale de fossés profond, doit être placé à 1 ou 2 m de la crête du
talus avec un espace nécessaire pour ses entretiens.
Cet ouvrage devra être dimensionné en capacité suffisante par tronçon homogène. Il convient de
prévoir les aménagements nécessaires à son entretien.

73. 68
Fig 6.2.1. Formes des fosses sur un talus en déblai (Van Tuu 1981).
b./ Réseaux de pieds de talus de déblai
C’est un réseau longitudinal constitué de fossés peu profonds appelés fossés plats comme par exemple
des cunettes aux formes douces pour améliorer la sécurité ou des caniveaux profonds revêtue,
chargés de récupérer les eaux issues de la chaussée, du talus et de l’accotement.
Les eaux récupérées par ce réseau sont rejetées dans un collecteur revêtu.
Fig 6.2.2. Réseau en pied de talus de remblai (Biaou 2009).

74. 69
Fig 6.2.3. Caniveau en pied de talus de déblai.
Des regards et avaloirs associés sont des ouvrages de concentration qui assurent la transmission des
eaux recueillies par les ouvrages de collecte vers les dispositifs d’évacuation situés hors de la
plateforme.
Si les eaux de ruissellement sont collectées à différents niveaux sur le talus en crête sur les risbermes,
il faudra prévoir des ouvrages de raccordements tels que les raccordements de descente d’eau à
cunette ou encore de descente d’eau à collecteur.
Fig 6.2.4. Raccordement de la descente d’eau au collecteur (Biaou 2009).
c./ Réseau de terre-plein central (TPC)
C’est un réseau qui a pour rôle de protéger toute la plate-forme, surtout lorsque le terre-plein central
n’est pas revêtu. En alignement droit le ruissellement sera canalisé par un ouvrage superficiel de
transport longitudinal (revêtu ou pas) de type fossé plat ou caniveau préfabriqué. Ce dispositif de
surface sera complété par la mise en place d’un drainage principal (décaler par rapport à l’axe du terre-
plein central (pour tenir compte de la présence de zones plantées et de glissières) pour protéger le

75. 70
corps de chaussée de la migration des eaux au travers du TPC vers les structures de chaussée et sol
support.
En déblai, pour une plate-forme assez large, il faudra prévoir une tranchée drainante profonde devrait
permettre de contribuer au rabattement d’éventuelle nappe.
Fig 6.2.5. Réseau de terre-plein central n’est pas revêtu avec un drain (Biaou 2009).
Lorsque le terre-plein central est revêtu, un caniveau situé dans la partie basse du terre-plein central va
permettre de drainer les eaux de la chaussée et de la plate-forme gravitairement vers les rives
extérieures de la chaussée.
Fig 6.2.6. Réseau de terre-plein central revêtu (Biaou 2009).
d./ Réseau d’assainissement de crête de talus de remblai
Lorsqu’une route est en remblai, l’une des choses les plus redoutées est l’érosion du talus due aux
eaux qui vont ruisseler. Le risque d’érosion est d’autant plus élevé lorsque le talus est important ou sa
pente est forte. Ce risque est généralement fonction de l’intensité locale des pluies, mais aussi de la
cohésion du sol et de la présence ou non de la végétation. C’est pour cela qu’il y a lieu de prévoir le
réseau de crête de talus de remblai, un réseau également longitudinal, pour empêcher les eaux de se
ruisseler directement sur le talus, le but étant de les dirigées (grâce à un raccordement aux descentes
d’eau) vers des emplacements aménagés en conséquence, c'est-à-dire les descentes d’eau qui sont
placées en moyenne tous les 30 m pour les régions de forte intensité de pluie, et de 50 m pour les
régions de faible intensité de pluie. Si la zone est caractérisée par les averses de fortes intensités, ce
réseau de descente est nécessaire dès que les talus dépassent 2 m, et pour les pluies moins intenses il
est nécessaire pour les talus qui dépassent 4 m.

76. 71
Fig 6.2.7. réseau de crête de talus remblai (Biaou 2009).
Le réseau de crête de talus de remblai est constitué de bourrelets en enrobé ou de bordures posés à
plat (type T1 ou T2), placés à la limite de la partie imperméabilisée de la chaussée ou de la bande
d’arrêt d’urgence à pour fonction de canaliser l’eau issue du ruissellement de la chaussée pour éviter
son déversement en rive sur le talus de remblai (Il protège donc le talus routier contre toute altération :
ravinement, érosion et en état limite, la rupture).
e./ Réseau d’assainissement de pied de talus de remblai
Les eaux interceptées par le réseau de crête de talus de remblai et collectées par les descentes d’eau
parviennent au pied du talus, au niveau de terrain naturel. Lorsque les débits qui y parviennent
commencent par devenir important, lorsque ces eaux sont évacuées librement, elles peuvent créer des
érosions au pied de talus ce qui pose un problème pour l’ouvrage routier ou encore créer des
dommages pour les riverains.
Fig 6.2.8. Fosses dans un terrain en remblai (Van Tuu 1981).

77. 72
Il faudra bien sûr les collecter et les canaliser vers les exutoires. Le réseau qui permet de récupérer ces
eaux est appelé réseau de pied de talus de remblai, disposé au moins de 1 à 2 m du pied de talus.
L’ouvrage de pied de talus de remblai est généralement un fossé trapézoïdal ou triangulaire enherbé à
forte capacité hydraulique, ou un fossé revêtu lorsque des risques d’érosion sont à craindre (la pente
critique est souvent de l’ordre de 3,5 ‰).
Photo 6.2.1 : Fossé revetu en béton au pied de talus en déblai (Hosni 2003) .
Photo 6.2.2 : Fossé en maçonné au pied de talus en déblai (Hosni 2003) .
Photo 6.2.3 : Fossé en maçonné au pied de talus en déblai (Hosni 2003) .

78. 73
6.2.4 Ouvrages transversaux et de raccordement
Les ouvrages transversaux sont ceux qui assurent le transfert d’écoulement de l’eau d’un réseau
longitudinal vers un autre. On distingue les ouvrages descentes d’eau et les traversées sous-
chaussées (collecteurs enterrés).
Les ouvrages de raccordement quand à eux sont situés à chaque point de ramification, de rejet ou
encore de changement de nature d’ouvrage (des différents raccordements des liaisons transversales
avec le réseau longitudinal). On distingue les regards de visite, regards avaloirs, les têtes de
collecteur et les ouvrages de raccordement. Ces ouvrages ces ouvrages sont préfabriqués et plus
rarement coulés en place.
Il est à signaler, qu’un un regard devra être impérativement prévu à chaque changement de direction
du tracé du collecteur, à une rupture de pente dans le profil en long et à une modification du diamètre
du collecteur.
Fig 6.2.9. Schéma général des ouvrages de collecte des eaux superficielles sur un ouvrage routier
(Ingérop 2015).
6.2.5 Ouvrages de contenance et de dépollution
Pour ouvrage de contenance, il faut entendre les bassins de régulation (écrêteurs, d’orage ou de
retenue) qui ont pour fonction principale de stocker et différer les débits à l’aval vers l’exutoire. Ces
bassins ont un rôle multifonction : décantation et lutte contre la pollution accidentelle. Les ouvrages de
contenance et de dépollution relèvent de techniques spécialisées.
6.2.6 Exutoires
Les exutoires pouvant recevoir les rejets en terme de quantité et qualité sont à identifier en amont de la
conception du réseau.

79. 74
6.2.7 Types et formes des fossés
Un fossé est creusé parallèlement à la route pour faciliter l'écoulement des eaux superficielles.
Les fossés ont un rôle principal, de recueillir les eaux de ruissellement de la surface de chaussée et les
évacuer pour qu'elles ne nuisent pas à la chaussée, aux utilisateurs de la route et autres ouvrages
(remblais, talus de déblais,...). Le fossé doit conserver son gabarit et ne pas présenter de points bas qui
entraîneraient des stagnations d'eau. Les fossés ont souvent aussi un rôle important d'interception des
eaux de l'environnement extérieur à la route. Ils ont également un rôle secondaire : assainir le corps de
chaussée voire, pour partie, le sol support (collecter les eaux des drains naturels ou artificiels, couper
les arrivées d'eaux souterraines). Très souvent, le fossé sert également à protéger les accotements des
riverains (délimitation nette des emprises). Mais le fossé profond peut être parfois dangereux pour
l’usager.
Il constitue un obstacle pouvant guider les véhicules vers les têtes de buses et des dalots. Un fossé est
caractérisé par son emplacement, sa forme, sa pente, sa profondeur, et la présence ou non d'un
revêtement.
On distingue en général deux type de fossés selon son emplacement :
- Les fossés extérieurs destinés à collecter principalement les eaux provenant du bassin versant
extérieur ;
- Les fossés latéraux situés dans les deux rives de la route, ou dans un seul côté de la route sont
destinées à collecter principalement les eaux de la plate-forme routière et des zones du talus, bande
d’arrêt …
Il est conseillé de mettre systématiquement des fossés extérieurs lorsqu’il y a un impluvium amenant
des débits non négligeables au pied de la route. On décharge ainsi les fosses latéraux de ces apports,
on évite leur comblement en diminuant les dépôts solides et on réduit les risques d’obstruction des
ouvrages de décharges par le charriage solide (branche, détritus divers).
Les fossés peuvent être de forme :
- Triangulaires, confectionnés par exemple au niveleuse. C’est le plus communément rencontré. Les
pentes des talus sont en général 1/2 et 2/1 ou bien 2/3 et 3/2 ;
Fig 6.2.10. Fosses de forme triangulaire (Van Tuu 1981).

80. 75
- Rectangulaires, confectionnés par exemple par la pelle mécanique ou au ripper en terrain rocheux ;
Fig 6.2.11. Fosses de forme rectangulaire (Van Tuu 1981).
- Trapézoïdaux, confectionnés par exemple par la niveleuse ou par la pelle mécanique en terrain
rocheux. Les pentes de talus peuvent être 1/2, 1/1, 2/1 ou 3/2 suivant la stabilité des talus, voire plus
raide en terrain rocheux.
Fig 6.2.12. Fosses de forme trapizoïdale (Van Tuu 1981).
- Circulaires (ou cunettes), confectionnés par exemple par la niveleuse, avec une hauteur
généralement < 0.6 m et des longueurs variables, elles sont parfois revêtues en béton/ béton armé, en
pierre, et par fois elles sont en terre.
Fig 6.2.13. Fosses de forme cunettes (Van Tuu 1981).
Les fossés sont généralement revêtus en béton, en béton armé ou en préfabriqué, surtout dans les
terrains meubles, pour éviter les affouillements. Compte tenu du coût de ces canaux, les profils
trapézoïdaux dits économiques sont parfois utilisés (un débit d’écoulement maximum pour une
longueur de revêtement minimale). Mais parfois les fossés sont non revêtus, s’ils ont des faibles
profondeurs et les terrains sont stables.

81. 76
Les dimensions peuvent être très variables, notamment pour les fossés extérieurs qui peuvent être
amenés à véhiculer des débits importants, mais généralement les profondeurs sont comprises entre 0.5
m ≤ h ≤ 1.0 m. Pour les fossés latéraux (intérieurs), on ne dépasse pas en général une profondeur de
0,6 m.
Les fossés extérieurs ou fossés latéraux doivent comporter les ouvrages de décharge en nombre
suffisant, pour éviter les débordements de l’eau.
Les ouvrages de décharge peuvent être des ouvrages sous-chaussés ou bien des ouvrages divergents,
selon la topographie de la zone traversée.
6.2.8 Autres ouvrages d’assainissement
a./ Les bordures, bourrelets et caniveaux
Ce sont des ouvrages situés en bordure de la chaussée ou de l’accotement, qui permettent de protéger
les talus contre le ravinement en guidant l’eau vers les avaloirs. Ils sont utilisés en crête de talus de
remblai et éventuellement sur terre-plein central, lorsqu’il est revêtu.
Fig 6.2.14. Profil d’un bourrelet et sa position par rapport une glissière (Biaou 2009).
Les caniveaux sont des ouvrages préfabriqués ou maçonnés (et soigneusement jointoyés) destinés à
recueillir et écouler les eaux superficielles le long de la chaussée.
Fig 6.2.15. Quelques formes de caniveaux (Nehaoua 2011).
D’autres type de caniveau est aussi existe, sont les caniveaux à grilles. Ce sont des ouvrages
préfabriqués ouverts à leur parte supérieure et recouverts d’une grille en métal ou en béton. Ils
assurent à la fois le rôle d'avaloirs longilignes et d'ouvrages de transport. Ils remplacent les fossés pour
recevoir les eaux de surface de la chaussée mais ils ne drainent pas. On les installe aussi parfois à
l'entrée de propriétés riveraines bâties pour éviter l'écoulement des eaux du domaine public vers le
domaine privé ou vice-versa. Les grilles sont justifiées par la nécessité d'arrêter les corps étrangers et
de permettre le passage occasionnel d'un véhicule. Il est conseillé de souder les grilles entre elles pour
éviter les risques de vol. La résistance des caniveaux doit être adoptée aux charges qu'ils sont
susceptibles de supporter.

82. 77
Fig 6.2.16. Caniveau rectangulaire couvert par une grille (Nehaoua 2011).
b./ Les avaloirs
Un avaloir est un ouvrage qui reçoit l’eau d’un caniveau, et permet à l'eau de descendre dans un
ouvrage situé à un niveau inférieur, généralement enterré (collecteur, buse de traversée,...).
Fig.6.2.17. a) Avaloir sous la chaussée b) avoir sous trottoir
Le rôle principal des avaloirs est de capter toute l’eau superficielle d’écoulement, descendre l’eau à un
niveau inférieur, arrêter les déchets solides emportés par l’eau, faire décanter les particules fines en
bas de l’avaloir.
Photo 6.2.4 : a) Avaloir a entrée verticale b) avoir à entrée latérale

83. 78
c./ Les descentes d’eau
Une descente d’eau est un ouvrage préfabriqué mis en place à la surface d’un talus ou enterrée.
Les descentes d'eau de surface sont constituées d'éléments emboîtés (tuiles) ou d'éléments en arc de
cercle (tôle ondulée galvanisée). En plus de la partie descendante, elles comprennent un ouvrage de
tête (entonnement) et un ouvrage de raccordement avec l'ouvrage inférieur (généralement fossé). Cet
ouvrage sert, en outre, de butoir et de calage pour les descentes d'eau.
Les descentes d'eau enterrées sont constituées d'une canalisation avec un avaloir à la partie supérieure
et un ouvrage de raccordement à la partie inférieure. Un regard intermédiaire permet d'assurer la
jonction entre la canalisation et l'ouvrage de raccordement.
Les descentes d’eau permettent de canaliser les eaux provenant d’un niveau haut vers un ouvrage situé
en bas. Les ouvrages implantés sur les crêtes de talus (de remblai ou de déblai), ils permettent
d’acheminer au pied de talus, les eaux collectées sur les crêtes. Les ouvrages utilisés sont des
caniveaux préfabriqués pour les débits faibles, et des ouvrages coulés sur place pour les débits plus
importants. On distingue les descentes d’eau suivant :
- Descentes d'eau de talus de remblais : Ce sont les plus fréquentes. Elles permettent à l'eau
collectée en bord de la chaussée de rejoindre un fossé ou un autre ouvrage situé en contrebas du
remblai,
- Descentes d'eau de talus de déblais : Elles permettent aux eaux collectées en haut des talus de
déblais de s'écouler vers les ouvrages d'assainissement qui bordent la route,
Nous pouvons dire que les avantages relatifs à la descente superficielle est que l’entretien est plus,
alors que ces inconvénients est qu’elle gêne parfois l’entretien des talus et aussi elle est plus fragile à
la dégradation.
La descente enterrée ne pose pas de problème lors de l’entretien du talus, mais elle a un problème
d’obturation.
Fig 6.2.18. descente d’eau de surface (Nehaoua 2011).

84. 79
Fig 6.2.19. descente d’eau enterrée (Nehaoua 2011).
d./ Les barbacanes
II s'agit des perforations situées à la base des dispositifs de retenue en béton destinées à l'écoulement
de l'eau. Ces barbacanes doivent être maintenues en parfait état de fonctionnement pour éviter toute
accumulation d'eau en amont de l'ouvrage en béton.
Fig 6.2.20. Emplacement des barbacanes sous un dispositif de béton (Nehaoua 2011).
6.2.9 Les ouvrages de concentration des eaux
Ce sont les regards et avaloirs associés qui sont des ouvrages de concentration qui assurent la
transmission des eaux recueillies par les ouvrages de collecte, les bordures et les bourrelets, vers les
dispositifs d’évacuation situés hors de la plate-forme.

85. 80
Fig 6.2.21. Modèle d’un regards
6.2.10 Ouvrages de franchissement
a./ Choix de la période de retour de pluie/débit
La pluviométrie de la zone de projet de route est l’une des données les plus importantes pour le
dimensionnement des ouvrages sous-chaussés, des différents réseaux, des ponts…. On peut y associer
l’évaporation de la zone, mais compte tenue des surfaces faibles à assainir dans la majorité des cas,
l’évaporation peut être négligée sans trop d’erreur. La courbe IDF reliant les intensités des pluies à
leurs durées pour chacune des fréquences de leur apparition est d’une importance capitale de cette
phase du projet. Elle permet d’estimer les débits des exutoires identifiés.
Pour la collecte des eaux superficielles, lorsqu’il s’agit des autoroutes et voies rapides urbaines, une
période de retour de 50 à 100 ans est généralement choisie pour les petits ouvrages hydrauliques, en
vérifiant que l’eau n’atteint pas le bord de la chaussée (ou de la bande d’arrêt d’urgence pour les
autoroutes, lorsqu’on suppose que les bermes font partie de l’ouvrage superficiel). Pour les routes de
moyenne importance, une période de retour de 10 à 25 ans est généralement choisie.
Alors que, s’il s’agit des ponts qui traversent les grands cours d’eau, des périodes de retour de 100,
200 et même 500 ans de débit de crue de projet sont pris en considération.
La période de retour « T » à prendre en compte doit dans chaque cas, faire l’objet d’une analyse
mettant en regard le coût d’investissement de l’infrastructure, ainsi que les conséquences d’un
débordement pour l’usager (l’impact sur la voie de circulation et sur le milieu naturel). Dans le cas des
zones inondables, il faut tenir compte des enjeux liés à la zone inondable. Pour chaque type
d’infrastructure, les conditions d’écoulement et l’effet d’une crue exceptionnelle doivent être
appréciés.

86. 81
b./ Protections des ouvrages hydrauliques sous-chaussés
Il est intéressant de caler le radier de l’ouvrage hydraulique à au moins 0,30 m sous le fond du lit du
cours d’eau pour permettre la reconstitution d’un fond naturel dans l’ouvrage.
La surélévation du niveau amont des écoulements et l’accroissement des vitesses en sortie d’ouvrage
nécessitent le plus souvent des protections en amont et en aval des ouvrages.
La protection efficace des berges aux changements de direction par des techniques pérennes relevant
prioritairement du génie végétal « Protection des berges de cours d’eau en techniques végétales ».
Les techniques de renforcement par enrochements et gabions devront être réservées aux sections
fortement sollicitées par la vitesse de l’écoulement, si les enjeux sont importants en terme de sécurité
des personnes et des biens à fortes valeurs ajoutées ;
L’accès aux ouvrages hydrauliques doit tenir compte des contraintes d’exploitation.
Une visite annuelle et une visite après une crue sont nécessaires pour les travaux d’entretien de
l’ouvrage et l’évacuation des différents atterrissements.
Pour certains ingénieurs de travaux publics, ils optent un diamètre minimal pour les ouvrages
hydrauliques sous les autoroutes de 1000 mm, et de 800 mm pour les routes de 2 ou 3 voies, tout en
garantissant les conditions d’exploitation et d’entretien.
Les contraintes de dimensionnement hydraulique auxquelles ces ouvrages doivent être soumis sont
essentiellement les contraintes de pente. En effet, pour des pentes inférieures à 3 ‰ des problèmes
décantation des sédiments et des éléments fins sont généralement observées, et pour des pentes fortes
> 6 %, des fortes vitesses sont générées, ce qui produit un érosion de l’ouvrage. Donc il est
recommandé de mettre en place les ouvrages nécessaires pour éviter un tel problème dans les deux
situations. Dans tous les cas, il reste l’entretien et l’exploitation de ces ouvrages le moyen le plus
fiable pour garder l’infrastructure routier dans les bonnes conditions, et par conséquence fournir une
sécurité aux usagers de la route.
c./ Ouvrages de traversées
Les ouvrages de traversés ou ouvrages de franchissement sont des ouvrages qui permettent de
traverser un cours d’eau, un talweg ou une dépression.
c.1./ Les buses et dalots
- Deux types de buses sont couramment utilisés : les buses en béton et les buses en métal.
Les buses sont utilisées exclusivement dans des sections où l’on dispose d’une épaisseur suffisante de
remblais (un minimum de 0.8 m de remblai est nécessaire au-dessus de la buse) et peuvent être
utilisées avec des hauteurs de remblais élevées.
Dans le cas des buses métalliques, cette hauteur de remblai admissible est fonction de l’épaisseur de la
buse.
Afin de permettre le nettoyage ou le curage des buses qui risquent souvent d’âtre obstruées
partiellement par les dépôts de sédiments et de pierres charriés par les eaux, il est conseillé de ne
jamais adopter un diamètre inférieur à 800 mm.
Les débits admissibles sont donc variables et peuvent être très élevés dans le cas d’une batterie de
plusieurs buses de grand diamètre quand la topographie du site permet un tel dispositif.
- Les dalots sont des ouvrages de franchissement placé sous chaussée qui nécessitent aucun remblai ou
admettre qu’une faible épaisseur de remblai (1 à 2 m), donc ils sont spécialement calculés pour les
surcharges.

87. 82
Trois types de dalots sont couramment utilisés :
- Les dalots ordinaires constitués de piédroits verticaux fondés sur semelles ou radier général et
sur lesquels repose une dalle en béton armé ;
- Les dalots cadres dans lesquels la dalle, les piédroits et le radier constituent une structure
rigide en béton armé (cadre) ;
- Les dalots portiques analogues aux dalots cadres, mais sans radier (piédroits verticaux fondés
sur semelles).
Les dalots sont en béton armé et résistent à toutes les contraintes extérieures et intérieures, ils sont
constitués par les éléments principaux suivants :
- Un radier ou une semelle en béton armé ;
- Si l’ouvrage de traversé est un matériau préfabriqué, il est généralement poser directement sur
la semelle ;
- S’il est couler sur place, il est généralement constituer de : piédroits, une dalle en béton armé,
deux murs de tête, quatre murs en aile (deux en amont et deux en aval) ;
- L’enrochement de protection amont et aval ;
- Les remblais d’accès ;
Les dalots de forme rectangulaire ou carrée sont généralement adoptés pour des débits
dépassant 10 m3
/s.
Ces ouvrages permettent le maintien du réseau hydrographique naturel au droit des arrivées d’eau.
Elles permettent aussi aux eaux collectées par les fossés de franchir la chaussée.
Seulement, il est nécessaire de mettre en place les aménagements nécessaires afin de minimiser
l’érosion et le transport solide vers ces ouvrages routiers.
Dans tous les cas, la hauteur d’eau amont ne doit pas excéder 1.2 fois la hauteur de l’ouvrage. Pour les
ouvrages d’ouverture ≤ 2 m. Les vitesses moyennes d’écoulements doivent respectées les critères de la
durabilité de l’ouvrage (doivent être inférieure à la vitesse admissible). En cas d’impossibilité de
satisfaire à ces conditions de la vitesse, il conviendra de prévoir des dispositifs de protection.
Le tirant d’air dans l’ouvrage de traversé correspond, en toute rigueur, à la hauteur libre entre la ligne
d’eau et la génératrice supérieure de l’ouvrage. Pour une ouverture ≤ 2,00 m, il est apprécié et
déterminé en fonction du débit de projet. Alors que pour une ouverture > 2,00 m, le tirant d’air est de
0,50 à 1,50 m. Et de préférence que le taux de remplissage de l’ouvrage hydraulique n’excède pas 75
% la hauteur totale de l’ouvrage.
Ces ouvrages hydrauliques sont généralement implantés dans l’axe du lit mineur du cours d’eau, et son
ouverture doit être égale au moins à celui du lit mineur. Il peut néanmoins être nécessaire de rectifier
le tracé naturel de l’écoulement sous l’infrastructure (la route) pour réaliser une traversée plus directe.
La continuité de l’écoulement hydraulique doit être respectée et les zones sensibles à l’érosion doivent
faire l’objet de protection.
Le contrôle de l’ouvrage est organisé après chaque saison pluvieuse, et après chaque crue importante
afin de détecter s’il y a lieu des anomalies ou des dégradations de l’ouvrage.
Une batterie de buses pourrait cependant être de coût moins élevé que le dalot, Néanmoins la
probabilité de risque d’obstruction des buses par branchages et souches en zone boisé est à traiter
sérieusement. Donc une rapide comparaison du coût des deux ouvrages, est nécessaire tous en tenant
compte du problème d’obstruction.

88. 83
Photo 6.2.5 : Vue de face d’une buse métallique en tôle ondulé galvanisée (à gauche)
et d’un dalot en béton armé (à droite).
Fig 6.2.22. Vue de dessus d’un dalot (Millogo 2009).
Il est signalé aussi que certains auteurs préfère la notion de « la revanche » au lieu de « le tirant
d’eau ». Ils ont proposés diverses formules pour l’estimation de la revanche :
On donne par exemple la formule de Mallet et Pacquant
en m
Avec :
h : est la hauteur de la vague formé sur le plan d’eau amont par le vent en m,
l : est la longueur du plan d’eau amont en Km,

89. 84
c.2./ Les ponts
Le pont est un ouvrage qui permet de franchir une dépression ou un obstacle (cours d’eau, voies de
communication) en passant par-dessus. Il est construit sur cours d’eau lorsque :
Le débit est important, la dépression est très profonde, ou le trafic routier est élevé.
Le pont est composé de trois parties principales :
- Les fondations qui permettent de transmettre les efforts au terrain ;
- Les appuis comprenant :
 Les culées qui servent d’appuis aux extrémités du tablier et supportent les poussées des
remblais ;
 Les piles qui supportent le tablier entre les culées ;
- Un tablier qui supporte les voies de circulation (automobiles, piétons, animaux) ; il peut être
en une ou plusieurs travées en fonction de la largeur de la vallée à traverser ;
L’étude hydraulique consiste à déterminer les caractéristiques suivant du pont :
- La hauteur d’eau est déterminée à partir de la crue de projet. Cette dernière est estimée par les
méthodes hydrologiques pour des périodes de retour prises égale à 200, 500 ou 1000 ans. La
crue de projet à prendre en compte dépend de l’importance de la route.
- Certains auteurs recommandent une estimation de la crue de projet centennale multiplie par un
facteur de sécurité variant de 1.5 à 2 ;
- La hauteur d’eau est calculée par la formule usuelle de débit de Manning-Strickler ;
- Le tirant d’air est prévu pour diminuer le risque d’obstruction partielle ou totale du pont. Il
dépend aux risques e charriage et de l’importance de l’ouvrage. Pour des ponts de longueur
inférieure à 50 m, on adopte généralement un tirant d’air au moins égal à :
 En zone désertique :
Si la portée du pont est < 50 m, le tirant d’air doit être ≥ 1.5 m ;
Si la portée du pont est > 50 m, le tirant d’air doit être ≥ 1.0 m ;
 En zone forestière :
Si la portée du pont est < 50 m, le tirant d’air doit être ≥ 3.0 m ;
Si la portée du pont est > 50 m, le tirant d’air doit être ≥ 2.0 m ;
- Il est recommadé d’estimer la profondeur d’affouillement au niveau des piles et d’évaluer
l’érosion des berges.
Fig 6.2.23. Coupe d’un pont à poutre droite (Millogo 2009).

90. 85
Les piles et les Culées des ponts qui sont en contact direct avec l’écoulement doivent avoir des profils
de formes hydrodynamiques pour résister à l’écoulement de l’eau et par suite une sollicitation
minimale des structures. D’autre part, ils doivent présenter une restriction minimale de la section
naturelle de l’écoulement pour réduire les effets des remous, la submersion des ouvrages et l’érosion
du lit de l’oued à l’aval (menaçant dans les deux cas et la vie de l’ouvrage et de ses usagers).
d./ Les radiers routiers
Un radier est un ouvrage qui permet de franchir les rivières en basses eaux et qui est submergé en cas
de crues. Le radier est établi sur le fond de la rivière et l’eau passe exclusivement par-dessus. Il est
donc construit sur un cours d’eau de faible pente, moyennement large, de faible hauteur des berges, et
qui reste sec en grande partie de l’année. Ce type d’ouvrage convient surtout en zone désertique.
Le radier routier est généralement composé de :
- Un radier en béton ou en béton armé ;
- Une protection en amont et une autre en avale ;
- Des balises de signalisation.
Le franchissement d’une rivière par un radier routier est moins coûteux qu’un dalot ou un pont, mais il
présente un inconvénient majeur : le trafic est interrompu lors des crues. L’interruption est due souvent
à la hauteur d’eau qui peut correspondre aussi à des vitesses excessives. On admet généralement des
hauteurs de 0.4 m pour les voitures et 0.6 m pour les camions, avec des vitesses moyennes
d’écoulement n’excédant pas 1.5 m/s.
Le radier lui-même est encré dans le sol et il est protégé à l’amont et l’aval conte l’érosion régressive
par un tapis de gabion semelle ou par un enrochement.
Les radiers routiers les plus réalisés sont : le radier horizontal et le radier courbe
Le radier horizontal
Il est réalisé pour le franchissement des cours d’eau de grandes largeurs, avec des lames d’eau faibles.
L’écoulement sur le radier est semblable à un écoulement sur un déversoir à seuil épais.
Le débit est déterminé par la formule de Bazin :
Q = 1.9 (0.7 + 0.185 HAM/B). L . HAM
3/2
Avec :
Q : débit de pointe de la crue en m3
/s ;
HAM : hauteur d’eau sur le seuil en m ;
B : largeur du radier (distance dans le sens d’écoulement) en m ;
L : longueur du radier en m.
Fig 6.2.24. Coupe d’un radier avec protection aval en escalier (Millogo 2009).

91. 86
Les risques d’affouillement à l’aval d’un radier sont élevés et pour assurer la pérennité de l’ouvrage, il
est nécessaire de réaliser une protection adéquate.
Les affouillements se produisent théoriquement sur une longueur maximale à l’aval du radier :
X = HAM + p
Avec :
X : la longueur de la zone d’affouillement ;
HAM : hauteur d’eau à l’amont du seuil ;
p : épaisseur du radier, ou hauteur de seuil.
Pour bien protéger l’ouvrage, on réalise la protection sur une longueur : L = 2 (HAM + p)
Cette protection aval est généralement faite en gabion semelle (2x1x0.5), et dans le cas d’un radier
surélevé, on réalise les gabions en forme d’escalier afin d’atteindre le fond de la rivière à l’extrémité
aval. Cette protection peut se terminer par un gabion cage (2x1x1) servant de dissipateur d’énergie.
Si les risques d’affouillements sont faibles, la longueur de protection aval peut être allégée (réduire la
distance, à la moitié, le tiers ou le quart…) ;
Si les risques d’affouillements sont élevés, la protection aval en escalier doit être effectuée en béton ou
en béton armé.
Photo 6.2.9 : Radier routier franchissant un cours d’eau (Hosni 2003).
Remarque :
Des balises de signalisation sont placées à l’entrée et à la sortie du radier, ainsi que sur les côtés des
radiers, pour signaler aux usagers la présence de l’ouvrage, ils sont généralement des piliers en béton
armés peints en rouge et blanc d’une hauteur moyenne de 1,50 m.

92. 87
Exercice 1 :
Il s’agit de dimensionner un dalot (ouvrage sous-chaussée). La chaussée à une largeur de 7 m, et le
dalot dépasse la chaussée de part et d’autre de 1.5 m
Fig 1. vue en plan de la route.
Pour pouvoir dimensionner le dalot, il faut évaluer le débit du bassin d’apport, dont les caractéristiques
figurent dans le tableau suivant :
Sous
bassin
Surface
S (ha)
Coeff. Ruissellement
Cr
Longueur d’écoulement
(m)
Côte amont
(m)
Côte aval
(m)
1 11.0 0.4 250 750.0 748.0
2 13.0 0.3 300 748.0 747.1
3 7.0 0.2 450 747.1 744.45
Fig 2. Schéma du bassin versant.
Partie 1- Calcul de débit
1. Calculer la pente équivalente du bassin versant ;
2. Calculer le coefficient de ruissellement équivalent ;
3. Calculer le temps de concentration dans le bassin versant (utiliser la formule de Kirpich );
4. Trouvez l’intensité pluviométrique à partir de la courbe IDF pour une période de retour de 10 ans ;
5. Evaluez le débit à l’aide de la formule rationnelle

93. 88
Fig 3. Courbe IDF (station Batna, code 07031, in Houichi 2017)
Partie 2- Dimensionnement di dalot
On suppose que le débit transporter est 3 m3
/s
1. calculer la hauteur d’eau dans le dalot de baéton (Ks = 60 m1/3
/s), en utilisant la formule de
Manning-Strickler,
2. Evaluer le tirant d’air (la revanche) dans le dalot,
3. Calucler la vitesse moyenne d’écoulement,
Fig 4. Coupe sur le dalot.

94. 89
Solution:
Partie 1
1.La pente équivalente du bassin versant :
Puisque les sous bassins 1, 2 et 3 sont sont en série, donc la pente équivalente est égale :
Avec :
Li : Longueur partielle du tronçon en m ;
Ii : pente du tronçon m/m ;
Sous
bassin
Longueur
(m)
Côte amont
(m)
Côte aval
(m)
Ii
(m/m)
Ieq
(m/m)
1 250 750.0 748.0 0.008
0.005
2 300 748.0 747.1 0.003
3 450 747.1 744.4 0.006
Donc Ieq = 0.005 (soit 0.5 %)
2.Coefficient de ruissellement équivalent
Puisque les sous bassins 1, 2 et 3 sont sont en série, donc le coefficient de ruissellement équivalent est
égal :
Cri : c’est le coefficient de ruissellemnt pour le bassin « i »
Ai : surface du bassin versant « i »
Sous
bassin
Surface
S (ha)
Coeff. Ruissellement
Cr
Cr equivant
1 11.0 0.4
0.31
2 13.0 0.3
3 7.0 0.2
Cr eq = 0.31
3.Temps de concentration
On utilise la formule de Kirpich :
On a Longueur totale : L = 1.0 Km ; la pente moyenne I = 0.00567
Tc = 2.78 heures
4. l’intensité pluviométrique à partir de la courbe IDF pour une période de retour de 10 ans
Donc à partir des courbes IDF, et pour une temps de concentration Tc=2.78h, on trouve une intesité
puluviométrique :
i = 13 mm/h

95. 90
5. Evaluation de débit de crue pour période de retour de 10 ans par la méthode rationnelle
Q = Cr. i. A / 360
avec :
Q : débit de pointe en m3
/s,
Cr : coefficient de ruissellement équivalent (Cr = 0.31),
i : l’intensité de pluie (mm/h) pour une durée égale Tc (i = 13 mm/h)
A : superficie du bassin versanten ha (A = 31 ha).
A.N :
Q = (Cr. i. A) / 360 = (0.31 x 13 x 31)/360 = 0.35 m3
/s
Q = 0.35 m3
/s
Partie 2
1.Calcul de débit au moyen de la formule de Manning-Strickler est :
On a : Ks = 60 m1/3
/s , I = 0.005 et Q = 3 m3
/s
Donc Sm * Rh
2/3
= 0.707
Pour une forme rectalgulaire: Sm = b * h = (0.8*2)*h , Pm = b + 2h = 2(0.8 + h)
Rh = Sm / Pm = 0.8h / (0.8 + h)
0.8 h * (0.8h/(0.8+h))2/3
= 0.707 on résout cette équation par itérations
Donc la hauteur d’eau h ≈ 0.81 m
2. Evaluation de la revanche (tirant d’eau) :
Puisque la hauteur de l’ouverture est < 2m, on peut estimer la revanche en fonction de débit de
transite, ou en utilisant les formules empiriques :
- Le débit est de 3 m3
/s, il est compris entre 1 à 4 m3
/s, on prend une revanche de 0.4 m ;
- On peut utiliser la formule : ce qui donne r = 0.42 m
- Comme on peut prendre pour un dalot de forme rectangulaire une revanche
r = h/3, soit r = 0.27 m ≈ 0.3m
donc on opte pour une revanche r = 0.4 m
3. La vitesse moyenne d’écoulement : V = Q / Sm = 3 / 1.297 = 2.31 m/s , V = 2.31 m/s
h 2* b Sm Pm Rh Sm*Rh
2/3
0.6 1.6 0.96 2.8 0.343 0.470
0.65 1.6 1.04 2.9 0.359 0.525
0.7 1.6 1.12 3 0.373 0.581
0.75 1.6 1.2 3.1 0.387 0.637
0.8 1.6 1.28 3.2 0.400 0.695
0.8106 1.6 1.297 3.22 0.403 0.707
0.85 1.6 1.36 3.3 0.412 0.753
0.9 1.6 1.44 3.4 0.424 0.812
I
R
S
Ks
Q h *
.
*
*
3
/
2


96. 91
Exercice 2 :
On se propose de déperminer l’emplacement des regards à grilles (avaloirs) au niveau de la route
représentée par le schéma suivant (Fig 3.11a et Fig 3.11b):
Fig 1. Vue en plan (Bahlous El Ouafi 2002).
Fig 2. Profil en travers (coupe A-A) (Bahlous El Ouafi 2002).
Le tronçon de la route étudiée a une longueur totale L = 500 m avec une pente globale
I= 1.5 %, et son profil en travers est representé par la coupe A-A.
La largeur de la route est 2 x 4m. le drainage longitudinal de la route est assuré par deux caniveaux
identiques disposés de part et d’autre de la route comme le montre la vue en plan. Ces caniveaux
drainent en plus de la surface de la chuassée, les accotements de largeur 20m chacun.
1. Déterminer la débitance Q des caniveaux en utilisant la formule de Manning-Strickler, avec Ks=
110 m1/3
/s ;
2. Dans le cas où le drainage de la route ne se ferait que superficiellement (c-à-d on ne prévoit pas
des avaloirs), calculer le débit dans chacune des sections S1, S2, S3, …Sx située à une abscisse
« x » sur l’axe de la chaussée (utilisé la formule rationnelle), avec un coefficient de ruissellement
Cr= 0.95 pour la chaussée et Cr=0.95 pour les accoutements aussi. L’intensité de pluie est i = 70
mm/h
3. Sachant que le débit transporté par le caniveau est égal à 72 l/s et que le débit d’un avaloir est
égal à 40 l/s :
- Est-il nécessaire de mettre des avaloirs dans les sections S2 et S3 ?
- Déterminer la distance maximale entre deux avaloirs successifs ;

97. 92
Solution :
1.Détermination du débit qui peut passer dans le caniveau, en fonction de son dimension :
On utilise la formule de Manning-Strickler : Q = Ks. Sm. Rh
2/3
I1/2
Les parameters hydrauliques du caniveau sont les suivants:
Sm = 0.4 x 0.15/2 = 0.03 m², Pm ≈ 0.4 m ; Rh = Sm/Pm = 0.075 m
Q = 110 x 0.03 x 0.0752/3
0.0151/2
= 0.072 m3
/s; Q = 0.072 m3
/s = 72 l/s
2. Calculer du débit dans les sections S1, S2, S3, …Sx située à une abscisse « x » sur l’axe de la
chaussée et à la fin du tronçon de la route :
La méthode superficielle Q = Cr . I . A/360 ; avec Cr = 0.95 et i = 70 mm/h et A (ha): variable
Q= 0.95 x 70 x A/360 = 0.185 A , avec A : surface en ha
Au niveau de la section S1 : A1 = 0 → Q1 = 0 m3
/s
Au niveau du S2 : A2 = 24 x 20 =480 m² = 0.048 ha → Q2 = 0.00888 m3
/s = 8.88 l/s
Au niveau du S3 : A3 = 24 x 40 =960 m² = 0.096 ha → Q3 = 0.01776 m3
/s = 17.76 l/s
Donc à une distance « x » Qx = 0.444 * x (l/s)
Et à la fin du tronçon, soit 500 m, Qtotal = 222 l/s
3. Est-il nécessaire de mettre des avaloirs dans les sections S2 et S3 ?
- Donc, il n’est pas nécéssaire de mettre les avaoirs dans les sections S2 et S3. Par ce que jusqu’à la
section S3, le débit pluvial estimé à 17.76 l/s est largement inférieur à la capacité du caniveau.
- La distance maximale entre deux avaoirs
Puisque la capacité maximale de l’avaloir est 40 l/s,
Donc on va mettre Qx = 40 = 0.444 * x ce qui donne x ≈ 90 m

98. 93
Références bibliographiques
Bahlous El-Ouafi S. (2002). Hydraulique, cours et exercices. CPU.
Beaudy J.P et Rolland J.C (1995). Mécanique des fluides appliquée. Berger.
Ben Hamouda R. (2008). Notions de mecaniqye des fluides. CPU.
Biaou A.C (2009). Cours d’hydraulique routière. 2iE.
Bniaiche E. (2013). Ecoulement à surface libre. ITSMAERB, PPT online.
Bourrier R. (1991). Les réseaux d’assainissement : calculs, applications,perspectives. Lavoisier TEC
et DOC.
Carlier M. (1998). Hydraulique générale et appliquée. Eyrolles.
Chow V.T. (1959). Open Channel hydraulics. McGraw-Hill.
Degoutte G. (2006). Diagnostic, aménagement et gestion des rivières (Hydraulique et morphologie
fluviales appliquées). Lavoisier TEC et DOC.
Gaaloul N. (2013). Notions de mécanique des fluides. Cours. CPU.
Ghernaout R. (2010). Mécanique des fluides et hydraulique. OPU.
Graf W. et Altinakar M. (1993) Hydraulique fluviale (tome I). Ecoulement permanent uniforme et
non uniforme. Presses polytechniques et universitaires romandes, Lausanne.
Houichi L. (2017). Formule appropriee pour l'estimation de l’intensite de pluie de duree et de
frequence voulue: un cas d’etude. Larhyss Journal, (30), 67-87.
Hosni S. (2003). L’assainissement des routes. Direction Générale des Ponts &Chaussées.
Kréménetski N., Schtérenliht D., Alychev V. et Yakovléva L. (1980). Hydraulique. Mir-Moscou.
INGEROP (2015). Adaptation des routes au risque et au changement climatique au Maroc.
Lachat B. (1994). Guide de protection des berges de cours d'eau en techniques végétales, Ministère de
l'Environnement
Lachat A. et Levy M. (1994). Hydraulique. CNFPT.
Lencastre A. (1995). Hydraulique générale. Eyrolles.
Maalel K. et Hafsia Z. (2012). Ouvrages hydrauliques, polycopié du cours. ENIT.
Melville B. (2008). The physics of local scour at bridge piers. 4th
ICSE
Millogo F.A (2009). Ouvrages hydrauliques. Polycopie de cours.
Nehaoua A. (2011). Assainissement routier, Société des études Techniques Sétif, ppt
ONF (2014). Guide technique des travaux routiers forestiers, plaine et collines. ONF.
Ouezdou M. B et Boudrigua A. (2004) les affouillements des ponts en Tunisie. Colloque les risques
en Génie Civil – ISET de Sfax-AIT - 18/19 mars 2004- Tunisie, 274-295.
Richardson E.V.et Davis S.R. (1995). Evaluating Scour at Bridges, 3ème
Edition, Federal Highway
Administration Hydraulic Engineering Circular 18, HEC-18, publication N° FHWA-IP-90-017.
Rocha N. R. (2014) Débits de crue et analyse hydrologique de petits bassins versants. Mémoire de
maîtrise en gérie agroalimentaire, université Laval.
Sari A. (2009). Initiation à l’hydrologie de surface : cours. Houma.
Satin M., Selmi B., Bourrier R. et Lemaire J.P (1995). Guide technique d’assainissement.
Le Monieur.
Sétra (2006). Assainissement routier, guide technique. Sétra
Sétra (2007). Cours d’eau et ponts, guide technique. Sétra.
Série Schaum (1995). M´ecanique des Fluides et hydraulique, Mc Graw hill.
Van Tuu N. (1981). Hydraulique routière. BCEOM.
White F.M. (2009). Fluid Mechanics, Seventh Edition, McGraw-Hill.