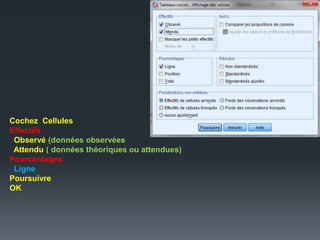
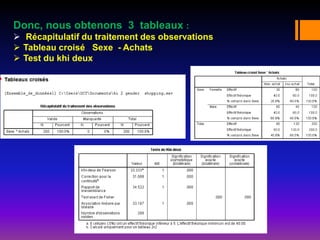
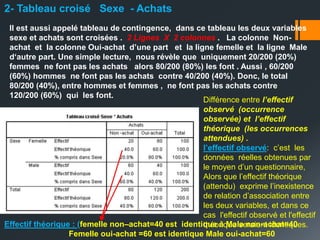
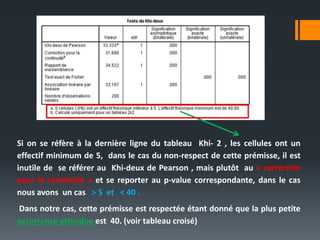
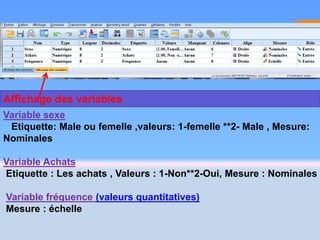
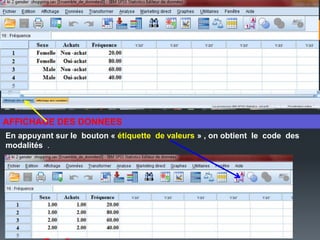
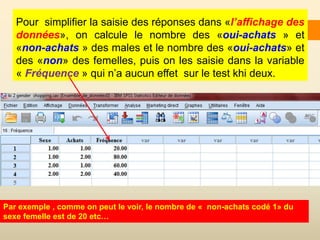
Le document traite du test Khi-deux, une analyse bi-variée utilisée pour déterminer l'association entre deux variables qualitatives nominales. Il illustre, à travers une étude sur la relation entre le sexe et les achats en Algérie, comment ce test évalue les hypothèses d'indépendance. Les résultats indiquent une association significative, avec une valeur p < 0,05, suggérant que les femmes achètent plus fréquemment que les hommes.

1. SPSSUniversité d’Oum El Bouaghi
Faculté des sciences de la terre et de
l’architecture

2. Le principe du test Khi 2 (Chi square)
 Cette analyse bi-variée consiste à déterminer s'il existe une
association entre deux variables qualitatives nominales . C’est-à-
dire déceler une éventuelle relation d’indépendance ou
d’influence d’une variable sur une autre. Le Chi-deux est une
analyse dite non-paramétrique, pas de prémisses des
paramètres de la distribution de la variable (moyenne, écart-type
et normalité).
• La variable qualitative catégorielle nominale est une
information non mesurable. Elle présente des catégories que l’on
nomme avec un nom codé qu’on appelle modalité . La variable
peut avoir plusieurs modalités codées . Par exemple: la variable
sexe avec 2 modalités (1- homme, 2- femme), la variable couleur
avec plusieurs modalités (1-rouge, 2-vert, 3-bleu, 4-…), variable
âge plusieurs modalités, variable fruit avec plusieurs
modalités(1-Banane, 2-Orange, 3-…) et variable logement avec
plusieurs modalités (1- logement individuel, 2- logement semi-
collectif, 3- logement collectif)

3. Ce test utilise tableau croisé (appelé aussi tableau de
contingence) pour examiner la relation entre deux variables
catégorielles. C’est un arrangement dans lequel les données sont
classées selon deux variables catégorielles. Les catégories d'une
variable apparaissent dans les lignes et les catégories de l'autre
variable apparaissent dans les colonnes.

4. Les conditions de l’utilisation de ce test
• Deux variables catégorielles nominales.
• Deux ou plusieurs catégories (modalités)
pour chaque variable.
• Indépendance des observations.
• Taille d'échantillon relativement grande et
aléatoire.
• les catégories des variables sont
mutuellement exclusive (Par exemple ,
oui –non ou male-femelle uniquement ,
pas de réponse intermédiaire)
• Les occurrences attendues doivent être
supérieures ou égales à 5 .

5. Hypothèses (H₀) et (H₁)
L'hypothèse nulle (H₀) et l'hypothèse alternative (H₁) du
test Chi-2 peuvent être exprimées de la manière
suivante :
H₀: « (Variable 1) n'est pas associée à (Variable 2) »
(Absence de relation entre les 2 variables
catégorielles)
H₁: «(Variable 1) est associée à (Variable 2) »
(Existence de relation entre les 2 variables )

6. La question de recherche
Est-ce qu’il a une relation entre le sexe et la fréquence
des achats dans une grande ville algérienne?
L’hypothèse nulle alternative H₀
Il n’ y a pas de relation significative entre le sexe et les
achats dans une grande ville algérienne.
.
L’hypothèse alternative HA
Il y a une relation significative entre le sexe et les achats
dans une grande ville algérienne. .

7. La 1ère variable : Sexe (Femelle et male)
Modalités :
 1- femelle
 2- Male
La 2ème variable: Achats (shopping dans une grande ville algérienne)
Modalités :
 1 - Non
 2 - Oui

8. Variable sexe
Etiquette: Male ou femelle ,valeurs: 1-femelle **2- Male , Mesure:
Nominales
Variable Achats
Etiquette : Les achats , Valeurs : 1-Non**2-Oui, Mesure : Nominales
Variable fréquence (valeurs quantitatives)
Mesure : échelle
Affichage des variables

9. En appuyant sur le bouton « étiquette de valeurs » , on obtient le code des
modalités .
AFFICHAGE DES DONNEES

10. Pour simplifier la saisie des réponses dans «l’affichage des
données», on calcule le nombre des «oui-achats » et
«non-achats » des males et le nombre des «oui-achats» et
des «non» des femelles, puis on les saisie dans la variable
« Fréquence » qui n’a aucun effet sur le test khi deux.
Par exemple , comme on peut le voir, le nombre de « non-achats codé 1» du
sexe femelle est de 20 etc…

11. La variable fréquence
Cliquez sur :
 Données
 Pondérer les observations
 Cochez Pondérer les observations
 Transférez « Fréquence » dans
le champs « Variable d’effectif »
 OK
 Puis saisissez les données dans la
variable fréquence 1
2
3
4

12. Traitement et interprétation des résultats
 Analyse
 Statistiques descriptives
 Tableaux croisés
1- Traitement et analyse (suivre la procédure)
1

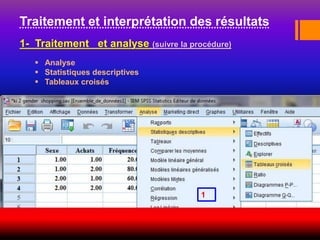
13. Dans cette fenêtre, placez
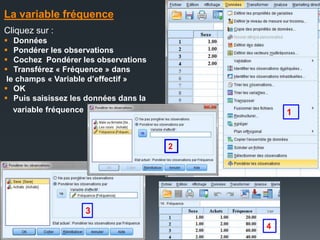
dans le champs « Ligne(s) »
la variable Sexe (Male ou
Femelle) et le champs
«Colonne» les achats,
rappelons qu’il est permis
d’intervertir les positions des
2 variables .
 Cliquer sur « Statistiques »
 Chi-deux
 Phi et V de Cramer [ La taille d'effet (Effect size): la
force de l'association]
 Poursuivre
3
2
2

14. Cochez Cellules
Effectifs
Observé (données observées
Attendu ( données théoriques ou attendues)
Pourcentages
Ligne
Poursuivre
OK

15. Donc, nous obtenons 3 tableaux :
 Récapitulatif du traitement des observations
 Tableau croisé Sexe - Achats
 Test du khi deux

16.  Sur ce tableau, un simple récapitulatif des observations,
il est indiqué, le nombre d’hommes et de femmes
interviewés N=200, dont le nombre qui n’a pas répondu à
la question N=0 ( Manquante) et le total =200,
2- interprétation
1-Tableaux : Récapitulatif du traitement des observations

17. 2- Tableau croisé Sexe - Achats
Il est aussi appelé tableau de contingence, dans ce tableau les deux variables
sexe et achats sont croisées . 2 Lignes X 2 colonnes . La colonne Non-
achat et la colonne Oui-achat d’une part et la ligne femelle et la ligne Male
d‘autre part. Une simple lecture, nous révèle que uniquement 20/200 (20%)
femmes ne font pas les achats alors 80/200 (80%) les font . Aussi , 60/200
(60%) hommes ne font pas les achats contre 40/200 (40%). Donc, le total
80/200 (40%), entre hommes et femmes , ne font pas les achats contre
120/200 (60%) qui les font.
Différence entre l’effectif
observé (occurrence
observée) et l’effectif
théorique (les occurrences
attendues) .
l’effectif observé: c’est les
données réelles obtenues par
le moyen d’un questionnaire,
Alors que l’effectif théorique
(attendu) exprime l’inexistence
de relation d’association entre
les deux variables, et dans ce
cas l'effectif observé et l'effectif
théorique seraient identiques.Effectif théorique : (femelle non–achat=40 est identique à Male non-achat=40
Femelle oui-achat =60 est identique Male oui-achat=60

18. Le résultat est significatif statistiquement car la valeur p =0,000 est inférieure
au niveau de signification choisi (α = 0,05), p-value < α=0,05 et donc nous
rejetons l’hypothèse nulle et nous acceptons l’hypothèse alternative qui stipule
que
« Il y a une significative association entre le sexe et les achats »
Donc, il s’avère que les femmes préfèrent souvent les achats (80/200)
plus que les hommes (40/200).
En d’autres termes, ll y a suffisamment de preuves pour dire que les achats
ne sont pas indépendants du sexe.
du fait que khi-deux de Pearson
2
3- Test du khi deux
p = 0,000 < 0,05
2 Lignes X 2 colonnes

19. Si on se réfère à la dernière ligne du tableau Khi- 2 , les cellules ont un
effectif minimum de 5, dans le cas du non-respect de cette prémisse, il est
inutile de se référer au Khi-deux de Pearson , mais plutôt au « correction
pour la continuité » et se reporter au p-value correspondante, dans le cas
nous avons un cas > 5 et < 40 .
Dans notre cas, cette prémisse est respectée étant donné que la plus petite
occurrence attendue est 40. (voir tableau croisé)

20. (Phi et V de Cramer) en tant que mesures d'associations, indique la force de la
relation entre le sexe des acheteurs et leur réponse à la question portant sur la
fréquence de leurs achats ,
Pour la mesure V Cramer
Elle s’applique lorsque au moins une variable a uniquement 2 modalités,
Plus V Cramer est proche de zéro, plus il y a indépendance entre les deux variables
étudiées. Valeur maximum 1 , signifie complète dépendance
Petite taille= 0.10
Taille moyen= 0.3
Grande taille =0.50
Pour notre cas V Cramer =0,408 , cette valeur indique que l’association entre les
2 variables (sexe et achats) est moyenne, elle est comprise entre 0,3 et 0,5. Aussi
p-value =0,000 < 0,05 , cette relation est assez significative .

21. Merci pour votre attention
 Université d’Oum El Bouaghi
 Faculté des sciences de la terre et de l’architecture