Téléchargé 21 fois
Analyses des données par SPSS et R
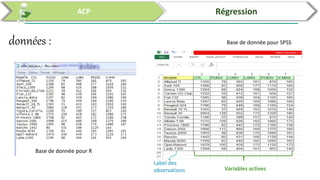
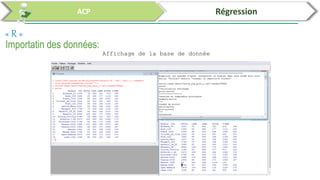
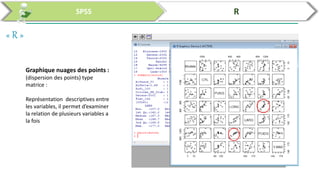
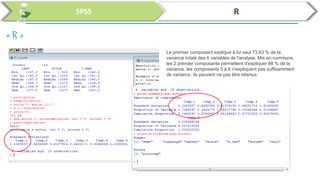
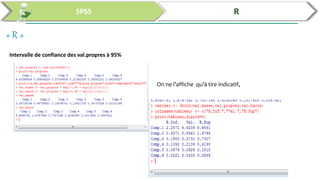
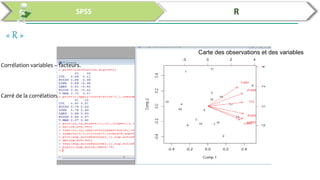
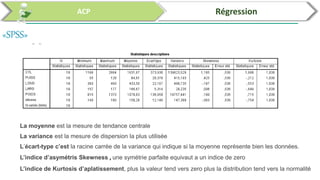
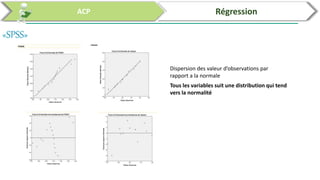
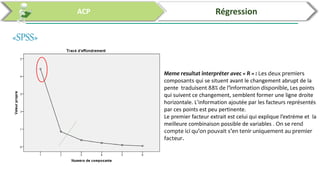
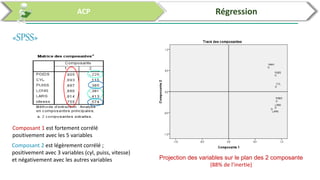
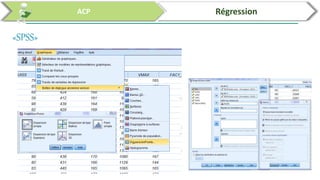
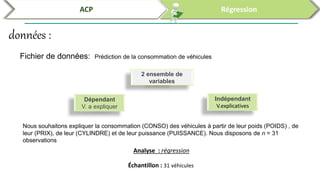
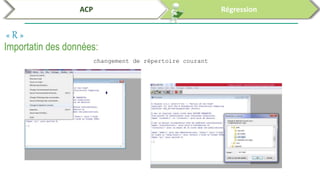
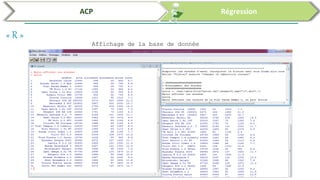
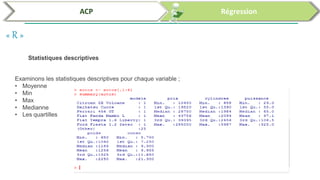
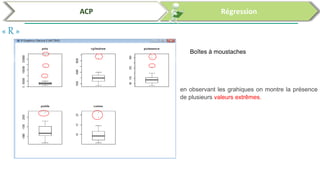
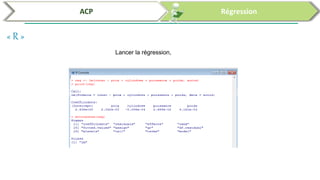
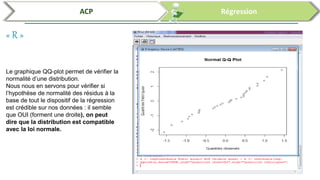
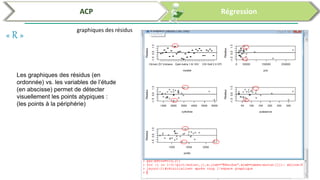
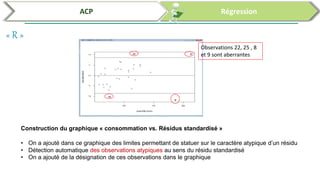
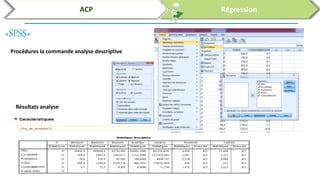
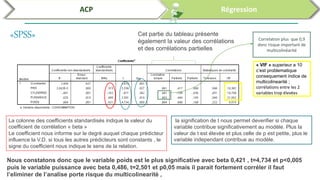
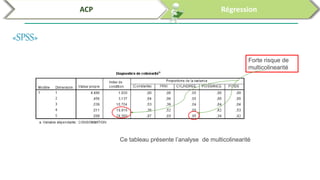
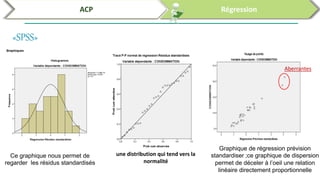
Ce document traite de l'utilisation des logiciels R et SPSS pour réaliser des analyses statistiques, notamment l'analyse en composantes principales (ACP) et la régression. Il présente les étapes d'importation de données, d'analyse descriptive et d'interprétation des résultats concernant les caractéristiques de véhicules, en soulignant l'importance des premiers composants qui expliquent une grande proportion de la variance. Enfin, il aborde la validation du modèle de régression en vérifiant la normalité des résidus et en analysant la significativité des prédicteurs.
![Ch4 andoneco [mode de compatibilité]](https://cdn.slidesharecdn.com/ss_thumbnails/ch4andonecomodedecompatibilit-140429111854-phpapp01-thumbnail.jpg?width=640&height=640&fit=bounds)
