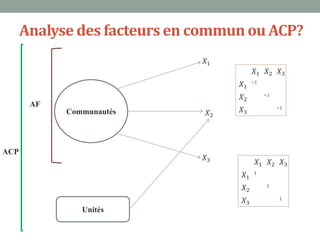
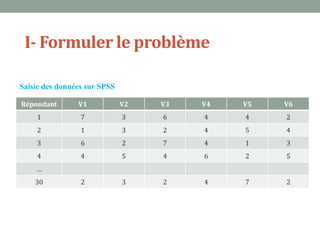
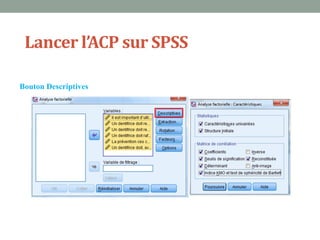
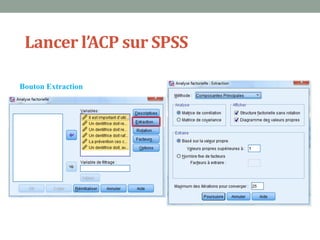
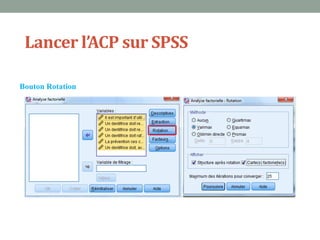
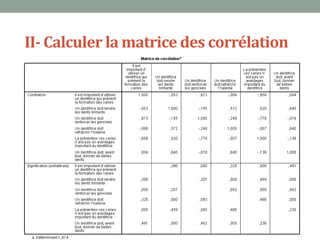
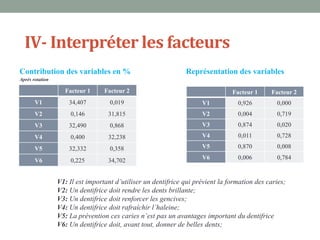
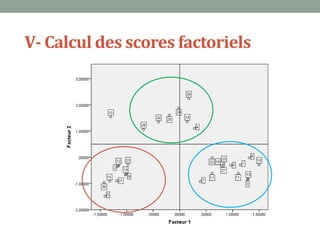
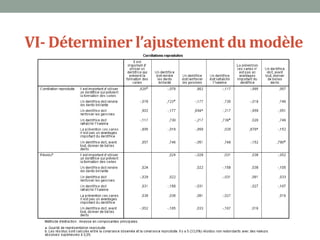
Ce document explique l'analyse en composantes principales (ACP), une méthode d'analyse multidimensionnelle utilisée pour réduire le nombre de variables tout en conservant l'information essentielle. Il détaille son application en marketing pour des études de segmentation, de positionnement et d'études publicitaires, ainsi que les prérequis statistiques nécessaires à son utilisation. En présentant un cas d'étude sur les critères d'achat des dentifrices, il illustre les étapes pratiques de mise en œuvre de l'ACP avec SPSS.

1. Royaume Du Maroc
Université Ibn Zohr
Ecole Nationale de Commerce et de Gestion d’Agadir
ANALYSE EN COMPOSANTES
PRINCIPALES
Mehdi AMAN
Décembre 2012

2. ANALYSE EN COMPOSANTES
PRINCIPALES
PRÉSENTATION DE LA MÉTHODE

3. L’Analyse en Composantes Principales
(ACP)
 L’analyse en composantes principales est une méthode
d’analyse multidimensionnelle des données.
 Les variables sujettes à cette analyse sont des variables
quantitatives.
 L’analyse en composantes principales repose sur l’analyse des
relations entre un nombre important de variables

4. Utilité de l’ACP
Cette méthode est utilisée pour identifier:
1. Les dimensions ou les facteurs fondamentaux qui expliquent
les corrélations entre plusieurs variables;
2. Un nouvel et plus petit ensemble de variables non corrélées;
3. Un ensemble plus petit des variables les plus déterminantes;

5. Avec la condition de…
G ARDER LE MAXIMUM
D’INFORMATION POSSIBLE

6. L’ ACP appliquée en Marketing
Cette méthode trouve de nombreuses applications dans le
domaine des études marketing:
1. Segmentation du marché;
2. Etudes de positionnement;
3. En recherche produit;
4. Etudes publicitaires;
5. Etudes prix…

7. Le Modèle d’ACP
Le modèle d’ACP : Le score Factoriel
𝐹𝑖𝑗 = 𝑋 𝑖1 𝐴1 + 𝑋 𝑖2 𝐴2 + ⋯ + 𝑋 𝑖𝑗 𝐴 𝑗
Où:
𝑭 𝒊𝒋 : est le score de l’individu i sur le
facteur j
𝑿 𝒊𝒋 : est la valeur centrée réduite de
l’individu i sur la variable j
𝑨 𝒋 : Coefficients Factoriels*
Nous avons autant de facteurs que de
variables
* Extraits des vecteurs propres

8. Analyse des facteurs en commun ou ACP?
𝑋1
𝑋1 𝑋2 𝑋3
𝑋1 <1
𝑋2 <1
AF
Communautés 𝑋2 𝑋3 <1
ACP
𝑋3
𝑋1 𝑋2 𝑋3
𝑋1 1
𝑋2 1
𝑋3 1
Unités

9. Glossaire ACP
 Tableau de données: Tableau croisant les individus i et les variables j;
 Matrice des corrélations: Corrélations entre l’ensemble des couples de variables;
 Matrice des corrélations reconstituée: A partir des composantes sélectionnées;
 Résidus: L’écart entre la matrice des corrélations et celle des corrélations reconstituée;
 Valeur propre: Représente la variance totale expliquée par chaque facteur, axe, composante;
 Vecteur propre: Représente les coefficients factoriels;
 Matrice des loadings: Corrélations entre les variables et les facteurs;
 Rotation: Technique qui consiste à pivoter les facteurs avec un angle θ;

10. Glossaire ACP
 Contribution: Contribution de chaque variable/individu dans la formation de les axes;
 Représentation: A quel degré les variables/individus sont bien représentés sur les axes;
 Score factoriel: Pour chaque i, ce sont les nouvelles coordonnées sur les facteurs principaux;
 Test de coude ou Scree Test: Graphique des valeurs propres, pris dans leur ordre
d’importance;
 Test de Sphéricité de Bartlett: Compare la matrice des corrélation à une matrice identité.
 Test Kaiser Mayer Olkin (KMO): Utilisé pour mesurer l’adéquation de l’ACP ou l’AF, il doit
être compris en 0,5 et 1;
 Pourcentage de variance (inertie): Part de la variance totale attribuée à chaque facteur;

11. ANALYSE EN COMPOSANTES
PRINCIPALES
PRE-REQUIS

12. Notions sur les vecteurs
Supposons les deux vecteur V1 et V2 :
2
V1 = 2 V2 = 2
1 2
Graphiquement les deux vecteurs se présentent comme suit:
Y
V1 V2
X

13. Notions sur les vecteurs
Y
Trois informations:
vα
vβ 1- La direction
2- Le sens
X 3- La norme (longueur)
𝑥1
𝑥
Soit le vecteur V = 2 𝒗 𝜶 .𝒗 𝜷
.
𝑥𝑛 ProjVα Vβ = ( )𝒗 𝒂
𝒗𝜶. 𝒗𝜶
𝑽 = 𝑥1 2 + 𝑥2 2 + ⋯ + 𝑥 𝑛 2

14. Rappel sur les statistiques descriptives
𝒏 𝒏
𝒊=𝟏(𝒙 𝒊 − 𝒙)²
𝒏
𝒊=𝟏 𝒙 𝟏 + 𝒙 𝟐 + ⋯+ 𝒙 𝒏 𝒙𝒊 − 𝒙 𝟐
𝒙=
𝒏 𝝈 𝒙² = 𝝈𝒙 =
𝒏 𝒊=𝟏
𝒏
𝒏
𝒊=𝟏(𝒙 𝒊 − 𝒙)(𝒚 𝒊 − 𝒚)
𝒓 𝒙𝒚 =
𝝈𝒙 𝝈𝒚

15. ANALYSE EN COMPOSANTES
PRINCIPALES
PRINCIPE

16. Principe de base dans l’estimation des
facteurs
 Nuage d’individus
ACP Normée: menée sur des données centrées et réduites

17. Principe de base dans l’estimation des
facteurs
 Nuage de variables
Le cosinus de l’angle formé par les deux vecteurs est égal au coefficient de corrélation
entre ces deux vecteurs

18. Principe de base dans l’estimation des
facteurs
 Ajustement du nuage d’individus: Projection des i

19. Principe de base dans l’estimation des
facteurs
 Ajustement du nuage des individus: Projection des d²(i , l)

20. Principe de base dans l’estimation des
facteurs
 Ajustement du nuage des variables

22. ANALYSE EN COMPOSANTES
PRINCIPALES
Mener une ACP sur SPSS

23. Mener une ACP sur SPSS
Calculer la Calculer les Estimer
Formuler le Extraire les Interpréter
matrice des scores l’adéquation
problème facteurs les facteurs
corrélations factoriels du modèle

24. I- Formuler le problème
 Objectif(s) de l’étude;
 Variables d’études;
 Echelle;
 Taille de l’échantillon;

25. Etude de cas
Les avantages fondamentaux recherchés
par les consommateurs lors de l’achat
d’un dentifrice

26. I- Formuler le problème
• Le sondage est réalisé sur un échantillon de 30 personnes
dans un centre commercial, ces dernières ont donné leur
avis sur les affirmations suivantes, sur une échelle de 1 à 7
(1: En total désaccord; 7: entièrement d’accord):
 V1: Il est important d’utiliser un dentifrice qui prévient la formation des caries;
 V2: Un dentifrice doit rendre les dents brillante;
 V3: Un dentifrice doit renforcer les gencives;
 V4: Un dentifrice doit rafraîchir l’haleine;
 V5: La prévention ces caries n’est pas un avantages important du dentifrice
 V6: Un dentifrice doit, avant tout, donner de belles dents;

27. I- Formuler le problème
Saisie des données sur SPSS
Répondant V1 V2 V3 V4 V5 V6
1 7 3 6 4 4 2
2 1 3 2 4 5 4
3 6 2 7 4 1 3
4 4 5 4 6 2 5
…
30 2 3 2 4 7 2

28. I- Formuler le problème
Saisie des données sur SPSS

29. Lancer l’ACP sur SPSS

30. Lancer l’ACP sur SPSS
Bouton Descriptives

31. Lancer l’ACP sur SPSS
Bouton Extraction

32. Lancer l’ACP sur SPSS
Bouton Rotation

33. Lancer l’ACP sur SPSS
Bouton Facteurs

34. II- Calculer la matrice des corrélation

35. II- Calculer la matrice des corrélation

36. III- Extraire les facteurs et déterminer leur
nombre

37. III- Extraire les facteurs et déterminer leur
nombre
 Détermination a priori ou considérations théoriques;
 Détermination fondée sur les valeurs propres;
 Scree-Test;
 Pourcentage de la variance;
 Test de fiabilité de deux sous-échantillons;
 Signification statistiques des valeurs propres;

38. IV- Interpréter les facteurs

39. IV- Interpréter les facteurs

40. IV- Interpréter les facteurs
Contribution des variables en % Représentation des variables
Après rotation
Facteur 1 Facteur 2 Facteur 1 Facteur 2
V1 34,407 0,019 V1 0,926 0,000
V2 0,146 31,815 V2 0,004 0,719
V3 32,490 0,868 V3 0,874 0,020
V4 0,400 32,238 V4 0,011 0,728
V5 32,332 0,358 V5 0,870 0,008
V6 0,225 34,702 V6 0,006 0,784
V1: Il est important d’utiliser un dentifrice qui prévient la formation des caries;
V2: Un dentifrice doit rendre les dents brillante;
V3: Un dentifrice doit renforcer les gencives;
V4: Un dentifrice doit rafraîchir l’haleine;
V5: La prévention ces caries n’est pas un avantages important du dentifrice
V6: Un dentifrice doit, avant tout, donner de belles dents;

41. IV- Interpréter les facteurs
V1: Prévention de la formation des caries;
Bienfaits sociaux
V2: Dents brillantes;
V3: Renforce les gencives;
V4: Rafraîchit l’haleine;
V5: La prévention des caries (NI)
V6: De belles dents;
Hygiène & santé des dents

42. V- Calcul des scores factoriels

43. V- Calcul des scores factoriels

44. VI- Déterminer l’ajustement du modèle
Une comparaison entre la matrice des
corrélations initiale et la matrice des
corrélations reconstituée à partir des
facteurs
Evaluation de la significativité des
résidus

45. VI- Déterminer l’ajustement du modèle

46. Quelques références