Présentation acp

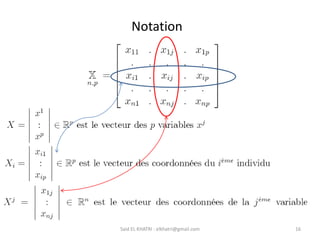
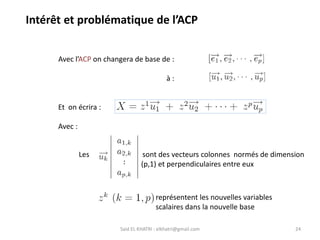
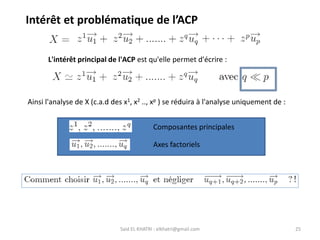
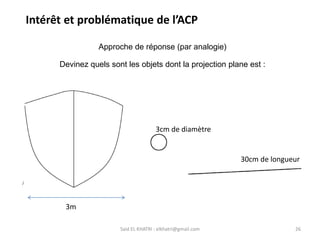
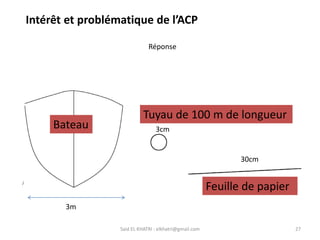
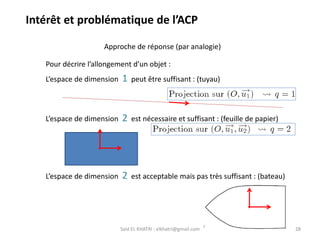
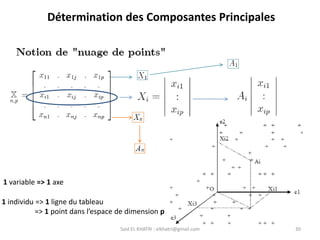
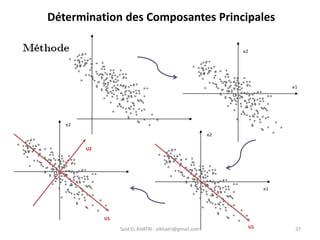
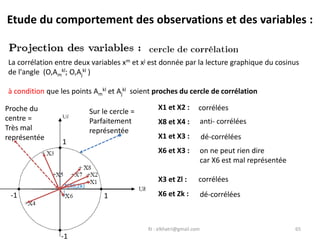
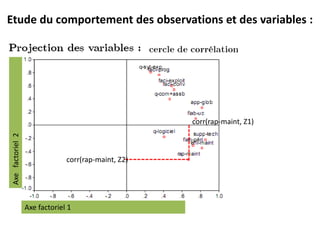
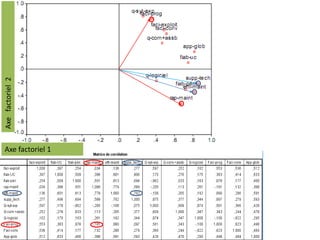
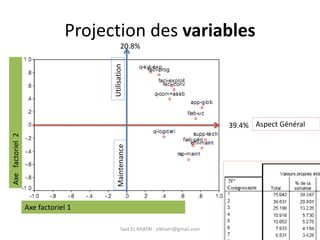
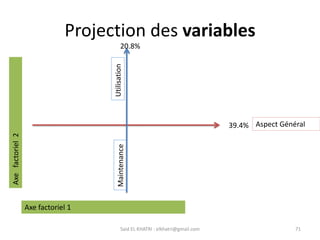
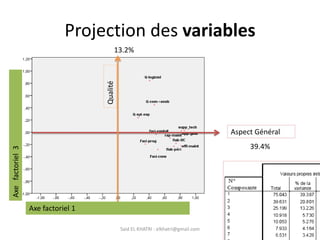
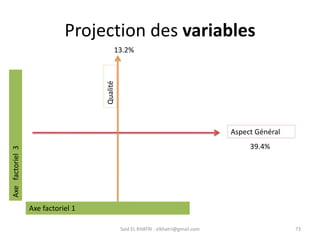
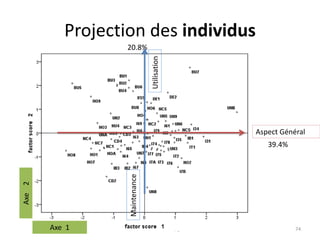
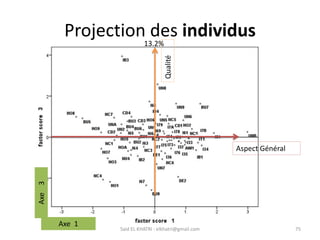
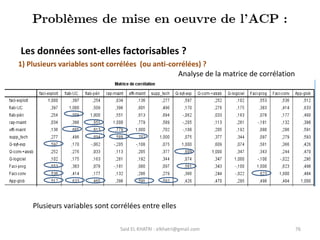
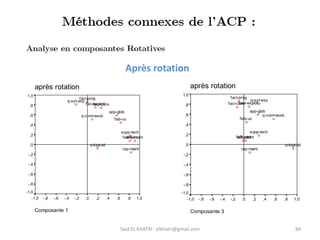
Analyse en Composantes Principales
ACP
1
Said EL KHATRI : elkhatri@gmail.com

But de l’ACP
2
L’ACP est une méthode descriptive
qui permet de résumer,
synthétiser
ou condenser
le comportement de p variables quantitatives
(observées n fois).

Rappel de statistiques de base
3

Notions de base
• Population (limitée ou de grande taille) :
ensemble des individus à étudier.
Said EL KHATRI : elkhatri@gmail.com 4
• Echantillon : partie de la population
(n individus) sur laquelle est effectuée l'étude.
• Individus : appartenant à la population
• Variable (caractère) : caractéristique des
individus, définie sur la population.

Notions de base
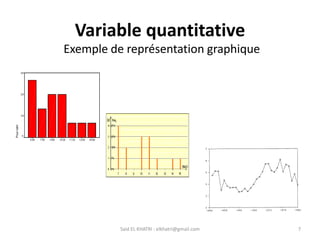
• Variable quantitative : =>valeurs réelles
• Variable qualitative :
* discrète (exemple : âge, nombre d'enfants)
* continue (exemple : taille, température)
* nominale (exemple: couleur [jaune, vert, ..], type de brouillard
[dense, de convection, néant])
* ordinale (exemple: type de voiture [aucune, petite, moyenne, grande]).
Deux types de variables :

Variable quantitative
Moyenne :
Variance :
Ecart type :
Variable centrée :
Variable centrée-réduite (ou centrée-normée) :
Variable normée (réduite) :

Exemple de représentation graphique
Variable quantitative

Analyse de la liaison entre 2
variables quantitatives
Covariance :
Corrélation :
Ŷ=r*Sy/Sx*x + b

Analyse de la liaison entre 2
variables quantitatives
Représentation graphique :
NOX
10
8
6
4
2
0
NOY
10
8
6
4
2
0 Rcarrée = 0,7579
xi
yi

ACP

But de l’ACP
11
L’ACP est une méthode descriptive
qui permet de résumer,
synthétiser
ou condenser
le comportement de p variables quantitatives
(observées n fois).

Exemple élémentaire
On considère l’échantillon constitué par :
16 pays (ou individus) => n=16
sur lesquels on a relevé les valeurs de
2 variables (p=2): l'espérance de vie (EVI), et le taux d'analphabétisme (ANA) en 1970

Exemple élémentaire

Analyse de p variables quantitatives
Observées n fois
À l’aide de
l’ACP
14

Notation
15
n individus
(scalaire)
(valeur de la j ème
variable pour le i ème
individu)
p colonnes
n lignes

Notation
16

Notation
17

Notation
18

1800 centres informatiques jugent les ordinateurs qu'ils utilisent.
Le questionnaire invitait les utilisateurs à juger "d'excellent à mauvais ", chaque
modèle d’ordinateur employé, en fonction des 12 (=p) critères suivants :
* Le nombre total des modèles d'ordinateur objets du questionnaire est 76 (=n)
* on retient, pour chaque modèle d'ordinateur la note moyenne relative à chaque
critère d’évaluation. (multiplié par 10)
La notation était :

Tableau des données :
: : : : : : : : : : : : : :
Question :
Analyser les jugements donnés par
les centres informatiques sur les
76 modèles d'ordinateurs selon les
12 critères ?
n=76
76 individus
76 modèles d’ordinateurs
p=12 => 12 variables = 12 critères d’évaluation des ordinateurs

On pourrait penser à :
*Analyser la variation des notes d'un critère à l'autre pour chaque modèle d'ordinateur
i (i=1,76)
Pourquoi faut il éviter cette méthode ?
* puis analyser la variation des notes d'un ordinateur à l'autre pour chaque critère
j (j=1,12)
• Si p et/ou n est grand, la méthode devient lourde et complexe
• Si des variables sont corrélées ou anti corrélées, l’analyse sera redondante
• Si des individus se ressemblent, l’analyse sera redondante aussi

• Condenser/synthétiser l'information :
• Rendre l’information plus facile à analyser;
et ce :
o en réduisant le nombre de données à analyser:
- regrouper des variables liées positivement ou négativement
o en visualisant les données par des graphes simples
 Ce qui revient à condenser la matrice d'observation initiale
Comment ?
Qu'apporte -t-elle l'ACP ?
Intérêt et problématique de l’ACP

FEX-FEX FUC-FUC AGL-AGL

Avec l’ACP on changera de base de :
à :
Et on écrira :
Avec :
Les sont des vecteurs colonnes normés de dimension
(p,1) et perpendiculaires entre eux
représentent les nouvelles variables
scalaires dans la nouvelle base

L'intérêt principal de l'ACP est qu'elle permet d'écrire :
Ainsi l'analyse de X (c.a.d des x1, x2 .., xp ) se réduira à l'analyse uniquement de :
Composantes principales
Axes factoriels

Approche de réponse (par analogie)
Devinez quels sont les objets dont la projection plane est :
3m
3cm de diamètre
30cm de longueur

Réponse
3m
3cm
30cm
Bateau
Tuyau de 100 m de longueur
Feuille de papier

Approche de réponse (par analogie)
Pour décrire l’allongement d’un objet :
L’espace de dimension 1 peut être suffisant : (tuyau)
L’espace de dimension 2 est nécessaire et suffisant : (feuille de papier)
L’espace de dimension 2 est acceptable mais pas très suffisant : (bateau)

En général:
L'information donnée sur la dispersion des points constituant un objet
dans un espace de dimension p est :
• très lisible lorsqu'on projette cet objet sur les axes (ou plans) de plus
grand allongement,
• et très peu importante en projection sur les axes de très faible
allongement.
L'objet décrit dans l'exemple d'analogie est, dans notre cas, un nuage
de n points dans l'espace de dimension =< p
Détermination des Composantes Principales

1 variable => 1 axe
1 individu => 1 ligne du tableau
=> 1 point dans l’espace de dimension p

1. Proximité:
❑ Deux individus proches sont semblables
(ils possèdent des valeurs proches pour l'ensemble
des variables)
❑ Deux individus éloignés sont dissemblables
(ils possèdent des valeurs éloignées sur 1 ou
plusieurs variables)
=> La mesure de ressemblance se fait par le calcul
d’une distance entre les deux individus
2. Centrer les variables ne modifie pas la
forme du nuage (C’est l’origine du repère qui
change et non le nuage)

Le principe de l'ACP consiste à représenter le nuage des n
points dans un espace
qui permettra, en des projections dans un sous espace
engendré par un nombre réduit de vecteurs, de montrer les
plus grands allongements de ce nuage.
Autrement : L'ACP vise à fournir une image simplifiée du nuage des
individus la plus fidèle possible .
 Trouver le sous-espace qui résume au mieux les données, c.a.d qui:
* Restitue grosso-modo la forme générale du nuage
* Ne perturbe pas trop les distances entre individus

Inertie du nuage de points:
• La dispersion du nuage de points est mesurée par son inertie par rapport au centre
de gravité :

On cherche des transformations linéaires orthogonales entre elles sur la
base du critère de la maximisation de la variance.
Etape 1: Recherche de l'axe (unitaire) tel que le nuage des points a une
variance (allongement) maximale sur cet axe
O
Ai
u1 (F1)
Hi
C.ad. Trouver l'axe factoriel (F1) qui déforme le moins possible le nuage
Maximiser σ𝑖=1
𝑛
𝑂𝐻𝑖
2
Minimiser σ𝑖=1
𝑛
𝐴𝑖𝐻𝑖
2

Etape 2: Recherche de l'axe (unitaire) tel que :
C.ad. Trouver l'axe factoriel (F2) tel que le plan (O,F1, F2) déforme le
moins possible le nuage Ai
Hi
O
u1 (F1)
u2 (F2)
Minimiser σ𝑖=1
𝑛
𝐴𝑖𝐻𝑖
2
Maximiser σ𝑖=1
𝑛
𝑂𝐻𝑖
2

Minimiser σ𝑖=1
𝑛
𝐴𝑖𝐻𝑖
2
Maximiser σ𝑖=1
𝑛
𝑂𝐻𝑖
2
𝐻𝑖 𝑒𝑠𝑡 𝑙𝑎 𝑝𝑟𝑜𝑗𝑒𝑐𝑡𝑖𝑜𝑛 𝑜𝑟𝑡ℎ𝑜𝑔𝑜𝑛𝑎𝑙𝑒 𝑑𝑒𝐴𝑖 sur (0,u1,..,uk)

G e1
e2
O
e1
e2
U1
O
e2
U1
U2
O

On montre que :
Les vecteurs directeurs des axes recherchés sont les vecteurs propres de la
matrice de variance covariance Σ (i.e. matrice d’inertie).
Ces vecteurs unitaires sont rangés dans l'ordre décroissant des valeurs
propres associées :
Le calcul des valeurs propres et les vecteurs propres peut s'effectuer en
résolvant les systèmes suivants :

Changement de base :

Les composantes principales sont des combinaisons
linéaires des variables initiales:

Soit la matrice diagonale des valeurs propres.
La matrice de variance-covariance des composantes principales est :
et
Propriété de la variance:
Propriété de la corrélation:

Notion de variance totale, variance expliquée et
variance résiduelle

(x100%)
Le pourcentage de variance expliqué par les q premiers axes principaux est :
La variance expliquée par les q premiers axes principaux est :
O
Ai
Fk
Hi
Fl
zik
zil
Ai
O
zik
Hi

Approximation de la reconstitution des variables initiales
Formule de reconstitution :
Formule d’approximation :
p variables q CP q << p

Approximation de la reconstitution des données initiales
Définir les coordonnées de l’oreille
gauche ?

(Critère de la valeur propre moyenne)
P=12
1/P=0,0833 =8,33%
On retient donc les 3 premières CP

Par exemple :
On retient dans ce cas les 9 premières CP

c/ Lorsque les données sont centrées réduites
On retient donc les 3
premières CP

d/ Critère de CATTELL : ( le plus utilisé ) connu sous le nom du "critère du coude".
On retient les q premières CP tel que l'apport en variance des dernières CP est
remarquablement plus faible par rapport aux premières.
En pratique, on trace -sur le graphe d'évolution des valeurs propres- la droite ajustant les
dernières valeurs propres et on garde les premières CP tel que les valeurs s'éloignent de
cette droite.
190.527 100.000

Etude du comportement des observations et des variables :
• Nécessite d'utiliser plusieurs projections
planes.
• On se limite souvent aux plans (O;U1;U2),
(O;U1;U3), et (O;U2;U3).
• Les points Aj et Ak paraissent très proches
sur le plan (O; U1;U3).
• Mais en réalité, ils sont très éloignés dans
l'espace: la projection sur le plan
(O;U1;U2) le montre facilement.

Attention : il ne faut commenter la position d’un individu sur un plan que s’il est bien
représenté sur ce plan;
Comment vérifier ?

Représentation d’un individu
L’inerte de Ai suivant l’axe Uk est :
Contribution de l’axe Uk à l’individu Ai :
Annexe mathématique
=
𝑂𝐻𝑖
2
𝑂𝐴𝑖
2

L’inerte de Ai suivant le plan dirigé par les axes Uk et Ul est :
Contribution du plan (O,Uk ,Ul) à l’individu Ai :
Uk
Ul
Ai
Zik
Zil
O
Hi
=

Règle empirique du seuil de la qualité de représentation
Il ne faut commenter la position d'un individu sur un plan
(Fk ; Fl ) que s’il est bien représenté sur ce plan.
C’est-à-dire : n’est pas faible (>0.25),
ie. Angle inférieur à 60°.
Cas extrêmes:
• =1
i.e. Ai est idéalement représenté sur le plan (=Hi)
• ~ 0
i.e Hi est proche de l’origine (Ai est mal représenté par Hi)
Uk
Ul
Ai
Zik
Zil
O
Hi

: : : : : : : : : : : : : :
zi,2
zi,1
i=
Remarque pratique
NB: Les individus projetés loin du centre O méritent plus d’attention car
leur contribution au calcul de l’inertie est grande

Z1 Z2 COS2_F1 COS2_F2 COS2_(F1,F2)
AM1 0,96827 -0,39538 69% 19% 88%
BU1 -0,50047 2,21635 6% 1% 7%
BU2 -0,50803 1,90542 3% 60% 63%
BU3 -0,88345 2,03428 3% 37% 40%
BU4 -0,88865 1,98165 6% 30% 36%
BU5 -2,33393 2,08892 8% 41% 49%
BU6 -0,37145 1,76014 15% 12% 26%
BU7 1,46471 2,75351 2% 47% 49%
BU8 -0,10818 1,26096 10% 34% 43%
CD1 0,57104 -0,35044 0% 6% 6%
CD2 -1,22644 -1,82901 2% 1% 2%
CD3 -0,38141 -0,3984 14% 32% 47%
CD4 -0,75267 -0,52764 3% 3% 6%
DE1 0,21089 1,26016 3% 1% 4%
DE2 0,75168 1,70319 1% 34% 35%
HO1 -1,44502 -0,72484 3% 17% 20%
HO2 1,19647 -1,05292 8% 2% 10%
HO3 -1,52104 0,42352 15% 12% 27%
HO4 0,09976 0,55875 26% 2% 28%
HO5 -0,80727 -0,163 0% 8% 9%
HO6 0,02829 0,93552 16% 1% 17%
X
X
X
X
X
X
X
X
X
Il faut se méfier de l’interprétation des individus mal représentés:
il ne faut les interpréter que sur les plans sur lesquels ils sont bien
représentés
L’individu BU5 est
bien représenté sur le
plan (F1,F2)
L’individu CD2 est
Très mal représenté sur
le plan (F1,F2)
L’individu AM1 est très
bien représenté sur le
plan (F1,F2)

Chaque Xj (vecteur des n coordonnées de xj est représenté sur le plan (O, Fk, Fl )
1
1
-1
-1
Fl
Fk
La qualité de représentation d’une variable
sur le plan (O, Fk, Fl) est mesurée par:
𝑟2 𝑥𝑗, 𝑧𝑘 + 𝑟2 𝑥𝑗, 𝑧𝑙

Cercle de corrélation:
B
O
B’
A’
A
α
1 α 0°
0 α 90°
-1 α 180°
r(x,y)
r(x,y)
r(x,y)

Chaque variable (ayant n coordonnées) est représentée par le point ‘
Et projetée sur le plan (O, Fk, Fl )
Aj
O
A’
j
1
Aj
O
A’
j
r(Xj ,Zk )
Zk’

Aj
O
A’
j
A’
m
Am
α
1 α 0°
0 α 90°
-1 α 180°

α α
α
Légère
déformation
de l’angle
Grande
déformation
de l’angle
A1 A2
A2
A1
Fk
Fl
A1
A2 R(X1,X2)=cos(α)
α
aucune
déformation
de l’angle

La corrélation entre deux variables xm et xj est donnée par la lecture graphique du cosinus
de l'angle (O,Am
kl; O,Aj
kl )
à condition que les points Am
kl et Aj
kl soient proches du cercle de corrélation
1
1
-1
-1
Sur le cercle =
Parfaitement
représentée
Proche du
centre =
Très mal
représentée
X1 et X2 :
X8 et X4 :
X1 et X3 :
X6 et X3 :
X3 et Zl :
X6 et Zk :
corrélées
anti- corrélées
dé-corrélées
on ne peut rien dire
car X6 est mal représentée
corrélées
dé-corrélées
r(X6,Zk)

Axe factoriel 1
Axe
factoriel
2
corr(rap-maint, Z2)
corr(rap-maint, Z1)

Axe factoriel 1
Axe
factoriel
2

1) Donner un sens à chaque axe factoriel
2) Interpréter la position des individus par rapport aux sens des axes.
* Etude des variables initiales fortement corrélées (positivement ou
négativement) avec cet axe.
* Ce sont les éléments extrêmes, éventuellement opposés, qui concourent à
l'élaboration des axes
* L'interprétation est parfois compliquée à cause de la combinaison de plusieurs
variables initiales; d'où la nécessité de bien connaitre les données de base
* Si l'interprétation des variables n'est pas évidente, il faut alors donner un sens
à l'axe à partir des individus qui ont les coordonnées extrêmes.
* Recherche lexicale (ou recherche de mots) qui peut résumer un ou des
groupe(s) de variables initiales corrélées avec l’axe …
+ : sens de Uk
- : sens inverse de Uk

Projection des variables
1) Un seul groupe de variables qui est corrélé (ou anti-corrélé) significativement
avec l’axe:
On dit que l’axe est expliqué par ce groupe de variables
Deux cas :
2) Deux groupes de variables: un corrélé positivement et significativement
avec l’axe et l’autre est corrélé négativement et significativement avec l’axe:
On dit que l’axe est expliqué par l’opposition entre ces deux groupes de
variables.

Axe factoriel 1
Axe
factoriel
2
Aspect Général
Utilisation
Maintenance
39.4%
20.8%

Aspect Général
Qualité
Axe factoriel 1
Axe
factoriel
3
39.4%
13.2%

Utilisation
Maintenance
Axe 1
Axe
2
39.4%
20.8%
Aspect Général
Projection des individus

75
Projection des individus
39.4%
Aspect Général
Qualité
13.2%
Axe 1
Axe
3

Les données sont-elles factorisables ?
1) Plusieurs variables sont corrélées (ou anti-corrélées) ?
Analyse de la matrice de corrélation
Plusieurs variables sont corrélées entre elles

2) L’indice de KMO (Kaiser-Meyer-Olkin) qui tend vers 1 ?
C’est le rapport :
somme des corrélations au carrée
somme des corrélations partielles au carrée
•0,50 et moins => misérable
•entre 0,60 et 0,70 => médiocre
•entre 0,70 et 0,80 => moyen
•entre 0,80 et 0,90 => méritoire
•plus que 0,9 => merveilleux.
Moyen

3) La signification de Bartlett tend vers 0 ?
(test de sphéricité)
Comparer la matrice de corrélation
à la matrice identité à l’aide de Khi2
• tend vers 0 => c’est très significatif,
• inférieur à 0.05 => significatif,
• entre 0.05 et 0.10 => acceptable
• au dessus de 0.10 => on rejette.
Très significatif

 En pratique:
Les données sont factorisables si au moins 2 conditions parmi
ces 3 conditions sont favorables
1) Plusieurs variables sont corrélées (ou anti-corrélées) ?
2) L’indice de KMO (Kaiser-Meyer-Olkin) tend vers 1 ?
3) La signification de Bartlett tend vers 0 ?

Variables hétérogènes => choisir Ω
Σ : variables centrées
Ω : Variables centrées réduites
Choix de Σ ou Ω ?
Si les variances des variables sont comparables, alors Σ
Variables homogènes
Si les variances des variables sont incomparables, alors Ω

Si p est grand => difficultés pour diagonaliser une matrice de dimension p×p
Solution : Méthode de DUAL => diagonaliser une matrice de petite taille : L
diagonaliser L  diagonaliser Σ

1. Lissage des données initiales
2. Reconstitution des données manquantes
3. Aide à alléger les modèles de prévision statistique

Permet d'améliorer l'interprétation des composantes principales de l'ACP en
effectuant des rotations sur les axes principaux retenus par l'ACP classique sur
la base de la maximisation de la variance de la série des corrélations au carré
avec les variables initiales
On cherche les CP sur la base la maximisation de l'autocorrélation à un décalage
temporel fixé
On cherche les CP sur la base la minimisation de l'erreur de prévision
appliquée lorsque les variables expriment l'espace et les individus le temps.
Elle tient compte des propagations spatio-temporelles.

après rotation
Composante 1
1,0
,8
,6
,4
,2
,0
-,2
-,4
-,6
-,8
-1,0
1,0
,8
,6
,4
,2
,0
-,2
-,4
-,6
-,8
-1,0
app-glob
faci-conv
faci-prog
q-logiciel
q-com+assb
q-syt-exp
supp-tech
effi-maint
rap-maint
fiab-péri
fiab-uc
faci-exploit
après rotation
Composante 3
1,0
,8
,6
,4
,2
,0
-,2
-,4
-,6
-,8
-1,0
Composante
2
1,0
,8
,6
,4
,2
,0
-,2
-,4
-,6
-,8
-1,0
app-glob
faci-conv
faci-prog
q-logiciel
q-com+assb
q-syt-exp
supp-tech
effi-maint
rap-maint
fiab-péri
fiab-uc
faci-exploit
Après rotation

Fin du chapitre
Analyse en Composantes Principales
ACP
85

Présentation acp

Contenu connexe

Tendances

Similaire à Présentation acp

Plus de grandprime1

Présentation acp