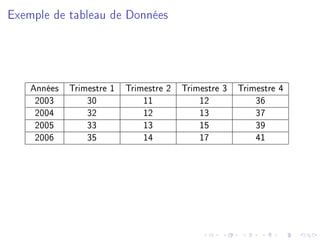
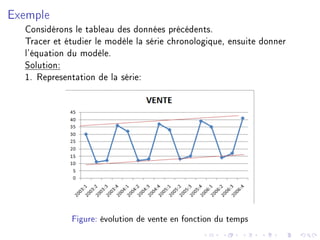
Le document présente un cours sur les séries temporelles, en abordant la définition, les composantes, les types de modèles et les méthodes d'analyse. Il décrit les concepts statistiques et mathématiques nécessaires pour étudier l'évolution des données chronologiques dans divers domaines. Enfin, des techniques pratiques, y compris des exercices d’application sous Microsoft Excel, sont proposées pour illustrer l'application de ces concepts.

1. Séries Temporelles
Cours, Exercices et Applications
Abdoulaziz A.Garba
Institut Communautaire Africain de Gestion et d'Ingénierie
12 décembre 2016

2. Plan du cours
1. Généralité
2. Dénition
3. Présentation graphique d'une série
4. Les composante d'une série et dénition
5. Les types de modèles
6. la décomposition d'une série
7. Les méthodes analytiques des chroniques et ajustement
8. Exercices d'applications
9. Application sous Microsoft Excel.

3. Généralité
les séries temporelles se rencontrent dans tous les domaines.
Economie: emploi, prix,...;
Bourse: BRVM10, CAC40, FTSE500, NASDAQ,....
Démographie: naissance, décès ...;
Sociologie: crime, mariage, divorces;
Météorologie: température, pluviométrie;
Ainsi, pour étudier une série chronologique, les méthodes pouvaient
se regrouper en deux: les méthodes classiques et les méthodes
proposées par Box Jenkins. Mais, ici, nous allons nous limiter
seulement aux méthodes classiques.

4. Dénitions
Dénition1
Une série temporelle, ou série chronologique se dénit comme une
suite d'observation indexée par le temps.
Avec T=t1, t2, ..., tn
Dénition2
On appelle série chronologique, ou chronique, ou série temporelle,
une suite d'observations chirées, ordonnées dans le temps.
Dénition3
Une chronique ou série chronologique est une distribution à deux
dimensions dont l'une est le temps.

5. Suite de dénition
C'est aussi une suite de valeurs numériques représentant l'évolution
d'une quantité spécique au cours du temps. De telles suites de
variables aléatoires peuvent être exprimées mathématiquement an
d'en analyser le comportement, généralement pour comprendre son
évolution passée et pour en prévoir le comportement futur. Une
telle transposition mathématique utilise le plus souvent des
concepts de probabilités et de statistique.

6. A savoir
Il y'a quelques points importants à retenir sur les chroniques:
Variable: Emploi, PIB, Consommation d'électricité, indice
boursier;
Unité de mesure: Milliers CFA, Pourcentage, en personne..;
Intervalle de temps: journalier, mensuel, annuel...;

7. Exemple de tableau de Données
Années Trimestre 1 Trimestre 2 Trimestre 3 Trimestre 4
2003 30 11 12 36
2004 32 12 13 37
2005 33 13 15 39
2006 35 14 17 41

8. Exemple de représentation graphique

9. Les composantes d'une série
Il existe plusieurs types de composantes:
La Trend: le trend schématise la tendance générale du
phénomène.Elle traduit aussi le comportement moyen de la
série. Elle est de la forme Yt = at + b.
La composante saisonnière ou saisonnalité (St): Elle
correspond à un phénomène qui se répète à intervalle de temps
régulier(périodique). D'ou le terme de variation saisonnières
avec les saisons, s1, s2, s3..., sp, st+p∀t ∈ N.
Selon des périodes plus courtes (de longue période), on
remarque des uctuations autour du trend de type sinusoïdale
qui se répète ce mouvement s'appelle cycle.
La composante résiduelle ou bruit blanc ou résidu(et): Ce sont
des uctuations régulières, en générale de faible intensités mais
de nature aléatoire. On parle aussi des aléas et.

10. Type de modèle
Il existe deux types de modèle: modèle additif et modèle
multiplicatif.
Pour identier le type de modèle, on peut se baser soit sur une
méthode graphique ou une méthode analytique.
A. méthode graphique: test de bande.
Sur le graphique de la série, on trace une droite passant par les
minima de la courbe et une autre droite passant par les maxima
pour chaque saison. Si ces droites sont parallèles, on est en
présence d'un modèle additif. Par contre, si les droites ne sont pas
parallèles, on est en présence d'un modèle multiplicatif.

11. suite type modèle
B. Méthode analytique:
Il existe plusieurs types de méthodes analytiques, mais la plus
courante est celle de BUYS BALLOT.
La méthode consiste à calculer d'abord les moyennes et les écarts
types de la série pour chaque année. Ensuite, on régresse σt en
fonction de la moyenne ¯Xt, pour avoir :
σt = α ¯Xt
Ainsi, si le coecient α = 0, alors on peut dire que le modèle est
additif.
Par contre, si le coecient α = 0, alors on peut dire que le modèle
est multiplicatif.

12. Exemple de schéma Additif
Figure: Yt = Ct + St + t.
Additif: ici, l'amplitude de la composante saisonnière et du bruit
reste constante au cours du temps. Ceci se traduit graphiquement
par des uctuations autour de la tendance d'amplitude constante.

13. Le schéma multiplicatif:
Figure: Yt = Ct ∗ St ∗ t
Multiplicatif: ici, l'amplitude de la composante saisonniere varie
dans le temps. Ainsi,
n
1
sj = p et
p
t=0 t = 1.

14. Décomposition d'une série
Pour étudier les séries chronologiques on doit suivre quatre étapes à
savoir:
Représenter la série graphiquement;
Modélisation statistique de la série;
Calcul des composantes (trend, saisonnière, aléatoire) ;
Prévision

15. Exemple
Considérons le tableau des données précédents.
Tracer et étudier le modèle la série chronologique, ensuite donner
l'équation du modèle.
Solution:
1. Representation de la série:
Figure: évolution de vente en fonction du temps

16. Détermination des composantes: trend et saisonnalités
1er méthode: on constate que la série chronologique oscille autour
d'une droite , donc trend.
2em: graphique, on constate que les pics des maxima s'ajustent sur
une droite, donc un trend.
Puis, on constate aussi que la courbe est périodique en forme
sinusoïdale, donc il ya la présence de saisonnalité Enn, à travers la
méthode de bande qui consiste à tracer deux lignes droites sur les
les sommets maxima et les minima, on constate que les deux lignes
sont parallèles. Ainsi, on peut dire que le modèle est additif, et
l'équation est donnée ci-dessous:
Yt = Ct + St + t, 1 t n (1)

17. Les méthodes empiriques de décomposition
Analyse de la saisonnalité
La désaisonnalisation d'une série consiste à utiliser certaines
techniques mathématiques an de séparer la série de ses variations
intra-annuelles périodiques.
Test de détection de la saisonnalité
Avant de désaisonnaliser une série, il faut au prealable tester
l'existance de la saisonnalité.
Parmi les tests de détection, il y'a :
L'analyse graphique: qui consiste à détecter d'éventuels pics et
creux périodiques de la série brute représentée dans le temps.
Le tableau de Buys Ballot: qui consiste à classer les périodes
par ordre de grandeur dans l'année. Si une période commune
est dégagée pour presque toutes les années par exemple, on
conrme la présence d'une saisonnalité.
Test de chorrelogramme: les coecients d'auto-corrélation
d'ordre k est le coecient de corrélation linéaire calculée entre
la série et la série décalée de k périodes.

18. Il est donné par la formule:
σk =
cov(xt, xt−k)
σxt.σxt−k
, k ∈ Z
Figure: le chorrélogramme

19. 2. Les méthodes de desaisonnalisation
La désaisonnalisation est une méthode qui consiste à éliminer la
saisonnalité sans modier les autres composantes de la série an
d'avoir unesérie corrigée de ses variations saisonnières(CVS) .
Ainsi, il est donné par les formules suivantes:
Si multiplicatif
St =
1
card(Ti)
n
i=1
Yt
Ct
(2)
Si additif
St =
1
card(Ti)
n
i=1
(Yt − Ct) (3)
Avec Sj = 1
p
n
p=1
Sp
et ¯S = Sj .

20. Si ¯S = 0 alors les Sj sont des coecients dénitifs. Par contre, si
¯S, alors les coecients dénitifs sont calculés par:
Sj ∗ = Sj − ¯S, avec
¯S =
1
p
p
j=1
Sj . (4)
Remarque: quand Sj = 0, on peut dire que le modèle est additif.
par contre, si
p
j=1
Sj = 1, le modèle est multiplicatif.

21. Technique de désaisonnalisation
Il existe deux grandes techniques de désaisonnalisation: les
techniques de régression et celles de ltrage.
Les modèles de désaisonnalisation par la méthode
d'ajustement linéaire
a. Modèle de régression linéaire
Un modèle consiste à supposer que:
Yt = aXt + b + t. (5)
Ou a et b son des paramètres inconnus,
t, un bruit blanc i-e
Bruit Blanc
E ( t) = 0, ∀t ∈ Z,
E 2
t = σ2
, ∀t ∈ Z,
Cov ( t, t+h) = 0, ∀t, h ∈ Z, h = o.

22. Ainsi, pour expliquer Y par X, il sut d'estimer les coecients a et
b par la méthode des moindres carrés ordinaires (M.C.O).
L'estimation de a et b est donnée par:
a =
Cov(x, y)
Var(x)
(6)
et
b = ¯y − a¯x (7)
b. désaisonnalisation avec la régression linéaire
Ici, on estime d'abord la tendance sous la forme:
Tt = b + at (8)
Une fois a et b connus, on calcule les coecients saisonniers
provisoires calculés en (2) ou (3).

23. Exemple
On donne la série chronologique suivante du phénomène Y qui suit
un modèle.
Vérier la saisonnalité?
Déterminer le type de modèle?
déterminer l'équation de la Trend et les coecients saisonniers?
Faire une prévision pour le 3ème trimestre 2007.
Années Trimestre1 Trimestre 2 Trimestre 3 Trimestre 4
2004 2 0,5 3,5 1
2005 5 2 5 3,5
2006 6,5 4 7,5 5

24. Solution
En appliquant la méthode de Buys Ballot on aura le tableau suivant:
Années Ti Ti Ti Ti
2004 T3 T1 T4 T2
2005 T3 T1 T4 T2
2006 T3 T1 T4 T2
On remarque que le troisième trimestre a tendance à enregistrer les
plus fortes valeurs (pics) en T3 traduisant ainsi la présence d'une
saisonnalité.

25. Figure: Courbe + droites de Buys Ballot
Avec cette gure, on constate que la courbe évolue presque entre
les deux droites parallèles Alors on conclut que le modèle est
ADDITIF.

26. Détermination de l'équation de la Trend
ft = at + b
Alors, ft = 0, 44t + 0, 94

27. Comme la somme des Sj n'est pas nulle, alors il faut retrancher
cette quantité à chaque saison:
Sj = 0, 01
ρ = 0.01
4
= 0.0025
Sj dénitifs sont:
S1 = 1.37 − 0.0025 = 1.37
S2 = −1.4027 − 0.0025 = −1.40
S3 = 1.375 − 0.0025 = 1.32
S4 = −1.2825 − 0.0025 = −1.28
Ainsi, la série est bien ajustée par les estimateurs.
l'équation de la série chronologique ajustée Y cvs
t s'écrit:
Y cvs
t = 0.44t + 0.93 + [+1.37; −1.40; 1.32; −1.28]
La valeur prévisionnelle de y au 3eme trimestre 2007 est:
Y cvs
15
= (0.44 ∗ 15) + 0.93 + 1.32
Y cvs
15
= 8.85

28. Filtrage: par les moyennes mobiles(MMt)
Dénition: On appelle moyenne mobile d'ordre p(pn), la série
constituée par les moyennes arithmétiques suivantes:
y1 + y2 + .... + yp
p
;
y2 + y3 + .... + yp+1
p
; etc. (9)
Ainsi, une moyenne d'ordre p s'écrit généralement par:
MMp =
1
p
p−1
i=0
yt+i (10)
t = 1, 2, ..., n
i ∈ N
Ainsi, deux types de moyennes mobiles généralement privilégiés
dans l'analyse des séries temporelles. Il s'agit de la moyenne mobile
symétrique équilibrée d'ordre impaire (2m+1), et de la moyenne
mobile équilibrée symétrique d'ordre paire (2m).
On appelle moyenne mobile équilibrée symétrique d'ordre impaire,

29. (p=2k+1), l'opérateur:
MMp,t =
1
p
p−1
i=−k
yt+i (11)
Exemple:
Si la moyenne mobile est d'ordre paire (p=2k), alors,
MMp,t =
1
p
[
1
2
yt−k +
k+1
i=−k+1
yt+i +
1
2
yt+k] (12)

30. Exercice sur les moyennes mobiles en TD et TP
F.I.N