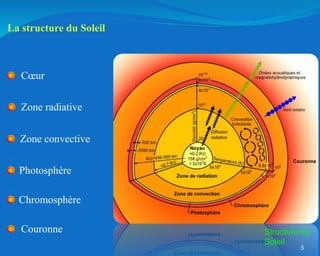
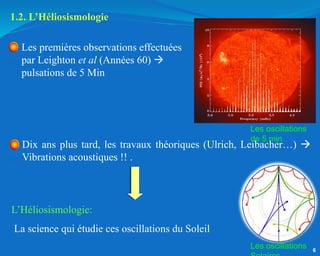
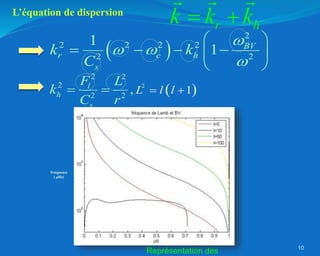
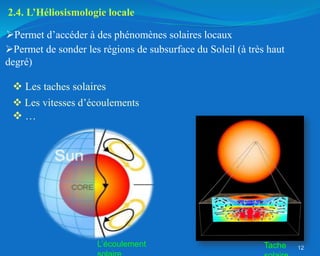
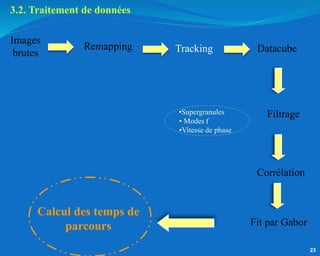
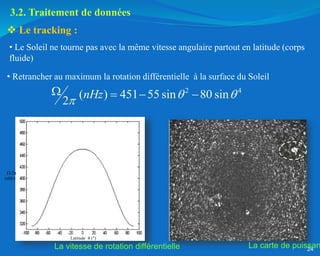
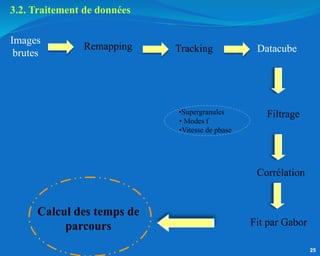
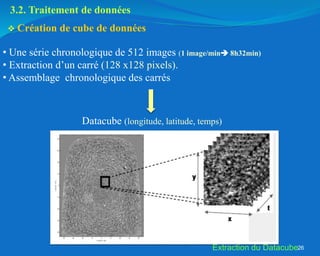
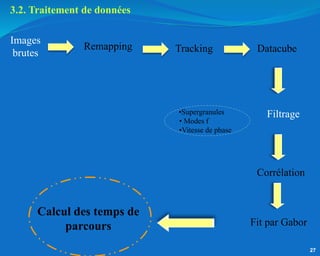
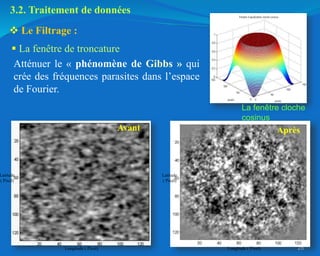
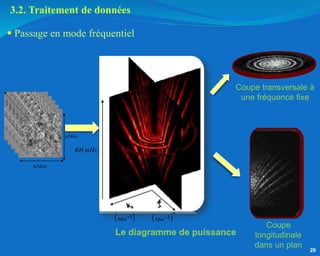
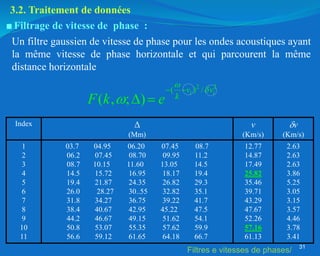
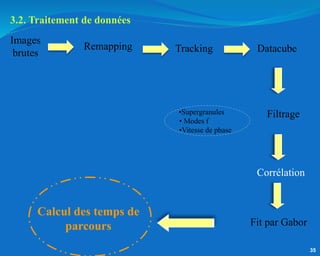
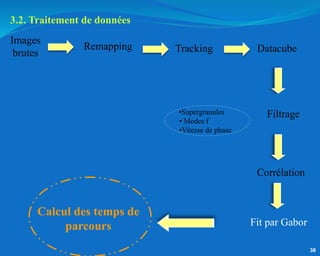
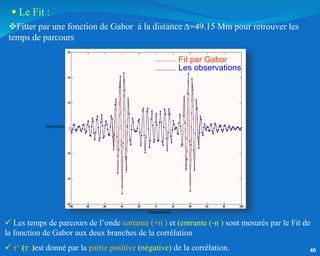
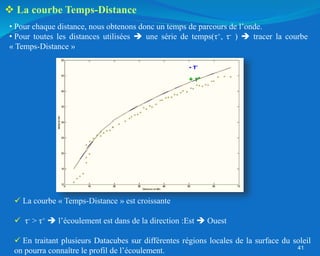
Ce document traite de l'héliosismologie, une science qui étudie les oscillations de la surface solaire pour en déduire des informations sur la structure interne du soleil grâce à la méthode temps-distance. Il présente une méthodologie théorique reliant les temps de parcours des ondes acoustiques aux propriétés internes du soleil, ainsi que les résultats obtenus via l'analyse d'images de la surface solaire. L'étude met en évidence le traitement des données et les techniques de filtrage nécessaires pour extraire des informations sur des phénomènes solaires locaux.

1. Problème Direct en Héliosismologie Temps-
Distance:
Etude & Interprétation Théorique
1
Université des Sciences et de la Technologie Houari Boumediene
Dirigé par
N. SEGHOUANI
Soutenance de Mémoire de Magister
Option: Physique théorique
Sujet:
Présenté par
BOUDERBA Yasmina
Faculté de physique
30 Mai 2010

2. 2
Étude des phénomènes solaires locaux à partir de l’étude de la
propagation des ondes acoustiques qui parcourent l’intérieur du
Soleil:
Etude théorique de la méthode Temps–Distance et mise
en place d’un modèle reliant le temps de parcours aux
propriétés internes (locales)
Détermination des temps de parcours à partir d’un
traitement d’images du Soleil
But et Méthodologie

3. 3
 Méthode Temps-Distance
Plan
 Généralités:
Le Soleil
L’Héliosismologie
 Conclusion et perspectives
 Temps de parcours: Résultats et discussions
 Introduction

4. 4
1. 1. Le Soleil
Le Soleil une étoile qui
produit sa propre énergie
1. Généralités
Ses caractéristiques:
R=696 Mm
M =1.98 1030 Kg
Age= 4,6 milliards d’années
Sa proximité, permet de l'étudier en détail
(précision temporelle et spatiale)
Situé à 150 millions de km de
la Terre (8 min lumière)
Le
Soleil/SOHO

5. 5
La structure du Soleil
Cœur
Zone radiative
Photosphère
Chromosphère
Couronne
Zone convective
Structure du
Soleil

6. Dix ans plus tard, les travaux théoriques (Ulrich, Leibacher…) 
Vibrations acoustiques !! .
Les premières observations effectuées
par Leighton et al (Années 60) 
pulsations de 5 Min
6
L’Héliosismologie:
La science qui étudie ces oscillations du Soleil
1.2. L’Héliosismologie
Les oscillations
de 5 min
Les oscillations

7. 7
 Le soleil est maintenu à l’équilibre grâce à deux forces
de rappels:
Les oscillations du Soleil
•La gravité •La pression
 Génère les ondes de gravité.
 Tend à faire imploser le Soleil
 Confiné à l’intérieur du Soleil
 se produisent à basses fréquences
 Génère les ondes de pression.
 Tend à faire exploser le Soleil
 Détectable à la surface du Soleil
 Se produisent à hautes fréquences
Mode p
Mode g

8. Modes propres du Soleil
 Le Soleil se comporte comme une cavité résonnante, où les ondes
acoustiques qui se propagent à l’intérieur forment les modes propres.
8
Mode: caractérisé par n, l et m
( )
( , ) ( ) ( , ) nlm
i t
nlm lm
nlm
f r t a r Y e  
   
 
l=6,m=0 l=6,m=3 l=6,m=6
Représentation des

9. .( ) 0
d
v
dt


 
( . )
P
v v
t 
 
    

( . ) .
N R
T v S E F
t
 

   

2
4 G
 
  
La conservation de la masse
L’équation du mouvement
La conservation d’énergie
L’équation de Poisson
Les équations de base en Héliosismologie
 L’Héliosismologie est basée sur des équations hydrodynamiques qui
considèrent le Soleil comme un corps fluide, à travers le système:
9

10. 10
L’équation de dispersion
 
2
2 2
2
2 2
1
,
l
h
s
L l l
F L
k
C r
 
 
 
2
2 2 2 2
2 2
1
1 BV
r c h
s
k k
C

 

 
   
 
 
r h
k k k
 
Représentation des
Fréquence
( μHz)

11. L’apport de l’Héliosismologie
 L’Héliosimologie nous permet de connaitre l’intérieur
du Soleil grâce à des mesures au niveau de la
photosphère
 L’Héliosismologie globale a permis d’étudier le Soleil dans
sa globalité et d’affiner les modèles solaires….
11

12. 12
Permet d’accéder à des phénomènes solaires locaux
 Les taches solaires
 Les vitesses d’écoulements
2.4. L’Héliosismologie locale
Permet de sonder les régions de subsurface du Soleil (à très haut
degré)
 …
Tache
L’écoulement

13. 13
 Méthode Temps-Distance
Plan
 Généralités:
Le Soleil
L’Héliosismologie
 Conclusion et perspectives
 Temps de parcours: Résultats et discussions
 Introduction

14. 14
 Cette méthode est inspirée de la sismologie
terrestre (Duvall,1993).
 
 
Temps f q r
i

 Elle est basée sur un modèle théorique reliant les temps de
parcours aux propriétés internes( la structure et la dynamique), en
modélisant la propagation des modes p moyennant certaines
approximations.
2. La méthode Temps-Distance
2.1. Le modèle théorique

15. 15
p
p
ds ds
k
v


 
 
 
 Les ondes p se propagent selon un parcours de rayon qui relie
les deux point de réflexions avec le centre du Soleil
« Approximation du rayon»
 A la subsurface du Soleil: BV<<c et BV<<
2 2 2 2
s c
k C
 
 
Les approximations à considérer pour ce modèle
r1
r2
(Δ)
r1
r2
(Δ)
r1
r2
(Δ)
Réflexion en surface
Reflectioninterne
Propagation de
l’onde
 En présence d’inhomogénéités locales dans le milieu, le parcours des modes p
reste inchangé. « principe de Fermat »
0
0
1
k ds
   
 
   
s c
s c
k k k
k C
C
   
 
  
  
  
δk :Perturbation du vecteur d’onde

16.  
0
2
0 2 2
2
s c c
moy
s c s
C k
ds
C C k
     
 
  
 

  
    
   
 
    
 
    
 

16
 
0
2
0 2 2 2
ˆ
. c c
c
u n c k
ds
c c c k
 
 
  
  
 

 
   
 
     
 
  
 
 
 
 
 
 

r2
-
r1
+
r2
r1
 Les temps de parcours en fonction des propriétés internes:
Les inhomogénéités locales
La vitesse de l’écoulement
0
2
ˆ
.
2
diff
s
u n
ds
C
  
 

    
L’équation de Fermat

17. 17
*
2 1
0
( , ) ( , ) ( , )
T
f r t f r t dt
  
  

 Plusieurs modes viennent se superposer sur un seul point sur la
surface du Soleil
2.2. Les temps de parcours Théoriques
 La fonction de corrélation donne la ressemblance du signal entre
deux points sur la surface du Soleil
2
2
0
( , ) exp ( ) cos ( )
4
g p

      
 
 
    
   
 
Amplitude
Temps
L’allure de la fonction de
 La fonction de corrélation est une somme de
fonctions de Gabor

18. 18
 Méthode Temps-Distance
Plan
 Généralités:
Le Soleil
L’Héliosismologie
 Conclusion et perspectives
 Temps de parcours: Résultats et discussions
 Introduction

19. Remapping Tracking
Images
brutes Datacube
Filtrage
Corrélation
Fit par Gabor
Calcul des temps de
parcours
•Supergranules
•Vitesse de phase
• Modes f
19
3. Temps de parcours: Résultats et discussions

20. 20
3.1. Les données
 Des images de vitesse Doppler de la
surface du Soleil (Dopplerogrammes)
 Les données sont obtenues des instruments d’observation (MDI/SOHO,
GONG)
Longitude ( Pixel)
Latitude
( Pixel)
La sonde
SOHO
Le réseau
GONG
Image

21. Remapping Tracking
Images
brutes Datacube
Filtrage
Corrélation
Fit par Gabor
Calcul des temps de
parcours
•Supergranules
•Vitesse de phase
• Modes f
21
3.2. Traitement de données

22.  Le Remapping :
3.2. Traitement de données
Avant Après
22
Latitude
( Pixel)
Longitude ( Pixel)
Longitude ( Pixel)
Latitude
( Pixel)
Re-projeter les images sur une grille équidistante (latitude, longitude)

23. Remapping Tracking
Images
brutes Datacube
Filtrage
Corrélation
Fit par Gabor
Calcul des temps de
parcours
•Supergranules
•Vitesse de phase
• Modes f
23
3.2. Traitement de données

24. 24
• Le Soleil ne tourne pas avec la même vitesse angulaire partout en latitude (corps
fluide)
 Le tracking :
2 4
( ) 451 55 sin 80 sin
2
nHz  

   
Latitude  (°)
/2π
(nHz)
La carte de puissan
La vitesse de rotation différentielle
3.2. Traitement de données
• Retrancher au maximum la rotation différentielle à la surface du Soleil

25. Remapping Tracking
Images
brutes Datacube
Filtrage
Corrélation
Fit par Gabor
Calcul des temps de
parcours
•Supergranules
•Vitesse de phase
• Modes f
25
3.2. Traitement de données

26. 26
 Création de cube de données
• Une série chronologique de 512 images (1 image/min 8h32min)
• Extraction d’un carré (128 x128 pixels).
• Assemblage chronologique des carrés
Datacube (longitude, latitude, temps)
3.2. Traitement de données
Extraction du Datacube

27. Remapping Tracking
Images
brutes Datacube
Filtrage
Corrélation
Fit par Gabor
Calcul des temps de
parcours
•Supergranules
•Vitesse de phase
• Modes f
27
3.2. Traitement de données

28. 28
Atténuer le « phénomène de Gibbs » qui
crée des fréquences parasites dans l’espace
de Fourier.
 Le Filtrage :
 La fenêtre de troncature
Avant Après
3.2. Traitement de données
La fenêtre cloche
cosinus
Latitude
( Pixel)
Longitude ( Pixel)
Latitude
( Pixel)
Longitude ( Pixel)

29.  Passage en mode fréquentiel
Coupe transversale à
une fréquence fixe
Coupe
longitudinale
dans un plan
29
X(Mm)
t(min)
y(Mm)
 
mHz

3.2. Traitement de données
 
1
Mm
 
1
Mm
Le diagramme de puissance

30. ■ Supergranulation :
•Leur signal se superpose à celui des
ondes p
•Oscillent à une fréquence de coupure
de 1.7 mHz.
•Un filtre passe haut qui élimine les
fréquences au dessous de la fréquence
de coupure
■ Les modes f
•Produits par les ondes de gravité de surface
•Se propagent horizontalement et ainsi
propagent les perturbations qui ne suivent pas
le pas du rayon acoustique .
•Un filtre passe bas spatial pour les éliminer.
Avant Après
Le Filtrage :
 
mHz

 
1
Mm
y
k   
1
Mm
y
k 
 
mHz

 
1
Mm
y
k   
1
Mm
y
k 
3.2. Traitement de données
30

31. ■Filtrage de vitesse de phase :
31
2 2
( ) /
( , ; )
i i
v v
k
F k e



 
 
Index Δ
(Mm)
v
(Km/s)
v
(Km/s)
1
2
3
4
5
6
7
8
9
10
11
03.7 04.95 06.20 07.45 08.7
06.2 07.45 08.70 09.95 11.2
08.7 10.15 11.60 13.05 14.5
14.5 15.72 16.95 18.17 19.4
19.4 21.87 24.35 26.82 29.3
26.0 28.27 30..55 32.82 35.1
31.8 34.27 36.75 39.22 41.7
38.4 40.67 42.95 45.22 47.5
44.2 46.67 49.15 51.62 54.1
50.8 53.07 55.35 57.62 59.9
56.6 59.12 61.65 64.18 66.7
12.77
14.87
17.49
25.82
35.46
39.71
43.29
47.67
52.26
57.16
61.13
2.63
2.63
2.63
3.86
5.25
3.05
3.15
3.57
4.46
3.78
3.41
Un filtre gaussien de vitesse de phase pour les ondes acoustiques ayant
la même vitesse de phase horizontale et qui parcourent la même
distance horizontale
3.2. Traitement de données
Filtres e vitesses de phases/

32. 
Ky (Mm-1)
( mHz)
 
1
Mm
y
k 
 
1
Mm
y
k 
■Exemples de filtrage de vitesse de phase :
Avant Après
V=25.82 km/s
V=57.16 km/s
32
Filtre
(mHz)
(mHz)
Ky (Mm-1)

(mHz)
 
1
Mm
y
k 

(mHz)

33. Latitude
( Pixel)
Longitude ( Pixel)
Latitude
( Pixel)
Longitude ( Pixel)
33
 Retour dans le domaine temporel
Avant
Après
V=57.16 Kms
Longitude ( Pixel)
Latitude
( Pixel)
Après
Visualisation d’une image du

34. Remapping Tracking
Image brute Datacube Filtrage
Récapitulation
34
 Modes f
 Supergranules
•
•
•
•
•
•
•
11 filtres de vitesse de
phase
11 Datacubes
V=25.82 km/s
V=57.16 km/s

35. Remapping Tracking
Images
brutes Datacube
Filtrage
Corrélation
Fit par Gabor
Calcul des temps de
parcours
•Supergranules
•Vitesse de phase
• Modes f
35
3.2. Traitement de données

36. 36
 La corrélation :
 La géométrie du quadrant(EST-OUEST):
 Cette géométrie correspond au modèle théorique de la différence
des temps de parcours en fonction de la vitesse d’écoulement.
3.3. Résultats et discussions
La géométrie (Est-
Ouest)
Longitude ( Pixel)
Latitude
( Pixel)
 On s’intéresse aux écoulements solaires
 la corrélation sera moyenner selon le
schémas des quadrants d’arc (Est-Ouest).
 Afin d’augmenter d’avantage le rapport signal/bruit, on passe d’une
simple corrélation entre deux point à une corrélation par rapport à un
schéma géométrique

37. 37
 Le diagramme Temps-Distance
 Chaque ligne verticale correspond à une corrélation effectuée et moyennée à une distance
donnée.
 La partie supérieure (inférieur) du diagramme correspond à la fonction de corrélation dans le sens
qui va nous fournir τ+ (τ- ).
Temps(min)
 La corrélation effectuée à tout les Datacubes nous donne le Diagramme Temps-Distance
 Chaque colonne correspond à un Datacube filtré à une vitesse de phase donnée
Distance(Mm))

38. Remapping Tracking
Images
brutes Datacube
Filtrage
Corrélation
Fit par Gabor
Calcul des temps de
parcours
•Supergranules
•Vitesse de phase
• Modes f
38
3.2. Traitement de données

39. 39
 Le Fit par la fonction de Gabor
 La fonction de Gabor :
   
 
2
0
( ) exp cos
4
g p
G A

     
 
   
 
 
La fonction de corrélation à une distance donnée montre que
la fonction de corrélation est une somme de fonctions de Gabor.
Ceci est confirmé par les résultats obtenus
 On utilise une approximation non linéaire des moindres carrés
(modèle théorique: une fonction type de Gabor)

40.  Le Fit :
Fitter par une fonction de Gabor à la distance Δ=49.15 Mm pour retrouver les
temps de parcours
40
Fit par Gabor
Les observations
 Les temps de parcours de l’onde sortante (+n ) et (entrante (-n ) sont mesurés par le Fit de
la fonction de Gabor aux deux branches de la corrélation
 τ+ (τ- )est donné par la partie positive (négative) de la corrélation.
Temps(min)
Amplitude

41. 41
 La courbe Temps-Distance
 La courbe « Temps-Distance » est croissante
 τ- > τ+  l’écoulement est dans de la direction :Est  Ouest
 En traitant plusieurs Datacubes sur différentes régions locales de la surface du soleil
on pourra connaître le profil de l’écoulement.
• Pour chaque distance, nous obtenons donc un temps de parcours de l’onde.
• Pour toutes les distances utilisées  une série de temps(τ+, τ- )  tracer la courbe
« Temps-Distance »
- τ-
+ τ+

42. 42
 Méthode Temps-Distance
Plan
 Généralités:
Le Soleil
L’Héliosismologie
 Conclusion et perspectives
 Temps de parcours: Résultats et discussions
 Introduction

43. 43
 Nous avons mis en place le modèle théorique de la méthode
Temps-Distance qui met en relation les temps de parcours avec les
propriétés internes du Soleil.
5. Conclusion et perspectives
 Pour déterminer ces temps de parcours, nous avons développé
toutes les procédures de traitement de données, qui pourrons servir à
d’autres investigations.
5.1. Conclusion
Ces temps de parcours calculés ont révélé l’existence et le sens de
l’écoulement solaire dans une région locale du Soleil.
 Nous avons étudié en particulier le modèle théorique de la
méthode Temps-Distance qui met en relation les temps de parcours
avec la vitesse d’écoulement.

44. 44
 Les temps de parcours déterminés dans ce travail seront exploités
pour nous permettre de calculer les vitesses d’écoulement par
simulation au 1er lieu , ensuite par l’inversion (problème inverse).
 Afin de comprendre les différents aspects de l’activité solaire et de son
influence sur l’héliosphère et la météo spatiale, il est intéressant de
surmonter les difficultés techniques qui nous permettent d’étudier les
oscillations des modes « p » avec plus de précision.
 Pour aller plus loin dans nos connaissances , on a besoin d’étudier l’activité
du Soleil avec plus de précision grâce à la nouvelle génération
d’instruments plus performants ( SDO)
5.2. Perspectives
 Mettre en évidence d’autres géométries (Quadrant: Nord-Sud,
Anneau concentrique) pour le calcul de la corrélation et les confronter
au modèles théoriques préalablement développés(les inhomogénéités
locales).

45. Merci
pour votre attention