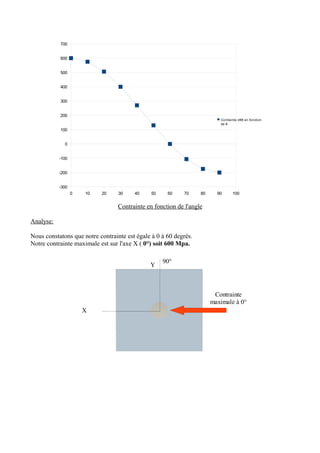
Cette étude analyse les contraintes sur une plaque carrée en aluminium avec un trou central, soumise à des efforts de traction, en utilisant le logiciel ProE pour vérifier la formule de contrainte. Les résultats montrent une contrainte maximale de 600 MPa à 0° et 617 MPa avec une autre méthode, ces résultats étant cohérents avec une différence de seulement 17 MPa. Les zones critiques se situent autour de l'axe x du trou, confirmant les résultats théoriques obtenus.

1. Lamarre Damien CICP 2
Cadoret Yohann
Calcul de structure
Étude d'une plaque percée
2009 – 2010

2. Problématique:
Vérifier la formule (F/(a x h)) x (1+2cos2θ) permettant de calculer la contrainte σθθ
en fonction de l'angle θ grâce au logiciel ProE.
Matériau:
Nous utilisons un alliage d'aluminium isotrope de caractéristique:
– E = 70 000 Mpa
– V = 0,3
Domaine d'étude:
Nous étudions une plaque carrée de dimension 100mm x 100mm x 5mm. Il y a un trou de 20mm
au milieu traversant de part en part.
Notre plaque est soumise à des efforts de traction de 100000N.
Nous sommes donc sur une problématique 2D car nous avons une contrainte plane.
Modèle étudié:
Il nous est impossible d'utiliser la symétrie de la pièce sur ProE. Il n'accepte pas les plans de
symétrie créés sur la pièce et exige plus de contraintes.
Nous allons donc travailler sur notre pièce pleine.
Cela ne fausse en aucun cas les résultats et nous pénalise légèrement sur le temps de calcul du
logiciel.
Détermination des contraintes suivant θ par calcul
Formule: (F/(a x h)) x (1+2cos2θ)
0 600
20 575
40 506
60 400
80 270
100 130
120 0
140 -106
160 -175
180 -200
angle 2θ σθθ

3. Contrainte en fonction de l'angle
Analyse:
Nous constatons que notre contrainte est égale à 0 à 60 degrés.
Notre contrainte maximale est sur l'axe X ( 0°) soit 600 Mpa.
0 10 20 30 40 50 60 70 80 90 100
-300
-200
-100
0
100
200
300
400
500
600
700
Contrainte σθθ en fonction
de θ
Contrainte
maximale à 0°
90°
X
Y

4. Détermination des contraintes suivant θ avec Mechanica
Nous obtenons une contrainte maximal de 617 Mpa.
Comparaison:
Après calcul et analyse grâce au logiciel, nous obtenons des résultats cohérent à 17 Mpa près soit
environs 3%.
Les zones critiques sur le logiciel sont sur l'axe X du trou soit les zones rouge de la photo ci dessus.
Les zones critique après nos calculs théorique sont sur notre axe X soir un angle de 0°.
Nos résultats concordes parfaitement au niveau norme et emplacement.
Y
X