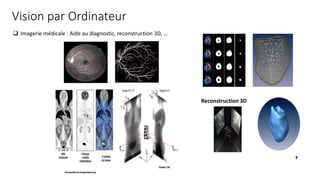
Computer vision is transforming industries by enabling computers to interpret and analyze visual data, bridging the gap between human perception and machine intelligence. This course provides a comprehensive introduction to computer vision, covering fundamental concepts, core techniques, and advanced applications. Designed for students, engineers, and professionals, it offers a balance between theory and practical implementation to help learners build real-world computer vision solutions. 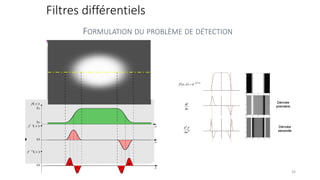The course begins with an overview of image processing, where students will learn about digital images, color spaces, and image transformations. Fundamental operations such as filtering, edge detection, thresholding, and morphological transformations will be covered, along with techniques for image enhancement and noise reduction. These concepts form the basis for more advanced topics in object detection, image segmentation, and feature extraction. A key component of the course is feature-based image analysis, which includes detecting and describing key points using algorithms such as SIFT, SURF, ORB, and FAST. Learners will explore how to match features across images and apply these techniques in applications like image stitching and panorama creation. Optical flow and motion tracking will be introduced to analyze moving objects in videos, providing a foundation for video-based applications. Deep learning has revolutionized computer vision, and this course integrates neural networks and deep learning frameworks to solve complex vision tasks. Students will work with convolutional neural networks (CNNs) to classify images, detect objects, and segment images. The course covers the architecture and inner workings of CNNs, including convolutional layers, pooling layers, activation functions, and backpropagation. Learners will implement models using popular frameworks such as TensorFlow and PyTorch. Beyond basic CNNs, the course explores state-of-the-art architectures such as ResNet, MobileNet, and Vision Transformers. Transfer learning and data augmentation techniques will be introduced to improve model performance with limited datasets. Object detection methods like YOLO and Faster R-CNN will be covered in detail, allowing students to build applications capable of detecting multiple objects in real-time. Image segmentation techniques such as U-Net and Mask R-CNN will be explored to perform pixel-level classification for medical imaging, autonomous driving, and other domains. The course also delves into generative models, including Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs), to create and manipulate images. Applications such as style transfer, super-resolution, and deepfake generation will be discussed. In addition, students will learn about facial recognition, pose estimation, and emotion detection, which are widely used in security, entertainment, and human-computer interaction.

1. Vision par Ordinateur
ComputerVision
Asma Ben Abdallah
ISIM, AU 2023-2024
Visionparordinateur2D
Visionparordinateur3D
1

2. Vision par ordinateur
I. Introduction
▪ La vision par ordinateur ou computer vision :
opermet aux ordinateurs et aux systèmes de
dériver des informations significatives à partir
d'images numériques, de vidéos et d'autres
entrées visuelles, et de prendre des mesures ou
de faire des recommandations sur la base de ces
informations.
opermet aux machines d’imiter la vision humaine
▪ Il s’agit d’un vaste champ pluridisciplinaire, pouvant
être considéré comme une branche de l’intelligence
artificielle et du Machine Learning.
o Quel type de scène ?
o Où se trouve la voiture?
o A quelle distance se trouve la
maison?
2

3. Vision par ordinateur
I. Introduction
• La vision par ordinateur se présente comme
un outil basé sur l’IA capable de traiter,
d’analyser, de comprendre, une image et de
traiter les informations qui en découlent
pour aider les systèmes à «voir» et à
identifier les objets.
• C’est l’équivalent, en termes d’IA, des yeux
humains et de la capacité de notre cerveau.
• Toutefois, il est aussi possible d’utiliser des
méthodes spécialisées et des algorithmes
d’apprentissage général n’étant pas
nécessairement liés à l’intelligence
artificielle.
3

4. ❑Les tâches de vision par ordinateur
comprennent des procédés pour acquérir,
traiter, analyser et « comprendre » des images
numériques, et extraire des données afin de
produire des informations numériques ou
symboliques, par exp sous forme de décisions.
❑Les données d'image peuvent prendre de
nombreuses formes, telles que des séquences
vidéo, des vues de plusieurs caméras, des
données multidimensionnelles à partir d'un
scanner 3D ou d'un appareil de numérisation
médical.
Vision par ordinateur
I. Introduction
4

5. Vision par Ordinateur
❑ Reconnaissance de caractères (OCR):
▪ Traitement de texte
▪ Tri Postal
▪ Reconnaissance d’un matricule
❑ Reconnaissance faciale
❑ Détection d’objet
❑ Suivi d’objet
II. Vision par ordinateur : Domaines d’application
5

6. Vision par Ordinateur
❑ Recherche d’une image
❑ Effets Spéciaux
❑ Identification
Reconnaissance d’empreinte,
Voix, Visage,
Œil, …
❑ Jeux vidéo
II. Vision par ordinateur : Domaines d’application
6

7. Reconstruction 3D
❑ Imagerie médicale : Aide au diagnostic, reconstruction 3D, …
7
Vision par Ordinateur

8. Vision par Ordinateur
❑ Robots mobiles
– évitement d'obstacles
– découverte d'un environnement inconnu et construction d'une carte
(exploration)
– conduite automatique / assistée
❑ Imagerie Médicale
❑ Robotique industrielle
II. Vision par ordinateur : Domaines d’application
8
Reconstruction 3D

9. III. Exemple de tâches de vision 2D-3D
1. Classification d'images : Attribuer une catégorie ou un
label prédéfini à une image. Par exemple, identifier si une
image contient un chien, un chat, une voiture, etc.
2. Détection d'objets : Identifier et localiser les objets
spécifiques dans une image. Cela implique de dessiner des
boîtes englobantes autour des objets et d'identifier leur
classe.
3. Suivi d'objets : Suivre le mouvement des objets dans une
séquence d'images, souvent utilisé dans la surveillance
vidéo.
4. Segmentation sémantique : Attribuer un label à chaque
pixel de l'image, en identifiant les régions correspondant à
différents objets ou structures.
Vision par Ordinateur 2D
9

10. 5. Restauration d’image : supprimer le ” bruit ” (grain, flou…) sur des
photos.
6. Reconstruction de scène : permet de créer un modèle 3D d’une
scène à partir d’images et de vidéos.
7. Estimation de pose d'un objet ou d'une personne dans
l'espace en fonction de l'image afin d’en extraire un modèle
biomécanique. Par exemple, la détection des articulations du
corps humain.
8. Reconnaissance faciale : Identifier et reconnaître les visages
humains dans une image. Par exemple, utilisation pour
l'authentification biométrique.
Vision par Ordinateur 2D
III. Exemple de tâches de vision 2D-3D
10

11. Vision par Ordinateur
IV. Système de Vision par Ordinateur
Connaissances et technologies qui permettent de
concevoir des machines qui peuvent « voir » :
• Les algorithmes de traitement d'images: Ces
algorithmes permettent de filtrer, de segmenter, de
renforcer ou de transformer des images
numériques.
• Les réseaux de neurones convolutifs (CNN)
• Les capteurs d'images: Caméras numériques…
• Les puces électroniques: Les GPU (processeurs
graphiques) sont particulièrement adaptés aux
calculs intensifs nécessaires à la vision par
ordinateur.
11

12. Vision par Ordinateur
IV. Système de Vision par Ordinateur
❑ Premier niveau : vision
acquiert une image grâce un capteur
❑ Deuxième niveau (bas niveau) : traitement de l'image
modifie le contenu de l'image afin de mettre en
évidence des éléments d'intérêt (objets,
contours)
❑ Troisième niveau (Haut Niveau) : reconnaissance
utilise des techniques d'intelligence artificielle pour
identifier des formes connues dans l'image
12

13. Partie 1 : Vision 2D
Rappel
❑Amélioration d’images :
▪ histogrammes,
▪ lissage, (filtrage médian,
moyenneur, Gaussien, …)
❑Contours d'une image de
dimension quelconque :
▪ extrema locaux du gradient
▪ ou zéros du laplacien
❑Segmentation d’une image
13

14. Vision 2D
Détection de contours
14

15. Transformations Locales d’images
Filtrage Spatial:
Détection de bruit
Détection de contours
15

16. CONVOLUTION NUMÉRIQUE
Rappel : la convolution est l'opérateur de base du traitement linéaire des images et a fait
le lien théorique avec les filtres et le traitement du signal.
16

17. 1. C’est une technique de réduction d'information dans les images.
2. L'image est transformée en un ensemble de courbes ( pas forcément fermées) formant les
frontières de l'image.
3. Les applications en traitement d’images sont diverses, citons : Reconnaissance d’objets, de
formes, reconstruction 3D, Compression d’images, …
Détection de contours
17

18. Détection de visages
Détection de contours : Exemples d’applications
Reconnaissance de
caractères : traitement
automatique de
chèques, de courrier, …
18

19. Mise en correspondance
Reconstruction 3D
des images
médicales à partir
d’images 2D
Détection de contours : Exemples d’applications
19

20. Détection de contours : Plan
1. Modélisation du contour
1.1 Modèle de contours
1.2 Formulation du problème de détection
2. Filtrage
2.1 Filtrage du premier ordre
2.2 Filtrage du second ordre
3. Post-traitements
20

21. I. Modèles de contours : Qu’est ce qu’un contour
21

22. I. Modèles de contours : Qu’est ce qu’un contour
Un profil d’intensité d’une ligne dans une image est représenté par des signaux
1D.
22

23. I. Modèles de contours : Qu’est ce qu’un contour
23

24. Modèles de contours
24

25. Détection des points de contours
Méthodes analytiques:
1) Approches par dérivées premières
2) Approches par dérivées secondes
Il existe plusieurs méthodes pour détecter les points de contours par exemple par
dérivées premières et par dérivées secondes.
25

26. Filtres différentiels
FORMULATION DU PROBLÈME DE DÉTECTION
26

27. FORMULATION DU PROBLÈME DE DÉTECTION
27

28. • La première dérivée ou gradient de l’image est l’opérateur de base
pour détecter les contours dans l’image.
• Gradient de l’image
= 0 si aucun changement de tons
≠ 0 si changement de tons
• Compare deux pixels
Filtres différentiels
DÉRIVÉE PREMIÈRE
28

29. II. Détection des contours:
Opérateur gradient
❑Le gradient de  au point (x,y) est un vecteur à deux dimensions
❑Le filtrage de l’image est effectué selon deux directions orthogonales : les
lignes ensuite selon les colonnes de l’image.
❑Pour chaque opérateur (Filtre), deux masques sont ainsi utilisées.
29

30. Gradient : Norme et Direction
30

31. Gradient : Norme et Direction
31

32. Calcul simple du gradient
32

33. Gradient : Norme et Direction
33

34. Gradient (version élémentaire 3x3)
34

35. Filtre de Roberts
35

36. Filtre de Roberts
36

37. Filtre de Roberts
37

38. Filtre de Prewitt
38

39. 39

40. 40

41. Filtre de Sobel
41

42. Exemple (Sobel)
42

43. 43

44. 44

45. En résumé
• Opérateur de Gradient
45

46. Deuxième dérivée de l’image:
Opérateur Laplacien
II. Détection des contours:
46

47. Filtres différentiels
47

48. Dérivées de l’image
48

49. Exemple avec un contour ‘rampe’
49

50. Le Laplacien
• Le Laplacien est le plus simple opérateur dérivatif
isotropique : c'est un scalaire
• Le Laplacien est un opérateur linéaire à deux
dimensions
 = +
2
2
2
2
2
f
f
x
f
y




50

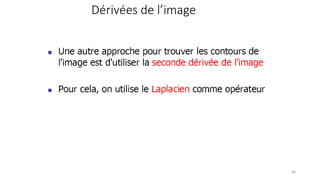
51. Le Laplacien : version discrète
• Dérivé partielle seconde de f(x,y) dans la
direction de x
• Dérivé partielle seconde de f(x,y) dans la
direction de y


2
2 1 1 2
f
x
f x y f x y f x y
= + + − −
( , ) ( , ) ( , )


2
2 1 1 2
f
y
f x y f x y f x y
= + + − −
( , ) ( , ) ( , )
 = + + −
+ + + − −
2
1 1
1 1 4
f f x y f x y
f x y f x y f x y
[ ( , ) ( , )
( , ) ( , )] ( , )
51

52. LE LAPLACIEN : FORMULATION D’UNE VERSION DISCRÈTE
52

53. LE LAPLACIEN : FORMULATION D’UNE VERSION DISCRÈTE
53

54. Le Laplacien
• Intensifie les discontinuités de tons
• Résulte en des images avec des arêtes et des discontinuités grises sur
fond noir sans détails
54

55. Comparaison Gradient / Laplacien
55

56. Dérivées
• Profil horizontal
• Différents types de contours
• Rampe
• Point isolé
• Ligne mince
• Marche (escalier)
• Plusieurs sections
constantes (plats)
56

57. Illustrations : Dérivées
 Dérivé première : points forts
 arêtes grossières
 changements brusques (escalier)
 Dérivé seconde : points forts
 détails fins : lignes, points
 double aux changements rudes
57

58. Exercices
Appliquer les 2 masques
Quel est le masque le plus efficace pour la détection des contours ?
58

59. Exercices
Appliquer les 2 masques
Quel est le masque le plus efficace pour détecter les contours ?
59

60. Exercices
Appliquer les 2 masques
Quel est le masque le plus efficace pour détecter les contours ?
60

61. II. Détection des points de contours
Le contour se matérialise par une rupture d’intensité dans l’image selon une direction
donnée. Pour détecter les contours, la méthodologie consiste en deux étapes
principalement:
61 61

62. II. Détection des points de contours
Etape 1 :
• Localiser et quantifier les contours par un calcul de gradient ou de Laplacien par
exemple, dans des directions privilégiées. Il repose sur l’étude des dérivées de la fonction
d’intensité dans l’image:
❖ Les extrema locaux du gradient de la fonction d’intensité
❖ Les passages par zéro du Laplacien.
* La difficulté réside dans la présence du bruit dans l’image.
62

63. II. Détection de contours
II.1 Laplacien
- Calculer le Laplacien en chaque pixel
- En théorie, les points de contours sont les points où le laplacien est nul
- En raison du bruit, en pratique on procède à détecter les changements de signe du laplacien
Le laplacien :
Sensible au bruit
Problème de seuillage 63

64. II. Détection des points de contours
II.2 SEUILLAGE DU GRADIENT
(MÉTHODE 1)
64

65. Une approche pour extraire les contours est de faire le seuillage pour l’amplitude
du gradient.
1. Calculer la norme du gradient en chaque point de l’image,
2. Calculer le contour en utilisant un seuil S pour décider si un pixel fait
partie ou non d’un contour.
Tous les pixels possédant une norme supérieure à un seuil S sont déclarés
appartenir à un contour.
Difficulté : quel seuil choisir ?
- Un seuillage trop bas nous amène à une sur- détection : on détecte
beaucoup de bruit et des contours épais apparaissent
- Un seuillage trop haut amène à une sous-détection : contours non
fermés
II.2 SEUILLAGE DU GRADIENT
(MÉTHODE 1)
65

66. Exemple de détection de contours par
Seuillage du gradient
66

67. Exemple de détection de contours par
Seuillage du gradient
❑Le principal inconvénient du seuil avec un simple gradient c’est la sensibilité au bruit.
❑Cette méthode ne fonctionne bien que pour les images sans bruit et avec de fortes
discontinuités.
67

68. Pour réduire l’effet du bruit: pré-filtrage
1. Filtrer l’image d’entrée avec un filtre
Gaussien.
2. Calculer la norme du gradient
3. Calculer 𝒄(𝒙, 𝒚) en utilisant un seuil 𝒔:
EXEMPLE DE DÉTECTION DE CONTOURS PAR SEUILLAGE DU GRADIENT
68

69. II.2 SEUILLAGE DU GRADIENT (MÉTHODE 2)
69

70. II.2 SEUILLAGE DU GRADIENT
(MÉTHODE 2 : SEUILLAGE DE L’AMPLITUDE DU GRADIENT )
70

71. II.2 SEUILLAGE DU GRADIENT
(MÉTHODE 2 : SEUILLAGE DE L’AMPLITUDE DU GRADIENT )
71

72. Seuillage global de l’histogramme:
1. Calculer la norme du gradient en chaque point de l’image:
2. Fixer le pourcentage de contours à garder ( exemple 80%)
3. Déterminer le seuil S à partir de l’histogramme cumulé du
module du gradient
II.2 SEUILLAGE DU GRADIENT (MÉTHODE 2)
72

73. II. DÉTECTION DES POINTS DE CONTOURS
II.2 SEUILLAGE DU GRADIENT
(MÉTHODE 3 : ALGORITHME DE CANNY)
C’est un des algorithmes de détection de contours parmi les plus utilisés.
Cet algorithme possède cinq étapes:
1. Lissage: éliminer le bruit de l’image à l’aide d’un filtre Gaussian.
2. Calcul des gradients: Détecter les contours en utilisant la méthode des gradients.
3. Suppression des non-maximums: pour détecter les contours filiformes.
4. Double seuillage: pour détecter les contours forts.
5. Seuillage par hystérésis: Éliminer les pixels de contours isolés et les segments trop
petits.
73

74. II.2 SEUILLAGE DU GRADIENT
(MÉTHODE 3 : ALGORITHME DE CANNY)
74

75. Extraction des maxima locaux de la norme du gradient dans la direction du gradient
Après lissage (Etape 1) de l’image et calcul du gradient (Etape 3), nous opérons à l’extraction des non-
maximum (Etape 3).
Suppression des non-maximums : il s’agit de supprimer de la norme du gradient toutes les valeurs
«faibles», les valeurs qui ne sont pas les plus grandes en suivant l’angle de leur gradien
75

76. Extraction des maxima locaux de la norme du gradient dans la direction du gradient
- Sélectionner les voisins du pixel en utilisant l’angle du gradient.
Exemple : si l’angle est de 90 degrés, les pixels voisins seront auront les coordonnées (x-
1,y) et (x+1,y)
- Pour la valeur de chaque voisin : si la valeur est plus grande que la valeur du pixel
courant, supprimer le pixel courant (attribuer la valeur 0), sinon le conserver
En pratique
On garde le pixel s’il est
supérieur à ces deux
pixels voisins dans la
direction considérée
76

77. Seuillage par hystéresis
77

78. SEUILLAGE DU GRADIENT PAR HYSTÉRÉSIS (MÉTHODE 3)
En résumé :
78

79. 79

80. 80

81. Vision 2D
Segmentation
81

82. Plan
• Qu’est ce que la segmentation
• Approches de la segmentation
• Méthodes de segmentation
• Seuillage
• Croissance de régions (Region growing)
• Décomposition et fusion (Split & Merge )
• Segmentation basée Deep Learning
82

83. •La segmentation d'images est l'un des
problèmes phares du traitement
d'images. Elle consiste à partitionner
l'image en un ensemble de régions
connexes Ri.
•L'intérêt de ces régions est de
pouvoir être manipulées ensuite via
des traitements de haut niveau pour
extraire des caractéristiques de forme,
de position, de taille, etc.
I. Qu’est ce que la segmentation
83

84. Segmentation: Exemple d’applications
84

85. ▪ La segmentation d’un point de vue formel, est un traitement de bas niveau qui consiste à créer une partition
d’une image A en sous ensemble de régions Ri.
▪ La région étant un ensemble connexe ayant des caractéristiques communes (intensité, texture, …)
▪ La segmentation est liée à la reconnaissance (quels objets voit-on dans l’image?
I. Qu’est ce que la segmentation
85

86. I. Qu’est ce que la segmentation-Notion de connexité
• La connexité est une propriété de liaison entre deux pixels
considérés de la même région dans une image.
•La 4-connexité : deux pixels sont 4-connexes s'ils se suivent sur la
même ligne ou la même colonne.
•Exemple : Dans l’image à droite, un exemple de paires de pixels
connexes : (A,B), (A,C), (A,D) et (A,E).
•A et F ne sont pas 4-connexes.
•La 8-connexité : deux pixels sont 8-connexes s'ils se suivent
verticalement, horizontalement ou en diagonale.
•Dans l'exemple ci-dessous, A et F sont 8-connexes.
86

87. I. Qu’est ce que la segmentation
• On appelle une composante k-connexe de l'image,
un ensemble de pixels tels que, si l'on prend 2 pixels
quelconques dans cet ensemble, il est possible de
trouver un chemin k-connexe qui les relie
(e,g k=4, 8).
•Exemple (A,B,C,D,E,F) est une composante connexe
NOTION DE CONNEXITÉ :
87

88. I. Qu’est ce que la segmentation
COMPOSANTE CONNEXE : EXEMPLE-2
étant donné une famille d'ensembles k-connexes ayant un pixel p en
commun, la réunion de ces ensembles est k-connexe.
❑ les composantes 4-connexes sont les
ensembles numérotés de 1 à 5,
❑ les composantes 8-connexes sont :
▪ d'une part la réunion des
ensembles 1 à 3,
▪ d'autre part la réunion des
ensembles 4 et 5.
88

89. NOTION DE CONNEXITÉ, DISTANCE
I. Qu’est ce que la segmentation
89

90. • La segmentation fait référence aux notions
de différence et de similarité comme les
perçoit le système visuel humain et ceci
donne naissance à deux approches
principalement :
• approche contour
• et approche région.
• Ces deux approches sont duales du fait que
chaque région possède un contour et qu’un
contour délimite nécessairement une
région.
II. Segmentation Région/Contours
90

91. II. Segmentation Région/Contours
La segmentation est basée sur:
▪ Les discontinuités : contours
▪ Rechercher les discontinuités entre régions (les changements abruptes,
frontières entre régions…)
▪ Les zones homogènes : régions
▪ Rechercher un critère d’homogénéité entre régions (Mêmes couleurs, textures,
intensités, …)
▪ La segmentation est le découpage d'une image en différentes régions
et/ou contours. Un contour fermé est équivalent à une région
Dualité Régions/Contours
91

92. II. Segmentation Région/Contours
92

93. III. Méthodes de segmentation
Plusieurs méthodes de segmentation:
• Seuillage : segmentation par histogramme
• Croissance de région
• Décomposition et fusion (Split & merge)
• Segmentation basée DL
93

94. ▪ Le seuillage est une méthode simple et très populaire pour le traitement
des images numériques.
▪ Ce n’est pas une méthode de segmentation en régions
▪ Approche pixel (ni région ni contour)
▪ Utilisée souvent en segmentation (avec post-traitements)
• Le seuillage peut être :
▪ Global : un seuil pour toute l'image
▪ Local : un seuil pour une portion de l'image
III.1 Segmentation par seuillage
94

95. Principe : trouver les déférents modes de l’histogramme, représentatifs d’autant de
classes d’objets dans l’image.
❑ On peut rechercher par exemple le(s) seuil(s) à partir d’une analyse de
l’histogramme.
❑ Exemple : Seuillage d’histogramme simple ou multi-seuils
❑ Le résultat du seuillage est une image binaire 0 ou 1
(qu’on transforme parfois en 0:255 pour l’affichage)
III.1 Segmentation par seuillage
95
Problème : choix du seuil !

96. Segmentation par seuillage
Comment définir le seuil?
96

97. Segmentation par seuillage
Seuillage global automatique
97

98. Segmentation par seuillage
Exemple : Seuillage simple
98

99. Segmentation par seuillage
Exemples : Seuillage simple
99

100. Seuillage global automatique :
exemple : Seuillage simple
100

101. Segmentation par seuillage multi-seuils
III.1 SEGMENTATION PAR SEUILLAGE
Seuillage d’histogramme multiple
Cas de deux seuils
10
1

102. Segmentation en pixels
Segmentation par seuillage :
+ Universel, temps réel, simplicité
+ Fonctionne bien sur des histogrammes multi-modaux
- Il faut connaître le nombre de classes
- Apparition de faux éléments (aucune prise en compte de la
composante spatiale)
- Le seuillage est une opération sur les pixels : ne produit
pas forcément des régions connexes,
- Il existe des méthodes de segmentation en régions
102

103. III.2 Segmentation en régions
Objectif : Trouver la partition de l’image tenant compte du double critère : Homogenéité de la région Ri
et Voisinage
103
1 : tout pixel de l'image appartient à
une région et une seule.
2 : toute région doit être connexe. La
connexité des régions est induite
par le voisinage défini sur l'image.
3 : chaque région doit être homogène.
4 : la fusion de deux régions ne doit pas
être homogène

104. III.2 Segmentation en régions
• Dans cette technique, on construit de façon itérative une région
partir d’un ensemble initial (qui peut être réduit à un pixel), qu’on fait
grossir en ajoutant des pixels en fonction de certaines conditions.
• Ces conditions peuvent être :
• relatives au niveau de gris (ou à la couleur) du nouveau pixel candidat,
comparé au niveau de gris (ou couleur) moyen de la région, …
• Adjacence de pixels
104
Méthode croissance des régions (Region growing)

105. III.2 Segmentation en régions - Méthode croissance
des régions
105

106. 106

107. 107

108. 108

109. III.2 Segmentation en régions
109
Méthode croissance des régions (Region growing)
Algorithme croissance de région

110. Exemple
Critère utilisé : Valeur Moyenne
110
Parcours des voisins se fait dans les directions : haut, bas, gauche,
droite

111. Exemple
Critère utilisé : Valeur Moyenne
111
Parcours des voisins se fait dans les directions : haut, bas, gauche,
droite

112. Exemple
Critère utilisé : Valeur Moyenne
112
Parcours des voisins se fait dans les directions : haut, bas, gauche,
droite

113. Exemple
Critère utilisé : Valeur Moyenne
• Evaluer le résultat d'une segmentation n'est pas facile :
• Il dépend de l’application
• Il dépend de ce qu’on veut
• Il est subjectif et varie d'une personne à l'autre
113
Parcours des voisins se fait dans les directions : haut, bas, gauche,
droite

114. Exemple-2
114
Parcours des voisins se fait dans les directions : haut, bas, gauche,
droite
Homogénéité : max-min <=5
5 5 100 100
5 5 100 100
5 100 100 20
5 100 100 22
5 20 22 24
Appliquer une segmentation par croissance de régions sur cette
image.
a) Comme germe de départ que proposez vous ?
b) Justifier formellement ce choix.
c) Appliquer une segmentation par croissance de régions sur
cette image. Détailler les résultats de la première, la seconde
et la dernière itération (résultat final de la segmentation). A
chaque itération, préciser le germe, son niveau de gris et ses
coordonnées
première itération :
Germe de départ : ...............,
Coordonnées du germe : ................

115. III.4 Segmentation en régions
Division et fusion (Split & Merge)
115

116. Etape de division
116

117. Etape de division
117

118. Etape de division
118

119. Etape de division
119

120. Etape de fusion
1- Sur-segmentation de l’image selon un prédicat très strict
2- Regroupement des régions adjacentes selon un prédicat plus lâche
120

121. Illustration 2 : Division ensuite fusion
121
Division
Fusion

122. 122

123. Split & Merge : conclusion
• Split : la géométrie du découpage a une grande influence sur le résultat
de la segmentation. Par exemple, le split en quadtree fait apparaître
des régions carrées.
• Merge : l'ordre dans lequel est réalisé le regroupement des régions a
aussi une influence sur le résultat. Comme illustré dans les figures
précédentes, les algorithmes commencent en général à fusionner les
régions les plus petites.
123

124. • Aucune méthode ne fonctionne pour toutes les images
• Pas de garantie, pas de recette miracle !
• Comment choisir convenablement les seeds de chaque région ?
• En général, l'ordre dans lequel les régions sont construites, mais aussi
l'ordre dans lequel sont ajoutés les pixels dans une région a une grande
influence sur le résultat.
124
Split & Merge : conclusion

125. Vision 3D
125