Le document présente une méthode automatique pour découvrir des relations intéressantes entre des objets à l'aide de règles d'association de la forme x ⇒ y, en utilisant des indicateurs tels que le support et la confiance. Il décrit l'algorithme a priori pour générer des ensembles d'items fréquents à partir de données et mentionne diverses applications pratiques dans des domaines tels que l'analyse de marché et la détection des fraudes. Malgré son efficacité, la méthode est coûteuse en termes de calcul et peut produire des règles triviales.

1. Règles d’association
Christelle Scharff
IFI
Juin 2004

2. Motivations et généralités
 Approche automatique pour découvrir des relations /
corrélations intéressantes entre des objets
 Règles de la forme: X  Y [support, confidence]
 X et Y peuvent être composés de conjonctions
 Support P(X  Y) = P(X et Y)
 Confidence P(X  Y) = P( Y | X) = P(X et Y)/P(X)
 Applications:
 Utilisé pour analyser le panier de la ménagère
 Design des rayons dans les supermarchés, ventes croisées,
segmentation du marché, design des catalogues de ventes
 Détection des fraudes
 Gestion des stocks

3. Exemples de règles
 Règle booléenne:
achète(x, “SQLServer”) ^ achète(x,
“DMBook”)  achète(x, “DBMiner”) [0.2%,
60%]
 Règle quantitative:
age(x, “30..39”) ^ salaire(x, “42..48K”) 
achète(x, “PC”) [1%, 75%]

4. Méthode Naïve
 Traiter toutes les combinaisons possibles des
attributs et de leurs valeurs pour créer toutes
les règles d’association possibles
 Exemple: 5 attributs prenant une seule valeur
 Combien de règles?
 Complexité computationnelle
 Nombre de règles gigantesque
 Amélioration: Garder les règles avec un
support et une confidence minimum
 Pas satisfaisant

5. L’algorithme A Priori [nom,
année]
 Un item est une paire (attribut, valeur)
 Un ensemble d’items regroupe des items
(sans duplication)
 Principe de l’algorithme A Priori:
 Génération d’ensembles d’items
 Calcul des fréquences des ensembles d’items
 On garde les ensembles d’items avec un support
minimum: les ensembles d’items fréquents
 On ne génère et on ne garde que les règles avec
une confidence minimum

6. Exemple:Météo et match de
foot

7. Exemple: Ensembles d’items
12 ensembles d’un item, 47 ensembles de deux items,
39 ensembles de trois items, 6 ensembles de quatre
items, 0 ensemble de cinq items = 104 ensembles
d’items avec un support >= 2
Supports

8. La propriété de fréquence des
ensembles d’items
 On utilise certaines propriétés pour construire
les ensembles d’items
 Les sous-ensembles d’un ensemble d’items
fréquent sont aussi des ensembles d’items
fréquents
 Par exemple, si {A,B} est un ensemble d’items
fréquents, alors {A} et {B} sont aussi des ensembles
d’items fréquents
 Plus généralement, les sous-ensembles de k-1 items
d’un ensemble de k items fréquent sont fréquents

9. Construction des ensembles
d’items
 En utilisant la propriété de fréquence des
ensembles d’items, on voit qu’on peut
construire les ensembles d’items
incrémentalement:
 On commence avec les ensembles à un item
 Un ensemble de k items peut être construit par
jointure d’un ensemble d’ensembles de k-1 items
avec lui-même, et en vérifiant la propriété de
fréquence

10. Exemple
 On suppose que les ensembles d’items sont
composés d’items ordonnés (par exemple
léxicographiquement)
 Considérons les ensembles de 3 items suivants:
 S = {(A,B,C), (A,B,D), (A,C,D), (A,C,E), (B,C,D)}
 S est joint avec lui-même
 (A,C,D,E) n’est pas un ensemble de 4 items
fréquent (car (C,D,E) n’est pas dans S)
 (A,B,C,D) est un ensemble de 4 items fréquent

11. Ensembles d’items et règles
 Un ensemble d’items peut représenter plusieurs
règles
 Exemple:
 A partir de {A,B,C}, on peut construire 7 règles avec le
même support:
 A  B, C
 B  A, C
 C  A, B
 A, B  C
 A, C  B
 B, C  A
 True  A, B, C
mais pas la même confidence

12. Générer les règles
 Transformer les ensemble d’items en
règles de manière efficace
 D’un ensemble de n items, on peut
générer 2n –1 règles potentielles
 On ne garde que les règles avec une
confidence minimum

13. Exemple: Ensembles d’items
 Règles
Support >= 2 (ou 2/14) et Confidence = 100%
58 règles
3 règles avec un support de 4
5 règles avec un support de 3
50 règles avec un support de 2

14. Exemple complet
TID Items
100 1 3 4
200 2 3 5
300 1 2 3 5
400 2 5
BD D itemset sup.
{1} 2
{2} 3
{3} 3
{4} 1
{5} 3
itemset sup.
{1} 2
{2} 3
{3} 3
{5} 3
Parcours D
C1
L1
itemset
{1 2}
{1 3}
{1 5}
{2 3}
{2 5}
{3 5}
itemset sup
{1 2} 1
{1 3} 2
{1 5} 1
{2 3} 2
{2 5} 3
{3 5} 2
itemset sup
{1 3} 2
{2 3} 2
{2 5} 3
{3 5} 2
L2
C2 C2
Parcours D
C3 L3
itemset
{2 3 5}
Parcours D itemset sup
{2 3 5} 2

15. Améliorer l’algorithme
 104 ensembles de 1 items peuvent générer
107 ensemble de 2 items
 Le calcul des supports est coûteux
 Générer les règles est coûteux
 Le calcul des confidences est coûteux
 Le parcours des données initiales est
récurrent

16. Calcul de la confidence d’une
règle: Optimisation naïve
 Calcul de 2n –1 confidences (une pour chaque
règle)
 Pour calculer la confidence d’une règle on
peut utiliser le support d’ensembles d’items
calculé auparavant (en utilisant une table de
hachage)
 Exemple:
 Pour calculer la confidence de:
 Température = cool, windy = false  humidity =
normal, play = yes
 On peut utiliser le support calculé pour:
 Température = cool, windy = false

17. La méthode
 Les règles sont faciles à interpréter
 La méthode réalise de l’apprentissage non
supervisé
 Elle est basée sur des calculs élémentaires
 Elle est très coûteuse
 Elle marche pour des découvertes de faits
fréquents
 Elle peut produire des règles triviales et
inutiles
 Exemple: Camembert  Vin rouge

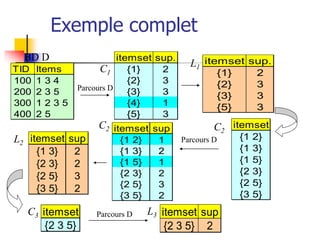
18. Autre algorithme
 L’algorithme d’arbre de modèles
fréquents (Frequent-pattern tree)
[name, année]

19. References
 I. H. Witten, and E. Frank. Data Mining :
Practical Machine Learning Tools and
Techniques with Java Implementations.
Morgan Kaufmann.
 J. Han, and M. Kamber. Data Mining
Concepts