Le document traite de l'intégration et du calcul d'aires délimitées par des fonctions, notamment des fonctions affines et des courbes comme les paraboles. Il présente des exemples pratiques où l'aire est calculée à l'aide de triangles et de trapèzes, ainsi qu'une méthode pour travailler avec des surfaces ayant un bord courbe en utilisant des rectangles pour approcher l'aire recherchée. La conclusion souligne l'importance de la limite des sommes de rectangles pour déterminer avec précision l'aire sous la courbe d'une fonction continue.

![Introduction
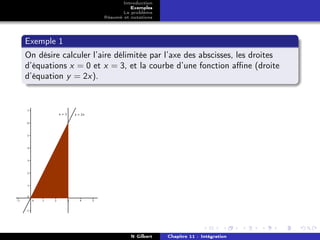
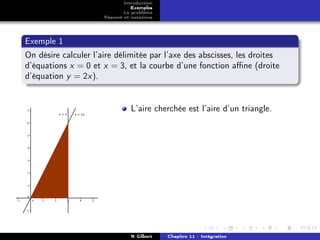
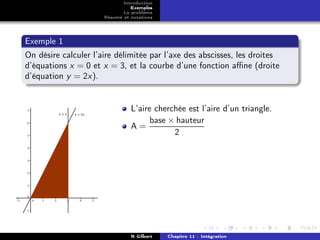
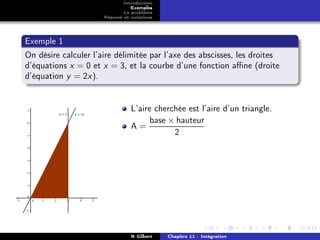
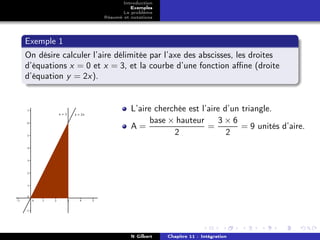
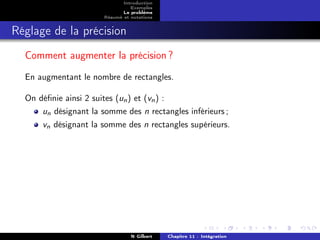
Exemples
Le problème
Résumé et notations
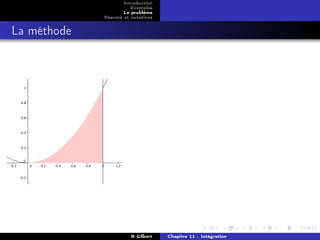
La méthode
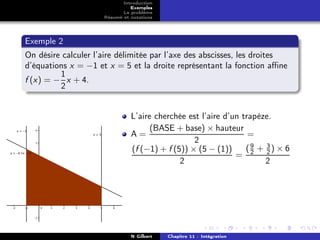
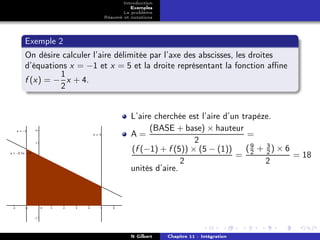
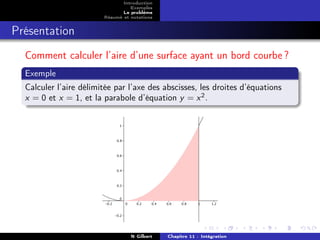
On travaille avec la fonction carrée sur [0; 1].
N Gilbert Chapitre 11 : Intégration](https://image.slidesharecdn.com/ts-integration-approche-120410192553-phpapp02/85/integration-19-320.jpg)
![Introduction
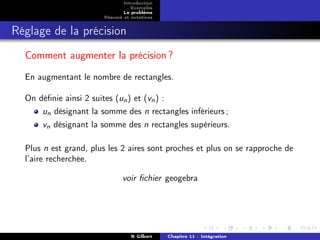
Exemples
Le problème
Résumé et notations
La méthode
On travaille avec la fonction carrée sur [0; 1].
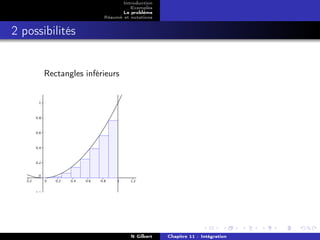
On découpe l’aire en un certain nombre de
rectangles et on ajoute les aires de ces rectangles.
N Gilbert Chapitre 11 : Intégration](https://image.slidesharecdn.com/ts-integration-approche-120410192553-phpapp02/85/integration-20-320.jpg)
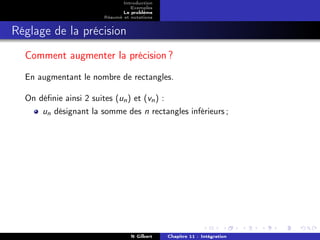
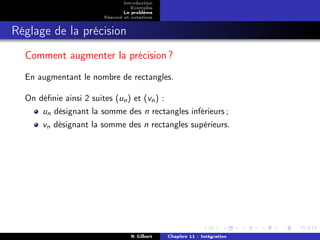
![Introduction
Exemples
Le problème
Résumé et notations
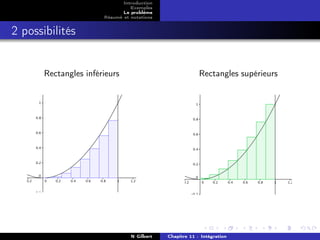
Calcul de un
On a partagé l’intervalle [0; 1] en n
Rectangles inférieurs intervalles.
Quelle est la largeur de chaque rectangle ?
Quelle est l’aire du premier rectangle ? du
deuxième ? ... du dernier ?
Écrire un sous la forme d’une somme et la
calculer.
N Gilbert Chapitre 11 : Intégration](https://image.slidesharecdn.com/ts-integration-approche-120410192553-phpapp02/85/integration-30-320.jpg)
![Introduction
Exemples
Le problème
Résumé et notations
Calcul de un
On a partagé l’intervalle [0; 1] en n
Rectangles inférieurs intervalles.
Quelle est la largeur de chaque rectangle ?
Quelle est l’aire du premier rectangle ? du
deuxième ? ... du dernier ?
Écrire un sous la forme d’une somme et la
calculer.
(n − 1)(2n − 1)
un =
6n2
N Gilbert Chapitre 11 : Intégration](https://image.slidesharecdn.com/ts-integration-approche-120410192553-phpapp02/85/integration-31-320.jpg)
![Introduction
Exemples
Le problème
Résumé et notations
Calcul de vn
On a partagé l’intervalle [0; 1] en n
Rectangles supérieurs intervalles.
Quelle est la largeur de chaque rectangle ?
Quelle est l’aire du premier rectangle ? du
deuxième ? ... du dernier ?
Écrire vn sous la forme d’une somme et la
calculer.
N Gilbert Chapitre 11 : Intégration](https://image.slidesharecdn.com/ts-integration-approche-120410192553-phpapp02/85/integration-32-320.jpg)
![Introduction
Exemples
Le problème
Résumé et notations
Calcul de vn
On a partagé l’intervalle [0; 1] en n
Rectangles supérieurs intervalles.
Quelle est la largeur de chaque rectangle ?
Quelle est l’aire du premier rectangle ? du
deuxième ? ... du dernier ?
Écrire vn sous la forme d’une somme et la
calculer.
(n + 1)(2n + 1)
un =
6n2
N Gilbert Chapitre 11 : Intégration](https://image.slidesharecdn.com/ts-integration-approche-120410192553-phpapp02/85/integration-33-320.jpg)
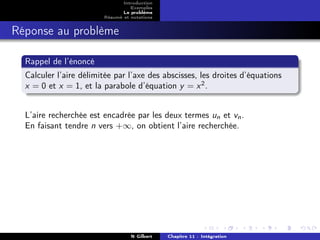
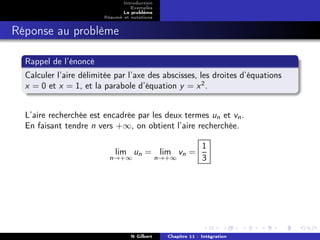
![Introduction
Exemples
Le problème
Résumé et notations
A retenir
Soit f une fonction continue et positive sur un intervalle [a; b] et C sa
courbe représentative.
L’aire du domaine délimité par l’axe des abscisses, C , et les droites
d’équations x = a et x = b est notée :
b
f (x)dx.
a
N Gilbert Chapitre 11 : Intégration](https://image.slidesharecdn.com/ts-integration-approche-120410192553-phpapp02/85/integration-38-320.jpg)