Introduction `a l’optimisation combinatoire
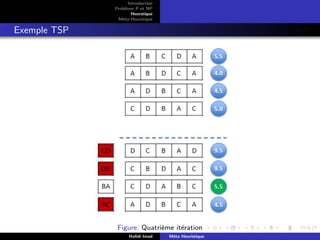
Sensibiliser sur les classes NP et r´esoudre des probl`emes classiques : TSP,
Sac `a dos...
se familiariser avec la conception des algorithmes heuristique et m´eta
heuristique
Organisation
cours sous formats de polycope, prise des notes recommand´ees.
pr´eparation des fiches TD et TP est obligatoire
mini projet `a r´ealiser `a la fin du semestre
Hafidi Imad M´eta Heuristique
D