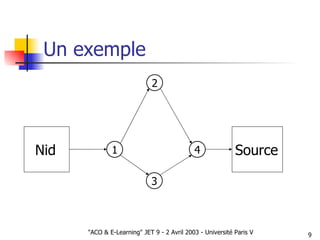
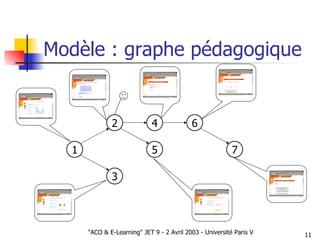
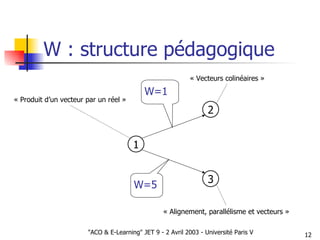
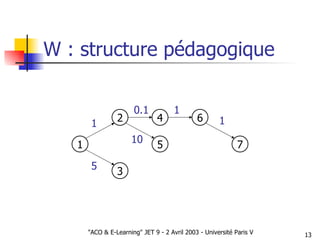
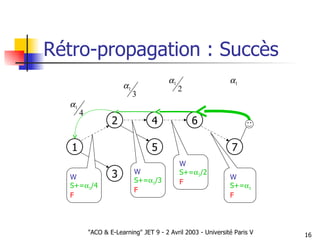
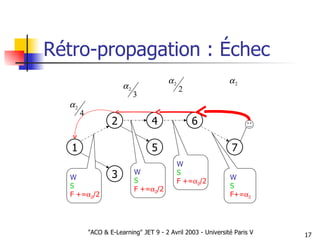
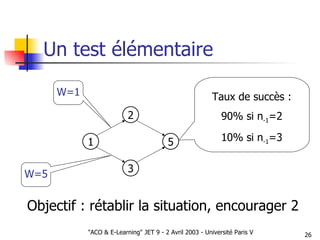
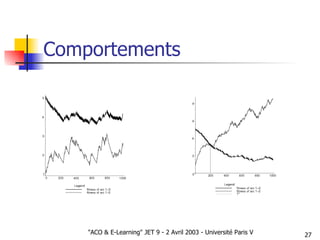
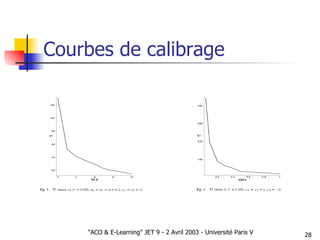
Le document présente une approche d'optimisation des parcours pédagogiques en e-learning utilisant l'optimisation par colonies de fourmis, qui s'inspire de comportements d'insectes sociaux. Il aborde des concepts tels que la communication stigmergique et la sélection d'arcs basés sur des critères de succès pédagogique, tout en incluant des simulations pour valider l'efficacité de cette méthode. Les premières observations signalent des résultats prometteurs concernant la structuration autonome des graphes pédagogiques.

1. Optimisation par Colonies de Fourmis pour le E-Learning : optimisation de parcours pédagogiques Yann SEMET Projet Fractales, INRIA Rocquencourt

2. Itinéraire Le site Paraschool Problème et solution Détails algorithmiques Procédures de sélection Simulations et tests réels Perspectives

3. Le site Paraschool

4. Le site Paraschool

5. Le site Paraschool

6. Le site Paraschool

7. Le site Paraschool

8. Optimisation par Colonies de Fourmis (A CO) Paradigme inspiré des colonies d’insectes sociaux Agents multiples et simples Balance information stigmergique et heuristique locale Solution « émergente » Efficace, souple, facile à écrire (métaphore des agents)

9. Un exemple 1 2 3 4 Nid Source

10. Fourmis et voyageurs de commerce (ACO&TSP) Application classique Excellents résultats obtenus par méthodes hybrides i l 1 j l n l k

11. Modèle : graphe pédagogique 1 2 3 5 4 6 7

12. W : structure pédagogique 1 2 3 « Produit d’un vecteur par un réel » « Vecteurs colinéaires » « Alignement, parallélisme et vecteurs » W=5 W=1

13. W : structure pédagogique 1 2 3 5 4 6 7 1 5 0.1 10 1 1

14. Un problème d’optimisation Maximiser : succès pédagogique Trouver la bonne valuation Contraintes : Pédagogiques Facteurs individuels Facteurs collectifs

15. Fourmis & Phéromones Communication stigmergique 2 types de phéromone : S et F Dépôt : mémoire Rétro-propagation : portée pédagogique Évaporation : dynamisme Pour une valuation plus pertinente

16. Rétro-propagation : Succès 1 2 3 5 4 6 7 W S+=  1 F W S+=  1 /2 F W S+=  1 /3 F W S+=  1 /4 F

17. Rétro-propagation : Échec 1 2 3 5 4 6 7 W S F+=  2 W S F +=  2 /2 W S F +=  2 /2 W S F +=  2 /2

18. S/F : évaporation  : taux d’évaporation ; x=  t Portée pédagogique temporelle Exploration dynamique Adaptabilité

19. Mémoire individuelle : H Un 1er facteur individuel Modèle de la mémoire volatile Une valeur par nœud et par étudiant Application de NxI dans R Nœud non visité : H=1 Nœud réussi : H=0.5 Nœud raté : H=0.75

20. H : anti-évaporation  =constante de temps ; x=  t H revient naturellement vers 1

21. Une mesure de fitness Mesure unifiée d’excellence locale Mesure la « désirabilité » des arcs

22. Désirabilité des arcs Balance heuristique locale/information stigmergique. Cf TSP Un arc est désirable lorsqu’il est : renforcé les professeurs (W élevé) témoin de succès (S élevé) non témoin d’échecs (F bas) nouveau ou oublié (H proche de 1)

23. Sélection d’arcs Sélection d’un arc à proposer parmi les arcs sortants Deux forces : Fitness (exploitation) Hasard (exploration) Balance réglable : s

24. Procédures implémentées Roulette Sélection par le rang : seuils automatiques et manuels Tournoi Tournoi stochastique

25. Tests : Simulations Une population d’étudiants : G(0.5,1/3) A chaque étudiant i son niveau A chaque nœud sa difficulté : 0.0 <d< 1.0 Si niveau(i)>d succès , sinon échec

26. Un test élémentaire 1 2 3 5 W=1 W=5 Taux de succès : 90% si n -1 =2 10% si n -1 =3 Objectif : rétablir la situation, encourager 2

27. Comportements

28. Courbes de calibrage

29. Application réelle En cours ! Mode silencieux Observations préliminaires encourageantes : Faisabilité technique Structuration autonome du graphe Émergence de nœuds singuliers Travail à venir

30. Résumé, Perspectives L’E-Learning comme un problème d’optimisation Un nouveau champ d’applications pour l’intelligence en essaim Une nouvelle façon de faire du design évolutionnaire interactif

31. MERCI ! « Ant Colony Optimisation for E-Learning : Observing the Emergence of Pedagogic Suggestions » Y.Semet, Y. Jamont, R. Biojout, E. Lutton, P. Collet - Projet Fractales, INRIA Rocquencourt Université de Technologie de Compiègne - Yann.Semet@tremplin-utc.net

32. Annexes

33. H : calibrage de  Oublier un exercice : H va de 0.5 à 0.9 Oublier prend 1 semaine (x=604800s)  =3.6E-6

34. La roulette E=nœuds accessibles depuis n i Probabilité proportionnelle au fitness Automatique mais pas réglable Sensible, parfois trop

35. Sélection par le rang I Probabilité de sélection inversement proportionnelle au rang Réduction automatique des écarts Non réglable Peut être insuffisamment subtil

36. Sélection par le rang II Probabilités attribuées manuellement pour chaque rang Complètement paramétrable Lourd

37. Sélection par tournoi S 1 arcs sortants tirés au hasard Le meilleur est choisi 1 paramètre de contrôle

38. Tournoi stochastique On choisit d’abord le pire arc S 1 « challengers » sont essayés l’un après l’autre Si plus fort, le « challenger » remplace son prédécesseur avec une probabilité s 2 2 paramètres de contrôle

39. Prolongements Nouveaux facteurs individuels (agenda, excellence, etc.) Nouveaux facteurs collectifs (e.g. coupe de re-médiation) Observation avant tout

40. Facteurs clés Écoute de l’équipe pédagogique Écoute des élèves Davantage que l’optimisation computationelle

41. Résumé Un problème d’optimisation : chercher la bonne valuation des arcs d’un graphe de navigation pédagogique Solution proposée : agents, communication stigmergique, sélection semi-aléatoire Éléments de calibrage Premières observations encourageantes