INTRODUCTION MATLAB pour bon démarrage.pdf

INITIATION A MATLAB
Jacques Tagoudjeu
ENSP 2012-2013
21/03/2013 1

INITIATION A MATLAB
1. GENERALITES
2. VARIABLES ET FONCTIONS PREDEFINIES
3. MATRICES ET TABLEAUX
4. OPERATIONS SOUS MATLAB
5. PROGRAMMATION MATLAB
6. GRAPHIQUES SOUS MATLAB
21/03/2013 J. Tagoudjeu, ENSP, 2
Référence:
http://enacit1.epfl.ch/cours_matlab/pdf/Matlab-Octave-Cours-JDBonjour-2012-09-24.pdf
http://enacit1.epfl.ch/cours_matlab

INTRODUCTION A MATLAB
1. GENERALITES
21/03/2013 J. Tagoudjeu, ENSP 3

GENERALITES: Introduction
• MATLAB = MATrix LABoratory;
• Logiciel de Calcul Scientifique en
développement depuis le début des années 80;
• Initialement conçu pour faciliter les opérations
de calcul matriciel
• Est aujourd'hui un outils assez puissant de calcul
numérique comportant plusieurs TOOLBOX
• Les objets de base de Matlab sont les matrices:
« comprend tout comme matrice et/ou
tableau »
• Un langage interprété

Environnement de Matlab
• Lancement:
Double cliquer sur
l’icône Matlab sur le
Bureau

• Accueil:
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 6

• Matlab comme calculatrice:
– Opérations classiques: +,-,*,/,^
– Par défaut, l’affichage des réels se fait sur 5 chiffres
significatifs et le stockage en mémoire se fait sur 16
chiffres en base 10.
– Modification du mode d’affichage des réels par la
commande: format
>> format; % affichage par défaut;
>> format short; % affichage par défaut;
>> format long; % affichage avec tous les chiffres significatif
>> format short e; >> formal long e; >> format short g; >> format long g
>> 6 + 7
>> ans =
13
>> 6 * 7
>> ans =
42
>> (6 +7)/(6 * 7+10)
>> ans =
0.2500

• Aide sous Matlab:
– Commande help
– Fenêtre d’aide
>> help % affiche l’aide de Matlab
>> help « mot clé » % affiche l’aide Matlab à propos de « mot clé »

• Historique des commandes:
– En plus de placer les commandes tapées dans la
fenêtre historique des commandes, toutes les
commandes d’une session Matlab peuvent être
rappelées à l’aide des touches flêchées.

1. GENERALITES
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 10

VARIABLES
• Une variable est identifiée par son identificateur;
• L’identificateur d’une variable est une suite
alphanumérique commençant par une lettre;
• Matlab est sensible à la case
• La définition d’une variable se fait en affectant à
celle-ci une valeur.
• La déclaration du type de la variable est implicite.
• Le type de la variable est déterminé automatique
par le type de la valeur qui lui est attribuée
– Syntaxe: « Nom_Variable » = « Valeur »

VARIABLES
• « Valeur » peut être:
– une constante scalaire (réelle, entière, complexe);
– une constante caractère ou chaîne de caractère;
– une constante booléenne;
– une matrice ou tableau;
– un tableau cellulaire;
– Le résultat de l’évaluation d’une expression ou d’une
fonction
• Exemple
21/03/2013 J. Tagoudjeu, ENSP, 12
>> a = 2.5
a = 2.5000
>> b = 3.75
b = 3.7500
>> c = (a + b)*4
c = 25.000
>> a =2.5, b=3.75, c=(a + b)*4
a = 2.5000
b = 3.7500
c = 25.000
>> a =2.5;
>> b=3.75;
>> c=(a + b)*4;
>> a
a = 2.5000
>> b = 3.75
b = 3.7500
>> c = (a + b)*4
c = 25.000

VARIABLES
• Valeur constante réelle:
25.675 0.006 4.25e12 -34.45e-33
• Valeur constante entière
35604 -1156785 10000
• Valeur constante complexe
5.0400+6.4000i
– Manipulation aisée des complexes: résolution de
l’équation x²+2x+5=0
– Affiche les solution
-1.0000 + 2.0000i et -1.0000 - 2.0000i

VARIABLES
• Constante booléenne:
true false
• Constante caractère ou chaîne
‘A’ ‘a’ ‘Bonjour’ ‘L’’épreuve de math’ ‘bonjour
monsieur!’
• constantes prédéfinies

VARIABLES
• Constantes prédéfinies (elles ne sont pas protégées)
Constante Description
pi 3.14159265358979 (la valeur de "pi")
i ou j racine de -1 (sqrt(-1)) (nombre imaginaire)
Inf ou inf infini (par exemple le résultat du calcul 5/0)
NaN ou nan indéterminé (par exemple le résultat du calcul 0/0)
realmin
env. 2.2e-308
: le plus petit nombre positif utilisable (en virgule flottante
double précision)
realmax
env. 1.7e+308
: le plus grand nombre positif utilisable (en virgule flottante
double précision)
eps
env. 2.2e-16
: c'est la précision relative en virgule flottante double
précision (ou le plus petit nombre représentable par l'ordinateur qui est
tel que, additionné à un nombre, il crée un nombre juste supérieur)
true
vrai ou 1 ; mais n'importe quelle valeur différente de 0 est aussi "vrai"
Ex: si nb vaut 0, la séquence if nb, disp('vrai'), else,
disp('faux'), end retourne "faux",
mais si nb vaut n'importe quelle autre valeur, elle retourne "vrai"
false faux ou 0

VARIABLES
• Variables prédéfinies
• Liste de variables actuelles et effacement des
variables
who
whos
clear NomVariable
clear all
Variable Description
ans
variable sur laquelle MATLAB retourne la valeur d'une expression qui
n'a pas été affectée à une variable (ou nomde variable par défaut pour
les résultats)
nargin nombre d'arguments passés à une fonction
nargout nombre d'arguments retournés par une fonction

FONCTIONS PREDEFINIES
• Matlab dispose d’une bibliothèque assez
fournie de fonctions prédéfinies qui comporte
entre autre:
– Les fonctions mathématiques élémentaires
– Les fonctions de conversion de type
– Les fonctions de manipulation des chaînes
– Les fonctions de calcul matriciel
– Les fonctions mathématiques spéciales
– De nombreuses autres fonctions dédiées contenues
dans les TOOLBOX

Fonctions numériques usuelles

21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 19

Fonctions complexes usuelles

1. GENERALITES

MATRICES : DEFINITION
• On distingue les vecteurs colonnes, vecteurs lignes, les
matrices à N lignes et M colonnes.
– Vecteur ligne: Nom_Vecteur = [ liste des valeurs séparées par
des espaces vides ou des virgules]
– Les valeurs sont de même type ou de types compatibles
– Exemple: définir les vecteurs v = (1,2,3); w = (0,1,-4,8+2i)
x = (-0.5,4,3.7,-1,1e-17), t=(1,3,5,7,9,11,13)
– Vecteur dont les éléments sont les termes d’une suite
arithmétique débutant par El_Min et <= El_Max:
Nom_Vect = El_Min : raison : El_Max
Lorsque la raison vaut 1, on a: Nom_Vect = El_Min : El_Max
– Vecteur contenant n valeurs équidistantes sur [a,b]
Nom_Vect = linspace(a,b,n)
Nom_Vect = a : h : b; avec h = (b-a)/(n-1)

– Vecteur colonne:
Nom_Vect = [ liste des valeurs séparées par des
points virgules ]
– Les valeurs sont de même type ou de types
compatibles
– Exemple: définir les vecteurs
- Définir le vecteur complexe de partie réelle v et de
partie imaginaire u







































13
25
1
.
0
5
8
4
1
0
3
2
1
u
i
w
v

– Matrice NxM = vecteur colonne de N vecteurs ligne de
taille M:
Nom_Mat = [ligne 1; ligne 2;…;ligne N]
– Matrice NxM = vecteur ligne de M vecteurs colonne
de taille N:
Nom_Mat = [Col 1, Col 2, …, Col M]
– Exemple: définir les matrices
- Définir la matrice complexe de partie réelle v et de
partie imaginaire u





































 

56
6
3
10
8
2
0
4
1
7
17
3
87
5
.
0
15
9
9
11
0
6
7
.
2
12
1
12
8
6
.
5
10
5
4
5
1
0
u
i
w
v


• Matrices particulières
– Matrices Nulles
Nom_Mat = zeros(N_lig,N_col)
– Matrices dont tous les éléments sont égaux à 1
Nom_Mat = ones(N_lig,N_col)
– Matrices dont tous les éléments sont égaux à une constante
Nom_Mat = repmat(const,N_lig,N_col)
– Matrices aléatoires
• Nom_Mat = rand(N_lig,N_col) : matrice de nombres aléatoires issus d’une
distribution sur ]0,1[
• Nom_Mat = randn(N_lig,N_col): matrice de nombre aléatoires issus d’une
distribution normale centrée réduite
– Matrices magiques:
Nom_Mat = magic(taille): taille>2
– Matrices diagonale: Nom_Mat = diag(vect)
vect est le vecteur diagonale de la matrice.
– Matrice identité:
Nom_Mat = eye(taille), Nom_Mat = eye(N_lig,N_col)

• Matrices définies par blocs
– Vecteur bloc ligne de N blocs
Nom_Mat = [Mat 1, Mat 2, …, Mat N] où les matrices
Mat 1, Mat 2, …, Mat N ont le même nombre de lignes
– Vecteur bloc colonne de M blocs
Nom_Mat = [Mat 1; Mat 2; …; Mat N] où les matrices
Mat 1, Mat 2, …, Mat M ont le même nombre de colonnes
– Matrices bloc de NxM blocs
Nom_Mat = [Bloc_Lig 1; Bloc_Lig 2; …; Bloc_Lig N]
Nom_Mat = [Bloc_Col 1, Bloc_Col 2, …, Bloc_Col M]
les matrices Bloc_Lig i sont les vecteurs bloc ligne de M
blocs
les matrices Bloc_Col i sont les vecteurs bloc colonne de
N blocs
– Matrices bloc de NxM blocs égaux à la matrice A
Nom_Mat = repmat(A,N,M)

• Matrices définies par blocs (exemples)































19
20
21
22
23
24
25
26
27
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
0
0
4
4
4
1
0
0
0
0
0
4
4
4
0
2
0
0
0
0
4
4
4
0
0
3
10
9
8
1
0
0
1
1
1
7
6
5
0
1
0
1
1
1
4
3
2
0
0
1
1
1
1
1
C































9
8
7
9
8
7
6
5
4
6
5
4
3
2
1
3
2
1
9
8
7
9
8
7
6
5
4
6
5
4
3
2
1
3
2
1
9
8
7
9
8
7
6
5
4
6
5
4
3
2
1
3
2
1
1
C

MATRICES : ACCES AUX ELEMENTS
• A est une variable contenant une Matrice de taille
NxM
– Accès à l’élément situé à la ligne i et à la colonne j: A(i,j)
– D’une manière générale, on a: a = A(Ind_Lig,Ind_Col), où
Ind_Lig est un vecteur d’entier compris entre 1 et N,
Ind_Col est un vecteur d’entier compris entre 1 et M.
– a est une matrice de taille pxq où p est le nombre
d’éléments de Ind_Lig et q le nombre d’éléments de
Ind_Col. a(i,j) = A(Ind_Lig(i),Ind_Col(j)).
– Lorsque A est un vecteur de taille N, on a A(i), A(Ind).
– Modification de la matrice A: A(Ind_Lig,Ind_Col) = a, a est
une matrice pxq.
– A(j) renvoie l’élément j du vecteur obtenu en alignant
successivement les colonnes de la matrice A.
– Exemple: Matrices C1 et C2 précédentes

MATRICES : TAILLE
• A est une variable Matrice
• [n,m] = size(A) : revoie dans la varible n le nombre de
lignes de A et dans m le nombre de colonne de A.
• l = size(A,Ndim): renvoie dans l le nombre de lignes
de A si Ndim=1 et le nombre de colonne si Ndim=2.
• la fonction size marche pour les vecteurs n=1 si
vecteur ligne et m=1 si vecteur colonne.
• Pour les vecteurs, la fonction appropriée est length
• l = length(Vec): renvoie dans l la taille du vecteur
Vect
• m = length(A): renvoie dans m la plus grande valeur
entre le nombre de lignes et le nombre de colonne de
A.
• N = numel(A): renvoie le nombre total d’éléments de
la matrice A

MATRICES : QUELQUES FONCTIONS ET OP.
• Réorganisation des matrices
Fonction Description
Opérateur '
ou fonction
ctranspose
Transposition normale de matrices réelles et
transposition conjuguée de matrices
complexes. Si la matrice ne contient pas de
valeurs complexes, ' a le même effet que .'
Ex: v=(3:5)' renvoie le vecteur colonne [3
; 4 ; 5]
Opérateur .'
ou fonction
transpose
Transposition non conjuguée de matrices
complexes
Ex: m=[1+5i 2+6i ; 3+7i 4+8i],
m.' fournit [1+5i 3+7i ; 2+6i 4+8i], alors que
m' fournit [1-5i 3-7i ; 2-6i 4-8i]

reshape(var,M,N)
Cette fonction de redimensionnement retourne une matrice de M
lignes x N colonnes contenant les éléments de var (qui peut être une
matrice ou un vecteur). Les éléments de var sont lus colonne après
colonne, et la matrice retournée est également remplie colonne après
colonne. Le nombre d'éléments de var doit être égal à MxN, sinon la
fonction retourne une erreur. Ex: reshape([1 2 3 4 5 6 7
8],2,4) et reshape([1 5 ; 2 6 ; 3 7 ; 4 8],2,4)
retournent [1 3 5 7 ; 2 4 6 8]
vec = mat(:)
Déverse la matrice mat colonne après colonne sur le vecteur-
colonne vec. Ex: si m=[1 2 ; 3 4] , alors m(:) retourne le
vecteur-colonne [1 ; 3 ; 2 ; 4]
sort(var
{,mode})
sort(var, d
{,mode})
Fonction de tri par éléments (voir aussi la fonction unique décrite
plus bas). Le mode de tri par défaut est 'ascend' (tri ascendant),
à moins que l'on spécifie 'descend' pour un tri descendant
 si l'on passe le paramètre d=2, trie les éléments à l'intérieur
des lignes (indépendemment les unes des autres)
Ex: si m=[7 4 6;5 6 3], alors sort(m) retourne [5 4 3 ; 7 6
6]
sort(m,'descend') retourne [7 6 6 ; 5 4 3]
et sort(m,2) retourne [4 6 7 ; 3 5 6]

sortrows(mat
{,no_col})
Trie les lignes de la matrice mat dans l'ordre croissant des valeurs de
la première colonne, ou dans l'ordre croissant des valeurs de la
colonne no_col
Ex: en reprenant la matrice m de l'exemple précédent : sortrows(m)
(identique à sortrows(m,1)) et sortrows(m,3) retournent [5 6 3 ; 7
4 6], alors que sortrows(m,2) retourne [7 4 6 ; 5 6 3]
fliplr(mat)
flipud(mat)
Retournement de la matrice mat par symétrie horizontale
(left/right),
respectivement verticale (up/down)
Ex: fliplr([1 2 3 ; 4 5 6]) retourne [3 2 1 ; 6 5 4], et
flipud([1 2 3 ; 4 5 6]) retourne [4 5 6 ; 1 2 3]
rot90(mat {,K})
Effectue une rotation de la matrice mat de K fois 90 degrés dans le
sens inverse des aiguilles d'une montre. Si K est omis, cela équivaut à
K=1
Ex: rot90([1 2 3 ; 4 5 6]) retourne [3 6 ; 2 5 ; 1 4], et rot90([1
2 3 ; 4 5 6],-2) retourne [6 5 4 ; 3 2 1]
flipdim, permute,
ipermute,
tril, triu
Autres fonctions de réorganisation de matrices : Tester sur une
matrice et donner leurs actions

• Calcul matriciel et statistique
norm(vec)
Calcule la norme (longueur) du vecteur vec.
On peut aussipasser à cette fonction une matrice (voir help)
dot(vec1,vec2)
Calcule la produit scalaire des 2 vecteurs vec1 et vec2 (ligne ou
colonne). Equivalent à vec1 * vec2' s'il s'agit de vecteurs-ligne, ou
à vec1' * vec2 s'ils'agit de vecteurs-colonne
On peut aussipasser à cette fonction des matrices (voir help)
cross(vec1,vec2)
Calcule la produit vectoriel (en 3D) des 2 vecteurs vec1 et vec2
(ligne ou colonne, mais qui doivent avoir 3 éléments !).
inv(mat)
Inversion de la matrice carrée mat. Une erreur est produite si la
matrice est singulière (ce qui peut être testé avec la fonction cond qui
est plus approprié que le test du déterminant)
det(mat) Retourne le déterminant de la matrice carrée mat
trace(mat)
Retourne la trace de la matrice mat, c'est-à-dire la somme des
éléments de sa diagonale principale

• .
rank(mat)
Retourne le rang de la matrice mat, c'est-à-dire le nombre de lignes
ou de colonnes linéairement indépendants
min(var{,d}) et
max(var{,d})
Appliquées à un vecteur ligne ou colonne, ces fonctions retournent le
plus petit, resp. le plus grand élément du vecteur. Appliquées à une
matrice var, ces fonctions retournent :
 si le paramètre d est omis ou qu'il vaut 1 : un vecteur ligne
contenant le plus petit, resp. le plus grand élément de chaque
colonne de var
 si le paramètre d vaut 2 : un vecteur colonne contenant le plus
petit, resp. le plus grand élément de chaque ligne de var
 ce paramètre d peut être supérieur à 2 dans le cas de "tableaux
multidimensionnels" (voir plus bas)
sum(var{,d}) et
prod(var{,d})
Appliquée à un vecteur ligne ou colonne, retourne la somme ou le
produit des éléments du vecteur. Appliquée à une matrice var,
retourne un vecteur ligne (ou colonne suivant la valeur de d, voir plus
haut sous min/max) contenant la somme ou le produit des éléments de
chaque colonne (resp. lignes) de var
Ex: prod([2 3;4 3] {,1}) retourne le vecteur ligne [8 9], prod([2
3;4 3],2) retourne le vecteur colonne [6 ; 12] et prod(prod([2 3;4
3])) retourne le scalaire 72

• ,
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 37
cumsum(var{,d})
et
cumprod(var{,d})
Réalise la somme partielle (cumulée) ou le produit partiel (cumulé)
des éléments de var. Retourne une variable de même dimension que
celle passée en argument (vecteur -> vecteur, matrice -> matrice)
Ex: cumprod(1:10) retourne les factorielles de 1 à 10, c-à-d. [1 2 6
24 120 720 5040 40320 362880 3628800]
mean(var{,d})
Appliquée à un vecteur ligne ou colonne, retourne la moyenne
arithmétique des éléments du vecteur. Appliquée à une matrice var,
retourne un vecteur ligne (ou colonne suivant la valeur de d, voir
plus haut sous min/max) contenant la moyenne arithmétique des
éléments de chaque colonne (resp. lignes) de var.
std(var{,f{,d}})
Appliquée à un vecteur ligne ou colonne, retourne l'écart-type des
éléments du vecteur. Appliquée à une matrice var, retourne un
vecteur ligne (ou colonne suivant la valeur de d, voir plus haut sous
min/max) contenant l'écart-type des éléments de chaque colonne
(resp. lignes) de var.
Attention : si le flag "f" est omis ou qu'il vaut "0", l'écart-type est
calculé en normalisant par rapport à "n-1" (où n est le nombre de
valeurs) ; s'il vaut "1" on normalise par rapport à "n"

median(var{,d}) Calcule la médiane
cov Retourne vecteur ou matrice de covariance
eig, eigs, svd, svds, cond,
condeig...
Fonctions en relation avec vecteurs propres et valeurs
propres
lu, chol, qr,
schur, svd,…
Fonctions en relation avec les méthodes de
décomposition/factorisation de type :
- LU, Cholesky, QR, Schur, valeurs singulières,

TABLEAUX MULTIDIMENSIONNELS
• Généralise la notion de matrice
• Peuvent être générer par indexation
• Un tableau à M dimensions peut être vue comme
un tableau à M1 dimensions de tableaux à M2
dimensions avec M=M1+M2.
• Ex:
C=ones(2,3,3) génère un tableau 3D de dimension 2x3x3
dont tous les éléments sont mis à la valeur 1
D=zeros(2,3,3) génère un tableau 3D de dimension
2x3x3 dont tous les éléments sont mis à la valeur 0
E=rand(2,3,3) génère un tableau 3D de dimension 2x3x3
dont les éléments auront une valeur aléatoire
comprise entre 0 et 1

1. GENERALITES

OPERATIONS SOUS MATLAB
• Composées d’opérateurs et d’opérandes
• Les opérandes sont des variables et/ou des
constantes de types compatibles
• Parmi les opérateurs, on distingue:
– Les opérateurs arithmétiques
– Les opérateurs logiques
– Les opérateurs de comparaison
– Les appels de fonctions

OPERATIONS SOUS MATLAB

1. GENERALITES

Instructions conditionnelles
• Condition simple
if expression logique
Suite d’instructions
end

• Alternative simple
if Expression logique1
Suite d’instructions 1
else
end

• Alternative Multiple
if Expression logique1
elseif Expression logique 2
…
else
Suite d’instructions N
end

• Choix Multiple
switch switch_Var
case val
Instructions
case {val1,val2,val3,…}
Instructions
…
otherwise
Instructions
end

Boucles
• Boucle for
for index = Ind_deb:pas:Ind_fin
end

Boucles
• Boucle while
while Expression logique
end
Exemple: Ecrire une fonction Matlab
permettant de générer les matrices de
Hilbert Hij=1/(i+j-1)

M-files : Scripts
et fonctions

M-file: Définition
• Un m-file est un fichier texte d’extension .m
contenant des commandes matlab.
• Remarque: Dans les m-file, les lignes de
commentaire sont précédées par le caractère %
• On distingue deux types de m-files:
– Les scripts
– Les fonctions

Script Matlab
• Un script matlab est un m-file contenant une suite
de commandes matlab destinées à être exécutées.
• L’exécution du script s’effectue en en le chargeant
dans la fenêtre de commande (on indique le chemin
d’accès de celui-ci)
• Les scripts sont conçus dans l’éditeur de matlab.
• Les variables déclarées dans un script sont
conservées en mémoire après son exécution.
• Exemple: Ecrire un script matlab qui étant donnée
deux vecteurs calcul leur produit scalaire.

function Matlab
• Une fonction matlab est un script qui commence
par une entête, dont la syntaxe est:
function [liste paramètres de sortie] =
Nom_fonction (liste paramètres d’appel)
• Ces paramètres sont séparés par des virgules. Il
peut arriver que ces listes soient vides.
• Il est vivement recommandé de sauvegarder la
fonction matlab sous: Nom_fonction.m.
• Les variables déclarées à l’intérieur d’une
fonction matlab sont locales à la fonction.

function Matlab (suite)
• On peut définir à l’intérieur d’une fonction matlab des
fonctions secondaires qui sont appelées par la fonction
principale et/ou s’appellent entre elles. La syntaxe est
identique à celle d’une fonction.
function [liste paramètres de sortie] =
Nom_fonction_k (liste paramètres d’appel)
• Une fonction secondaire se termine par le mot clé
return.
• La portée des fonctions secondaires est interne à la
fonction principale.
• Exemple: écrire une fonction matlab permettant de
calculer le factoriel d’un entier strictement positif.

1. GENERALITES
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 55

Graphiques sous Matlab
• Matlab dispose d’une bibliothèque assez
fournie de fonctions graphiques en 2D et 3D
• Le tracé des courbes sous Matlab procède
généralement en trois étapes:
– La discrétisation du domaine de représentation;
– L’évaluation de la fonction à tracer en chaque
point du domaine discret
– L’exécution d’une commande graphique en
utilisant les données précédentes.
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 56

Graphique 2D
• La commande plot:
• plot(x,y): Tracer le vecteur y en fonction
du vecteur x
• plot(t,x,t,y,t,z) : Tracer x(t), y(t) et
z(t) sur le même graphique
• plot(x,y,‘ctm') : Tracer y(x) en couleur
m avec le trait de type t et le marqueur m
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 57

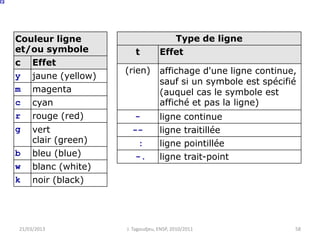
Couleur ligne
et/ou symbole
c Effet
y jaune (yellow)
m magenta
c cyan
r rouge (red)
g vert
clair (green)
b bleu (blue)
w blanc (white)
k noir (black)
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 58
Type de ligne
t Effet
(rien) affichage d'une ligne continue,
sauf si un symbole est spécifié
(auquel cas le symbole est
affiché et pas la ligne)
- ligne continue
-- ligne traitillée
: ligne pointillée
-. ligne trait-point

Marqueur
m Effet
(rien) pas de symbole
o cercle
* étoile de type astérisque
+ signe plus
x croix oblique (signe fois)
. (point) petit disque rempli
^ < > v triangle (orienté selon symbole)
s carré vide (square)
d losange vide (diamond)
p étoile à 5 branches (pentagram)
h étoile à 6 branches (hexagram)
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 59

Ajout de texte sur un graphique
• Pour améliorer la lisibilité d’un graphique, on peut
utiliser les commandes suivantes:
• title(‘titre du graphique’) : pour ajouter
un titre au graphique;
• xlabel(‘label de l’axe des
abscisses’) : labéliser l’axe des abscisses;
• ylabel(‘label de l’axe des
ordonnées’) : labéliser l’axe des ordonnées;
• legend(‘courbe 1’,’courbe 2’) : pour
ajouter une légende à la figure;
• text(a,b,’texte’) : pour ajouter un texte à
partir de du point (a,b)
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 60

x = linspace(0,30,200);
y1 = sin(x)./exp(x/10);
y2 = 1.5*sin(2*x)./exp(x/10);
plot(x,y1,x,y2);
xlabel('Duree [ms]');
ylabel('Amplitude[mm]');
title('Comparaison amortisseurs');
legend('amortisseur 1','amortisseur 2',4);
text(6,1,'Experience A', ...
'FontSize',14,'Rotation',-20, ...
'Color','red');
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 61

• Afficher plusieurs courbes sur un graphique: commandes
hold on et hold off: plot(x1,y1); hold
on; plot(x2,y2); plot(x3,y3);
fplot(‘fun’,[a,b]); hold off
• Créer une nouvelle fenêtre graphique: figure(n)
% n désigne le numéro de la fenêtre
• Créer plusieurs graphiques dans une même fenêtre
graphique
• subplot(m,n,i) :
– m nombre de sous fenêtre verticalement;
– n nombre de sous fenêtre horizontalement;
– i position du graphique à représenter, comptée de
gauche à droite et de haut en bas
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 62

Exemple
subplot(2,3,1); fplot(‘sin’,[pi,10*pi]);
title(‘Sinus’);
subplot(2,3,2); fplot(‘cos’,[pi,10*pi]);
title(‘Cosinus’);
subplot(2,3,3); fplot(‘sin(x)/x’,[pi,10*pi]);
title(‘Oscillations amorties 1’);
subplot(2,3,4); fplot(‘cos(x)/x’,[pi,10*pi]);
subplot(2,3,5);
fplot(‘sin(x)/(x*x)’,[pi,10*pi]);
subplot(2,3,6); fplot(‘cos(x)/x^3’,[pi,10*pi]);
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 63

Autres formes de graphiques 2D
• semilogx(f,A) : Tracer A(f) avec échelle
log(f)
• semilogy(w,B) : Tracer B(w) avec échelle
log(B)
• polar(theta,r): Tracer r(theta) en
coordonnées polaires
• bar(x,y) : Tracer y(x) sous forme des barres;
• fplot(‘Nom_fonction’, [a,b]):
permet de représenter la fonction Nom_fonction
sur l’intervalle [a,b] .
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 64

Graphique 3D
• Tracer les lignes de niveau d’une fonction de 2
variables f(x,y):
• contour(X,Y,Z) :
• X,Y,Z sont des matrices de même taille telles que
Z(i,j)=f(X(i,j),Y(i,j));
• contour(X,Y,Z,n) : permet de tracer n
lignes de niveau
• [C,h]=contour(X,Y,Z);
clabel(C,h): permet d’afficher les valeurs
des lignes de niveau
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 65

Graphique 3D
• Tracer la surface d’équation z= f(x,y):
• mesh(X,Y,Z) :
• X,Y,Z sont des matrices de même taille telles que
Z(i,j)=f(X(i,j),Y(i,j));
• meshc(X,Y,Z,n) : trace les lignes de
niveau sous la courbe dans le plan z=zmin;
• meshz(X,Y,Z): permet de tracer une boîte
en dessous de la surface
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 66

Graphique 3D
• Courbe paramétrée en 3D:
• plot3(x,y,z) :
• x=x(t); y=y(t) ,z=z(t);
• Surface paramétrée:
• surf(X,Y,Z):
• x=f1(u,v); y=f2(u,v); z=f3(u,v)
21/03/2013 J. Tagoudjeu, ENSP, 2010/2011 67

INTRODUCTION MATLAB pour bon démarrage.pdf

Contenu connexe

Similaire à INTRODUCTION MATLAB pour bon démarrage.pdf

Dernier

INTRODUCTION MATLAB pour bon démarrage.pdf