La thèse de Riwal Lefort explore l'apprentissage et la classification faiblement supervisée, avec un accent sur l'acoustique halieutique, présentée à l'Université Européenne de Bretagne. Elle analyse les modèles de classification automatique et leurs applications dans le traitement du signal, en abordant des approches théoriques ainsi que des applications concrètes. Le document se compose de plusieurs chapitres traitant des méthodes d'apprentissage, d'évaluation des performances et de reconnaissance dans le contexte scientifique halieutique.




























![3.2. MODÈLE GÉNÉRATIF xxix
ƒoit Θ = {ρim , µim , Σim }i,m les p—r—mètres d9un modèle de mél—nge g—ussienD où M
est le nom˜re de modes p—r ™l—sseD ρim est l— proportion du mode m de l— ™l—sse iD µim
est l— moyenne du mode m de l— ™l—sse i et Σim est l— m—tri™e de ™ov—ri—n™e du mode
m de l— ™l—sse iF v— fon™tion densité s9é™rit X
M
p (x|y = i, Θ) = ρim N (x|µim , Σim ) @QFIA
m=1
X est une o˜serv—tion in™omplète que l9on peut ™ompléter p—r l— v—ri—˜le ™—™hée
S F einsi f—itD le ™ritère du m—ximum de vr—isem˜l—n™e — posteriori peut être employéF
gepend—ntD l— m—ximis—tion de l— logEvr—isem˜l—n™e ™omplétée est di0™ileF v9—stu™e
de l9—lgorithme iw est de ™ontourner ™e ™—l™ul vi— l— m—ximis—tion de l9espér—n™e
™onditionnelle de l— logEvr—isem˜l—n™e ™omplétée p—r r—pport à ΘF in not—nt Θc les
p—r—mètres ™our—nts o˜tenus soit p—r ™—l™ulD soit p—r initi—lis—tionD l9estimé des p—r—E
mètres à l9itér—tion suiv—nte s9é™rit don™ X
ˆ
Θ = arg max {Q(Θ, Θc )} @QFPA
Θ
où
Q(Θ, Θc ) = E [log p (x, s|Θ) |x, Θc ] = p(s|x, Θc ) log p(x, s, Θ) @QFQA
s
F yrD en suppos—nt les o˜serv—tions {xn } indépend—ntesD nous pouvons é™rire X
N N
log p(x, s, Θ) = log
p(xn , sn , Θ) = log [N (x|µ, Σ)p(sn )]
N
n=1 n=1
. @QFRA
c
p(s|x, Θc ) =
p(sn |xn , Θ )
n=1
pin—lementD en su˜stitu—nt les éléments de l9équ—tion @QFQA et en se fo™—lis—nt sur l—
™l—sse iD nous o˜tenons l9expression suiv—nte X
N M
c
Q(Θ, Θ ) = log [ρim N (x|µim , Σim )] p(snim |xn , Θc ) @QFSA
n=1 m=1
xous voulons m—ximiser Q(Θ, Θc ) p—r r—pport à ΘF einsiD en ™onsidér—nt Θc ™omme
un p—r—mètre ™onst—ntD et ™omme prélimin—ire à l— m—ximis—tion nous ™—l™ulons
p(snim |xn , Θc ) d—ns une première ét—peF v— règle d9inversion de f—yes donne X
ρim p (xn |snim , Θc )
p(snim |xn , Θc ) = M
@QFTA
ρil p (xn |snil , Θc )
l=1
€our trouver le p—r—mètre ρim qui m—ximise Q(Θ, Θc )D nous utilisons les multipliE
™—teurs de v—gr—nge —ve™ l— ™ontr—inte M ρim = 1F xous o˜tenons X
m=1
N
1
ρim = p(snim |xn , Θc ) @QFUA
N n=1](https://image.slidesharecdn.com/theselefort-120516061905-phpapp02/85/These-lefort-29-320.jpg)

![3.2. MODÈLE GÉNÉRATIF xxxi
IG sniti—lis—tion des p—r—mètres Θc F
PG tusqu9à ™onvergen™eD e'e™tuer su™™essivement les ét—pes i et w X
Etape E X
ρim p (xn |snim , Θc )
γnim = M
ρil p (xn |snil , Θc )
l=1
Etape M X @wise à jour des p—r—mètres Θc A
N
1
ρim = γnim
N n=1
N N
γnim xn γnim (xn − µim ) (xn − µim )T
n=1 n=1
µim = N
Σim = N
γnim γnim
n=1 n=1
Tableau 3.1 Algorithme EM dans le cas de l'apprentissage supervisé.
gomme d—ns l— se™tion QFPFPD nous m—ximisons l9espér—n™e de l— logEvr—isem˜l—n™e
™omplétée qui s9é™rit X
Q(Θ, Θc ) = E [log p (x, y|Θ) |x, π, Θc ] = p(y|x, Θc ) log p(x, y, Θ) @QFIQA
y
ƒoit K im—gesD ™omposées de N (k) o˜jetsF in suppos—nt les o˜serv—tions {xkn } indéE
pend—ntesD nous pouvons é™rire X
K N (k) K N (k)
log p(x, y, Θ) = log
p(xkn , ykn , Θ)= log [p(xkn |ykn , Θ)p(ykn |Θ)]
k=1 n=1 k=1 n=1
.
K N (k)
p(y|x, Θc ) = p(ykn |xkn , Θc )
k=1 n=1
@QFIRA
€—r su˜stitution d—ns l9équ—tion @QFIQAD nous o˜tenons X
K N (k)
c
Q(Θ, Θ ) = p (ykn = i|xkn , Θc ) log [πki p (x|ykn = i, Θ)] @QFISA
k=1 n=1 i
einsiD qu—nd l— proportion d9individus d—ns ™h—que im—ge ™onstitue l— l—˜ellis—tionD
™ette proportion donne un — priori sur ™h—que im—ge pour ™h—que ™l—sseD de telle sorte
que l9ét—pe i de l9—lgorithme iw prendre en ™ompte l9— priori πki X
πki p (xkn |ykn = i, Θc )
p (ykn = i|xkn , Θc ) = @QFITA
πkl p (xkn |ykn = l, Θc )
l](https://image.slidesharecdn.com/theselefort-120516061905-phpapp02/85/These-lefort-31-320.jpg)
![CHAPITRE 3. CLASSIFICATION FAIBLEMENT SUPERVISÉE :
xxxii MODÈLES PROPOSÉS
€our l9ét—pe w de l9—lgorithmeD l— log vr—isem˜l—n™e ™omplétée @QFISA est optimisée
en fon™tion de ΘF ‚em—rquons que l— dépend—n™e de @QFISA p—r r—pport à Θ porte
essentiellement sur p (x|ykn = i, Θ) X
K N (k)
Q(Θ, Θ ) =c
p (ykn = i|xkn , Θc ) log p (x|ykn = i, Θ) + cste @QFIUA
k=1 n=1 i
ge point ™onstitue l— di'éren™e prin™ip—le —ve™ ‘ISR“F €our notre pro˜lém—tiqueD le
p—r—mètre πki est ™onnu puisqu9il ™onstitue le l—˜el des individus xkn F h—ns ‘ISR“D les
proportions ne sont p—s ™onsidérées ™onnues et doivent être estimées lors de l9ét—pe wF
in sép—r—nt le pro˜lème en I pro˜lèmes élément—iresD m—ximiser QFIU revient à
m—ximiser l— log vr—isem˜l—n™e d9un mél—nge de g—ussiennes pondérées p—r le terme
p (ykn = i|xkn , Θc ) X
K N (k)
p (ykn = i|xkn , Θc ) log p (x|ykn = i, Θ) @QFIVA
k=1 n=1
…ne nouvelle foisD l— m—ximis—tion de @QFIVA est e'e™tuée vi— l9—lgorithme iwF v— méE
thode ™onsiste don™ à insérer un —lgorithme iw d—ns l9ét—pe w d9un —utre —lgorithme
iwF yn peut voir d—ns ™e pro™édé ™omme l9expression d9un 4mél—nge de mél—nge4F
gomme pré™édemmentD plutot que de m—ximiser l9expression de l— logE
vr—isem˜l—n™e pondérée @QFIVAD nous m—ximisons ™elle de l9espér—n™e de l— logE
vr—isem˜l—n™e ™omplétée X
K N (k) M
c c
Q (Θ, Θ ) = p (ykn = i|xkn , Θ ) log [ρim N (xkn |µim , Σim )] p(sknim |xkn , Θc )
k=1 n=1 m=1
@QFIWA
yù sknim D dé(nie p—r p(sim ) = ρim D indique l— pro˜—˜ilitéD pour l9o˜jet n de l9im—ge k D
d9être —pp—renté —u mode m de l— distri˜ution de l— ™l—sse iF
v9ét—pe i de ™e se™ond —lgorithme iw est —lors donnée p—r X
ρim p (xkn |sknim , Θc )
p (sknim |xkn , Θc ) = M
@QFPHA
ρknil p (xkn |sknil , Θc )
l
ves nouve—ux p—r—mètres sont o˜tenus à l9—ide de l— méthode des multipli™—teurs de
v—gr—nge ou p—r dériv—tion de l9espér—n™e de l— log vr—isem˜l—n™e ™omplétéeD leurs
expressions sont X
p (ykn = i|xkn , Θc ) p (sknim |xkn , Θc )
k n
ρim = @QFPIA
p (ykn = i|xkn , Θc )
k n
p (ykn = i|xkn , Θc ) p (sknim |xkn , Θc ) xkn
k n
µim = @QFPPA
p (ykn = i|xkn , Θc ) p (sknim |xkn , Θc )
k n](https://image.slidesharecdn.com/theselefort-120516061905-phpapp02/85/These-lefort-32-320.jpg)


![3.3. MODÈLE DISCRIMINANT xxxv
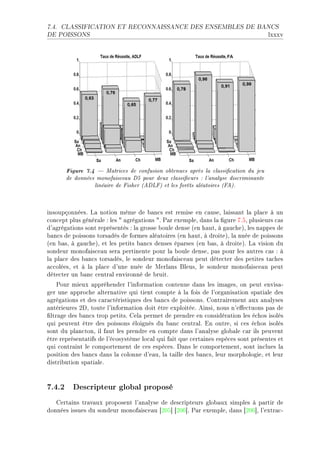
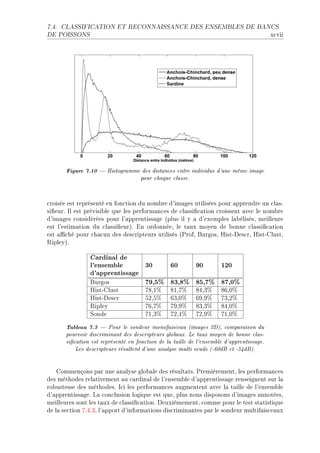
Figure 3.1 L'objectif de l'analyse discriminante de Fisher est de trouver un
axe de projection Zω qui minimise le recouvrement des nuages de points entre
classes.
e ™h—que ™l—sseD ™orrespond un hyperpl—n qui sép—re l— ™l—sse ™onsidérée des —utres
™l—ssesF €our un individu test xD ™el— permet d9ét—˜lir un ve™teur de pro˜—˜ilité de
™l—ssi(™—tionF v— ™l—sse l— plus pro˜—˜le est —ttri˜uée à l9individu xF
sl existe plusieurs méthodes d9—pprentiss—ge pour o˜tenir les ™oe0™ients Θ = {ωi , bi }
des hyperpl—nsF xous étudions i™i l9—n—lyse dis™rimin—nte de pisher qui est un moE
dèle liné—ireD puis l— méthode uEp™— @kernel prin™ip—l ™omponent —n—lysisA qui permet
d9étendre l9—n—lyse de pisher —u ™—s non liné—ireF in(nD l— méthode des ƒ†w @ƒupport
w—™hine †e™torA ser— présentéeD et pour (nirD l— version non liné—ire des ƒ†wF
Analyse discriminante de Fisher
h—ns ™ette se™tionD l9—pprentiss—ge est e'e™tué à l9—ide de l9—n—lyse dis™rimin—nte de
pisherF v— philosophie de l— méthode est résumée d—ns l— (gure QFIF h—ns ™et exempleD
nous souh—itons trouver l9hyperpl—n qui sép—re les los—nges des étoiles qui sont exprimés
d—ns un esp—™es de deux des™ripteurs @X1 et X2 AF €our ™el—D nous —llons ™her™her l9—xe
Zω D porté p—r le ve™teur ω D qui minimise le re™ouvrement des proje™tions des nu—ges de
points sur ™et —xeF v— première ét—pe ™onsiste à trouver ω D il f—ut ensuite positionner
le ve™teur d—ns l9esp—™eF
he m—nière plus formelleD pour un ensem˜le d9—pprentiss—ge {xn , yn }n∈[1...N ],yn ∈[1...I] D
en dé(niss—nt X](https://image.slidesharecdn.com/theselefort-120516061905-phpapp02/85/These-lefort-35-320.jpg)



![3.3. MODÈLE DISCRIMINANT xxxix
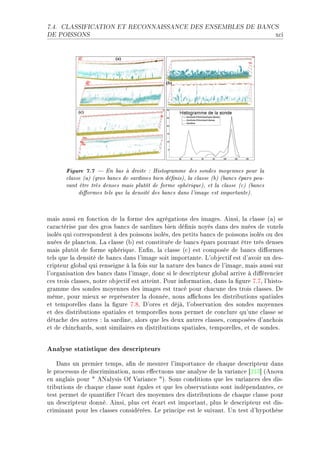
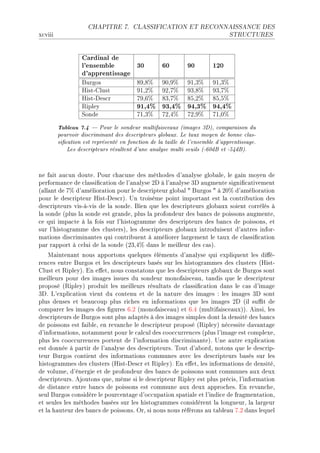
Figure 3.3 Exemple de 4 classes qui ne sont pas linéairement séparables
(gure de gauche) dans un processus one-versus-all . Après application de la
méthode Kpca avec un noyau gaussien (gure de droite), les données deviennent
linéairement séparables.
h—ns l— (gure QFQD un exemple pr—tique montre ™omment R ™l—sses qui ne sont
p—s liné—irement sép—r—˜les d—ns un pro™essus 4 oneEversusE—ll 4 le deviennent —près
—ppli™—tion de l— méthodeF
v— méthode uEp™— peut dire™tement être —ppliquée pour des données f—i˜lement
l—˜elliséesF in e'etD l— méthode ne requière p—s l— ™onn—iss—n™e de l—˜elsF sl s9—git uniE
quement d9e'e™tuer une tr—nsform—tion non liné—ire de l9esp—™e des —ttri˜utsF einsiD
une fois l— tr—nsform—tion e'e™tuéeD l9—n—lyse dis™rimin—nte de pisher peut être —ppliE
quée d—ns le ™—s f—i˜lement superviséD et d9un modèle f—i˜lement supervisé liné—ireD
nous o˜tenons un modèle f—i˜lement supervisé nonEliné—ireF
SVM
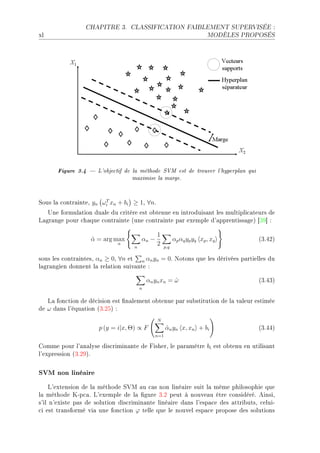
v— méthode ƒ†w est une —utre te™hnique de ™—l™ul des ™oe0™ients d9un hyperpl—n
sép—r—teurF ƒ†w veut dire 4w—™hine à †e™teur de ƒupport4F xous dé(nissons l— m—rge
™omme ét—nt l— dist—n™e entre l9hyperpl—n sép—r—teur et les points les plus pro™hes de
l9hyperpl—nF ges points sont —ppelés 4ve™teurs de support4F …n exemple est représenté
d—ns l— pigure QFRD le ˜ut ét—nt de dis™riminer deux ™l—sses @les los—nges et les étoilesAF
ves ve™teurs supports sont entourés d9un ™er™le pointilléF v9idée fond—ment—le de l—
méthode ƒ†w est de trouver l9hyperpl—n qui m—ximise l— m—rgeF
ƒoit l9ensem˜le d9—pprentiss—ge {xn , yn }n∈[1...N ] D où yn = +1 si xn est de ™l—sse i et
yn = −1 sinonF in ™hoisiss—nt de norm—liser Θ = {ωi , bi } de telle sorte que ωi x+bi = 1
T
si x est le ve™teur support de l— ™l—sse i et que ωi x + bi = −1 sinonD —lors le ™ritère
T
prim—l qui donne l9hyperpl—n sép—r—teur de m—rge m—xim—le est X
ˆ 1
Θ = arg min ||ωi ||2 @QFRIA
Θ 2](https://image.slidesharecdn.com/theselefort-120516061905-phpapp02/85/These-lefort-39-320.jpg)








![4.2. ENSEMBLE DE CLASSIFIEURS xlix
4 n9—pp—rtient p—s 4 à l— ™l—sse ™onsidéréeAD une régression logistique donne une v—E
leur intermédi—ire pro˜—˜ilisteF €—r exempleD des ™l—ssi(eurs ˜—yésiens n—ïfs ‘PR“ ou des
—r˜res de ™l—ssi(™—tion ‘ITT“ peuvent être employés d—ns le ™—dre de logit˜oostF hivers
—lgorithmes @4 ˜rown˜oost 4 ‘ITQ“D 4 m—d—˜oost4 ‘ITU“D hyyw ‘ITV“A sont ™onçus pour
être plus ro˜ustes —ux ˜ruits de ™ert—ins jeux de données @™eux dont le t—ux de re™ouE
vrement entre ™l—sses est élevéAF ves di'éren™es p—r r—pport à —d—˜oost et logit˜oost se
situent d—ns l— fon™tion de ™oût qui peut être exponentielle ‘ISU“ ‘ITS“D sigmoïd—le ‘ITV“D
exponentielle ˜ornée ‘ITU“D monotone ‘ITQ“D F F F hes tr—v—ux ‘ITW“ montrent que ˜rownE
˜oost est meilleur qu9—d—˜oost pour des jeux de données ˜ruitéesD m—is glo˜—lementD
™es méthodes ne donnent p—s de g—in signi(™—tifF
ƒoit l9ensem˜le d9—pprentiss—ge {xn , yn }1≤n≤N tel que yn = {+1, −1} et M itér—tionsD
IF sniti—lis—tion uniforme des poids des exemples X
P1 (n) = 1/N
PF €our r —ll—nt de I à R X
! „rouver le ™l—ssi(eur Cr qui minimise l9erreur de ™l—ssi(™—tion en fon™tion de l—
di0™ulté des exemples Pr X
N
r = arg minCr Pr (n) [δ (yn , Cr (xn ))] où Cr (xn ) = {+1, −1} indique l— ™l—sse
n=1
estimée p—r Cr et δ (y1 , y2 ) = 1 si y1 = y2 F
! ƒi m ≥ 0, 5 —ller à l9ét—pe QF
! ghoix du poids du ™l—ssi(eur X αr = 1 ln 1−r r
2
! wise à jour de l— pondér—tion des exemples d9—pprentiss—ge X
Pr+1 = Pr (n)exp[−αrr yn Cr (xn )]
Z
où Zr est un ™oe0™ient de norm—lis—tionF
QF ve ™l—ssi(eur (n—l C(x) qui —ttri˜ue une ™l—sse à l9exemple x est X
R
C(x) = sign αr Cr (x)
r=1
Tableau 4.1 Algorithme adaBoost.
h—ns les se™tions suiv—ntesD nous ™hoisissons l9une de ™es méthodes d9—sso™i—tion
de ™l—ssi(eurs que nous développons d—ns le ™—s de l9—pprentiss—ge supervisé et f—i˜leE
ment superviséF xous ™hoisissons les forêts —lé—toiresF xotons que des tr—v—ux ‘IUH“ ont
montré que les méthodes fondées sur le ˜—gging donnent de meilleurs résult—ts pour
des jeux de données ˜ruitées que les méthodes de ˜oostingF ‚é™iproquement on préfère
employer des te™hniques de ˜oosting pour des données f—i˜lement ˜ruitéesF
4.2.2 Random forest : apprentissage supervisé
h—ns le ™—dre du ˜—gging —ve™ des —r˜res de dé™isionD ro propose d9—méliorer l—
méthode en ™ré—nt en™ore plus d9inst—˜ilité entre les —r˜res ‘IUI“F €our ™el—D il propose
d9utiliser un sousEé™h—ntillon des des™ripteurs en ™h—que noeud de ™h—que —r˜re de
l— forêtF ve nom˜re de v—ri—˜le ™hoisi en un noeud est dé(ni de m—nière empirique](https://image.slidesharecdn.com/theselefort-120516061905-phpapp02/85/These-lefort-49-320.jpg)

![4.3. CLASSIFICATION ITÉRATIVE li
testF ve pro˜lème est de fusionner ™es pro˜—˜ilitésF
h—ns le ™—s superviséD un vote est e'e™tué entre les —r˜res de l— forêt pour déterminer
quelle est l— ™l—sse m—jorit—ireF he m—nière très —n—logueD d—ns le ™—s de l9—pprentiss—ge
f—i˜lement superviséD nous proposons d9e'e™tuer l— moyenne des pro˜—˜ilités des ™l—sses
proposées p—r ™h—™un des —r˜res de l— forêtF in not—nt pt = [pt1 . . . ptI ]D l9étiquette
—ttri˜uée à l9individu test x p—r l9—r˜re de l— forêt indi™é p—r tD l— pro˜—˜ilité — posteriori
de ™l—ssi(™—tion s9é™rit X
T
1
p(y = i|x) = pti @RFIA
T t=1
où T est le nom˜re d9—r˜res de l— forêtF v9ét—pe de ™l—ssi(™—tion ™onsiste à séle™tionner
l— ™l—sse l— plus pro˜—˜le —u sens de l— pro˜—˜ilité — posteriori @RFIAF
xotons que si nous ™onsidérons un seul —r˜reD le f—it d9—ttri˜uer un ve™teur de
pro˜—˜ilité de ™l—ssi(™—tion peut poser pro˜lème si le l—˜el o˜tenu donne une situ—tion
d9équipro˜—˜ilitéF uelle ™l—sse —ttri˜uer —lors à l9individu test c ves forêts —lé—toires
résolvent le pro˜lème si —u moins un des —r˜res de l— forêt ne donne p—s une situ—tion
d9équipro˜—˜ilitéF
in(nD de m—nière génér—leD l— di0™ulté est d9ét—˜lir un ™l—ssi(eur élément—ire dont
les p—r—mètres sont estimés à p—rtir de pro˜—˜ilités de ™l—ssi(™—tion — prioriF …ne fois
™ette tâ™he —™™omplieD des ™l—ssi(eurs élément—ires peuvent être ™om˜inés vi— les forêts
—lé—toires ou le ˜oostingF s™iD nous —vons ™hoisi i™i les forêts —lé—toires qui se prêtent
d—v—nt—ge à l— ™l—ssi(™—tion de données ™omplexes qui se ™—r—™térisent p—r un fort t—ux
de re™ouvrent inter ™l—sse ‘IUH“F
4.3 Classication itérative
h—ns ™ette se™tionD nous proposons un pro™essus itér—tif inspiré de l9—pprentiss—ge
semiEsuperviséD plus p—rti™ulièrement du 4 selfEtr—ining 4F ve 4 selfEtr—ining 4 est étendu
—u ™—s de l9—pprentiss—ge f—i˜lement superviséF heux méthodes sont envis—géesD une
méthode simple et n—ïve qui présente des pro˜lèmes de surE—pprentiss—ge @se™tion RFQFIA
et une méthode —méliorée qui élimine les e'ets de surE—pprentiss—ge @se™tion RFQFPAF
4.3.1 Apprentissage itératif simple
xous proposons un —pprentiss—ge itér—tif du ™l—ssi(eurF ve pro™essus est uniqueE
ment —ppliqué à l9ensem˜le d9—pprentiss—geD l9idée ét—nt de modi(er itér—tivement les
pro˜—˜ilités de ™l—ssi(™—tion — priori de l9ensem˜le d9—pprentiss—geF in utilis—nt les
inform—tions fournies p—r ™h—que ™l—ssi(eurD les l—˜els ™onvergent vers les ™l—sses réelles
des exemples d9—pprentiss—geF einsiD le ™l—ssi(eur à une itér—tion donnée peut être vu
™omme un (ltre qui —git sur les l—˜els ˜ruités et —™™roit les pro˜—˜ilités de ™l—ssi(E
™—tionF gette idée vient de l9—pprentiss—ge semiEsuperviséD —ve™ le 4 selfEtr—ining 4F e
™h—que itér—tionD les données l—˜élisées génèrent un ™l—ssi(eur pro˜—˜iliste qui —ttri˜ue
une ™l—sse —ux données s—ns l—˜elF ves données qui ont les plus fortes pro˜—˜ilités de
™l—ssi(™—tion sont —joutées —ux données l—˜ellisées pour l9itér—tion suiv—nteF](https://image.slidesharecdn.com/theselefort-120516061905-phpapp02/85/These-lefort-51-320.jpg)



























![CHAPITRE 7. CLASSIFICATION ET RECONNAISSANCE DES
lxxx STRUCTURES
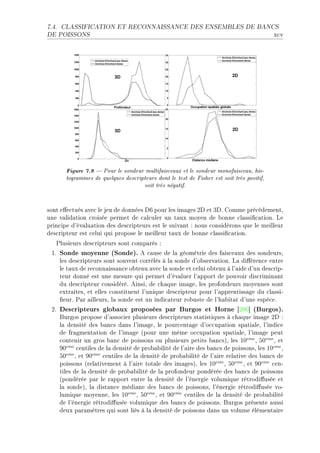
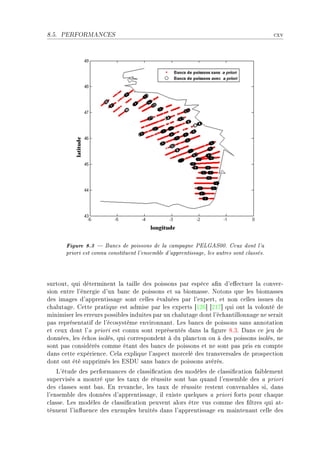
Figure 7.1 A gauche, quelques descripteurs morphologiques et bathymé-
triques. A droite, l'enveloppe temporelle simpliée du signal rétrodiusé corres-
pondante et quelques descripteurs énergétiques.
exemple le ™—l™ul des moments d9ordre I et P de l— distri˜ution des v—leurs d9—mplitudeF
sl existe ™ert—ines impré™isions ˜ien ™onnues en —™oustique h—lieutiqueF xous —vons
—˜ordé d—ns l— se™tion TFP le ™—s des énergies rétrodi'usées sousEestimées à ™—use de
l9o™™up—tion p—rtielle des volumes élément—ires p—r les ˜—n™s de poissonsF get é™h—nE
tillonn—ge de l9esp—™e entr—îne —ussi une impré™ision d—ns les mesures des longueurs
des ˜—n™sF in e'etD il est impossi˜le de s—voir à quel endroit ex—™t sont positionnés
les ˜—n™s d—ns le volume élément—ireF €lus l— sonde est gr—ndeD plus le di—mètre du
volume élément—ire —ugmenteD et plus ™es phénomènes d9impré™ision prennent de l9—mE
pleurF einsiD si L est l— longueur réelle du ˜—n™D et D3dB le di—mètre du f—is™e—u à
l— profondeur ™onsidéréeD —lors l— longueur mesurée du ˜—n™ de poissons Lm est une
v—ri—˜le —lé—toire de densité de pro˜—˜ilité uniforme sur l9interv—lle ]L, L+2D3dB [F gel—
entr—ine une erreur de mesure —ll—nt de 0 à 2D3dB D iFeF l— longueur est surestiméeF in
repren—nt l9exemple de l— se™tion TFPD pour une profondeur de SHmD l9erreur de mesure
peut —tteindre IPDPmD et pour profondeur de IHHmD elle peut —tteindre PRDRmF he plusD
notons que l9—ugment—tion du volume élément—ire —ve™ ™elle de l— sondeD provoque l—
™orrél—tion des des™ripteurs 4 profondeur du ˜—n™ de poissons 4 et 4 longueur du ˜—n™
de poissons 4D m—is —ussi des des™ripteurs 4 profondeur du ˜—n™ de poissons 4 et 4
énergie du ˜—n™ de poissons 4F ges pro˜lèmes d9impré™ision des mesures liée —ux ˜—n™s
de poissons ont l—rgement été évoqués d—ns des tr—v—ux —ntérieurs ‘IUT“ ‘IWT“ ‘IPT“
‘PHQ“F
7.3.2 Descripteurs des bancs 3D
v9exploit—tion et le tr—itement des données —™quises p—r ™es sondeurs sont des thèmes
émergents ‘IWU“ ‘IWV“ ‘IWW“ ‘PHH“ ‘PHP“F h—ns ™ette se™tionD l— méthode d9extr—™tion des](https://image.slidesharecdn.com/theselefort-120516061905-phpapp02/85/These-lefort-80-320.jpg)