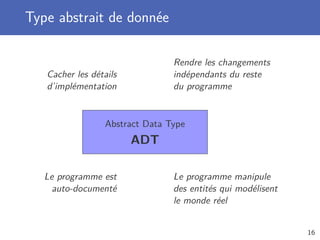
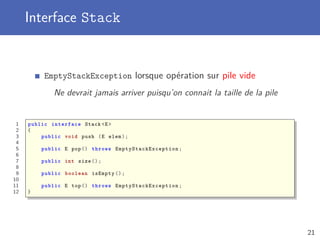
Le document présente les concepts de la programmation orientée objet, en particulier les types abstraits de données (TAD) tels que les piles, files et déques. Il discute également de la complexité temporelle et spatiale des algorithmes, ainsi que de la modélisation par diagrammes UML. Enfin, il fournit des exemples d'implémentation et d'utilisation des TAD en Java.

1. PO3T Programmation orientée objet
Séance 6
Type abstrait
de données
Sébastien Combéfis, Quentin Lurkin mercredi 28 octobre 2015

2. Ce(tte) œuvre est mise à disposition selon les termes de la Licence Creative Commons
Attribution – Pas d’Utilisation Commerciale – Pas de Modification 4.0 International.

3. Rappels
Modélisation d’un logiciel
Le langage de modélisation UML
Aspect statique sur la structure « physique »
Aspect dynamique sur l’exécution du logiciel
Exemples de diagrammes UML
Diagramme de classe
Diagramme d’activité
3

4. Objectifs
Structure de données
Complexité temporelle et spatiale
Type abstrait de données (TAD)
Séquence d’éléments
TAD Queue, Stack et Deque
Structure chainée
4

5. Complexité calculatoire

6. Temps d’exécution
Évaluer le temps d’exécution d’un algorithme
Comme une fonction de la taille de ses entrées
Plusieurs méthodes possibles
Étude expérimentale en mesurant le temps d’exécution
Compter le nombre d’opérations primitives
Analyse asymptotique en fournissant des bornes
6

7. Somme d’entiers
Somme des n premiers nombres entiers positifs
La taille du problème est représentée par n
Algorithme pour résoudre le problème exprimé en pseudo-code
Permet une analyse indépendante du langage de programmation
1 Input : n, un entier strictement positif
2 Output : la somme des n premiers entiers positifs (n compris) est
renvoyée
3
4 sum ← 0
5 for (i ← 1 to n)
6 {
7 sum ← sum + i
8 }
9 return sum
7

8. Opération primitive
Compte du nombre d’opérations primitives
En considérant l’affectation sum ← sum + i comme une opération
Algorithme de complexité temporelle linéaire
0 1 2 3 4 5
0
1
2
3
4
5
n
Nombred’opérationsélémentaires
8

9. Variante en temps constant
Exploitation de la propriété
n
i=1
i =
n(n + 1)
2
1 Input : n, un entier strictement positif
2 Output : la somme des n premiers entiers positifs (n compris) est
renvoyée
3
4 return n(n + 1)/2
0 1 2 3 4 5
0
1
2
3
4
5
n
Nombred’opérationsélémentaires
9

10. Recherche d’un élément dans un tableau
Algorithme qui cherche un élément donné dans un tableau
La taille du problème est n, la taille du tableau
1 Input : tab, un tableau d’entiers
2 n, entier positif , taille du tableau tab
3 value, un entier
4 Output : true si value est un des éléments du tableau tab, et false
sinon
5
6 for (i ← 0 to n − 1)
7 {
8 if (tab[i] = value)
9 {
10 return true;
11 }
12 }
13 return false
10

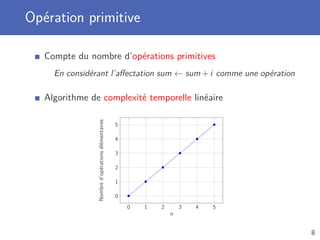
11. Analyse expérimentale (1)
Expérience avec le même tableau
Le nombre d’opérations primitives n’est pas le même
Trois situations possibles, complexité...
...dans le meilleur des cas
...dans le pire des cas
...moyenne
tab value Opérations primitives
[8, 2, 3, −1, 0] 8 1
[8, 2, 3, −1, 0] −1 4
[8, 2, 3, −1, 0] 99 5
11

12. Analyse expérimentale (2)
Nombres d’opérations primitives pour différents tests
Apparition du pire cas et du meilleur cas
0 1 2 3 4 5
0
1
2
3
4
5
n
Nombred’opérationsélémentaires
Meilleur des cas
Pire des cas
Cas moyen
12

13. Notation Big-Oh
Notation big-Oh pour une borne supérieure de la complexité
Pour les valeurs de n plus grande qu’un certain seuil n0
Notation Type
O(1) constante
O(log n) logarithmique
O(n) linéaire
O(n log n) quasi-linéaire
O(n2) quadratique
O(n3) cubique
O(np) polynomiale
O(nlog n) quasi-polynomiale
O(2n) exponentielle
O(n!) factorielle 0 2 4 6 8 10
0
10
20
30
40
50
60
n
Nombred’opérationsélémentaires
O(2n)
O(n2)
O(n log(n))
O(n)
O(log(n))
O(1)
13

14. Complexité temporelle et spatiale
Complexité temporelle
Borne supérieure sur le nombre d’opérations primitives
En fonction de la taille du problème
Complexité spatiale
Borne supérieure sur l’espace mémoire utilisé
En fonction du nombre d’éléments stockés
14

15. Type abstrait
de données

16. Type abstrait de donnée
Abstract Data Type
ADT
Cacher les détails
d’implémentation
Rendre les changements
indépendants du reste
du programme
Le programme est
auto-documenté
Le programme manipule
des entités qui modélisent
le monde réel
16

17. Caractérisation
Choix d’un nom pour le TAD
Noms usuels connus comme pile, file...
Définition des opérations du TAD à l’aide d’une interface
Opérations permettant d’interroger et manipuler les données
Choix d’implémentation de l’interface
Définit les complexités temporelle et spatiale
17

18. Pile

19. TAD Pile (1)
Une pile est une séquence d’éléments (stack)
Éléments empilés les uns sur les autres
Séquence suit le principe LIFO
Last-In First-Out, dernier élément ajouté sera premier à sortir
0 1 2 3 4
pop
push
haut
de pile
19

20. TAD Pile (2)
Méthodes spécifiques au TAD pile
push(e) ajoute l’élément e sur la pile
pop() retire l’élément en haut de pile (erreur si vide)
Méthodes additionnelles
size() renvoie la taille de la pile
isEmpty() teste si la pile est vide
top() renvoie l’élément en haut de pile (erreur si vide)
20

21. Interface Stack
EmptyStackException lorsque opération sur pile vide
Ne devrait jamais arriver puisqu’on connait la taille de la pile
1 public interface Stack <E>
2 {
3 public void push (E elem);
4
5 public E pop() throws EmptyStackException ;
6
7 public int size ();
8
9 public boolean isEmpty ();
10
11 public E top() throws EmptyStackException ;
12 }
21

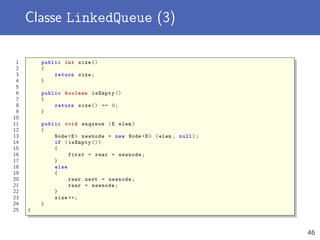
22. Classe ArrayStack (1)
1 public class ArrayStack <E> implements Stack <E>
2 {
3 private final int capacity;
4 private final E[] data;
5 private int top;
6
7 @SuppressWarnings ("unchecked")
8 public ArrayStack ()
9 {
10 capacity = 100;
11 data = (E[]) new Object[capacity ];
12 top = -1;
13 }
14
15 public int size ()
16 {
17 return top + 1;
18 }
19
20 public boolean isEmpty ()
21 {
22 return size () == 0;
23 }
22

23. Classe ArrayStack (2)
1 public void push (E elem) throws FullStackException
2 {
3 if (size () == capacity)
4 {
5 throw new FullStackException ();
6 }
7 data [++ top] = elem;
8 }
9
10 public E pop() throws EmptyStackException
11 {
12 if (isEmpty ())
13 {
14 throw new EmptyStackException ();
15 }
16 E elem = data[top];
17 data[top --] = null;
18 return elem;
19 }
20
21 public E top() throws EmptyStackException
22 {
23 if (isEmpty ())
24 {
25 throw new EmptyStackException ();
26 }
27 return data[top];
28 }
29 }
23

24. Complexité de ArrayStack
Complexité temporelle des opérations
Méthode Complexité
size O(1)
isEmpty O(1)
top O(1)
push O(1)
pop O(1)
Complexité spatiale en O(n)
En notant bien qu’il y a une capacité maximale fixée
24

25. File

26. TAD File (1)
Une file est une séquence d’éléments (queue)
Éléments ajoutés les uns derrière les autres
Séquence suit le principe FIFO
First-In First-Out, premier élément ajouté sera premier à sortir
0 1 2 3 4
dequeue enqueue
queue
de file
tête
de file
26

27. TAD File (2)
Méthodes spécifiques au TAD file
enqueue(e) ajoute l’élément e dans la file
dequeue() retire l’élément en début de file (erreur si vide)
Méthodes additionnelles
size() renvoie la taille de la file
isEmpty() teste si la file est vide
front() renvoie l’élément en début de file (erreur si vide)
27

28. Interface Queue
EmptyQueueException lorsque opération sur file vide
Ne devrait jamais arriver puisqu’on connait la taille de la file
1 public interface Queue <E>
2 {
3 public void enqueue (E elem);
4
5 public E dequeue () throws EmptyQueueException ;
6
7 public int size ();
8
9 public boolean isEmpty ();
10
11 public E front () throws EmptyQueueException ;
12 }
28

29. Classe ArrayQueue (1)
1 public class ArrayQueue <E> implements Queue <E>
2 {
3 private final int capacity;
4 private final E[] data;
5 private int front;
6 private int rear;
7
8 @SuppressWarnings ("unchecked")
9 public ArrayQueue ()
10 {
11 capacity = 100;
12 data = (E[]) new Object[capacity ];
13 front = 0;
14 rear = 0;
15 }
16
17 public int size ()
18 {
19 return (capacity - front + rear) % capacity;
20 }
21
22 public E front () throws EmptyQueueException
23 {
24 if (isEmpty ())
25 {
26 throw new EmptyQueueException ();
27 }
28 return data[front ];
29 }
29

30. Classe ArrayQueue (2)
1 public boolean isEmpty ()
2 {
3 return front == rear;
4 }
5
6 public void enqueue (E elem) throws FullQueueException
7 {
8 if (size () == capacity - 1)
9 {
10 throw new FullQueueException ();
11 }
12 data[rear] = elem;
13 rear = (rear + 1) % capacity;
14 }
15
16 public E dequeue () throws EmptyQueueException
17 {
18 if (isEmpty ())
19 {
20 throw new EmptyQueueException ();
21 }
22 E elem = data[front ];
23 data[front] = null;
24 front = (front + 1) % capacity;
25 return elem;
26 }
27 }
30

31. Complexité de ArrayQueue
Complexité temporelle des opérations
Méthode Complexité
size O(1)
isEmpty O(1)
front O(1)
enqueue O(1)
dequeue O(1)
Complexité spatiale en O(n)
En notant bien qu’il y a une capacité maximale fixée
31

32. TAD Deque (1)
Une file à deux bouts est une séquence d’éléments (deque)
Éléments ajoutés les uns derrière les autres, des deux côtés
Ajout et retrait d’éléments des deux côtés de la file
Même principe que la liste, mais avec deux bouts
0 1 2 3 4
removeFirst
insertFirst
removeLast
insertLast
début de
deque
fin de
deque
32

33. TAD Deque (2)
Méthodes spécifiques au TAD deque
insertFirst(e) ajoute l’élément e au début du deque
insertLast(e) ajoute l’élément e à la fin du deque
removeFirst() retire l’élément en début de deque (erreur si vide)
removeLast() retire l’élément en fin de deque (erreur si vide)
Méthodes additionnelles
size() renvoie la taille de la file
isEmpty() teste si la file est vide
first() renvoie l’élément en début de deque (erreur si vide)
last() renvoie l’élément en fin de deque (erreur si vide)
33

34. Interface Deque
EmptyDequeException lorsque opération sur deque vide
Ne devrait jamais arriver puisqu’on connait la taille du deque
1 public interface Deque <E>
2 {
3 public void insertFirst (E elem);
4
5 public void insertLast (E elem);
6
7 public E removeFirst () throws EmptyDequeException ;
8
9 public E removeLast () throws EmptyDequeException ;
10
11 public int size ();
12
13 public boolean isEmpty ();
14
15 public E first () throws EmptyDequeException ;
16
17 public E last () throws EmptyDequeException ;
18 }
34

35. Structure chainée

36. Classe Node
Stockage des éléments dans des nœuds
Un objet de type Node stocke une référence vers l’élément
1 public class Node <E>
2 {
3 private final E data;
4 private final Node <E> next;
5
6 public Node (E data , Node <E> next)
7 {
8 this.data = data;
9 this.next = next;
10 }
11
12 public E getData ()
13 {
14 return data;
15 }
16
17 public Node <E> getNext ()
18 {
19 return next;
20 }
21 }
36

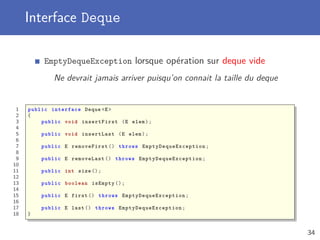
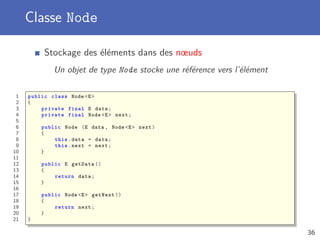
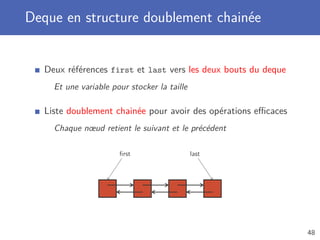
37. Chainage d’objets
Création de plusieurs instances que l’on chaine ensemble
Un objet Node stocke une référence vers un autre
1 public static void main (String [] args)
2 {
3 Node <String > n2 = new Node <String > ("World", null);
4 Node <String > n1 = new Node <String > ("Hello", n2);
5 }
n1
Node
Node
data
String
next
Node
String
Hello
n2
Node
Node
data
String
next
Node
String
World
37

38. Pile en structure chainée
Garder en mémoire une référence top vers le haut de la pile
Et une variable pour stocker la taille
Une pile vide est caractérisée par top == null
top
38

39. Classe LinkedStack (1)
1 public class LinkedStack <E> implements Stack <E>
2 {
3 private Node <E> top;
4 private int size;
5
6 public LinkedStack ()
7 {
8 top = null;
9 size = 0;
10 }
11
12 public int size ()
13 {
14 return size;
15 }
16
17 public boolean isEmpty ()
18 {
19 return size () == 0;
20 }
39

40. Classe LinkedStack (2)
1 public void push (E elem)
2 {
3 top = new Node <E> (elem , top);
4 size ++;
5 }
6
7 public E pop() throws EmptyStackException
8 {
9 if (isEmpty ())
10 {
11 throw new EmptyStackException ();
12 }
13 E elem = top.getData ();
14 top = top.getNext ();
15 size --;
16 return elem;
17 }
18
19 public E top() throws EmptyStackException
20 {
21 if (isEmpty ())
22 {
23 throw new EmptyStackException ();
24 }
25 return top.getData ();
26 }
27 }
40

41. Complexité de LinkedStack
Complexité temporelle des opérations
Méthode Complexité
size O(1)
isEmpty O(1)
top O(1)
push O(1)
pop O(1)
Complexité spatiale en O(n)
Il y a exactement un nœud par élément de la pile
41

42. File en structure chainée
Deux références front et rear vers le début et fin de la file
Et une variable pour stocker la taille
Une file vide est caractérisée par front == null
Et on a automatiquement rear == null
front rear
42

43. Classe interne
Construire une classe à partir d’autres
En utilisant par exemple une relation de composition
Encapsulation des détails d’implémentation
Cacher la relation de composition du monde extérieur
Une classe interne est définie à l’intérieur d’une autre
Seule la classe « hôte » peut utilise la classe interne, si privée
43

44. Classe LinkedQueue (1)
1 public class LinkedQueue <E> implements Queue <E>
2 {
3 private Node <E> front;
4 private Node <E> rear;
5 private int size;
6
7 public LinkedQueue ()
8 {
9 front = null;
10 rear = null;
11 size = 0;
12 }
13
14 private static class Node <E>
15 {
16 private E data;
17 private Node <E> next;
18
19 public Node <E> (E data , Node <E> next)
20 {
21 this.data = data;
22 this.next = next;
23 }
24 }
44

45. Classe LinkedQueue (2)
1 public E front () throws EmptyQueueException
2 {
3 if (isEmpty ())
4 {
5 throw new EmptyQueueException ();
6 }
7 return front.getData ();
8 }
9
10 public E dequeue () throws EmptyQueueException
11 {
12 if (isEmpty ())
13 {
14 throw new EmptyQueueException ();
15 }
16 E elem = front.getData ();
17 front = front.next;
18 size --;
19 if (isEmpty ())
20 {
21 rear = null;
22 }
23 return elem;
24 }
45

46. Classe LinkedQueue (3)
1 public int size ()
2 {
3 return size;
4 }
5
6 public boolean isEmpty ()
7 {
8 return size () == 0;
9 }
10
11 public void enqueue (E elem)
12 {
13 Node <E> newnode = new Node <E> (elem , null);
14 if (isEmpty ())
15 {
16 first = rear = newnode;
17 }
18 else
19 {
20 rear.next = newnode;
21 rear = newnode;
22 }
23 size ++;
24 }
25 }
46

47. Complexité de LinkedQueue
Complexité temporelle des opérations
Méthode Complexité
size O(1)
isEmpty O(1)
front O(1)
enqueue O(1)
dequeue O(1)
Complexité spatiale en O(n)
Il y a exactement un nœud par élément de la file
47

48. Deque en structure doublement chainée
Deux références first et last vers les deux bouts du deque
Et une variable pour stocker la taille
Liste doublement chainée pour avoir des opérations efficaces
Chaque nœud retient le suivant et le précédent
first last
48

49. Complexité de LinkedDeque
Complexité temporelle des opérations
Méthode Complexité
size O(1)
isEmpty O(1)
first, last O(1)
insertFirst, insertLast O(1)
removeFirst, removeLast O(1)
Complexité spatiale en O(n)
Il y a exactement un nœud par élément du deque
49

50. Vecteur

51. TAD Vecteur (1)
Un vecteur est une séquence d’éléments (vector)
Éléments ajoutés les uns derrière les autres
Chaque élément d’un vecteur possède un rang
Le rang de e est le nombre d’éléments qui se trouvent avant lui
0 1 2 3 4
51

52. TAD Vecteur (2)
Méthodes spécifiques au TAD vecteur
elemAtRank(r) renvoie l’élément de rang r (erreur si invalide)
replaceAtRank(r, e) remplace l’élément de rang r par e et
renvoie l’ancien élément de rang r (erreur si invalide)
insertAtRank(r, e) insère un nouvel élément e pour qu’il soit
de rang r (erreur si invalide)
removeAtRank(r) supprime l’élément de rang r (erreur si
invalide)
Méthodes additionnelles
size() renvoie la taille de la file
isEmpty() teste si la file est vide
52

53. Complexité de ArrayVector
Complexité temporelle des opérations
Méthode Complexité
size O(1)
isEmpty O(1)
elemAtRank, replaceAtRank O(n)
insertAtRank, removeAtRank O(n)
Complexité spatiale en O(n)
Où n est la taille du tableau sous-jacent
53

54. Crédits
https://www.flickr.com/photos/bitterjug/7670055210
https://www.flickr.com/photos/67755197@N00/1096645153
https://www.flickr.com/photos/bobafred/3149722
https://www.flickr.com/photos/hktang/4243300265
https://www.flickr.com/photos/86530412@N02/8210762750
https://www.flickr.com/photos/dominicspics/4626264814
54