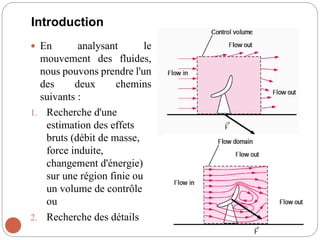
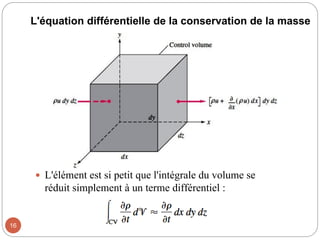
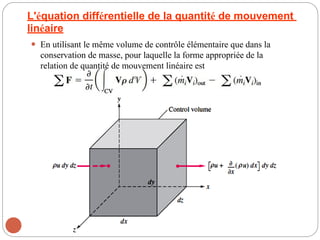
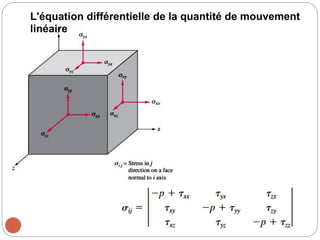
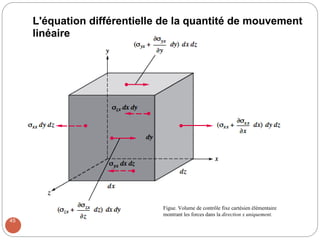
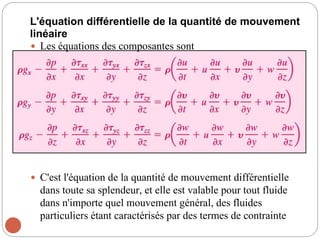
Le chapitre 3 traite des relations différentielles dans la mécanique des fluides, notamment l'accélération des fluides, la conservation de la masse et la quantité de mouvement linéaire. Il introduit des concepts clés tels que le champ de vitesse, l'accélération locale et convective, ainsi que les équations correspondantes pour des conditions d'écoulement spécifiques, y compris les fluides incompressibles. Les équations de Navier-Stokes et d'Euler pour différents types de fluides sont également discutées.

1. Mécanique des
fluides
Chapitre 3
Relations différentielles pour un écoulement
de fluide
1

2. ❖ Introduction
❖ Champ d'accélération
❖ Équation différentielle Conservation de la masse
❖ Équation différentielle de la quantité de mouvement linéaire
❖ Écoulement visqueux
❖ Problèmes résolus
2
Table des matiéres du chapitre

3. Introduction
 En analysant le
mouvement des fluides,
nous pouvons prendre l'un
des deux chemins
suivants :
1. Recherche d'une
estimation des effets
bruts (débit de masse,
force induite,
changement d'énergie)
sur une région finie ou
un volume de contrôle
ou
2. Recherche des détails

4. point par point d'un
modèle d'écoulement
en analysant une
région infinitésimale
de l'écoulement.
3

5. Introduction
 La technique du volume de contrôle est utile lorsque
nous nous intéressons aux caractéristiques globales d'un
écoulement, telles que le débit massique à l'intérieur et à
l'extérieur du volume de contrôle ou les forces nettes
appliquées aux corps.
 L'analyse différentielle, quant à elle, implique
l'application d'équations différentielles du mouvement des
fluides à n' importe quel point du champ d'écoulement sur
une région appelée domaine d'écoulement.
 Une fois résolues, ces équations différentielles donnent
des détails sur la vitesse, la densité, la pression, etc., en
chaque point de l'ensemble du domaine d'écoulement.

6. Le champ d'accélération d'un fluide
 La vitesse est une fonction vectorielle de la position et du
temps et a donc trois composantes u, v et w, chacune
étant un champ scalaire en soi.
 C'est la variable la plus importante en mécanique des
fluides : la connaissance du champ vectoriel de vitesse est
presque équivalente à la résolution d'un problème
d'écoulement de fluide.
 Le champ vectoriel d'accélération a de l'écoulement est dérivé de la
deuxième loi de Newton en calculant la dérivée temporelle totale du
vecteur vitesse :

7. Le champ d'accélération d'un fluide
 Comme chaque composante scalaire (u, v, w) est fonction des
quatre variables (x, y, z, t), nous utilisons la règle de dérivation
en chaîne pour obtenir chaque dérivée temporelle scalaire. Par
exemple
 Mais, par définition, dx/dt est la composante locale
de la vitesse u, et dy/dt =v, et dz/dt = w.
 La dérivée temporelle totale de u peut donc s'écrire comme
suit, avec des expressions exactement similaires pour les
dérivées temporelles de v et w :
6

8. Le champ d'accélération d'un fluide
7
1. En les additionnant en un vecteur, on obtient le total accélération:

9. Le champ d'accélération d'un fluide
 Le terme δV/δt est appelé l'accélération locale, qui disparaît si
l'écoulement est stable, c'est-à-dire indépendant du temps.
 Les trois termes entre parenthèses sont appelés accélération
convective, qui se produit lorsque la particule se déplace à travers des
régions de vitesse variant dans l'espace, comme dans une tuyère ou un
diffuseur.
 L'opérateur de gradient est donné par :
8

10. Le champ d'accélération d'un fluide
 La dérivée temporelle totale, parfois appelée dérivée
substantielle ou dérivée matérielle, peut être appliquée
à n'importe quelle variable, telle que la pression :
 Partout où les effets convectifs se produisent dans les
lois de base impliquant la masse, la quantité de
mouvement ou l'énergie, les équations différentielles de
base deviennent non linéaires et sont généralement plus
compliquées que les écoulements qui n'impliquent pas
de changements convectifs.
9

11. Exemple 1. Champ d'accélération
10
Étant donné le champ vectoriel de vitesse eulérien
déterminez l'accélération totale d'une particule.

12. Étape de solution 2 : De la même manière, les termes
d'accélération convective sont
11

13. Exemple 2. Champ d'accélération
 Un champ de vitesse idéalisé est donné par la formule
 Ce champ d'écoulement est-il stable ou instable ? Est-ce
bidimensionnel ou tridimensionnel ? Au point (x, y, z) =
(1, 1, 0), calculez le vecteur d'accélération.
Solution
 L'écoulement est instable car le temps t apparaît
explicitement dans les composants.
 L'écoulement est tridimensionnel parce que les trois vitesses
Les composants sont non nuls.
 Évaluer, par dérivation, le vecteur accélération en (x, y, z)
= (−1, +1, 0).
12

14. Exemple 2. Champ d'accélération
13

15. Exercice 1
 La vitesse dans un certain champ d'écoulement
bidimensionnel est donnée par l'équation
où le vecteur vitesse est en m/s lorsque x, y et t sont
respectivement en mètre et en secondes.
1. Déterminer les expressions du local et du convectif
composantes de l'accélération dans les directions x et y.
2. Quelle est l'intensité et la direction de la vitesse et de
l'accélération au point x = y = 2 m à l'instant t = 0 ?
14

16. L'équation différentielle de la conservation de la masse
 La conservation de la masse, souvent appelée relation de continuité,
indique que la masse de fluide ne peut pas changer.
 Nous appliquons ce concept à une très petite région. Toutes les
équations différentielles de base peuvent être dérivées en
considérant soit un volume de contrôle élémentaire, soit un système
élémentaire.
 Nous choisissons un volume de contrôle fixe infinitésimal (dx, dy,
dz), comme le montre la figure ci-dessous, et utilisons des relations
de volume de contrôle de base.
 L'écoulement de chaque côté de l'élément est approximativement
unidimensionnel, et la relation de conservation de masse appropriée
à utiliser ici est donc la suivante :
15

17. L'équation différentielle de la conservation de la masse
 L'élément est si petit que l'intégrale du volume se
réduit simplement à un terme différentiel :
16

18. L'équation différentielle de la conservation de la masse
 Les termes de débit massique se produisent sur les six faces, trois
entrées et trois sorties.
 En utilisant le concept de champ ou de continuum où toutes les
propriétés d'un fluide sont considérées comme des fonctions
uniformément variables du temps et de la position, telles que ρ= ρ
(x, y, z, t).
 Ainsi, si T est la température sur la face gauche de l'élément,
Le visage droit aura une température légèrement différente
 Pour la conservation de masse, si ρu est connu sur la face gauche, le
La valeur de ce produit sur la face droite est
17

19. L'équation différentielle de la conservation de la masse
 Introduire ces termes dans la relation principale
 La simplification donne
18

20. L'équation différentielle de la conservation de la masse
 L'opérateur de gradient vectoriel
nous permet de réécrire l'équation de continuité
sous une forme compacte
de sorte que la forme compacte de la relation de continuité est

21. L'équation différentielle de la conservation de la masse
Écoulement incompressible
 Un cas particulier qui offre une grande simplification est
l'écoulement incompressible, où les changements de densité
sont négligeables.
 Le résultat
est valable pour un écoulement incompressible stable
22

22. L'équation différentielle de la conservation de la masse
 Le critère de l'écoulement incompressible est
 où Ma = V/a est le nombre de Mach sans dimension de
l'écoulement.
 Pour l'air dans des conditions standard, un écoulement peut
donc être considéré comme incompressible si la vitesse est
inférieure à environ 100 m/s.

23. Exemple
 Pour un certain champ d'écoulement bidimensionnel
incompressible, la composante de vitesse dans la
direction y est donnée par l'équation
 Déterminez le vecteur vitesse dans la direction x
de sorte que l'équation de continuité soit satisfaite.
28

24. Exemple - solution
29

25. L'équation différentielle de la quantité de mouvement
linéaire
 En utilisant le même volume de contrôle élémentaire que dans la
conservation de masse, pour laquelle la forme appropriée de la
relation de quantité de mouvement linéaire est

26. L'équation différentielle de la quantité de mouvement
linéaire
Encore une fois, l'élément est si petit que le volume intégral
se réduit simplement à un terme dérivé :
Les flux de quantité de mouvement se produisent sur les six
faces, trois entrées et trois sorties.
40

27. L'équation différentielle de la quantité de mouvement
linéaire
 Présentation de ces termes
 Une simplification se produit si nous divisons le terme
entre parenthèses comme suit :
 Le terme entre parenthèses du côté droit est considéré
comme l'équation de continuité, qui disparaît à l'identique

28. L'équation différentielle de la quantité de mouvement
linéaire
 Le long terme entre parenthèses du côté droit est
l'accélération totale d'une particule qui occupe
instantanément le volume de contrôle :
 Ainsi, nous avons maintenant
 Cette équation indique que la force nette sur le volume de
contrôle doit être de taille différentielle et proportionnelle
au volume de l'élément.
42

29. L'équation différentielle de la quantité de mouvement
linéaire
 Ces forces sont de deux types, les forces corporelles et les forces de
surface.
 Les forces du corps sont dues à des champs externes (gravité,
magnétisme, potentiel électrique) qui agissent sur toute la masse de
l'élément.

 La seule force corporelle que nous considérerons est la gravité.
 La force de gravité sur la masse différentielle ρ dx dy dz à l'intérieur
Le volume de contrôle est

 Les forces de surface sont dues aux contraintes exercées sur les côtés
de la surface de contrôle. Ces contraintes sont la somme de la pression
hydrostatique et des contraintes visqueuses τij qui résultent du
mouvement avec des gradients de vitesse
43

30. L'équation différentielle de la quantité de mouvement
linéaire

31. L'équation différentielle de la quantité de mouvement
linéaire
Figue. Volume de contrôle fixe cartésien élémentaire
montrant les forces dans la direction x uniquement.
45

32. L'équation différentielle de la quantité de mouvement
linéaire
 La force superficielle nette dans la direction x est donnée par
 Séparation en pression et contraintes visqueuses
 où dv = dx dy dz.
 De même , nous pouvons dériver les forces y et z par unité
de volume sur la surface de contrôle

33. L'équation différentielle de la quantité de mouvement
linéaire
 La force superficielle vectorielle nette peut être écrite comme
suit :

34. L'équation différentielle de la quantité de mouvement
linéaire
 Sous forme de divergence
est le tenseur de contrainte visqueuse agissant sur l'élément
 La force superficielle est donc la somme du vecteur
gradient de pression et de la divergence du tenseur de
contrainte visqueuse

35. L'équation différentielle de la quantité de mouvement
linéaire
 L'équation de base de la quantité de mouvement
différentielle d'un élément infinitésimal est donc
 En mots:

36. L'équation différentielle de la quantité de mouvement
linéaire
 Les équations des composantes sont
 C'est l'équation de la quantité de mouvement différentielle
dans toute sa splendeur, et elle est valable pour tout fluide
dans n'importe quel mouvement général, des fluides
particuliers étant caractérisés par des termes de contrainte

37. visqueuse particuliers.
50

38. Écoulement invisqueux : équation d'Eulers
 Pour un écoulement sans frottement τij =0, 
 Il s'agit de l'équation d'Eulers pour l'écoulement non
visqueux

39. Fluide newtonien : équations de Navier-Stokes
 Pour un fluide newtonien, les contraintes visqueuses sont
proportionnelles aux vitesses de déformation de l'élément et au
coefficient de viscosité.
 où μ est le coefficient de viscosité
 La substitution donne l'équation de la quantité de mouvement différentielle
pour un Fluide newtonien à densité et viscosité constantes :

40. Fluide newtonien : équations de Navier-Stokes
 Il s'agit des équations de Navier-Stokes à écoulement
incompressible nommées d'après C. L. M. H. Navier
(1785-1836) et Sir George G. Stokes (1819-1903), à qui
l'on attribue leur dérivation.
53

41. Flux invisqueux
 Des contraintes de cisaillement se développent dans un
fluide en mouvement en raison de la viscosité du fluide.
 Nous savons que pour certains fluides courants, tels que
l'air et l'eau, la viscosité est faible, il semble donc
raisonnable de supposer que dans certaines circonstances,
nous pouvons simplement négliger l'effet de la viscosité
(et donc les contraintes de cisaillement).
 Les champs d'écoulement dans lesquels les contraintes
de cisaillement sont supposées être négligeables sont
dits non visqueux ou sans frottement.
 Pour les fluides dans lesquels il n'y a pas de contraintes de
cisaillement, la contrainte normale en un point est
indépendante de la direction, c'est-à-dire σxx = σyy = σzz.
54

42. Flux invisqueux
Équations du mouvement d'Euler
 Pour un écoulement NON visqueux dans lequel toutes les contraintes de
cisaillement sont zéro et l'équation du mouvement d'Euler s'écrit
 En notation vectorielle, les équations d'Euler peuvent être exprimées
comme suit :