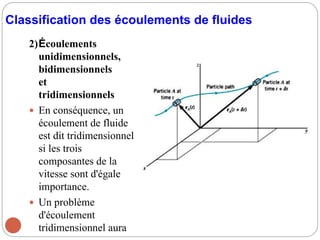
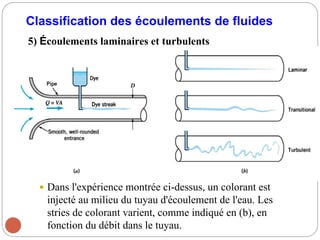
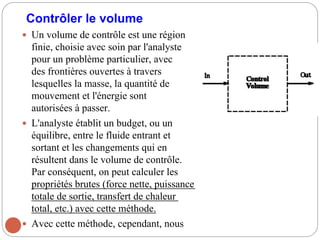
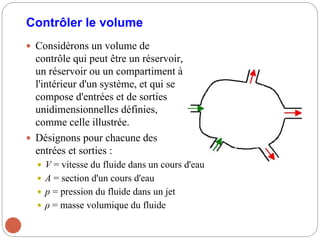
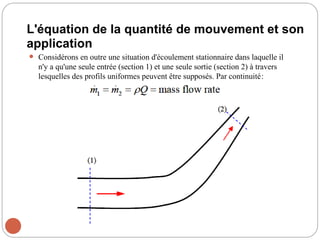
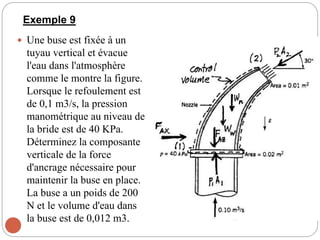
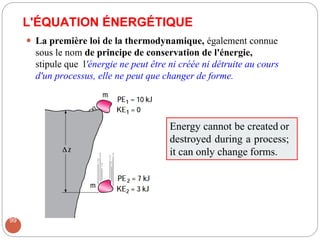
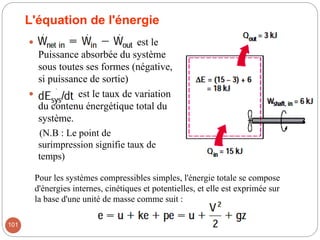
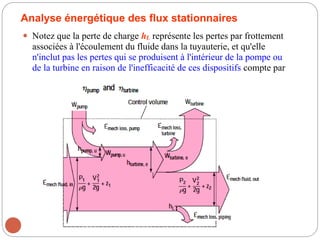
Le chapitre 2 de la mécanique des fluides traite des relations intégrales pour un volume de contrôle, en classifiant les écoulements de fluides selon divers critères tels que la dimensionnalité, la viscosité et la compressibilité. Les méthodes d'analyse incluent l'analyse de volume de contrôle, l'analyse différentielle, et l'analyse expérimentale. Les lois physiques de base de la mécanique des fluides, telles que la conservation de la masse, l'équation de mouvement, et les principes d'énergie, sont également abordées.