Ce document présente une introduction aux tableaux à une dimension, connus comme vecteurs, en expliquant leur déclaration, accès aux éléments et opérations de base. Il aborde la création, l'édition et les manipulations des tableaux, ainsi que des exemples d'algorithmes en Pascal pour saisir et afficher des éléments. Des exercices d'application sont également fournis pour renforcer la compréhension des concepts liés aux vecteurs.

1. CHAPITRE:
Structuresdedonnées
(tableauxàunedimension
:Vecteurs) 1ere année LMD Sciences
et Technologies

2. Introduction
Notion d’un tableau (vecteur)
Déclaration d’un Vecteur
Accès aux éléments d’un Vecteur
Quelques opérations de base sur les Vecteurs
Exercices d'applications
Sommaire:
1
2
3
4
5
6

3. INTRODUCTION

4. Tableaux à une
dimension:
Tableaux
OU
Tableaux à deux
dimensions:
1 seule indice
2 indices

5. NOTION D’UN
TABLEAU
(VECTEUR)

6. On appelle généralement un tableau un ensemble fini d’éléments de
même type et subissent les mêmes traitements.
Un tableau monodimensionnel ( ou vecteur) est caractérisé par:
 Son nom (identificateur du vecteur)
Le nombre d’ éléments d’un tableau définit sa cardinalité (taille,
longueur), et le type des éléments définit le type du tableau.
Chacune des valeurs est repérée par un indice indiquant la position
de la donnée dans le tableau compris entre 1 et N.

7. Schématiquement, un vecteurT contenant 10 éléments peut être
représenté par :
T: est le nom du vecteur,
T[1] : désigne le contenu de l'élément numéro 1 du vecteurT,
T[2] : désigne le contenu de l'élément numéro 2 du vecteurT,
...
T[i] : désigne le contenu de l'élément numéro i du vecteurT.
1 2 3 4 5 6 7 8 9 10
19 9 0 -6 4,7 -5 110 -0,7 5 -11T:
Indices
Eléments

8. DÉCLARATION
D’UN VECTEUR

9. Exemple:
Variable
A :Tableau [1..35] d’entiers;
T:Tableau [1..10] de chaine de caractères;
Syntaxe (algorithme):
Variable
nom_tableau: TABLEAU [indice_min..indice_max] de type;
Valeur de l’indice initial Valeur de l’indice final

10. Exemple:
Var
Tab :array[1..7] of integer;
T: array [1..20] of real;
Remarque: en cas d’un tableauT de n valeurs entières, on déclare:
T:array[1..100] of integer;
On parle ici des tableaux statiques
Syntaxe (Pascal):
Var
Nom_tableau :array[indice_min..indice_max] of type;
Valeur de l’indice initial Valeur de l’indice final

11. ACCÈS
AUX ÉLÉMENTS
D’UNTABLEAU

12. 1. Création d’un tableau (Lire/remplir un tableau):
La saisie des éléments du tableau se fait par le clavier.
Pour lire (remplir) un tableau, il faut parcourir tous ces éléments
afin de donner à chaque élément une valeur. Pour se faire, nous
utilisons une BOUCLE.
T[1]= 10 T[2] T[3] T[10]=-2.9
1 2 3 4 5 6 7 8 9 10
ELEMENTS
INDICES
lire (T[1]);
lire (T[2]);
lire (T[3]);
……
lire (T[10]);
Pour i← 1 à 10 faire
lire (T[i]);

13. Création du tableau en Algorithmique:
Algorithme saisie;
Variable
T:Tableau[1..10] de Réel;
i: entier;
Debut
Pour i← 1 à 10 faire
Ecrire ('Donner l''élément numéro ', i, ' du
tableau‘);
Lire (T[i]);
Finpour;
Fin.
Création du tableau en Pascal:
Program saisie;
Var
T: array[1..10] of real;
i: integer;
begin
for i:=1 to 10 do
begin
write('Donner l''élément numéro ', i, ' du
tableau');
read(T[i]);
end;
End.
Exemple: écrire un algorithme et un programme
pascal permettant de saisir dix valeurs réelles
dans un tableau.

14. 2. Edition d’un tableau (affichage des éléments d’un tableau)
Pour afficher un tableau il faut parcourir tous ces éléments et afficher par
la commande écrire chaque élément. Pour se faire, nous utilisons une
BOUCLE.
Exemple: écrire un algorithme/programme Pascal permettant d’afficher le
tableau suivant:
1 2 3 4 26
A B C ….. Z
Ecrire (T[1]);
Ecrire (T[2]);
Ecrire (T[3]);
……
Ecrire (T[26]);
Pour i← 1 à 26 faire
Ecrire (T[i]);

15. Affichage d’un tableau en Algorithmique :
Algorithme affichage;
Variable
T: Tableau[1..26] de caractère;
i: entier;
Debut
Pour i← 1 à 26 faire
Ecrire (' l''élément numéro ', i, ' du
tableau=‘, T[i]);
Finpour;
Fin.
Affichage d’un tableau en Pascal:
Program saisie;
Var
T: array[1..10] of real;
i: integer;
begin
for i:=1 to 26 do
begin
write(' l''élément numéro ', i, ' du
tableau=‘,T[i]);
end;
End.

16. LESOPÉRATIONS
SUR LESTABLEAUX

17. Soit le tableauT suivant:
T:
On accède à la i eme valeur d'un tableau en utilisant la syntaxe suivante :
Nom du tableau [indice].
Exemple.
T[3] le troisième élément du tableauT. T[3]=10
T[2] ← 20 : mettre la valeur 20 dans la 2 eme case du tableauT. Soit le nouveau
tableau deT:
T:
3 -5 10 9 -6
1.Affectation:
3 20 10 9 -6

18. Soit le tableauT suivant:
T:
En considérant le cas ou x est une variable de type Entier,
x ←T[2] : mettre la valeur de la 2 eme case du tableauT dans x, c'est-a-dire
mettre la valeur -5 dans x.
x
lire(T[1]) : mettre la valeur saisi par l'utilisateur dans la première case du
tableauT.
écrire(T[1]): afficher la valeur de la première case du tableau.
3 -5 10 9 -6
-5

19. 2. Autres manipulations dans les tableaux:
Avec les vecteurs, on peut réaliser les manipulations suivantes:
Le rangement des valeurs dans un tableau;
La récupération, la consultation des valeurs rangées dans un tableau;
 La recherche si une valeur existe dans un tableau;
 La mise à jour des valeurs dans un tableau;
 La modification de la façon dont les valeurs sont rangées dans un tableau (par
exemple : les trier de différentes manières);
La manipulation des opérations entre tableaux : comparaison de tableaux,
multiplication, etc.
Exercice 1: Donner l’algorithme qui calcul la moyenne des notes des étudiants
dans un vecteur A de taille n.

20. 1 2 3 4 5 6
A:
0
S i
11,33
M
13 1
S i
22 2
S i
32,5 3
S i
44,5 4
S i
60,5 5
S i
68 6
S i
68/6
TraitementA
n S M
6
n
1 2 3 4 5 6
13 9 10.5 12 16 7.5A:

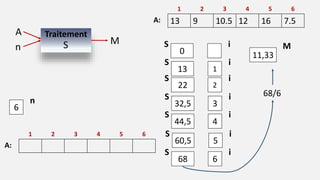
21. Algorithme Som_Moy;
Variable
A: tableau [1..100] de réel;
S, M : réel;
i, n : entier;
début
Écrire (‘donner le nombre d’’ étudiants’);
Lire (n);
S← 0;
pour i ← 1 a n faire
Ecrire(‘donner les éléments du tableau’);
Lire (A(i));
S ← S + A(i);
Finpour;
M ← S/n;
Ecrire (‘La moyenne=‘,M);
Fin.

22. Le traitement que l’on doit répéter plusieurs fois par l'utilisation d’une boucle
est un bloc qui contient une suite d’instructions à exécuter. Ces instructions
peuvent être une affectation, un appel de méthode, une structure
conditionnelle (le test SI) ou une autre boucle.
Dans le cas d'une boucle à l’intérieur d’une autre boucle, on parle de boucles
imbriquées.
Dans l'exemple suivant, nous présentons le cas d'un test SI à l'intérieur d'une
boucle pour.
Exemple. Donner l’algorithme qui calcul le nombre d'étudiants ayant une note
supérieure ou égale à 10 sachant que le tableau contient N étudiants:
3.Lesblocsimbriquées(bouclesimbriquées):

23. TraitementTab
n note >=10
nb
1 2 3 4 5
Tab:
5
n
1 2 3 4 5
12 8 7 10 19Tab:
0nbi
11i
12i
nb
nb
12Tab[1]
8
7
Tab[2]
Tab[3]
10Tab[4]
19Tab[5]
2
3
nb
nb
1nb3i
4i
5i
T[i]>=10 nb←nb+1

24. Solution:
Algorithme Notes;
Variable
Tab: Tableau [1..100] de réel;
i ,nb, N : entier ;
Début
Ecrire (‘donner la taille du
tableau’);
Lire(N);
nb ← 0;
Pour i ← 1 à n faire
écrire(‘ donner l’’élément’ , i,
’du tableau’);
lire (Tab [i]);
Si (Tab[i] >=10) alors
nb ←nb+1
FSi ;
FPour ;
écrire ('le nombre de notes
supérieures à 10 est : ', nb);
Fin.

25. EXERCICES
D'APPLICATIONS

26. Exercice N°1 :
Ecrire un algorithme qui permet de calculer et
afficher le nombre d’éléments positifs, négatifs
et nuls dans un tableau de 100 éléments réels.

27. Exercice N°2 :
Ecrire un algorithme/ programme Pascal qui
détermine la symétrique d’un vecteurT de taille
n dont les éléments sont des entiers.

28. Exercice N°3 :
Ecrire l’algorithme qui multiplie et additionne
chaque élément d’un vecteur «V1 » de taille n
par chaque élément d’un vecteur «V2 » de
taille m.

29. Exercice N°4 :
Ecrire un algorithme/programme Pascal qui permet
de:
1. Remplir un tableauT de taille N d’entiers.
2. Rechercher et afficher le nombre d’occurrences
(d’apparition) d’un nombre dans le tableauT.