Le mémoire de Gabriel Garcia-Prieto se concentre sur le pricing des produits dérivés climatiques, soulignant leur importance croissante face aux risques économiques liés aux variations climatiques. Le document explore le marché des produits dérivés climatiques, les types de produits disponibles, et les méthodes de pricing adoptées par les acteurs du marché. Il aborde également les implications pour diverses industries et propose des stratégies de couverture contre les aléas climatiques.







![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 8 / 118 Mémoire du DEA Finance de Marché
IIInnntttrrroooddduuuccctttiiiooonnn
« Weather is big business. [It] is
not just an environmental issue – it is a
major economic factor… One seventh of
our economy, about $1 trillion a year, is
weather sensitive ».
William M. Daley,
U.S. Secretary of Commerce
Aujourd’hui, on estime que 20% de l’économie américaine est concernée par
le temps qu’il fait : le risque climatique affecte non seulement la vie des particuliers,
mais aussi l’activité générale des entreprises. Les revenus des entreprises peuvent
donc être très fortement influencés par un été plus chaud que la normale ou un hiver
plus doux que prévu.
Bien que les travaux des centres de recherche météorologiques soient de plus
en plus avancés et que les prévisions se fassent sur des durées toujours plus
longues, il nous est tous arrivés de s’encombrer d’un parapluie pour rien ou d’avoir
prévu un maillot de bain alors qu’un pull se serait révélé plus adéquat. La
météorologie n’est pas une science exacte, d’où l’existence de risque.
La plupart des entreprises incluent dans leurs états financiers annuels un
paragraphe expliquant leur stratégie en matière de gestion des risques. Elles sont
ainsi souvent amenées à utiliser des produits financiers dérivés pour se couvrir
contre leur risque de taux d’intérêt ou leur risque de change. Les produits dérivés
climatiques résultent de la même problématique afin de couvrir un risque immuable.
Citons à titre d’exemple les risques contre lesquels une entreprise voudrait se
couvrir :
Température
Précipitation (pluie ou neige)
Vitesse du vent
Chaleur et humidité](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-8-320.jpg)






![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 16 / 118 Mémoire du DEA Finance de Marché
1.3.1. Indices Heating Degree Day (HDD)
Un HDD mesure la fraîcheur d’une journée par rapport au standard de 65°
Fahrenheit durant la saison hivernale (de novembre à mars).
Mathématiquement, on a
HDD Journalier = MAX [0, 65°F – Température moyenne journalière]
Une température moyenne de 45° donne donc 20 HDD. Une température de
68° donne 0 HDD.
Ces résultats journaliers peuvent être accumulés pour former des périodes
diverses : 1 semaine (Noël – Nouvel An = 80.5 HDD), 1 mois (ventes d’hiver = 345
HDD), un trimestre (saison des vacances = 1035HDD).
Dans ce cas, on parle d’HDD cumulés tels que avec n = date de fin du contrat:
ni
i
sjournalierHDDHDDCum
1
1.3.2. Indices Coolind Degree Day (CDD)
Un CDD mesure l’intensité de la chaleur d’une journée par rapport au
standard de 65° Fahrenheit durant la saison estivale(d’avril à septembre).
CDD Journalier = MAX [0, Température moyenne journalière - 65°F]
Une température moyenne de 77° Fahrenheit donne un CDD journalier de 12.
Une température moyenne de 55 donne 0 CDD.
De même que pour les HDD, les CDD peuvent être accumulés sur une
période bien spécifiée : 2 semaines (Tournoi de Wimbledon = 63 CDD), 2 mois
(période des récoltes = 274.5 CDD), 6 mois (période des crèmes glacées = 873
CDD)
Là aussi, on parle de CDD cumulés:
ni
i
sjournalierCDDCDDCum
1](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-16-320.jpg)

![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 18 / 118 Mémoire du DEA Finance de Marché
1.4.1.1. Le Cap
Encore appelé option d’achat – call option – le Cap donne à l’acheteur un
payout non -linéaire basé sur la différence entre la valeur spot du sous – jacent et le
prix d’exercice défini contractuellement.
L’acheteur de Cap paie une prime au vendeur afin de posséder ce droit au
payout.
Si le prix spot est supérieur au strike, le vendeur va payer la différence de prix
à l’acheteur ; dans le cas contraire, aucun versement n’est effectué.
Le montant à payer est calculé comme la différence entre le prix spot et le
strike, multiplié par un certain prix par unité d’indice, majoré par un certain montant.
Le cap permet à l’acheteur de s’assurer une protection contre des conditions
climatiques qui lui seraient défavorables, tout en bénéficiant de conditions plus
favorables.
Notons enfin qu’à l’image des contrats de réassurance où le réassureur
« achète » à l’assureur ses sinistres au – dessus d’un certain niveau et jusqu’à une
certaine limite (contrats en « excess of loss »), le pay-off en T est limité dans tous les
cas (contractuellement) par un montant B, ce qui donne
CSP (T) = min (B, C(T)), soit
CSP (T) = min [B, A max [0,
n
j
j k
1
)65,0max( ]]
L’instrument décrit par le cash – flow terminal peut aussi bien être appelé
« capped call » que « cal spread » car il correspond à la détention en position longue
d’un call de strike k et en position courte d’un call de strike B / A.](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-18-320.jpg)












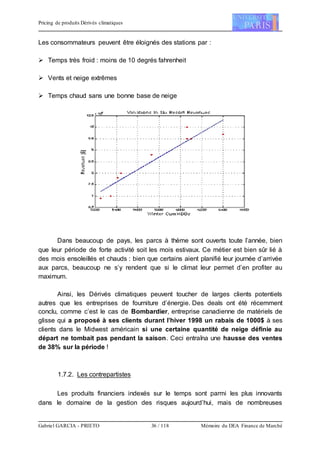






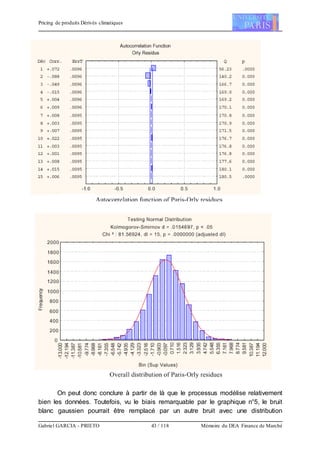

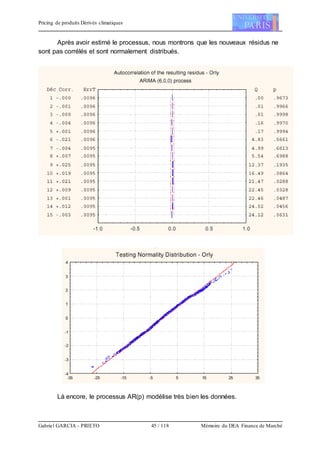


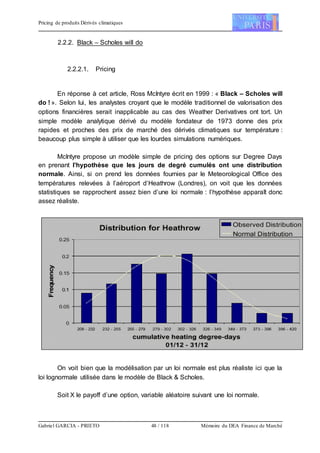
![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 49 / 118 Mémoire du DEA Finance de Marché
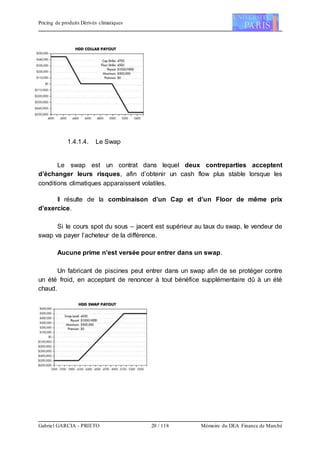
Si on note V la valeur de l’option, on a
V = E [X], i.e. V =
dssPX )(
avec P(s) =
²2
)²(
2
1
ms
e
en prenant s : nombre de jours de degré cumulés
m : moyenne
: écart type ou volatilité
Pour les options européennes, le payoff s’écrit X = Max [ (S-K), o] ; K étant le strike
et = + / - 1 pour le call et le put respectivement..
Nous pouvons maintenant discuter des solutions analytiques des principales
options météorologiques traitées sur le marché. En reprenant des résultats connus
d’algèbre linéaire, on peut écrire pour les options de type européennes:
VE = (m - K)
)( Km
+ ² P (K)
Où (x) est la loi normale
Le pricing d’option financière pose l’existence d’une mesure de probabilité dite
risque neutre sous laquelle les prix de tous les actifs financiers actualisés au taux
sans risque sont martingales. Le seul paramètre inconnu dans le pricing d’options
financières est la volatilité.
Dans le cas des options climatiques, la moyenne et la volatilité sont
inconnues. La moyenne des options climatiques est similaire au forward des options
financières. La moyenne implicite du sous jacent d’une option climatique indique
l’espérance du prix de marché des observations futures et tient donc compte des
prévisions et tendances les plus récentes.
Les moyenne et volatilité implicites représentent toutes les deux le
risque et sont donc déterminantes du prix de l’option. A partir de là, on peut
donc facilement déterminer le prix de l’option.
Par exemple, si on reprend l’exemple mentionné plus haut de l’entreprise ABC
Jacket se couvrant par achat d’un put, avec une moyenne de 2000 HDD, un strike de](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-49-320.jpg)

![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 51 / 118 Mémoire du DEA Finance de Marché
2.3. The Dischel D1 Stochastic Temperature Model
2.3.1. Le modèle théorique
Pour résoudre le problème de détermination du prix de l’option, l’auteur
suggère de se référer aux données météorologiques passées pour prévoir les
données futures, mais seulement pour la détermination de la volatilité. Il pense
que par un modèle stochastique, on est plus à même de décrire des données qu’en
calculant simplement une moyenne et une variance à partir de données historiques
de court terme.
Bien que ce modèle serve avant tout à pricer une option sur température,
l’auteur suggère qu’il peut être parfaitement appliqué à d’autres facteurs climatiques.
Les séries temporelles recherchées ne peuvent se trouver dans les données
passées de prix payés pour les dérivés car de nombreuses informations y sont
perdues et des séquences météorologiques masquées. Pour cela , on va utiliser les
valeurs climatiques journalières, comme les jours de degré.
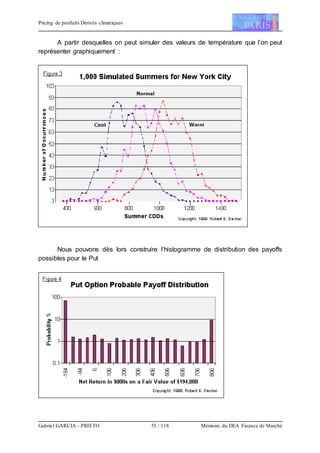
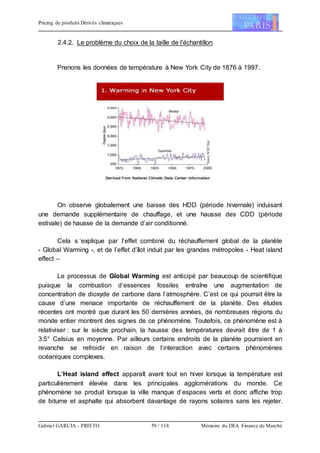
L’idée de ce modèle est de simuler le plus de scénarios possible afin de
quantifier les températures potentielles futures, et en attribuant à chacune une
probabilité de réalisation. On calcule pour chaque scénario le prix du dérivé. Le prix
théorique aujourd’hui est alors la somme des prix probabilisés selon chaque
scénario.
L’auteur dit avoir testé son modèle durant le printemps 1998 pour une dizaine
de produits financiers et sur une dizaine de sites différents. Les prix calculés se
révèlent très proches des prix de marché, selon l’auteur.
Sur certains sites, le climat change radicalement ces dernières années, d’où
une nécessité de retravailler les données.
Le processus stochastique utilisé est donné par
dT = [ (t) * (t) - T(t)] dt + dm1 + dm2 (1)
Le paramètre T est une variable climatique : température, précipitation,… qui
varie selon le temps t](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-51-320.jpg)












![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 66 / 118 Mémoire du DEA Finance de Marché
2.6. Le modèle de Dornier & Queruel (Barep Asset
Management)
2.6.1. Non applicabilité du processus Mean Reverting standard
Reprenons la dynamique Mean Reverting utilisée dans la plupart des modèles
Mean Reverting
dT = [ (t) * (t) - T(t)] dt + t dWt
avec , moyenne fonction du temps
Les auteurs montrent alors que ce processus n’a pas en fait pour espérance la
moyenne , i.e. E [Tt] t. Nous en verrons par la suite les impacts énormes sur le
Fair Price de l’option.
Soit le processus
)(0
tt
dsa
t TeZ
t
s
avec Tt suivant le processus Stochastique défini. Ainsi,
))(*( '0
ttttt
dsa
t TadTdteZ
t
s
))()(*( '0
dtTadWdtTadte ttttttttt
dsa
t
s
)( '0
ttt
dsa
dWdte
t
s
avec ’ dérivée de par rapport au temps
On peut résoudre cette Equation Différentielle Stochastique puisque le
terme de droite ne dépend pas de Zt.](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-66-320.jpg)
![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 67 / 118 Mémoire du DEA Finance de Marché
t
s
dua
s
duat
st dWedseZZ
s
u
s
u
00
'
0
00
Par intégration par parties pour le second terme et en remplaçant Zt par
son expression, on a
t
s
dua
s
duaduat
ss
duadua
t dWeedseeeTT
s
u
t
u
s
u
t
u
t
u
00
0
00000
Le dernier terme est simplement gaussien de moyenne nulle. En passant à
l’espérance, on a donc
dseeeTTE
s
u
t
u
t
u duat
ss
duadua
000
0
0][
Il n’y a alors aucune raison pour que cette expression soit égale ou même
proche de la moyenne attendue t
Si on avait E [Tt] = t, on aurait
dseTe
s
u
t
u duat
ss
dua
t
00
0
0
En dérivant cette expression, on obtient 0'
t .
Avec ce modèle, la seule possibilité d’avoir une moyenne de t est de
prendre t contant, ce qui est bien le cas dans le modèle de Vasicek. Pour les
produits dérivés climatiques, cette restriction s’avère aberrante.
Analysons l’erreur de ce modèle en supposant fonction de la
saisonnalité et d’une tendance linéaire :
t = S * t + C + E * sin (wt)](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-67-320.jpg)
![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 68 / 118 Mémoire du DEA Finance de Marché
avec S, C et E constants, et w =
365
2
a, paramètre de force de retour à la moyenne est supposé constant.
Nous voulons l’espérance de Tt avec la même tendance et les mêmes
oscillations que t
. Pour T0 = 0 = C, on a
])([cos
²²
)(sin
²²
²
)1(][ atatat
tt ewt
wa
aw
Ewt
wa
w
EeCe
a
S
TE
Lorsque t est grand, on peut éliminer e-at, mais il reste un biais
)(cos
²²
)(sin
²²
²
1 wt
wa
aw
Ewt
wa
w
E
a
S
Il reste, dans ce modèle, des parasites qui influencent l’amplitude et la phase
de la moyenne réelle. Le processus est bien Mean Reverting, mais pas vers t
a doit être choisi en fonction des données historiques par technique de
maximum de vraisemblance, par exemple.
2.6.2. Illustration numérique
Illustrons ces résultats avec des données sur 20 ans à Chicago.
Nous discrétisons le processus
Tn+1 – Tn = a * (n - Tn) + * n
a et > 0 et constants, n bruit gaussien standard
n est estimé à partir de données historiques
Biais du à la
pente de la
tendance
Biais du à la
moyenne de
la température
Biais du à la
saisonnalité](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-68-320.jpg)
![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 69 / 118 Mémoire du DEA Finance de Marché
On trouve alors
a 299.0
189.6
On peut remarquer ici que comme le paramètre a est assez petit, le bruit
explicité va être assez grand.
On peut alors simuler les espérances par
E [Tn+1]– E [Tn] = a * (n – E [Tn])
Le graphe n°2 montre les variations de E [Tn] - n
On voit que cette différence ne tend pas vers 0, mais au contraire possède
des valeurs extrêmes de 5 °F à – 6 °F.
2.6.3. Apport des auteurs
Les auteurs sont parfaitement d’accord sur le concept que les températures
journalières tendent vers une moyenne ajustée quotidiennement de référence. Selon
eux, c’est simplement la formulation mathématique qui est mauvaise.
Ils proposent alors une dynamique
dTt = dt + at (t – Tt) dt + t dWt](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-69-320.jpg)
![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 70 / 118 Mémoire du DEA Finance de Marché
C’est alors le processus Tt – t qui suit le processus d’Ornstein Uhlenbeck de
moyenne nulle.
On peut alors simuler les trajectoires de la température attendue Tt avec le
processus discrétisé, en utilisant des techniques de maximum de vraisemblance
pour estimer a et , et des simulations de Monte Carlo.
Tn+1 – Tn = n+1 - n + a * (n - Tn) + * n
En passant à l’espérance
E [Tn+1]– n+1 = (1 – a) * (E [Tn] - n )
Les erreurs entre la moyenne de Tn et n diminuent géométriquement pour
0 < a < 2.
Dans ce cas, Tn est réellement Mean Reverting vers n et le modèle est correct
pour les estimateurs :
a 296.0
356.6
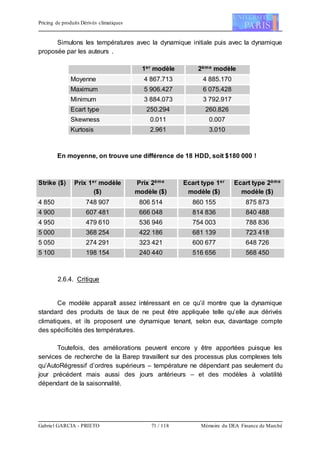
Essayons de valoriser le call suivant :
Produit : Call HDD
Lieu de mesure : Chicago
Période : 1er Novembre – 31 Mars
Nominal : $10 000 par HDD](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-70-320.jpg)


![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 74 / 118 Mémoire du DEA Finance de Marché
Tableau A
1 2 3 1 Log -
vraisem
blance
Atlanta 0.8833
(0.01170)
-0.3035
(0.01520)
0.0322
(0.01169)
7.5980
(0.12086)
5.0912
(0.14603)
-0.1881
(0.01067)
-20 626
Chicago 0.7989
(0.01170)
-0.2570
(0.01467)
0.0428
(0.01170)
7.8289
(0.13922)
3.1294
(0.18181)
-0.2014
(0.02316)
-23 130
Dallas 0.8158
(0.01170)
-0.2436
(0.01483)
0.0201
(0.01170)
8.9378
(0.14060)
6.3349
(0.16800)
-0.1418
(0.00953)
-21 381
New York 0.7558
(0.01169)
-0.263
(0.01433)
0.0463
(0.01169)
6.5372
(0.11241)
2.7035
(0.14520)
-0.2432
(0.02238)
-21 719
Philadelphia 0.7726
(0.01169)
-0.2595
(0.01446)
0.0473
(0.01169)
6.9034
(0.11957)
3.1654
(0.15360)
-0.2015
(0.01932)
-21 792
2.7.2. Evaluation des dérivés
Les auteurs montrent que le prix de marché du risque est insignifiant et que
l’évaluation en univers risque neutre peut donc être menée.
Considérons un contrat forward sur HDD dont la période d’accumulation
commence en T1 et se termine en T2
2
1
)0,65(),( 21
T
T
YMaxTTHDD
Le prix de ce contrat est simplement la valeur attendue des HDD cumulés sur
cette période. Avec les termes d’auto corrélation, il est difficile d’obtenir une formule
fermée. Si nous posons l’hypothèse de zéro auto corrélation, les prix forward sont
donnés par :
])
2
)²ˆ65(
[exp
2
)
ˆ65
(*]ˆ65[),,(
2
1
2
,
,,
,
,
,21
T
T yr
uryr
yr
yr
yrHDD
YY
NYTTtF
(3)](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-74-320.jpg)
![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 75 / 118 Mémoire du DEA Finance de Marché
])
2
)²ˆ65(
[exp
2
)
65ˆ
(*]65ˆ[),,(
2
1
2
,
,,
,
,
,21
T
T yr
uryr
yr
yr
yrCDD
YY
NYTTtF
(4)
De là les expressions des calls et puts de strike X et de maturité T2. r est le
taux sans risque :
CHDD (t, T1, T2, X) =
)( 2 tTr
e
Et [max (HDD(T1, T2) – X, 0)] (5)
PHDD (t, T1, T2, X) =
)( 2 tTr
e
Et [X - max (HDD(T1, T2), 0)] (6)
Il est très difficile d’obtenir des solutions analytiques aux équations
précédentes en raison de la double présence de l’opérateur Max. Il faut alors
procéder par simulations.
2.7.3. Critique
Le modèle est intéressant car :
Il tient compte des prévisions climatiques comme input
Il permet d’évaluer des contrats sur température de différentes maturités et
pour différentes saisons puisqu’il se fonde sur la prévision des
températures quotidiennes, il requiert donc une estimation pas à pas ; à la
différence d’une modélisation de HDD ou CDD qui impliquerait une procédure
d’estimation propre à chaque contrat.
Toutefois, on peut y déceler une limite en ce sens que le modèle prend
comme input les prévisions météorologiques. Or, celles – ci bien qu’émises par
des centres de recherche d’état (National Weather Services aux Etats – Unis), ne
portent que sur des périodes relativement courtes et surtout ne se révèlent que très
peu fiables. Ainsi, même si les acteurs du marché des produits dérivés climatiques
s’entendaient pour prendre ce modèle comme référence, le large panel de prévisions
climatiques à horizon 6 mois entraînerait toujours d’importants bid / ask spreads.](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-75-320.jpg)


![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 78 / 118 Mémoire du DEA Finance de Marché
La quantité d’HDD est un facteur non traité suivant la dynamique
dh = m(h, t) dt + s(h, t) dz
L’entreprise subit aussi une fonction de coût C(p, h, t). Le prix de l’énergie achetée
est un actif traité de dynamique
dp = u(p, t) dt + (p, t) dw
z et w sont deux processus de Wiener corrélés de coefficient
On construit un portefeuille par n1 futures sur HDD pricés à F(h, t) et n2 futures de
gaz naturel pricés à f(p, t) pour couvrir les coûts et les revenus.
Les variations du portefeuille s’écrivent :
d = dR (h, t) – dC(h, p, t) + n1 dF(h, t) + n2 df(p, t)
En appliquant le lemme d’Itô :
d={ ),²(
²2
²
),( ths
h
R
thm
h
R
t
R
} dt + ),( th
h
R
dz
+ n1{[ ),²(
²2
²
),( ths
h
F
thm
h
F
t
F
]dt + ),( ths
h
F
dz }
– {[ ),²(
²2
²
),²(
²2
²
),(),(
²
),(),( tp
p
C
ths
h
C
tpths
ph
C
tpu
p
C
thm
h
C
t
C
] dt
+ ),( ths
h
C
dz+ ),( tp
p
C
dw }+n2 {[ ),²(
²2
²
),( tp
p
f
tpu
p
f
t
f
]dt+ ),( tp
p
f
dw }
On veut un portefeuille sans risque, i.e.
0),(),(),( 1
ths
h
C
ths
h
F
nths
h
R
et
0),(),( 2
tp
p
f
ntp
p
C
](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-78-320.jpg)



![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 82 / 118 Mémoire du DEA Finance de Marché
Nous allons alors essayer de changer le drift de I(t) de à = - , et
ensuite faire comme si les investisseurs étaient risque neutre, pour avoir la valeur de
l’obligation.
Le prix à t = 0 de l’obligation climatique zéro – coupon est donnée par la
valeur actualisée de l’espérance des flux futurs sous cette probabilité « risque –
neutre ».
)]1)1(1([ ,,0 TKIKI TTT
rT
Q FFeEP
On veut faire apparaître explicitement la probabilité du 1er passage de I(t) par
K :
P0 = e
-rT
F ( TKITQ
,
1 )
On peut donc obtenir une formule fermée à l’obligation climatique :
))]()()((1[ 2
²
2
1
0
10 dN
K
I
dNeFP
r
rT
avec
T
Tr
K
I
Ln
d
)
2
²
(0
1
T
Tr
K
I
Ln
d
)
2
²
(0
2
Lorsque K tend vers l’infini, le prix de l’obligation climatique se rapproche de
l’obligation sans risque équivalente.
3.1.1.2. Evaluation du spread entre deux bonds
Supposons que la valeur faciale soit de 1. Notons Y0, le taux de rendement de
l’obligation de maturité T :](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-82-320.jpg)
![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 83 / 118 Mémoire du DEA Finance de Marché
00
1
PLn
T
Y
En remplaçant le prix par son expression :
))]()()((1[
1
2
²
2
1
0
10 dN
K
I
dNLn
T
rY
r
Le spread S0 se définit comme la différence entre Y0 et le taux de rendement
d’une obligation zéro – coupon sans risque.
Il est donné par :
))]()()((1[
1
2
²
2
1
0
10 dN
K
I
dNLn
T
S
r
Cette formule permet de comparer le rendement d’une obligation climatique et
d’une obligation classique sans risque (obligation d’état ou d’entreprise AAA).
Toute chose égale par ailleurs, le spread est une fonction décroissante de la
maturité. C’est une fonction croissante du pourcentage à risque : plus les
investisseurs peuvent perdre, plus ils demandent un rendement supplémentaire
3.1.1.3. Elasticité et Duration
Les concepts d’élasticité et de duration sont des indicateurs du risque de taux
pour une obligation.
L’élasticité est donnée par
r
P
P
n
0
0
0
1
En appliquant cette formule à l’expression
P0 = e
-rT
F ( TKITQ
,
1 )](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-83-320.jpg)
![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 84 / 118 Mémoire du DEA Finance de Marché
On obtient
r
Q
Q
Tn TKI
TKI
T
T
,
,
1
0
Si = 0, on retombe sur la duration standard de Macaulay
Pour les obligations exposées au risque climatique, le signe dépend de la
dérivée de la probabilité risque neutre de premier passage par rapport au taux
d’intérêt
)()(
²
2
)(]))((')('[ 0²
2
1
0
2
²
2
1
0
21
,
K
I
Ln
K
I
dN
K
I
dNdN
T
r
Q rr
T TKI
3.1.1.4. Weather bonds et Treasury bonds
Une obligation climatique peut s’analyser comme un portefeuille composé de
deux actifs :
Une position longue sur une obligation de même risque de défaut
Une position courte sur une option binaire
L’option binaire a un payout discontinu et paie un montant fixe si le sous –
jacent satisfait un certain niveau prédéterminé.
Le rendement moyen d’une obligation climatique est donné par :
E[RP0] = B E[RB] -D E[RD]
Avec E[RB] : taux de rendement attendu sur l’obligation sans risque équivalente
E[RD] : taux de rendement attendu sur l’option binaire
B : poids de l’obligation sans risque dans le portefeuille
D : poids de l’option binaire dans le portefeuille
Les poids de chaque composante peuvent être exprimés en terme de la
probabilité risque neutre de 1er passage.](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-84-320.jpg)



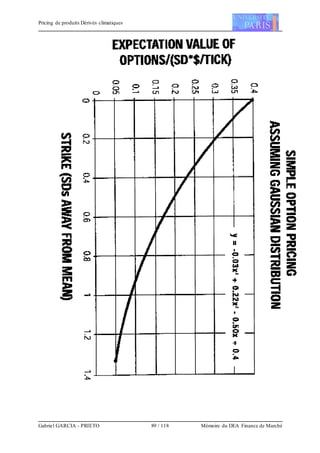





![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 96 / 118 Mémoire du DEA Finance de Marché
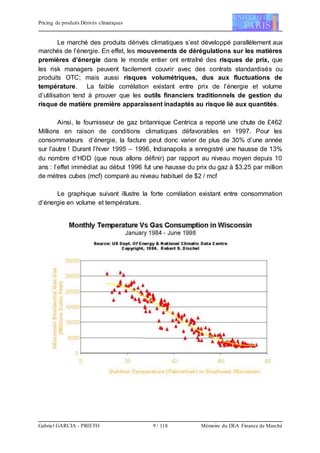
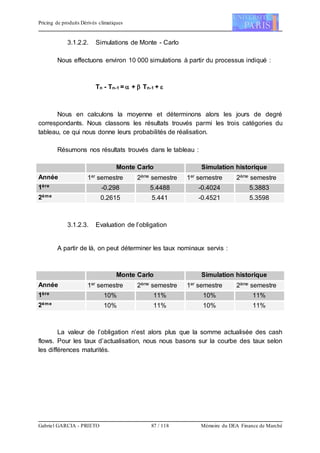
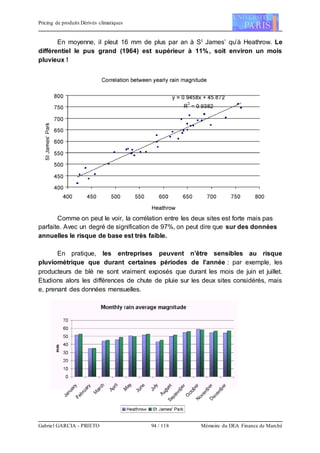
Si on représente sur un graphique la fréquence de pluie sur une année, on
s’aperçoit qu’il pleut plus souvent en hiver qu’en été (ce dont on pouvait s’attendre
intuitivement). La distribution n’est toutefois pas symétrique et une fonction
sinusoïdale apparaît inadéquate pour la modélisation.
Par ailleurs, on peut s’apercevoir qu’il existe un phénomène de mémoire entre
les jours pluvieux et les jours secs : un jour sec est généralement suivi d’un jour sec,
et vice versa. La probabilité de pluie est donc conditionnelle au passé.
Notons Xt l’événement « il pleut à la date t ». Xt suit une loi de Bernoulli
Xt = 0 de probabilité 1- pt
1 de probabilité pt
1 = « il pleut »
Nous connaissons la moyenne historique de Xt. C’est toutefois insuffisant pour
modéliser les séries temporelles Xt. Supposer l’indépendance des Xi revient à avoir
E [Xt / Xt-1, Xt-2, Xt-3] = E [Xt] = pt
Ce qui est différent de EH [Xt] (opérateur d’espérance historique).
Ainsi, la probabilité pt a une espérance dépendant du passé et est
conditionnelle à Xt-1, Xt-2, Xt-3,…
Nous sommes amenés à raisonner par récurrence pour déterminer le
degré de retard.
La probabilité pt est donnée par : pt = P (Xt =1 / Xt-1, Xt-2, Xt-3,…, Xt-k)
L’objectif est de déterminer la valeur minimale de k qui modélise au mieux la
distribution sur la période considérée.
Pour une année de 365 jours, on suppose E [pt] = E [pt+365], ce qui suppose
que le climat ne varie pas d’une année sur l’autre, i.e. il pleuvra toujours plus
fréquemment en hiver qu’en été.
Nous estimons tout d’abord les probabilités conditionnelles pour k = 1,
simulons le processus et comparons distribution simulée avec la distribution
historique. Nous reprenons la méthode pour plusieurs valeurs de k. La valeur la plus
petite estimant au mieux les données historiques est retenue..](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-96-320.jpg)


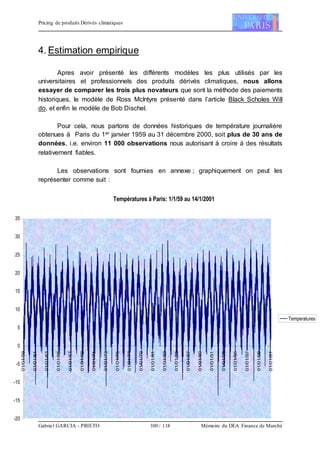
![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 101 / 118 Mémoire du DEA Finance de Marché
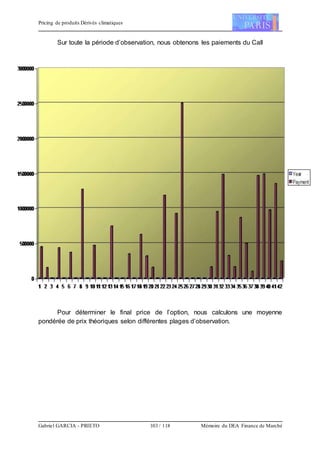
Par ces trois modèles, nous allons pricer un Call CDD. Ce produit paie si les
températures estivales se vérifient supérieures à la moyenne (65° Fahrenheit ou
ici 18° Celsius). Ce produit pourrait par exemple intéresser une entreprise de
cinéma qui craindrait que si le temps se révèle trop ensoleillé, les gens n’aillent
« s’enfermer » dans une salle de cinéma mais plutôt aller à la plage,… La période à
couvrir est de 6 mois : du 1er avril au 30 septembre, le strike de 100 CDD. Selon les
standards de marché, le Call paie 10 000$ par CDD.
4.1. Méthode des paiements historiques (Burn analysis)
Bien que peu satisfaisante d’un point de vue théorique puisqu’on ne tient pas
compte de quelconque prévision météorologique, cette méthode se révèle en fait la
plus utilisée par les acteurs du marché des produits dérivés climatiques par sa
simplicité d’utilisation et par la relative pertinence des prix donnés.
L’idée est de se demander ce qu’aurait payé le produit financier les années
passées. Pour cela,
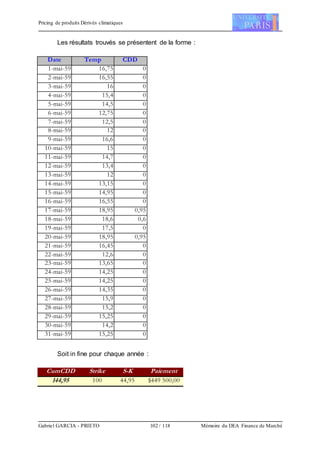
A partir des données historiques nous calculons pour chaque jour
Max [(Température– 18) ; 0]
Pour chaque année nous sommons les CDD trouvés afin de déterminer
Max [ (CumCDD - Strike) ; 0]](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-101-320.jpg)

![Pricing de produits Dérivés climatiques
Gabriel GARCIA - PRIETO 107 / 118 Mémoire du DEA Finance de Marché
4.3. Le modèle de Bob Dischel
The Dischel D1 Stochastic Temperature Model est mathématiquement le plus
abouti. On ne cherche pas à modéliser ici les Degree Days, et encore moins les
paiements passés mais bien les températures elles –mêmes ! Ainsi, la perte
d’information est minimale, et le modèle se veut non pas à vocation purement
financière mais permettrait aussi de prévoir globalement les températures futures.
Comme on l’a vu la dynamique utilisée est un processus Mean Reverting avec
deux sources de risque : température et variations de température :
dT = [ (t) * (t) - T(t)] dt + dm1 + dm2 (1)
est la moyenne historique variant avec le temps, et représente le centre de
gravité vers lequel le paramètre revient
et sont deux coefficients constants
Le grand apport de ce modèle est que les processus m1 et m2 sont
quelconques, ce qui permet de lever l’hypothèse relativement lourde de normalité
imposée par les autres modèles.
En pratique, l’auteur propose de prendre une version discrétisée du processus
est de n’utiliséer qu’une seule source de risque : les variations de température.
Tˆ signifie que la valeur de la variable est simulée ou projetée.
est la moyenne pour toutes les dates qui nous intéressent.
annéesdNombre
T
année
dateannée
date
'
,
La première étape consiste donc à déterminer les valeurs constantes et
sous l’hypothèse que + = 1 et = 1. Par un algorithme d’optimisation relativement](https://image.slidesharecdn.com/682f4eeb-9625-4b3c-a25e-de090d7b4437-151103224315-lva1-app6892/85/Gab-107-320.jpg)