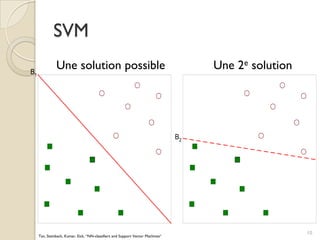
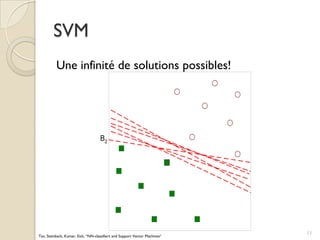
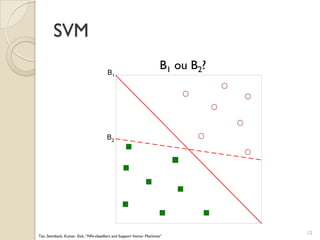
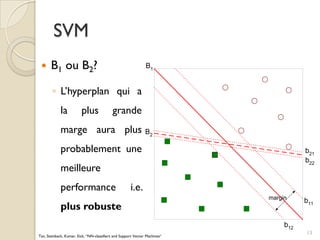
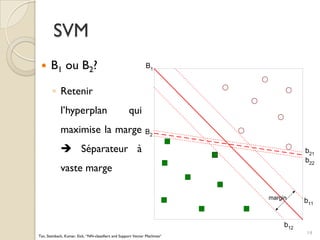
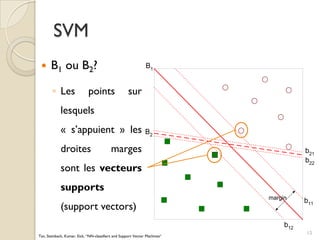
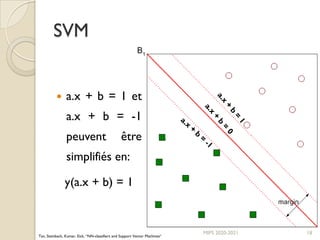
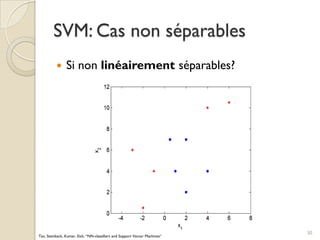
Le document traite des machines à vecteurs de support (SVM) dans le cadre de l'apprentissage supervisé, en expliquant leur fonctionnement, leurs applications et les défis associés. Il présente des concepts clés tels que la maximisation de la marge et l'utilisation de noyaux pour traiter des données non linéairement séparables. Enfin, le texte aborde les avantages et les inconvénients des SVM en termes de robustesse et de complexité de modélisation.