Métriques pour l'évaluation de l'Annotation

Métriques pour l’évaluation de l’Annotation
Jean-Philippe Fauconnier

Institut de Recherche en Informatique de Toulouse
Équipe MELODI

25 novembre 2013


Métriques pour l’Annotation

1 / 71

Introduction
1. Annotation au sens Linguistique et TAL
Annotation de corpus
Annotation : une méta-donnée sur du texte (Pustejovsky et Stubbs, 2012)
(...) it is not enough to simply provide a computer with a large
amount of data and expect it to learn to speak—the data has
to be prepared in such a way that the computer can more
easily ﬁnd patterns and inferences. This is usually done by
adding relevant metadata to a dataset. Any metadata tag used
to mark up elements of the dataset is called an annotation
over the input.
Corpus annoté : ensemble de textes annotés (Pustejovsky et Stubbs, 2012)
Datasets of natural language are referred to as corpora, and a
single set of data annotated with the same speciﬁcation is
called an annotated corpus.



2 / 71

Introduction
2. Pourquoi annoter ? (Rosset, 2013)
• Évaluer un modèle théorique (Péry-Woodley, et al., 2009)
• Développer/Évaluer un système TAL (Afantenos et al., 2010)
• Observer des phénomènes (Pascual, 1995 ; Rebeyrolle, 2009)
3. Cadre pour l’annotation
• Corpus
Pré-annoté ou non
• Annotateurs (≥2)
Étudiants, chercheurs, experts, etc.
• Guide d’annotation
Description de la tâche et rédaction itérative
• Schéma d’annotation
Conventions pour représenter l’annotation
• Outils
MAE (Stubbs, 2011), Glozz (Widlöcher et Mathet, 2009 ; 2012), etc.


3 / 71

Introduction
4. Pourquoi bien annoter ?
• Risque de silence pour les approche symboliques
• Risque de bruit dans les tâches en ML
• Faire des hypothèses et les éprouver empiriquement
• Assurer la reproductibilité de ces expériences
Constitution d’un corpus // méthodologie expérimentale (stat.)
→ Relation entre var. indépendantes et dépendantes
→ Diminuer les variables cachées (confounding factors)
→ Corpus et annotateurs "représentatifs"
→ Objectif : dégager des liens causalité
Cependant
• Mais en réalité, beaucoup de facteurs interviennent
• Et peut-on réellement considérer un annotateur comme un processus
aléatoire et indépendant ?

D’où un réel besoin d’évaluer.


4 / 71

Introduction
5. Évaluer pour :
-

Qualité du corpus
Qualité des annotations
Estimateurs stat. pour un phénomène
Produire un alignement consistant

6. Qu’est-ce qu’on évalue ?
-

Le corpus ?
Les annotateurs ?
Le guide d’annotation ?
Le schéma d’annotation ?

7. Et comment ?
- Tests d’hypothèse ?
- Corrélation intra-classes ?
- Coeﬃcients d’accord ?


5 / 71

Introduction
Validity vs. Reliability :
Notions reprises de l’Analyse de Contenu (Krippendorf, 2004), où les chercheurs
visent à diminuer les biais, et adaptées au TAL (Artstein et Peosio, 2008).

1. Validity :
Vérifier la validité du schéma d’annotation.
• Les catégories définies sont-elles correctes ?
• Est-ce qu’il s’agit de la vérité ?
• Validity ← Reliability

2. Reliability :
Vérifier la fiabilité de la tâche d’annotation
• Stability :
Accord intra-annotateur
• Reproductibility :
Accord inter-annotateurs
• Accuracy :
Comparaison à un "gold standard"


6 / 71

Introduction
Et après l’évaluation de la validité/fiabilité ?
⇒ Question de l’alignement
Comment choisir l’annotation finale ?
- Un annotateur expert ?
- Un vote majoritaire ?
- Discussion entre annotateurs ?
→ Dépendances entre annotateurs ?
→ Mise à mal de la situation expérimentale ?

Dans les prochaines sections :
- Section 1 : Retour sur les coefficients d’accord
- Section 2 : Une approche unifiée pour l’accord et l’alignement
- Section 3 : Corpus LARAt - Un cas concret



7 / 71

1

Coeﬃcients pour l’accord
Nécessité d’une mesure du hasard
2 annotateurs : s, π et κ
Multiples-annotateurs : multi-π, multi-k
Métriques pondérées : α, kw et αk
Interprétation

2

Une approche holiste et uniﬁée

3

Corpus LARAt : un cas concret



8 / 71


Les coefficients d’accord (Artstein & Peosio, 2008)
- forment une famille de métriques
- mesurent l’accord entre codeurs
- sont contraints dans un intervalle [-1,1]
accord = 1 accord parfait
accord = 0 aucun accord
accord = -1 désaccord parfait
Pourquoi les coefficients d’accord ?
Il existe d’autres métriques/tests.
- Accord observé
- Test d’hypothèse du χ2
- Coefficients de corrélation


9 / 71

Nécessité d’une mesure du hasard : Accord observé

Accord Observé
Ao est la plus simple mesure pour l’accord
(1) Dénombrer les items i où les codeurs c sont en accord
(2) Accord = quand à un item i est assigné une même catégorie k
(3) Diviser par le nombre N d’items pour obtenir un pourcentage.
A2
isA instOf Synon Multi Total
isA
20
5
25
10
15
25
instOf
A1
Synon
15
10
25
Multi
5
20
25
Total
25
25
25
25
100
Ao =

1
N

nk =
k∈K

60
= 0, 60
100

10 / 71


Accord Observé
- Ao rentre dans le calcul de tous les coeﬃcients
- Cependant Ao seul n’est pas suﬃsant
- Le facteur de "chance" est ignoré
- → impossibilité de comparer les études
Deux facteurs :
Variation de ces deux facteurs d’une étude à l’autre.
- Le nombre K de catégories (Scott, 1955)
- Distribution des items i (Di Eugenio et Glass, 2004)



11 / 71


(Scott, 1955)
"[percentage agreement] is biased in favor of dimensions with a
small number of categories."

k1
k2
Total

k1
1/4
1/2

k2
1/4
1/2

k1
k2
k3
Total

k1
1/9
1/3

k2
1/9
1/3

k3
1/9
1/3

K =2

Total
1/2
1/2
1


Par "chance" : 1/4 des i
dans chaque cellule
Ao = 1/2
Total
1/3
1/3
1/3
1

K =3
Par "chance" : 1/9 des i
dans chaque cellule
Ao = 1/3

12 / 71


(Arstein & Peosio, 2008)
"(...) we expect a higher percentage agreement when one category
is much more common than the other."
Supposons la distribution suivante :
- 95 % des i d’un domaine sont k1
- 5 % des i d’un domaine sont k2

k1
k2
Total

k1
0,95
0,95

k2
0,05
0,05


Total
0,95
0,05
1

• Par "chance" : (0, 95)2
des i classés en k1 et
(0, 05)2 classés en k2 .
• Par "chance" :
Ao = (0, 95)2 + (0, 05)2
= 90,5 %

13 / 71

Nécessité d’une mesure du hasard : Test du Chi-2

Un test statistique pour l’accord ?
- Tests d’hypothèses évaluent une hypothèse statistiquement
- Ces tests produisent une p-value qui permet de rejeter ou
accepter une hypothèse selon un risque alpha (souvent à 0,05)
Test du Chi-2
- Le χ2 teste l’indépendance entre deux V.A X et Y
- Sous H0 : X et Y sont indépendants
- Sous H1 : X et Y ont une "relation"

- Comparaison des distributions de X et Y pour choisir l’hypothèse
- Cependant, (Cohen, 1960) montre que le χ2 mesure l’association
et non l’accord.



14 / 71

Nécessité d’une mesure du hasard : Test du Chi-2

Test du χ2 de Pearson

isA
instOf
Synon
Multi
Total

isA
20

instOf

Synon

10
15

15
10

25

25

isA
isA
instOf
Synon
Multi
Total

5
25

instOf

Synon

10
15

15
10

25

25

Multi
5

25
25


20
25
Multi
25

25

Total
25
25
25
25
100
Total
25
25
25
25
100

Ao = 0,60
X 2 = 140
p-value < 0,01
→ Accord

Ao = 0,20
X 2 = 204
p-value < 0,01
→ Désaccord


15 / 71

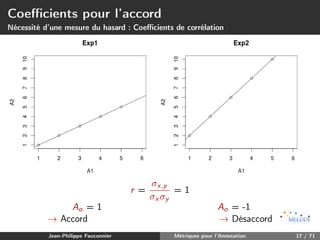
Nécessité d’une mesure du hasard : Coeﬃcients de corrélation

Coeﬃcients de corrélation r et rs
- mesurent la corrélation entre une V.A X et Y
- prennent une valeur entre [-1,1]
- Cependant, mesurent l’existence d’une relation et non l’accord
Supposons l’exemple suivant :
- Deux expériences avec chacune 2 codeurs et 5 items
- À chaque item est attribué une valeur entre [1,5] (rating)
Item
a
b
c
d
e

Exp1
A1 A2
1
1
2
2
3
3
4
4
5
5

Exp2
A1 A2
1
2
2
4
3
6
4
8
5
10

16 / 71

Nécessité d’une mesure du hasard : Coeﬃcients de corrélation

Existence d’une relation aﬃne

r =
Ao = 1
→ Accord

σx,y
=1
σx σy
Ao = -1
→ Désaccord

17 / 71


Nécessiter d’une correction par la chance
- Ao ne suﬃt pas
- χ2 , r et rs ne sont pas adaptés
- il est nécessaire de prendre en compte la "chance" avec laquelle
les annotateurs auraient pu tomber d’accord.
Accord attendu
- Ae une mesure pour estimer le "hasard"
- Une formule qui corrige Ao
- Mesure corrigée de ce que serait l’accord "réel" sous l’eﬀet du hasard.
- Si Ao élevé, mais que Ae l’est aussi 0
- Si Ao moyen, mais que Ae est bas, → 1

Ao − Ae
1 − Ae


18 / 71

1

Interprétation

2


3




19 / 71

2 annotateurs : S, Pi et Kappa

Comment estimer le hasard pour 2 annotateurs ?
- L’estimation de Ae diﬀère dans les métriques :
- S (Bennett et al., 1954)
- π (Scott, 1955)
- κ (Cohen, 1960)

- Mais la formule reste identique :

S, π, κ =


Ao − Ae
1 − Ae

20 / 71


Comment calculer Ae ?
Situation expérimentale avec des annotateurs indépendants
Implique :
• Indépendance entre deux événements (d’annotation)
• Ainsi, si A et B, deux événements, sont indépendants :

P(A ∩ B) = P(A).P(B)
(*) L’hypothèse d’indépendance est très controversée (cf. John Uebersax)

Ae : la somme des produits sur toutes les catégories k :

AS , Aπ , Aκ =
e
e
e

P(kc1 ).P(kc2 )
k∈K



21 / 71


Comment calculer

k∈K

P(kc1 ).P(kc2 ) ?

C’est dans l’estimation du hasard que S, π, κ diﬀèrent :

- S = Distribution uniforme
1
Pas de distinction p(k) = k
As =
e

1 1
k∈K k . k

- π = Une seule distribution
ˆ
Distinction des catégories p (k) =
Aπ =
e

k∈K

1
= k.( k )2 =

nk
2N

ˆ
ˆ
P(k).P(k) =

- κ = Distributions individuelles
Distinction des catégories et des codeurs

Aκ =
e

k∈K


1
k

nk 2
k∈K ( 2N )
nc1 k
N
nc1 k nc2 k
k∈K N . N

ˆ
p (k|ci ) =

ˆ
ˆ
P(k|ci ).P(k|ci ) =


22 / 71

2 annotateurs : comparaison

Comparaison des métriques
Pour Ao ﬁxé à 0,60
isA
instOf
Synon
Multi
Total

isA
instOf
Synon
Multi
Total

isA
20

Synon

10
15
5
25

instOf

15
10

25

25

isA
20
10
10

instOf
10
10

Synon
10

40

20

Multi
5

20
25
Multi

10


20

20
20

Total
25
25
25
25
100
Total
40
20
20
20
100

S = 0,467
π = 0,467
κ = 0,467

S = 0,467
π = 0,444
κ = 0,444


23 / 71

2 annotateurs : comparaison

Comparaison des métriques
Pour Ao ﬁxé à 0,60

isA
instOf
Synon
Multi
Total

isA
20

20

instOf
5
10
5

Synon
5
5
10

20

20

Multi
10
5
5
20
40

Total
40
20
20
20
100

S = 0,467
π = 0,460
κ = 0,474

"Paradoxe" du Kappa
Le κ augmente lorsque les distributions des annotateurs divergent
et, inversement, pénalise les distributions similaires.


24 / 71

1

Interprétation

2


3




25 / 71

Multiples annotateurs : multi-Pi et multi-kappa

Multi-π et Multi-k
- Métriques π et κ ont leur généralisation à de multiples codeurs
- π (Scott, 1955) ⇒ k de Fleiss (Fleiss, 1971), appelé multi-π
- κ (Cohen, 1960)⇒ k de (Davies et Fleiss, 1982), appelé multi-κ

"Accident" terminologique
En TAL :
• Proposition d’un "kappa" (Carletta, 1996)
• issu du K (Siegel et Castellan, 1988)
• lui-même issu du κ de Fleiss (Fleiss, 1971)
• Et le κ de Fleiss est une généralisation du π (Scott, 1955)


26 / 71

Multiples annotateurs : multi-Pi et multi-kappa

Principe
- Utilisation de tables d’accord
- Impossibilité d’utiliser des tables de contingence
- Divergences :
- Distribution seule : multi-π
- Distributions individuelles : multi-κ

Item
i1
i2
.
.
iN
Total

isA
1
3

instOf
0
1

Synon
2
0

Multi
1
0

0
60 (0,4)

4
15 (0,1)

0
30 (0,2)

0
45 (0,3)



27 / 71

1

Interprétation

2


3




28 / 71

Coefficient cube

Coefficient cube (Artstein et Peosio, 2008)
- Classification des coefficients selon 3 axes



29 / 71

Métriques pondérées

Métriques pondérées
- α (Krippendorf, 1980)
- κw (Cohen, 1968)
- αk (Artstein et Peosio, 2008)
Principe
• Utilisation d’une fonction de distance δ
• Mesurer le désaccord Do
De
-

Do
De
Do
De
Do
De

= 0 accord parfait
= 1 aucun accord
> 1 désaccord systématique

• Que l’on soustrait à 1 pour la comparaison entre coeﬃcients
Do
1−
De


30 / 71

Métriques pondérées : fonction de distance

Fonction de distance δ
- Donner des coûts diﬀérents aux erreurs
- Utilisation d’une matrice de distance entre les catégories
- Permet de déﬁnir une distance pour plusieurs types de variables :
nominale, ordinale, rating, ratio
δki ,kj = (ki − kj )2 =

0
si ki = kj
0 < x ≤ 1 si ki = kj

- Croissance quadratique pour pénaliser les écarts
- La matrice de distance doit être symétrique
isA
instOf
Synon
Multi

isA
0
0.5
1
1

instOf
0.5
0
1
1

Synon
1
1
0
1

Multi
1
1
1
0


31 / 71

Métriques pondérées : alpha de krippendorf

α (Krippendorf, 1980)
- Multiples codeurs et types de variables
- Autorise les annotations manquantes
- Reste signiﬁcatif avec de petits échantillons (Krippendorf, 2004)
- S’apparente au test ANOVA
Test ANOVA (Analysis of Variance)
- Le test ANOVA teste si deux V.A X et Y proviennent de la
même population
- Sous H0 : X et Y < même population
- Sous H1 : X et Y ne proviennent pas de la même population

- Comparaison des variances de X et Y pour choisir l’hypothèse
- Dans l’α :
- Faible variance
0 Accord
- Variance limitée 1 Aucun accord
- Variance élevée > 1 Désaccord


32 / 71

1

Interprétation

2


3




33 / 71

Interprétation des coeﬃcients d’accord

Échelle d’interprétation (Fort, 2011 ; Rosset, 2013)
- (Landis & Koch, 1977)
0,00-0,20 0,21 - 0,40
mauvais
médiocre

0,41 - 0,60
moyen

- (Krippendorf, 1980)
0,00 - 0,67
0,67 - 0,80
incohérence aucune décision
- (Green, 1997)
0,00 - 0,40 0,40 - 0,75
faible
moyen

0,61 - 0,80
bon

0,81 - 1,00
excellent

0,81 - 1,00
cohérence

0,75 - 1,00
élevé

34 / 71

Interprétation des coefficients d’accord : biais et prévalence

Biais : le "paradoxe du k"
- Le k paraît récompenser les distributions qui diffèrent
- (Di Eugenio et Glass, 2004) : utiliser le κ en discours où les
distributions diffèrent, π/α quand les distributions sont similaires.
- (Artstein et Peosio, 2008) : bien qu’il y ait divergence pour un Ao
fixé, dans la pratique Ao et Ae sont dépendants (car issus des
mêmes données).

isA
instOf
Synon
Multi
Total

isA
20

20

instOf
5
10
5

Synon
5
5
10

20

20


Multi
10
5
5
20
40

Total
40
20
20
20
100

S = 0,467
π = 0,460
κ = 0,474


35 / 71

Interprétation des coefficients d’accord : biais et prévalence

Prévalence :
- La distribution des items tend à diminuer le coefficient.
- (Artstein et Peosio, 2008) : les coefficients corrigés par une
mesure de hasard sont sensibles à l’accord sur les catégories rares.

isA
Multi
Total

isA
0,90
0
0,90

Multi
0,05
0,05
0,10


Total
0,95
0,05
1

• Ak = 0,95
o
• Ak = 0,86
e
• k

= 0,63


36 / 71

Interprétation des coefficients d’accord

Quels coefficients pour quelle évaluation ?
(Artstein et Peosio, 2008)

1. Validité du schéma d’annotation
- Les coefficients à distributions individuelles k, kw et αk
reflètent mieux le travail individuel des annotateurs.
Les annotateurs ont-ils bien compris ?
Le schéma reflète-t-il la réalité/vérité ?
Le guide d’annotation est-il pertinent ?

2. Fiabilité de la tâche d’annotation
- Les coefficients à simple distribution π, multi-π, α
diminuent la variance et permettent la généralisation.
La tâche est-elle reproductible ?
L’annotation est-elle cohérente ?
Les résultats tirés de ce corpus sont fiables ?


37 / 71

1


2

Le désaccord comme créateur de désordre
Alignement
Alignement idéal et mesure d’accord

3




38 / 71

Problématique : Accord et Alignement

Accord sur des unités non-prédéﬁnies
- Les coef. fonctionnent pour les cas où les unités sont prédéﬁnies
(e.g : PosTag, annotation syntaxique, etc.)

- Comment estimer l’accord avec des unités qui "pavent" le texte ?
(e.g : REN, chaînes anaphoriques, Discours, etc.)



39 / 71


- F-Mesure :
- Une annotation est considérée comme annotation de référence
- Une moy. harmonique est eﬀectuée entre le rappel et la précision
- Moy. sur le corpus (micro-avg) ou sur chaque doc./cat. (macro-avg)
- Pour codeurs>2 , on préférera l’exactitude

Présent
Absent
precision =

Présent
TP
FP

TP
TP + FP

F (β) = (1 + β 2 )

TPci ,cj
N.C

c∈C

(micro-avg)

Absent
FN
TN
recall =

TP
TP + FN

precision.recall
β 2 .precision + recall

- Alternative : adaptation de α (voir Krippendorf, 2004)


40 / 71


- Comment définir un TP ?
À partir de quel écart est-on prêt à dire que 2 unités ayant une
position légèrement différente (chez c1 , c2 et c3 ) désignent bien
le même phénomène ?

Problème de l’alignement
- Le choix d’une métrique d’accord ne résout pas l’alignement :
Comment choisir la position finale ?
Comment choisir la catégorie finale ?
Comment produire un alignement consistant ?


41 / 71

(Mathet, 2011)

Une approche holiste et unifiée (Mathet et Widlöcher, 2011)
- unifiée : définit l’accord et l’alignement en utilisant la position et
la catégorisation des items
- holiste : prend en compte tous les items pour l’alignement final
Principes :
- accord et alignement = tâches inter-dépendantes
- Meilleur alignement = alignement qui minimise le désordre
- Meilleur accord = valeur de désordre



42 / 71

1


2

Alignement

3




43 / 71


Désaccord = Désordre
- Hypothèse : Pour c codeurs, même si position et catégorisation
diffèrent, elles devraient en grande partie converger (dans le cas
contraire, tâche = échec).
- Idée : calculer le désordre pour estimer le désaccord
- Accord parfait : les unités i ont les mêmes bornes et catégories
- Désaccord : les unités i n’ont pas les mêmes bornes et catégories

- Combien de transformations entre accord parfait et désaccord ?
Transformations
1. déplacement de bornes de début et de fin
2. requalification de catégories
3. suppression d’unités


44 / 71


Fonction de Dissimilarité d
- La fonction de dissimilarité d s’apparente à la fonction δkrippendorf
- Diﬀérence : elle s’applique directement aux items i (et non aux k)

diu ,iv =

0
si iu = iv
0 < x si iu = iv

- Diﬀérence : elle est appliquée à la position et la catégorisation
• dpos mesure la distance dans le texte
• dcat mesure la distance entre catégories



45 / 71


Dissimilarité positionnelle
- Soit start(i) et end (i) pour l’indice de début et de ﬁn de l’item i
dans le texte

2
|start(iu ) − start(iv )| + |end (iu ) − end (iu )| 
dpos iu ,iv = 
(end(iu )−start(iu ))+(start(iv )+end(iv ))
2

• Croissance quadratique pour pénaliser les écarts importants
• |start(iu ) − start(iv )| + |end (iu ) − end (iu )|
Somme des écarts absolus pour deux items
•

(end(iu )−start(iu ))+(end(iv )+start(iv ))
2

Moyenne des unités. Permet le passage à des échelles diﬀérentes.



46 / 71


Dissimilarité catégorielle
- Deux fonctions :
- dcat : dissimilarité entre deux unités
- distcat : diﬀérence entre les catégories dans la matrice symétrique

- où dcat est :
dcat

iu ,iv

= distcat (kiu , kiv ).∆∅

- où distcat retourne la valeur dans la matrice :
isA
instOf
Synon
Multi

isA
0
0.5
1
1

instOf
0.5
0
1
1

Synon
1
1
0
1

Multi
1
1
1
0


47 / 71


Dissimilarité combinée
- dcombi est une combinaison linéaire de dpos et dcat

dcombi

iu ,iv

= a.dpos (iu , iv ) + b.dcat (iu , iv )

- où si a = 0, 5 et b = 0, 5, un poids égal est donné aux deux
dissimilarités :

dcombi

iu ,iv


=

dpos (iu , iv ) + dcat (iu , iv )
2


48 / 71

1


2

Alignement

3




49 / 71

Alignement

Distinction entre alignement unitaire et alignement
.

- a = un alignement unitaire entre deux unités
- ¯ = un ensemble d’alignements unitaires pour un jeu d’annotation
a
Alignement unitaire
.

- a, un n-uplet, avec n compris dans l’intervalle [1, C ]
.
- a contient, au plus, une unité de chaque annotateur
Alignement
c1
c2
1
( i1 , i∅ )
1
2
( i1 , i1 )
( ... , ... )
1
2
( i3 , i12 )

→ alignement vide avec unité ﬁctive i∅
→ vrai alignement
→ "faux" alignement

Nombre d’alignements unitaires générables : (

c∈C

Nc ) − 1


50 / 71

Alignement et Entropie

Entropie dans le sens de désordre (et non de (Shannon, 1948))

Alignement unitaire :
- Idée : mesurer le désordre d’un alignement unitaire en utilisant
une fonction de dissimilarité
- On mesure l’"entropie" d’un alignement unitaire, pour une dx
donnée, en faisant la moyenne de ses dissimilarités.
. .

e(a) =

1
n
2

dx (iu , iv )
.

iu ,iv ∈a

Intuition
Au plus un alignement unitaire aura de grandes distances entre ses
unités, au plus il aura de "désordre", c’est-à-dire d’entropie au sens
de (Mathet, 2011).


51 / 71


Entropie dans le sens de désordre (et non de (Shannon, 1948))

Alignement :
- On mesure l’"entropie" d’un alignement en faisant la moyenne de
.
l’entropie de chacun de ses alignements unitaires a
1
¯a
e (¯) =
|¯|
a

|¯|
a
. .

e(a)
i=1

- Ici, la moyenne est considérée aﬁn d’éviter, dans le cas de
comparaison entre deux jeux, l’un avec doublons et l’autre sans,
qu’il y ait une diﬀérence d’entropie.


52 / 71

1


2

Alignement

3




53 / 71


Alignement idéal :
- ˆ est l’alignement ¯ qui minimise l’entropie pour tous les
a
a
.
alignements unitaires a possibles pour un jeu d’annotations j.
Mesure d’accord
- Pour un jeu d’annotations j et un corpus c (textes nus) :
ealeatoire (c) − e(j)
ealeatoire (c)
- où ealeatoire est une estimation du "hasard" (cf. section 1), c-à-d
de ce que pourrait être l’entropie pour un corpus donné.
accord (j) =

Interprétation
• Si accord (j) = 1, accord parfait et entropie nulle.
• Si accord (j) ≤ 0, aucun accord.


54 / 71

Alignement idée et mesure d’accord

Ainsi :
- le choix de l’alignement idéal se fait sur base de l’entropie
- réciproquement, la mesure d’accord se fait sur base de
l’alignement idéal.

Dans la pratique :
.

- Réduction de l’espace de recherche en enlevant les a improbables
- Algorithme d’approximation pour une solution approchée de ˆ
a
- Nécessité, cependant, de déﬁnir un ∆∅ pour chaque campagne


55 / 71

1


2


3

Cadre
Retour sur la tâche d’annotation
Exploitation



56 / 71

Corpus LARAt
Cadre

Une campagne d’annotation
- Objectif : Annoter des structures énumératives selon une
typologie multi-dimensionnelle avec plusieurs axes.
- Corpus :
- 249 documents de Wikipédia (< GEONTO)
- 87 documents de Annodis

- Un guide d’annotation
- 2 annotateurs étudiants
Outil :
- Les SE sont objets discursifs où la mise en forme du texte est
nécessaire pour l’annotation en texte.
- Les outils tels que Callisto, MMAX2, Glozz ne conviennent pas.
- Nécessité d’un outil adapté :
Développement de LARAt


57 / 71

Corpus LARAt
Cadre

Interface de LARAt


58 / 71

Corpus LARAt

Des distributions diﬀérentes pour les annotateurs :
- Annotateur 1 sur Axe Sémantique



59 / 71

Corpus LARAt

Des distributions diﬀérentes pour les annotateurs :
- Annotateur 2 sur Axe Sémantique



60 / 71

Corpus LARAt

Distributions diﬀérentes au niveau du nombre d’items :
- Les classes InstanceOf et isA : grand nombre d’items + outliers



61 / 71

Corpus LARAt
Exploitation

Exploitation :
1. Nécessité de déﬁnir un alignement pour calculer les accords
2. Calculer des coef. à distributions individuelles pour évaluer la
typologie (k)
3. calculer des coef. à distribution simple pour évaluer le
corpus/tâche (α)
1. Alignement par le positionnement
- Les multiples axes empêchent une approche uniﬁée
- Alternative : estimer les paramètres de distance
- qui nécessite d’annoter un petit set d’annotations ..



62 / 71

Corpus LARAt
Exploitation : alignement par le positionnement

Génération d’alignements unitaires
- Sous-ensemble restreint du corpus (env. 300 annot.)
- Objectif : estimer des seuils sur diﬀ − start et diﬀ − end



63 / 71

Corpus LARAt

Annotation semi-automatique des alignements "réels"



64 / 71

Corpus LARAt

Estimation d’une frontière de décision
- Par Support Vector Machine (SVM)



65 / 71

Corpus LARAt

Estimation d’une frontière de décision
- Par régression logistique (ici sur la seule variable diﬀ − start)
- Moyennement eﬃcace mais modèle moins "boîte noire"



66 / 71

Conclusion
L’annotation
- est à la base de la majorité des systèmes TAL
- est un sujet non clos :
-

L’annotation multi-labels
Le seuil d’accord humain et les performances en ML
Les annotateurs réellement "aléatoires" sous A. Mechanical Turk
etc.

Accord et Alignement :
- ne sont pas des problèmes indépendants
- il existe de nombreuses métriques :
- Nécessité d’un choix conscient
- Et d’intervalles de conﬁance ?



67 / 71

Références
• S. Afantenos, P. Denis, P. Muller, and L. Danlos, "Learning recursive
segments for discourse parsing," in Proc. Proceedings of 7th Language
Resources and Evaluation Conference (LREC 2010), 2010.
• R. Artstein and M. Poesio, "Inter-coder agreement for computational
linguistics," Computational Linguistics, vol. 34, iss. 4, pp. 555-596, 2008.
• E. M. Bennett, R. Alpert, and A. Goldstein, "Communications through
limited-response questioning," Public Opinion Quarterly, vol. 18, iss. 3, pp.
303-308, 1954.
• Y. Bestgen, "Quels indices pour mesurer l’efficacité en segmentation
thématique ?," in Proc. Actes de la 16e Conférence sur le Traitement
Automatique des Langues Naturelles (TALN 2009), 2009.
• J. Carletta, "Assessing agreement on classification tasks : the kappa
statistic," Computational linguistics, vol. 22, iss. 2, pp. 249-254, 1996.
• J. Cohen and others, "A coefficient of agreement for nominal scales,"
Educational and psychological measurement, vol. 20, iss. 1, pp. 37-46, 1960.
• J. Cohen, "Weighted kappa : Nominal scale agreement provision for scaled
disagreement or partial credit.," Psychological bulletin, vol. 70, iss. 4, p.
213, 1968.
• B. Di Eugenio and M. Glass, "The kappa statistic : A second look,"
Computational linguistics, vol. 30, iss. 1, pp. 95-101, 2004.


68 / 71

Références
• J. L. Fleiss, "Measuring nominal scale agreement among many raters.,"
Psychological bulletin, vol. 76, iss. 5, p. 378, 1971.
• Fort, K., Corpus Linguistics : Inter-Annotator Agreements, INIST, 2011.
• A. M. Green, "Kappa statistics for multiple raters using categorical
classifications," in Proc. Proceedings of the 22nd annual SAS User Group
International conference, 1997, pp. 1110-1115.
• C. Grouin, S. Rosset, P. Zweigenbaum, K. Fort, O. Galibert, and L.
Quintard, "Proposal for an extension of traditional named entities : From
guidelines to evaluation, an overview," in Proc. Proceedings of the 5th
Linguistic Annotation Workshop, 2011, pp. 92-100.
• K. Krippendorff, Content analysis : An introduction to its methodology,
Sage Publications, 1980.
• K. Krippendorff, "On the reliability of unitizing continuous data,"
Sociological Methodology, pp. 47-76, 1995.
• K. Krippendorff, "Measuring the reliability of qualitative text analysis data,"
Quality & Quantity, vol. 38, pp. 787-800, 2004.
• R. J. Landis and G. G. Koch, "The measurement of observer agreement for
categorical data," biometrics, pp. 159-174, 1977.


69 / 71

Références
• Y. Mathet and A. Widlöcher, "Une approche holiste et uniﬁée de
l’alignement et de la mesure d’accord inter-annotateurs," in Proc. Actes de
la 18e Conférence sur le Traitement Automatique des Langues Naturelles
(TALN 2011), 2011.
• C. Müller and M. Strube, "Multi-level annotation of linguistic data with
MMAX2," , Braun, S., Kohn, K., and Mukherjee, J., Eds., Frankfurt a.M.,
Germany : Peter Lang, 2006, pp. 197-214.
• E. Pascual and M. P. Pery-Woodley, "La déﬁnition dans le texte," Textes de
type consigne–Perception, action, cognition, pp. 65-88, 1995.
• M. Péry-Woodley, N. Asher, P. Enjalbert, F. Benamara, M. Bras, C. Fabre,
S. Ferrari, L. Ho-Dac, A. Le Draoulec, Y. Mathet, and others, "ANNODIS :
une approche outillée de l’annotation de structures discursives," in Proc.
Actes de la 16e Conférence sur le Traitement Automatique des Langues
Naturelles (TALN 2009), 2009.
• J. Pustejovsky and A. Stubbs, Natural language annotation for machine
learning, O’Reilly, 2012.
• J. Rebeyrolle, M. P. Jacques, M. P. Péry-Woodley, and others, "Titres et
intertitres dans l’organisation du discours 1," Journal of French Language
Studies, vol. 19, iss. 2, p. 269, 2009.


70 / 71

Références
• Rosset, S., Accords inter-annotateurs dans une campagne d’annotation : de
la théorie à la pratique, CLEE-ERSS, 2013.
• W. A. Scott, "Reliability of content analysis : The case of nominal scale
coding.," Public opinion quarterly, 1955.
• S. Siegel and J. N. Castellan, Nonparametric Statistics for the Behavioral
Sciences, McGraw-HiU Book Company, N. Y., Ed., , 1988, vol. 2nd edition.
• C. E. Shannon, "A mathematical theory of communication," The Bell
System Technical Journal„ vol. 27, iss. 1, pp. 379-423, 1948.
• A. Stubbs, "MAE and MAI : Lightweight Annotation and Adjudication
Tools," in Proc. Proceedings of the 5th Linguistic Annotation Workshop,
Association of Computational Linguistics, Portland, 2011.
• A. Widlöcher and Y. Mathet, "La plate-forme Glozz : environnement
d’annotation et d’exploration de corpus," in Proc. Actes de la 16e
Conférence sur le Traitement Automatique des Langues Naturelles (TALN
2009), 2009.
• A. Widlöcher and Y. Mathet, "The Glozz platform : a corpus annotation
and mining tool," in Proc. Proceedings of the 2012 ACM symposium on
Document engineering, 2012, pp. 171-180.



71 / 71

Métriques pour l'évaluation de l'Annotation

Contenu connexe

Tendances

En vedette

Métriques pour l'évaluation de l'Annotation