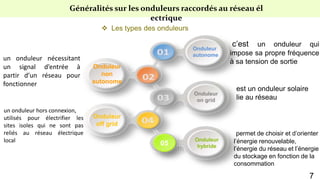
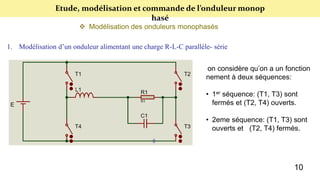
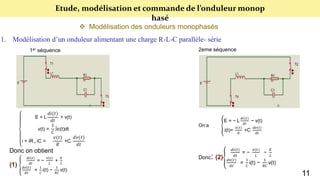
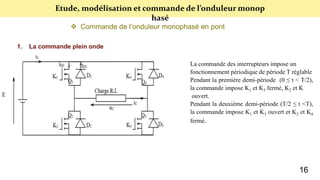
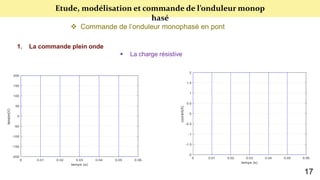
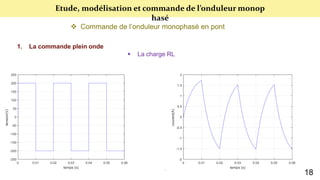
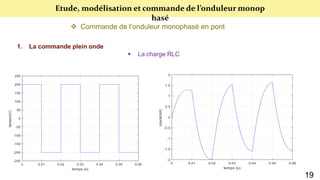
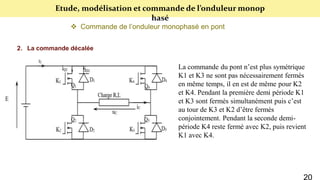
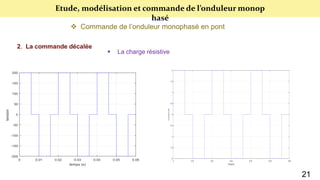
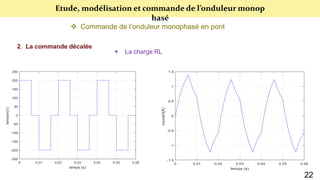
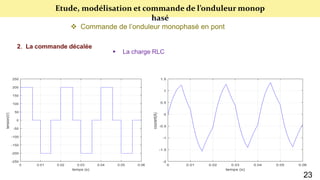
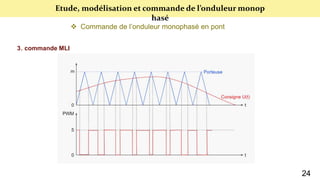
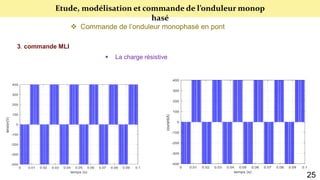
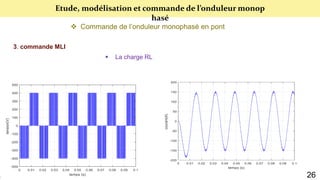
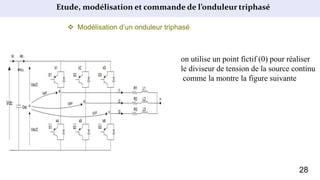
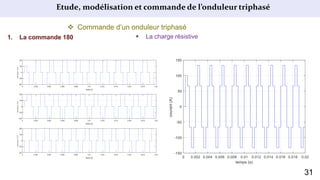
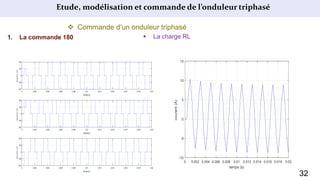
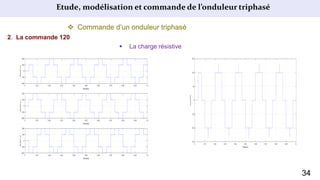
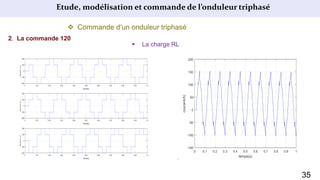
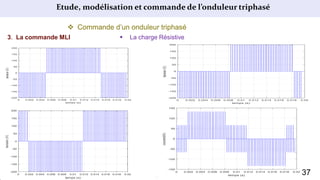
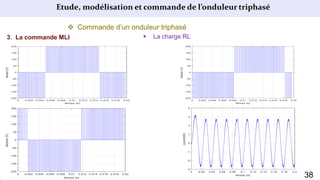
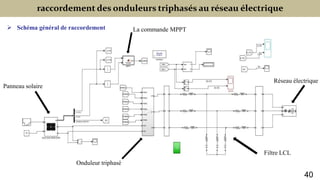
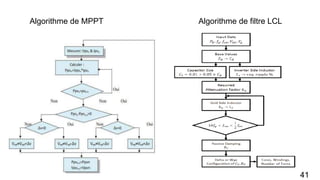
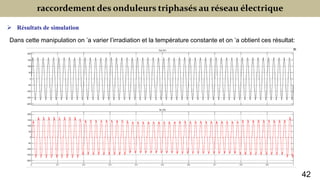
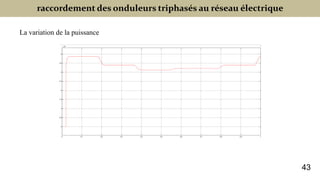
Le document présente une étude sur le raccordement des panneaux photovoltaïques au réseau électrique, en se concentrant sur la modélisation et la commande des onduleurs monophasés et triphasés. Il aborde les types d'onduleurs, leurs applications et les méthodes de commande, tout en soulignant l'importance croissante des énergies renouvelables dans le contexte des besoins énergétiques mondiaux. Les résultats de simulation sont également présentés, démontrant la variabilité de la puissance injectée en fonction de l'éclairement et de la température.