Le document traite de la stabilité des navires, en mettant l'accent sur la relation entre le poids, la forme, et le centre de gravité. Il décrit différentes conditions d'équilibre (stable, instable, et indifférent) en fonction de la position du centre de gravité par rapport au centre de carène. Des calculs pratiques pour déterminer la stabilité longitudinale et transversale sont également présentés, incluant des exemples et des méthodologies spécifiques.

1. 1
RESUME STABILITE.
STABILITE DE FORME.
STABILITE DE POIDS.
On appelle « MODULE DE STABILITE INITIALE TRANSVERSALE Msi », le
produit du poids (DEPLACEMENT) par la hauteur métacentrique. Gm. P. Gm
Msi = P. Gm
P (r-a) = P (TKM – KG)
KM – KG = (r – a) = GoM.
HAUTEUR METACENTRIQUE. Gm.
Gm = h = (r-a) = TKM – KG? À calculer par les moments.
m
TKm *
h. θ
r. L1
*G
Fo. a. θ Gîte. Lo
*Co C1
F1
KC KG
K
Supposons l’action d’une force qui tend à incliner transversalement le navire.
La FORME de la CARENE changera en même temps que la position du CENTRE de
CARENE. Tandis que le centre de gravité « G », qui dépend que de la répartition ou distribution
des POIDS reste INVARIABLE.
Dans ces conditions, les lignes d’action des deux forces P et π ne seront plus coïncidentes.
KG. KC. TKm.
GC = a.
Gm = h.
Cm = r = φ.

2. 2
Vu que P = π il en résulte un « MOMENT » oppose à l’action inclinante entre les deux
lignes d’action // entre elles de P et π.
* m *m
π
π
C
* Co *
Co
* G * G ne change pas.
P
STABILITE TRANSVERSALES.
Pour des inclinaisons transversales < de 10 à 12°, la ligne d’action de π rencontre le plan
longitudinal de symétrie en un point que nous pouvons faire coïncider avec le métacentre initial
correspondant à la position droite du navire. Trois cas se présentent.
I. «G.» AU-DESSOUS DE «C.» cargaison Fond de cale.
Le MOMENT qui résulte de l’inclinaison initiale est un moment redresseur qui tend à ramener
le navire à la position initiale.
h * m. L1
r.
F θ
Fo. Lo
θ
F1 π
Co C1
X
Go
a. P
*
K
Sinus = Côté oppose sur Hypoténuse
Sin O = X/Gom; X = Gom. Sin O
Le Couple de redressement est. Poids x Bras de levier. PX.

3. 3
P.X = P. GoM sin θ = P. (r + a). Sin θ
Msi = P. (r + a) > O
En inclinant légèrement le navire d’un angle θ (faible), Co passe en C1 tandis que G ne varie
pas. Les deux forces ne sont plus sur la même verticale, donc il s’est créé un COUPLE qui a
tendance à ramener le navire à sa position initiale.
On peut donc dire que pour ce cas, L’EQUILIBRE EST STABLE.
II. «G» AU-DESSUS DE «C.» / Cargaison en pontée.
En inclinant le navire d’un angle θ (faible), Co passe en C1. Les deux forces ne sont plus sur la
même verticale. Donc il s’est crée un COUPLE PX dont le msi est positif, il y a réaction d’un
COUPLE DE REDRESSEMENT.
* m.
L1 π
X
r. G * θ
Fo. Lo
P
F1 a
C0 C1
*
π
LE COUPLE DE REDRESSEMENT PX.
PX = P. mG. Sin θ = P (r – a) sin θ
P (r – a) = msi > 0 donc PX est positif.
C’est un équilibre stable.

4. 4
m. CONFONDU AVEC G.
Le navire, une fois, incliné restera en équilibre dans sa nouvelle position à la cessation de
la courbe inclinante donc l’équilibre est INDIFFERENT.
Une inclinaison ultérieure provoquera un changement d’équilibre.
COUPLE PX = P. Gm. Sin θ
r. = a.
Donc:
P(r – a) sin θ = O. PX = O
Msi = P(r – a) = O.
m. AU-DESSOUS DE G.
A la moindre inclinaison initiale, le MOMENT qui en résulte est un moment inclinant qui
accentue le mouvement, donc, l’EQUILIBRE EST INSTABLE.
*G
a. π P.
* m. L1
r.
Fo θ Lo
*
F π
F1 C1
Co.
Couple PX = P. Gm. Sin θ = Couple de redressement.
PX = P (a – r) Sin θ
msi = P ( a – r) < O. Equilibre INSTABLE.
Le couple ainsi a tendance à augmenter la gîte, c’est un COUPLE DE CHAVIREMENT.
C’est le cas de l’équilibre instable.
En définitive, on peut dire que l’équilibre est stable si la stabilité de FORME est
supérieure à la stabilité de POIDS.

5. 5
STABILITE TRANSVERSALE.
* m.
GM = r – a θ Couple de redressement L1. P = v. w = H
Z (+) Couple de redressement
G* Cm = r.
r. Z’
Fo. C. Chavirement.(-) θ CG = a.
a. Lo
P H GM = (r – a)
F1 *C’ GZ = (r – a) sin θ
C*
C GZ= Bras de levier.
MOMENT DU COUPLE DE STABILITE.
P x GZ = P (r - a) Sin θ
MODULE DE STABILITE.
P (r – a)o > O
VALEUR DE r = φ = I/V
I = L.l³ / I2. Moment d’inertie / axe longitudinal
V = L. l. Tm. Volume de carène.

6. 6
CORRECTION D’ASSIETE. (ONGLET). MN.
O PPM
TAR² L
A’
θ
TAR1 ∆TAR. F? M A AV1
θ Cor.
δ ∆T
N.
TAR
∆TAV
TF? TF. Tm.
L’
TAV²
TAV
TF = Tm + MN
Tg θ = MN = ∆TAV = δ∆T
FM FA. L
MN = Tgθ. FM = δ ∆T. (± FM)
L
TF = TAV + TAR ± FM. ∆T
2 L.
TF = Tm + FM. ∆T
L.
POUR UNE ASSIETE POSITIVE.
AR AV AR AV
F F
(+) (-)
TF TF

7. 7
CALCUL PRATIQUE.
Si TM > Tm. C/Arc. TM + I/3 C/Arc
Si TM < Tm. Arc. TM – I/3 Arc
T’m = TAR + TAV ± ONGLET ± Arc D’T
2
EXEMPLE.
Tm D TM = 7m20
7m20 12150 TAR = 8m10
7m40 12535 TAV = 6m60 Calculer D’ ?
7m45 12678 F sur AV de M à 3m.
L = 160m.
TM = 7m20
TF = Tm + Cor. MN + Arc Tm = 7.35 m.
MN = FM. ∆T/L
MN = 3m. x 1,5 = 0,03m Tm > TM. Arc. (-)
160
ARC = TM – Tm = 7m20 – 7,35 = 0.15 le tiers.= 0.05
TF = 7.35 + 0.03 + 0.05 = 7.43 m.
D’= Voir table. Avec TF.

8. 8
THEOREME DES MOMENTS. KG? OG?
OG K O
Poids KG PPAR Mt / Quille Mt / PPAR
Navire lège ------ ----- --------- ------------- --------------
P x KG P x OG
Cale 1 p1
Cale 2 p²
Soute p3…
Σ poids ΣMt Σ Mt
Mt = P x Dist.
KG = Σ Mt ; OG = Σ Mt / PPAR
Σ Poids Σ Poids
STABILITE LONGITUDINALE.
PPAR. m. PPAV.
F G
O* C’ *
* C. Centre de flottaison.
K.
Lorsque le navire est droit, G et C sont à égale distance / PPAR/M
Et même alignement / m, msi.
Lorsque le navire gîte ou prend une assiette. C se déplace en C’
Et Co en C1. G ne change pas de position. TOUT TOURNE
AUTOUR DE G.

9. 9
M.
*
PPAR PPM PPAV
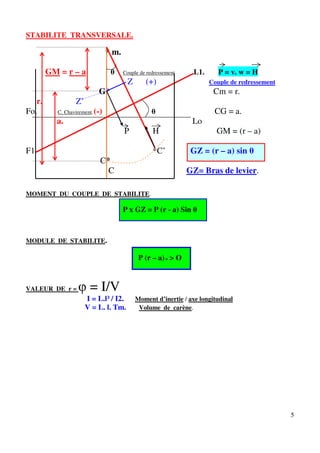
F1 LCG
* G.
Fo. LCF. F. M Lo
N ψ
d.
LCB C1 * Co
Tm. TM. L1
TF
*
K.
Lpp
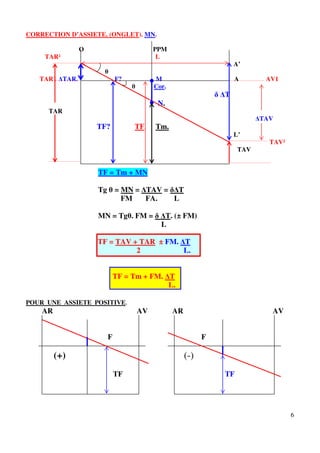
Tm = TM si navire droit.
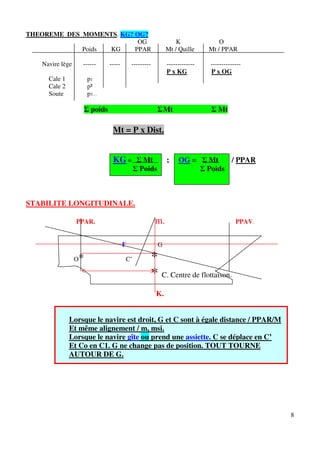
LCB. – LCF. – LCG.
LEST LIQUIDE.
m
*i * *Dx. Le liquide étant mobil, on doit considérer qu’il est
Transféré en D Métacentre.
I / V = φ
g.1 D = φ = I / V / axe longitudinal
p = V d
g.²
g.1 Mvt de poids vers le haut. Stabilité diminue.
p
[P (φ – a)]’ = P (φ – a)o – pgiD.
p
p. gi. D = vd. I/V = id.
(φ – a)’ = (φ – a)o – id / P

10. 10
Exemple.
Id = 30 x 15³ x 1.025 = 8648 m4
L = 30 m. 12
l. = 15 m.
d. = 1.025
P = 10.000 ts (φ – a)’ = 0.50 - 8648 = - 0.36 m
(φ – a) o = 0.50 m 10.000
New (φ – a)’?
Stabilité négative. Couple de chavirement.
UTILISATION DES COURBES HYDROSTATIQUES.
RESOLUTION DES PROBLEMES DE STABILITE.
Courbe hydrostatique.
TF D TPC LCB LCF TKm MTC.
m tonnes e/cm/t/cm OC/Mt / PPAR OFMt / PPAR m 1°/t. m / cm
6.20 8.104 14.93 54.98 53.18 7.02 88.10
7.60 10.252 15.98 53.93 50.69 7.28 104.35
Tm ; TE navire droit – TE moyen. TE Corrigé. Onglet + ARC et C/arc.
D ; Poids total ; Déplacement du navire.
TPC ; Poids nécessaire pour faire enfoncer le navire de e = 1 cm
LCB ; position du centre de carène / PPAR. OC.
LCF ; Position du centre de gravité de la flottaison / PPAR « C ». OF.
MTC ; Couple nécessaire pour varier une gîte de 1°. Pd.

11. 11
CALCUL DE STABILITE.
DESIGNATION P LCG/OG Mo/m
P. OG
KG Mo/m
P. KG
ωi
D. Lège 2695 47,04 126772,8 7,39 11916,05 ---------
Cale N°1
Entre-pont N°1.
Cales N°2 - 3.
Entrepont N°2 – 3.
Pontée
Total Cargaison.
Gas – Oil. / D.O 64,65 10,40 671,84 6,46 417,31 27,5
FO.
Huiles.
F.Water. 215. 37,20 16.070,40 1,59 686,88 226,8
Total Machine
CST. 250
GRAND TOTAL 10.130 52,18 528671,96 6,03 61.142,67 ----
Mt = P.D D = Mt/D KG = S. Mt / S. P
Pour un Déplacement de 10.130 ts, on lit sur la table hydrostatique.
Tm = 7,52m. ∆T = 1,75.
TPC = 15,92. LCF = 50,80.
LCB = 53,97.
LCF = 50,80. TEAV = 6,59 Ht métacentrique GoM = 1,20 m.
TKm 7,26. TEAR = 8,34
MTC = 103,30
KG = 1,23. Tm = 7,46
Cor. GGo = 8,03
METHODE DE CALCUL.
Déplacement total = 10.130 ts.
LCG = ΣMt = 528.677,96 = 52,8 m.
ΣPt 10.130
KG = 61.1425,67 = 6,03
10.130
GMs = TKM – KG = 7,28 – 6,03 = 1,23 m
GoM = GMs – ωi / Dt = 1,23 – 293 / 10.130 = 1,23.
COUPLE INCLINANT.
CI = P x BG = Dt x BG.

12. 12
BG = LCB – LCG = OG – OC
BG = 53,97 – 52,18 = 1,79.
CI = 18.132,70.
CALCUL DE ∆T = Différence d’assiette.
∆T m = CI / MTC = 18.132,7 / 103,6 = 1,75 m.
TgΨ = ∆T / Lpp = 1,75 / 108 = 0,01
TAR = Tm + LCF x TgΨ
TAR = 7,52 + (50,80 x 0,01) = 8m02.
TAV = TAR – ∆T
TAV 8,02 – 1,75 = 6m27
Tm = TAV = TAR = 6.27 – 8.02 / 2 = 7.14m
2
GGo = GMs – GoM
GGo = 1,23 – 1,20
GGo = 0.03 m
M/V IBN KHALDOUN. II. 7 TGI.
CALCUL DE STABILITE. P =φ.V
DESIGNATION POIDS LCG / OOO GGG Moment KKK GGG Moment Wi.
Peack Avant. 359 6,50 2333,5 10 cm.
N°1 Bd & Td 298 1.0 298,0
N°2 Bd & Td 260 0,74 192,4
N°4 Bd & Td 235 0,75 176,3
N°19 Central 200 0,71 142,0
Total EM / 1,025 1352 tonnes 2,32 3142,2
N°17 Bd 14 9,40 131,6
N°17 Td 44 9,22 405,7
Peack AR. 86 6,56 564,2
Total F / Water. 144 tonnes 7,7 1101,5
N°3 Bd 383 0,73 279,6
N°3 Td 112 0,73 81,7
N°5 C 112 0,71 79,5

13. 13
N°6 C 124 0,71 88,0
N°14.15.16.21. 69 5,60 386,4
Total FO / 0,90 688 tonnes 1,33 915,2
N°7 62 1,20 74,4
N°12 09 8,30 74,7
N°18 55 6,10 335,5
Total DO / 0,84 126 tonnes 3,84 484,6
LO/0,9.8.9.10.11 19,5 tonnes 5,07 98,9
Cale I 4,34 5742,5
Cale II 4,07 4,13
Cale III 4,10
Faux-Pont I 8,82
Faux-pont II 8,75 8,77
Faux-pont III 8,75
Pontée I 10m+ 14,43
Pontée II 12m+
Total Cargaison
NAVIRE - LEGE 2940 tonnes 7,25 21315,0 GM/3,5
Constante 250 tonnes? 6m 1500,0
DEPLACEMENT 5519 ts. KM/7,70 5,20 m. 28557.5 GoM/2,5
Déplacement:T’m 3,90
Différence.
TAR. = f (Déplacement), la table Hydrostatique.)
TAV. = LCB/OC LCF/OF TKM TPC MTC
∆T =
Tm. =
TM. =

14. 14
A.
C/Arc = GGG ooo MMM = TKM – KG?
Onglet. =
T’m =
Lpp =117,70 m.
19,50 m x 10,50 26 x 10,50 2 T/m² 13 x 7,80
2 m. 2 m 55 19% 33,4% 47%
1722 m³. 2,92 m. 2300 m³. 4,62 m. 1114 m³. 2,96
10m.
2,3 T/m²
2075 m³. 4,70 m. 3043 m³. 4,80 m. 1066 m³. 4,30 m.
4,40 m.
10 T/m²
2m10
3796 m³. 5343 m³. 2181 m³.
26,60 m. 37,80 m. 22 m.
TOTAL CALES... = 6185 m³. TOTAL = 11.321 m³
TOTAL Fx–PONTS = 5136 m³.
JB = 5331,59 Tx. Observateur = 19m50 – TE.
JN = 3812,93 Tx.
P/L ETE = 8190 Tx.
P/L HIVER = 7810 Tx. Conteneur 20’ = 6,10 m x 2,43.
1m³ = 35,32 CF.
LHT = 126,60 m 1 CF = 0,028 m³.
Largeur = 17,23 m 1 Ft. = 0,3048 m
Lpp = 117,70 m. 1 m = 3,281 Feet.
TE Maximum = 7,33 m.