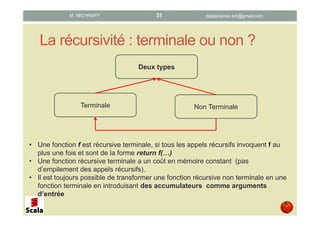
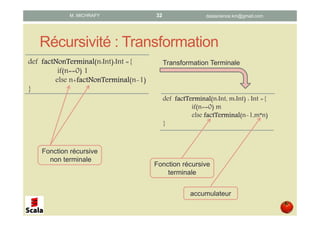
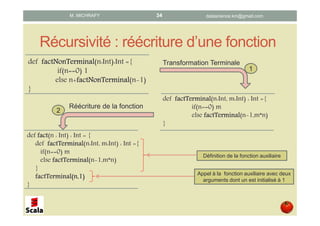
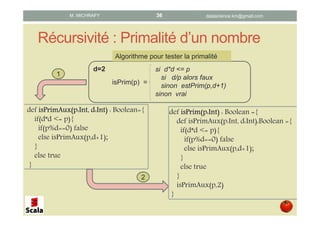
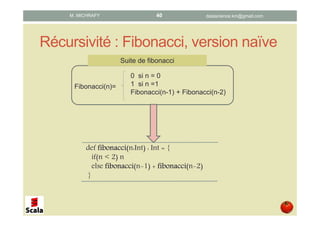
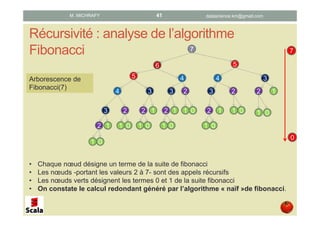
Ce document présente les concepts de la programmation fonctionnelle en Scala, en abordant des éléments tels que les fonctions pures, anonymes, la récursivité et la closure. Il détaille également des exemples pratiques et des syntaxes pour illustrer ces concepts. L'objectif principal est d'initier les lecteurs à la programmation fonctionnelle tout en utilisant Scala comme langage d'implémentation.











![Fonction anonyme : construction
scala> val add1:(Int, Int) => Int = (x:Int, y:Int) => x+y
add1: (Int, Int) => Int = <function2>= <function2>= <function2>= <function2>
scala> add1(1,10)
res0: Int = 11
scala> val add2: Function2[Function2[Function2[Function2[Int,Int,IntInt,Int,IntInt,Int,IntInt,Int,Int]]]] = ((((x:Intx:Intx:Intx:Int, y:Int) =>, y:Int) =>, y:Int) =>, y:Int) => x+yx+yx+yx+y
add2: (Int, Int) => Int = <function2><function2><function2><function2>
scala> add2.applyapplyapplyapply(1,10)
res1: Int = 11
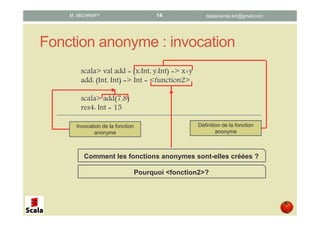
• Une fonction anonyme est instanciée par un objet de type « fonction »
• L’objet étend le type FonctionNFonctionNFonctionNFonctionN, N désignant l’arité de la fonction anonymes
• L ’objet FonctionN dispose d’une méthode « apply »
datascience.km@gmail.comM. MICHRAFY 15](https://image.slidesharecdn.com/scalaprogrammationfonctionnelle-160221102918/85/Scala-programmation-fonctionnelle-15-320.jpg)

![Fonction comme argument : déclaration
• Il est aussi possible de définir une fonction qui prend en
entrée une fonction
• Ce principe est similaire au pointeur de fonction en
C/C++ ou aux interfaces fonctionnelles en Java
• Il suffit de déclarer la signature de la fonction
defdefdefdef nomFonctionnomFonctionnomFonctionnomFonction(fctfctfctfct:([:([:([:([paramsparamsparamsparams]) =>]) =>]) =>]) => typeRetourtypeRetourtypeRetourtypeRetour, arg:type, ...) : typeRetourtypeRetourtypeRetourtypeRetour = {....}
Fonction comme argument d’une autre fonction
datascience.km@gmail.comM. MICHRAFY 17](https://image.slidesharecdn.com/scalaprogrammationfonctionnelle-160221102918/85/Scala-programmation-fonctionnelle-17-320.jpg)