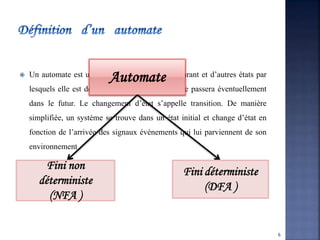
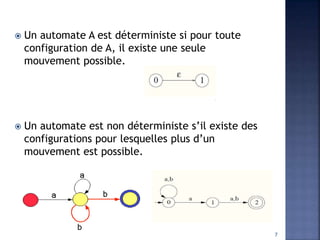
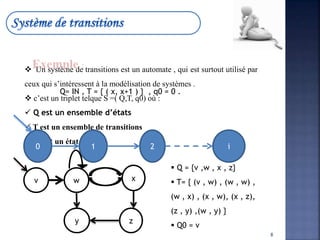
Le document traite des systèmes de transitions étiquetés, qui sont des structures utilisées pour modéliser des systèmes par des automates. Il décrit leur définition, leurs propriétés, ainsi que les différences entre systèmes déterministes et non déterministes. Les applications comprennent la reconnaissance des langages formels et la nécessité d'un formalisme pour représenter des systèmes complexes.

1. Ministère de L’Enseignement
Supérieur, de la Recherche
Scientifique et de la Technologie
Institut Supérieur des Sciences
Appliquées et de Technologie de
Mateur
Réalisée par: Intissar DGUECHI
Encadré par :
 Mr . Bchini Tarek
@mail: intissarstic@gmail.com

2. INTRODUCTION
SYSTÈME DE TRANSITION
SYSTÈME DE TRANSITION ÉTIQUETÉ
COMPOSITION DE SYSTÈMES DE TRANSITIONS ÉTIQUETÉ
CONCLUSION &PERSPECTIVES
PROPRIÉTÉS DES SYSTÈMES DE TRANSITIONS ÉTIQUETÉS
2

3.  Complexité des protocoles de communication :
systèmes distribués
ligne de transmission non fiable
Matériels hétérogènes
Nécéssité d’un formalisme de description
formelle
3

4.  Formalisme de base:
o Automates a état fini
o Réseau de pétri
o Systèmes de transitions étiquetés
o Algèbre de processus
o Formalisme de haut niveau:
o Lotos, Estelle
o SDL
o VHDL
4

5. Le comportement de système est la dimension la plus
cruciale et la plus difficile à modéliser aujourd’hui car :
 Les concepts à utiliser sont nombreux
 Il n’existe pas de modèle théorique permettant de
représenter ces concepts pour tous les systèmes.
Ce qui conduit à représenter le système de façon précise et
non-ambigüe du comportement comme le système de transition
5

6.  Un automate est une machine ayant un état courant et d’autres états par
lesquels elle est déjà passée ou par lesquels elle passera éventuellement
dans le futur. Le changement d’état s’appelle transition. De manière
simplifiée, un système se trouve dans un état initial et change d’état en
fonction de l’arrivée des signaux événements qui lui parviennent de son
environnement .
Automate
Fini déterministe
(DFA )
Fini non
déterministe
(NFA )
6

7.  Un automate A est déterministe si pour toute
configuration de A, il existe une seule
mouvement possible.
 Un automate est non déterministe s’il existe des
configurations pour lesquelles plus d’un
mouvement est possible.
7

8.  Un système de transitions est un automate , qui est surtout utilisé par
ceux qui s’intéressent à la modélisation de systèmes .
 c’est un triplet telque S =( Q,T, q0) où :
 Q est un ensemble d’états
 T est un ensemble de transitions
 q0 est un état initial
Exemple :
Q= IN , T = { ( x, x+1 ) } , q0 = 0 .
0 1 2 i
w x
y z
v
 Q = {v ,w , x , z}
 T= { (v , w) , (w , w) ,
(w , x) , (x , w), (x , z),
(z , y) ,(w , y) }
 Q0 = v
8

9. Différences avec un automate :
Une transition n'est pas causée par l'environnement
Pas d‘états terminaux
Nombre d‘états infini possible
Exécution infinie possible
9

10.  Un système de transitions étiqueté est un quadruplet
 S= ( Q , A , T , q0 )
 Q = est un ensemble d’états
 A = est un alphabet fini d’actions étiquetant les transitions
 T = est un ensemble de transitions reliant les états deux à deux
w x
y z
v
b
a
b
bc
a
a
• Q = { v , w , x , z , y }
• A = { a, b , c }
• T = { (v , a , w) , ( w, b , w )
(w , a , x ) , (w , b , x )
, (x ,b , z ) , ( z , a , y ),
(w , c , y ) }
• q0 = v
10

11. Exemple :
L’automate modélise un compteur modulo 4 . Les états de cet
automate correspondent aux quatre valeurs du compteur (0, 1, 2, 3).
Les transitions traduisent les opérations inc (incrémentation) et dec
(décrémentation) du compteur.
0
23
1
inc
Formellement, l’automate est décrit par :
 S = {0, 1, 2, 3}
 s0 = {0}
 E = {inc, dec}
T = {(0, inc, 1), (1, inc, 2), (2, inc, 3), (3, inc, 0), (0, dec, 3),
(1, dec, 0), (2, dec, 1), (3, dec, 2)}
inc
inc dec
dec
dec
11

12.  Syntaxe pour les étiquettes :
Selon la classe d’automate considérée , la forme des étiquettes change
Alors , La syntaxe des étiquettes est définie par :
<étiquette> ::= [ <garde> ‘:’ ] [ <Liste d’événements>[ ; <condition sur
horloge>] ‘/’ ] [ <liste d’actions> ]
 [<x>] signifie que le champ <x> est peut être vide .
 <garde> est une condition exprimée à l’aide de variables de
l’automate.
 <Liste d’événements> contient le nom d’un événement
<liste d’actions> contient le littéral τ .
 <condition sur horloge> est utilisable dans les automates temporisés .
12

13.  L’étiquette associée à une transition peut être composée de
trois types d’éléments :
 Evénements : permettent le franchissement de transition
 Une garde : qui définit une condition , Le franchissement de la
transition ne peut se faire que si la condition est vraie .
 Des actions : effectuées par l’automate avant de changer
d’état.
 Si l’étiquette associée à une transition est vide, cela signifie
que la transition se fait de manière aléatoire ou de manière
implicite connue par celui qui a fait la modélisation. On peut
avoir un automate où il n’y a que les états interconnectés avec
des transitions sans étiquettes.
 Si l’étiquette ne contient pas d’événement, cela signifie que
le franchissement est aléatoire et est lié uniquement à la garde
si elle existe. Pour des raisons de déterminisme, il faut éviter
d’utiliser des transitions sans événements .
13

14.  Soit S = { Q ,α , T , q0 }
 Le franchissement d’une transition (q , a , q’ ) appartient à « T »
Est noté :
a
Q’Q
 Le franchissement d’une séquence de transitions (qi, ai , qi +1 )
appartient à « T » avec 1 ≤ i < 0 est noté :
q1 q2 qn
a1 a n+1
14

15.  Soient S1= (Q1, A1 , T1 , q0 ) et S2= ( Q2 , A2 , T2 , q1 ) deux
symboles de transition étiquetés .
 Le comportement du système global peut être représenté par un
système de transitions étiqueté S= ( Q , A , T , q0 ) tel que :
Q ⊂ Q1 * Q2
A ⊂ A1 * A2
T ⊂ T1 * T2
q = ( q0 , q1 )
15

16. Un système de transitions étiqueté est fini si et seulement si :
Q et T sont des ensembles finis
Un système de transitions étiqueté est déterministe si et seulement si :
Si pour tout couple <état, étiquette>, le choix de la transition est
unique.
Un système de transitions étiqueté est indéterministe si et seulement si :
S’il existe au moins un état qui a deux transitions étiquetées de
la même .
16

17. Les systèmes de transitions jouent
un rôle important dans
la reconnaissance des langages
formels, notamment aussi dans
leur classification
17

18. Merci pour votre
attention
18