La thèse de Benoît Boulinguiez, soutenue à l'Université de Rennes 1, explore les procédés d'adsorption et de régénération électrothermique sur textile de carbone activé, visant à traiter les composés organiques volatils (COV) dans des gaz énergétiques. Le document présente des modèles de traitement du biogaz en Europe, les matériaux et méthodes utilisés, ainsi que des études sur les dynamiques d'adsorption et de désorption. Cette recherche contribue à résoudre la problématique des COV dans le contexte de l'énergie durable.





































































![1.4. Filières et procédés unitaires de traitement
Figure 1.10 – Structure d’un gel de silice
L’adsorption sur gel de silice a également été testée pour l’adsorption des siloxanes (Schweigkofler
and Niessner, 2001; Ricaurte Ortega, 2009; Finocchio et al., 2009; Matsui and Imamura, 2010). Les capacités d’adsorption mesurées sur les gels de silice sont proches de 100 mg.g−1 , pour des concentrations
en siloxanes de l’ordre du gramme par mètre cube (Schweigkofler and Niessner, 2001; Matsui and Imamura, 2010). Les auteurs de ces recherches ont comparé ces capacités d’adsorption avec d’autres types
d’adsorbants (charbon actif et zéolite) et ont montré que les gels de silice avaient des capacités d’adsorption supérieures aux zéolites mais inférieures aux charbons actifs. Les faibles porosités des gels de silice
en comparaison à celles des charbons actifs expliquent ces observations.
Une autre famille d’adsorbants abondamment employés dans la purification de gaz est celle des zéolites. Les zéolites sont des structures cristallines de silicate d’aluminium contenant un cation métallique,
n+
Mx/n [Alx Siy O2 x+y ] x – · zH2 O de type X ou Y, en fonction de l’agencement cristallin des atomes. Les
zéolites existent à l’état naturel, mais une grande partie de celles utilisées industriellement sont manufacturées. Leur structure cristalline ordonnée détermine la structure poreuse et donc en grande partie les
propriétés adsorbantes de la zéolite. L’intérêt de fabriquer des zéolites réside dans le contrôle de la distribution poreuse, pour la rendre anisotrope et très étroite, augmentant alors la sélectivité pour l’adsorption
(Zhao et al., 1998). Les zéolites synthétiques sont souvent référencées dans la littérature sous le terme de
tamis moléculaire.
Le cation métallique présent dans la structure cristalline est responsable des propriétés acido-basiques
de la zéolite, indirectement du caractère hydrophobe de cette dernière et de la dimension des cages
formées par la structure cristalline. Il est possible de distinguer les zéolites en deux groupes, le premier
étant les zéolites hydrophiles, le second, les hydrophobes. Les premières sont souvent employées dans
des procédés de déshumidification poussée du gaz, alors que les dernières peuvent être utilisées pour
l’adsorption de composés organiques comme les COV (Clausse et al., 1998; López-Fonseca et al., 2003;
Ko et al., 2007; Ricaurte Ortega, 2009).
L’adsorption d’H2 S dans les biogaz fait partie du champ d’application envisagé avec des zéolites
(Cosoli et al., 2008; Yasyerli et al., 2002). Les capacités d’adsorption mesurées restent largement en
dessous des rendements d’épuration pouvant être obtenus avec d’autres systèmes, Yasyerli et al. (2002)
ont déterminé des capacités de 30 mg.g−1 sur de la clinoptilolite, une zéolite naturelle, avec un biogaz
réel. Cosoli et al. (2008) ont rapporté des capacités de 40 mg.g−1 sur des zéolites synthétiques pour des
concentrations d’H2 S de 1000 mg.m−3 .
Le traitement des COV constitue un enjeu clé dans les filières de valorisation de biogaz, cependant
l’utilisation de zéolite pour l’adsorption d’un large spectre de composés — aux propriétés divergentes
— est à l’encontre de l’avantage de ces adsorbants à la porosité spécifique. Par conséquent, un nombre
restreint de recherches s’est intéressé à l’adsorption de différents COV sur une même zéolite (Zhao et al.,
1998).
42](https://image.slidesharecdn.com/theseboulinguiez-140115081139-phpapp02/85/These-boulinguiez-70-320.jpg)



























































































































































































![4.2. ADSORPTION DYNAMIQUE MONO-COMPOSÉ ET MODÉLISATION
kg
le coefficient de transfert de masse global (s−1 )
qe
¯
la quantité d’adsorbat en équilibre avec la concentration en phase gaz (mol.kg−1 )
En dépit des résultats discutés dans la section 3.2 sur la modélisation des isothermes d’adsorption
des COV dans leur matrice respective, les limites de la résolution numérique employée ont contraint
l’utilisation d’un modèle à deux paramètres ajustables uniquement. Celui de Langmuir a été préféré à
celui de Freundlich, en lieu du modèle de Langmuir-Freundlich pour décrire la relation entre la phase
gaz et la quantité adsorbée du COV. Cependant, afin de compenser les faiblesses du modèle de Langmuir
dans la modélisation des isothermes d’adsorption, les valeurs des paramètres bL et qm sont ajustées par
régression non linéaire2 à partir des points à basses concentrations des courbes isothermes.
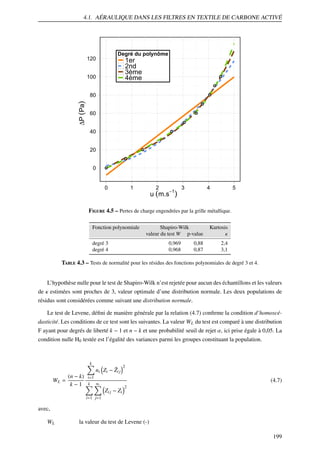
Les résultats de l’ajustement des valeurs des paramètres du modèle de Langmuir sont listés dans
le tableau 4.17 et la figure 4.42 illustre cette démarche par une comparaison des modélisations à basses
concentrations par les modèles de Langmuir et de Freundlich, par rapport au modèle optimal de LangmuirFreundlich déterminé sur la gamme complète de l’isotherme d’adsorption.
qm
(mol.kg−1 )
bL
×103 (m3 .mol−1 )
r2
(-)
toluène
isopropanol
dichlorométhane
éthanethiol
siloxane D4
4,322
5,852
2,870
3,865
1,599
14,038
0,153
0,081
0,063
65,167
0,915
0,992
0,996
0,986
0,962
THT
5,709
0,697
0,997
COV
Table 4.17 – Valeurs des paramètres ajustés du modèle de Langmuir à partir des points à basse concentration
pour les différents COV et à 25 °C.
La relation d’équilibre entre la concentration en phase gaz et la quantité adsorbée dans les simulations
numériques d’adsorption dynamique est par conséquent définie par l’équation de Langmuir (1.22). Le
système algébrico-différentiel définissant les considérations physiques du « modèle 1 » est résumé.
2
¯
−D ∂ C + v ∂C + ∂C + 1 − ρ ∂q = 0
L
s
2
∂z
∂t
∂t
∂z
∂q
¯
− kg (qe − q) = 0
¯
¯
∂t
qm bLC
qe −
¯
=0
1 + bLC
Le système d’équations est adimensionnalisé préalablement à la simulation numérique, afin de borner
toutes les variables sur l’intervalle [0,1]. L’adimensionnalisation fait appel à un changement de variable
et par commodité à des nombres adimensionnels, tel que le nombre de Peclet, noté Pe (Hwang et al.,
1997; Giraudet, 2006; Yao et al., 2009; Fournel et al., 2010). Les relations d’adimensionnalisation sont
les suivantes :
2
La procédure employée pour effectuer l’ajustement des paramètres est identique à celle présentée dans la section 3.2
231](https://image.slidesharecdn.com/theseboulinguiez-140115081139-phpapp02/85/These-boulinguiez-259-320.jpg)
















































![Bibliographie
Condon, J. (2006). Surface area and porosity determinations by physisorption : measurements and
theory. Elsevier, Amsterdam ; ;Boston, 1st ed. edition.
Cosoli, P., Ferrone, M., Pricl, S., and Fermeglia, M. (2008). Hydrogen sulphide removal from biogas by
zeolite adsorption : Part i. GCMC molecular simulations. Chemical Engineering Journal, 145(1) :86–
92.
Coulson, J. M., Richardson, J. F., Backhurst, J. R., and Harker, J. H. (1999). Coulson and Richardson’s
Chemical Engineering Vol.1, volume 1 of Chemical Engineering. Butterworth-Heinemann, Oxford, 6
edition.
Cui, H. and Turn, S. Q. (2009). Adsorption/desorption of dimethylsulfide on activated carbon modified
with iron chloride. Applied Catalysis B : Environmental, 88(1-2) :25–31.
Cui, H., Turn, S. Q., and Reese, M. A. (2009). Removal of sulfur compounds from utility pipelined
synthetic natural gas using modified activated carbons. Catalysis Today, 139(4) :274–279.
Dalai, A. K., Majumdar, A., and Tollefson, E. L. (1999). Low temperature catalytic oxidation of hydrogen sulfide in sour produced wastewater using activated carbon catalysts. Environmental Science &
Technology, 33(13) :2241–2246.
Dalai, A. K., Tollefson, E. L., Yang, A., and Sasaoka, E. (1997). Oxidation of methyl mercaptan over an
activated carbon in a Fixed-Bed reactor. Industrial & Engineering Chemistry Research, 36(11) :4726–
4733.
Das, D., Gaur, V., and Verma, N. (2004). Removal of volatile organic compound by activated carbon
fiber. Carbon, 42(14) :2949–2962.
de Wild, P., Nyqvist, R., de Bruijn, F., and Stobbe, E. (2006). Removal of sulphur-containing odorants
from fuel gases for fuel cell-based combined heat and power applications. Journal of Power Sources,
159 :995–1004.
Deed, C., Rosevear, A., Gronow, J., Braithwaite, P., and Smith, R. (2004a). Guidance on gas treatment
technologies for landfill gas engines. Technical report, UK Environment Agency, Bristol, UK.
Deed, C., Rosevear, A., Gronow, J., Braithwaite, P., and Smith, R. (2004b). Guidance on monitoring
trace components in landfill gas. Technical report, UK Environment Agency, Bristol, UK.
Desikan, P. and Amber, C. (1964). Catalytic hydrodesulphurization of thiophene v. the hydrothiophenes.
selective poisoning and acidity of the catalyst surface. Canadian Journal Chemistry, 42 :843–850.
Deublein, D. (2008). Biogas from waste and renewable resources : an introduction. Wiley-VCH, Weinheim [Germany].
Dewil, R., Appels, L., and Baeyens, J. (2006). Energy use of biogas hampered by the presence of
siloxanes. Energy Conversion and Management, 47(13-14) :1711–1722.
Dowd, J. E. and Riggs, D. S. (1965). A comparison of estimates of Michaelis-Menten kinetic constants
from various linear transformations. Journal of Biological Chemistry, 240(2) :863–869.
Dufour, A., Celzard, A., Ouartassi, B., Broust, F., Fierro, V., and Zoulalian, A. (2009). Effect of micropores diffusion on kinetics of CH4 decomposition over a wood-derived carbon catalyst. Applied
Catalysis A : General, 360(2) :120–125.
Dwivedi, P., Gaur, V., Sharma, A., and Verma, N. (2004). Comparative study of removal of volatile
organic compounds by cryogenic condensation and adsorption by activated carbon fiber. Separation
and Purification Technology, 39(1-2) :23–37.
v](https://image.slidesharecdn.com/theseboulinguiez-140115081139-phpapp02/85/These-boulinguiez-309-320.jpg)



















