Cette thèse examine l'impact de l'activité humaine sur la composition chimique de la troposphère au-dessus de l'océan Pacifique, en développant un modèle téléscopique de chimie et de transport atmosphériques. Les recherches, menées au National Center for Atmospheric Research, impliquent des analyses des processus chimiques et dynamiques ainsi que des aspects mathématiques et météorologiques associés. L'étude inclut également des développements de modèles de chimie-transport tridimensionnels et évalue diverses variables influençant la composition atmosphérique.

1. UNIVERSITE LIBRE DE BRUXELLES
Facult´e des Sciences Appliqu´ees
L’impact de l’activit´e humaine sur la
composition chimique de la troposph`ere
au-dessus de l’Oc´ean Pacifique:
D´eveloppement d’un mod`ele t´el´escopique de chimie et de
transport atmosph´eriques et interpr´etation des r´esultats
de la campagne de mesures MLOPEX.
Th`ese pr´esent´ee en vue de l’obtention du
grade de Docteur en Sciences Appliqu´ees par
Paul Ginoux
Ann´ee acad´emique 1996-1997

2. 2
A la m´emoire d’Antonio

3. 3
Avant-propos
Les recherches pr´esent´ees dans cet ouvrage ont ´et´e effectu´ees au D´epartement
de chimie atmosph´erique (ACD) du National Center for Atmospheric Research
(NCAR) `a Boulder (Colorado). J’adresse ma profonde gratitude `a Guy Brasseur,
directeur de ACD au NCAR et co-promoteur de cette th`ese, pour l’´energie et le
temps qu’il a bien voulu me consacrer. Je remercie toutes les personnes de ACD
qui ont accept´e de m’aider tout au long de ce travail et particuli`erement J.-F.
Lamarque, D. Hauglustaine, Cl. Granier, B. Ridley, E. Atlas et S. Madronich.
Un grand merci `a X. Tie qui partage avec moi cet exceptionnel bureau du NCAR
pour son encouragement dans les moments de doutes.
Je tiens `a t´emoigner sp´ecialement ma reconnaissance `a J.-F. M¨uller,
chercheur `a l’Institut d’A´eronomie Spatiale de Belgique `a Uccle, qui m’a g´en´ereusement
fourni son code chimique et ses cartes globales d’´emission. Je remercie ´egalement
les autres chercheurs de l’Institut d’A´eronomie Spatiale de Belgique, ainsi que
son directeur actuel, P. Simon, pour leur chaleureux accueil qu’ils me r´eservaient.
Mr. H. DecKoninck, professeur `a la facult´e des Sciences Appliqu´ees de
l’Universit´e de Bruxelles et professeur `a l’Institut Von Karman de Rhode-St.-
Gen`ese, a accept´e de promouvoir cette th`ese. Qu’il trouve ici l’expression de mes
sinc`eres remerciements.
C’est pour moi un agr´eable devoir de remercier l’Organisme de la poli-
tique Scientifique, Technique et Culturel (OSTC) et sa responsable Mme
M. Van-
derstraeten pour l’octroi d’un contrat de recherche dans le cadre du programme
d’impulsion ”Global Change” (contrat no
GC/11/018).
Merci `a mon p`ere pour son ´efficacit´e `a corriger le pr´esent manuscrit, `a
ma m`ere et `a ma soeur Isabelle pour leur chaleureux accueil lors de mes visites `a
Bruxelles. Qu’il me soit enfin permis d’exprimer ma tendre affection `a Catherine
avec qui je languis d’impatience de reprendre nos activit´es artistiques communes.
Boulder, le 19 avril 1997.
P.G.

4. 4

5. Contents
1 Introduction 7
2 Processus chimiques et dynamiques en relation avec les donn´ees
MLOPEX 19
2.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2.2 Processus dynamiques dans la troposph`ere . . . . . . . . . . . . . 20
2.2.1 Circulation g´en´erale . . . . . . . . . . . . . . . . . . . . . 22
2.2.2 Circulation au-dessus du Pacifique Nord . . . . . . . . . . 22
2.2.3 Trajectoires . . . . . . . . . . . . . . . . . . . . . . . . . . 29
2.2.4 Transport convectif . . . . . . . . . . . . . . . . . . . . . . 31
2.2.5 Circulation `a proximit´e de l’ˆıle de Hawaii . . . . . . . . . . 32
2.2.6 M´et´eorologie `a l’Observatoire de Mauna Loa . . . . . . . . 36
2.2.7 Etude du traceur isotopique 2
22Rn . . . . . . . . . . . . . 39
2.3 Processus chimiques dans la tropopsh`ere . . . . . . . . . . . . . . 41
2.3.1 M´ecanismes chimiques . . . . . . . . . . . . . . . . . . . . 41
2.3.2 Les d´epˆots sec et humide . . . . . . . . . . . . . . . . . . . 49
2.3.3 Les donn´ees de la campagne MLOPEX-I . . . . . . . . . . 49
2.4 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
3 Aspects math´ematiques 55
3.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
3.2 Les variables d´ependantes . . . . . . . . . . . . . . . . . . . . . . 56
3.3 Les ´equations primitives . . . . . . . . . . . . . . . . . . . . . . . 57
3.3.1 Equation d’´etat . . . . . . . . . . . . . . . . . . . . . . . . 57
3.3.2 Conservation de la masse . . . . . . . . . . . . . . . . . . . 57
3.3.3 Conservation de la quantit´e de mouvement . . . . . . . . . 58
3.3.4 Conservation de l’´energie . . . . . . . . . . . . . . . . . . . 59
3.3.5 Conservation de la vapeur d’eau . . . . . . . . . . . . . . . 60
3.3.6 Conservation des constituants chimiques . . . . . . . . . . 60
3.4 Simplifications des ´equations . . . . . . . . . . . . . . . . . . . . . 61
3.5 Transformations des coordonn´ees . . . . . . . . . . . . . . . . . . 64
5

6. 6 CONTENTS
3.5.1 Transformation des coordonn´ees horizontales . . . . . . . . 64
3.5.2 Transformation de la coordonn´ee verticale. . . . . . . . . . 67
3.6 Param´etrisation des flux turbulents . . . . . . . . . . . . . . . . . 69
3.7 Ensemble des ´equations `a r´esoudre . . . . . . . . . . . . . . . . . 70
3.8 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
4 Variables m´et´eorologiques 73
4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
4.2 Les variables m´et´eorologiques `a l’´echelle globale . . . . . . . . . . 76
4.3 Les variables m´et´eorologiques `a m´eso-´echelle . . . . . . . . . . . . 80
4.4 Comparaison avec les observations . . . . . . . . . . . . . . . . . . 82
4.5 Comparaison avec la climatologie . . . . . . . . . . . . . . . . . . 95
4.6 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95
5 D´eveloppement d’un mod`ele de la couche limite plan´etaire 99
5.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99
5.2 Processus de transport dans la couche limite . . . . . . . . . . . . 99
5.2.1 Echelles caract´eristiques . . . . . . . . . . . . . . . . . . . 100
5.2.2 Param´etrisations du coefficient Km . . . . . . . . . . . . . 102
5.2.3 Hauteur de la couche limite . . . . . . . . . . . . . . . . . 102
5.3 Conditions aux limites . . . . . . . . . . . . . . . . . . . . . . . . 106
5.3.1 Flux turbulents `a la surface . . . . . . . . . . . . . . . . . 106
5.3.2 Longueur de rugosit´e . . . . . . . . . . . . . . . . . . . . . 107
5.3.3 Temp´erature de surface . . . . . . . . . . . . . . . . . . . . 108
5.3.4 Humidit´e sp´ecifique `a la surface terrestre . . . . . . . . . . 114
5.4 Convection par les nuages convectifs profonds . . . . . . . . . . . 115
5.5 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 118
6 D´eveloppement d’un mod`ele de chimie-transport tridimension-
nel de la troposph`ere 121
6.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
6.2 D´efinition du domaine . . . . . . . . . . . . . . . . . . . . . . . . 122
6.3 Maillage du domaine . . . . . . . . . . . . . . . . . . . . . . . . . 125
6.3.1 G´en´eration de la grille structur´ee globale . . . . . . . . . . 126
6.3.2 Maillage de la grille structur´ee . . . . . . . . . . . . . . . . 127
6.3.3 G´en´eration d’une grille non-structur´ee . . . . . . . . . . . 127
6.3.4 Maillage de la grille non-structur´ee . . . . . . . . . . . . . 129
6.4 R´esolution num´erique de l’´equation de continuit´e . . . . . . . . . 131
6.4.1 D´ecouplage des ´equations . . . . . . . . . . . . . . . . . . 133
6.5 Equations photochimiques . . . . . . . . . . . . . . . . . . . . . . 134
6.5.1 Mod`ele photochimique . . . . . . . . . . . . . . . . . . . . 134

7. CONTENTS 7
6.5.2 R´eactions chimiques . . . . . . . . . . . . . . . . . . . . . 136
6.5.3 R´eactions photochimiques . . . . . . . . . . . . . . . . . . 140
6.5.4 R´eactions h´et´erog`enes . . . . . . . . . . . . . . . . . . . . 144
6.5.5 Production de NO par les ´eclairs . . . . . . . . . . . . . . 145
6.5.6 M´ethode num´erique . . . . . . . . . . . . . . . . . . . . . . 146
6.6 Advection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 147
6.6.1 Calcul des lignes caract´eristiques . . . . . . . . . . . . . . 149
6.6.2 Recherche des valeurs de la concentration aux points origines151
6.6.3 M´ethodes d’int´egration . . . . . . . . . . . . . . . . . . . . 153
6.6.4 Filtrage des bruits . . . . . . . . . . . . . . . . . . . . . . 156
6.6.5 Fixeur de masse . . . . . . . . . . . . . . . . . . . . . . . . 157
6.6.6 Tests du sch´ema num´erique . . . . . . . . . . . . . . . . . 158
6.7 Diffusion verticale . . . . . . . . . . . . . . . . . . . . . . . . . . . 168
6.8 Convection . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 168
6.9 Les conditions initiales et aux limites . . . . . . . . . . . . . . . . 169
6.10 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 169
7 Conditions aux limites du mod`ele de Chimie-Transport 171
7.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171
7.2 Emissions des gaz dans la r´egion d’Hawaii . . . . . . . . . . . . . 171
7.3 Vitesse de d´epˆot sec . . . . . . . . . . . . . . . . . . . . . . . . . 188
7.3.1 Les variables d’entr´ee . . . . . . . . . . . . . . . . . . . . . 194
7.3.2 Effets de la pluie et de la ros´ee . . . . . . . . . . . . . . . . 194
7.3.3 Extension aux autres gaz . . . . . . . . . . . . . . . . . . . 194
7.4 Liste des param`etres . . . . . . . . . . . . . . . . . . . . . . . . . 195
7.5 Donn´ees additionnelles . . . . . . . . . . . . . . . . . . . . . . . . 197
7.6 Interpolation des donn´ees . . . . . . . . . . . . . . . . . . . . . . 201
7.7 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203
8 Analyse et interpr´etation des donn´ees MLOPEX-II 205
8.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 205
8.2 Etude de r´etro-trajectoires . . . . . . . . . . . . . . . . . . . . . . 206
8.2.1 Variations saisonni`ere . . . . . . . . . . . . . . . . . . . . . 206
8.2.2 Variations journali`eres . . . . . . . . . . . . . . . . . . . . 208
8.2.3 Variations diurnes . . . . . . . . . . . . . . . . . . . . . . . 210
8.3 Etude de traceurs passifs . . . . . . . . . . . . . . . . . . . . . . . 210
8.3.1 Comparaison des simulations avec les observations . . . . . 210
8.3.2 Origines des masses d’air `a MLO . . . . . . . . . . . . . . 214
8.3.3 Influence des sources am´ericaines en janvier . . . . . . . . 216
8.3.4 Cheminement des polluants locaux vers MLO . . . . . . . 219
8.4 Analyse de la chimie . . . . . . . . . . . . . . . . . . . . . . . . . 222

8. 8 CONTENTS
8.4.1 Donn´ees relatives `a MLOPEX-II . . . . . . . . . . . . . . . 222
8.4.2 Simulations . . . . . . . . . . . . . . . . . . . . . . . . . . 225
8.4.3 Comparaison entre les r´esultats du mod`ele et les observations226
8.5 Analyse des r´esultats du mod`ele . . . . . . . . . . . . . . . . . . . 244
8.5.1 Analyse locale . . . . . . . . . . . . . . . . . . . . . . . . . 244
8.5.2 Analyse r´egionale . . . . . . . . . . . . . . . . . . . . . . . 247
8.6 Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 261
9 Conclusions 263
9.1 Param´eterisation du transport convectif de constituants gazeux par
un ensemble de nuages cumuliformes. . . . . . . . . . . . . . . . . 269
9.1.1 Param´eterisation du flux massique Mc . . . . . . . . . . . 269
9.1.2 D´etermination de Xci . . . . . . . . . . . . . . . . . . . . . 272
9.2 Approximation par ´el´ements finis . . . . . . . . . . . . . . . . . . 275
9.2.1 El´ement rectiligne lin´eaire . . . . . . . . . . . . . . . . . . 276
9.2.2 El´ement triangulaire lin´eaire . . . . . . . . . . . . . . . . . 277
9.2.3 El´ement quadratique complet . . . . . . . . . . . . . . . . 278
9.2.4 El´ements tridimensionnels . . . . . . . . . . . . . . . . . . 278

9. Chapter 1
Introduction
Les recherches entreprises depuis plusieurs d´ecennies indiquent ample-
ment que l’augmentation de la population et des activit´es industrielles et agricoles
exercent une influence significative sur la composition chimique de l’atmosph`ere
terrestre. Ces recherches ont ´et´e r´esum´ees dans les rapports de l’Organisation
M´et´eorologique Mondiale ([244], [245] et [246]). Outre l’apparition de gaz de
synth`ese tels que les chloro-fluoro-carbones (CFC), les concentrations de nom-
breux gaz en trace ont plus que doubl´e depuis la r´evolution industrielle, comme
l’indique la figure 1.1. Cependant cette augmentation est ralentie par l’existence
de processus physiques et chimiques de destruction qui compensent en grande par-
tie l’accroissement des ´emissions. Sans ces processus, la composition chimique de
l’atmosph`ere serait totalement diff´erente, entraˆınant une modification profonde
du climat.
La photochimie troposph´erique est pr´epond´erante dans le ”nettoyage”
des polluants gazeux de l’atmosph`ere. En effet, les compos´es r´eduits ´emis `a
la surface terrestre sont oxyd´es dans l’atmosph`ere et transform´es en compos´es
chimiquement inertes, par exemple la transformation du CO en CO2, ou ils sont
´elimin´es par pr´ecipitation apr`es transformation en une esp`ece soluble, par exem-
ple la transformation du monoxyde d’azote (NO) en acide nitrique qui se dissoud
rapidement dans les gouttes de pluie. L’´el´ement moteur de cette oxydation est
l’ozone. Son rˆole central provient de sa photodissociation par les radiations so-
laires dans l’ultra-violet lib´erant ainsi un atome d’oxyg`ene dans son premier ´etat
d’excitation ´electronique:
O3 + hν (λ <310 nm) → O(1
D) + O2 (jO3b)
L’atome d’oxyg`ene O(1
D) est rapidement d´esactiv´e par collision avec l’azote ou
l’oxyg`ene mol´eculaire. La reaction de d´esactivation de O(1
D) avec la vapeur d’eau
est nettement moins proble mais elle est la premi`ere source du radical hydroxyle:
O(1
D)+H2O → 2OH (rO-H2Ob)
9

10. 10 Chapitre 1: Introduction
Figure 1.1: Evolution du rapport de m´elange du m´ethane mesur´e `a partir
de carottes glaciaires en Antarctique (DEO8: Etheridge et al., 1992; Mizuho:
Nakazawa et al., 1993) et au Groenland (Summit: Blunier et al., 1993; Site J:
Nakazawa et al., 1993) sur les mille derni`eres ann´ees. Les donn´ees atmosph´eriques
au Cap Grim (Tasmanie) sont incluses pour d´emontrer la bonne transition avec
les donn´ees de carottes glaciaires.
Ce radical est le principal agent oxydant de l’atmosph`ere et d´etermine en cons´equence
la capacit´e oxydante de l’atmosph`ere.
Si l’ozone stratosph´erique nous prot`ege des radiations solaires dans l’ultra-
violet, il agit, pr`es de la surface terrestre, comme un polluant important dans les
r´egions industrialis´ees. Des concentrations ´elev´ees, d´epassant les seuils l´egaux de
toxicit´e (au-del`a de 120 parties par milliard), sont fr´equemment observ´ees dans les
zones urbaines et p´eri-urbaines lors de conditions m´et´eorologiques particuli`eres.
Enfin, l’ozone joue un rˆole important dans l’´evaluation du changement
climatique. En vertu de son influence sur la capacit´e oxydante de l’atmosph`ere,
il d´etermine la dur´ee de vie des gaz radiativement actifs. De plus, il est lui-mˆeme
un gaz absorbant important dans l’infra-rouge pour une longueur d’onde centr´ee
`a 9.6 µm.
Il apparaˆıt donc que, tant pour la qualit´e de l’air au niveau r´egional
que pour les changements globaux, une meilleure connaissance de la chimie tro-
posph´erique et en particulier de celle de l’ozone est cruciale.
Si un effort important a ´et´e entrepris depuis plusieurs d´ecennies pour
comprendre les m´ecanismes chimiques conduisant `a la formation de brouillard
acide au-dessus des villes et r´egions industrielles (Vall´ee de la Meuse en 1930,
Donora en Pennsylnanie en 1948, Poza Rica au Mexique en 1950, et Londres en

11. Introduction 11
1952), c’est seulement depuis la fin des ann´ees 1970 que les probl`emes `a l’´echelle
globale ont ´et´e ´etudi´es. Auparavant seuls les effets sur les villes industrielles
´etaient pris en consid´eration. On pensait alors que l’atmosph`ere ´etait suffisam-
ment vaste pour absorber ces sources de pollution sans provoquer de changements
significatifs. Afin de garder les concentrations locales aussi basses que possible
les chemin´ees des usines furent rehauss´ees. Cette solution ne fit qu’augmenter
l’acidit´e des pr´ecipitations au travers de l’Europe. Entre 1972 et 1977, le pro-
gramme Long Range Transport of Air Pollutants a ´et´e mis en place par l’OCDE
pour d´eterminer l’impact des gaz de combustion ´emis dans les r´egions industrielles
sur la composition chimique de l’atmosph`ere ´eloign´ee de ces r´egions. Il faut cepen-
dant attendre le d´ebut des ann´ees 80 pour voir apparaˆıtre des ´etudes d’impact `a
l’´echelle globale, par exemple dans le rapport Global Tropospheric Chemistry: A
plan for Action, de l’Acad´emie des Sciences des Etats-Unis (1984). En 1985, le
Global Tropospheric Chemistry Program a ´et´e lanc´e par les instances f´ed´erales des
Etats-Unis. En Belgique, depuis 1990, le gouvernement a support´e un programme
d’impulsion `a l’´etude du changement global, contribution au International Geop-
shere and Biosphere Program (IGBP), et coordonn´e par les Services f´ed´eraux des
affaires Scientifiques, Techniques et Culturelles (SSTC). Notre recherche a ´et´e
financ´ee dans le cadre de ce dernier programme.
En relation avec ces programmes, des campagnes de mesures simultan´ees
de gaz r´eactifs dans les r´egions de la troposph`ere ´eloign´ee ont ´et´e organis´ees
afin d’´etudier l’impact des activit´es humaines sur la composition chimique de
la troposph`ere. Parmi celles-ci, on peut citer par exemple Tropospheric Ozone,
TROPOZ II [232]; East Asia/North Pacific Regional Study, APARE, [3], Pa-
cific Exploratory Mission West-A, PEM West-A [118], et Mauna Loa Observatory
Photochemistry Experiment, MLOPEX-II [13], effectu´ees durant quatre p´eriodes
d’un mois pour chacune des saisons couvrant les ann´ees 1991 et 1992, `a l’Obser-
vatoire de Mauna Loa (situ´e au milieu du Pacifique sur l’ˆıle d’Hawaii). Durant
cette campagne les compos´es cl´es dans la chimie de l’ozone ont ´et´e mesur´es si-
multan´ement, et parmi ceux-ci le radical OH dont la faible concentration rend
la mesure particuli`erement difficile. De plus, certains compos´es particuliers ont
´et´e mesur´es simultan´ement `a l’aide de plusieurs instruments afin de permettre
une intercomparaison. Nous avons repris au tableau 1.1 la liste des compos´es
mesur´es, ainsi que le type d’instruments, les exp´erimentateurs et les institutions
auxquelles ils sont affili´es. Le nombre impressionant de compos´es mesur´es ainsi
que d’exp´erimentateurs impliqu´es dans cette campagne rend celle-ci relativement
unique.

12. 12 Chapitre 1: Introduction
Table 1.1: Ensemble des mesures effectu´ees au site de l’Observatoire de Mauna
Loa, pendant la campagne MLOPEX-II (1991/1992)
Compos´es Instruments Exp´erimentateurs Institutions
H2O2, CH3O2H, CH2O EF B. Heikes, B. McCully Univ. of RI
H2O2, CH3O2H HPLC G. Kok, T. Staffelbach NCAR
CH2O IEF T. Campos NCAR
H2O2, CH2O TDLAS G. Mackay, D. Karecki UNISEARCH
Carboniles HPLC K. Mpooper, X. Chen
C. Schultz Wash. State Univ.
X. Zhou, Y-N Lee Brookhaven NL
HNO3, NO−
3 Denuder R. Norton, S. Buhr NOAA AL,CIRES
HCOOH, CH3COOH Filter/IC R. Norton, S. Buhr NOAA AL,CIRES
HNO3, NO−
3 Denuder/IC J. Lind, T. Campos,E. Atlas NCAR
NMHC, CO GC/FID J. Greenberg, P. Zimmerman
GR/RGD S. Schauffler, D. Helmig
GC/MS A. Wedel, G. Brailsford
W. Pollock NCAR
J(NO2), J(O3) Actinom`etre R. Shetter, T. Gilpin NCAR
RO2 CA C. Cantrell, J. Calvert
G. GIlliland NCAR
J(O3) Radiom`etre W. Junkeman Fraunhofer Inst
OH CI/MS F. Eisele, D. Tanner Georgia Tech RI
PAN, MN, O3 GC, UV B. Ridley, J. Walega,
NO, NO2 CL F. Grahek NCAR
NOy, SO2 CL, PF G. H¨ubler NOAA AL, CIRES
Nitrates organiques GC/ECD E. Atlas NCAR
A´erosols fins SMPS R. Weber, P. McMurry Univ of Minn.
Radon, Thoron Compteur α S. Whittlestone ANSTO
Variables m´et´eo Station PAM J. Walega, D. Montzka NCAR
O3, colonne d’O3, CFC - R. Schnell, P. Tans,
CH4, N2O, CO, CO2 E. Dlugokencky, J. Elkins
Vents, Noir de carbone S. Oltmans, B. Bodhaine
Particules G. Herbert NOAA
EF=Enzyme Fluorescence; HPLC=High Performance Liquid Chromatography;
IEF=Immobilized Enzyme fluorescence;RGD=Reduction Gas Detector;
IC=Ion Chromatography; GC=Gas Chromatography;
FID=Flame Ionization Detection; MS=Mass Spectrometry;
CA=Chemical Ampifier; CI=Chemical Ionization;
UV=UltraViolet; CL=Chemi-Luminescence;
PF=photo-fluorescence;ECD=electron capture detection;
SMPS=scanning differential mobility particule spectrometer.
NOAA AL=National Oceanographic and Atmospheric Administration-Aeronomy Laboratory;
NCAR=National Center for Atmospheric Research;
CIRES=Cooperative Institute for Research in Environmental Science

13. Introduction 13
L’objectif du pr´esent travail est de d´evelopper un mod`ele de chimie at-
mosph´erique pour analyser et interpr`eter les donn´ees mesur´ees lors de la
campagne MLOPEX afin de mieux comprendre la distribution, les varia-
tions et le bilan de l’ozone dans la troposph`ere au-dessus du Pacifique.
Le site de l’Observatoire de Mauna Loa (MLO) est situ´e `a 3.4 kilom`etres
d’altitude sur les pentes du volcan de Mauna Loa de l’ˆıle d’Hawaii (figure 1.2)
qui se trouve au centre de l’oc´ean Pacifique nord (204,422 degr´es de longitude
ouest et 19,539 degr´es de latitude nord). L’´eloignement du site des continents
asiatique et am´ericain -6000 et 4000 kilom`etres s´eparent respectivement Hawaii
du Japon et de la Californie- permettent de supposer que la plupart des compos´es
produits au-dessus des continents sont proches de l’´equilibre photochimique. De
plus, l’altitude ´elev´ee du site rend les mesures repr´esentatives d’une fraction im-
portante de la troposph`ere libre1
non-pollu´ee. En effet, la nuit, lors du refroidisse-
ment radiatif de la surface du volcan, l’air froid descend les pentes du volcan et
limite ainsi l’influence des ´emissions locales. L’altitude du site correspond `a la
zone de transition entre les vents aliz´es du Nord-Est entraˆınant au-dessus de la
surface oc´eanique les masses d’air d’origine am´ericaine et les vents rapides d’ouest
apportant les masses d’origine asiatique.
L’Observatoire de Mauna Loa est donc un site particuli`erement int´eressant
pour l’´etude de la composition chimique de la troposph`ere ´eloign´ee et en partic-
ulier ses variations associ´ees avec les ´emissions anthropiques continentales. C’est
pourquoi le Laboratoire de Diagnostic et de Mod´elisation du Climat g`ere le site
depuis une trentaine d’ann´ees et mesure en continu les concentrations de gaz tels
que le CO2, CH4, CO et O3.
L’analyse des donn´ees obtenues lors d’une campagne pilote en mai 1988,
MLOPEX-I [203], a montr´e qu’il existait certains d´esaccords entre les ´evaluations
th´eoriques et les observations, en particulier en ce qui concerne le bilan des oxy-
des d’azote [152]. D’autre part, Greenberg et al. [94] ont d´etect´e la nuit des
concentrations non nulles d’hydrocarbures non-m´ethaniques, vraisemblablement
d’origine locale. Ceci pourrait signifier qu’il existe une certaine contamination
par les ´emissions locales des mesures effectu´ees dans la troposph`ere libre. S’il
existe une influence des ´emissions locales, il est difficilement justifiable d’analyser
les donn´ees sans consid´erer celles-ci.
Pour mener `a bien notre ´etude, il nous a donc sembl´e n´ecessaire de pou-
voir ´evaluer `a Hawaii l’impact des:
• Emissions continentales (Asie, Am´eriques, Europe),
1
Partie de la troposph`ere qui n’est pas directement sous l’influence des ´emissions de surface
grˆace `a la pr´esence d’une couche d’inversion qui la s´epare de la couche limite plan´etaire.

14. 14 Chapitre 1: Introduction
Figure 1.2: Vue de l’archipel d’Hawaii, indiquant les noms des diff´erentes ˆıles
ainsi que les villes et les volcans principaux.

15. Introduction 15
• Emissions des autresˆıles de l’archipel d’Hawaii et en particulier celle d’Oahu
o`u se trouve la ville industrielle d’Honolulu,
• Emissions locales de l’ˆıle d’Hawaii.
• • •
La grande dispersion des ´echelles caract´eristiques des ph´enom`enes de transport at-
mosph´erique rend leur mise en ´equation tr`es complexe et nous incite par cons´equent
`a employer un mod`ele math´ematique simplifi´e. L’approche g´en´eralement adopt´ee
consiste `a se fixer une valeur d’´echelle en de¸c`a de laquelle les ph´enom`enes sont
param´etris´es. Cette simplification conduit malgr´e tout `a un syst`eme d’´equations
aux d´eriv´ees partielles non-lin´eaires et seule une m´ethode num´erique permet-
tra de le traiter en l’absence de solutions analytiques. Malheureusement, la ca-
pacit´e des ordinateurs actuels ne permet pas de r´esoudre ces ´equations pour
toute la troposph`ere avec une r´esolution horizontale inf´erieure `a plusieurs cen-
taines de kilom`etres. Etant donn´e que la dimension d’Hawaii est de l’ordre de
200 kilom`etres, deux approches diff´erentes sont offertes:
• Approche globale: le domaine couvre toute la troposph`ere et il est fait
abstraction d’Hawaii tant du point de vue dynamique que chimique,
• Approche r´egionale: le domaine ´etudi´e est limit´e `a l’archipel d’Hawaii, ce
qui oblige `a fixer des conditions aux limites sur les fronti`eres lat´erales.
La premi`ere approche a ´et´e utilis´ee par Brasseur et al. [32] pour analyser les
donn´ees MLOPEX obtenues pour les conditions de vents descendants. De telles
conditions se produisant en g´en´eral la nuit quand la plupart des radicaux ont
disparu, l’´etude se limite `a l’analyse des gaz `a longue dur´ee de vie. La deuxi`eme
approche a ´et´e suivie par le groupe de mod´elisation r´egionale du National Center
for Atmospheric Research (NCAR) qui a choisi un domaine limit´e au Pacifique
avec une r´esolution horizontale de 80 kilom`etres. Un tel choix ne pouvait nous
satisfaire car, d’une part, avec une r´esolution de 80 kilom`etresi, Hawaii est tr`es
mal repr´esent´e et, d’autre part, l’influence des ´emissions anthropiques continen-
tales sur la composition chimique `a Hawaii, qui est une inconnue fondamentale,
apparaˆit comme une condition aux limites mal d´efinie.

16. 16 Chapitre 1: Introduction
En cons´equence, nous avons ´et´e amen´e `a d´evelopper une approche orig-
inale qui nous permet de consid´erer tout `a la fois l’influence des ´emissions
continentales ´eloign´ees et celle des ´emissions locales d’Hawaii. Elle consiste
`a r´esoudre les ´equations d’un mod`ele de chimie-transport tridimensionnel
de la troposph`ere en des points concentr´es autour d’Hawaii et dont la den-
sit´e diminue au fur et `a mesure que l’on s’en ´eloigne (figure 1.3).
Un tel choix nous a conduit `a d´evelopper un nouveau mod`ele et `a met-
tre en oeuvre des techniques num´eriques originales, notamment en ce qui
concerne l’advection, ainsi qu’`a cr´eer un programme graphique de visuali-
sation des r´esultats dont les figures 1.2 et 1.3 sont des exemples.
• • •
La complexit´e de la chimie troposph´erique -plus de cinq mille gaz diff´erents
ont ´et´e r´epertori´es [162]- et de la circulation `a Hawaii, nous a amen´e `a commencer
notre pr´esentation par une description des aspects chimiques et dynamiques fon-
damentaux relatifs `a notre ´etude.
Le deuxi`eme chapitre pr´esente une synth`ese des connaissances actuelles,
d’une part, sur la chimie de l’ozone troposph´erique pour une r´egion non-pollu´ee
et, d’autre part, sur la circulation au-dessus du Pacifique et particuli`erement dans
la r´egion d’Hawaii.
La formulation math´ematique du transport des compos´es chimiques dans
l’atmosph`ere est d´ecrite au troisi`eme chapitre. En partant des principes de con-
servation, nous sommes amen´es `a r´esoudre un syst`eme d’´equations aux d´eriv´ees
partielles non-lin´eaires. Un certain nombre de simplifications peuvent ˆetre ap-
port´ees `a ces ´equations, en particulier aux ´equations de Navier-Stokes. Cepen-
dant, aucune solution analytique de ces ´equations ne peut ˆetre trouv´ee. Il faut,
par cons´equent, faire appel aux m´ethodes num´eriques. Pour faciliter la r´esolution
num´erique les coordonn´ees sont transform´ees `a la fois selon la verticale (coor-
donn´ee suivant le relief) et selon l’horizontale (projections st´er´eo-polaire et de
Mercator). Les ph´enom`enes de transport `a petite ´echelle tels que la convection
forc´ee dans la couche limite plan´etaire et le transport vertical intense dans les
nuages de type cumulo-nimbus introduisent un ensemble incomplet d’´equations
(plus d’inconnues que d’´equations). La solution g´en´eralement adopt´ee dans les
mod`eles de chimie consiste `a param´etriser ces ph´enom`enes.

17. Introduction 17
Figure 1.3: Grille de calcul projet´ee sur la Terre avec une vue centr´ee sur le
Pacifique Nord o`u la grille est ´etendue au sud de l’´equateur.

18. 18 Chapitre 1: Introduction
Au quatri`eme chapitre, l’obtention des variables m´et´eorologiques et leur
comparaison avec les observations ont ´et´e abord´ees. La r´esolution num´erique de
l’ensemble des ´equations aurait n´ecessit´e le travail d’une ´equipe pendant plusieurs
d´ecennies. Nous avons par cons´equent pr´ef´er´e d´ecoupler la dynamique de la
chimie. De cette fa¸con les variables dynamiques deviennent des donn´ees pour le
mod`ele de chimie-transport atmosph´erique. Nous nous sommes servis des donn´ees
du Centre Europ´een de Pr´evision du Temps `a Moyen terme (ECMWF) qui fournit
les champs de variables m´et´eorologiques analys´ees toute les douze heures sur une
grille espac´ee de 2,5o
(∼ 275 km `a l’´equateur). Une telle grille ne d´ecrivant la
m´et´eorologie de l’ˆıle d’Hawaii que par un seul point, nous avons utilis´e un mod`ele
r´egional existant qui traite les ´equations de la dynamique avec une r´esolution
num´erique d’une dizaine de kilom`etres.
Les donn´ees ECMWF ne contiennent aucune valeur `a la surface terrestre
et ne fournissent pas d’information sur les flux turbulents dans la couche limite
plan´etaire. Le calcul des variables de surface ainsi que la param´eterisation des
flux turbulents sont d´ecrites au cinqui`eme chapitre.
Au sixi`eme chapitre, nous avons d´ecrit le d´eveloppement d’un mod`ele
num´erique de chimie-transport tridimensionnel de la troposph`ere. Nous expliquons
´egalement la m´ethode de construction de la grille de calcul qui constitue l’originalit´e
de ce mod`ele. La r´esolution num´erique des ´equations aux points de cette grille a
n´ecessit´e des d´eveloppements originaux, principalement pour le transport advec-
tif. Le nombre de points de grille ´etant tr`es ´elev´e dans le cas des mod`eles tridi-
mensionnels (∼ 106
) nous avons attach´e un soin particulier `a choisir ou d´evelopper
des m´ethodes efficaces.
Les conditions aux limites du mod`ele de chimie-transport sont d´ecrites
au septi`eme chapitre. Une partie importante de notre travail a consist´e `a ´etablir,
dans la r´egion d’Hawaii, des cartes `a haute r´esolution (∼ 10 km) pour les multiples
donn´ees n´ecessaires `a la sp´ecification des flux d’´emission des diff´erents gaz et du
d´epˆot sec `a la surface terrestre. Nous avons param´etris´e le d´epˆot sec par analogie
avec les circuits ´electriques: le transfert de compos´es chimiques vers la surface
d´epend de multiples r´esistances plac´ees en s´eries et en parall`eles. Nous avons
termin´e ce chapitre en d´ecrivant bri`evement la technique d’interpolation -non
triviale- d´evelopp´ee pour la d´etermination aux points de grille de notre mod`ele
des valeurs des donn´ees fournies sur une grille diff´erente.
Le huiti`eme chapitre est consacr´e `a l’analyse et l’interpr´etation des donn´ees
de la campagne de mesures MLOPEX-II. Nous avons d´ebut´e cette analyse en
effectuant une ´etude de r´etro-trajectoire qui nous a permis d’interpr´eter les vari-
ations diurnes et saisonni`eres des concentrations des constituants chimiques. En
fonction de la distance parcourue, de la position du point de d´epart et d’autres
param`etres caract´erisant les trajectoires, il est alors possible de classifier les
masses d’air arrivant `a l’Observatoire de Mauna Loa en fonction du temps. Cette

19. Introduction 19
´etude ne consid`ere que le transport advectif et n´eglige les ph´enom`enes de dilution
par m´elange turbulent ou par convection au travers des cumulonimbi. Or ces
derniers processus contrˆolent l’influence des ´emissions continentales sur la chimie
de la troposph`ere libre. En effet les vitesses des vents `a la surface sont nettement
inf´erieures aux vitesses en altitude et le transport `a grande ´echelle des gaz pollu-
ants d’origine continentale n’aura lieu que s’il y a transfert vertical depuis leurs
sources jusqu’`a la troposph`ere libre, L’´etude de r´etro-trajectoires n´egligeant ce
transfert, nous avons entrepris une ´etude du traceur isotopique 222
Rn en distin-
guant les ´emissions pour chaque continent. Nous avons r´ep´et´e cette exp´erience en
distinguant les ´emissions des diff´erentes ˆıles de l’Archipel d’Hawaii afin d’´evaluer
l’impact des ´emissions des villes industrrielles telles que Honolulu ou Wailukuku
sur la composition chimique de l’air `a l’Observatoire de Mauna Loa. Un dernier
probl`eme que nous avons trait´e est de savoir comment les gaz ´emis sur la cˆote Est
de l’ˆıle d’Hawaii atteignent l’Observatoire de Mauna Loa: suivent-ils un chemine-
ment direct ou contournent-ils l’ˆıle par ses cˆot´es en montant ensuite par le versant
oppos´e? Une telle ´etude est importante car elle permet d’´evaluer le temps mis
au transport des gaz ´emis localement jusqu’`a leur arriv´ee `a l’Observatoire, et
de d´eduire ´egalement leur taux d’oxydation et de d´epˆot sec. Nous avons ensuite
simul´e chacune des quatre p´eriodes de mesure couvrant huit jours en octobre 1991,
janvier 1992, mai 1992 et juillet 1992. Les r´esultats du mod`ele fournissent toutes
les heures sur tout l’h´emisph`ere Nord et de la surface terrestre `a la tropopause
les concentrations de 46 constituants chimiques. Ces r´esultats ont ´et´e compar´es
aux mesures effectu´ees lors de la campagne MLOPEX-II tant `a l’Observatoire
que le long de trajectoires prises par les avions de mesure. En nous servant des
´etudes de r´etro-trajectoires et de traceurs, nous avons interpr´et´e les variations
saisonni`ere, journali`ere et diurne des r´esultats de nos simulations. Nous avons
enfin calcul´e le bilan de l’ozone et d’autres constituants cl´es par sous-domaines,
en distinguant d’une part la couche limite plan´etaire de la troposph`ere libre et
d’autre part les continent des oc´eans.
Le neuvi`eme chapitre est consacr´e aux conclusions de la pr´esente ´etude.
Elles visent `a montrer que nos objectifs ont ´et´e atteints mais aussi que certaines
id´ees pr´e-´etablies du transport de polluants doivent ˆetre reconsider´ees.
En vue d’all´eger le texte, nous avons report´e au dixi`eme chapitre, sous
forme d’annexes, quelques d´etails de calcul.

20. 20 Chapitre 1: Introduction

21. Chapter 2
Processus chimiques et
dynamiques en relation avec les
donn´ees MLOPEX
2.1 Introduction
La distribution spatiale et temporelle des constituants chimiques dans
l’atmosph`ere est d´etermin´ee par de multiples processus dont notamment les ´emissions
`a la surface terrestre, le d´epˆot sec et humide, les r´eactions chimiques et photochim-
iques et le transport. Les ´emissions de surface sont associ´ees aux ´eruptions vol-
caniques, aux activit´es biologiques continentale et oc´eanique, la combustion de la
biomasse et des combustibles fossiles, etc. Les transformations chimiques font es-
sentiellement intervenir les r´eactions de collision entre deux ou trois mol´ecules et
la photodissociation par la radiation solaire pour des longueurs d’onde sup´erieures
`a 295 nm (UV). Le transport est habituellement repr´esent´e par le transport advec-
tif `a grande ´echelle et les processus `a plus petite ´echelle tels que les mouvements
convectifs associ´es aux nuages et la turbulence dans la couche limite plan´etaire.
Le d´epˆot humide r´esulte de la pr´ecipitation d’esp`eces solubles par les pluies alors
que le taux de d´epˆot sec d´epend de la nature de la surface terrestre.
Au cours de ce chapitre, nous allons aborder ces processus dans le cadre
des donn´ees MLOPEX `a Hawaii. Il existe de nombreuses publications relatives
`a la chimie et `a la dynamique d’Hawaii en raison de son ´eloignement des sources
continentales de pollution et de sa circulation particuli`ere. Nous tenterons donc
d’en faire ici une synth`ese.
Nous aborderons le probl`eme du transport de compos´es gazeux en dis-
tinguant trois ´echelles spatiales: g´en´erale, r´egionale et locale. Nous nous at-
tacherons ´egalement `a la variation temporelle du transport, saisonni`ere au-dessus
du Pacifique et diurne sur l’ˆıle d’Hawaii. Les ´etudes de trajectoires et du traceur
21

22. 22 Chapitre 2: Processus chimiques et dynamiques
radio-actif 222
Rn seront utilis´ees pour interpr´eter les variations saisonni`eres des
concentrations des gaz `a Hawaii.
Apr`es avoir d´ecrit les types de transformations chimiques dans la tro-
posph`ere, nous isolerons les m´ecanismes chimiques fondamentaux qui contrˆolent
la distribution et les variations de la teneur en ozone, en s´eparant les r´egions
recul´ees non-pollu´ees comme Hawaii des r´egions continentales pollu´ees. La com-
position chimique caract´eristique `a l’Observatoire de Mauna Loa sera r´esum´ee `a
partir des donn´ees de la campagne pilote MLOPEX-I [203].
2.2 Processus dynamiques dans la troposph`ere
La troposph`ere est la partie inf´erieure de l’atmosph`ere caract´eris´ee par
une d´ecroissance de la temp´erature moyenne avec l’´el´evation en altitude (figure
2.1). Celle-ci augmentant dans la stratosph`ere, son minimum d´etermine la posi-
tion de la tropopause qui s´epare la troposph`ere de la stratosph`ere. La hauteur de
la troposph`ere varie avec la latitude: elle est maximum `a l’´equateur (18 km), min-
imum aux pˆoles (8 km), et d’environ 15 km dans la r´egion d’Hawaii. L’influence
de la surface terrestre s’exerce surtout dans la couche limite plan´etaire dont la
hauteur est limit´ee en g´en´eral, par une inversion thermique. Cette inversion re-
streint les ´echanges avec le restant de la troposph`ere appel´ee pour cette raison la
troposph`ere libre.
Les processus de transport dans la troposph`ere se distinguent de ceux de
la stratosph`ere par l’influence de la surface terrestre, la valeur ´elev´ee du rapport
de m´elange de la vapeur d’eau et la faible concentration d’ozone. La capacit´e
d’absorption des radiations solaires par le sol et le refroidissement radiatif net de
la troposph`ere sup´erieure dˆu aux ´emissions dans l’infra-rouge par le CO2, H2O
et O3 cr´eent une condition d’instabilit´e thermique. Elle est principalement com-
pens´ee par la convection dans les nuages cumuliformes qui m´elange globalement
la troposph`ere en quelques mois [40].
D’autre part, il y a plus d’´energie absorb´ee aux latitudes tropicales (0o
- 30o
) et subtropicales (30o
-40o
) que d’´energie ´emise par la radiation terrestre.
Dans les r´egions temp´er´ees (40o
-60o
) et polaires (60o
-90o
), l’inverse se produit.
En cons´equence, il y a toute l’ann´ee un transfert d’´energie depuis les basses vers
les hautes latitudes maintenu par les courants oc´eaniques et atmosph´eriques. Ce
processus de transfert est `a l’origine de la circulation g´en´erale de l’atmosph`ere.
Le transport d’un h´emisph`ere `a l’autre est un processus plus lent `a cause
de la convergence des aliz´es le long de la zone de convergence inter-tropicale,
dans la troposph`ere inf´erieure et de la divergence des vents dans la troposph`ere
sup´erieure. L’´echelle de temps du transport interh´emisph´erique est de l’ordre
d’un an [90].

23. 2.2 Processus dynamiques 23
Figure 2.1: Profil vertical de la temp´erature entre la surface terrestre et 100 km
d’altitude d´efinissant les diff´erentes couches de l’atmosph`ere (d’apr`es Atmospheric
Chemistry and Global Change, 1997).

24. 24 Chapitre 2: Processus chimiques et dynamiques
L’´echelle de temps du transport entre la troposph`ere et la stratosph`ere est
de l’ordre de plusieurs ann´ees `a cause du faible m´elange entre ces deux couches
au-travers de la tropopause. Par contre au niveau du jet polaire, localis´e aux
latitudes moyennes, lors du passage de perturbations cycloniques, il y a injection
´episodique d’air stratosph´erique vers la troposph`ere. Brasseur et al. [32] ont ainsi
montr´e que certains ´episodes marqu´es par une augmentation des oxydes d’azote
`a Hawaii pouvaient s’expliquer par l’injection d’air stratosph´erique au-dessus des
Etats-Unis, suivi d’un transport horizontal vers Hawaii.
En raison de la lenteur des ´echanges entre les deux h´emisph`eres d’une
part et entre la troposph`ere et la stratosph`ere d’autre part, nous limiterons notre
´etude `a la troposph`ere dans l’h´emisph`ere nord.
2.2.1 Circulation g´en´erale
La circulation g´en´erale est forc´ee par le d´es´equilibre thermique radiatif
`a la surface terrestre. La structure zonale de cette circulation est caract´eris´ee
par trois cellules dans chaque h´emisph`ere. La premi`ere, Cellule de Hadley, est
marqu´ee par un d´eplacement vers le haut des masses d’air ´equatoriales et une
subsidence subtropicale. Dans les r´egions polaires, l’affaissement les masses d’air
froides se dirigent vers les latitudes temp´er´ees. En altitude, la convergence vers le
pˆole boucle la circulation au sein de la cellule directe polaire ainsi cr´e´ee. La cellule
indirecte des latitudes subtropicales et temp´er´ees, cellule de Ferrel, est forc´ee par
les deux autres. Aux latitudes de 60o
, la rencontre des masses d’air polaire et
d’air tropical forme le front polaire o`u l’air chaud s’´el`eve en pente douce au-dessus
de l’air froid. La d´eflexion du vent par la force de Coriolis finit par donner `a la
circulation g´en´erale ainsi d´efinie ses caract´eristiques au sol: aliz´es ´equatoriaux
et subtropicaux, courants d’ouest dans les latitudes temp´er´ees et d’est dans les
r´egions polaires. Dans les couches sup´erieures de la troposph`ere, aux latitudes
temp´er´ees, l’´ecoulement d’ouest stationnaire atteint son maximum d’intensit´e au
niveau des courants jets `a une altitude comprise entre 10 et 12 km.
La variation saisonni`ere de cette circulation g´en´erale suit celle de la radia-
tion solaire: en ´et´e, pour l’h´emisph`ere nord, la zone de convergence intertropicale
se d´eplace vers le nord alors qu’en hiver elle se d´eplace vers le sud.
2.2.2 Circulation au-dessus du Pacifique Nord
La circulation au-dessus du Pacifique est conditionn´ee par la position de
l’anticyclone du Pacifique et les courants jets subtropicaux et polaires ainsi que
la subsidence associ´ee avec la branche descendante de la cellule de Hadley [101].

25. 2.2 Processus dynamiques 25
Figure 2.2: Sch´ema de la circulation troposph´erique id´ealis´ee dans l’h´emisph`ere
Nord. La direction des vents `a la surface terrestre est repr´esent´ee par des fl`eches.
Aux tropiques, les vents dominants sont du Nord-Est. Aux latitudes moyennes les
vents sont modul´es par les syt`emes synoptiques auxquels sont associ´es des fronts
froids (triangles), chauds (demi-cercles) et occlus (triangles et demi-cercles). Sur
la partie de droite, la structure verticale de la circulation formant trois cellules
(la cellule de Hadley aux tropiques, la cellule de Ferrel aux latitudes moyennes et
la cellule polaire aux latitudes ´elev´ees) est dessin´ee en relation avec la tropopause
polaire et tropicale, le front polaire (PF), le courant jet polaire (Jp), et le courant
jet subtropical (Js) d’apr`es Atmospheric Chemistry and Clobal Change (1997).

26. 26 Chapitre 2: Processus chimiques et dynamiques
Anticyclone du Pacifique
La haute pression associ´ee `a l’anticylone du Pacifique peut ˆetre repr´esent´ee par la
valeur de la hauteur du g´eopotentiel 1
. Les valeurs de la hauteur du g´eopotentiel `a
700 mb sont dessin´ees pour quatre mois de l’ann´ee sur la figure 2.3 . On constate
que cet anticyclone migre aux cours des saisons. Au cours de l’´et´e il se renforce
et occupe sa position la plus au nord, alors qu’en hiver il s’affaiblit et occupe sa
position la plus au sud. Par rapport `a Hawaii, cet anticyclone passe du nord-est
en ´et´e au sud-ouest en hiver.
La circulation `a 700 mb, repr´esent´ee par les vecteurs du vent sur la
figure 2.4, est associ´ee `a l’anticyclone du Pacifique Nord et d´ecrit un mouvement
horlogique anticyclonique. En ´et´e (figure 2.4.d) Hawaii est sous l’influence des
vents d’Est associ´es `a la branche Sud de l’anticylone, alors qu’en hiver (figure
2.4.b) ce sont les vents d’Ouest de la branche Nord de l’anticyclone qui passent
par Hawaii. Au printemps et en automne, les vents sont principalement du Nord-
Est (figures 2.4 c et a).
Si l’on compare la circulation `a 700 mb avec celle `a la surface (figure 2.5),
on constate que Hawaii est continuellement sous l’influence des vents dominants
du Nord-Est en provenance de la cˆote californienne. Il faut noter en janvier
(figure 2.5.b) la basse pression sur le golfe d’Alaska qui m´elange les masses d’air
d’Am´erique du Nord `a celles en provenance d’Asie.
Jets polaire et subtropical
Le jet polaire occupe une position permanente tout au long de l’ann´ee, centr´ee `a
200 mb et 45o
N, comme l’indiquent les figures (2.6 a-d) qui reprennent les valeurs
zonales du vent le long d’un m´eridien passant par Hawaii. Le jet subtropical qui
se d´etache du jet polaire sur le Pacifique passe `a proximit´e d’Hawaii et est marqu´e
par des vents zonaux d’ouest. Ces vents atteignent une valeur maximum en hiver
sup´erieure `a 50 m.s−1
vers 200 mb. On constate que l’Observatoire de Mauna
Loa situ´e `a une pression d’environ 700 mb est dans la zone de transition entre
les vents d’est et d’ouest au printemps et en automne. En hiver (figure 2.6.a), la
pression de transition entre les vents d’est et d’ouest, est de l’ordre de 800 mb,
alors qu’en ´et´e elle s’´el`eve jusqu’`a 250 mb.
Subsidence subtropicale
Le Pacifique Nord est influenc´e dans la r´egion ´equatoriale par la branche montante
de la cellule de Hadley et subtropicale par la branche descendante. Nous nous
1
La hauteur du g´eopotentiel est l’altitude en m`etres, compt´ee `a partir du niveau de la mer,
d’une surface de pression donn´ee. Elle est maximum pour un anticyclone et minimum pour un
cyclone.

27. 2.2 Processus dynamiques 27
Figure 2.3: Hauteur du g´eopotentiel (m) `a 700 mb pour les mois de a) Octobre,
(b) Janvier, c) Mai et d) Juillet. Les isocontours correspondent `a 2750, 2850,
2950, 3000, 3060, 3120, 3140, 3160, 3180 et 3200 m.

28. 28 Chapitre 2: Processus chimiques et dynamiques
Figure 2.4: Vecteurs du vent `a 700 mb pour les mois de a) Octobre, b) Janvier,
c) Mai et d) Juillet.

29. 2.2 Processus dynamiques 29
Figure 2.5: Vecteurs du vent `a 1000 mb pour les mois de a) Octobre, b) Janvier,
c) Mai et d) Juillet.

30. 30 Chapitre 2: Processus chimiques et dynamiques
Figure 2.6: Moyenne zonale de la vitesse du vent horizontal (m.s−1
) au-dessus
du Pacifique pour les mois de a) Octobre, b) Janvier, c) Mai et d) Juillet. Les
isocontours correspondent `a -5, -3, 0, 5, 10, 15, 20, 25, 30, 40 et 40 m.s−1
.

31. 2.2 Processus dynamiques 31
sommes servis des moyennes sur 10 ans (1978-1989) des valeurs du vent vertical,
en coordonn´ees de pression, calcul´ees `a partir des donn´ees du Centre Europ´een de
pr´evision du temps [226] pour indiquer le ph´enom`ene d’affaissement subtropical
au-dessus du Pacifique nord. Les figures 2.7 a), b), c) et d) reprennent les valeurs
positives du vent vertical (vers le bas) moyenn´ees entre les niveaux de pression
de 300 `a 700 mb, pour les mois d’octobre, janvier, mai et juillet. On constate
que tout au long de l’ann´ee il existe un flux descendant qui s’´etend dans la r´egion
tropicale depuis la cˆote ouest des Etats-Unis au-del`a d’Hawaii. En janvier cette
zone s’´etend jusqu’en Mongolie. Elle correspond `a la branche descendante de la
cellule tropicale de Hadley et s’accompagne de faible valeur d’humidit´e relative.
On peut donc s’attendre `a ce que les masses d’air en provenance d’Asie
ou mˆeme d’Europe, d´eplac´ees depuis la surface jusqu’au niveau des courants jets
soient transport´ees rapidement vers l’Est et descendent sur Hawaii (figure 2.8).
2.2.3 Trajectoires
L’´etude de trajectoires permet de classifier les masses d’air de diff´erentes
origines, et en particulier de d´eterminer leurs origines continentales. Ce type
d’´etude consiste `a remonter dans le temps la trajectoire suivie par une parcelle
d’air connaissant son point d’arriv´ee et les champs de vitesse du vent en chaque in-
stant. Les champs de vitesse proviennent soit d’assimilation d’observations dans
un mod`ele m´et´eorologique (vents analys´es) soit d’un mod`ele climatique (vents
climatologiques). La m´ehode de calcul est relativement simple, une fois le champ
de vitesse connu, car elle consiste principalement `a interpoler les vitesses connues
en un nombre de points limit´es le long de la trajectoire. L’exactitude des interpo-
lations ´etant limit´ee, les erreurs introduites s’accumulent rapidement et Merrill et
al. [173] estiment que l’erreur sur la position est ´egale `a la moiti´e de la distance
parcourue. Si donc l’´etude des trajectoires est tr`es utile, elle ne permet qu’une
analyse qualitative de l’origine des masses d’air.
En utilisant les moyennes mensuelles des vents analys´es du National Me-
teorological Center (NMC) entre les p´eriodes 1981-1988, Harris et Kahl [103] ont
calcul´e les trajectoires arrivant apr`es dix jours aux niveaux de longitude et de
latitude de l’Observatoire de Mauna Loa (204.422o
E, 19.539o
N), sur deux sur-
faces isobariques 500 et 700 mb. De leur ´etude il apparait que les masses d’air
sont essentiellement d’origine asiatique en hiver et d’Am´erique centrale en ´et—’e.
Au printemps et en automne une partie significative des masses d’air stagne aux
environs de Hawaii, l’apport d’air frais venant principalement d’Asie apr`es avoir
tourn´e autour de l’anticyclone du Pacifique nord. Il semble ´egalement qu’il n’y a
pas de transport significatif des sources de pollution depuis l’Am´erique du Nord
et aucune trajectoire ne traverse l’´equateur.

32. 32 Chapitre 2: Processus chimiques et dynamiques
Figure 2.7: Composante verticale du vent moyenn´ee entre 300 et 700 mb, pour les
mois de a) Octobre, b) Janvier, c) Mai et d) Juillet. Les isocontours correspondent
`a 0, 1, 2, 3, 4, 5, 7.5 et 10 × 10−2
Pa.s−1
.

33. 2.2 Processus dynamiques 33
Figure 2.8: Sch´ematisation du transport depuis le continent asiatique jusqu’`a
Hawaii. Depuis la source d’´emission (a), les gaz polluants sont transport´es hori-
zontalement vers l’Est pr`es de la surface o`u ils sont m´elang´es par turbulence (b),
avant d’ˆetre entraˆın´es verticalement par les nuages convectifs profonds `a haute
altitude (c). Le transport rapide sur le Pacifique s’accompagne d’une subsidence
(d) avant d’atteindre Hawaii (e).
2.2.4 Transport convectif
La convection se d´eveloppe sur des ´echelles spatiales variant de quelques
kilom`etres carr´es (cumulus par beau temps) `a quelques milliers de kilom`etres
carr´es et peut s’´etendre depuis la surface terrestre jusqu’`a la tropopause, tels que
les cumulo-nimbus ou nuages convectifs profonds. Les cumulus et cumulonimbus,
`a la diff´erence des autres types de nuages qui apparaissent lors du passage d’un
front, se d´eveloppent lors d’un r´echauffement intense des couches de surface.
Les cumulus sont des nuages bas qui se forment au sommet de la couche limite
plan´etaire. Ces nuages ne s’accompagnent en g´en´eral pas de pr’ecipitation et on
parlera de convection s`eche `a l’oppos´e des cumulonimbus (profondeur de 5 `a 10
km), auxquels sont associ´es ´eclairs, tonnerres, et fortes pr´ecipitations.
Les nuages convectifs profonds (cumulo-nimbus) ont le potentiel de trans-
porter les constituants en trace depuis la couche limite plan´etaire vers les couches
sup´erieures de la troposph`ere ainsi que de modifier la composition chimique par la
dissolution des compos´es solubles. Il peut donc exister une dualit´e entre l’apport
vers la troposph`ere libre de gaz solubles produits au niveau de la couche limite
plan´etaire et leur lessivage par les pr´ecipitations.
Pour ´etudier la distribution des cumulonimbus, nous nous sommes servis
d’une climatologie de nuages ´etablie `a partir des donn´ees du programme ”Inter-

34. 34 Chapitre 2: Processus chimiques et dynamiques
national Satellite Cloud Climatology Project” (ISCCP). Le programme ISCCP
[209] fournit des moyennes mensuelles (version C2) de certaines caract´eristiques
temporelles et spatiales, telles que les fractions de surface occup´ees par un type
de nuage ou l’ensemble des nuages, leurs altitudes au sommet et leurs ´epaisseurs
optiques. Ces donn´ees, disponibles de 1983 `a 1991, ont ´et´e moyenn´ees sur la
p´eriode 1984-1987 sur une grille de 5o
par 5o
[192]. La figure 2.9 donne les dis-
tributions spatiales du pourcentage de couverture par les cumulonimbus pour les
mois d’octobre, janvier, mai et juillet. En ´et´e, le contraste thermique entre le
sol chaud et l’air froid au-dessus des continents est `a l’origine des zones de max-
ima sur les continents alors qu’en hiver ce contraste se marque surtout au-dessus
de l’oc´ean. Les maxima en Mai et en Octobre sont moins marqu´es. Au niveau
de l’´equateur, les masses d’air humide transport´ees depuis l’oc´ean subtropical
convergent le long de la zone de convergence intertropicale (ZCIT). Cette con-
vergence induit la formation de cumulo-nimbus et est accompagn´ee d’abondantes
pr´ecipitations tout au long de l’ann´ee. Aux latitudes temp´er´ees, un large syst`eme
convectif est associ´e au front entre la d´epression polaire et l’anticyclone du Paci-
fique. Ces nuages convectifs inclin´es verticalement vers le nord transf`erent vers
les r´egions polaires l’´energie re¸cue aux latitudes subtropicales. En hiver (figure
2.9.a), l’instabilit´e thermique entre la couche de surface atmosph´erique et l’oc´ean
plus chaud est `a l’origine du d´eveloppement de cumulus et cumulo-nimbus. En
´et´e, le rayonnement intense `a la surface des continents et l’apport d’air humide
maritime expliquent l’augmentation de la fr´equence des cumulo-nimbus au-dessus
des continents (figure 2.9.c).
2.2.5 Circulation `a proximit´e de l’ˆıle de Hawaii
La circulation, `a proximit´e de l’ˆıle de Hawaii, refl`ete l’interaction entre
quatre facteurs: la latitude, l’influence oc´eanique, la position relative de l’ˆıle
par rapport `a l’anticyclone du Pacifique Nord et l’orographie. Avec une surface
d’environ 10,500 kilom`etres carr´es, l’ˆıle de Hawaii occupe les deux-tiers de la
surface totale de l’archipel. Cinq larges cˆones volcaniques forment le relief; le
plus haut est Mauna Kea qui s’´el`eve `a 4205 m`etres au-dessus du niveau de la mer
(figure 2.10). Les autres volcans sont Mauna Loa (4169 m`etres), Hualalai (2521
m`etres), Kohala (1670 m`etres), et Kilauea (1248 m`etres). Kilauea et Mauna Loa
sont des volcans actifs.
La taille et l’´el´evation de la chaˆıne volcanique contribuent `a une grande
diversit´e climatique. Les cˆot´es face au vent de Mauna Loa sont humides, avec
des pr´ecipitations accumul´ees de l’ordre de 10 m`etres par an. Par contre les faces
sous le vent sont `a l’abri des pluies, et certains endroits sont classifi´es comme
semi-d´esertiques. La plus grande partie de la population (92.053 habitants en
1980) est concentr´ee dans la ville de Hilo (35.269 habitants en 1980), qui est

35. 2.2 Processus dynamiques 35
Figure 2.9: Distribution de la couverture par les cumulo-nimbus pour les mois de
a) Octobre, b) Janvier, c) Mai et d) Juillet. Les valeurs ont ´et´e obtenues `a partir
des valeurs satellitaires du ISCCP et moyenn´ees entre 1984-1987. Les isocontours
correspondent `a 4, 8, 12, 16 et 20 %.

36. 36 Chapitre 2: Processus chimiques et dynamiques
Figure 2.10: Orographie et v´eg´etation de l’ˆıle d’Hawaii.

37. 2.2 Processus dynamiques 37
le port principal de l’ˆıle. Avec une d´enivellation de plus de 4000 m`etres sur
approximativement 70 kilom`etres et une disparit´e dans la distribution spatiale
des pr´ecipitations, l’ˆıle de Hawaii subit des climats simultan´es tr`es vari´es: de
tropical `a semi-d´esertique. La v´eg´etation refl`ete cette disparit´e et on y trouve
quasiment cˆote-`a-cˆote la forˆet tropicale, le semi-d´esert et la toundra (figure 2.10).
Influence de l’orographie sur la circulation
L’orographie de Hawaii influence profond´ement les aspects du climat au-
dessus et au voisinage de l’ˆıle. Le r´echauffement des pentes des montagnes par la
radiation solaire pendant la journ´ee, ou le refroidissement radiatif nocturne, sont
transmis aux couches d’air avoisinantes par conduction et convection turbulente et
g´en`erent une circulation locale complexe (figure 2.11). Le refroidissement radiatif
Figure 2.11: Repr´esentation sch´ematique de la circulation le long des pentes de
l’ˆıle d’Hawaii, a) le jour et b) la nuit.
nocturne de surface cr´ee un vent froid descendant le long des pentes de Mauna
Kea et Mauna Loa. Ce vent forme une couche d’une cinquantaine de m`etres
d’´epaisseur qui descend avec une faible vitesse de l’ordre de 3 ms−1
. Au-dessus de
cette couche, il y a une circulation de retour montante qui diverge aux sommets.
Au cours de la nuit les vents descendants, ou vents catabatiques, se renforcent et
repoussent les vents dominants du nord-est `a l’est de Hilo sur plusieurs dizaines
de kilom`etres [126]. Apr`es le lever du jour, le r´echauffement radiatif modifie
la direction du vent et cr´ee des vents chauds et humides ascendants (ou vents
anabatiques), accompagn´es de nuages de type cumulus. D’autre part, ces vents
catabatiques et anabatiques sont renforc´es par les brises qui agissent dans le mˆeme
sens. Le contraste thermique entre l’air au-dessus de l’ˆıle et de l’oc´ean g´en`ere des

38. 38 Chapitre 2: Processus chimiques et dynamiques
brises de mer ou brises de terre suivant qu’ils prennent naissance au-dessus de
l’oc´ean ou de la terre. La capacit´e thermique ´elev´ee de l’eau r´eduit la variation
diurne de la temp´erature de surface de l’oc´ean, alors que la faible conductivit´e
mol´eculaire et la capacit´e thermique des sols renforcent l’amplitude de variation
de la temp´erature de l’air dans la couche de surface. Il en r´esulte un gradient de
temp´erature positif (n´egatif), vers la terre, pendant la journ´ee (nuit). Le front
de la brise de mer est caract´eris´e par une discontinuit´e du degr´e d’humidit´e et
une couverture nuageuse de type cumulus [215]. Ces vents locaux sont limit´es `a
la couche limite plan´etaire dont la hauteur est d’environ 2 kilom`etres [101].
Influence de l’orographie sur les nuages
Au-dessus de l’oc´ean et `a proximit´e de Hawaii, les pr´ecipitations accu-
mulent entre 50 et 75 cm d’eau par an. Par contraste, les ˆıles re¸coivent jusqu’`a 15
fois cette valeur par endroits et moins d’un tiers en d’autres. Les diff´erents types
de nuages sont, en g´en´eral, d´eclench´es et renforc´es par l’orographie [121]. D’autre
part dans la zone de convergence entre les masses d’air maritime et insulaire, `a
la limite de la zone de bloquage, il y a formation d’une bande nuageuse de type
cumulus quasi-stationnaire [215]. La nuit cette bande de nuages se positionne
`a l’est de l’ˆıle. Pendant la journ´ee le refroidissement ascensionnel d’air chaud
et humide maritime, le long des pentes est `a l’origine de formations nuageuses
et d’abondantes pr´ecipitations. Les pr´ecipitations associ´ees `a ces nuages peu-
vent accumuler jusqu’`a dix m`etres de pluie par an. La variabilit´e spatiale des
pr´ecipitations est essentiellement li´ee au terrain et aux vents locaux [84] Les
niveaux de pr´ecipitations suivent approximativement l’orographie [88]. Elles at-
teignent une valeur maximum aux environs de 750 m d’altitude et ensuite dimin-
uent rapidement avec l’´el´evation. Cette r´epartition spatiale fluctue d’un jour `a
l’autre et d´epend entre autres de l’inversion thermique [44]. Le maximum de
pr´ecipitation a lieu d’octobre `a mai alors que l’anticyclone du Pacifique s’affaiblit
et occupe sa position la plus au sud.
2.2.6 M´et´eorologie `a l’Observatoire de Mauna Loa
L’´el´evation de l’Observatoire de Mauna Loa, o`u la pression atmosph´erique
moyenne est de 680 mbar, est telle qu’il se situe dans la zone de transition entre
deux r´egimes synoptiques superpos´es. Les vents dominants du nord-est, forc´es
par l’anticyclone du Pacifique, sont limit´es en altitude par les vents d’ouest du
courant jet subtropical. La hauteur de la transition varie avec les saisons, de 500
mbar en ´et´e, elle descend `a 700 mbar en hiver. L’Observatoire est donc influenc´e
par un r´egime de vents d’est en ´et´e et d’ouest en hiver. Mais le r´egime des vents
affectant l’Observatoire peut varier d’un jour `a l’autre, sp´ecialement au print-

39. 2.2 Processus dynamiques 39
emps.
Une couche d’inversion se maintient tout au long de l’ann´ee s´eparant l’air
maritime de la troposph`ere libre, aux environs de 2 kilom`etres d’altitude [101].
L’Observatoire est avec une altitude de 3.5 km, au-dessus de cette inversion.
L’Observatoire se trouve sur la partie sup´erieure du col en forme de selle
de cheval qui s´epare Mauna Loa, au sud, de Mauna Kea, au nord, et la partie
face aux vents dominants de l’est de la partie aride `a l’ouest. Typiquement, le
r´echauffement de surface `a l’Observatoire commence apr`es le lever du soleil avec
un taux de 8o
C.hr−1
, alors que la temp´erature de l’air `a 1.8 m au-dessus du sol
augmente de 1.7o
C.hr−1
. Nous avons repris `a la figure 2.12 la variation diurne
moyenne de la temp´erature `a 2 m`etres et 40 m`etres, et la temp´erature de ros´ee `a
MLO pendant la campagne MLOPEX-I. Quelques heures apr`es le lever du soleil,
Figure 2.12: Variation diurne de la temp´erature (o
C) `a diff´erentes hauteurs (2 et
40 m`etres), ainsi que la temp´erature de ros´ee Td `a MLO pendant la campagne
MLOPEX-I.
les vents secs et descendants nocturnes se dissipent. Il s’ensuit une p´eriode de
vents faibles et variables. Aux environs de midi, alors que la temp´erature du sol
et de l’air continuent d’augmenter, un ´ecoulement turbulent et sec apparaˆıt et des
cumulus ou stratocumulus montent vers le col, auparavant sous un ciel ´eclairci
par les vents drainants nocturnes. En d´ebut d’apr`es-midi l’´ecoulement ascendant
devient humide et augmente de vitesse et de turbulence, et si l’inversion des vents
dominants est faible ou absent, des nuages orographiques prennent naissance sur
les pentes. Au coucher du soleil, les vents ascendants faiblissent et sont remplac´es
par une p´eriode de calme, et les nuages se dissipent rapidement au-dessus de
l’Observatoire. Vers 21 heures, le sol s’est refroidi suffisamment pour permettre

40. 40 Chapitre 2: Processus chimiques et dynamiques
le retour des vents secs descendants. La figure 2.13 reprend la variation diurne des
composantes horizontales du vent (U,V) `a MLO pendant la campagne MLOPEX-
I. La variation diurne de la direction du vent `a l’Observatoire refl`ete le passage de
Figure 2.13: Variation diurne des deux composantes du vent horizontal (m.s−1
)
`a MLO pendant la campagne MLOPEX-I.
vents descendants catabatiques la nuit `a des vents montants anabatiques le jour.
La nuit, la direction du vent est d’environ 200o
et indique des vents descendants
du sommet de Mauna Loa. Pendant la journ´ee la direction du vent oscille autour
de 90o
en ´et´e et de 300o
en hiver. Cette variation est due `a l’influence des vents
d’ouest en hiver et des vents du nord-est en ´et´e. Les masses d’air maritime arrivent
en fin de matin´ee `a l’Observatoire par un ´ecoulement direct depuis le versant est
(face au vent) et par un ´ecoulement de retour g´en´er´e par la zone turbulente du
versant ouest, situ´ee sous le vent (cf. variation de la temp´erature de ros´ee sur
la figure 2.13). L’air analys´e `a MLO est donc form´e d’un m´elange complexe
d’air provenant de l’ouest et correspondant `a la troposph`ere libre, d’air stable
du nord-est li´e aux vents dominants de l’anticyclone du Pacifique, d’air chaud
et humide de la couche limite maritime et enfin d’air appartenant `a la couche
limite insulaire, contamin´e par la pollution locale et les ´emissions naturelles. La
mesure simultan´ee de l’humidit´e, de la direction du vent et de la concentration
des noyaux de condensation permet de classifier les masses d’air et de ne retenir
que les p´eriodes non-pollu´ees par la pollution locale et les ´emissions naturelles
des ˆıles et de l’oc´ean.

41. 2.2 Processus dynamiques 41
2.2.7 Etude du traceur isotopique 2
22Rn
Le Radon 222, 222
Rn, est un gaz inerte dont la perte est due seulement
`a sa d´esint´egration radioactive et dont la p´eriode de demi-vie est de 3.83 jours
(soit une dur´ee de vie de 5.5 jours). Il est ´emis par les sols non gel´es `a un taux
quasiment constant de 1 atome.cm−2
.s−1
[136]. Les ´emissions oc´eaniques sont de
trois ordres de grandeur plus faibles [243]. Il est donc repr´esentatif des masses
d’air d’origines continentales. D’autre part il a une dur´ee de vie sup´erieure `a celle
d’un nuage convectif, mais inf´erieure au temps n´ecessaire pour ˆetre homog´en´eis´e
dans toutes les couches de la troposph`ere. Il constitue de ce fait un excellent
traceur de l’activit´e convective et permet dans les mod`eles de valider les sch´emas
num´eriques du transport convectif.
Le 222
Rn est ´emis principalement par les sols bien a´er´es et sa concen-
tration diminue rapidement en s’´ecartant des continents. La concentration du
222
Rn s’exprime en pico Curie pour des conditions standards de pression et de
temp´erature ou par l’abr´eviation pCi/SCM. La valeur moyenne de la concen-
tration du 222
Rn pr`es de la surface terrestre varie entre 100 et 300 pCi/SCM
au-dessus des continents et de 0.01 `a 100 pCi/SCM au-dessus des oc´eans [128];
[17]; [86]. Liu et al. [150] ont ´etudi´e l’ensemble des profils verticaux de 222
Rn
mesur´es en diff´erents endroits de la Terre. La figure 2.14 reprend la moyenne de
ces mesures pour les diff´erentes saisons. Il apparait de leur ´etude que le m´elange
vertical est plus intense en ´et´e en raison du renforcement radiatif. D’autre part
il faut noter que le gradient vertical est plus ´elev´e entre 3 et 8 km qu’entre 0 et
3 km d’altitude. Cette variation de pente est le r´esultat du transport vertical
associ´e aux nuages convectifs qui pompent l’air de la couche limite plan´etaire
et l’advectent verticalement jusqu’`a leur sommet [89]; [150]. Nous savons que
l’activit´e convective, au au-dessus du Pacifique Nord, s’intensifie en ´et´e sur les
continents, avec un maximum pr`es des Philipines, et sur l’oc´ean en hiver avec
un maximum aux latitudes moyennes (figure 2.9). Or, d’apr`es Harris et Kahl
[103], les vents dominants en hiver sont de secteur ouest avec 37% des masses
d’air qui viennent d’Asie, alors qu’en ´et´e les vents d’est apportent des masses
d’air d’Am´erique centrale (22%) ou du Pacifique (15%). Donc le transport ver-
tical au-dessus de l’Asie est efficace en ´et´e alors qu’un faible pourcentage d’air
asiatique est transport´e vers Hawaii et inversement en hiver. Etant donn´e que le
transport vertical convectif est limit´e en hiver au-dessus de l’Asie (figure 2.9.a), la
contribution de masses d’air d’autres origines sera tout aussi significative dans la
concentration totale du 222
Rn. La variation saisonni`ere du 222
Rn `a l’Observatoire
de Mauna Loa sur la figure 2.15 est calcul´ee `a partir d’un mod`ele de transport
utilisant des donn´ees climatologiques [17]., La contribution asiatique `a la con-
centration totale est ´egalement indiqu´ee. Le maximum au printemps est dˆu `a
la contribution asiatique, alors que le maximum secondaire en ´et´e a une autre

42. 42 Chapitre 2: Processus chimiques et dynamiques
Figure 2.14: Profils verticaux moyens de la concentration de 222
Rn (pCi/SCM)
pour les quatre saisons. Les barres d’erreur repr´esentent la variance dans le cas
de l’´et´e (Liu et al., 1984).
Figure 2.15: Variations saisonni`eres de la concentration du 222
Rn calcul´ees (Balka-
nski et al., 1992) `a MLO. Les traits pleins repr´esentent la valeur de la concen-
tration calcul´ee, et les traits interrompus donnent la partie de la concentration
originaire d’Asie.

43. 2.3 Processus chimiques dans la troposph`ere 43
origine.
Wilkening [242], apr`es avoir analys´e l’activit´e de nombreux ´echantillons
pr´elev´es dans les sols de l’ˆıle d’Hawaii, a montr´e qu’il existait une ´emission deux
fois plus ´elev´ee que normalement par les sols profonds organiques que l’on trouve
au nord et `a l’est de l’ˆıle. Or en ´et´e la direction moyenne du vent `a MLO est
de 90o
, soit des vents d’est. Il pourrait donc y avoir contamination des mesures
par les sources locales. En analysant les donn´ees observ´ees du Radon 222 `a
MLO entre aoˆut et d´ecembre 1989 par Whittlestone et al. [241], on constate que
d’une part la contribution des sources locales `a la concentration totale moyenne
sur une journ´ee du Radon 222 est dominante en ´et´e et d’autre part les maxima
correspondent `a des vents ascendants du nord ou de l’est. Moore et al. [177] ont
calcul´e que 74% du 222
Rn sous la couche d’inversion ´etait dˆu aux ´emissions locales
de l’ˆıle. D’autre part ils estiment que le temps de r´esidence du 222
Rn au-dessus
de l’ˆıle est de 13 heures. Ce qui veut dire que les ´emissions locales pourraient
influencer les valeurs mesur´ees de nuit.
En r´esum´e, nous dirons que la contribution asiatique lors de la mesure des
concentrations de gaz d’origine anthropique `a MLO est majoritaire au printemps,
minoritaire en ´et´e, et significative, mais non pr´epond´erante, en automne et en
hiver.
2.3 Processus chimiques dans la tropopsh`ere
Les processus chimiques de la troposph`ere sont essentiellement les m´ecanismes
de r´eaction photochimiques et d’autre part les ´echanges avec la surface terrestre
(´emissions et d´epˆots).
2.3.1 M´ecanismes chimiques
Les constituants chimiquement actifs de la troposph`ere incluent les com-
pos´es organiques tels que le m´ethane (CH4) et les hydrocarbones non-m´ethaniques
(NMHC) et leurs produits de r´eaction (ald´ehydes, peroxydes, hydro-peroxydes,
etc.), ainsi que les compos´es inorganiques tels que le monoxyde de carbone (CO),
les oxydes d’azote (NO, NO2), l’acide nitrique (HNO3), le peroxy-ac´ethyl-nitrate
(PAN), les compos´es hydrog´en´es (OH, HO2, H2O2) et l’ozone (O3), [79]; [149];
[127].
Chimie de l’ozone
Dans ce paragraphe, nous allons d´ecrire les m´ecanismes chimiques prin-
cipaux qui interviennent dans la chimie de l’ozone, en distinguant les cycles

44. 44 Chapitre 2: Processus chimiques et dynamiques
pr´epond´erants pour une zone pollu´ee et non-pollu´ee (cas d’Hawaii). Ces pro-
cessus ont ´et´e sch´ematis´ees `a la figure 2.16.
Figure 2.16: Diagramme sch´ematique des processus chimiques fondamentaux af-
fectant la composition de la troposph`ere, d’apr`es Atmospheric Chemistry and
Global Change (1997).
L’ozone
L’ozone, principalement produit dans la stratosph`ere, ne constitue dans
la troposph`ere que 10% de l’ozone total [90]. Son abondance est contrˆol´ee prin-
cipalement par des processus photochimiques qui font intervenir, en pr´esence de
lumi`ere, les oxydes d’azote et les radicaux peroxydes, et dans une moindre mesure
par injection stratosph´erique occasionnelle li´ee `a des perturbations synoptiques
aux latitudes moyennes. [144]. Il est d´etruit `a la surface terrestre par d´epˆot sur
la v´eg´etation. La r´eaction cl´e qui d´eclenche ces m´ecanismes chimiques, est la
photodissociation de l’ozone (O3) qui lib`ere un atome d’oxyg`ene `a l’´etat excit´e
O(1
D),
O3 + hν (λ <310 nm) → O(1
D) + O2 (jO3b)
Alors que les plupart des atomes d’oxyg`ene, `a l’´etat excit´e, O(1
D) form´es sont
ramen´es `a leur ´etat fondamental par r´eaction avec les gaz majoritaires O2 et N2:
O(1
D) + O2 → O(3
P) + O2 (rO-O2)
O(1
D) + N2 → O(3
P) + N2 (rO-N2)

45. 2.3 Processus chimiques dans la troposph`ere 45
une faible portion (≈ 1 %) r´eagit avec la vapeur d’eau pour produire deux radicaux
hydroxyles:
O(1
D) + H2O → 2OH (rO-H2Oa)
L’atome d’oxyg`ene d´esactiv´e O(3
P) va r´eagir avec une mol´ecule d’oxyg`ene, en
pr´esence d’un troisi`eme corps (M), pour former une mol´ecule d’ozone:
O(3
P) + O2 + M → O3 + M (rO-O2a)
M´ethane
Les r´eactions mises en jeu dans la chaˆıne d’oxydation du m´ethane et
les esp`eces qui vont ˆetre form´ees diff`erent suivant la teneur troposph´erique en
oxydes d’azote (NOx). Cette chaˆıne est initi´ee par l’oxydation de 80 `a 90 %
du CH4 troposph´erique par OH. Dans une atmosph`ere pauvre en oxydes d’azote
(NOx ≤ 5–30 pptv2
) deux cycles sont `a distinguer :
CH4 + OH → CH3 + H2O (rCH4-OH)
CH3 + O2 + M → CH3O2 + M (rCH3-O2)
CH3O2 + HO2 → CH3O2H + O2 (rCH3O2-HO2)
CH3O2H + hν → CH3O + OH (jCH3O2H)
CH3O + O2 → CH2O + HO2 (rCH3O-O2)
CH4 + O2 + hν → CH2O + H2O Bilan
et
CH4 + OH → CH3 + H2O (rCH4-OH)
CH3 + O2 + M → CH3O2 + M (rCH3-O2)
CH3O2 + HO2 → CH3O2H + O2 (rCH3O2-HO2)
CH3O2H + OH → CH2O + OH + H2O (rCH3O2H-OH)
CH4 + OH + HO2 → CH2O + 2 H2O Bilan
Le m´ethyle hydroperoxyde (CH3O2H) peut ´egalement r´eagir avec OH pour for-
mer:
2
pptv= parts par 1012
en volume

46. 46 Chapitre 2: Processus chimiques et dynamiques
CH3O2H + OH → CH3O2 + H2O (rCH3O2H-OH)
qui est suivie de (rCH3O2-HO2).
Dans une atmosph`ere riche en NOx, le radical dioxyde de m´ethyle (CH3O2)
r´eagit pr´ef´erentiellement avec NO :
CH4 + OH → CH3 + H2O (rCH4-OH)
CH3 + O2 + M → CH3O2 + M (rCH3-O2)
CH3O2 + NO → CH3O + NO2 (rCH3O2-NO)
CH3O + O2 → CH2O + HO2 (rCH3O-O2)
HO2 + NO → OH + NO2 (rHO2-NO)
2 × (NO2 + hν → NO + O) (jNO2)
2 × (O + O2 + M → O3 + M) (rO-O2)
CH4 + 4 O2 + 2 hν → CH2O + H2O + 2 O3 Bilan
L’oxydation de CH4 en formald´ehyde (CH2O) se fait donc avec ou sans produc-
tion d’ozone suivant la teneur troposph´erique en oxydes d’azote.
Formald´ehyde
La d´ecomposition de CH2O en monoxyde de carbone se produit par pho-
todissociation suivant deux voies possibles:
CH2O + hν → CO + H2 (jCH2Oa)
ou
CH2O + hν → CHO + H (jCH2Ob)
Cette photodissociation est suivie du cycle chimique:
CHO + O2 → HO2 + CO (rCHO-O2)
H + O2 + M → HO2 + M (rH-O2)
2 × (HO2 + O3 → OH + 2 O2) (rHO2-O3)
CH2O + 2 O3 → CO + 2 O2 + 2 OH Bilan
Au lieu d’ˆetre photodissoci´e, CH2O peut ˆetre oxyd´e par le radical OH:

47. 2.3 Processus chimiques dans la troposph`ere 47
CH2O + OH → CHO + H2O (rCH2O-OH)
CHO + O2 → HO2 + CO (rCHO-O2)
HO2 + O3 → OH + 2 O2 (rHO2-O3)
CH2O + O3 → CO + H2O + O2 Bilan
Comme dans le cas de la d´ecomposition du m´ethane, l’abondance en OH d´eterminera
le cycle pr´ef´erentiel de destruction de CH2O.
Dans une atmosph`ere riche en NOx, HO2 r´eagit pr´ef´erentiellement avec
NO et la d´ecomposition de CH2O se fera suivant le sch´ema :
CH2O + hν → CHO + H (jCH2Ob)
CHO + O2 → HO2 + CO (jCHO-O2)
H + O2 + M → HO2 + M (rH-O2)
2 × (HO2 + NO → OH + NO2) (rHO2-NO)
2 × (NO2 + hν → NO + O) (jNO2)
2 × (O + O2 + M → O3 + M) (rO-O2)
CH2O + 4 O2 + 2 hν → CO + 2 OH + 2 O3 Bilan
ou bien :
CH2O + OH → CHO + H2O (rCH2O-OH)
CHO + O2 → HO2 + CO (rCHO-O2)
HO2 + NO → OH + NO2 (rHO2-NO)
NO2 + hν → NO + O (jNO2)
O + O2 + M → O3 + M (rO-O2)
CH2O + 2 O2 + hν → CO + H2O + O3 Bilan
On assistera donc `a une production d’ozone dans une atmosph`ere pollu´ee en
oxydes d’azote et `a une destruction de O3 dans le cas contraire.
Monoxyde de carbone
L’´etape finale de cette chaˆıne est l’oxydation de CO en CO2. De nouveau,
il convient de diff´erencier les atmosph`eres riches et pauvres en NOx. En pr´esence
de faibles concentrations d’oxydes d’azote :

48. 48 Chapitre 2: Processus chimiques et dynamiques
CO + OH → CO2 + H (rCO-OH)
H + O2 + M → HO2 + M (rH-O2)
HO2 + O3 → OH + 2 O2 (rHO2-O3)
CO + O3 → CO2 + O2 Bilan
Signalons que la r´eaction de HO2 avec lui-mˆeme pour produire du peroxyde
d’hydrog`ene (H2O2) entre en comp´etition avec (rHO2-O3) et constitue une perte
pour les constituants hydrog´en´es HOx (= H + OH + HO2), par l’interm´ediaire
du d´epˆot sec et du lessivage de H2O2. Lorsque l’abondance des NOx est plus
importante, l’oxydation de CO se fait suivant le sch´ema :
CO + OH → CO2 + H (rCO-OH)
H + O2 + M → HO2 + M (rH-O2)
HO2 + NO → OH + NO2 (rHO2-NO)
NO2 + hν → NO + O (jNO2)
O + O2 + M → O3 + M (rO-O2)
CO + 2 O2 + hν → CO2 + O3 Bilan
On voit donc que la teneur troposph´erique en NOx non seulement contrˆole la
production ou la destruction de l’ozone, mais qu’elle joue, ´egalement, un rˆole
critique dans les r´eactions qui d´eterminent l’abondance du radical OH, pour des
concentrations donn´ees de CO et CH4. La variation des taux de production et
de destruction de l’ozone en fonction de la concentration du NOx est reprise `a la
figure 2.17. Les valeurs de concentrations de NOx mesur´ees durant la campagne
MLOPEX-I varient entre 25 et 50 ppt, ce qui correspond d’apr`es le graphique
2.17 `a une destruction nette d’ozone.
Hydrocarbures non-m´ethaniques
Les activit´es biologiques et humaines sont responsables de l’´emission
abondante de compos´es organiques autres que le m´ethane. Parmi ces compos´es
organiques, il faut citer les alcanes (´ethane C2H4) et les alc`enes (´ethyl`ene C2H4,
propyl`ene C3H6, isopr`ene C5H8, α-pin`ene C10H16). Les effets nets de l’oxydation
de ces hydrocarbures sont
• la conversion de OH en HO2,
• la transformation d’oxyde d’azote en nitrates organiques RONO2,
• la formation de monoxyde de carbone CO,
• la formation de formald´ehyde CH2O.

49. 2.3 Processus chimiques dans la troposph`ere 49
Figure 2.17: Variations des taux de production et destruction de l’ozone en fonc-
tion du rapport de m´elange de NOx.
Les oxydes d’azote
Les oxydes d’azote NOx (NOx = NO + NO2) contrˆolent le taux de pro-
duction de l’ozone ainsi que celui du radical hydroxyle OH [51]. Ils d´eterminent
donc indirectement le taux d’oxydation de la plupart des gaz en trace. Leur
taux d’´emissions est le plus abondant dans les r´egions industrielles d’o`u ils sont
transport´es. La dur´ee de vie de NOx est relativement courte dans la troposph`ere
variant de moins d’un jour en ´et´e jusqu’`a plusieurs jours en l’absence d’une ac-
tivit´e photochimique [154]; [151]. L’Observatoire de Mauna Loa ´etant distant
de plusieurs miliers de kilom`etres des continents, les concentrations de NOx sont
seulement de quelques dizaines de ppt [35], compar´e `a plusieurs milliers dans les
r´egions industrielles. Sur l’oc´ean Pacifique la production de NO par les ´eclairs
peut devenir la source dominante de NOx [134], sp´ecialement en ´et´e.
Les r´eservoirs d’azote
Par photochimie, NOx est converti en d’autres compos´es azot´es organiques
et inorganiques moins r´eactifs tels que le nitrate de peroxy-ac´etyle (PAN), l’acide
nitrique (HNO3) et les particules de nitrate (NO−
3 ). Le PAN, qui est omnipr´esent
dans la troposph`ere, est principalement d´etruit par d´ecomposition thermique. De
par sa longue dur´ee de vie `a basse temp´erature, il peut v´ehiculer efficacement des
atomes d’azote sur de grandes distances. Sa distribution horizontale pr´esente un
gradient m´eridional tr`es marqu´e, avec un maximum vers 60o
N et un minimum `a
l’´equateur.

50. 50 Chapitre 2: Processus chimiques et dynamiques
Table 2.1: Intervalles de concentration de gaz r´eactifs correspondant `a diff´erents
taux de pollution (d’apr`es Finlayson-Pitts et Pitts, 1986).
Taux de pollution
Gaz Nul Faible Mod´er´e Elev´e
[CO] ≤ 0.2 ppm 0.2-1 ppm 1-10 ppm 10-50 ppm
[NO2] ≤ 1 ppb 1-20 ppb 0.02-0.2 ppm 0.2-0.5 ppm
[O3] ≤ 0.005 ppm 0.02-0.08 ppm 0.1-0.2 ppm 0.2-0.5 ppm
[NMHC] ≤ 65 ppbC 100-500 ppbC 300-1500 ppbC ≥ 1.5 ppmC
[SO2] ≤ 1 ppb 1-30 ppb 0.03-0.2 ppm 0.2-2 ppm
ppb: parties par 10−9
en volume
ppm: parties par 10−6
en volume
ppbC: parties par 10−9
d’atomes de carbone
ppmC: parties par 10−6
d’atomes de carbone
L’acide nitrique est form´e par la r´eaction entre le radical hydroxyle OH et
le dioxyde d’azote NO2. Il est d´etruit par photodissociation, oxydation par OH,
et d´epˆots sec et humide. Ces deux derniers processus constituent une perte nette
d’azote. Sa distribution horizontale refl`ete sa formation au-dessus des sources
continentales de NOx et son transport par les vents dominants. Au niveau de
MLO, il constitue le r´eservoir d’azote le plus abondant. Mais le PAN qui est
moins abondant constitue la premi`ere source chimique de NOx (sa d´ecomposition
thermique est beaucoup plus rapide que la vitesse de r´eaction HNO3 + OH). Sa
variation saisonni`ere pr´esente un maximum en hiver et un minimum en ´et´e. En
ce qui concerne les valeurs de HNO3 calcul´ees `a MLO `a l’aide de mod`eles, elles
sont pratiquement toutes sous-estim´ees d’un facteur 2 [145]; [146]; [130]; [179].
Diff´erentes th´eories tentent d’expliquer ce d´esaccord, et la plus plausible fait ap-
pel `a la conversion en acide nitrique de nitrates organiques dont on ne tient pas
compte.
On voit donc que si les processus chimiques d´ependent des concentrations
des NOx celles-ci sont li´ees au taux de pollution. Nous avons donn´e au tableau
2.1 les valeurs de concentration de CO, O3, NO2, et NMHC pour diff´erents taux
de pollution. On constate une forte augmentation des compos´es azot´es avec le
niveau de pollution, due `a l’intensit´e des ´emissions de NOx.

51. 2.3 Processus chimiques dans la troposph`ere 51
2.3.2 Les d´epˆots sec et humide
La plupart des gaz ´emis ou produits pr`es de la surface sont d´etruits
par d´epˆot avant d’avoir pu quitter la couche limite plan´etaire. Il existe deux
types de d´epˆot. L’un est le d´epˆot sec qui est dˆu `a l’adsorption dans les mat´eriaux
organiques `a la surface terrestre (feuilles, branches d’arbres, sol, etc.) en l’absence
de pr´ecipitation (la surface elle-mˆeme peut ˆetre s`eche ou humide, dans le cas de
surface d’eau ou apr`es une pluie) et l’autre est le d´epˆot humide qui correspond `a
la dissolution de gaz solubles dans les gouttes de pluie. Les gaz tels que les acides
sont rapidement ´elimin´es par le d´epˆot humide alors que les gaz moins solubles (par
exemple l’ozone et les hydrocarbures) sont d´etruits par d´epˆot sec. Le d´epˆot sec
est g´en´eralement repr´esent´e `a l’aide d’une vitesse qui fournit le temps n´ecessaire
`a une mol´ecule de gaz pour ˆetre adsorb´e `a la surface. Ainsi pour l’ozone, cette
vitesse de d´epˆot est de l’ordre de 1 cm.s−1
[239]. Lee et al. [140] ont mesur´e des
vitesses comprises entre 0.27 et 4 cm.−1
pour l’acide nitrique `a l’Observatoire de
Mauna Loa.
2.3.3 Les donn´ees de la campagne MLOPEX-I
Du 1er
mai au 4 juin 1988, des mesures simultan´ees de constituants
azot´es, d’hydrocarbures, de peroxydes, d’acides organiques, du formald´ehyde et
d’autres constituants ont ´et´e effectu´ees `a l’Observatoire de Mauna Loa (MLO).
Les valeurs moyennes des concentrations de ces compos´es sont donn´ees au tableau
2.2 pour les deux r´egimes de vent (ascendant et descendant) et la valeur moyenne
pour les deux r´egimes. Les mesures de la troposph`ere libre sont celles prises entre
22h00 et 10h00 (heure locale) quand la vitesse du vent descendant est d’au moins
1m.s−1
[203]. Les mesures correspondant au r´egime de vents ascendants sont
prises entre 11h00-19h00 (heure locale). Ce sont ces mesures que nous d´esirons `a
pr´esent discuter.
Les oxydes d’azote
Les oxydes d’azote NO et NO2 ont ´et´e mesur´es simultan´ement par les
techniques de chimiluminescence pour NO et de conversion photolytique pour
NO2 [204]. Dans les conditions de vents descendants (troposph`ere libre), les
valeurs moyennes sont de 10 ppt pour NO et 24 ppt pour NO2. L’apr`es-midi les
valeurs typiques sont de 12 ppt pour NO et 25 `a 30 ppt pour NO2 indiquant une
influence mod´er´ee des sources de l’ˆıle.

52. 52 Chapitre 2: Processus chimiques et dynamiques
Table 2.2: Concentrations moyennes et variance (entre parenth`eses) de quelques
compos´es mesur´es entre le 1er
mai et le 4 juin 1988 `a l’Observatoire de Mauna
Loa.
Conditions du vent
Gaz Toutes Descendantes Ascendantes
[O3] (ppb) 39.9 (11) 43.3 (12) 34.5 (7.6)
[NOx] (ppt) 38 (20) 32 (13) 43 (21)
[PAN] (ppt) 21 (17) 17 (14) 27 (20)
[HNO3] (ppt) 123 (79) 109 (60) 130 (80)
[NOy] (ppt) 272 (128) 271 (111) 255 (106)
[CH3ONO2] (ppt) 3.9 (1.8) 3.7 (2.1) 4 (1.5)
Σ[RONO2] (ppt) [1] 3.8 (2.2) 2.7 (1.4) 5.0 (2.2)
[CO] (ppb) 143 (17) 136 (11) 148 (16)
[CH4] (ppb) 1657 (46) 1655 (41) 1660 (49)
[H2O2] (ppt) 1017 (424) 1053 (265) 903 (409)
[CH2O] (ppt) 138 (70) 105 (42) 190 (72)
[CH3O2H] (ppt) 153 (64) 137 (52) 154 (62)
[C2H4] (ppt) 81 (76) 53 (40) 89 (71)
[C2H6] (ppt) 819 (216) 751 (151) 867 (258)
[C5H8] (ppt) 13.6 (34) 1 (3) 26 (46)
[1] ΣRONO2 est la somme des nitrates d’alkyles avec au moins 3 atomes de carbone
ppt: parties par 10−12
en volume
ppb: parties par 10−9
en volume

53. 2.3 Processus chimiques dans la troposph`ere 53
Table 2.3: Rapport de concentrations de certains gaz et de l’ensemble des com-
pos´es azot´es NOy `a partir des mesures de MLOPEX-I. Les valeurs de la table
sont les valeurs moyennes mesur´ees durant la campagne MLOPEX-I.
Conditions du vent
Rapport Toutes Descendantes Ascendantes
[Ox]/[NOy] 0.155 0.143 0.171
[HNO3]/[NOy] 0.454 0.427 0.511
[PAN]/[NOy] 0.087 0.07 0.111
[NO−
3 ]/[NOy] 0.204 0.145 0.238
Σ[NOy]i/[NOy] 0.934 0.789 1.0721
[1]: La somme des concentrations des esp`eces azot´ees mesur´ees s´epar´ement ne coˆıncide pas avec
la mesure de la concentration de la somme des compos´es azot´es. [CH3NO2] et Σ[RONO2] ne
compte que pour 1% de [NOy].
Famille des compos´es azot´es
La famille des compos´es azot´es non-appari´es NOy est la somme de tous les
constituants azot´es impairs (NOy)i qui sont r´eactifs dans l’atmosph`ere [12]. Pour
la basse et moyenne troposph`ere, les constituants principaux sont NO, NO2, NO3,
N2O5, HNO3, HNO2, PAN, RONO2, NO−
3 . Les valeurs de [NO3] et [N2O5] sont
de l’ordre de quelques ppt et peuvent ˆetre n´eglig´ees dans le calcul de [NOy]. La
mesure de NOy consiste `a convertir tous les compos´es azot´es r´eactifs en NO avant
quantification. Les mesures s´epar´ees des constituants azot´es par des techniques
diff´erentes permet d’´etablir la r´epartition des compos´es azot´es impairs au sein
de NOy. Normalement la somme des concentrations des constituants mesur´es
s´epar´ement doit ˆetre ´egale `a la valeur mesur´ee pour NOy. Cependant plusieurs
´etudes ont montr´e qu’il existe un d´es´equilibre significatif au profit de NOy [73];
[202]; [123]; [12]. Ce d´eficit indique qu’il y a un constituant azot´e manquant dans
la liste de la famille NOy. Nous avons repris `a la table 2.3 les valeurs des rapports
entre la concentration des constituants azot´es impairs (NOy)i et la concentration
de NOy en distinguant le r´egime des vents (ascendant, descendant). Dans les
conditions de vents descendants correspondant `a la troposph`ere libre, la somme
des concentrations de NOx, HNO3, PAN, NO3−
, CH3ONO2, et ΣRONO2 est
en moyenne 25% inf´erieure `a la concentration mesur´ee de NOy. HNO3 est le
principal compos´e azot´e impair.
L’ˆage photochimique d’une masse d’air peut se mesurer par la conversion

54. 54 Chapitre 2: Processus chimiques et dynamiques
Table 2.4: Concentrations moyennes du m´ethane, monoxyde de carbone et de
quelques hydrocarbures non-m´ethaniques mesur´es `a MLO pendant la campagne
MLOPEX-I.
Conditions du vent
Gaz Toutes Descendantes Ascendantes
[CH4] (ppb) 1670 1666 1677
[CO] (ppb) 138 136 143
[C2H6] (ppt) 773 742 820
[C2H4] (ppt) 60 44 62
[C3H8] (ppt) 35 29 44
[C3H6] (ppt) 17 11 17
[C5H8] (ppt) 2 0 11
ppb: parties par 10−9
en volume
ppt: parties par 10−12
en volume
de NOx en HNO3 ou d’autres r´eservoirs azot´es. Une diminution du NOx refl`ete
le temps de transformation en d’autres compos´es au sein de la famille NOy et
´egalement la dilution due au m´elange pendant le transport. L’ˆage photochimique
peut aussi ˆetre mesur´e par le rapport NOx/NOy, ´etant donn´e que NOx diminue
avec le temps au profit de NOy. Cependant NOy n’est pas conserv´e `a cause du
d´epˆot `a la surface terrestre et du lessivage rapide de HNO3. Quand des masses
d’air sont originaires du Pacifique central et se d´eplacent lentement, on observe un
rapport [HNO3]/[NOy] ´elev´e et un faible rapport [NOx]/[NOy] [12]. A l’oppos´e,
quand des masses d’air proviennent d’Asie, le rapport NOx/NOy est ´elev´e et
[HNO3]/[NOy] est faible. Il pourrait sembler qu’il existe une corr´elation entre
le rapport [NOx]/[NOy] et [NOy]. Cependant il n’en est rien, car l’air analys´e
`a MLO est en g´en´eral un m´elange de masses d’air d’origines diff´erentes qui ont
donc des ˆages photochimiques diff´erents [12].
Les hydrocarbures et le monoxyde de carbone
Le m´ethane, CH4, les hydrocarbures non-m´ethaniques (NMHC) et le
monoxyde de carbone, CO, ont ´et´e mesur´es pendant la campagne MLOPEX-I
[94]. Les valeurs des concentrations d’un certain nombre de ces compos´es sont
reprises `a la table 2.4. Les valeurs mesur´ees pour des vents descendants, entre
22h00 et 10h00 (heure locale d’Hawaii) sont caract´eristiques de la troposph`ere
libre non-pollu´ee. Les concentrations des hydrocarbures `a courte dur´ee de vie qui

55. 2.3 Processus chimiques dans la troposph`ere 55
sont ´emis `a la surface de l’oc´ean ou de l’ˆıle d’Hawaii, augmentent significativement
`a l’Observatoire de Mauna Loa lorsqu’il y a un apport d’air maritime pendant
la journ´ee. Dans le cas de l’isopr`ene les ´emissions par la v´eg´etation sont peu
prononc´ees compar´ees `a celles des forˆets continentales [94] et les concentrations
mesur´ees `a MLO sont faibles.
Bilan photochimique de l’ozone
L’ozone est produit par la r´eaction (rO-O2a), et la principale production de O(3
P)
dans la troposph`ere est la photodissociation de NO2. Le NO2 est quant `a lui
produit par l’oxydation de NO par O3. Ces trois r´eactions constituent un cycle
nul et n’ont aucun effet net sur l’ozone. Mais dans les r´egions peu pollu´ees
(faible concentration de NO2) les radicaux hydroxyle, hydro-peroxyle, m´ethyle-
peroxyde et autres peroxydes organiques peuvent oxyder NO en NO2. Dans ce cas,
les r´eactions rNO-HO2, rNO-CH3O2, et rNO-RiO2 constituent une production
d’ozone et le taux de production est donn´e par la relation:
P(O3) = (kNO−HO2[HO2] + kNOCH3O2[CH3O2] + ΣikNO−RiO2[RiO2])[NO] (2.1)
o`u k sont les constantes cin´etiques de r´eaction. La destruction photochimique
dans les r´egions peu pollu´ees (faible abondance en NO) de l’ozone est le fait de
sa photodissociation et sa r´eduction par OH et HO2. Le taux de destruction
s’exprime alors par la relation:
D(O3) = jO3b[O3] + (rHO2−O3[HO2] + rOH−O3[OH])[O3] (2.2)
La production nette de l’ozone pour un ´etat stationnaire se calcule en prenant
la diff´erence entre P(O3) et D(O3). En contraignant ce calcul avec les valeurs
mesur´ees correspondant `a la troposph`ere libre, il est possible de calculer la vari-
ation diurne moyenne de la production d’ozone: en moyenne diurne une faible
destruction de 0.91×105
molec.jour−1
[204] est calcul´ee.
Durant la journ´ee, le minimum mesur´e du rapport de m´elange d’environ
35 ppb refl`ete l’apport d’air maritime pauvre en ozone. La nuit, l’apport des
couches sup´erieures de la troposph`ere augmente la concentration d’O3 jusqu’`a
une valeur d’environ 45 ppb. Il a ´et´e d´emontr´e [206] que ce maximum d’ozone
dans la troposph`ere libre au-dessus d’Hawaii n’´etait pas dˆu `a une injection depuis
la stratosph`ere o`u l’ozone est principalement produit mais ´etait reli´e `a un apport
d’air continental. Quant `a la question de savoir si l’ozone a ´et´e produit au-
dessus du continent et ensuite transport´e ou si il a ´et´e produit localement apr`es
le transport de pr´ecurseurs, elle a ´et´e d´ebattue depuis quelques temps [188]; [4];
[206].

56. 56 Chapitre 2: Processus chimiques et dynamiques
2.4 Conclusions
Dans ce chapitre, pour mieux comprendre l’influence des ´emissions de
polluants associ´ees aux activit´es humaines sur la composition chimique d’une
partie recul´ee de la troposph`ere, `a Hawaii au milieu du Pacifique, nous avons
r´esum´e les ph´enom`enes de transport et les processus chimiques fondamentaux
tels qu’ils ont ´et´e d´ecrits lors de l’analyse des donn´ees de la campagne pilote
MLOPEX-I et dans les nombreuses publications concernant Hawaii.
Il en ressort qu’il existe une forte saisonnalit´e de cette influence marqu´ee
par la position de l’anticyclone du Pacifique et des zones de convection par les
cumulonimbus. En hiver la position au sud-ouest d’Hawaii de cet anticyclone
favorise l’apport d’air asiatique transport´e `a hautes altitudes, alors qu’en ´et´e sa
position au nord d’Hawaii apporte pr´ef´erentiellement des masses d’air d’origine
am´ericaine `a basse altitude. La circulation `a Hawaii est marqu´ee par l’interaction
entre des vents dominants du nord-est et la topographie domin´ee par deux volcans
culminants `a plus de 4000 m`etres. Sur les flancs de ces volcans les vents sont
soumis `a une forte variation diurne: vents ascendants de jour et vents descendants
de nuit.
Les ´etudes du transport effectu´ees `a l’aide du traceur isotopique 222
Rn
ont montr´e qu’il existait un d´esaccord syst´ematique entre les mod`eles et les ob-
servations `a Hawaii. Ce d´esaccord n’a pu encore ˆetre expliqu´e. Ces ´evaluations
supposent qu’il n’y a pas d’influence des ´emissions locales la nuit, bien qu’aucune
´etude n’at v´erifi´e cette hypoth`ese. Nous montrerons au huiti`eme chapitre, que
les concentrations atteintes de jour sont dues aux ´emissions locales.
Les cycles chimiques de l’ozone, du m´ethane, du formald´ehyde, du monoxyde
de carbone et des hydrocarbures non-m´ethaniques sont contrˆol´es par l’abondance
des oxydes d’azote (NOx). Pour une r´egion non-pollu´ee, comme celle d’Hawaii,
la faible concentration de NOx conduit `a une destruction nette d’ozone. Cepen-
dant il existe un certain d´esaccord dans la r´epartition des compos´es azot´es entre
les observations durant MLOPEX-I (pour les p´eriodes de vents descendants) et
les mod`eles photochimiques, en particulier en ce qui concerne la concentration
calcul´ee de l’acide nitrique qui est cinq fois trop ´elev´ee. Un tel d´esaccord existe
´egalement pour le formald´ehyde et le peroxyde de m´ethyle. Malheureusement du-
rant cette campagne de mesure, le radical hydroxyle, ´el´ement d´eterminant pour
la chimie troposph´erique, n’a pas ´et´e mesur´e ce qui a ´et´e par contre r´ealis´e du-
rant la seconde campagne MLOPEX-II. A l’oppos´e notre mod`ele, pour certaines
saisons, calcule trop peu d’acide nitrique, comme nous en parlerons au huiti`eme
chapitre.

57. Chapter 3
Aspects math´ematiques
3.1 Introduction
L’atmosph`ere aux altitudes inf´erieures `a 100 kilom`etres (l’homosph`ere)
peut ˆetre consid´er´ee comme un milieu continu compressible dont l’´etat est car-
act´eris´e par des quantit´es physiques (pression, densit´e, temp´erature) et chim-
iques (concentrations des constituants chimiques). Ces variables sont suppos´ees
ˆetre continues dans l’espace et le temps. D’autre part les constituants chim-
iques sont consid´er´es comme parfaitement m´elang´es en n’importe quel point de
l’homosph`ere. L’atmosph`ere ´etant en mouvement, elle peut ˆetre d´ecrite par un
champ vectoriel de vitesse. Les lois fondamentales de la m´ecanique des fluides et
de la thermodynamique qui r´egissent les mouvements de l’atmosph`ere peuvent
ˆetre exprim´ees `a l’aide d’´equations aux d´eriv´ees partielles. Celles-ci sont parti-
culi`erement complexes, notamment du fait de la disparit´e des ´echelles de temps
et d’espace des ph´enom`enes `a traiter, et aucune solution g´en´erale ne peut ˆetre
d´etermin´ee. Il est donc n´ecessaire de faire appel `a des hypoth`eses simplificatrices
pour pouvoir r´esoudre ces ´equations.
Dans ce chapitre, nous commencerons, apr`es avoir d´efini la liste des vari-
ables d´ependantes, par ´ecrire les ´equations fondamentales du transport des com-
pos´es gazeux dans la troposph`ere. Un certain nombre d’hypoth`eses nous permet-
tera d’´etablir un ensemble d’´equations simplifi´ees avec leurs conditions initiales et
aux limites. Ces ´equations font apparaˆıtre de nouvelles variables `a petite ´echelle,
qui sont param´etris´ees `a l’aide de coefficients de diffusion. Nous terminerons ce
chapitre en ´etablissant la liste des ´equations `a r´esoudre.
57

58. 58 Chapitre 3: Aspects math´ematique
3.2 Les variables d´ependantes
A l’´epoque de la seconde guerre mondiale, on consid´erait que l’atmosph`ere
´etait compos´ee d’une vingtaine de constituants chimiques. Une d´ecennie plus tard
ce nombre ´etait port´e `a une centaine. Actuellement plusieurs milliers de consti-
tuants gazeux ont ´et´e r´epertori´es [90].
Parmi cette multitude de compos´es chimiques, il faut distinguer les com-
pos´es majoritaires (N2, O2) et les gaz rares (Ar, Ne, He, Kr, Xe) qui ont un
rapport de m´elange 1
constant dans la troposph`ere des compos´es minoritaires ou
en trace qui ont une distribution spatio-temporelle d’autant plus variable que leur
dur´ee de vie photochimique est courte.
Nous consid´erons un nombre N de compos´es gazeux qui interviennent
significativement dans la chimie de l’ozone troposph´erique. La distribution des
rapports de m´elange des N gaz va d´ependre des variables m´et´eorologiques suiv-
antes:
• la pression p (Pa)
• la densit´e de l’air ρ (kg.m−3
)
• la temp´erature T (K)
• les trois composantes de la vitesse du vent (u, v, w) (m.s−1
)
• la concentration de H2O dans ses trois phases
Nous avons `a pr´esent N + 9 inconnues, d´ependant des coordonn´ees d’espace
(x, y, z) et du temps t, qui peuvent ˆetre d´etermin´ees `a partir des ´equations exp-
rimant les lois de conservation:
• de la masse de l’air
• de la quantit´e de mouvement
• de l’´energie
• de l’eau dans ses trois phases
1
Le rapport de m´elange est soit massique soit volumique. Si ρ est la masse sp´ecifique de l’air
et si ρi est la masse sp´ecifique d’un gaz i, le rapport de m´elange massique sera µi=ρi
ρ , dont les
unit´es sont exprim´ees en parties par 103
(ppthm), par 106
(ppmm), par 109
(ppbm) ou par 1012
(pptm). Si [d] est la densit´e de l’air, exprim´ee en mol´ecules par centim`etre cube (molec.cm−3
)
et [Ci] est la concentration d’un constituant i, ´egalement exprim´e en molec.cm−3
, le rapport
de m´elange volumique sera fi=[Ci]
[d] dont les unit´es sont exprim´ees en parties par 103
(ppthv ou
ppth), par 106
(ppmv ou ppm), par 109
(ppbv ou ppb) ou par 1012
(pptv ou ppt).

59. 3.3: Equations primitives 59
• des N constituants chimiques gazeux
et la loi consitutive du milieu:
- loi des gaz parfaits.
A ces ´equations, il faut ajouter les conditions aux limites et initiales. Nous allons
`a pr´esent ´etablir ces ´equations de conservation et d’´etat au cas de la troposph`ere.
3.3 Les ´equations primitives
3.3.1 Equation d’´etat
La loi des gaz parfaits d´ecrit l’´etat d’un m´elange de gaz `a faible densit´e
et est donn´ee par la relation suivante
p α = n R T (3.1)
o`u
p est la pression (N.m−2
),
α est le volume sp´ecifique (m3
.kg−1
),
T est la temp´erature absolue (K), et
R est une constante qui d´epend de la composition chimique du m´elange.
L’air ´etant compos´e majoritairement de O2, N2 et de Ar, la valeur de la constante
pour l’air sec est de 287 J.K−1
.kg−1
. La concentration de la vapeur d’eau est tr`es
variable dans la troposph`ere mais ne peut ˆetre n´eglig´ee dans le calcul de R. Si l’on
d´efinit l’humidit´e sp´ecifique q comme le rapport entre la masse de vapeur d’eau
et la masse de l’air, une nouvelle constante doit ˆetre d´efinie en chaque point de
la troposph`ere en fonction de q. Par cons´equent, la relation qui est g´en´eralement
utilis´ee pour d´efinir l’´equation d’´etat de l’atmosph`ere est la suivante
p = ρRTv (3.2)
o`u
ρ = 1/α est la masse sp´ecifique de l’air (kg.m−3
),
Tv = T(1 + 0.61q) est la temp´erature virtuelle de l’air (K),
R = 287 J.kg−1
.K−1
est la constante des gaz pour l’air sec.
3.3.2 Conservation de la masse
La conservation de la masse de l’air s’exprime par son ´equation de con-
tinuit´e:
∂
∂t
ρ + ∇(ρv) = 0 (3.3)

60. 60 Chapitre 3: Aspects math´ematique
qui relie la masse sp´ecifique de l’air ρ au champ de vitesse du vent v. En utilisant
l’´egalit´e: ∇(ρv) = v.∇ρ + ρ∇v, l’´equation de continuit´e (3.3) peut s’´ecrire sous
la forme d’une diff´erentielle totale:
dρ
dt
=
∂
∂t
ρ + v.∇ρ = −ρ ∇v (3.4)
3.3.3 Conservation de la quantit´e de mouvement
Dans un r´ef´erentiel fix´e `a la Terre, la conservation de la quantit´e de
mouvement peut s’exprimer par l’´equation vectorielle suivante [117]:
∂v
∂t
= −v.∇v −
1
ρ
∇p + g − 2Ω × v + T (3.5)
o`u
v est le vecteur de la vitesse du vent,
ρ est la masse sp´ecifique de l’air,
1
ρ
∇p est la force du gradient de pression,
g est la force de gravit´e,
Ω × v est la force de Coriolis,
Ω est le vecteur de la vitesse angulaire de rotation de la Terre (Ω =
7.292 × 10−5
rad.s−1
), et
T sont les forces de friction par unit´e de masse.
Les forces de friction peuvent ˆetre n´eglig´ees dans l’homosph`ere car le coefficient
de diffusion mol´eculaire est tr`es faible (∼ 1.5 × 10−5
m2
.s−1
).
Si nous choisissons un syst`eme d’axes de coordonn´ees (x, y, z) fix´e `a la
surface terrestre tel que d´efini `a la figure 3.1, en fonction de la latitude Φ et de la
longitude λ, le produit vectoriel de la force de Coriolis s’exprime suivant les trois
composantes de la quantit´e de mouvement par les expressions [111]:
2Ωv sin Φ − 2Ωw cos Φ suivant x
−2Ωu sin Φ suivant y (3.6)
2Ωu cos Φ suivant z
o`u (u, v, w) sont les composantes du vent.
Dans la premi`ere expression, le terme en w peut ˆetre n´eglig´e puisque la vitesse
verticale est de plusieurs ordres de grandeur inf´erieure `a la vitesse horizontale.
De plus, la composante verticale de la force de Coriolis est de plusieurs ordres
de grandeur inf´erieure aux autres termes de l’´equation 3.5 suivant z et est donc
n´eglig´ee.

61. 3.3: Equations primitives 61
Figure 3.1: Syst`eme de coordonn´ees (x, y, z) li´e `a la Terre.
Les composantes de l’´equation de la quantit´e de mouvement peuvent
s’´ecrire de la mani`ere suivante:
∂u
∂t
+ u
∂u
∂x
+ v
∂u
∂y
+ w
∂u
∂z
= −
1
ρ
∂p
∂x
+ fcv
∂v
∂t
+ u
∂v
∂x
+ v
∂v
∂y
+ w
∂v
∂z
= −
1
ρ
∂p
∂y
− fcu (3.7)
∂w
∂t
+ u
∂w
∂x
+ v
∂w
∂y
+ w
∂w
∂z
= −
1
ρ
∂p
∂z
− g
o`u fc = 2Ω sin Φ est le param`etre de Coriolis.
3.3.4 Conservation de l’´energie
L’´equation de conservation de l’´energie peut ˆetre d´eriv´ee des lois de la
thermodynamique pour prendre la forme suivante [117]
dθv
dt
=
θv
cpTv
Sθ (3.8)
o`u
θv est la temp´erature potentielle virtuelle d´efinie par l’expression:
θv = Tv
1000
p
R
cp
(3.9)
p est la pression atmosph´erique (mb),
cp=1004 J.kg−1
.K−1
est la chaleur sp´ecifique de l’air sec `a pression con-
stante,
Tv est la temp´erature virtuelle d´efinie en 3.2, et

62. 62 Chapitre 3: Aspects math´ematique
Sθ est le taux de r´echauffement diabatique par unit´e de masse (J.kg−1
.s−1
).
Les sources et les pertes principales du r´echauffement diabatique sont:
-l’absorption des radiations solaires,
-l’absorption et l’´emission des radiations dans l’infra-rouge,
-les changements de phase de la vapeur d’eau.
La dissipation d’´energie par mouvement mol´eculaire peut ˆetre n´eglig´ee dans l’homosph`ere
en raison de la tr`es faible valeur du coefficient de diffusion mol´eculaire.
3.3.5 Conservation de la vapeur d’eau
L’abondance de l’eau dans ses trois phases peut s’obtenir `a l’aide d’une
´equation de conservation pour chaque phase:
dqi
dt
= Sqi i = 1, 2, 3 (3.10)
o`u q1, q2 et q3 sont les rapports de masse de l’eau sous forme de vapeur, liquide
et solide. Sqi repr´esente les diff´erents processus de changement de phase et de
production ou perte chimique. Dans la troposph`ere, les changements de masse
par les r´eactions chimiques sont n´egligeables et les diff´erents processus intervenant
dans le calcul de Sqi sont les suivants:
Sq1 = (+´evaporation - condensation) + ( +sublimation - d´eposition)
Sq2 = (+fusion - cong´elation) + (+condensation - ´evaporation) + (+pr´ecipitation
du dessus - pr´ecipitation vers le bas)
Sq3= (+cong´elation - fusion) +(+d´eposition - sublimation) + (+pr´ecipitation du
dessus - pr´ecipitation vers le bas)
3.3.6 Conservation des constituants chimiques
Pour tous les compos´es gazeux consid´er´es nous avons `a ´ecrire une ´equation
de conservation. Nous utilisons une ´equation similaire `a celle de la vapeur d’eau,
mais qui exprime la conservation du rapport de m´elange f:
dfi
dt
= Sni (3.11)
o`u Sni repr´esente les termes de production et de perte photochimiques qui sont
fonction des concentrations des gaz.
La concentration ni d’un gaz i se calcule en utilisant la loi des gaz parfait, si on
connait le rapport de m´elange fi, par la relation
ni =
pNav
104RdTv
fi molecules.cm−3 (3.12)

63. 3.4: Simplification des ´equations 63
Table 3.1: Nomenclature des ´echelles caract´eristiques des ph´enom`enes de trans-
port atmosph´eriques, d’apr`es Atkinson 1995.
Echelles
Micro M´eso Synoptique
P´eriode < 1 hr 1-48 hr > 48 hr
Longueur d’onde < 20 km 20-500 km > 500 km
o`u p est la pression (mb), Nav = 6, 02 × 1023
est le nombre d’Avogadro, Rd =
8, 3143 J.K−1
.mole−1
est la constante universelle des gaz et Tv est la temp´erature
virtuelle (K).
L’ensemble des N ´equations de continuit´e des constituants gazeux forme un
syst`eme non-lin´eaire dont les valeurs propres (temps de vie photochimique) sont
fortement dispers´ees.
3.4 Simplifications des ´equations
Les ´equations de conservation que nous avons d´efinies pr´ec´edemment
sont exprim´ees en fonction des op´erateurs diff´erentiels (∂/∂t, ∂/∂xi) et peuvent
ˆetre discr´etis´ees en termes de diff´erences finies δt, δx, δx, δy et δz pour autant
que ces diff´erences tendent vers zero. Cependant, l’atmosph`ere ´etant consid´er´ee
comme un milieu continu, ces dif´erences doivent ˆetre nettement sup´erieurs au
rayon moyen des mol´ecules. Actuellement les valeurs utilis´ees de ces diff´erences
sont de l’ordre du centim`etre et de la seconde [193]. Or nous d´esirons r´esoudre
ces ´equations avec une r´esolution de l’ordre d’une dizaine de kilom`etres au-
dessus d’Hawaii et de plusieurs centaines de kilom`etres dans les r´egions distantes
d’Hawaii. Une telle r´esolution permet de simuler correctement les ph´enom`enes `a
m´eso-´echelle, d’apr`es la classification de Atkinson [10] reprise au tableau 3.1.
Les variables d´ependantes sont d´ecompos´ees en une variable moyenne
explicitement r´esolue et une variable fluctuante qui doit ˆetre exprim´ee en fonction
des variables moyennes.
Une variable X est d´ecompos´ee suivant l’expression:
X = X + X (3.13)
o`u X est la valeur moyenne de X:
X =
t+∆t
t
x+∆x
x
y+∆y
y
z+∆z
z X dz dy dx dt
∆t ∆x ∆y ∆z
(3.14)

64. 64 Chapitre 3: Aspects math´ematique
et X est la d´eviation de X par rapport `a la moyenne, appel´ee g´en´eralement
perturbation `a sous-´echelle.
Les intervalles ∆t, ∆x, ∆y, ∆z sont sup´erieurs `a la minute pour l’intervalle de
temps et `a la centaine de m`etres pour les intervalles d’espace (cf. tableau 3.1)
La moyenne d’une quantit´e ob´eit aux r`egles suivantes:
X = X, X = 0,
∂X
∂t
=
∂X
∂t
,
∂X
∂xj
=
∂X
∂xj
, etc. (3.15)
Si l’on substitue les variables dans les ´equations par la somme d’une variable
moyenne et d’une fluctuation nous obtenons une ´equation qui peut ˆetre moyenn´ee
par une expression similaire `a 3.14 tout en suivant les r`egles d´efinies en (3.15).
Ces ´equations se simplifient si l’on fait les approximations suivantes
1. Approximation de Boussinesq: Les variables moyennes `a m´eso-´echelle
X peuvent s’exprimer en terme d’une variable qui ne d´epend que de l’altitude
X0(z) et d’une perturbation X . La variable X0 est la moyenne int´egr´ee, sur
plusieurs centaines de kilom`etres et sur plusieurs heures, de X. Elle corre-
spond donc `a une variable `a l’´echelle synoptique. Cette d´ecomposition est
r´ealis´ee pour la pression p (p = p0 +p ), la masse sp´ecifique ρ (ρ = ρ0 +ρ ) et
la temp´erature (T = T0 + T ). L’approximation de Boussinesq consiste, de
plus, `a traiter la masse sp´ecifique comme une constante dont les variations
sont dues `a de faibles perturbations, except´e quand elle est coupl´ee avec la
gravit´e [117].
2. Approximation hydrostatique: La force de gravit´e est enti`erement com-
pens´ee par le gradient vertical de pression, `a l’´echelle synoptique [117].
−
1
ρ0
∂p0
∂z
= g (3.16)
Martin et Pielke [168] ont montr´e que cette approximation est toujours
valide pour des longueurs d’´echelle sup´erieures `a une dizaine de kilom`etres.
3. Approximation d’an´elasticit´e: Pour les mouvements `a l’´echelle synop-
tique, le flux de masse d’air est non-divergent. L’´equation de continuit´e se
r´esume donc au terme de divergence:
∇.(ρ0v) = 0 (3.17)
o`u
ρ0 est la masse sp´ecifique de l’air moyenne `a l’´echelle synoptique,
v est le vecteur de la vitesse instantan´ee.

65. 3.4: Simplification des ´equations 65
Les d´eveloppements de substitution de variables, d’int´egration moyennes des
´equations et de simplification peuvent ˆetre trouv´es dans des ouvrages de r´ef´erence
[193]; [222]; [10]. Nous donnerons ici uniquement la forme finale des ´equations:
∂u
∂t
= −
j
uj
∂u
∂xj
−
j
1
ρ0
∂ρ0u uj
∂xj
−
1
ρ0
∂p
∂x
+ fcv (j = 1, .., 3) (3.18)
∂v
∂t
= −
j
uj
∂v
∂xj
−
j
1
ρ0
∂ρ0v uj
∂xj
−
1
ρ0
∂p
∂y
− fcu (j = 1, .., 3) (3.19)
∂w
∂t
= −
j
uj
∂w
∂xj
−
j
1
ρ0
∂ρ0w uj
∂xj
−
1
ρ0
∂p
∂z
−
ρ
ρ0
g (3.20)
∂ni
∂t
= −uj
∂ni
∂xj
−
1
ρ0
∂ρ0uj ni
∂xj
+ Sni, i = 1, .., Nt
(3.21)
∂ρ
∂t
= −
∂ρuj
∂xj
−
∂ρ uj
∂xj
(3.22)
∂θ
∂t
= −uj
∂θ
∂xj
−
1
ρ0
∂ρ0uj θ
∂xj
+ Sθ (3.23)
∂qi
∂t
= −uj
∂qi
∂xj
−
1
ρ0
∂ρ0uj qi
∂xj
+ Sqi i = 1, 2, 3 (3.24)
o`u Sni, Sθ, Sqi sont les termes de perte et de production int´egr´es sur les intervalles
∆t, ∆x, ∆y, ∆z,
les variables ( )0, ( )’ et ( )” sont respectivement les variables moyenn´ees
sur tout le domaine, les variables `a meso-´echelles apparues en introduisant l’approximation
de Boussinesq, et les variables `a sous-´echelle qui sont param´etris´ees.
Nous voyons que pour chacune de ces ´equations primitives simplifi´ees nous avons
une nouvelle inconnue, `a savoir le terme de corr´elation entre fluctuations (overlineu uj ,
uj ni ,...) qui est appel´e flux turbulent. Nous avons d’autre part deux inconnues
suppl´ementaires: les perturbations `a sous-´echelle pour la masse sp´ecifique (ρ )
et la pression (p ). Cette derni`ere variable est calcul´ee `a partir d’une ´equation
´evolutive qui est d´eriv´ee de l’´equation de continuit´e. Apr`es quelques d´eveloppements
d´etaill´es par exemple par Atkinson [10], nous obtenons l’´equation suivante:
∂p
∂t
= −ρ0gw − γp
j
∂uj
∂xj
−
j
uj
∂p
∂xj
+
γp
T
Sθ j = 1, .., 3 (3.25)
o`u γ = cp/cv est le rapport entre les chaleurs sp´ecifiques `a pression et `a volume
constants.

66. 66 Chapitre 3: Aspects math´ematique
La fluctuation de la masse sp´ecifique peut ˆetre calcul´ee par la relation suivante
[193]:
ρ = ρ
p0
p
(
T
T0
−
p
p0
) (3.26)
o`u T = T −T0(z) est la fluctuation de la temp´erature absolue autour d’une valeur
de r´ef´erence T0(z).
Les valeurs de r´ef´erence ρ0, T0 et p0 sont pr´ecalcul´ees en int´egrant respectivement
les variables p, θ, p sur tout le domaine horizontal et la p´eriode de simulation
pour chaque niveau vertical.
3.5 Transformations des coordonn´ees
3.5.1 Transformation des coordonn´ees horizontales
Le choix d’un syst`eme de coordonn´ees doit permettre une plus grande
simplicit´e des ´equations et ´eviter d’introduire des points de discontinuit´e. Dans le
cas des mod`eles globaux, il est en g´en´eral fait usage d’un syst`eme de coordonn´ees
li´e `a la surface terrestre et dont l’axe x est dirig´e le long d’un paral`ele, l’axe y
suivant un m´eridien et z suivant l’altitude compt´ee `a partir du sol (cf. figure 3.1).
Un tel syst`eme d’axes est non cart´esien et les mod`eles `a m´eso-´echelle, ayant un
domaine limit´e, utilisent un plan de projection o`u l’on peut d´efinir un syst`eme
cart´esien. La surface de projection est un plan interceptant la Terre dans la
r´egion ´etudi´ee et la projection est de type conforme (Mercator, Lambert, st´er´eo-
polaire) et un choix particulier se fonde sur la latitude du domaine: pour la r´egion
´equatoriale, la projection de Mercator est utilis´ee; aux latitudes moyennes ce sera
la projection de Lambert alors qu’un domaine proche des pˆoles est projet´e sur
un plan st´er´eo-polaire. A part la projection st´er´eo-polaire, tous ces syst`emes de
coordonn´ees ont un point de discontinuit´e aux pˆoles. Les pˆoles n´ecessitent donc
un traitement particulier qui d´et´eriore en g´en´eral la solution. Un autre probl`eme
qui se pose avec ces deux premiers syst`emes de coordonn´ees est la connectivit´e
entre les bords fictifs du domaine, la Terre ´etant une sph`ere. Ce probl`eme se
pose principalement pour la r´esolution des ph´enom`enes de transport lors de flux
traversant ces bords: une masse d’air traversant le cˆot´e droit du domaine doit
traverser identiquement le cˆot´e gauche pour assurer la continuit´e.
Pour la r´esolution des variables m´et´eorologiques nous utilisons une pro-
jection de Mercator et pour la r´esolution des variables chimiques nous employons
la projection st´er´eopolaire.

67. 3.5: Transformations des coordonn´ees 67
Figure 3.2: G´eom´etrie de la projection st´er´eopolaire. Les arcs AB et CD sur la
surface de la Terre sont projet´es respectivement sur les lignes A’B’ et C’D’.
Projection st´er´eopolaire
La projection st´er´eopolaire est une projection conforme qui pr´eserve la
forme d’une surface, mais non ses dimensions. Une distance s mesur´ee sur la
surface terrestre est li´ee `a la distance projet´ee sp par la relation (figure 3.2):
sp = s
1 + sin Φv
1 + sin Φ
(3.27)
o`u
m = 1+sin Φv
1+sin Φ
est le facteur d’´echelle de la projection,
Φ est la latitude,
Φv est la ”vraie” latitude.
La vraie latitude correspond `a la latitude du plan de projection, en supposant
qu’il est parall`ele au plan ´equatorial. Hawaii est situ´e autour de 20o
N et nous
avons donc choisi Φv = 20o
N. Sur ce plan nous d´efinissons un syst`eme d’axes
cart´esiens (˜x, ˜y, ˜z) dont l’origine correspond au pˆole nord, l’axe ˜x suit le m´eridien
de Greenwich et l’axe ˜y suit le m´eridien de longitude 90o
O (cf. figure 3.3). Le
syst`eme de coordonn´ees (˜x, ˜y) ainsi choisi est cart´esien.
Les ´equations (3.18)-(3.25) qui ont ´et´e exprim´ees dans les axes (x, y, z),
peuvent ˆetre transform´ees vers le nouveau syst`eme (˜x, ˜y, ˜z) apr`es une s´erie de
transformations qui peuvent ˆetre trouv´ees dans la litt´erature [193]. Les donn´ees
globales qui servent `a initialiser les variables et les param`etres sont en g´en´eral
exprim´ees dans le syst`eme d’axes (λ, Φ). Il est donc utile de rappeler les relations
entre ces coordonn´ees et les coordonn´ees cart´esiennes (˜x, ˜y) qui sont les suivantes
⎧
⎪⎨
⎪⎩
˜x
˜y
˜z
⎫
⎪⎬
⎪⎭
=
⎧
⎪⎨
⎪⎩
m a cos Φ cos λ
m a cos Φ sin λ
z
(3.28)

68. 68 Chapitre 3: Aspects math´ematique
Figure 3.3: Syst`eme de coordonn´ees (˜x, ˜y) utilis´e sur le plan de projection st´er´eo-
polaire qui coupe la surface terrestre `a une latitude de 20o
Nord. L’axe ˜x suit le
m´eridien de Greenwich et l’axe ˜y suit le m´eridien de longitude 90o
Ouest.
o`u a est le rayon terrestre (6371 km). Quant aux vecteurs (u, v, w) projet´es sur
(˜u, ˜v, ˜w), ils sont li´es entre eux par les relations
⎧
⎪⎨
⎪⎩
˜u
˜v
˜w
⎫
⎪⎬
⎪⎭
=
⎛
⎜
⎝
−m sin λ −m cos λ 0
+m cos λ −m sin λ 0
0 0 1
⎞
⎟
⎠
⎧
⎪⎨
⎪⎩
u
v
w
⎫
⎪⎬
⎪⎭
(3.29)
Projection de Mercator
La projection de Mercator est une projection conforme dont le facteur
d’´echelle m est donn´e par la formule (figure 3.4):
m = cos Φv (3.30)
o`u Φv est la vraie latitude.
Le syst`eme d’axes cart´esiens (˜x, ˜y, ˜z) est choisi de sorte que l’origine est plac´ee
`a l’intersection entre l’´equateur et le m´eridien de Greenwich, ˜y est dirig´e vers
le nord suivant un m´eridien, ˜x est dirig´e vers l’est suivant un parall`ele et ˜z est
l’altitude compt´ee `a partir du sol. Les relations entre les coordonn´ees sph´eriques
(λ, Φ, z) et Mercator (˜x, ˜y, ˜z) sont les suivantes
⎧
⎪⎨
⎪⎩
˜x
˜y
˜z
⎫
⎪⎬
⎪⎭
=
⎧
⎪⎪⎨
⎪⎪⎩
m a λ
m a ln 1+sin Φ
cos Φ
z
(3.31)
o`u a est le rayon terrestre (6371 km).

69. 3.5: Transformations des coordonn´ees 69
Figure 3.4: G´eom´etrie de la projection de Mercator. Les arcs AB et CD sur la
surface de la Terre sont projet´es sur A’B’ et C’D’.
3.5.2 Transformation de la coordonn´ee verticale.
Coordonn´ee verticale σ
La plupart des mod`eles utilisent une coordonn´ee verticale ind´ependante
de la topographie, en prenant le rapport entre la pression, p, et la pression au
sol, ps. Afin d’att´enuer la d´eformation due au relief, la coordonn´ee verticale au
sommet du domaine repr´esente un niveau de pression, pt (figure 3.5). La nouvelle
coordon´ee verticale σ est d´efinie par la relation:
σ =
p(x, y, z, t) − pt
ps(x, y, t) − pt
(3.32)
Calcul du vent vertical en coordonn´ee σ
Pour le calcul de la vitesse verticale il faut distinguer deux cas, celui
de l’approximation hydrostatique et le cas non-hydrostatique. L’approximation
hydrostatique suppose que les fluctuations de la vitesse verticale sont n´egligeables
face `a la gravit´e et au gradient vertical de pression. Il n’y a donc plus d’´equation
´evolutive pour la vitesse verticale. Cependant, sa valeur peut ˆetre d´etermin´ee `a
partir de l’´equation de continuit´e. En introduisant la variable p telle que
p (x, y, t) = ps(x, y, t) − pt (3.33)
l’´equation de continuit´e, exprim´ee dans le syst`eme de coordonn´ees (˜x, ˜y, σ), de-
vient
∂p
∂t
+
∂p ˜u
∂˜x
+
∂p ˜v
∂˜y
+
∂p ˙σ
∂σ
= 0 (3.34)

70. 70 Chapitre 3: Aspects math´ematique
Figure 3.5: Coordonn´ee verticale σ qui suit la surface terrestre produisant un
syst`eme d’axes non-orthogonaux en pr´esence de reliefs mais dont l’effet s’att´enue
avec l’altitude.
En imposant l’´equation ´evolutive suivante pour la pression de surface,
∂p
∂t
= −
1
0
∂p ˜u
∂˜x
+
∂p ˜v
∂˜y
dσ (3.35)
il est n´ecessaire que ˙σ satisfasse l’´equation
˙σ = −
1
p
σ
0
∂p
∂t
+
∂p ˜u
∂˜x
+
∂p ˜v
∂˜y
dσ (3.36)
o`u σ est la variable d’int´egration telle qu’`a la surface (σ = 1) la vitesse ˙σ=0.
Dans le cas non-hydrostatique, nous avons une ´equation d´eterministe pour la
vitesse verticale w (´equation 3.20) et la perturbation de pression p (´equation
3.25). La pression s’obtient alors par la relation
p(x, y, σ, t) = p (x, y, t)σ + pt + p (x, y, σ, t) (3.37)
En admettant que les variables synoptiques satisfont l’approximation hydrosta-
tique dp = −ρ0gdz, en rempla¸cant p par la relation pr´ec´edente et en isolant ˙σ,
on obtient
˙σ ≡
dσ
dt
= −ρ0g
p
dz
dt
− σdp
dt
(3.38)
= −ρ0g
p
w − σ∂p
∂˜x
˜u − σ∂p
∂˜y
˜v (3.39)

71. 3.6: Param´etrisation des flux turbulents 71
3.6 Param´etrisation des flux turbulents
Les termes de divergence du flux turbulent, tels que
∂ρ0 ˜uj X
∂˜xj
, sont apparus
en moyennant les ´equations primitives quand les variables instantan´ees ont ´et´e
exprim´ees sous la forme d’une variable moyenne (X) et d’une variable fluctuante
(X ). La sp´ecification de ces termes en fonction des autres variables est appel´ee
le probl`eme de fermeture des ´equations car le nombre d’inconnues est sup´erieur
au nombre d’´equations [222]. Il est possible de d´evelopper des ´equations pour
les flux turbulents inconnus (X ˜uj ), qui sont des termes du second ordre. Mais
ces nouvelles ´equations font apparaˆıtre de nouvelles inconnues du troisi`eme ordre
(produit de trois quantit´es turbulentes). Au fur et `a mesure que de nouvelles
´equations sont ajout´ees, de nouvelles inconnues apparaissent. Pour pallier ce
probl`eme, les variables turbulentes inconnues sont param´etris´ees en fonction des
variables et des param`etres connus. Ces param`etres sont g´en´eralement d´etermin´es
`a partir de donn´ees observ´ees ou de mod`eles plus complets. L’ordre de fermeture
correspond `a l’ordre du produit des variables turbulentes qui sont param´etris´ees:
la param´etrisation des termes (X ˜uj ) en fonction de X et de ˜uj est une fermeture
du premier ordre. La plupart des mod`eles atmosph´eriques se limitent au premier
ordre de fermeture et les flux turbulents sont param´etris´es `a l’aide d’un coefficient
de diffusion turbulente par analogie avec la viscosit´e.
Ainsi pour un fluide Newtonien, la contrainte de cisaillement (force visqueuse
par unit´e de surface) peut ˆetre approch´ee par
τ = ρν
∂v
∂z
(3.40)
o`u ν est le coefficient de viscosit´e cin´ematique, ρ est la masse sp´ecifique de l’air
et ∂v/∂z est le cisaillement.
Par analogie, on peut s’attendre `a ce que la contrainte turbulente puisse ´egalement
s’exprimer en utilisant le terme de cisaillement (∂v/∂z) si l’on fait correspondre
`a la viscosit´e mol´eculaire ν une viscosit´e turbulente Km. Il existe des diff´erences
entre ν et Km. Premi`erement la valeur de ν = 1.5 × 10−5
m2
.s−1
est nettement
plus faible que Km dont les valeurs typiques varient entre 1 et 10 m2
.s−1
[222].
Deuxi`emement ν est une fonction du fluide alors que Km est une fonction de
l’´ecoulement et doit ˆetre param´etris´e en fonction d’autres variables. Derni`erement
il faudrait consid´erer un coefficient Km diff´erent pour les flux turbulents de la
chaleur, de la quantit´e de mouvement et pour chaque compos´e gazeux `a trans-
porter, y compris la vapeur d’eau.
Il existe une ´evidence exp´erimentale qui sugg`ere que le coefficient Km pour la
vapeur d’eau et la chaleur sont identiques [222]. Par simplicit´e et par manque
de donn´ees, on fait l’hypoth`ese que le coefficient Km pour la vapeur d’eau et les
autres compos´es gazeux sont identiques. Nous discuterons de la param´etrisation
de ces coefficients Km au cinqui`eme chapitre.

72. 72 Chapitre 3: Aspects math´ematique
3.7 Ensemble des ´equations `a r´esoudre
Le syst`eme d’´equations 3.18-3.24, exprim´e dans le syst`eme d’axes (˜x, ˜y, σ),
des variables moyennes, pour lesquelles nous avons supprim´e dans leur notation
la surligne, devient
∂p fi
∂t
= fi
∂p ˜u
∂˜x
+ ∂p ˜v
∂˜y
+ ∂p ˙σ
∂σ
− ∂p ˜ufi
∂˜x
+ ∂p ˜vfi
∂˜y
+ ∂p ˙σfi
∂σ
+1
ρ
∂ρfi ˜uj
∂˜xj
+ p ˜Sni (i = 1, ..., N) (3.41)
∂˜uj
∂˜xj
= 0 (3.42)
∂p θ
∂t
= θ ∂p ˜u
∂˜x
+ ∂p ˜v
∂˜y
+ ∂p ˙σ
∂σ
− ∂p ˜uθ
∂˜x
+ ∂p ˜vθ
∂˜y
+ ∂p ˙σθ
∂σ
(3.43)
+1
ρ
∂ρθ ˜uj
∂˜xj
+ p ˜Sθ (3.44)
∂p ˜u
∂t
= ˜u ∂p ˜u
∂˜x
+ ∂p ˜v
∂˜y
+ ∂p ˙σ
∂σ
− ∂p ˜u˜u
∂˜x
+ ∂p ˜v˜u
∂˜y
+ ∂p ˜u ˙σ
∂σ
(3.45)
−mp
ρ
∂p
∂˜x
− σ
p
∂p
∂˜x
∂p
∂σ
+ p f˜v + 1
ρ
∂ρ˜u ˜uj
∂˜xj
(3.46)
∂p ˜v
∂t
= ˜v ∂p ˜u
∂˜x
+ ∂p ˜v
∂˜y
+ ∂p ˙σ
∂σ
− ∂p ˜u˜v
∂˜x
+ ∂p ˜v˜v
∂˜y
+ ∂p ˜v ˙σ
∂σ
(3.47)
−mp
ρ
∂p
∂˜y
− σ
p
∂p
∂˜y
∂p
∂σ
+ p f˜v + 1
ρ
∂ρ˜v ˜uj
∂˜xj
(3.48)
∂p ˜w
∂t
= ˜w ∂p ˜u
∂˜x
+ ∂p ˜v
∂˜y
+ ∂p ˙σ
∂σ
− ∂p ˜u ˜w
∂˜x
+ ∂p ˜v ˜w
∂˜y
+ ∂p ˜w ˙σ
∂σ
(3.49)
−p gρ0
ρ
1
p
∂p
∂σ
+ Tv
T
− T0p
Tp0
p g(q2 + q3) + 1
ρ
∂ρ ˜w ˜uj
∂˜xj
(3.50)
∂p p
∂t
= p ∂p ˜u
∂˜x
+ ∂p ˜v
∂˜y
+ ∂p ˙σ
∂σ
− ∂p ˜up
∂˜x
+ ∂p ˜vp
∂˜y
+ ∂p ˙σp
∂σ
(3.51)
−p γp ∂˜u
∂˜x
− σ
p
∂p
∂˜x
∂˜u
∂σ
+ ∂˜v
∂˜y
− σ
p
∂p
∂˜y
∂˜v
∂σ
+ p f˜v
(3.52)
+ρ0gγp∂ ˜w
∂σ
+ p ρ0gw (3.53)

73. 3.8: Conclusions 73
∂p qi
∂t
= qi
∂p ˜u
∂˜x
+ ∂p ˜v
∂˜y
+ ∂p ˙σ
∂σ
− ∂p ˜uqi
∂˜x
+ ∂p ˜vqi
∂˜y
+ ∂p ˙σqi
∂σ
(3.54)
+1
ρ
∂ρqi ˜uj
∂˜xj
+ p ˜Sqi (i = 1, 2, 3) (3.55)
˙σ = −
ρ0g
p
˜w −
σ
p
∂p
∂˜x
˜u −
σ
p
∂p
∂˜y
˜v (3.56)
p = p σ + pt + p (3.57)
∂p0
∂z
= −ρ0g (3.58)
p = p0 + p (3.59)
p = ps − pt (3.60)
θ = Tv
1000
p(mb)
R
cp
(3.61)
p = ρRTv (3.62)
ρ = ρ0 + ρ (3.63)
Tv = T(1 + 0.61q1) (3.64)
Ce syst`eme d’´equations peut ˆetre r´esolu une fois les conditions aux limites et
initiales sp´ecifi´ees. Les param´etrisations des termes de production des variables
qi (i=1,2,3) et θ que nous avons utilis´ees sont d´ecrites en d´etail par Grell et al.
[93]. Quant au terme de production chimique ˜Sni il est calcul´e `a partir d’un
mod`ele photochimique de la troposph`ere d´ecrit au sixi`eme chapitre.
3.8 Conclusions
Dans ce chapitre, nous avons ´etabli l’ensemble des ´equations `a r´esoudre
pour ´etudier l’´evolution de compos´es chimiques dans la troposph`ere. Nous avons
pour ce faire effectu´e deux d´ecompositions successives des variables instantan´ees,
faisant apparaˆıtre des variables `a macro, m´eso et micro ´echelles. Les premi`eres
sont constantes dans le temps et ne d´ependent que de l’altitude. Elles satisfont
l’approximation hydrostatique et de Boussinesq. Les secondes sont explicite-
ment r´esolues `a l’aide d’´equations diff´erentielles, alors que les derni`eres sont
param´etris´ees `a l’aide de coefficients de diffusion dont le calcul est d´ecrit au
cinqui`eme chapitre. Nous avons introduit de nouvelles coordonn´ees d’espace qui
permettent suivant la verticale de suivre la topographie et suivant l’horizontale
d’avoir un syst`eme cart´esien, dans un plan de projection de Mercator ou st´er´eopolaire.
Nous allons aborder au cours des trois chapitres suivants la r´esolution num´erique
de ces ´equations.

74. 74 Chapitre 3: Aspects math´ematique

75. Chapter 4
Variables m´et´eorologiques
4.1 Introduction
Nous avons vu au chapitre pr´ec´edent que pour r´esoudre l’´equation de con-
tinuit´e des compos´es gazeux atmosph´eriques, nous avons besoin de connaˆıtre les
variables m´et´eorologiques (p, T, q1, q2, q3, u, v, w) en tout point de la troposph`ere
durant les p´eriodes de mesures de la campagne MLOPEX-II. Ces variables sont
calcul´ees par des mod`eles de circulation g´en´erale, tels que ceux du European Cen-
ter for Medium Range Forecasting (ECMWF) en Europe et le National Meteoro-
logical Center (NMC) aux Etats-Unis. De tels mod`eles sont utilis´es pour assim-
iler les observations disponibles par mesures au sol, ballon-sondes, et satellites.
Nous avons utilis´e les donn´ees du ECMWF qui couvrent toute la troposph`ere
et une partie de la stratosph`ere sont fournies en des points r´eguli`erement dis-
tribu´es suivant les latitudes et longitudes (2.5o
× 2.5o
) toutes les 12 heures. Une
telle distribution est insuffisante pour caract´eriser la variation spatiale et diurne
de la dynamique `a Hawaii. Nous avons, en cons´equence, effectu´e des simula-
tions dans la r´egion d’Hawaii `a l’aide d’un mod`ele `a m´eso-´echelle `a deux grilles
imbriqu´ees dont les espacements sont respectivement 27 et 9 kilom`etres. Pour
assurer une continuit´e des champs, les valeurs globales observ´ees servent de con-
ditions aux limites et initiales au mod`ele. La figure 4.1 donne la grille du mod`ele
du ECMWF et du mod`ele `a m´eso-´echelle. La figure 4.2 est un agrandissement de
la figure pr´ec´edente centr´ee sur Hawaii. Nous y voyons une portion de la grille du
ECMWF de 2.5o
×2.5o
, et les deux domaines imbriqu´es du mod`ele `a m´eso-´echelle.
Dans ce chapitre, nous commencerons par d´efinir les donn´ees observ´ees
`a l’´echelle globale que nous avons utilis´ees sans rentrer dans la description du
mod`ele de pr´evision, ce qui d´epasserait tr`es largement le cadre de ce travail. De
mˆeme, en ce qui concerne le mod`ele r´egional nous ne d´ecrirons que les partic-
ularit´es des simulations sans rentrer dans les aspects num´eriques. Les r´esultats
75

76. 76 Chapitre 4: Variables m´et´eorologiquess
Figure 4.1: Grilles des variables m´et´eorologiques: grille globale du mod`ele eu-
rop´een de pr´evision du temps (ECMWF), 2 grilles r´egionales imbriqu´ees utilis´ees
pour simuler la m´et´eorologie dans la r´egion d’Hawaii.

77. 4.1: Introduction 77
Figure 4.2: Agrandissement des grilles des variables m´et´eorologiques centr´e sur
Hawaii. Il y a trois grilles dont la taille des mailles r´eguli`eres est de 2.5o
× 2.5o
pour les donn´ees ECMWF (grille A), 27 km (pour le premier niveau de grille du
mod`ele MM5, not´ee B sur la figure) et 9 km (pour le deuxi`eme niveau du mod`ele
MM5, not´ee C sur la figure).

78. 78 Chapitre 4: Variables m´et´eorologiquess
seront compar´es aux climatologies d´ecrites au premier chapitre.
4.2 Les variables m´et´eorologiques `a l’´echelle glob-
ale
Les donn´ees m´et´eorologiques `a l’´echelle globale que nous avons utilis´ees
proviennent du European Centre for Medium Range Wheater Forecasts ou (ECMWF).
Ces donn´ees ont ´et´e analys´ees `a partir des multiples stations couvrant la Terre
et constituent les meilleurs donn´ees m´et´eorologiques accessibles [225]. Les vari-
ables archiv´ees au National Center for Atmospheric Research depuis 1985 sont:
la hauteur du g´eopotentiel (m), la temp´erature (K), les composantes de la vitesse
du vent (m.s−1
) et l’humidit´e relative (%). Elles sont d´efinies sur une grille de
2.5 × 2.5 degr´es (cf. figure 4.1) en 14 niveaux verticaux 1
(1000, 850, 700, 500,
400, 300, 250, 200, 150, 100, 70, 50, 30, 10 mb) et 2 fois par jour (0h00 et 12h00
GMT). La seule variable de surface ´egalement archiv´ee est la pression.
Les vents `a l’´echelle synoptique sont essentiellement le r´esultat de gradi-
ents de pression et de la force de Coriolis (cf. Chapitre 2). Le Pacifique est domin´e
par une zone de haute pression, l’anticyclone du Pacifique dont les mouvements
saisoniers r´egissent la circulation (cf. Chapitre 1). Cette derni`ere est, pour les
p´eriodes ´etudi´ees (octobre 1991, janvier 1992, mai 1992 et juillet 1992), similaire
`a la climatologie [112]. Cependant l’anticylone du Pacifique est constamment plus
`a l’ouest d’Hawaii et est moins intense [112]. Ceci est peut ˆetre li´e `a la formation
du ph´enom`ene El Nin˜o 2
`a partir d’Octobre 1991 d’apr`es Bachmeier et al. [16].
L’absence de station m´et´eorologique sur la partie Nord de l’oc´ean Paci-
fique et particuli`erement entre Hawaii et les Etats-Unis, rend l’analyse des vari-
ables m´et´eorologiques incertaine. Par contre entre Hawaii et le continent asia-
tique, il en existe une dizaine, mais la plupart sont situ´ees plus au sud, pr`es de
l’´equateur. Or le transport depuis le continent asiatique se situe `a une latitude
´equivalente ou sup´erieure `a celle d’Hawaii. Seules trois stations sont align´ees en-
tre Hawaii et le continent asiatique (figure 4.3): Chichijima (142.11 o
E, 27.05o
N),
Minamitorishima (153.58o
E, 24.18o
N) et Wake (166.39o
E, 17o
N). Les profils ver-
ticaux observ´es de la vitesse du vent (figure 4.4) et de la direction du vent (figure
4.5) ont ´et´e compar´es `a ceux interpol´es sur notre grille de calcul (cf. Chapitre
6). Premi`erement nous constatons que malgr´e la complexit´e des interpolations
il existe un bon accord entre les variables mesur´ees et interpol´ees. Cependant les
1
Depuis 1992, il existe un niveau suppl´ementaire `a 925 mb
2
El Nino est le nom port´e par une anomalie des courants oc´eaniques ´equatoriaux qui trans-
portent des masses d’eau chaude en surface le long de la cˆote en Am´erique centrale, modifiant
ainsi la cellule de Walker et donc la m´et´eorologie pour tout le Pacifique et les continents asiatique
et am´ericain.

79. 4.2: Variables globales 79
Figure 4.3: Stations m´et´eorologiques situ´ees entre Hawaii et le continent asia-
tique. Elles servent `a pouvoir comparer les valeurs des variables m´et´erologiques
observ´ees et calcul´ees sur notre grille.

80. 80 Chapitre 4: Variables m´et´eorologiquess
Figure 4.4: Profil de la vitesse interpol´ee sur la grille du mod`ele (ligne continue)
et mesur´ee (ligne interrompue) du vent moyenn´e sur 8 jours en Octobre 1991 (a),
Janvier 1992 (b), Mai 1992 (c) et Juillet 1992 (d), au dessus de Chichijima.

81. 4.2: Variables globales 81
Figure 4.5: Profil de la direction du vent interpol´ee sur la grille du mod`ele (ligne
continue) et mesur´ee (ligne interrompue) du vent moyenn´e sur 8 jours en Octo-
bre 1991 (a), Janvier 1992 (b), Mai 1992 (c) et Juillet 1992 (d), au dessus de
Chichijima.

82. 82 Chapitre 4: Variables m´et´eorologiquess
valeurs de la vitesse du vent sur la grille de calcul (ligne continue sur les figures)
sont syst´ematiquement plus faibles de 20% que les valeurs observ´ees, ce qui n’est
pas le cas aux autres stations. La direction du vent `a Chichijima varie entre 180o
et 270o
tout au long de l’ann´ee, soit des vents de secteur Sud-Ouest, except´e en
juillet quand les vents tournent de secteur Sud-Est. Ce qui signifie que les masses
d’air en provenance d’Asie se d´eplacent en g´en´eral vers le Nord-Est, `a l’exception
des mois d’´et´e quand il peut exister des vents locaux d’Est.
Le maximum de la vitesse du vent `a 200 mb (10 kilom`etres d’altitude)
au niveau des courants jets est clairement visible avec une vitesse atteignant 60
m.s−1
en janvier au-dessus de Chichijima. Le minimum vers 15 kilom`etres de la
vitesse du vent co¨ıncide avec la tropopause qui est marqu´ee par un minimum de la
temp´erature (∼ -70 o
C). La vitesse d´ecroˆıt en g´en´eral depuis la tropopause jusqu’`a
la surface terrestre. Cependant, au dessus de Wake la vitesse vers 5 kilom`etres
d’altitude atteint un minimum et s’accroˆıt dans la couche limite. L’analyse de
la direction du vent aux trois stations fait ressortir la permanence des vents de
secteur est ou nord-est `a Wake dans la couche limite et la partie de la troposph`ere
libre en-dessous de 5 kilom`etres d’altitude.
4.3 Les variables m´et´eorologiques `a m´eso-´echelle
Les variables m´et´eorologiques `a m´eso-´echelle dans la r´egion desˆıles d’Hawaii
proviennent de simulations que nous avons effectu´ees avec la version 5.1 du mod`ele
`a m´eso-´echelle (MM5) du Pennsylvania State University/National Center for At-
mospheric Research (PSU/NCAR). La description du mod`ele MM5 est donn´ee
en d´etail par Manning et Haagenson [167], Grell et al. [93], Haagenson et Dud-
hia [99], Haagenson [100], Guo et Chen [98]. Le mod`ele poss`ede de nombreuses
options, en particulier il peut ˆetre utilis´e soit pour la pr´evision du temps soit
pour l’analyse dans sa version hydrostatique (la force du gradient de pression
est ´equilibr´ee par la gravit´e) ou non-hydrostatique (l’acc´el´eration verticale est
r´esolue).
Nous avons utilis´e le mod`ele dans sa version non-hydrostatique, c’est-
`a-dire que nous r´esolvons les ´equations 3.46-3.55 pour un facteur d’´echelle m
relatif `a la projection de Mercator avec une vraie latitude Φv=0 (formule 3.30).
Le syst`eme de coordonn´ees (˜x, ˜y) est obtenu `a partir des relations 3.31, et la
coordonn´ee verticale σ est d´efinie en 3.32 avec pt =50 mb.
Nous allons `a pr´esent d´ecrire bri`evement les diff´erentes options utilis´ees
et les modifications que nous y avons apport´ees. Le mod`ele MM5 est constitu´e
de plusieurs modules de pr´eparation des donn´ees et du code de simulation pro-
prement dit. A chacun des modules nous donnons la liste des options utilis´ees et
les modifications ´eventuelles.

83. 4.3: Variables `a m´eso-´echelle 83
1. D´efinition du domaine et des param`etres relatifs `a la surface terrestre
• D´efinition du domaine: Le domaine est centr´e `a 19.5o
de latitude
Nord et 205o
de longitude Est. Il est compos´e de deux sous domaines
imbriqu´es, le premier form´e de 40 × 40 points de grille distants de
27 kilom`etres et le second de 40 × 37 points de grille distants de
9 kilom`etres (cf. figure 4.2). Les deux sous-domaines interagissent
(”two-way nesting”).
• Modifications: Les donn´ees topographiques et de la v´eg´etation utilis´ees
dans MM5 ont une r´esolution de 30 d’arc ce qui repr´esente un peu plus
de 50 kilom`etres. En interpolant de telles donn´ees sur la grille de 9
kilom`etres de r´esolution, l’ˆıle n’est plus form´ee que d’un seul volcan
atteignant 1600 m`etres d’altitude au lieu de deux volcans l’un culmi-
nant `a 4205 m`etres (Mauna Kea) et l’autre `a 4167 m`etres (Mauna
Loa). Quant `a la v´eg´etation il n’existe qu’un seul type d’´ecosyst`eme
correspondant `a la savanne. L’obtention d’une topographie correcte
pour les simulations est fondamentale pour des raisons dynamique (le
fondement de la campagne MLOPEX est li´e `a l’existence d’une varia-
tion diurne du r´egime de vents dont l’existence d´epend de la pr´esence
d’un relief ´elev´e) et chimique (les r´eactions chimiques sont sensibles
aux valeurs de la temp´erature et de la vapeur d’eau qui diminuent avec
l’altitude). En cons´equence, nous avons ´etabli des cartes de v´eg´etation
et de topographie avec une r´esolution de 2.5’ (∼ 3 km) d’arc `a partir
de l’Atlas d’Hawaii [11]. Cette grille couvre la surface comprise entre
(200o
E, 17.5o
N) et (205o
E, 22.5o
N). L’altitude maximum voisine alors
3244 m`etres et les types d’´ecosyst`emes reproduisent correctement la
diversit´e de la v´eg´etation propre `a Hawaii.
2. Interpolation horizontale
Les mˆemes donn´ees ECMWF utilis´ees pour les variables m´et´eorologiques
`a l’´echelle synoptique sont interpol´ees sur la grille du mod`ele pour chaque
niveau de pression et toutes les 12 heures. ECMWF ne fournit pas la
temp´erature `a la surface, elle est par cons´equent initialis´ee `a partir des
donn´ees du National Meteorological Center (NMC).
3. Interpolation verticale
Les champs de variables interpol´es horizontalement sur les 12 niveaux de
pression ECMWF sont interpol´es verticalement sur les 23 niveaux σ (1.,
0.99, 0.98, 0.96, 0.93, 0.89, 0.85, 0.8, 0.75, 0.7, 0.65, 0.6, 0.55 0.5, 0.45, 0.4,
0.35, 0.3, 0.25, 0.2, 0.15, 0.1, 0.05, 0.0) du mod`ele MM5.
4. Simulation `a m´eso-´echelle avec la premi`ere version du mod`eles MM5

84. 84 Chapitre 4: Variables m´et´eorologiquess
Les ´equations 3.46-3.55 sont r´esolues sur le domaine `a deux grilles im-
briqu´ees en utilisant les param´etrisations suivantes des processus physiques,
(leur description peut ˆetre trouv´ee dans Grell et al. [93]:
• Le r´echauffement radiatif de l’atmosph`ere est param´etris´e en con-
sid´erant pour le rayonnement infra-rouge l’absorption par la vapeur
d’eau et pour le rayonnement ultra-violet la r´eflexion et l’absorption
par les nuages et la diffusion multiple et l’absorption par la vapeur
d’eau. Le calcul radiatif est effectu´e toutes les 30 minutes.
• L’eau condens´ee (q2) est calcul´ee explicitement en r´esolvant l’´equation
(3.55)
• La param´etrisation du transport dans la couche limite est due `a Black-
adar [21], [22] avec les modifications apport´ees par Zhang et Anthes
[252]. Elle est du premier ordre de fermeture et utilise des crit`eres de
stabilit´e et des coefficients de diffusion turbulente dont la param´etrisation
est similaire `a celle d´ecrite au chapitre suivant.
• Le transport convectif par les nuages est param´etris´e suivant Grell
[93] qui ne consid`ere que l’ascendance dans le nuage et la subsidence
dans l’environnement. Il n’y a donc pas d’´echange entre le nuage et
l’environnement except´e `a la base et au sommet.
• La temp´erature de surface est calcul´ee `a partir de l’´equilibre ´energ´etique
d´ecrit au chapitre suivant. Le contenu en eau du sol est constant au
cours de la simulation et est fix´e suivant le type de v´eg´etation.
Les 4 simulations de 8 jours chacune couvrent les p´eriodes qui vont
- du 15 au 23 octobre 1991,
- du 21 au 29 janvier 1992,
- du 1 au 9 mai 1992, et
- du 22 au 30 juillet 1992.
Le pas de temps est de 30 secondes et une simulation n´ecessite approxima-
tivement 30 heures CPU sur un CRAY-Y-MP8/864.
4.4 Comparaison avec les observations
La direction du vent observ´ee `a 40m au-dessus du sol `a l’Observatoire
de Mauna Loa est compar´ee `a la valeur calcul´ee `a la figure 4.6. Premi`erement
nous constatons un cycle diurne de la direction du vent calcul´ee qui indique
un ´ecoulement nocturne descendant (de 90o
`a 270o
) et un ´ecoulement diurne
ascendant (de 270o
`a 360o
et de Oo
`a 90o
). Ces deux types d’´ecoulement peuvent
ˆetre isol´es en fonction du temps suivant des crit`eres ´etablis par Walega et al.

85. 4.4: Comparaison avec les observations 85
Figure 4.6: Evolution de la direction du vent `a l’Observatoire de Mauna Loa,
observ´ee `a 40 m`etres (trait interrompu) et calcul´ee `a 35 m`etres (trait continu)
pour les quatre p´eriodes de simulation: (a) Octobre 1991, (b) Janvier 1992, (c)
Mai 1992 et (d) Juillet 1992.

86. 86 Chapitre 4: Variables m´et´eorologiquess
Table 4.1: P´eriodes (heure locale `a Hawaii) durant les quatre simulations pour
lesquelles les vents sont descendants, comme ´etablies par Walega et al., 1992.
Octobre 91 Janvier 92 Mai 92 Juillet 92
Jour d´ebut fin Jour d´ebut fin Jour d´ebut fin Jour d´ebut fin
14 0 10 20 0 10 30 0 7 23 5 6
15 0 1 20 22 24 1 0 10 24 22 24
15 3 6 21 0 10 1 22 24 25 0 10
15 22 24 21 22 24 2 0 6 26 0 8
16 0 9 22 0 10 2 22 24 28 4 7
17 22 24 22 22 24 3 0 10
18 0 10 23 0 10 3 22 24
18 22 24 23 22 24 4 0 10
19 0 9 24 0 9 5 0 6
19 22 24 24 22 24 5 22 24
20 0 10 25 0 10 6 0 10
20 22 24 25 22 24 6 22 24
21 0 9 26 0 10 7 0 10
21 22 24 26 22 24 7 22 24
22 0 10 27 0 10 8 0 10
27 22 23 8 22 24
28 0 23
[234] et bas´es sur la direction et la vitesse du vent, le point de ros´ee et l’humidit´e
relative. La table 4.1 reprend les p´eriodes de vents descendants ´etablies par
ces auteurs. Except´e pour le mois de juillet, au cours duquel les conditions
pr´edominantes correspondent `a des vents montants, les vents sont descendants
quasiment tous les jours de 22 heures `a 10 heures. Durant ces p´eriodes la direction
du vent oscille autour de 180o
en Octobre et en Juillet (vents du sud), et 225o
en
Janvier et en Mai (vents du sud-ouest). Pendant la journ´ee, la direction du vent
varie autour de 100o
en Octobre et en Juillet (vents d’est) et de 300o
en Janvier
et en Mai (vents du nord-ouest). Les directions de nuit et de jour peuvent ˆetre
associ´ees respectivement avec les vecteurs du vent au-dessus de 700 mb et dans la
couche limite. Cependant si nous prenons la valeur moyenne sur toute la p´eriode
(tableau 4.2) la distinction entre les deux types de condition du vent devient
confuse en raison de la variabilit´e du vent.
Nous constatons que si les variations journali`ere et saisonni`ere calcul´ees
de la direction du vent correspondent aux variations observ´ees, par contre les
variations diurnes calcul´ees sont inexistantes. Les vents de nuit au lieu d’ˆetre de
secteur Sud sont de mˆeme secteur que pendant la journ´ee. La variation diurne de

87. 4.4: Comparaison avec les observations 87
Table 4.2: Vitesse et direction du vent pour les condition ascendantes, descen-
dantes et pour toutes conditions, telles qu’elles ont ´et´e mesur´ees et calcul´ees au
cours des 4 p´eriodes de l’ann´ee.
Octobre 1991 Janvier 1992 Mai 1992 Juillet 1992
Alt (m) Asc Dsc Ttes Asc Dsc Ttes Asc Desc Ttes Asc Dsc Ttes
Mesures
Vitesse du vent (m.s−1
)
8 2.9 3.0 3.0 4.0 4.4 4.2 4.3 3.8 4.1 3.6 7.4 4.0
40 4.0 3.5 3.8 5.7 6.2 6.0 5.4 4.7 5.1 4.8 10.9 5.5
Direction du vent
8 147 181 160 242 235 238 236 226 232 156 173 158
40 148 175 158 239 229 234 243 216 232 151 149 151
Mod`ele
Vitesse du vent (m.s−1
)
40 3 3.4 3.2 3.7 4.0 3.8 3.4 3.5 3.5 3.1 6.2 3.5
400 3.9 3.7 3.8 4.5 5.3 5.0 3.9 4.6 4.3 3.4 7.7 4.0
Direction du vent
40 133 173 151 238 224 229 297 294 296 129 101 124
400 126 164 143 272 243 255 307 280 293 124 125 124
la direction du vent est due `a al variation de la temp´erature de surface: refroidisse-
ment la nuit et r´echauffement la journ´ee. Or le mod`ele simule bien l’´evolution
de la vitesse du vent (figure 4.8) ainsi que celle de la variation de temp´erature
`a l’Observatoire (figure 4.7). Les valeurs moyennes calcul´ees de la vitesse du
vent pour les deux types de conditions sont similaires avec celles observ´ees (table
4.2) et il y acc´el´eration la nuit avec des vents qui atteignent 8 m.s−1
en juillet.
Il semble que le d´esaccord entre les variations diurnes calcul´ees et mesur´ees de la
direction du vent soit du `a un trop faible gradient La r´esolution sur Hawaii est
de 9 kilom`etres, ce qui correspond `a la distance entre l’Observatoire et le sommet
du volcan Mauna Loa. D’autre part, le sommet de Mauna Loa, pour le mod`ele
`a m´eso-´echelle, est de 3244 m`etres au lieu de 4167 m`etres. En cons´equence, la
direction du vent est bien simul´ee en contrebas de l’Observatoire de Mauna Loa
mais pas entre celle-ci et le sommet de Mauna Loa. En d’autres termes le mod`ele
voit la position de l’Observatoire plus proche du sommet que ce qu’elle est en

88. 88 Chapitre 4: Variables m´et´eorologiquess
Figure 4.7: Evolution de la vitesse du vent `a l’Observatoire de Mauna Loa, ob-
serv´ee `a 40 m`etres (trait interrompu) et calcul´ee `a 35 m`etres (trait continu) pour
les quatre p´eriodes de simulation: (a) Octobre 1991, (b) Janvier 1992, (c) Mai
1992 et (d) Juillet 1992.

89. 4.4: Comparaison avec les observations 89
Figure 4.8: Evolution de la temp´erature `a l’Observatoire de Mauna Loa, observ´ee
`a 40 m`etres (trait interrompu) et calcul´ee `a 35 m`etres (trait continu) pour les
quatre p´eriodes de simulation: (a) Octobre 1991, (b) Janvier 1992, (c) Mai 1992
et (d) Juillet 1992.

90. 90 Chapitre 4: Variables m´et´eorologiquess
r´ealit´e.
La temp´erature `a une pression de 700 mb au-dessus de Hilo (204.953o
E,
19.73o
N), niveau de pression correspondante `a celle de l’Observatoire, est quasi-
ment constante et est proche de la temp´erature moyenne `a Mauna Loa. Les vents
dominants ´etant de l’Est ou du Nord-Est, les masses d’air arrivant `a l’Observatoire
passent d’abord au-dessus de Hilo sur une surface isobarique de 700 mb. Si nous
comparons la direction du vent calcul´ee `a 700 mb au-dessus de Hilo (figure 4.9)
avec celle mesur´ee par ballon-sonde, nous constatons que le mod`ele simule bien
les variations journali`eres et saisonni`eres. Pr`es de la surface (1000 mb) `a Hilo, le
mod`ele est capable de reproduire les variations diurnes de la direction du vent,
comme l’indique la figure 4.10.
En moyennant les vents pour chacun des deux r´egimes de vent dont les
p´eriodes sont d´efinies au tableau 4.1, nous avons repr´esent´e les vecteurs du vent
calcul´es et interpol´es sur notre grille de calcul `a la figure 4.11 pour le r´egime
des vents descendants et `a la figure 4.12 pour la p´eriode des vents montants.
Sur la figure 4.11, l’´ecoulement est essentiellement descendant, pour toutes les
saisons, avec une zone de divergence des vents au niveau de Hilo (cˆote Est). Sur
la cˆote Ouest, il y a en permanence un ´ecoulement de retour montant. Pour
l’autre r´egime de vent (figure 4.12), l’´ecoulement montant le long des pentes
volcaniques est bien caract´eris´e. Nous constatons qu’il existe en g´en´eral deux
zones de divergence sur le versant Est: la premi`ere par les vents dominants au
niveau de Hilo et la seconde `a mi-hauteur par les vents montants. Cet aspect
est important, car les zones d’´emission d’hydrocarbures par la forˆet tropicale et
les ´emissions anthropiques `a Hilo sont situ´ees en-dessous de cette deuxi`eme zone
de divergence et les polluants n’acc`edent pas `a l’Observatoire directement mais
contournent l’ˆıle. Un autre aspect qui va influencer la composition chimique `a
l’Observatoire est l’extension des zones montantes au col entre Mauna Kea et
Mauna Loa. En mai, le col est sous l’influence des vents d’Ouest alors qu’en
juillet les vents d’Est passent au-del`a du col. En cons´equence, les hydrocarbures
´emis par la forˆet tropicale de la cˆote Est atteignent rapidement l’Observatoire
(s’ils ne sont pas pris dans la zone de divergence) en juillet alors qu’en Mai il
faut s’attendre `a de faibles valeurs de concentration. En effet la dur´ee de vie
des hydrocarbures est inf´erieure `a un jour et le temps mis `a contourner l’ˆıle et `a
monter par le versant Ouest est d’au moins un jour.
Comme nous d´esirons connaˆıtre l’impact des ´emissions des autres ˆıles de
l’archipel d’Hawaii, nous avons ´egalement compar´e les variables m´et´eorologiques
calcul´ees avec celles mesur´ees `a l’a´eroport d’Honolulu (202.302o
E, 21.302o
N) qui
se situe au bord de la mer au sud de l’ˆıle d’Oahu. A l’instar de l’ˆıle d’Hawaii,
la pr´esence d’un volcan est ´egalement `a l’origine d’un renforcement des brises de
mer et de terre. Nous constatons que le mod`ele est capable de reproduire les
changements de direction associ´es au changement de brises `a la surface (figure

91. 4.4: Comparaison avec les observations 91
Figure 4.9: Evolution de la direction du vent `a 700 mb au dessus de la ville
de Hilo observ´ee (ligne interrompue) et calcul´ee (ligne continue) pour les quatre
p´eriodes de simulation: (a) Octobre 1991, (b) Janvier 1992, (c) Mai 1992 et (d)
Juillet 1992.

92. 92 Chapitre 4: Variables m´et´eorologiquess
Figure 4.10: Evolution de la direction du vent `a la surface de la ville de Hilo
observ´ee (ligne interrompue) et calcul´ee (ligne continue) pour les quatre p´eriodes
de simulation: (a) Octobre 1991, (b) Janvier 1992, (c) Mai 1992 et (d) Juillet
1992.

93. 4.4: Comparaison avec les observations 93
Figure 4.11: Vecteurs du vent calcul´e et moyenn´e `a la surface sur la p´eriode
d´efinie comme vents descendants.

94. 94 Chapitre 4: Variables m´et´eorologiquess
Figure 4.12: Vecteurs du vent calcul´e et moyenn´e `a la surface sur la p´eriode
d´efinie comme vents montants.

95. 4.5: Comparaison avec la climatologie 95
4.13). A 850 mb au-dessus de Honolulu, nous avons ´egalement un bon accord
entre les observations et les valeurs calcul´ees tant pour la direction et la vitesse
du vent que la temp´erature. Les directions de vent associ´ees `a chaque p´eriode
sont similaires `a 850 mb au-dessus d’Honolulu et 700 mb au-dessus de Hilo:
• Octobre 91: En d´ebut de p´eriode les vents sont du sud et viennent progres-
sivement de l’est `a partir du 18 et ensuite du nord vers le 21.
• Janvier 92: La direction du vent est initialement du nord-est, passe au sud
le 21, puis au nord `a partir du 23 et revient ensuite vers l’est.
• Mai 92: La direction du vent du nord-est passe au nord-ouest du 2 au 5
mai, et revient `a une direction du nord-est pour le restant de la simulation.
• Juillet 92: La direction du vent se maintient autour de 90o
(vents d’est)
tout au long de la simulation avec une direction franchement nord en fin de
simulation.
4.5 Comparaison avec la climatologie
Au premier chapitre, nous avons d´ecrit la circulation au-dessus de l’oc´ean
Pacifique `a l’aide d’une climatologie ´etablie sur dix ans. La comparaison entre
la climatologie et la m´et´eorologie durant la campagne MLOPEX-II permet de
d´egager certaines particularit´es propres aux ann´ees 1991-1992. Nous n’allons ici
comparer que le champ de vitesse. Il est important de noter que nos simulations
ne couvrent que 8 jours pour chaque saison et ne sont donc pas n´ecessairement
repr´esentatives de toute la p´eriode de mesure qui est d’un `a deux mois. La
figure 4.14 reprend les vecteurs du vent `a 700 mb moyenn´es sur les huit jours
de simulation en chacun des points de grille de notre mod`ele. La position de
l’anticyclone du Pacifique est clairement visible par sa circulation horlogique. En
comparant cette figure avec celle ´etablie pour les vents climatologiques (figure
2.4), on constate que les circulations de janvier et de mai sont similaires. Par
contre, la circulation en octobre 1991 et juillet 1992 pr´esente une beaucoup plus
grande variabilit´e spatiale. Le vent vertical moyen calcul´e sur notre grille et
moyenn´e verticalement entre 700 et 300 mb est donn´e `a la figure 4.15. On constate
une similarit´e d’ensemble avec les valeurs de la vitesse verticale climatologique
(figure 2.7). En particulier l’ordre de grandeur (10−2
Pa.s−1
) est le mˆeme et la
variation saisonni`ere de l’extension de la zone de subsidence sur le Pacifique est
similaire. En relation avec la largeur des mailles de notre grille (cf. figure 1.3),
les valeurs pour les ann´ees 1991-1992 pr´esentent une variabilit´e plus grande dans
la r´egion d’Hawaii et moindre sur le continent asiatique.

96. 96 Chapitre 4: Variables m´et´eorologiquess
Figure 4.13: Evolution de la direction du vent `a 1000 mb au niveau de l’a´eroport
de Honolulu observ´ee (ligne interrompue) et calcul´ee (ligne continue) pour les
quatre p´eriodes de simulation: (a) Octobre 1991, (b) Janvier 1992, (c) Mai 1992
et (d) Juillet 1992.

97. 4.5: Comparaison avec la climatologie 97
Figure 4.14: Vecteurs du vent horizontal `a 700 mb repr´esent´es en chacun des
points de grille du mod`ele et moyenn´es durant les huit jours de simulation pour
les mois de: (a) Octobre 1991, b) Janvier 1992, c) Mai 1992 et d) Juillet 1992.

98. 98 Chapitre 4: Variables m´et´eorologiquess
Figure 4.15: Composante verticale du vent moyenn´ee entre 300 et 700 mb, pour
les simulations des mois de a) Octobre 1991, b) Janvier 1992, c) Mai 1992 et d)
Juillet 1992. Les isovaleurs correspondent `a 0, 1, 2, 3, 4 et 5 4× 10−2
Pa.s−1
.

99. 4.6: Conclusions 99
4.6 Conclusions
Les variables m´et´eorologiques sont obtenues `a partir de donn´ees analys´ees
globales du ECMWF et de simulations effectu´ees `a l’aide du mod`ele `a m´eso-´echelle
MM5. Nous avons compar´e les variables globales avec la climatologie au-dessus du
Pacifique. Les diff´erences entre les variables analys´ees globales et la climatologie
sont faiblement marqu´ees par une position plus `a l’ouest de l’anticylcone du Paci-
fique qui est ´egalement moins intense. Les r´esultats des simulations avec MM5 ont
´et´e compar´ees avec les mesures prises `a l’Observatoire de Mauna Loa, Hilo et Hon-
olulu. Il existe un bon accord en ce qui concerne la temp´erature, l’amplitude et
la vitesse du vent. En particulier la variation diurne de la temp´erature de surface
du sol induit un changement dans la direction du vent qui est bien simul´e. Cepen-
dant il semble que le mod`ele ne puisse reproduire `a l’Observatoire de Mauna Loa
les conditions nocturnes (vents descendants). Le refroidissement de surface re-
sponsable de ce type de vent est pourtant en bon accord avec les observations. La
distance qui s´epare l’Observatoire du sommet du volcan Mauna Loa correspond
`a la r´esolution du mod`ele MM5 et donc la pente prise entre ces deux points est
mal repr´esent´ee.
Parmi les donn´ees m´et´eorologiques globales, la temp´erature et l’humidit´e
de surface et les coefficients de diffusion de la couche limite plan´etaire doivent
doivent encore ˆetre calcul´es, ce qui consitue l’objet du prochain chapitre.

100. 100 Chapitre 4: Variables m´et´eorologiquess

101. Chapter 5
D´eveloppement d’un mod`ele de
la couche limite plan´etaire
5.1 Introduction
La couche limite plan´etaire (CLP) est la r´egion inf´erieure de la tro-
posph`ere o`u les variables m´et´eorologiques s’ajustent aux conditions aux limites `a
la surface terrestre. Ces conditions sp´ecifient une vitesse nulle pour le vent et un
flux de chaleur et d’humidit´e. Le transport vertical dans la CLP est essentielle-
ment turbulent et se formule math´ematiquement `a l’aide d’une param´etrisation.
Nous avons vu au paragraphe 6.3 que cette param´etrisation utilisait l’analogie
avec la diffusion mol´eculaire nous pouvions introduire un coefficient de diffusion
turbulente pour la quantit´e de mouvement, la chaleur et les gaz. Les valeurs de
ces coefficients sont inconnues `a l’´echelle globale, de mˆeme que les flux `a la sur-
face. Nous avons donc d´evelopper un mod`ele de couche limite qui nous permet
de les ´evaluer.
5.2 Processus de transport dans la couche limite
On d´efinit la couche limite plan´etaire comme la partie de la troposph`ere
qui est directement influenc´ee par la pr´esence de la surface terrestre, et r´epond
aux for¸cages de cette surface par un transport vertical turbulent sur une ´echelle
de temps d’environ une heure [222].
L’existence d’un r´egime turbulent d´epend du cisaillement du vent et de
la stabilit´e thermique auxquels il faut ajouter l’effet de viscosit´e de l’air. Dans
l’atmosph`ere le nombre de Reynolds1
est tr`es ´elev´e (> 105
) et les effets de viscosit´e
1
Re = UL/ν o`u U et L sont respectivement la vitesse (∼ 1 m.s−1
) et la longueur (> 1 m)
caract´eristique d’un ´ecoulement dans la couche limite [222], et ν est la viscosit´e cin´ematique
101

102. 102 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire
sur l’´ecoulement peuvent ˆetre n´eglig´es. Pour caract´eriser le r´egime d’´ecoulement
on se sert g´en´eralement du nombre de Richardson, Ri qui fournit le rapport entre
l’acc´el´eration par flottabilit´e et celle due au cisaillement:
Ri =
g∂θv
∂z
θvh(∂v
∂z
)2
(5.1)
o`u
θv est la temp´erature potentielle,
h est la hauteur de la couche limite plan´etaire,
v est l’amplitude de la vitesse horizontale.
Si Ri < 0 l’´ecoulement sera instable et il y aura formation de turbulence. Pour
0 < Ri < 1, l’´ecoulement est stable mais l’existence d’un r´egime turbulent d´epend
alors de son histoire ant´erieure. Dans le cas o`u Ri > 0.25 l’´ecoulement sera
laminaire. La valeur de Ri = 0.25 est appel´e nombre critique de Richardson, Ric.
Comme nous l’avons d´ej`a dit au troisi`eme chapitre, par analogie avec la
viscosit´e mol´eculaire, on introduit g´en´eralement une viscosit´e turbulente appel´e
coefficient de diffusion turbulente qui d´epend de l’´ecoulement. De plus nous
supposons que les coefficients sont identiques pour la quantit´e de mouvement, la
chaleur et les compos´es gazeux. Ayant d´efini trois r´egimes d’´ecoulement, nous
allons pour chacun de ces r´egimes ´etablir une param´etrisation du coefficient de
diffusion turbulente, Km, en utilisant des ´echelles caract´eristiques.
5.2.1 Echelles caract´eristiques
Nous faisons deux hypoth`eses. Premi`erement nous supposons que la CLP
est horizontalement homog`ene (u = v). Deuxi`emement, nous d´efinissons un flux
turbulent effectif qui est la somme des flux mol´eculaire et turbulent. En effet pr`es
de la surface le seul transfert a lieu par diffusion mol´eculaire, mais par simplicit´e
nous utilisons un seul coefficient [222]. Dor´enavant, lorsque nous parlerons de flux
de surface nous entendons flux effectifs de surface et nous ignorerons les processus
mol´eculaires. Ces flux sont mesur´es `a deux hauteurs standards `a 2 m`etres (sous-
abri) et `a 10 m`etres (niveau an´emom´etrique). En ce qui concerne les mod`eles, `a
m´eso-´echelle ou les mod`eles de chimie-transport, les flux de surface sont calcul´es
au premier niveau vertical dont l’altitude est d’environ 35 m`etres. Donc lorsque
nous parlons de flux de surface nous entendons en r´ealit´e un flux `a 35 m`etres
d’altitude.
Le flux de quantit´e de mouvement τs `a la surface donne la mesure de la contrainte
de cisaillement du vent. Le premier param`etre adimensionnel donne l’´echelle de
(1.5 m2
.s−1
).

103. 5.2: Processus de transport dans la couche limite 103
Figure 5.1: Enveloppe des valeurs de la longueur de Monin-Obukhov LMO au
cours d’un cycle diurne
vitesse et est donn´e par la relation:
u =
τs
ρ
(5.2)
Cette ´echelle de vitesse est appel´ee la vitesse de friction et est utilis´ee pour car-
act´eriser la turbulence produite par cisaillement dans la CLP.
Le deuxi`eme param`etre est le rapport entre l’altitude z et la hauteur
d’´echelle o`u la production d’´energie cin´etique turbulente par flottabilit´e domine
celle par cisaillement. Cette hauteur d’´echelle est donn´ee par la longueur de
Monin-Obukhov, LMO:
LMO = −
u3
k g
θvs
(w θv )s
(5.3)
o`u
g est l’acc´el´eration de la gravit´e,
θv est la temp´erature potentielle virtuelle,
θvs est la temp´erature potentielle virtuelle `a la surface terrestre,
(w θv )s est le flux de quantit´e de chaleur `a la surface terrestre,
k est la constante de von Karman dont la valeur habituellement prise
´egale `a 0.35 [222].
Les valeurs de LMO sont marqu´ees par de fortes variations diurnes et l’enveloppe
de ces valeurs en fonction de l’heure de la journ´ee est reprise `a la figure 5.1 d’apr`es
Stull [222].

104. 104 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire
5.2.2 Param´etrisations du coefficient Km
Les param´etrisations de Km en fonction des valeurs du nombre de Richard-
son proviennent des ´etudes de Troen et Mahrt [230], et Mahrt et al. [166]. Elles
sont donn´ees par les formules suivantes:
Km = kw z(1 −
z
hCLP
)2
Ri < 0 (5.4)
Km = ku z(1 −
z
hCLP
)2
0 < Ri < 0.25 (5.5)
Km = kRicu LMO(1 −
z
hCLP
)2
Ri > 0.25 (5.6)
o`u Ric est le nombre de Richardson critique (=0.25) et hCLP est la hauteur de la
couche limite plan´etaire qui est une nouvelle inconnue.
La valeur moyenne sur huit jours et sur la hauteur de la couche limite du coeffi-
cient de diffusion turbulente est donn´ee `a la figure 5.2. Les valeurs du coefficient
sont toujours ´elev´ees sur le continent asiatique (> 10 m2
.s−1
) ce qui signifie que
d’une part les gaz ´emis sur ce continent sont bien m´elang´es et d’autre part un
certain pourcentage d’entre eux sera entraˆın´e hors de la couche limite vers la
troposph`ere libre, facilitant le transport rapide par les courants d’altitude vers
Hawaii. Sur le continent am´ericain il y a un maximum tr`es prononc´e (> 30
m2
.s−1
) en Octobre, favorisant le transport par les vents dominants du Nord-Est,
pr`es de la surface terrestre, vers Hawaii.
5.2.3 Hauteur de la couche limite
La hauteur de la couche limite est calcul´ee `a partir de la formule ´etablie
par Troen et Mahrt [230]:
hCLP =
Ricθvs | v(hCLP ) |2
g(θv(hCLP ) − θvs)
(5.7)
o`u
θvs est la temp´erature potentielle virtuelle `a la surface,
θv(hCLP ) est la temp´erature potentielle virtuelle au sommet de la CLP,
| v(hCLP ) | est le module du vecteur vitesse horizontale au sommet de la
CLP,
θvs est la temp´erature potentielle virtuelle telle que
θvs =
⎧
⎪⎪⎨
⎪⎪⎩
θvs cas stable
θvs + 6.5(w θv )s
w
cas instable
(5.8)

105. 5.2: Processus de transport dans la couche limite 105
Figure 5.2: Valeur moyenne du coefficient de diffusion turbulente dans la couche
limite plan´etaire calcul´ee par notre mod`ele et pour les quatre simulations des
mois de: a) Octobre 1991, b) Janvier 1992, c) Mai 1992 et d) Juillet 1992.

106. 106 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire
La formule de calcul de hCLP est non-lin´eaire et un processus it´eratif est n´ecessaire.
Comme premi`ere estimation on prend 100 m et hCLP est incr´ement´e de 100 m
jusqu’`a ce que la relation soit v´erifi´ee. Nous avons sch´ematis´e l’´evolution de hCLP
au-dessus des continents `a la figure 5.3 Les valeurs moyennes calcul´ees de hCLP
Figure 5.3: Evolution sch´ematique de la hauteur de la couche limite plan´etaire sur
une journ´ee au-dessus des continents. Avec l’apparition du soleil, le r´echauffement
de surface g´en`ere de la convection. La production d’´energie cin´etique turbulente
par cisaillement et flottabilit´e est marqu´ee par des tourbillons dont l’amplitude
augmente avec le temps jusqu’`a atteindre la couche d’inversion en d´ebut d’apr`es-
midi. Pour des conditions instables, cette couche d’inversion est travers´ee par
des masses d’air humide qui forment des nuages. A la tomb´ee de la nuit, le
refroidissement de surface engendre une stabilit´e thermique qui d´eveloppe une
couche laminaire stable de faible hauteur, au-dessus de laquelle l’´energie cin´etique
turbulente se dissipe petit `a petit (couche r´esiduelle).
avec les variables m´et´eorologiques donn´ees au chapitre pr´ec´edent sont donn´ees `a
la figure 5.4. Les maxima de hCLP sont situ´es principalement sur les oc´eans, ceci
en raison de sa faible variation diurne. En effet l’inertie thermique de l’oc´ean
maintient une temp´erature de surface quasiment constante `a l’inverse de ce qui
se produit au-dessus des sols.

107. 5.2: Processus de transport dans la couche limite 107
Figure 5.4: Hauteur moyenne de la couche limite plan´etaire calcul´ee par notre
mod`ele et pour les quatre simulations des mois de: a) Octobre 1991, b) Janvier
1992, c) Mai 1992 et d) Juillet 1992.

108. 108 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire
5.3 Conditions aux limites
La complexit´e des conditions aux limites pour les variables turbulentes
provient de l’interaction entre l’atmosph`ere et la biosph`ere. En particulier, la
temp´erature et la vapeur d’eau d´ependent de ces interactions. Les valeurs de
ces variables ne sont pas fournies par les donn´ees du ECMWF. Nous avons par
cons´equent utilis´e des param´etrisations qui malgr´e leur simplicit´e relative permet-
tent d’obtenir les valeurs des variables `a la surface et de d´eduire les flux turbulents
de celles-ci.
5.3.1 Flux turbulents `a la surface
Les flux de surface sont calcul´es d’apr`es Mahrt [165] pour le cas stable et
d’apr`es Louis et al. [157] pour le cas instable, en tenant compte des modifications
apport´ees par Holtslag et Beljaars [119]. En utilisant une approximation du
premier ordre comme pr´ec´edemment pour les flux turbulents, ceux-ci peuvent
s’exprimer par les relations suivantes:
(w u )s = Cm | v0 |
(w v )s = Cm | v0 |
(w θ )s = Ch(θs − θ0) (5.9)
(w q1 )s = Ch(q1s − q10)
(w ni )s = Ch(nis − ni0)
o`u
Cm et Ch sont les coefficients d’´echange de la quantit´e de mouvement et
de la chaleur,
| v0 | est le module du vecteur vitesse du vent `a la hauteur sous abri
(2m) ou au premier niveau du mod`ele,
θ0, q10 et ni0 sont respectivement la temp´erature potentielle, l’humidit´e
sp´ecifique et la concentration du compos´e gazeux i `a 10 m de hauteur (hauteur
an´emom´etrique),
θs, q1s et nis sont respectivement la temp´erature potentielle, l’humidit´e
sp´ecifique et la concentration du compos´e gazeux i `a la surface. Les valeurs de
θs et q1s sont obtenues `a partir d’un bilan ´energ´etique et de l’eau `a la surface
terrestre. Les valeurs de nis sont difficiles `a mesurer, par contre il est possible
de calculer directement le flux d’´emission et la d´eposition s`eche `a la surface pour
chacun des compos´es i. Nous d´evelopperons la m´ethode de calcul au chapitre
sept.
Les coefficients d’´echange sont calcul´es `a partir des param´etrisations suiv-

109. 5.3: Conditions aux limites 109
antes
Cm = k2
| v1 |
F1(z, z0m, RiB)
ln( z
z0
)
2 (5.10)
Ch = k2
| v1 |
F2(z, z0m, z0h, RiB)
ln( z
z0
)ln( z
z0h
)
(5.11)
o`u
RiB est le nombre volumique de Richardson pour la couche de surface 2
,
z0 est la longueur de rugosit´e a´erodynamique3
z0m est la longueur de rugosit´e a´erodynamique pour la quantit´e de mou-
vement,
z0h est la longueur de rugosit´e pour la chaleur.
La fonction F1 est d´efinie par la relation [166]:
F1 =
⎧
⎪⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎪⎩
e−RiB
cas stable (RiB > 0)
1 − 10.0RiB
1+7.5
10.0k2
(−RiB
z
z0m
)
1
2
(ln( z
z0m
))
2
cas instable (RiB < 0) (5.13)
La fonction F2 est d´efinie par la relation [166]:
F2 =
⎧
⎪⎪⎪⎪⎨
⎪⎪⎪⎪⎩
e−RiB
cas stable (RiB > 0)
1 − 15.0RiB
1+7.5
10.0k2
(−RiB
z
z0m
)
1
2
ln( z
z0m
)ln( z
z0h
)
cas instable (RiB < 0) (5.14)
5.3.2 Longueur de rugosit´e
Pour calculer les flux turbulents de surface nous avons besoin de connaˆıtre
les valeurs de z0 pour la quantit´e de mouvement z0m et la chaleur z0h qui sont
respectivement les hauteurs pour lesquelles u = 0 et θ = θs.
D’apr`es Lettau [143], et Kondo et Akashi [132], z0m au-dessus d’une surface hor-
izontalement homog`ene peut ˆetre exprim´e en fonction de la hauteur et de la den-
sit´e spatiale des ´el´ements rugueux. De nombreuses ´etudes, r´esum´ees par Wieringa
[240], ont ´etabli des valeurs de z0m pour divers types d’´ecosyst`emes. Dans le cas
2
RiB =
gz(θv0 − θvs)
θv0 | v0 |2
(5.12)
o`u θvs et θv0 sont les temp´eratures potentielles virtuelles `a la surface et `a 10 m.
3
La longueur de rugosit´e a´erodynamique z0 est la hauteur `a laquelle la vitesse horizontale
du vent s’annule.

110. 110 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire
d’une surface de terrain complexe, la densit´e et la forme des ´el´ements rugueux ne
sont plus homog`enes et une valeur moyenne est calcul´ee suivant la m´ethode de
Kondo et Yamazawa [133]:
z0m =
0.25
S
(Ls)isi (5.15)
o`u S, Ls et si sont respectivement l’aire de la r´egion, les longueurs de rugosit´e
et l’aire occup´ee par le type d’´el´ement rugueux i. Nous avons utilis´e un nom-
bre r´eduit d’´ecosyst`emes (14) ´etablis par Matthews et al. [170] pour lesquels on
consid`ere que les propri´et´es physiologiques sont homog`enes et constantes. Les
valeurs de Ls pour les 14 ´ecosyst`emes sont reprises au tableau 7.11.
Connaissant la distribution des ´ecosyst`emes et leurs rugosit´es g´eom´etriques re-
spectives, il est alors possible de calculer z0m sur la r´egion qui entoure les points
de grille. Dans le cas des surfaces d’eau (lacs et oc´eans) la hauteur g´eom´etrique
des vagues d´epend de la contrainte de cisaillement exerc´ee par le vent de surface.
Chamberlain [37] a ´etabli une relation pour Locean au-dessus de l’oc´ean qui tient
compte de l’effet du vent via la vitesse de friction u∗:
Locean = 0.016
u2
∗
g
(5.16)
o`u la constante 0.016 a ´et´e ´etablie empiriquement par Wu [247].
Quand l’aire de la r´egion occupe plusieurs kilom`etres carr´es, il faut ´egalement
tenir compte des variations topographiques [78]. Pour cela, la variance de la
surface topographique σtopo est calcul´ee pour chaque point de grille `a partir des
´el´evations zs au centre des ´el´ements entourant le point consid´er´e. Nous utilisons
ensuite la formule de Hansen et al. [102] qui permet de calculer une longueur de
rugosit´e, ztopo
0m , en fonction de la topographie:
ztopo
0m = 0.041σ0.71
topo (5.17)
La valeur choisie pour z0 est la valeur maximum entre z0m calcul´ee `a partir de
(5.15) et ztopo
0m .
5.3.3 Temp´erature de surface
La temp´erature de surface peut s’obtenir `a partir du bilan thermique `a la
surface terrestre. En choisissant la convention que les flux montants sont positifs,
la relation d’´equilibre s’exprime de la mani`ere suivante:
−Qs = Qh + Qe − Qg + ∆Qs (5.18)
o`u

111. 5.3: Conditions aux limites 111
Qs est la radiation nette `a la surface vers l’atmosph`ere,
Qh est le flux de chaleur sensible vers l’atmosph`ere,
Qe est le flux de chaleur latente vers l’atmosph`ere,
Qg est le flux mol´eculaire de chaleur vers le sol, et
∆Qs est le stockage de l’´energie interne par le sol.
Les flux sont ´evalu´es par unit´e de surface.
Equilibre radiatif La radiation nette `a la surface Qs peut ˆetre s´epar´ee en
quatre composantes:
Qs = S ↑ + S ↓ + L ↑ + L ↓ (5.19)
o`u
S ↑ est la radiation solaire `a courte longueur d’onde r´efl´echie par la
surface,
S ↓ est la radiation solaire `a courte longueur d’onde transmise par l’air
vers la surface,
L ↑ est la radiation dans l’infrarouge ´emise par le sol,
L ↓ est la radiation dans l’infrarouge diffus´ee vers le sol.
Les flux radiatifs descendants sont n´egatifs par d´efinition, et ceux ascendants
sont positifs. Chacun des termes de la relation (5.19) repr´esente la somme des
composantes radiatives directe et diffuse traversant un plan horizontal attach´e `a
la surface.
Radiation `a courte longueur d’onde L’intensit´e de la radiation solaire au
sommet de l’atmosph`ere, appel´ee irradiance solaire, S0, varie entre 1360 et 1380
W.m−2
, et nous avons utilis´e S0=1370 W.m−2
[182]. Une partie de cette radiation
est att´enu´ee par dispersion et absorption par les mol´ecules de gaz et les a´erosols,
et r´eflexion par les nuages. L’att´enuation de la radiation peut ˆetre param´etris´ee `a
l’aide d’un facteur de transmission pour un ciel clair, τd, et un facteur de r´eduction
par les nuages, τc. Un autre facteur important est l’angle solaire z´enithal, χ, qui
est l’angle entre la verticale et la direction du soleil.
La r´eduction de la radiation par unit´e de surface varie comme cos χ. L’expression
pour S ↓ `a la surface peut ˆetre approch´ee par la relation [20]:
S ↓=
S0τcτd cos(χ) si −90o
< ψ < 90o
0 si | ψ |> 90o (5.20)
avec
τd qui est estim´e ´egal `a 65%,

112. 112 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire
τc est le facteur de r´eduction dˆu aux nuages4
.
Si on d´efinit l’alb´edo, αs, comme la fraction de la radiation incidente r´efl´echie `a
la surface, la radiation r´efl´echie, S ↑ est donn´ee par:
S ↑ = −αsS ↓ (5.22)
Les valeurs de l’alb´edo d´ependent du type d’´ecosyst`eme au sol et sont donn´ees
au tableau 7.11.
Radiation dans l’infrarouge Les flux radiatifs dans l’infrarouge, L ↑ et L ↓,
ont des valeurs ´elev´ees et de signes oppos´es. Le flux descendant L ↓ est surtout le
fait de la vapeur d’eau, principal ´emetteur dans l’infrarouge. Ce flux est renforc´e
par la pr´esence de nuages qui r´efl´echissent vers le bas une partie ∆ du flux L ↑.
Pour tenir compte de ces diff´erents ´el´ements nous avons utilis´e la param´etrisation
de Staley et Jurica [220]:
L ↓ = 0.67
psqs
0.622
0.08
σSBT4
1 + ∆L ↓ (5.23)
o`u
ps est la pression de surface (Pa),
qs est l’humidit´e sp´ecifique de surface (kg.kg−1
)
σSB est la constante de Stefan-Boltzmann (=1.38 × 10−23
J.K−1
)
T1 est la temp´erature au 1er
niveau du mod`ele num´erique, et
∆L ↓ est l’accroissement du flux radiatif en pr´esence de nuages5
.
Le flux radiatif dans l’infrarouge ´emis par le sol, L ↑, est d´efini par la loi de
Boltzmann:
L ↑ = sσSBT4
s (5.25)
o`u s est l’´emissivit´e de la surface.
4
τc est ´evalu´e, suivant Coiffier et al. [50], en fonction du pourcentage de couverture nuageuse
par les nuages bas (Fcl), moyens (Fcm), et hauts (Fch) fournis par les donn´ees satellitaires du
ISCCP [209]:
τc = (1 − 0.7Fcl)(1 − 0.7Fcm)(1 − 0.4Fch) (5.21)
5
∆L ↓ est param´etris´e [50] en fonction du pourcentage de couverture nuageuse (Fcl, Fcm,
Fch pour les nuages bas, moyens et hauts, respectivement):
∆L ↓ = σSB 0.25 T 4
(σl) Fcl + 0.27 T 4
(σm) Fcm (1 − Fcl))
+ 0.32 T 4
(σh) Fch (1 − Fcm) (1 − Fcl)
(5.24)
o`u
T (σl), T (σm), T (σh) sont les temp´eratures `a la base des nuages de type bas, moyens et hauts.
La base des nuages est fix´ee suivant les valeurs de pression ´etablies par l’ISCCP [209]: 900mb
pour les nuages bas, 700 mb pour les nuages moyens et 400 mb pour les nuages hauts. La
relation (3.32) permet de d´eterminer les coordonn´ees verticales σl, σm, σh `a partir de ces valeurs
de pression.

113. 5.3: Conditions aux limites 113
Flux de chaleur sensible et latente Les flux de chaleur sensible, Qh, et de
chaleur latente, Qe, sont calcul´es par les relations
Qh = ρ1cp(
T
θ
)1(w θ )s (5.26)
Qe = ρ1(w q )s (5.27)
o`u
ρ1 est la masse sp´ecifique de l’air au premier niveau du mod`ele num´erique
(kg.m−3
)
w est la composante turbulente de la vitesse verticale,
θ est la composante turbulente de la temp´erature potentielle,
(T
θ
)1 est le rapport de la temp´erature absolue et potentielle au premier
niveau du mod`ele num´erique,
q est la composante turbulente de l’humidit´e sp´ecifique,
cp est la chaleur massique (J.kg−1
.K−1
).
Dans ces relations les flux turbulents sont param´etris´es `a l’aide d’une approxi-
mation du premier ordre, telles que celles d´efinies en 5.9. Dans le cas du flux
de chaleur latente, on peut consid´erer que si le sol est satur´e en eau, l’humidit´e
sp´ecifique est satur´ee, qSAT . Le rapport entre la teneur en eau du sol, ωg, qui
est une inconnue calcul´ee par l’´equation (5.42), et la porosit´e du sol, ωk, dont
les valeurs sont donn´ees au tableau 7.12, exprime le degr´e de saturation en eau.
Nous pouvons r´e´ecrire les relations 5.26 et 5.27:
Qh = Chcpρ1(Ts − T1) (5.28)
o`u Ch est le coefficient de transfert dans la couche de surface (m.s−1
), param´etris´e
en (5.11),
Ts est la temp´erature inconnue `a la surface, et
T1 est la temp´erature au premier niveau du mod`ele num´erique.
Qe = Chρ1
ωg
ωk
(qSAT (Ts) − q1) (5.29)
o`u
q1 est l’humidit´e sp´ecifique au premier niveau du mod`ele num´erique,
qSAT (Ts) est l’humidit´e sp´ecifique `a saturation `a la surface calcul´ee par
la formule (Holton, 1979):
qSAT =
pSAT
p − (1 − )pSAT
(5.30)
o`u

114. 114 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire
=0.622 est le rapport des poids mol´eculaires de la vapeur d’eau et de
l’air sec,
pSAT est la pression `a saturation de la vapeur d’eau. Elle est fonction
uniquement de la temp´erature et se calcule `a partir de la formule de Bolton
(1981):
pSAT = 6.11 × exp
17.27(T(o
K) − 273.15)
T(oK) − 35.86
(mb) (5.31)
Echanges avec le sol Pour calculer les flux entre le sol et l’atmosph`ere, nous
supposons que d’une part le flux net de chaleur est nul sur une p´eriode de 24
heures, et que d’autre part il existe une profondeur ds au-del`a de laquelle la
temp´erature ”profonde” du sol Tp est constante pendant le temps de la simulation.
En tenant compte de ces hypoth`eses, le flux de chaleur net du sol peut ˆetre
approch´e par l’expression (Deardroff, 1978):
G = Csds2
√
π
∂Ts
∂t
+
2π
τ
(Ts − Tp) (5.32)
o`u
Cs est la capacit´e calorifique6
du sol par unit´e de volume (J.m−3
.K−1
),
ds est la profondeur du sol o`u les variations de la temp´erature de surface
ne se font plus sentir et est suppos´ee ´egale `a la racine carr´ee du produit de la
diffusivit´e thermique du sol (Ks) et de la p´eriode de variation (τ=24 heures),
La valeur de Tp provient des moyennes mensuelles moyenn´ees sur dix
ans de la temp´erature `a 1000mb du Centre Europ´een de pr´evision du temps
(Trenberth et al., 1992).
En rempla¸cant dans l’´equation d’´equilibre ´energ´etique (5.18), les diff´erents termes
par leurs expressions donn´ees ci-dessus, il est possible d’exprimer la variation de
6
Pour la d´etermination de la capacit´e calorifique des sols, nous supposons que le sol est
form´e des fractions fm de mati`ere solide, fv d’air, et fw d’eau telle que fm + fv + fw = 1.
Parmi les donn´ees des caract´eristiques du sol, nous avons la porosit´e, ω (cf. tableau 7.12), nous
avons alors fv = ω et fm + fw = (1 − ω). La valeur de fw est connue grˆace au calcul de la
teneur en eau dans la couche de profondeur ds (5.42): fw = ωg. La capacit´e thermique du sol
´etant surtout d´etermin´ee par le contenu en eau, nous supposons que la valeur de la capacit´e
thermique de la fraction solide est constante quel que soit le type de sol et est ´egal `a 0.48 106
J.m−3
.K−1
(Hillel, 1982). La capacit´e thermique de l’air est de 0.6 × 106
J.m−3
.K−1
. Nous
pouvons alors calculer la capacit´e thermique du sol, Cs (J.m−3
.K−1
):
Cs = (0.48fm + 0.6fv + fw)106
J.m−3
.K−1
(5.33)

115. 5.3: Conditions aux limites 115
la temp´erature7
, Ts, en fonction du temps:
∂Ts
∂t
=
−2
√
π
Csds
Hs + LvEs + s(σSBT4
s − L ↓) − (1 − αs)S ↓ −
2π
τ
(Ts − Tp)
(5.34)
o`u Lv est la chaleur latente de vaporisation calcul´ee `a l’aide de la formule [222]
suivante:
Lv = (2.501 − 0.00237T(o
C)) × 106
(J.kg−1
) (5.35)
L’´equation 5.34 est r´esolue par un sch´ema num´erique implicite avec un pas de
temps de 10 min. Le membre de droite de l’´equation (MD) est pond´er´e entre
l’instant tn
et l’instant suivant tn+1
par le facteur α = 3
4
[20]:
∆Ts
∆t
=
(Tn+1
s − Tn
s )
(tn+1 − tn)
= α(MD)n+1
+ (1 − α)(MD)n
(5.36)
Le terme T4
s est lin´earis´e suivant la relation:
(Tn+1
s )4
= (Tn
s )4
+ 4(Tn
s )3
(Tn+1
s − Tn
s ) (5.37)
De mˆeme, l’humidit´e sp´ecifique `a saturation, qSAT , est une fonction exponentielle
de la temp´erature, et est lin´earis´ee dans le terme de flux de chaleur latente:
qSAT (Tn+1
s ) = qSAT (Tn
s ) +
∂qSAT
∂T Tn
s
(Tn+1
s − Tn
s ) (5.38)
o`u ∂qSAT
∂T Tn
s
est la variation de l’humidit´e sp´ecifique `a saturation en fonction de
la temp´erature8
7
Le calcul de Ts est effectu´e aux points de grille de la surface du domaine o`u les terres
´emergent. Au-dessus des surfaces d’eau et des oc´eans, la temp´erature de surface est suppos´ee
´egal `a Tp.
8
∂qSAT
∂T
Ts
= 0.622LvqSAT
Rv(Ts)2 (Deardroff, [58] (5.39)
o`u
Lv est la chaleur latente de vaporisation et est calcul´ee suivant (5.35),
Rv est la constante des gaz pour la vapeur d’eau (=461.51 J.kg−1
.K−1
).

116. 116 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire
Apr`es lin´earisation des termes en Ts, l’´equation 5.36 devient [20]:
∆Ts
∆t
= α−2
√
π
Csds
{Chcpρ1(Tn+1
s − Tn
1 )
+Lvρ1Ch
ωn
g
ωk
qn
SAT +
∂qn
SAT
∂T
(Tn+1
s − Tn
s ) − qn
1
+ sσSB [(Tn
s )4
+ 4(Tn
s )3
(Tn+1
s − Tn
s )]}
−α2π
τ
(Tn+1
s − Tp)
+(1 − α) −2
√
π
Csds
[ sσSB(Tn
s )4
+ Hs + LvEs] − 2π
τ
(Tn
s − Tp)
−−2
√
π
Csds
{(1 − αs)S ↓ − sL ↓}
(5.40)
La r´esolution de cette ´equation converge en g´en´eral apr`es trois it´erations.
5.3.4 Humidit´e sp´ecifique `a la surface terrestre
De la mˆeme mani`ere que pour la temp´erature de surface, nous pouvons
obtenir l’humidit´e sp´ecifique `a la surface terrestre en ´etablissant un bilan de la
vapeur d’eau `a la surface. Cet ´equilibre est donn´e par la relation
Eg − Prec = Gw (5.41)
o`u
Prec est le taux de pr´ecipitation,
Gw est le taux d’infiltration vers le sol, et
Eg est le taux d’´evaporation `a la surface.
Ces grandeurs s’expriment en (kg.m−2
.s−1
). En supposant que les mou-
vements verticaux intersticiels de la vapeur d’eau dans le sol puissent s’exprimer
par un processus de diffusion, la variation avec le temps du contenu en eau du
sol ωg peut s’exprimer par (Deardroff,1978):
∂ωg
∂t
= −C1
(Eg − Prec)
ρwds
− C2
(ωg − ω2)
τ1
(5.42)
o`u
ρw est la densit´e de l’eau (1 kg.m−3
),
C1 et C2 sont des constantes respectivement ´egales `a 0.1 et 0.9,
d’s est la profondeur le long de laquelle la variation diurne s’´etend dans
le sol9
,
9
d1’ est calcul´ee d’apr`es Hillel (1982) comme une fonction de la perm´eabilit´e du sol Kw:
ds = τ1Kw
ωg
ωk

117. 5.4: Convection par les nuages convectifs profonds 117
ω2 est la valeur moyenne du contenu en eau du sol10
sur la profondeur11
ds au del`a de laquelle le flux vertical du contenu en eau est n´egligeable et
τ est la p´eriode de variation diurne soit 86400 s.
Si le contenu en eau ωg est sup´erieur `a la porosit´e du sol ωk, il y a ´ecoulement en
surface. Donc dans l’´equation (5.42), les valeurs de ωg sont comprises entre 0 et
ωk. Si ωg est ´egal `a ωk on dira que le sol est satur´e.
L’´equation (5.42) ´etant non-lin´eaire, elle est r´esolue par it´eration. Con-
naissant ωg, l’humidit´e sp´ecifique `a la surface du sol se d´etermine par la relation:
qg = α qSAT (Ts) + (1 − α )q1 (5.45)
o`u
qSAT est l’humidit´e sp´ecifique `a saturation pour la temp´erature de surface
Ts (calcul´ee `a partir de l’´equation 5.40),
q1 est l’humidit´e sp´ecifique au premier niveau du mod`ele, et
α = min(1, ωg
ωk
).
5.4 Convection par les nuages convectifs pro-
fonds
L’´echelle horizontale des nuages cumuliformes est de plusieurs ordres de
grandeur inf´erieure `a l’´echelle caract´eristique des mod`eles synoptique et m´eso-
´echelle. Le transport convectif associ´e `a ces nuages est par cons´equent param´etris´e
dans les ´equations de transport. Cette param´eterisation tient compte des trois
processus fondamentaux: l’entraˆınement `a la base, le d´etraˆınement dans la partie
haute du nuage, et la subsidence lente `a l’ext´erieur du nuage (figure 5.5)). La
plupart des multiples param´etrisations du transport convectif par les cumulonim-
bus se fondent sur l’existence d’une surface suffisamment grande pour contenir un
ensemble de tels nuages et en mˆeme temps plus petite que l’´echelle des syt`emes
10
La valeur de ω2 est d´eduite de l’´equation:
∂ω2
∂t
= −
(Eg − Prec)
ρwd2
(5.43)
o`u la valeur initiale de ω2 est arbitrairement choisie en prenant le rapport de l’humidit´e moyenne
`a la surface qp et l’humidit´e `a saturation qSAT pour la temp´erature moyenne Tp,
ω2 =
qpωk
qSAT (Tp)
(5.44)
Ces valeurs moyennes de la temp´erature, Tp, et de l’humidit´e sp´ecifique, qp, proviennent des
moyennes mensuelles sur 10 ans des donn´ees analys´ees de ECMWF (Trenberth et al., 1992).
11
(ds =
√
365ds)

118. 118 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire
Figure 5.5: Repr´esentation sch´ematique d’un ensemble de nuages cumuliformes
et des mouvements qui les accompagnent: entraˆınement sur les cˆot´es, ascension
dans le nuage, d´etraˆınement dans l’enclume et subsidence dans l’environnement.
synoptiques (Arakawa et Schubert, 1974). Math´ematiquement, le transport con-
vectif peut ˆetre trait´e de la mˆeme mani`ere que la turbulence: les variables sont
scind´ees en variables moyennes et fluctuations autour de cette moyenne. Le trans-
port convectif d’une grandeur X est repr´esent´e par le flux trubulent suivant:
Transport convectif = w X (5.46)
Pour permettre la param´etrisation du transport convectif, on suppose
que l’influence statistique d’une famille de nuages de diff´erentes formes et tailles,
occupant une fraction de surface donn´ee, peut ˆetre repr´esent´ee par une famille de
nuages types uniform´ement r´epartis sur la surface.
Le flux moyen de masse au travers de cette surface est donn´e par
M = Mc + Me (5.47)
o`u
Mc est le flux vertical montant dans le nuage convectif, et
Me est le flux vertical descendant dans l’environnement.
On suppose que les nuages convectifs occupent une fraction σ de l’aire horizontale.
Alors
Mc = −σwcMe = −(1 − σ)we (5.48)

119. 5.4: Convection par les nuages convectifs profonds 119
o`u
wc est la vitesse verticale dans le ou les nuages convectifs
we est la vitesse verticale dans l’environnement.
On fait l’hypoth`ese que σ 1 et we wc. On suppose d’autre part que la
grandeur X peut ´egalement ˆetre scind´ee entre environnement et nuage convectif:
X = σXc + (1 − σ)Xe ≈ Xe (5.49)
Si le transport vertical turbulent de la grandeur X est uniquement dˆu `a la con-
vection, alors
w X = wX − wX = σ(1 − σ)(wc − we)(Xc − Xe) (5.50)
En tenant compte des hypoth`eses pr´ec´edentes, on obtient:
−w X ≈ −σwc(Xc − Xe) = Mc(Xc − Xe) (5.51)
Le terme de transport convectif dans les ´equations (3.41) et (3.55) peut ˆetre
remplac´e par la relation (5.51):
−w X ≈ Mc(Xc − Xe) ≈ Mc(Xc − X) (5.52)
Les relations pr´ec´edentes sont valables si les valeurs de Xc, wc, `a une hauteur
donn´ee, sont les mˆemes dans tous les nuages. Nous utilisons la g´en´eralisation
de Yanai et al. (1973) qui ´etend les relations pr´ec´edentes `a des nuages de car-
act´eristiques diff´erentes. La relation (5.52) est remplac´ee par la somme des con-
tributions des nuages:
−w X ≈
i
Mci(Xci − X) (5.53)
o`u l’indice i r´ef`ere au ieme
nuage.
Dans cette ´equation Mci et Xci sont des nouvelles inconnues qui sont `a leur tour
param´etris´ees. Nous nous sommes bas´es sur la m´ethode de Feichter et Crutzen
(1990) pour exprimer Mci en fonction du taux de pr´ecipitation, de la couverture
nuageuse et du profil de la vapeur d’eau dans l’environnement. Xci est calcul´e
`a partir d’une solution analytique. Les m´ethodes de calcul de Mci et Xci sont
reprises en Annexe 1. Suivant cette m´ethode, Mci est proportionnel `a la quan-
tit´e d’eau contenue dans les nuages cumuliformes qui pr´ecipite (variable C de
l’´equation 9.9). En utilisant la distribution des fractions nuageuses de l’ISCCP
[209] (cf. § 7.5.3), des valeurs de pr´ecipitations de Shea [212] (cf. § 7.5.5) et des
r´esultats du mod`ele MM5 (cf. chapitre pr´ec´edent), il est possible de calculer la
distribution moyenne journali`ere de la variable C que nous avons repr´esent´e `a la

120. 120 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire
figure 5.6. Les mois pour lesquels le transport `a grande ´echelle des polluants con-
tinentaux est le plus efficace, sont janvier et mai. Les valeurs sont relativement
faibles durant ces deux mois sur le continent asiatique. Par contre il existe des
valeurs ´elev´ees, en janvier, sur l’Europe et l’est des Etats-Unis. Par cons´equent,
les polluants asiatiques qui atteignent Hawaii doivent d’abord ˆetre transport´es
jusqu’`a l’est du Japon avant d’ˆetre transport´es verticalement vers la troposph`ere
sup´erieure et ˆetre entraˆın´es par les courants jets d’ouest. C’est ´egalement `a l’est
du Japon qu’il y a m´elange avec les masses d’air d’origine am´ericaine, en raison
de la pr´esence d’une circulation cyclonique sur le golfe d’Alaska (cf. chapitre
pr´ec´edent).
5.5 Conclusions
Nous avons d´evelopp´e un mod`ele de couche limite qui nous a permis de calculer
les flux turbulents des compos´es gazeux ainsi que les flux `a la limite inf´erieure du
mod`ele. Ceci nous a conduit `a d´evelopper un bilan ´energ´etique et de la vapeur
d’eau pour calculer respectivement la temp´erature et l’humidit´e de surface. La
param´etrisation des coefficients de diffusion turbulente est bas´ee sur le nombre
de Richardson qui permet de d´eterminer trois types de stabilit´e: stable, neutre
et instable. L’amplitude des coefficients est fonction de la production d’´energie
cin´etique turbulente par cisaillement et flottabilit´e. Nous avons ins´er´e dans ce
chapitre la description d’une param´etrisation qui permet de calculer le flux ver-
tical et la concentration des compos´es gazeux dans les cumulonimbus.

121. 5.5: Conclusions 121
Figure 5.6: Distribution moyenne journali`ere de la quantit´e de pr´ecipitation par
les nuages de type cumulonimbus (kg.m2
.jour−1
) calcul´ee par notre mod`ele pour
les simulations du mois de: a) Octobre 1991, b) Janvier 1992, c) Mai 1992 et d)
Juillet 1992.

122. 122 Chapitre 5: D´eveloppement d’un mod`ele de couche limite plan´etaire

123. Chapter 6
D´eveloppement d’un mod`ele de
chimie-transport tridimensionnel
de la troposph`ere
6.1 Introduction
Connaissant les champs de variables m´et´eorologiques durant quatre p´eriodes
de huit jours couvrant les p´eriodes de mesures intesnisves pendant la campagne
MLOPEX-II, il nous reste `a r´esoudre l’ensemble des ´equations de continuit´e
pour chacun des constituants chimiques composant la troposph`ere (´equation
3.41). La solution de ces ´equations ne peut ˆetre obtenue qu’`a l’aide d’une
m´ethode num´erique approch´ee. Nous consacrons ce chapitre au d´eveloppement
d’un mod`ele num´erique de r´esolution des ´equations de continuit´e de compos´es
gazeux.
Nous allons commencer par d´efinir le domaine d’int´egration. La r´esolution
num´erique des ´equations est effectu´ee en un nombre fini de points (points de grille)
dont la distribution horizontale `a la base du domaine (la surface terrestre) doit
caract´eriser aux mieux les ´emissions continentales `a grande ´echelle et r´egionales
correspondant aux ˆıles de l’archipel d’Hawaii. Les points de grille forment alors
un ensemble d´efini comme non-structur´e: les points sont non-colin´eaires dans les
deux directions. La r´esolution des termes d´ependant de l’espace devient non-
triviale et une technique particuli`ere, que nous d´ecrirons, a ´et´e utilis´ee. Cette
grille ne correspondant pas `a celle des variables m´et´eorologiques nous devrons
interpoler celles-ci sur notre grille. Ce faisant, le vent vertical doit ˆetre recalcul´e
pour assurer la conservation du flux massique de l’air.
L’approximation num´erique de chacun des termes de l’´equation de conti-
nuit´e sera d´evelopp´ee, en particulier la m´ethode des ´el´ements finis. Cette m´ethode
consiste `a approcher la solution par un nombre fini de polynˆomes orthogonaux.
123

124. 124 Chapitre 6: D´efinition du domaine et conditions aux limites
Ces polynˆomes sont d´efinis sur des mailles (ensemble de points de grille) appel´e
´el´ement fini. La solution est d´efinie en tout point du domaine `a l’aide de fonctions
d’interpolation construites `a partir de ces polynˆomes.
Certaines techniques num´eriques originales seront test´ees, en particulier
pour la r´esolution de l’advection.
6.2 D´efinition du domaine
La d´efinition du domaine est contrainte par les deux conditions suivantes:
• Prise en compte des principales sources de polluants susceptibles d’influencer
la composition chimique de l’atmosph`ere au-dessus d’Hawaii,
• Eloignement autant que possible des fronti`eres lat´erales de la r´egion d’Hawaii
pour y att´enuer l’influence des conditions aux limites.
Comme semblent l’indiquer les ´etudes de trajectoires du deuxi`eme chapitre, les
principales sources de polluants contaminant l’atmosph`ere `a Hawaii sont localis´ees
en Asie. Cependant on ne peut exclure les continents europ´eens et am´ericains
qui sont `a l’´echelle terrestre les sources principales de polluants. La zone de
convergence intertropicale peut ˆetre consid´er´ee comme une barri`ere imperm´eable
entre les deux h´emisph`eres dans la troposph`ere. Il est donc logique pour une
simulation d’une semaine de limiter le domaine `a l’h´emisph`ere nord.
L’´equateur est cependant trop proche d’Hawaii (1500 km) pour le choisir
comme fronti`ere lat´erale. Par cons´equent, nous avons ´etendu le domaine au Sud
de l’´equateur sur le Pacifique. A l’oppos´e, le domaine ne couvre que le Nord de
l’Afrique. Nous d´efinissons le domaine dans le plan de projection st´er´eopolaire1
comme un rectangle dont les quatre sommets sont d´efinis par les longitudes et
latitudes suivantes: (55o
E, 0o
N), (144o
E, 18o
S), (225o
E, 25o
S), (297o
E, 12o
S). La
vraie latitude de la projection est ´egale `a 20o
N, et plus on s’´eloigne vers le nord
plus les longueurs d’arc seront raccourcies, inversement plus on s’´eloigne vers le
sud plus les distances seront allong´ees. La figure 6.1 reprend la configuration de
la grille sur le plan de projection st´er´eo-polaire et la figure 1.3 son recouvrement
sur la Terre. Le domaine est limit´e verticalement par la surface terrestre et la
basse stratosph`ere (100 mb). La solution est calcul´ee en 23 niveaux verticaux
concentr´es dans la couche limite plan´etaire et qui s’espacent de plus en plus au
fur et `a mesure que l’on s’´ecarte de la CLP. Ces niveaux, exprim´es en coordonn´ees
de rapport de pressions σ = p/ps, sont donn´es au tableau 6.1.
1
Nous avons justifi´e un tel choix, au 3eme
chapitre, en faisant remarquer qu’une telle pro-
jection ne pr´esente pas de discontinuit´e au pˆole nord et le long d’un m´eridien.

125. 6.2 D´efinition du domaine 125
Figure 6.1: Grille de calcul sur le plan de projection st´er´eo-polaire dont la vraie
latitude est `a 20o
N. La taille des mailles se ress`ere sur la r´egion d’Hawaii.

126. 126 Chapitre 6: D´efinition du domaine et conditions aux limites
Table 6.1: Niveaux verticaux du mod`ele exprim´es en coordonn´ee σ et leur altitude
approximative en kilom`etres.
σ1 0.1 17.5
σ2 0.14008 16.5
σ3 0.18023 14.5
σ4 0.22047 12.7
σ5 0.26078 11.3
σ6 0.30117 10.1
σ7 0.34164 9.0
σ8 0.38219 8.1
σ9 0.42282 7.3
σ10 0.46353 6.5
σ11 0.50431 5.8
σ12 0.54518 5.1
σ13 0.58613 4.5
σ14 0.62715 3.9
σ15 0.66826 3.4
σ16 0.70944 2.9
σ17 0.75071 2.4
σ18 0.79206 2.0
σ19 0.83348 1.5
σ20 0.87499 1.1
σ21 0.91658 0.7
σ22 0.95825 0.36
σ23 0.99500 0.04

127. 6.3: Maillage du domaine 127
6.3 Maillage du domaine
Apr`es avoir d´efini le domaine, nous cherchons `a d´efinir les points de grille
respectant les crit`eres suivants:
• Espacement entre points de grille de l’ordre de 300 km `a l’´echelle globale
pour caract´eriser les ph´enom`enes synoptiques
• Espacement entre points de grille de l’ordre de quelques kilom`etres `a Hawaii
pour caract´eriser d’une part la dynamique r´egionale complexe et d’autre
part les diff´erentes sources d’´emission
• Taille des mailles variant graduellement depuis l’espacement le plus fin `a
Hawaii `a l’espacement maximum le long de la fronti`ere la plus ´eloign´ee
Les diff´erentes sources d’´emission `a Hawaii sont caract´eris´ees par les diff´erents
types d’´ecosyst`emes qui suivent les lignes de niveau. Donc en coupant l’orographie
d’Hawaii en tranches d’altitude constante il est possible de s´eparer les diff´erents
´ecosyst`emes. La projection horizontale des points le long des lignes de niveau
produit un ensemble non-structur´e de points de grille. Pour cr´eer des points de
grille sur l’oc´ean entourant Hawaii, nous avons utilis´e l’analogie avec le calcul des
lignes d’´equipotentielles ´electrique (´equation de Poisson).
Il est toujours possible de couvrir un ensemble arbitraire de points par
des ´el´ements finis en combinant des triangles et des rectangles. Cependant, la
pr´ecision de la m´ethode d´epend du nombre de points composant ces ´el´ements.
Plus le nombre est ´elev´e plus la m´ethode est pr´ecise. Etant donn´e que l’espacement
entre points de grille sur le domaine global est relativement important nous
d´esirons maintenir une certaine pr´ecision en d´efinissant le cˆot´e d’un ´el´ement par
trois points (´el´ements quadratiques).
Le maillage du domaine d´epend du type de grille. Dans le cas d’une grille
structur´ee, les relations entre points de grille sont assez imm´ediates. Par contre
dans le cas d’une grille non-structur´ee il n’est plus possible d’effectuer un maillage
sans l’aide d’algorithmes particuliers. Parmi ceux-ci, la m´ethode de triangulation
de Delaunay [60] offre l’avantage de n’exiger aucune propri´et´e g´eom´etrique par-
ticuli`ere (exception faite que trois points ne peuvent ˆetre colin´eaires).
Le maillage complet du domaine comprend les ´etapes suivantes:
1. Cr´eation des points du domaine global avec une progression de l’espacement
depuis un maximum aux bords du domaine global vers un minimum aux
bords de la r´egion ´etudi´ee, partie du domaine que nous appelerons la fenˆetre
2. Cr´eation de points suivant les lignes de niveau sur les ˆıles d’Hawaii

128. 128 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
3. Cr´eation de points entre les ˆıles de la r´egion d’Hawaii et les bords de la
fenˆetre
4. Maillage de la grille structur´ee globale
5. Maillage de la grille non-structur´ee couvrant la fenˆetre
6.3.1 G´en´eration de la grille structur´ee globale
Si l’on se fixe le nombre total de points, l’espacement minimum pour la
fenˆetre, et les coordonn´ees des points extrˆemes du domaine et de la fenˆetre, il est
possible de calculer un facteur d’´elongation des points de grille. D’apr`es l’´etude
de Staniforth et Mitchell [219], la pr´ecision des r´esultats sera d’autant meilleure
que ce facteur sera proche de l’unit´e. Nous cherchons donc `a minimiser, dans
deux directions, une fonction de trois variables: les deux facteurs d’´elongation et
le nombre de points.
Nous supposons que nous avons N points distribu´es entre les points
extrˆemes de coordonn´ees ˜x1 et ˜xN sur le plan de projection et une distance ∆
entre points de grille le long de la fenˆetre. Soit hi = ˜xi+1 − ˜xi (i = 1, ..., N − 1)
l’intervalle entre points, et entre les L points de la fenˆetre h = ∆, les valeurs hi
sont calcul´ees sur les trois parties du domaine de la mani`ere suivante:
hi =
⎧
⎪⎨
⎪⎩
R1hi+1 1 ≤ i ≤ M R1 > 1
∆ 1 + M ≤ i ≤ M + L
R2hi−1 1 + M + L ≤ i ≤ N R2 > 1
(6.1)
o`u
M est le nombre de points `a gauche de la fenˆetre,
L est le nombre de points le long de la fenˆetre,
N − M − L est le nombre de points `a droite de la fenˆetre,
R1 et R2 sont les facteurs d’´elongation respectivement `a gauche et `a
droite.
En exprimant les relations (6.1) uniquement en fonction de l’espacement ∆ entre
points de grille de la fenˆetre et en supposant une progression g´eom´etrique des
facteurs d’´elongation R1 et R2, nous obtenons les relations:
hi =
⎧
⎪⎪⎨
⎪⎪⎩
R
(M+1−i)
1 ∆ 1 ≤ i ≤ M
∆ 1 + M ≤ i ≤ M + L
R
(i−M+L+1)
2 ∆ 1 + M + L ≤ i ≤ N
(6.2)
En sommant ces relations sur les portions d’intervalle o`u elles sont d´efinies et
en sachant que (˜xi − ˜xj) = i−1
k=j hk, nous obtenons les trois ´equations `a trois

129. 6.3: Maillage du domaine 129
Table 6.2: Valeurs des donn´ees et des param`etres utilis´es pour construire la grille
h´emisph´erique structur´ee sur le plan de projection st´er´eo-polaire.
L ∆ (km) M N R1 R2
˜x 12 39 20 49 1.30 1.53
˜y 12 94 14 43 1.42 1.43
inconnues (M, R1, R2) suivantes:
˜xM+1 − ˜x1 = R1∆
R1−1
(RM
1 − 1)
˜xM+L − ˜xM+1 = ∆(L − 1)
˜xN − ˜xM+L = R2∆
R2−1
(RN−M−L
2 − 1).
(6.3)
En sommant ces trois ´equations, on obtient une relation qui lie R1, R2 et M,
R1
R1−1
(RM
1 − 1) + R2
R2−1
(RN−M−L
2 − 1) = ˜xN −˜x1
∆
− (L − 1)
avec la condition 1 ≤ M ≤ N − L − 1
(6.4)
Les valeurs de R1 et R2 et M qui satisfont cette relation et cette condition sur
M, et minimisent la fonction f = (R1 − R2)2
, sont la solution du probl`eme.
Nous avons r´esum´e l’ensemble des r´esultats et des donn´ees utilis´ees au
tableau 6.2. Les coordonn´ees des sommets extrˆemes du domaine sont (55o
E,0o
N)
et (225o
E,-250
N), et pour la fenˆetre encadrant la r´egion d’Hawaii (200o
E,24o
N)
et (208o
E, 16o
N).
6.3.2 Maillage de la grille structur´ee
Les points de grille une fois d´efinis, nous pouvons cr´eer les ´el´ements finis pas-
sant par ces points. Le meilleur choix entre pr´ecision et efficacit´e d’ex´ecution
est l’´el´ement fini `a 9 noeuds. L’erreur d’approximation sur cet ´ele´ement est du
troisi`eme ordre (cf. Annexe 2).
6.3.3 G´en´eration d’une grille non-structur´ee
Les points de grille dans la fenˆetre sont g´en´er´es en deux ´etapes. La
premi`ere consiste `a produire des points relatifs aux ˆıles et la deuxi`eme `a cr´eer des
points entre ces ˆıles.

130. 130 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Grille sur les ˆıles d’Hawaii
Comme nous l’avons vu au deuxi`eme chapitre, les types de v´eg´etation sont tr`es
vari´es sur lesˆıles d’Hawaii et peuvent ˆetre reli´es aux taux de pr´ecipitation. Comme
les isocontours de ces taux correspondent relativement bien `a l’orographie, nous
coupons le relief par des plans horizontaux r´eguli`erement espac´es suivant l’altitude.
Pour ce faire nous utilisons une carte topographique avec une r´esolution de 2.5’
par 2.5’. Les points d’intersection entre les mailles et les plans horizontaux four-
nissent les points de grille. En se fixant une tol´erance entre points de grille, telle
que si la distance entre deux points de grille est inf´erieure `a cette tol´erance ces
deux points sont fusionn´es, nous obtenons ainsi 734 points qui caract´erisent les
ˆıles d’Hawaii.
Grille entre les ˆıles et les bords de la fenˆetre
Nous cherchons maintenant `a g´en´erer une grille qui co¨ıncide avec la grille globale
sur les bords de la fenˆetre de la r´egion d’Hawaii, et qui caract´erise l’´ecoulement
autour des ˆıles. Le probl`eme de la g´en´eration d’une grille o`u les points fronti`eres
sont impos´es peut se poser comme un probl`eme de conditions aux limites [81]: se
donnant les fonctions ξ(˜xb, ˜yb) et η(˜xb, ˜yb) sur les points (˜xb, ˜yb) des fronti`eres ∂Ωw,
on cherche ξ(˜x, ˜y) et η(˜x, ˜y) en tous points du domaine Ωw limit´e par les fronti`eres
∂Ωw. Les coordonn´ees physiques (x, y) sont les variables ind´ependantes et les
coordonn´ees g´en´eralis´ees (ξ, η) sont les variables d´ependantes. Nous d´esirons une
variation r´eguli`ere depuis les fronti`eres ∂Ωw jusqu’aux points li´es aux ˆıles. Pour
ce faire nous utilisons l’´equation de Poisson:
∂2ξ
∂˜x2 + ∂2ξ
∂˜y2 = P(ξ, η)
∂2η
∂˜x2 + ∂2η
∂˜y2 = Q(ξ, η)
(6.5)
o`u P et Q sont des fonctions qui d´eforment le maillage autour des points li´es aux
ˆıles. Ces ´equations sont transform´ees depuis (˜x, ˜y) vers (ξ, η):
α∂2 ˜x
∂ξ2 − 2β ∂2 ˜x
∂ξ∂η
+ γ ∂2 ˜x
∂η2 + δ(P ∂˜x
∂ξ
+ Q∂˜x
∂η
) = 0
α∂2 ˜y
∂ξ2 − 2β ∂2 ˜y
∂ξ∂η
+ γ ∂2 ˜y
∂η2 + δ(P ∂˜y
∂ξ
+ Q∂˜y
∂η
) = 0
(6.6)
o`u
α = ∂˜x
∂η
2
+ ∂˜y
∂η
2
β = ∂˜x
∂ξ
∂˜x
∂η
+ ∂˜y
∂ξ
∂˜y
∂η
γ = ∂˜x
∂ξ
2
+ ∂˜y
∂ξ
2
δ = αγ − 2β
(6.7)
Les deux ´equations (6.6) et les termes (6.7) sont discr´etis´es par la m´ethode des
diff´erences centr´ees. Les fonctions P et Q sont reprises de Thompson et al. [224]

131. 6.3: Maillage du domaine 131
et sont donn´ees par les relations suivantes:
P(ξ, η) = −
L
l=1
alsgn(ξ − ξl)e−c1|ξ−ξl|
(6.8)
−
M
m=1
bmsgn(ξ − ξm)e−dm
√
(ξ−ξm)2+(η−ηm)2
(6.9)
Q(ξ, η) = −
L
l=1
alsgn(η − ηl)e−c1|η−ηl|
(6.10)
−
M
m=1
bmsgn(η − ηm)e−dm
√
(ξ−ξm)2+(η−ηm)2
(6.11)
o`u
al, bm, cl, dm
2
sont des param`etres de contrˆole des d´eformations autour
des L + M points (ξl, ηl) et (ξm, ηm), et
sgn(x) =
⎧
⎪⎨
⎪⎩
1 si x > 0
0 si x = 0
−1 si x < 0
(6.12)
La proc´edure de calcul consiste `a d’abord r´esoudre le syst`eme (6.6) avec P = Q =
0, comme valeur initiale des ´equations non-lin´eaires qui sont r´esolues it´erativement
par une m´ethode de relaxation [195]. Nous avons ainsi form´e une grille de 289
points en se fixant L = 0, M = 1 et (a = 0, b = 10, c = 0, d = 0.25). En com-
binant les deux derni`eres grilles et en se fixant une tol´erance pour la fusion des
points proches, on obtient une grille form´ee de 920 points (figure 6.2).
6.3.4 Maillage de la grille non-structur´ee
Le maillage d’une grille non-structur´ee est nettement moins facile que
pour une grille structur´ee. Pour ce faire, on d´efinit pour chaque point un poly-
gone convexe tel que l’espace int´erieur est plus proche de ce point que de n’importe
quel autre point (Dirichlet, 1850). La m´ethode de Delaunay [60] fournit un crit`ere
pour d´efinir ces polygones: il existe un seul cercle de rayon minimum passant par
trois points dans lequel il n’y a aucun autre point. La proc´edure de triangula-
tion est telle que la diagonale d’un quadrilat`ere form´e de deux triangles max-
imise le minimum des six angles internes [237]. Nous avons employ´e l’algorithme
d´evelopp´e par Fang et Piegl [74] qui utilise une grille uniforme pour trianguler
2
al et cl ont pour effet de d´eplacer les lignes ξ=const. et η=const vers les lignes ξl et ηl; bm
et dm attirent les lignes ξ=const et η=const vers le point (ξm, ηm).

132. 132 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Figure 6.2: Grille non-structur´ee form´ee de 920 points dans la r´egion d’Hawaii.

133. 6.4: R´esolution de l’´equation de continuit´e 133
par la m´ethode de Delaunay3
. Cet algorithme poss`ede de multiples avantages
et entre autres de diminuer le temps de calcul au fur et `a mesure que la trian-
gulation avance4
. Nous utilisons ensuite la m´ethode d’Anderson [5] qui g´en`ere
de nouveaux points afin d’´eviter un brusque changement de taille d’un triangle
`a l’autre. Apr`es retriangulation les points qui n’appartiennent ni aux bords de
la fenˆetre ni aux ˆıles sont d´eplac´es pour avoir autant que possible des triangles
´equilateraux (triangle non-d´eform´e). Ceci est accompli par l’algorithme it´eratif
suivant:
xj+1
i = xj
i + ω
n
n
k=1(xk − xi)
yj+1
i = yj
i + ω
n
n
k=1(yk − yi)
(6.13)
o`u ω < 1 est un facteur de relaxation et la somme porte sur les n cot´es de
triangles de sommet i. Le nombre d’it´erations j est de l’ordre d’une centaine
avant convergence.
La combinaison de la grille structur´ee globale et non-structur´ee r´egionale
constitue la grille compl`ete du domaine. Pour chacune des mailles nous d´efinissons
un ´el´ement fini qui est soit un triangle `a trois noeuds (erreur d’approximation du
deuxi`eme ordre) soit un rectangle `a 9 noeuds (erreur d’approximation du troisi`eme
ordre). Nous avons ainsi 3027 points formant 2214 ´el´ements finis compos´es de
1774 triangles et de 440 rectangles sur chacun des 23 niveaux.
6.4 R´esolution num´erique de l’´equation de con-
tinuit´e
Nous avons vu au chapitre pr´ec´edent que l’´equation de conservation d’un
compos´e gazeux atmosph´erique s’exprimait, par l’´equation de continuit´e suivante:
∂p fi
∂t
= fi
∂p ˜u
∂˜x
+
∂p ˜v
∂˜y
+
∂p ˙σ
∂σ
−
∂p ˜ufi
∂˜x
+
∂p ˜vfi
∂˜y
+
∂p ˙σfi
∂σ
+
p
ρ
∂ρfi ˜uj
∂˜xj
+p ˜Sni
(6.14)
o`u
fi est le rapport de m´elange volumique du compos´e i,
3
Cet algorithme ne converge qu’`a la condition qu’il n’y ait pas plus de trois points sur un
mˆeme cercle (aucune forme carr´ee ou rectangulaire). Or, pour assurer une continuit´e avec
les mailles rectangulaires de la grille globale et les mailles triangulaires de la fenˆetre, nous
avons d´ecompos´e, aux bords de la grille globale avec la fenˆetre, les ´el´ements rectangulaires
en triangles. Pour ´eviter que l’algorithme diverge, les coordonn´ees sont d’abord normalis´ees.
Ensuite un nombre al´eatoire est g´en´er´e et est multipli´e par un nombre correspondant `a l’erreur
d’arrondi de l’ordinateur (10−8
). Ce nombre est alors ajout´e aux coordonn´ees normalis´ees des
points de grille.
4
La v´erification de l’absence de trou ou de recouvrement est op´er´ee visuellement `a l’aide
d’un algorithme graphique qui r´etr´ecit les dimensions des triangles

134. 134 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
p = ps si l’on choisit comme coordonn´ee verticale, σ = p
ps
,
˜Sni est le terme de production chimique (s−1
),
1
ρ
∂ρfi ˜uj
∂˜xj
est le terme de transport `a sous-´echelle (diffusion turbulente et
convection),
(˜u, ˜v) sont les composantes de vitesse dans le plan de projection st´er´eopolaire,
sur lequel est attach´e le syst`eme d’axes cart´esiens (˜x, ˜y) d´efinis par les transfor-
mations 3.28, et sont reli´ees aux composantes (u, v) par la transformation 3.29.
Les champs m´et´eorologiques calcul´es par le mod`ele `a m´eso-´echelle sont des valeurs
moyennes sur deux heures.
Nous faisons l’hypoth`ese que les valeurs moyennes sur deux heures des acc´el´erations
verticales sont n´egligeables [193]. Une telle hypoth`ese revient `a utiliser l’approximation
hydrostatique. Dans ce cas, en moyennant sur deux heures les vents horizontaux
calcul´es par le mod`ele `a m´eso-´echelle (chapitre 4), la vitesse verticale en coor-
donn´ee verticale σ peut se calculer `a partir de l’´equation suivante [93]:
˙σ = −
1
ps
σ
0
∂ps
∂t
+
∂ps ˜u
∂˜x
+
∂ps˜v
∂˜y
dσ (6.15)
si l’´equation ´evolutive de la pression de surface est calcul´ee par l’int´egrale sur la
hauteur du domaine de la divergence du vent horizontal:
∂ps
∂t
= −
∂ps
∂t
+
∂ps ˜u
∂˜x
+
∂ps˜v
∂˜y
+
∂ps ˙σ
∂σ
(6.16)
Si, dans l’´equation 6.14 on d´erive le premier et le deuxi`eme termes, et que l’on
tient compte de l’´equation ´evolutive 6.16, on obtient l’´equation simplifi´ee suivante:
∂fi
∂t
= −
∂˜ufi
∂˜x
+
∂˜vfi
∂˜y
+
∂ ˙σfi
∂σ
+
1
ρ
∂ρfi ˜uj
∂˜xj
+ ˜Sni (6.17)
Pour r´esoudre cette ´equation il faut sp´ecifier les conditions initiales et aux limites
doivent ˆetre sp´ecifi´ees. Les conditions initiales fi(X,0) `a l’instant t=0 et en tout
point X du domaine Ω sont donn´ees par une relation du type suivant
fi(X, 0) = fi
0
(X) (6.18)
Les conditions aux limites `a la surface terrestre imposent un flux turbulent qui
se d´ecompose en un flux d’´emission et d’un d´epˆot sec:
(w ni )s = −vdini0 + ϕi (6.19)
o`u vdi est la vitesse de d´epˆot sec (cm.s−1
), ϕi est l’´emission du compos´e i (molec.
cm−2
. s−1
), et ni0 est la concentration (molec.cm−3
) du compos´e i au premier

135. 6.4: R´esolution de l’´equation de continuit´e 135
niveau du mod`ele (∼ 35 m). La d´etermination des valeurs de vd et ϕ est le sujet
du prochain chapitre.
Sur les faces lat´erales nous fixons la concentration aux valeurs calcul´ees par le
mod`ele troposph´erique global de M¨uller et Brasseur [179], et au sommet nous
imposons un flux nul except´e pour l’ozone et l’acide nitrique, compos´es princi-
palement produits dans la stratosph`ere, pour lesquels nous fixons sur les deux
derniers niveaux les valeurs calcul´ees par M¨uller et Brasseur [179].
6.4.1 D´ecouplage des ´equations
La plupart des mod`eles de chimie-transport actuels emploient la tech-
nique de ”time-splitting” [250] qui consiste `a s´eparer la solution num´erique de
l’´equation de continuit´e en diff´erentes ´etapes, l’une pour le transport (advection,
diffusion et convection), et l’autre pour les transformations chimiques. Cette
technique est valide parce que les ´echelles de temps des transformations chim-
iques des compos´es cl´es sont beaucoup plus courtes que l’´echelle de temps du
transport. La variation dans le temps des variables d´ependantes f est donc la
somme de leurs variations dues aux processus chimiques, de transport advectif,
de diffusion turbulente, et de transport convectif:
∂f
∂t
=
∂f
∂t chem
+
∂f
∂t adv
+
∂f
∂t diff
+
∂f
∂t conv
(6.20)
o`u
∂f
∂t chem
= Sn (6.21)
∂f
∂t adv
= −
∂˜ufi
∂˜x
+
∂˜vfi
∂˜y
+
∂ ˙σfi
∂σ
(6.22)
∂f
∂t diff
= −
1
ρ
∂
∂σ
ρKσσ
∂f
∂z
(6.23)
∂f
∂t conv
=
n
Mn
c (fn
ci − fi) (6.24)
o`u n est la somme sur les nuages de hauteurs diff´erentes et fn
ci est le rapport de
m´elange du constituant i dans le nuage n (cf. ´equation 5.53).
Le coefficient de diffusion turbulente en coordon´ee verticale σ, Kσσ, s’exprime en
fonction de Km par la relation:
Kσσ =
ρg
ps
2
Km (6.25)
Nous allons `a pr´esent d´ecrire les m´ethodes de r´esolution de chacun de ces
termes.

136. 136 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
6.5 Equations photochimiques
6.5.1 Mod`ele photochimique
La troposph`ere est compos´ee d’une multitude de constituants gazeux
dont une grande majorit´e ont une influence n´egligeable sur la chimie des com-
pos´es observ´es `a Hawaii. Madronich et Calvert [162] ont ´etabli un m´ecanisme de
4930 r´eactions entre plus de 3000 constituants gazeux. Un tel m´ecanisme permet
de s´electionner les esp`eces et les r´eactions qui sont utiles pour des mod`eles tridi-
mensionnels de la troposph`ere globale. M¨uller et Brasseur [179] ont ainsi ´etabli
un mod`ele chimique de la troposph`ere form´e de 41 compos´es et de 125 r´eactions,
centr´e sur l’´etude de la capacit´e oxydante de l’atmosph`ere. Ce faisant, ils ont
attribu´e un rˆole important `a l’isopr`ene qui est l’hydrocarbure non-m´ethanique le
plus abondamment ´emis dans la troposph`ere [178]. Nous avons repris leur mod`ele
chimique, dont les esp`eces peuvent ˆetre regroup´ees suivant que leurs concentra-
tions puissent ˆetre fix´ees, calcul´ees avec ou sans transport selon leur dur´ee de vie
photochimique.
• Esp`eces fix´ees:
– O2 oxyg`ene mol´eculaire5
– N2 azote mol´eculaire6
– H2O vapeur d’eau7
– H2 hydrog`ene mol´eculaire8
– N2O protoxyde d’azote9
• Esp`eces transport´ees
– Compos´es inorganiques
∗ O3 ozone
∗ H2O2 peroxyde d’hydrog`ene
∗ HNO3 acide nitrique
∗ N2O5 h´emipentoxyde d’azote
∗ NOx ≡ NO + NO2 oxydes d’azote impairs
– Compos´es organiques
5
Fraction molaire de O2=0.20
6
Fraction molaire de N2=0.78
7
D´eduit des donn´ees ECMWF et des r´esultats du mod`ele MM5
8
Fraction molaire de H2=5.6×10−7
9
Fraction molaire de N2O=3×10−7

137. 6.5: Equations photochimiques 137
∗ CH4 m´ethane
∗ C2H6 ´ethane
∗ C2H4 ´ethyl`ene
∗ C3H6 propyl`ene
∗ C4H10 butane
∗ C5H8 isopr`ene
∗ C10H16 α-pin`ene
∗ CO monoxyde de carbone
∗ CH2O formald´ehyde
∗ PAN (CH3CO3NO2) nitrate de peroxy-ac´etyle
∗ MPAN (CH2CCH3CO3NO2) nitrate peroxym´ethacrylique
∗ MVK (CH2CHCOCH3) m´ethyle-vinyle-c´etone
∗ MACR (CH2CCH3CHO) m´ethyle-acrol´eine
∗ CH3OOH peroxyde de m´ethyle
∗ C2H5OOH peroxyde d’´ethyle
∗ C3H6OHOOH peroxyde issu du propyl`ene
∗ CH3COOOH acide perac´etique
∗ ONIT nitrates organiques
• Esp`eces non transport´ees
– Compos´es inorganiques
∗ O(1
D) atome d’oxyg`ene (excit´e)
∗ O(3
P) atome d’oxyg`ene (fondamental)
∗ OH radical hydroxyle
∗ HO2 radical hydroperoxyle
∗ NO monoxyde d’azote
∗ NO2 dioxyde d’azote
∗ HNO2 acide nitreux
∗ HNO4 acide pernitrique
∗ NO3 trioxyde d’azote
– Compos´es organiques
∗ CH3CHO ac´etald´ehyde
∗ CH2OHCHO glycolald´ehyde
∗ CHOCHO glyoxal
∗ CH3COCHO m´ethyle-glyoxal

138. 138 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
∗ CH3O2 radical m´ethyle-peroxyle
∗ C2H5O2 radical ´ethyle-peroxyle
∗ ISO1 produit de d´egradation de ISO
∗ MOHO2 radical peroxyle du MVK et du MACR
∗ CH3CO3 radical peroxy-ac´etyle
∗ MCO3 (CH2CCH3CO3) radical peroxy-m´ethacrylique
6.5.2 R´eactions chimiques
L’ensemble des r´eactions s´electionn´ees par M¨uller et Brasseur [179], ainsi
que les constantes de r´eaction, sont repris au tableau 6.3 o`u T est la temp´erature
exprim´ee en o
K. Les coefficients des r´eactions du second ordre sont exprim´es en
(cm3
.molec−1
.s−1
). Les constantes des r´eactions `a trois corps sont calcul´ees par
la formule:
k =
k0[M]
1 + k0[M]
k∞
F
(1+(log10(
k0[M]
k∞
))2)−1
c (cm3
.molec−1
.s−1
) (6.26)
o`u [M] est la concentration du troisi`eme corps qui absorbe l’exc`es d’´energie, (O2
ou N2).
Les r´eactions d’´equilibre (constante Keq) sont scind´ees en une r´eaction de forma-
tion (constante kf ) et de destruction (constante Keq × kf ).
Toutes ces constantes de r´eaction ont ´et´e ´etablies `a partir de mesures en labora-
toire et le Jet Propulsion Laboratory effectue p´eriodiquement leur r´evision. Nous
nous sommes bas´es sur la r´evision du JPL dat´ee de 1990 [61].

139. 6.5: Equations photochimiques 139
Tableau 6.3: Liste des r´eactions chimiques
R´eactions Constantes cin´etiques
Chimie de l’oxyg`ene
1 O(1
D) + N2 → O + N2 1.8 × 10−11
× exp(110/T )
2 O(1
D) + O2 → O + O2 3.2 × 10−11
× exp(70/T )
3 O + O2 + M → O3 + M 6.0 × 10−34
(300/T )2.3
4 O + O3 → 2 O2 8.0 × 10−12
× exp(−2060/T )
Chimie des hydrog`enes impairs
5 O(1
D) + H2O → 2 OH 2.2 × 10−10
6 O(1
D) + H2 → OH + HO2 1.0 × 10−10
7 HO2 + O3 → OH + 2 O2 1.1 × 10−14
× exp(−500/T )
8 OH + O3 → HO2 + O2 1.6 × 10−12
× exp(−940/T )
9 OH + HO2 → H2O + O2 4.8 × 10−11
× exp(250/T )
10 2 OH → H2O + O 4.5 × 10−12
× exp(−240/T )
11 OH + H2 → H2O + H 5.5 × 10−12
× exp(−2000/T )
12 2 HO2 → H2O2 2.2 × 10−13
× exp(619/T )
13 2 HO2 + M → H2O2 + M 1.9 × 10−33
[M] × exp(980/T )
14 2 HO2 + H2O → H2O2 + H2O 3.1 × 10−34
exp(2820/T )
15 2 HO2 + H2O + M → H2O2 + H2O + M 2.7 × 10−54
× exp(3180/T )
16 H2O2 + OH → H2O + HO2 2.9 × 10−12
× exp(−160/T )
Chimie de l’azote
17 O(1
D) + N2O → N2 + O2 4.9 × 10−11
18 O(1
D) + N2O → 2 NO 6.7 × 10−11
19 O3 + NO → O2 + NO2 2.0 × 10−12
× exp(−1400/T )
20 HO2 + NO → OH + NO2 3.7 × 10−12
× exp(240/T )
21 NO2 + O → NO + O2 6.5 × 10−12
× exp(120/T )
22 NO2 + OH + M → HNO3 + M k0 = 2.5 × 10−30
(300/T )2.9
k∞ = 5.2 × 10−11
Fc = exp(−T/353)
23 HNO3 + OH → NO3 + H2O k = k0 + k3[M]
1+
k3[M]
k2
k0 = 7.2 × 10−15
× exp(785/T )
k2 = 4.1 × 10−16
× exp(1440/T )
k3 = 1.9 × 10−33
× exp(725/T )
24 NO + OH + M → M + HNO3 k0 = 7.4 × 10−31
(300/T )2.4
k∞ = 1.0 × 10−11
Fc = exp(−T/1300)
25 NO2 + HO2 + M → M + HNO4 k0 = 1.8 × 10−31
× (300/T )3.2
k∞ = 4.7 × 10−12
(300/T )1.4
Fc = 0.6

140. 140 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Tableau 6.3 (suite)
26 HNO4 + M → HO2 + NO2 + M Keq = 2.1 × 10−27
×
exp(10900/T )
27 HNO4 + OH → H2O + NO2 + O2 1.3 × 10−12
× exp(380/T )
28 O3 + NO2 → O2 + NO3 1.2 × 10−13
× exp(−2450/T )
29 NO3 + HO2 → 0.4 (HNO3 + O2) + 0.6 (OH + NO2) 2.3 × 10−12
× exp(170/T )
30 NO3 + NO2 + M → N2O5 + M k0 = 2.2 × 10−30
(300/T )4.3
k∞ = 1.5 × 10−12
(300/T )0.5
Fc = 0.6
31 N2O5 + M → NO3 + NO2 + M Keq = 4.0 × 10−27
×
exp(10930/T )
32 N2O5 + H2O → 2 HNO3 2.7 × 10−22
Oxydation du m´ethane
33 OH + CH4 → CH3O2 + H2O 2.95 × 10−12
× exp(−1820/T )
34 O(1
D) + CH4 → CH3O2 + OH 1.4 × 10−10
35 O(1
D) + CH4 → CH2O2 + H2 1.4 × 10−11
36 CH3O2 + NO → CH2O + NO2 + HO2 4.2 × 10−12
× exp(180/T )
37 CH3O2 + HO2 → CH3OOH + O2 3.3 × 10−13
× exp(800/T )
38 2 CH3O2 → 0.6 ( CH3OH + CH2O)
+ 0.8 (CH2O + HO2) 2.2 × 10−13
× exp(220/T )
40 CH3OOH + OH → 0.58 (CH3O2 + H2O)
+ 0.42 (CH2O + H2O + OH) 3.8 × 10−12
× exp(200/T )
41 CH2O + OH → CO + HO2 + H2O 1.0 × 10−11
42 CH2O + NO3 → CO + HO2 + HNO3 6.0 × 10−13
× exp(−2058/T )
43 CO + OH → CO + HO2 1.5 × 10−13
× (1 + 0.6p(mb))
Oxydation des hydrocarbures non-m´ethaniques
44 OH + C2H6 → C2H5O2 + H2O 1.1 × 10−11
× exp(−1100/T )
45 NO + C2H5O2 → CH3CHO + HO2 + NO2 8.9 × 10−12
46 HO2 + C2H5O2 → C2H5OOH + O2 6.5 × 10−13
× exp(650/T )
47 CH3O2 + C2H5O2 → 0.7 CH2O + 0.8 CH3CHO
+ HO2 + 0.3 CH3OH + 0.2 C2H5OH 3.75 × 10−13
× exp(−40/T )
48 2 C2H5O2 → 1.6 CH3CHO + 1.2 HO2
+ 0.4 C2H5OO + O2 1.6 × 10−13
× exp(−300/T )
49 OH + C2H5OOH → 0.5 (C2H5O2 + CH3CHO + OH)
+ H2O 3.8 × 10−12
× exp(200/T )
50 C2H4 + OH + M → 2/3 C3H6OHO2 + M k0 = 9.5 × 10−29
(300/T )0.8
k∞ = 9.5 × 10−12
Fc = exp(−T/840)
51 O3 + C2H4 → CH2O + 0.4 HCOOH + 0.52 HO2
+ 0.4 OH + 0.18 CO2 + 0.42 CO
+ 0.12 H2 + 0.02 H2O 1.2 × 10−14
× exp(−2630/T )

141. 6.5: Equations photochimiques 141
Tableau 6.3 (suite)
52 C3H6 + OH + M → C3H6OHO2 + M k0 = 8.0 × 10−27
(300/T )3.5
k∞ = 3.0 × 10−11
Fc = exp(−T/433)
53 C3H6 + O3 → 0.1 CH3COOH + 0.08 CH4
+ 0.585 HO2 + 0.2875 CH3O2 + 0.37 CO
+ 0.5325 CH2O + 0.4575 OH + 0.06 H2
+ 0.5 CH3CHO + 0.2 HCOOH + 0.33 CO2 6.5 × 10−15
× exp(−1900/T )
54 C3H6 + NO3 → ONIT 4.0 × 10−15
55 C3H6OHO2 + NO → CH3CHO + CH2O
HO2 + NO2 4.2 × 10−12
× exp(180/T )
56 C3H6OHO2 + HO2 → CH6OHOOH + O2 6.5 × 10−13
× exp(650/T )
57 C3H6OHOOH + OH → 0.5 (C3H6OHO2 + OH
+ CH3COCH2OH) + H2O 3.8 × 10−12
× exp(200/T )
58 CH3CHO + OH → CH3CO3 + H2O 6.0 × 10−12
× exp(250/T )
59 CH3CHO + NO3 → CH3CO3 + HNO3 1.4 × 10−12
× exp(−1900/T )
60 CH3CO3 + NO → CH3O2 + NO2 + CO2 5.1 × 10−12
× exp(200/T )
61 CH3CO3 + NO2 → CH3CO3NO2 2.8 × 10−12
× exp(181/T )
62 CH3CO3 + HO2 → 2/3 (CH3COOOH + O2)
+ 1/3 (CH3COOH + O3) 4.3 × 10−13
× exp(1040/T )
63 CH3CO3 +CH3O2 → CH3O2 + CH2O
+ CO2 + HO2 1.8 × 10−9
× exp(−1800/T )
64 CH3CO3 + CO3O2 → CH3COOH + CH2O + O2 4.1 × 10−15
× exp(2100/T )
65 2 CH3CO3 → 2 CH3O2 + CO2 2.5 × 10−12
× exp(550/T )
66 CH3CO3NO2 + M → CH3CO3 + NO2 + M k0 = 5.0 × 10−2
× exp(−12875/T )
k∞ = 2.2 × 10+16
× exp(−13435/T )
Fc = 0.27
67 CH3COOOH + OH → CH3CO3 + H2O 1.0 × 10−11
Oxydation de l’isopr`ene et des terp`enes
68 C5H8 + OH → ISO1 2.5 × 10−11
× exp(409/T )
69 C5H8 + O3 → 0.25 MVK + 0.25 MACR
+ 0.6 CH2O + 0.22 CH3O2 + 0.21 HCOOH
+ 0.79 HO2 + 0.49 OH + 0.025 CH3COOOH
+ 0.63 CO + 0.34 CO2 + 0.2 CH3CO3
+ 0.15 (0.13 CH2O + 1.87 CO + 0.87 H2) 1.2 × 10−14
× exp(−2013/T )
70 C5H8 + NO3 → ONIT 3.0 × 10−12
× exp(−450/T )
71 C4H10 + OH → 0.8 ISO1 1.55 × 10−11
× exp(−540/T )
72 ISO1 + NO → 0.5 MVK + 0.5 MACR
+ CH2O + HO2 + NO2 3.7 × 10−12
× exp(180/T )
73 ISO1 + NO → 0.59 (CH3CO3 + CH2O
+ CH2OHCHO + NO2) + 0.41 (ONIT + CH2O) 4.5 × 10−13
× exp(180/T )
74 ISO1 + HO2 → 0.15 (MVK + MACR)
+ 0.3 (CH2O + HO2) 6.5 × 10−13
× exp(650/T )
75 ISO1 + CH3O2 → MACR + CH2O + 2 HO2 1.3 × 10−14

142. 142 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Tableau 6.3 (suite)
76 ISO1 + CH3CO3 → MACR + HO2
+ 0.8 CH3O2 + 0.8 CO2 + 0.2 CH3COOH 4.9 × 10−14
77 MVK + OH → MOHO2 8.6 × 10−12
× exp(500/T )
78 MVK + O3 → 0.5 (CH3CO3 + CO + HO2)
+ 0.46 HO2 + 0.5 CH2O + 0.2 HCOOH
+ 0.19 CO2 + 0.06 H2 + 0.4 CH3O2
+ 0.8 OH + 0.1 CH3COOOH + 1.1 CO 4.0 × 10−15
× exp(−2000/T )
79 MACR + OH → 0.4 MOHO2 + 0.6 H2O + 0.6 MCO3 4.9 × 10−12
× exp(500/T )
80 MACR + O3 → 0.6 (CH3CO3 + CO + HO2
+ 0.76 HO2 + 0.4 CH3O2 + 0.2 HCOOH + 0.61 CO
+ 0.1 OH + 0.59 CO2 + 0.06 H2 + 0.4 CH2O 4.4 × 10−15
× exp(−2500/T )
81 MOHO2 + NO → CH2OHCHO + CH3CO3 + NO2 3.7 × 10−12
× exp(180/T )
82 MOHO2 + NO → ONIT 4.5 × 10−13
× exp(180/T )
83 MOHO2 + HO2 → 0.3 CH3CO3 + 0.3 CH2OHCHO 6.5 × 10−13
× exp(650/T )
84 CH2OHCHO + OH → 0.5 CH3CO3 + 0.5 HO2
0.5 (0.13 CH2O + 1.87 CO + 0.87 H2) 6.0 × 10−12
× exp(250/T )
85 CH2OHCHO + NO3 → CH3CO3 + HNO3 1.4 × 10−12
× exp(−1900/T )
86 MCO3 + NO → 0.4 (CH3CO3 + CH2O)
+ 0.6 (CH3CO3 + CO + 2 HO2) + CO2 + NO2 5.1 × 10−12
× exp(200/T )
87 MCO3 + NO2 → MPAN 2.8 × 10−12
× exp(181/T )
88 MCO3 + HO2 → MOHO2 4.5 × 10−13
× exp(1040/T )
89 MCO3 + CH3O2 → 1.4 CH2O + 1.6 HO2 + CO2
+ 0.4 CH3CO3 + 0.6 (CH3CO3 + CO + HO2) 2.2 × 10−12
× exp(490/T )
90 MCO3 + CH3CO3 → 0.4 (CH3CO3 + CH2O)
+ 0.6 (CH3CO3 + CO + 2 HO2)
+ 2 CO2 + CH3O2 2.8 × 10−12
× exp(530/T )
91 2 MCO3 → 0.8 (CH3CO3 + CH2O)
+ 1.2 (CH3CO3 + CO + 2 HO2) + 2 CO2 2.8 × 10−12
× exp(530/T )
92 MPAN + M → MCO3 + NO2 + m k0 = 5.0 × 10−2
×
exp(−12875/T )
k∞ = 2.2 × 1016
×
exp(−13435/T )
Fc = 0.27
93 C10H16 + OH → ISO1 1.2 × 10−11
× exp(444/T )
94 C10H16 + O3 → idem reac ISO+O3 9.9 × 10−16
× exp(−730/T )
95 C10H16 + NO3 → ONIT 5.6 × 10−11
× exp(−650/T )
6.5.3 R´eactions photochimiques
L’absorption des photons dans le domaine de longueurs d’onde ultra-
violette et visible par les mol´ecules atmosph´eriques induit une transition vers
des ´etats ´electroniquement excit´es. Nous avons vu que la formation de l’ozone
d´ependait de ce processus. Une r´eaction de photodissociation peut s’exprimer
comme une r´eaction du premier ordre, et dans le cas d’une mol´ecule A, nous

143. 6.5: Equations photochimiques 143
Table 6.4: Liste des r´eactions de photodissociation
Photodissociation Coefficient
1 O2 + hν → O + O J(O2)
2 O3 + hν → O2 + O J1(O3)
3 O3 + hν → O2 + O(1
D) J2(O3)
4 H2O2 + hν → 2 OH J(H2O2)
5 NO2 + hν → NO + O J(NO2)
6 HNO3 + hν → OH + NO2 J(HNO3)
7 HNO4 + hν → HO2 + NO2 J(HNO4)
8 NO3 + hν → O + NO2 J1(NO3)
9 NO3 + hν → O2 + NO J2(NO3)
10 N2O5 + hν → NO3 + NO2 J(N2O5)
11 CH3OOH + hν → CH2O + HO2 + OH J(CH3OOH)
12 CH2O + hν → CO + 2 HO2 J1(CH2O)
13 CH2O + hν → CO + H2 J2(CH2O)
14 C2H5OOH + hν → CH3CHO + HO2 + OH J(CH3OOH)
15 C3H6OHOOH + hν → CH3CHO + CH2O
+ HO2 + OH J(CH3OOH)
16 CH3CHO + hν → CH3O2 + CO + HO2 J(CH3CHO)
17 CH3CO3NO2 + hν → CH3CO3 + NO2 J(PAN)
18 CH3COOOH + hν → CH3O2 + OH + CO2 0.28 ×J(H2O2)
19 MVK + hν → CH3CO3 + HO2
+ 0.25 (CH2O + CO) + 0.75 CHOCHO J(MVK)
20 MACR + hν → MCO3 + HO2 J(MACR)
21 CH2OHCHO + hν → CH2O + CO + 2 HO2 2 × J(CH3CHO)
22 MPAN + hν → MCO3 + NO2 J(PAN)
aurons
d[A]
dt
= −JA[A] (6.27)
o`u [A] est la concentration (molec.cm−3
) de A et JA est le coefficient de pho-
todissociation (s−1
). Nous avons repris au tableau (6.4) la liste des r´eactions de
photodissociation prises en compte avec les coefficients correspondants. Si les
donn´ees sont manquantes pour un compos´e, le J d’un constituant photochim-
iquement similaire est choisi.
Pour un intervalle de longueur d’onde dλ, JA est proportionnel au flux de pho-
tons jλdλ (photon.cm−2
.s−1
), `a la section efficace d’absorption σA(λ, T) (cm2
) et
du rendement quantique A(λ, T) de la mol´ecule A. En consid´erant que la par-
tie du spectre solaire qui peut photodissocier la mol´ecule est comprise entre les

144. 144 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
longueurs d’onde [λ1, λ2], le coefficient de photodissociation est donn´e par:
JA(z, χ) =
λ2
λ1
A(λ, T)σA(λ, T)jλ(λ, z, χ)dλ (6.28)
o`u z est l’altitude consid´er´ee et χ est l’angle z´enithal.
Les distributions spectrales des sections efficaces d’absorption et des rendements
quantiques sont d´etermin´ees en laboratoire et sont revues p´eriodiquement par le
JPL 1990 [61]. Le calcul exact de cette int´egrale doit tenir compte des radiations
directes incidentes et r´efl´echies `a la surface terrestre et de la diffusion multiple. En
pratique cette int´egrale est discr´etis´ee en un ensemble limit´e de longueurs d’ondes
et la diffusion multiple est calcul´ee suivant diff´erentes approximations qui sont
d´ecrites dans l’ouvrage de Finlayson-Pitts et Pitts [80]. Malgr´e tout, les mod`eles
tridimensionnels utilisent presque tous une table des valeurs pr´ecalcul´ees des J
pour tous les constituants et pour certaines valeurs des param`etres dominants:
altitude, colonne d’ozone, angle z´enithal, temp´erature de l’air et alb´edo de la
surface terrestre. M¨uller et Brasseur [179] ont realis´e un tel tableau `a partir d’un
mod`ele unidimensionnel de calcul des J tr`es pr´ecis [161]. Les param`etres d’entr´ee
sont l’altitude (de 1 `a 25 km tous les 3 km), l’angle z´enithal (10 valeurs), l’alb´edo
de surface (0.05, 0.1, 0.2, 0.5 et 0.75) et la colonne d’ozone (0.5, 0.75, 1, 1.25, 1.5,
1.75 et 2 fois la colonne d’ozone standard de 300 unit´es Dobson10
). Connaissant
les valeurs de ces cinq param`etres en tous points du domaine, nous pouvons
interpoler les valeurs des J fournies par la table. L’altitude est une variable
ind´ependante et est donc connue. Les valeurs d’alb´edo d´ependent du type de
terrain situ´e directement en dessous du point consider´e. Elles sont reprises au
tableau 7.11 pour les 14 types d’´ecosyst`emes que nous avons consid´er´es. L’angle
z´enithal est calcul´e `a partir d’une expression relativement complexe qui fait appel
`a la g´eom´etrie sph´erique et qui tient compte entre autres de la courbure de la
Terre [161].
La colonne d’ozone `a un niveau de pression du mod`ele est d´etermin´ee `a partir de
la valeur calcul´ee entre ce niveau de pression et le sommet du mod`ele (100mb),
et la colonne au-dessus de 100 mb qui a ´et´e mesur´ee par l’appareil Total Ozone
Mass Spectrometer (TOMS) embarqu´e sur le satllite NIMBUS 7.
Les valeurs de J calcul´ees dans le tableau correspondent `a un ciel clair. Or les
nuages d’une part r´efl´echissent efficacement les radiations incidentes directes et
r´efl´echies `a la surface terrestre et d’autre part renforcent la diffusion multiple entre
cristaux de glace et gouttes d’eau condens´ee. Il y a donc un renforcement de la
photodissociation au sommet du nuage et une att´enuation en dessous avec un
maximum secondaire sous la base du nuage. Ici encore un calcul pr´ecis de l’effet
des nuages est trop coˆuteux en temps de calcul pour un mod`ele tridimensionnel.
10
1 unit´e Dobson = 2.69 × 1016
molec.cm−2

145. 6.5: Equations photochimiques 145
Table 6.5: Facteurs de correction αi pour les diff´erentes r´eactions de photodisso-
ciation
J2(O3) 0.7
J(NO2) 1.2
J(NO3) 1.3
J1(CH2O) 1.0
J2(CH2O) 1.1
J(CH3CHO) 0.9
autres r´eactions 1.0
Nous nous sommes donc servis de la param´etrisation de Chang et al. [39]. Le
taux de photodissociation effectif J est calcul´e par la formule:
J = Jclair 1 −
3
l=1
Fcl(Fl − 1) (6.29)
o`u
Jclair est la valeur de J interpol´ee `a partir de la table,
Fcl est la fraction nuageuse de la couche l,
l est le num´ero d’une des trois couches de nuages observ´es par mesure
satellitaire lors du programme ISCCP [209],
Fl est le rapport entre Jcouvert/Jclair calcul´e, pour χ ≤ 60o
, en fonction
de la position verticale par rapport aux nuages
Fl =
⎧
⎪⎨
⎪⎩
1 + αi(1 − tr) cos χ au-dessus
1.4 cos χ `a l’int´erieur
1.6tr cos χ en-dessous
(6.30)
Pour χ > 60o
, la valeur de Fl est maintenue constante et est ´egale `a celle pour
χ = 60o
. Dans ces expressions, αi est un facteur de correction d´ependant de la
r´eaction de photodissociation. Les valeurs de αi sont donn´ees au tableau (6.5).
La variable tr est le coefficient de transmission de l’´energie incidente au travers
des nuages et se calcule par la formule [129]:
tr =
5 − exp(−τ)
4 + 3τ(1 − 0.86)
(6.31)
o`u τ est l’´epaisseur optique.
Les valeurs d’´epaisseur optique varient en fonction du type de nuage et de son
contenu en eau condens´ee: 1 `a 5 pour les cumulus, altocumulus et cirrus; 5 `a
25 pour les cirro-cumulus et 25 `a 125 pour les cumulonimbus [209]. Quand le

146. 146 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
contenu en eau condens´ee, q2, est connu, on utilise la formule de Chang et al.
[39]:
τ =
3
l=1
3q2l∆zl
2ρwrdroplet
(6.32)
o`u
q2l est le contenu en eau condens´ee moyenn´e sur la hauteur de la couche
nuageuse l,
∆zl est l’´epaisseur de la couche de nuage l (m),
ρw est la masse sp´ecifique de l’eau (g.m−3
),
rdroplet est le rayon moyen des gouttes d’eau (10−5
m).
Si la valeur de q2 n’est pas connue en un point, on utilise la formule de M¨uller et
Brasseur [179] qui relie directement la valeur de l’´epaisseur optique `a l’extension
verticale du nuage:
τ = 0.16
3
l=1
∆pl (6.33)
o`u ∆pl est la diff´erence de pression entre le sommet et la base de la couche l.
Un autre facteur significatif est la variation annuelle de la distance Terre/Soleil,
l’´energie incidente par unit´e de surface ´etant en effet une fonction de cette dis-
tance. La valeur corrig´ee de J s’obtient par
J = J × LTS (6.34)
o`u LTS est le facteur correctif donn´e par la formule [163]:
LTS = 1.00011 + 0.034221 cos(θ0) + 0.00128 sin(θ0)
+0.000719 cos(2θ0) + 0.000077 sin(2θ0) (6.35)
o`u θ0= 2π(Jour Julien
365.25
)
6.5.4 R´eactions h´et´erog`enes
En raison du manque de connaissance des r´eactions h´et´erog`enes `a la
surface des a´erosols et des gouttes d’eau, nous n’avons consid´er´e que la dissolution
des gaz dans les gouttes de pluie. En supposant que les gouttes de pluie ne
s’´evaporent pas, la dissolution peut ˆetre trait´ee simplement comme une perte
suppl´ementaire dans l’´equation de continuit´e.
Nous avons utilis´e les mˆemes param´etrisations que M¨uller et Brasseur
[179] pour tenir compte du lessivage par les pluies des compos´es solubles. Le
taux de lessivage au sol est suppos´e proportionnel au taux de pr´ecipitation:
βsurf
i = fpi × 3 × 10−8
× Prec (6.36)

147. 6.5: Equations photochimiques 147
Table 6.6: Facteurs fpi pour la param´etrisation du lessivage par les pluies des
compos´es solubles
H2O2 1
HNO3 2
HNO4 0.5
CH2O 0.7
CH3OOH 0.5
C2H5O2H 0.7
C3H6OHO2H 0.7
CH3CO3H 0.7
CHOCHO 2
autres compos´es 0
o`u
Prec est le taux de pr´ecipitation (mm/mois),
3 × 10−8
est un facteur dimensionnel qui convertit des (mm/mois) en
(s−1
),
fpi est un facteur qui tient compte de la solubilit´e du gaz i dont les valeurs
sont donn´ees au tableau (6.6).
Au-dessus de la CLP, la contribution de la couche l au taux de lessivage `a un
niveau σ du mod`ele est donn´e par la formule:
βi(σ) = βsurf
i × fl(σ) ×
cl
ctot
(6.37)
avec
fl(σ) =
⎧
⎪⎨
⎪⎩
1 σ > σl−1
σl−σ
σl−σl−1
σl < σ < σl−1
0 σ < σl
(6.38)
et ctot = c1 + c2 + c3 est la somme des fractions de nuages pour les trois couches.
6.5.5 Production de NO par les ´eclairs
La dissociation thermique de N2 et O2 par les ´eclairs produirait entre 1
Tg(N)/an `a 220 Tg(N)/an [227]; [38]; [57]; [113], [154]; [26]; [196]). Ces incer-
titudes sont tr`es ´elev´ees et les valeurs pourraient ˆetre sup´erieures aux ´emissions
globales de NO par les sols. En adoptant une source globale de NO par les ´eclairs
de 8 Tg(N)/an [154], en supposant qu’elle est constante avec l’altitude en dessous
de la tropopause (100mb) et en connaissant la distribution du nombre d’´eclairs
par minute et par unit´e de surface [229], nous pouvons calculer la production de
NO par unit´e de volume et de temps en tous points du domaine.

148. 148 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
6.5.6 M´ethode num´erique
En chaque point de grille, nous r´esolvons le terme de production pho-
tochimique, Sni, pour chaque constituant i. Nous avons donc en un point de
grille une ´equation diff´erentielle ordinaire non-lin´eaire pour la concentration ni
du compos´e i:
d[ni]
dt
= Pi(nj) − Li(nj)[ni] (6.39)
o`u [ni] est la concentration (molec.cm−3
) du constituant i,
Pi et Li sont les termes de production et de perte photochimiques qui
d´ependent de la concentration d’un ou plusieurs autres constituants.
La dispersion des valeurs propres de ce syst`eme d’´equations qui ne sont autres que
les dur´ees de vie photochimique (τ = P/L) ne permet pas d’utiliser un sch´ema
explicite de discr´etisation pour des raisons de stabilit´e. La m´ethode de Gear [85]
`a pas multiples et `a contrˆole automatique du pas de temps maximum en fonction
d’une pr´ecision fix´ee est trop coˆuteuse en temps de calcul pour ˆetre utiliser dans un
mod`ele tridimensionnel. Nous lui avons pr´ef´er´e la m´ethode implicite pour laquelle
le terme de destruction Li est une fonction des concentrations au temps t + ∆t.
Cette m´ethode est inconditionnellement stable quel que soit le pas de temps.
Cependant `a chaque pas de temps un ensemble d’´equations non-lin´eaires doit
ˆetre r´esolu `a l’aide d’une m´ethode it´erative. Au lieu de r´esoudre l’ensemble des N
´equations alg´ebriques par inversion de la matrice jacobienne, nous ne consid´erons
que les termes diagonaux. La concentration d’un constituant i au temps t + ∆t
se calcule alors par la formule suivante
[ni]t+∆t
=
[ni]t
+ P∆t
1 + L∆t
(6.40)
Cette m´ethode converge moins vite que si nous avions introduit la matrice ja-
cobienne mais offre l’avantage de ne pas n´ecessiter d’inversion de matrice. Une
technique g´en´eralement utilis´ee pour diminuer la dispersion des valeurs propres
est de grouper certains constituants r´eagissant entre eux suivant des cycles nuls ou
quasiment nuls [228]. Les groupes de constituants sont appel´es familles. Parmi
celles-ci, nous avons form´e: la famille d’oxyg`enes impairs (Ox=O3 + O(1
D) +
O(3
P)) et celle des azotes impairs (NOx = NO + NO2). Au sein d’une famille,
on suppose qu’un constituant est transport´e et les autres sont `a l’´equilibre pho-
tochimique: la production P est ´equilibr´ee par la destruction L[n]. Au d´ebut de
chaque pas de temps, le fractionnement de chaque famille est effectu´e, ensuite en
trois it´erations les concentrations des constituants non-transport´es sont ´evalu´ees
par la formule (6.41) ou (6.42), suivi alors du calcul des concentrations des familles
et des constituants transport´es par la formule (6.40). La proc´edure est it´erative
et d’apr`es nos tests trois it´erations sont n´ecessaires et cinq it´erations sont suff-
isantes. Par soucis d’efficacit´e, nous it´erons trois fois. Pour les constituants `a

149. 6.6: Advection 149
l’´equilibre photochimique, la concentration est ´evalu´ee suivant l’expression:
[ni]t+∆t
=
P
L
(6.41)
`a moins que le terme de destruction ne devienne tr`es petit auquel cas nous util-
isons un sch´ema explicite:
[ni]t+∆t
= [ni]t
+ (P − L[ni]t
)∆t (6.42)
Les expressions (6.41) ou (6.42) de chacun des constituants `a l’´equilibre sont
recalcul´ees trois fois avant l’´evaluation de l’expression (6.40) des constituants
transport´es, ce qui correspond `a neuf it´erations `a chaque pas de temps.
6.6 Advection
Il n’existe pas de m´ethode id´eale de discr´etisation de l’´equation d’advection.
La difficult´e provient de sa nature hyperbolique, dont l’expression est la suivante
∂f
∂t
+ ˜v•∇f = 0 (6.43)
Les lignes caract´eristiques de la solution sont d´efinies par l’´equation indicielle
suivante
d˜xi
dt
= ˜ui i=1,2,3 (6.44)
La recherche pr´ecise des lignes caract´eristiques pose un probl`eme ´etant donn´e
qu’elles relient les variables ind´ependantes (˜xi, t): la discr´etisation d’une variable
influence celle des autres. Certains crit`eres de stabilit´e doivent ˆetre respect´es
lors de la discr´etisation des variables. En particulier, la condition de Courant-
Friedricks-Lewy (CFL) impose une limite maximum au pas de temps en fonction
de la distance entre points de grille et la vitesse du vent:
| ˜ui | ∆t
∆xi
≤ 1 (6.45)
o`u
∆t est le pas de temps,
∆xi est la plus petite distance entre points de grille dans la direction i,
| ˜v | est la valeur absolue de la composante i de la vitesse du vent.
Avec une r´esolution de l’ordre de quelques kilom`etres dans la r´egion d’Hawaii et
en consid´erant une vitesse des vents dominants de l’ordre de 10 m.s−1
, le pas de
temps doit ˆetre inf´erieur `a deux minutes. Par contre, le long du bord le plus
´eloign´e d’Hawaii, ∆x est d’environ 1500 km, le pas de temps peut atteindre un

150. 150 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
jour. En principe, la formulation lagrangienne, qui consiste `a fixer les axes de
coordon´ees sur la parcelle d’air en mouvement, permet d’´eviter cette limitation
du pas de temps. Si l’on effecte un changement des variables ind´ependantes (˜xi)
vers (˜xi) tel que:
d˜xi = d˜xi − ˜uidt (6.46)
et pour f = f(˜xi, t), on a
∂f
∂t
|˜x=
∂f
∂˜xi
∂˜xi
∂t
+
∂f
∂t
|˜x = −ui
∂f
∂˜xi
+
∂f
∂t
|˜x (6.47)
et l’´equation (6.43) se r´esume alors `a l’´equation suivante
∂f
∂t
= 0 (6.48)
dont la solution est imm´ediate, c(˜xi) = f(˜xi−uit) = constante, une fois connue les
lignes caract´eristiques. Leur d´etermination n´ecessite, de par la nature discr`ete
des mod`eles num´eriques, de multiples interpolations qui entachent la solution
d’erreurs syst´ematiques et rendent la m´ethode non-conservative.
La m´ethode semi-lagrangienne combine les avantages de la formulation
lagrangienne (pas de restriction sur le pas de temps) et eul´erienne (pas d’accumulation
d’erreurs dans la recherche de trajectoire). Le principe de la m´ethode semi-
lagrangienne consiste `a consid´erer un ensemble de volumes d’air, tels qu’`a chaque
pas de temps ces volumes viennent co¨ıncider avec le volume entourant les points
de grille (figure 6.3). L’erreur sur le calcul des trajectoires depuis une position in-
connue vers un point de grille se r´ep`ete `a chaque pas de temps mais ne s’accumule
pas. Cependant elle ne r´esoud pas le probl`eme de conservation de la masse. Une
possibilit´e serait de diminuer l’erreur d’approximation en utilisant des fonctions
d’interpolation de degr´e sup´erieur. Mais une telle solution devient rapidement
prohibitif en temps de calcul lorsqu’il s’agit d’advecter plus d’une vingtaine de
compos´es gazeux. Dans le cas de simulation relativement courte, la perte de la
masse, dues aux incertitudes num´eriques, est relativement insignifiante compar´ee
aux autres erreurs, telle que la diffusion num´erique. Nous avons cependant veill´e
`a maintenir la masse constante.
La m´ethode semi-lagrangienne offre un avantage suppl´ementaire qui est
d’effectuer deux op´erations successives. La premi`ere consiste `a rechercher les
lignes caract´eristiques qui ne d´ependent que des variables ind´ependantes. Cette
op´eration repr´esente pr`es de 90% du temps de calcul en raison principalement
de la difficult´e de localiser un point dans une grille non-structur´ee. Apr`es avoir
interpol´e les variables m´et´eorologiques, cette op´eration est effectu´ee une fois pour
toutes et les valeurs des trajectoires `a chaque pas de temps sont sauvegard´ees sur
fichier. La deuxi`eme op´eration qui consiste `a r´esoudre l’´equation (6.47), peut ˆetre

151. 6.6: Advection 151
Figure 6.3: M´ethode semi-lagrangienne de r´esolution du transport advectif.
Les points de grille i, j, k, l sont d´eplac´es par advection le long des lignes car-
act´eristiques
divis´ee en une s´erie de calculs qui ne font appel qu’`a la g´eom´etrie et le calcul d’une
somme de produits qui d´ependent des variables d´ependantes. Nous avons donc
pr´ecalcul´es les trajectoires de chaque point de grille et durant les simulations nous
effectuons seulement les interpolations. Nous sommes ainsi capable de r´eduire le
temps de calcul d’un facteur 100 pour le transport advectif.
6.6.1 Calcul des lignes caract´eristiques
La recherche des lignes caract´eristiques se limite, pour la m´ethode semi-
lagrangienne, `a d´eterminer pour chaque point de grille une origine. Celle-ci est
telle que sur un intervalle de temps fix´e un ´el´ement de volume qui lui est attach´e
vient co¨ıncider exactement avec le volume entourant le point de grille correspon-
dant (figure 6.3). A chaque pas de temps les vitesses du vent ayant chang´e, la
position d’origine est diff´erente et doit donc ˆetre recalcul´ee.
Soit (xn+1
i ) la position d’un point de grille au temps tn+∆t
, et (xn
i ) la position
du point origine correspondant au temps tn
. La position du point d’origine se
calcule en int´egrant l’´equation (6.44):
xn
i = xn+1
i −
tn+∆t
tn
ui dt i=1,2,3 (6.49)

152. 152 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Ces int´egrales sont discr´etis´ees dans le temps, en consid´erant que la vitesse varie
lin´eairement le long de la trajectoire. La vitesse moyenne est donc la moyenne
des vitesses aux points (xn
i ) et (xn+1
i ). Etant donn´e que (xn+1
i ) d´epend de ui, le
probl`eme est non-lin´eaire, et il faut donc utiliser une m´ethode it´erative dont nous
avons sch´ematis´e le principe `a la figure 6.4. L’algorithme utilis´e est le suivant
Figure 6.4: Recherche it´erative des trajectoires depuis la position xn+1
i `a xn
i , en
passant par les points interm´ediaires de chaque it´eration k, (xn
i )k
.
(xn
i )k
= xn+1
i − ∆t
ui((xn
j )k−1
) + ui(xn+1
j )
2
i=1,2,3 et j=1,2,3 (6.50)
o`u l’indice k repr´esente le num´ero de l’it´eration. Cinq it´erations sont effectu´ees
`a moins que la diff´erence entre (xn
i )k
et (xn
i )k−1
ne soit inf´erieure `a une valeur
fix´ee. Les vitesses ui(xn
j ) sont initialement (pour k = 0) choisies arbitrairement
´egales `a ui(xn+1
j ). Ensuite, `a chaque nouvelle it´eration elles sont calcul´ees par
interpolation `a l’aide de fonctions tridimensionnelles. Le degr´e d’interpolation
est suivant la verticale (σ) lin´eaire et suivant l’horizontale (˜x, ˜y) quadratique ou
lin´eaire. Les interpolations sont effectu´ees sur l’´el´ement fini qui contient le point
(xn
i )k
. Les composantes du vent sont connues toutes les deux heures et sont
interpol´ees toutes les 10 minutes avant d’utiliser l’algorithme (6.50).

153. 6.6: Advection 153
6.6.2 Recherche des valeurs de la concentration aux points
origines
Connaissant la position (xn,yn,σn) occup´ee par tous les points de grille
apr`es un pas de temps, les concentrations peuvent ˆetre calcul´ees par interpolation
`a partir des valeurs connues aux points de grille. De mani`ere `a r´eduire les erreurs
d’approximation par interpolation, la m´ethode des r´esidus pond´er´es est utilis´ee
conjointement avec la m´ethode des caract´eristiques comme propos´e par Hasbani
et al. [105]. La m´ethode des ´el´ements finis diff`ere dans la r´esolution d’´equations
diff´erentielles de la m´ethode des diff´erences finies, en ce sens qu’elle ne discr´etise
pas les op´erateurs mais approche la solution par des fonctions d’interpolation
d´efinies sur des ´el´ements finis (figure 6.5).
Figure 6.5: M´ethode semi-lagrangienne combin´ee `a la m´ethode des ´el´ements fi-
nis. L’ensemble des neuf noeuds formant l’´el´ement quadratique complet au temps
t ´etaient au pas de temps pr´ec´edent aux points marqu´es des chiffres romains.
Puisqu’il y a conservation le long des caract´eristiques au cours du temps, les
concentrations aux noeuds des deux ´el´ements doivent ˆetre les mˆemes. Ces con-
centrations sont connues au pas de temps pr´ec´edent, donc en interpolant ces
valeurs sur les noeuds de chiffres romains on obtient les nouvelles valeurs. Les
int´egrales pond´er´ees des concentrations sur les ´el´ements finis sur les deux grilles
permettent de conserver la masse aux erreurs d’interpolation pr`es.

154. 154 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Ainsi, la valeur du rapport de m´elange d’un constituant transport´e `a
l’instant t, f(x, y, σ, t) est approch´ee en tout point j d’un ´el´ement fini e, du
domaine par un ensemble de polynˆomes orthogonaux, N(x, y, σ), par la relation
suivante:
f(xn, yn, σn, t) =
e
ne
j=1
Nj(xn, yn, σn)fj(t) (6.51)
o`u
Nj(xn,yn,σn) est la jeme
fonction d’interpolation au point origine de la
trajectoire (cf. Annexe 2),
ne est le nombre de points de grille qui d´efinissent l’´el´ement fini e.
En rempla¸cant la relation (6.51) dans l’´equation diff´erentielle (6.48), nous intro-
duisons une erreur qui est ´egale `a,
=
e
ne
j=1
d(Njfj)
dt
= 0 (6.52)
Les erreurs sur chaque ´el´ement fini e
sont minimis´ees par des fonctions de
pond´eration (m´ethode des r´esidus pond´er´es). Le choix des coefficients de pond´eration
varie suivant diff´erentes m´ethodes. La m´ethode de Galerkin consiste `a choisir les
mˆemes fonctions d’interpolation N(x,y,σ). En int´egrant l’ensemble des erreurs e
sur le domaine Ω et en les pond´erant par les fonctions N, on obtient:
Ω Ni dΩ = 0
e Ωe Ni(x, y, σ) e
dΩe
= 0
e j Ωe Ni(x, y, σ)Nj(x, y, σn)dΩe
{dfj
dt
} = 0
(6.53)
o`u
i est l’indice portant sur tous les noeuds du domaine Ω
j est l’indice portant sur les noeuds de l’´el´ement fini Ωe
e est l’indice sur tous les ´el´ements finis couvrant le domaine Ω,
Ni(x, y, σ) sont les fonctions de pond´eration,
Nj(x, y, σ) sont les fonctions d’interpolation.
En discr´etisant dans le temps le terme
dfj
dt
aux instant t et t + ∆t, le syst`eme
d’´equations int´egrales (6.53) devient:
⎡
⎣
e j Ωe
Ni(x, y, σ)Nj(x, y, σ)dΩe
⎤
⎦ {fj(t + ∆t)}
=
⎡
⎣
e j Ωe
Ni(x, y, σ)Nj(xn, yn, σn)dΩe
⎤
⎦ {fj(t)} (6.54)

155. 6.6: Advection 155
Les valeurs de vitesse horizontale ´etant de plusieurs ordres de grandeur sup´erieures
(> 106
) `a celles de la vitesse verticale, nous pouvons d´ecomposer le transport ad-
vectif en sa composante horizontale (H) et verticale (V ). Ce qui se traduit pour
les fonctions Ni et Nj par l’expression suivante:
Ni(x, y, σ) = NH
i (x, y)NV
i (σ) (6.55)
Le syst`eme (6.54) peut alors ˆetre scind´e en deux sous-syt`emes
e j NH
i (x, y)NH
j (x, y)dxdy {fj}
= e j NH
i (x, y)NH
j (xn, yn)dxdy {fj(t)}
e j NV
i (σ)NV
j (σ)dσ {fj(t + ∆t)} =
e j NV
i (σ)NV
j (σn)dσ {fj}
(6.56)
o`u fj est une solution interm´ediaire. Cette simplification permet de ne consid´erer
que les caract´eristiques g´eom´etriques d’un seul plan, puisqu’elles sont les mˆemes
pour chaque plan. Cependant l’int´egration num´erique diff`ere d’un ´el´ement fini `a
l’autre. Pour augmenter la rapidit´e d’ex´ecution nous projetons les ´el´ements finis
vers des ´el´ements de formes simples (carr´e et triangle ´equilat´eral) et de dimensions
unitaires qui s’int`egrent tr`es facilement. Cette projection n´ecessite n´eanmoins la
connaisance du jacobien de la transformation. La m´ethode d’int´egration la plus
usit´ee pour sa pr´ecision est la m´ethode de Gauss. Cette m´ethode ne peut ˆetre
utilis´ee avec les triangles pour lesquels nous employons les formules de Hammer.
6.6.3 M´ethodes d’int´egration
La m´ethode de Gauss consiste `a d´eterminer r coefficients i et r coordonn´ees ξi
de mani`ere `a int´egrer exactement des polynˆomes d’ordre m ≤ 2r − 1:
1
−1
f(ξ)dξ =
r
i=1
if(ξi) (6.57)
Dans le cas d’un ´el´ement de forme carr´ee, nous aurons la formule suivante
1
−1
1
−1
f(ξ, η)dξdη =
r1
i=1
r2
j=1
i jf(ξi, ηj) (6.58)
Dans le cas d’un triangle, les formules de Hammer permettent d’obtenir une
expression identique aux cas pr´ec´edents:
1
0
1−ξ
0
f(ξ, η)dξdη =
r
i=1
if(ξi, ηi) (6.59)

156. 156 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Table 6.7: Int´egration num´erique de Gauss `a une dimension
Ordre Nombre de ξi wi
m points r
3 2 1/
√
3 1
−1/
√
3
0 8/9
5 3 3/5 5/9
− 3/5 5/9
Table 6.8: Int´egration num´erique de Hammer `a deux dimensions
Ordre Nombre de ξi ηi wi
m points r
1/6 1/6 1/6
2 3 2/3 1/6 1/6
1/6 2/3 1/6
Les d´etails de cette m´ethode peuvent ˆetre trouv´es dans l’ouvrage de Davis et
Rabinowitz [56]. Nous nous limiterons `a donner les valeurs utilis´ees. Dans le
cas de l’´el´ement lin´eaire `a deux noeuds nous utilisons deux points d’int´egration
(tableau 6.7), pour l’´el´ement carr´e nous utilisons l’int´egration `a trois noeuds dans
les deux directions (tableau 6.7) et pour le triangle nous utilisons trois points
d’int´egration (tableau 6.8).
Ayant d´efini le nombre de points d’int´egration par ´el´ement, les fonctions
d’interpolation et le jacobien sont calcul´es en ces points.
Apr`es transformation des coordonn´ees (x, y, σ) par les coordonn´ees (ξ, η, ζ),
et sommation sur les (r1 × r2) points d’int´egration de coordonn´ees (ξr, ηr) et r
points d’int´egration de coordonn´ee ζr, suivant la verticale, les deux syst`emes
(6.56) s’´ecrivent `a pr´esent:
r1 r2 e j r1 r2NH
i (ξr1, ηr2)NH
j (ξr1, ηr2)det[Je
(ξr1, ηr2)]dξdη {fj}
= r1 r2 e j r1 r2NH
i (ξr1, ηr2)NH
j (ξn, ηn)det[Je
(ξr1, ηr2)]dξdη {fj(t)}
r e j rNV
i (ζr)NV
j (ζr)det[Je
(ζr)]dζ {fj(t + ∆t)}
= r e j rNV
i (ζr)NV
j (ζn)det[Je
(ζr)]dζ {fj}
(6.60)

157. 6.6: Advection 157
o`u (ξn, ηn) sont les coordonn´ees (xn, yn) transform´ees.
La solution est obtenue en r´esolvant successivement ces deux syst`emes en in-
versant les matrices du membre de gauche. La matrice du 1er
syst`eme contient
des termes non nuls dispers´es. La plus grande distance entre la diagonale et le
dernier terme non nul sur une rang´ee, est appel´ee la demi largeur de bande de la
matrice. Plus cette largeur de bande est ´elev´ee plus l’inversion sera coˆuteuse en
place m´emoire et en temps d’ex´ecution. Cette largeur d´epend de la num´erotation
des points de grille. Hasbani et al. [105] ont not´e que la pr´ecision du r´esultat
d´ependait surtout de la pr´ecision dans le calcul des termes du membre de droite
des syst`emes (6.60). Etant donn´e que la taille des matrices est de plusieurs mil-
liers de lignes et de colonnes, leur inversion serait prohibitive, nous avons adopt´e
la technique de ”lumping” [254] qui consiste `a diagonaliser une matrice Mij de la
mani`ere suivante:
Mij = k Ω NiNkdΩ i = j
0 i = j
(6.61)
Si d’autre part, ces int´egrales sont ´evalu´ees par la m´ethode de Simpson (les points
d’int´egration co¨ıncident avec les points de grille), alors le calcul de ces int´egrales
se r´eduit `a multiplier la somme des aires des ´el´ements finis entourant le noeud
i, e Se(ξ, η) ou e le(σ), par un coefficient de pond´eration, βi pour le plan
horizontal ou γi pour la ligne verticale. Finalement la solution de l’´equation
d’advection s’obtient par l’algorithme suivant:
fi = r1 r2 e j r1 r2NH
i (ξr1,ηr2)NH
j (ξn,ηn)det[J(ξr1,ηr2)]∆ξ∆η
βi( e
Se)
fj(t)
fi(t + ∆t) = r e j rNV
i (ζr)NV
j (ζn)det[J(ζr)]∆ζ
γi( e
le)
fj
(6.62)
o`u
Se est la surface de l’´el´ement fini horizontal e,
le est la longueur de l’´el´ement fini vertical e,
βi et γi sont des coefficients de pond´eration qui permettent de conserver
la masse apr`es ”lumping”, leurs valeurs sont donn´ees au tableau 6.9
Par souci de rapidit´e d’ex´ecution, les termes li´es `a la g´eom´etrie des ´el´ements
horizontaux sont pr´ecalcul´es et stock´es dans une fonction Ξ, et le calcul de fi
dans l’algorithme pr´ec´edent devient
fi =
e
Ξe,i[
j
NH
j (ξn, ηn)fj(t)] (6.63)
o`u
Ξe,i = r1 r2 NH
i (ξr1, ηr2)det[J(ξr1, ηr2)]∆ξ∆η
βi e Se
(6.64)

158. 158 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Table 6.9: Coefficients de pond´eration pour diff´erents ´el´ements `a une (segment
de droite) et deux dimensions (triangle `a 3 noeuds, carr´e `a 4 noeuds et carr´e `a 9
noeuds).
Nombre de Num´ero des noeuds
noeuds 1 2 3 4 5 6 7 8 9
2 1/2 1/2
3 1/3 1/3 1/3
4 1/4 1/4 1/4 1/4
9 1/36 4/36 1/36 4/36 1/36 4/36 4/36 1/36 16/36
N.B. Les noeuds sont compt´es dans le sens anti-horlogique en commen¸cant par le coin inf´erieur
gauche.
D’autre part les fonctions NH
j (ξr1, ηr2) sont identiques pour un mˆeme type d’´el´ement
fini. Elles sont par cons´equent pr´ecalcul´ees directement aux r1 × r2 points de
Gauss. Finalement il nous reste uniquement `a calculer pour chaque pas de temps
et chaque point de grille la valeur de la solution au point (ξn, ηn) par la formule
(6.63).
Nous voyons que le nombre d’op´erations a ´et´e fortement r´eduit et comme
nous le verrons en comparant avec d’autres algorithmes semi-lagrangiens, notre
algorithme est significativement plus rapide.
Si une masse d’air ext´erieure au domaine y rentre, la valeur des rapports
de m´elange `a l’intersection de la trajectoire et de la ligne fronti`ere est impos´ee
comme conditions aux limites.
Cet algorithme offre l’avantage d’ˆetre efficace en temps de calcul, d’ˆetre
flexible par rapport `a n’importe quel type de maillage, de ne pas d´ependre des
conditions CFL et de minimiser les erreurs d’interpolation. Par contre, il ne
conserve pas la masse ni les gradients (diffusion num´erique). Nous ´evaluerons ces
probl`emes en fin de chapitre et les comparerons `a ceux des autres m´ethodes.
6.6.4 Filtrage des bruits
Selon le th´eor`eme de Godunov, tout sch´ema num´erique lin´eaire de r´esolution
de l’´equation d’advection ne peut ˆetre `a la fois conservatif et pr´eserver la solution
stationnaire exacte. Les sch´emas d’ordre ´elev´e qui satisfont la deuxi`eme pro-
pri´et´e ne peuvent garantir la premi`ere. Quant aux sch´emas lin´eaires d’ordre un,
`a l’oppos´e ils sont conservatifs mais diffusent artificiellement la solution et ne satis-
font plus la deuxi`eme propri´et´e. Dans notre cas, nous utilisons un sch´ema d’ordre
un sur les triangles `a trois noeuds et un sch´ema d’ordre deux sur les ´el´ements `a
neuf noeuds. Si les gradients ´elev´es de la solution sont rapidement diminu´es sur

159. 6.6: Advection 159
les triangles, leur haute densit´e de distribution dans la r´egion d’Hawaii comble
partiellement ce probl`eme. Par contre, un gradient ´elev´e sur les rectangles `a neuf
noeuds peut cr´eer des extr´ema locaux et donc produire des oscillations de la con-
centration, et en particulier cr´eer des valeurs n´egatives. En cons´equence, apr`es
r´esolution de l’´equation d’advection, la solution est filtr´ee en appliquant de la dif-
fusion autour des valeurs n´egatives. La technique consiste `a r´esoudre l’´equation de
la diffusion horizontale par la m´ethode des ´el´ements finis. La th´eorie est identique
`a celle d´evelopp´ee pr´ec´edemment, et nous donnons directement l’algorithme:
fcorr
i =
e j
[Ξe,i,j,1Kxx + Ξe,i,j,2Kyy]fj(t)∆t (6.65)
o`u les fonctions Ξ(e, i, j, 1) et Ξ(e, i, j, 2) pr´ecalcul´ees ne d´ependent que de la
g´eom´etrie:
Ξe,i,j,1 =
r1 r2
∂NH
i (ξr1,ηr2)
∂ξ
∂ξ
∂x
+
∂NH
i (ξr1,ηr2)
∂η
∂η
∂x
det[J(ξr1, ηr2)]∆ξ∆η
βi e Se
(6.66)
Ξe,i,j,2 =
r1 r2
∂NH
i (ξr1,ηr2)
∂ξ
∂ξ
∂y
+
∂NH
i (ξr1,ηr2)
∂η
∂η
∂y
det[J(ξr1, ηr2)]∆ξ∆η
βi e Se
(6.67)
o`u les d´eriv´ees partielles des coordonn´ees dans l’espace de r´ef´erence par rapport
`a celles dans l’espace r´eel sont les termes de la matrice jacobienne inverse.
La propri´et´e de sym´etrie en i et j des matrices Ξ est exploit´ee lors du stockage
de ces valeurs. Les coefficients de diffusion Kxx et Kyy sont non nuls uniquement
au-dessus des ´el´ements finis qui contiennent un noeud o`u la concentration est
n´egative. Apr`es trois it´erations, si des valeurs n´egatives persistent, la valeur
absolue est impos´ee. Ensuite la masse totale du domaine est modifi´ee pour assurer
la conservation, `a l’aide d’un ”fixeur de masse”.
6.6.5 Fixeur de masse
La masse totale de chaque constituant chimique est conserv´ee en chaque
niveau vertical du domaine apr`es advection horizontale `a l’aide d’un fixeur de
masse. L’´ecart de masse avant et apr`es l’advection horizontale est redistribu´e de
la mani`ere suivante.
Soit α le rapport entre la masse, sur un plan horizontal Ω, avant (m0) et apr`es
(m1) advection horizontale:
α =
m1dΩ − Φ0∆t
m0dΩ − Φ1∆t
(6.68)

160. 160 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
o`u Φ0 et Φ1 sont les flux sortants sur la fronti`ere lat´erale avant et apr`es advection
horizontale, et ∆t est le pas de temps.
La masse du constituant en un point du plan sera alors corrig´ee par la relation:
mcorr = αm1 (6.69)
Les int´egrales dans le calcul de α sont effectu´ees par la m´ethode des ´el´ements finis
suivant une technique identique `a celle d´ecrite pr´ec´edemment. En se r´eferant `a
l’algorithme (6.62), on obtient un algorithme similaire pour le coefficient α:
α =
r1 r2 e j r1 r2NH
i (ξr1, ηr2)NH
j (ξr1, ηr2)det[J(ξr1, ηr2)]∆ξ∆ηmj
0 − Φ0∆t
r1 r2 e j r1 r2NH
i (ξr1, ηr2)NH
j (ξr1, ηr2)det[J(ξr1, ηr2)]∆ξ∆ηmj
1 − Φ1∆t
(6.70)
o`u les sommes portent successivement sur les r1 × r2 points de Gauss dans les
deux directions horizontales, tous les ´el´ements finis et l’ensemble des noeuds j de
chaque ´el´ement e.
Les flux sur les cˆot´es sont calcul´es en consid´erant des ´el´ements finis lin´eaires `a une
dimension. Pour de tels ´el´ements finis l’int´egrale du flux le long d’un ´el´ement de
longueur L et situ´e entre les noeuds i et i + 1 se calcule par l’algorithme suivant
Φi = vi cos θ+ui sin θ
3
+ vi+1 cos θ+ui+1 sin θ
6
L
Φi+1 = vi cos θ+ui sin θ
6
+ vi+1 cos θ+ui+1 sin θ
3
L
(6.71)
o`u les termes sont repr´esent´es `a la figure 6.6.
6.6.6 Tests du sch´ema num´erique
Au cours des paragraphes suivants, nous testerons notre sch´ema de trans-
port en comparant les r´esultats avec ceux d’une solution analytique et d’autres
sch´emas num´eriques pour des probl`emes simples.
Autres sch´emas num´eriques
Le sch´ema de Taylor-Galerkin eul´erien explicite, d´enom´e FETG, est bas´e
sur les ´el´ements finis et a ´et´e d´ecrit par Chock [47]. Il consiste `a d´evelopper en
s´erie de Taylor, jusqu’au troisi`eme ordre, la valeur de la variable au temps t + ∆t
autour de la valeur au temps t. L’int´egration dans le temps est effectu´ee par la
m´ethode explicite d’Euler. FETG est un sch´ema qui est tout `a la fois pr´ecis, peu
dispersif et rapide en temps de calcul. Cependant il est limit´e par la condition
CFL.
Le sch´ema de Hughes et Brooks [124], ”Streamline Upwind Petrov Galerkin”
(SUPG), est ´egalement bas´e sur les ´el´ements finis mais les fonctions de pond´eration

161. 6.6: Advection 161
Figure 6.6: Sch´ema de calcul du flux sur l’´el´ement fronti`ere compris entre les
noeuds i et i + 1, de longueur L, et faisant un angle θ par rapport `a l’axe des x.
Les composantes (ui, vi) et (ui+1, vi+1) des vecteurs Ui et Ui+1 sont projet´ees sur
la normale `a l’´el´ement fronti`ere.
sont modifi´ees pour ajouter plus de poids dans la direction de l’´ecoulement, ce
qui r´eduit la dispersion lat´erale. Certaines modifications apport´ees par Hughes
[125] en ont fait un excellent sch´ema dans le cas o`u il y a des discontinuit´es dans
l’´ecoulement. Ce sch´ema est par cons´equent fr´equemment utilis´e en dynamique
des fluides pour l’´etude d’´ecoulement avec ondes de choc. Dans le cadre de la
chimie atmosph´erique ce sch´ema est trop coˆuteux en temps de calcul pour pouvoir
ˆetre utilis´e dans un mod`ele tridimensionnel.
Le sch´ema des fonctions chapeaux (CF) est bas´e sur les ´el´ements finis et
utilise des polynˆomes de Lagrange du premier degr´e comme fonctions de poids et
d’interpolation. Cette m´ethode est tr`es simple `a programmer et est tr`es rapide
d’ex´ecution. Cependant elle est limit´ee par les conditions CFL et ne peut ˆetre
utilis´ee que pour une grille structur´ee r´eguli`ere. D’autre part elle engendre des
oscillations importantes qui se propagent rapidement sur tout le domaine.
Les sch´emas semi-lagrangiens consistent comme nous l’avons expliqu´e
pr´ec´edemment en deux ´etapes. La premi`ere recherche l’origine des points de
grille le long des caract´eristiques sur un pas de temps. La deuxi`eme effectue les
interpolations n´ecessaires pour connaˆıtre la solution en ces points origines. La
m´ethode n’a pas de restriction sur le pas de temps mais elle n’est pas conservative.
Il existe diff´erentes versions de ce sch´ema et nous comparerons nos r´esultats avec
celle d´evelopp´ee par Smolarkiewicz et Rasch [218] pour des degr´es d’interpolation:

162. 162 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
deux (SLT2), quatre (SLT4) et six (SLT6). Leur sch´ema pr´eserve le signe de la
solution.
Nous appellons notre sch´ema SLFEM-Q9 ou SLFEM-T3 suivant qu’il
s’agit de rectangles `a neuf noeuds ou de triangles `a trois noeuds. Nous d´esignons
par SLFEM le sch´ema qui combine les deux types d’´el´ements.
Advection pure bidimensionnelle
Nous avons utilis´e le test classique [45] qui consiste `a advecter un cˆone
dans un mouvement circulaire sur un domaine bidimensionnel. La concentration
initiale est d´efinie en tous points de coordonn´ees (x, y) par,
c(t = 0) =
50(1 + cos πR
R0
) pour R ≤ R0
0 pour R ≥ R0
(6.72)
R = (x − x0)2 + (y − y0)2 (6.73)
o`u (x0, y0) est la position du maximum de la concentration.
Les composantes de vitesse sont d´efinies `a partir de la vitesse angulaire ω:
u = −ωy
v = +ωx (6.74)
Une rotation est effectu´ee en 240 pas de temps. Le domaine est form´e de 33 × 33
points espac´es r´eguli`erement d’une unit´e, et centr´e en (0,0). La distribution
conique du traceur est initialement centr´ee en (-8,0) avec une base circulaire de
rayon R0 = 4. A partir de cette grille, nous formons deux maillages, l’un form´e
d’´el´ements rectangulaires `a 9 noeuds et l’autre de triangles `a 3 noeuds. Dans le
cas du premier maillage nous effectuons un test avec et sans fixeur de conservation
de masse. Pour ces trois cas nous comparons les valeurs de quatre param`etres
avec celles obtenues pour les m´ethodes SLT2, SLT4, SLT6 et FETG par Chock
et Winkler [48]. Les param`etres sont:
Rapport de masse c(t)dΩ/ ce
(t)dΩ
Rapport de distribution de masse c(t)2
dΩ/ ce
(t)2
dΩ
Erreur absolue moyenne | c(t) − ce
(t) | dΩ/ dΩ
Erreur absolue maximum max(| c(t) − ce
(t) |)
(6.75)
o`u ce
est la solution exacte qui n’est autre que la solution initiale d´eplac´ee d’une
rotation ωt.
Le premier param`etre permet de v´erifier la conservation de la masse. Le deuxi`eme
donne la mesure de la dispersion num´erique. Le troisi`eme permet d’´evaluer

163. 6.6: Advection 163
l’importance des distorsions, quant au dernier il est sensible au d´ephasage et
`a la conservation des gradients.
Nous avons repris les valeurs de ces quatre param`etres aux figures (6.7a,
b, c, d) pour SLFEM-T3, SLFEM-Q9, SLFEM-Q9 avec fixeur de masse et pour
les quatre autres m´ethodes num´eriques: FETG, SLT2, SLT4 et SLT6. Nous
constatons que le sch´ema SLFEM-Q9 ne conserve pas la masse mais malgr´e que
la pr´ecision soit ´equivalente `a celle du sch´ema SLT2, les valeurs des param`etres se
rapprochent plus des sch´emas pr´ecis SLT4 ou SLT6. Le sch´ema SLFEM-T3 est
tr`es diffusif, mais par contre il conserve parfaitement la masse et distord moins les
r´esultats que SLT2. Le sch´ema FETG est sans conteste le plus pr´ecis. La figure
6.8a et b donne la distribution pour la m´ethode SLFEM-Q9 et SLFEM-Q9 avec
fixeur. Nous constatons que le minimum `a la base du cˆone cr´e´e artificiellement
par la m´ethode disparaˆıt en utilisant le fixeur au prix d’un accroissement de
la diffusion num´erique. La figure 6.8.c donne la distribution avec la m´ethode
SLFEM-T3 qui est comme on le voit excessivement diffusive, mais par contre
conserve la masse. En ce qui concerne le temps d’ex´ecution SLFEM-Q9 est 1.2,
4, 8, 19, 46 fois plus rapide que FETG, SLT2, SLT4, SLT6, SUPG. 11
Le sch´ema
num´erique que nous avons d´evelopp´e se compare donc bien aux autres m´ethodes
et il est de plus efficace `a l’ex´ecution.
Test de la m´ethode d’advection avec chimie
Dans un mod`ele de chimie-transport, les constituants chimiques r´eagissant
entre eux, leur concentration fluctue en fonction du transport suivant leur dur´ee
de vie. Un constituant tr`es r´eactif aura une dur´ee de vie trop courte pour ˆetre
transport´e (par exemple O(1
D)). Au contraire un constituant faiblement r´eactif
d´ependra essentiellement du transport. La distribution des autres constituants
d´ependra tout autant du transport que de la chimie (par exemple O3 et NOx).
Les distributions ´evoluant constamment, il en sera de mˆeme des gradients. Or
les sch´emas d’int´egration de l’advection conservent difficilement les gradients. En
cons´equence, pour tester l’aptitude de notre sch´ema num´erique `a conserver les
gradients en pr´esence de r´eactions chimiques, nous avons utilis´e le test de Hov et
al. [122]. Les auteurs consid`erent un ensemble de 10 r´eactions (tableau 6.10) o`u
interviennent 11 constituants chimiques ( tableau 6.11) dont les concentrations
initiales sont constantes sur le domaine `a l’exception de NO, NO2, ALD et HC
dont la distribution forme un cˆone `a base circulaire centr´ee en (-8,0) et de rayon
´egal `a 4. La concentration hors du cˆone repr´esente 2.5% de la valeur maximum
au sommet. L’´ecoulement ´etant purement rotatif, le transport ne devrait pas
modifier la distribution des concentrations, et donc ne pas avoir d’influence sur la
chimie. En effet si la concentration d’un constituant au temps t1 est n1 en (x1, y1)
11
Les calculs ont ´et´e effectu´es sur un IBM 560.

164. 164 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Figure 6.7: Evolution de 4 param`etres pour la comparaison de 6 m´ethodes
num´eriques de r´esolution de l’´equation d’advection: a. le rapport de conser-
vation de masse, b. le rapport de la distribution de masse, c. l’erreur moyenne
absolue, d. l’erreur absolue maximum.

165. 6.6: Advection 165
Figure 6.8: Distribution d’un traceur apr`es une rotation en utilisant le sch´ema
num´erique SLFEM-Q9 (interpolation quadratique sur maille `a 9 noeuds) sans
fixeur (a), avec fixeur (b) et SLFEM-T3 (interpolation lin´eaire sur maille trian-
gulaire).

166. 166 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Table 6.10: R´eactions chimiques et constantes cin´etiques. Les constantes de
r´eaction k s’expriment en [cm3
.s.molec−1
], alors que les constantes de photodis-
sociation j ont pour unit´e des [s−1
].
HC + OH → 4 RO2 + 2 ALD k1 = 6.0 × 10−12
ALD + hν → 2 HO2 + CO j2 = 7.8 × 10−5
× exp(−0.87/ cosθ)
RO2 + NO → NO2 + ALD + HO2 k3 = 8.0 × 10−12
NO + HO2 → NO2 + OH k4 = 8.3 × 10−12
NO2 + hν → NO + O3 j5 = 1.0 × 10−2
× exp(−0.39/ cosθ)
NO + O3 → NO2 + O2 k6 = 1.6 × 10−14
O3 + hν → O2 + O(1
D) j7 = 1.9 × 10−4
× exp(−1.9/ cosθ)
O(1
D) + H2O → 2 OH k8 = 2.3 × 10−10
NO + OH → HNO3 k9 = 1.0 × 10−11
CO + OH → CO2 + HO2 k10 = 2.9 × 10−13
sa concentration au temps t2 sera pour l’advection seulement n1 en (x2, y2) et
pour la chimie sans transport n2 en (x1, y1). Une rotation est effectu´ee en 24
heures d´ecompos´ees en 576 pas de temps. Le domaine est form´e de 16 × 16
´el´ements carr´es `a 9 noeuds (33 × 33 noeuds au total), de cˆot´e ´egal `a 2 unit´es et
centr´e en (0,0). Les composantes de la vitesse en un point (x, y) sont donn´ees
par les relations (6.74). Les valeurs `a la base et au sommet du cˆone de la concen-
tration initiale et apr`es 24 heures d’int´egration chimique sont donn´ees au tableau
6.11. Le rapport entre la solution avec chimie et advection et la solution avec
chimie uniquement, au points (9,17) pour les 10 constituants chimiques est donn´e
au tableau 6.12 pour SLFEM-Q9, SLFEM-Q9 avec fixeur de masse, FETG, FC,
SUPG, SLT6. Except´e pour NO pour lequel notre sch´ema surestime de 300%
la valeur, les r´esultats sont ´equivalents `a SLT6. D’autre part, il n’y a pas de
d´ephasage comme pour SUPG ni d’oscillations (Chapeau et SUPG) et de valeurs
n´egatives (SUPG). Les diff´erences de rapport entre constituants s’expliquent par
une variation diff´erente de leur distribution. Pour les oxydes d’azote, la destruc-
tion chimique inverse le pic et la concentration `a la base est plus ´elev´ee apr`es une
r´evolution (figure 6.9a et 6.10b). Sur les figures 6.10, la valeur au centre de la
grille correspond `a la valeur exacte, ce qui cr´ee cet aspect visuel particulier. En
effet, comme nous l’avons vu la m´ethode des ´el´ements finis donne la valeur exacte
aux noeuds, or le centre de rotation est fixe et l’interpolation se r´esume `a prendre
la valeur en ce noeud o`u finalement il n’y a que la chimie qui agit. Le monoxyde
d’azote ´etant essentiellement d´etruit par l’ozone, la diffusion num´erique d´ecroˆıt
la valeur maximum de celui-ci et ´egalement le taux de destruction de NO cr´eant
un rapport sup´erieur `a 1. La mˆeme chose est vraie pour NO2 (figure 6.9b et
6.10b) mais son taux de destruction est plus faible que celui de NO et sa valeur

167. 6.6: Advection 167
Figure 6.9: Distribution, en consid´erant uniquement la chimie, de la concentra-
tion: (a) du monoxyde d’azote (NO), (b) du dioxyde d’azote (NO2), (c) de l’ozone
(O3) et (d) de l’ald´ehyde (ALD).

168. 168 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Figure 6.10: Distribution, en consid´erant la chimie et l’advection r´esolue par la
m´ethode SLFEM-Q9 avec fixeur, de la concentration: (a) du monoxyde d’azote
(NO), (b) du dioxyde d’azote (NO2), (c) de l’ozone (O3) et (d) de l’ald´ehyde
(ALD).

169. 6.6: Advection 169
Table 6.11: Valeurs des concentrations initiales et apr`es 24 heures d’int´egration
de la chimie exprim´ee en [molec.cm3
]
Concentrations initiales Concentrations apr`es chimie
Constituant Base Sommet Base Sommet
NO 2.5 × 109
1.0 × 1011
2.47 × 105
9.75 × 103
NO2 2.5 × 109
1.0 × 1011
4.66 × 107
2.52 × 107
HC 2.5 × 109
1.0 × 1011
1.36 × 108
4.32 × 108
ALD 1.25 × 1010
5.0 × 1011
1.68 × 1010
6.74 × 1011
O3 5.0 × 1011
5.75 × 1011
1.15 × 1012
CO 1.0 × 1012
8.66 × 1011
1.11 × 1012
HO2 1.0 × 106
6.39 × 1010
8.48 × 1011
RO2 1.0 × 106
1.53 × 109
6.39 × 1010
OH 1.0 × 105
2.66 × 106
3.60 × 106
O(1
D) 1.0 × 103
4.76 × 100
9.52 × 100
H2O 2.5 × 1015
2.5 × 1015
finale est plus proche de l’unit´eq que pour NO. Dans le cas de l’ald´ehyde (figure
6.9d et 6.10d), constituant moins r´eactif, le rapport inf´erieur `a l’unit´e est dˆu `a la
diffusion num´erique. La mˆeme remarque s’applique pour l’ozone (figure 6.9b et
6.10b). L’atome d’oxyg`ene O(1
D) est `a l’´equilibre photochimique avec O3 ce qui
explique la valeur identique de leur rapport. La diff´erence des valeurs du rapport
au tableau 6.12 si le fixeur de masse est appliqu´e ou non est surtout marqu´ee pour
les constituants `a longue dur´ee de vie chimique qui pr´esentent de forts gradients
de concentration. Le facteur α de la relation (6.68) est de l’ordre de 10−4
pour le
NO. L’atome d’oxyg`ene et le radical hydroxyle ont une tr`es courte dur´ee de vie,
inf´erieure `a la seconde, et ne sont donc pas sensibles au transport et par voie de
cons´equence la correction due au transport advectif est n´egligeable.
En r´esum´e, nous voyons que l’erreur produite par la diffusion num´erique
sur la concentration de constituants chimiques est de l’ordre de 30% et dans
certains cas atteint 300%. Il faut cependant noter que les gradients dans ce test
sont tr`es ´elev´es. Mais avec notre grille tr`es fine de tels gradients peuvent exister
dans la r´egion d’Honolulu o`u les ´emissions de monoxyde de carbone et de CO
sont ´elev´ees. Cependant de telles conditions n’existent qu’`a la surface terrestre
et la nuit, quand il y a peu de m´elange au sein de la couche limite plan´etaire.

170. 170 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
Table 6.12: Valeurs du rapport entre la concentration avec chimie et advec-
tion et la chimie uniquement au point de grille (9,17) pour diff´erentes m´ethodes
num´eriques
Constituant SLFEM-Q9 SLFEM-Q9 FETG CF SUPG SLT6
fixeur
NO 3.01 3.06 1.17 1.1 0.01,2
2.5
NO2 1.34 1.39 1.03 1.02 0.7 1.24
HC 0.88 0.92 1.0 1.02 1.23 0.82
ALD 0.4 0.4 0.87 0.9 1.16 0.47
O3 0.71 0.71 0.95 0.96 1.12 0.76
CO 0.87 0.87 0.96 0.97 1.02 0.86
HO2 0.45 0.45 0.88 0.91 1.16 0.51
RO2 0.36 0.38 0.83 0.86 1.09 0.41
OH 0.86 0.86 0.99 0.99 1.072
0.91
O(1
D) 0.71 0.71 0.95 0.96 1.12 0.76
1. Valeur n´egative mise `a z´ero.
2. Le maximum n’est pas localis´e au point (9,17).
6.7 Diffusion verticale
Le transport vertical par diffusion turbulente est exprim´e, en coordonn´ee
σ, par l’´equation suivante
∂fi
∂t
=
1
ρ
∂
∂σ
ρKσσ
∂fi
∂σ
(6.76)
o`u Kσσ est le coefficient de diffusion turbulente en coordonn´ee verticale σ. Il se
calcule `a partir de Km suivant la relation (6.25).
La discr´etisation de cette ´equation est r´ealis´ee par la m´ethode implicite
des diff´erences finies [81] qui est inconditionnellement stable. Pour les conditions
aux limites on impose un flux nul ou non nul `a la surface `egal au taux d’´emission
du gaz consid´er´e et un flux nul au sommet except´e pour O3 et HNO3 o`u leurs
rapports de m´elange sur les deux derniers niveaux sont impos´es. Les valeurs
d’´emission `a la surface seront ´etablies au chapitre suivant.
6.8 Convection
Au chapitre pr´ec´edent nous avons montr´e comment calculer le flux mas-
sique dans les nuages et la concentration des gaz `a l’aide d’une param´etrisation
bas´ee sur celle de Feichter et Crutzen [77] suivant des d´eveloppements repris

171. 6.9: Les conditions initiales et aux limites 171
en Annexe. Pour tester la param´etrisation du transport convectif, il est clas-
siquement fait usage du traceur istopique 222
Rn dont la distribution verticale est
modifi´ee de mani`ere caract´eristique par les nuages convectifs: le maximum sec-
ondaire au milieu de la troposph`ere libre est dˆu au transport convectif (cf. figure
2.14).
6.9 Les conditions initiales et aux limites
Les variables chimiques sont initialis´ees `a partir des distributions de con-
centration calcul´ees par le mod`ele tridimensionnel global de chimie-transport de la
troposph`ere IMAGES [179]. Etant donn´e que nous utilisons le mˆeme m´ecanisme
chimique d´evelopp´e pour IMAGES, les valeurs des concentrations interpol´ees
sur notre grille sont proches de l’´equilibre quasi-stationnaire. Les r´esultats de
ce mod`ele sont des moyennes mensuelles distribu´ees sur une grille de 5o
× 5o
(∼ 500 × 500 km `a l’´equateur). Les variables m´et´eorologiques utilis´ees par ce
mod`ele sont obtenues `a partir de climatologies mensuelles.
Les conditions aux limites seront envisag´ees au prochain chapitre.
6.10 Conclusions
Au cours de ce chapitre nous avons examin´e le d´eveloppement d’un
mod`ele num´erique de r´esolution de l’ensemble des ´equations de continuit´e des
constituants chimiques de la troposph`ere.
Nous avons en premier lieu d´efini le domaine d’int´egration qui a la forme
d’un rectangle sur le plan de projection st´er´eopolaire, couvrant l’h´emisph`ere nord
et une partie de l’h´emisph`ere sud. Sur ce plan de projection nous avons d´efini
un syst`eme d’axes cart´esiens. La distribution des points de grille est cr´e´ee pour
caract´eriser les sources d’´emissions globales et locales. La densit´e des points de
grille est en cons´equence ´elev´ee autour d’Hawaii et diminue au fur et `a mesure
qu’on s’en ´eloigne. Les points forment alors un ensemble non-structur´e dans la
r´egion d’Hawaii et structur´e ailleurs. Nous avons ensuite mailler la grille `a l’aide
de triangles `a 3 noeuds et de rectangles `a 9 noeuds. Cette grille et ce maillage
sont reproduits sur 23 niveaux verticaux.
La r´esolution des ´equations de continuit´e sur une telle grille utilise la
technique de s´eparation des processus chimique et de transport: chimie, advec-
tion, diffusion, convection. Nous avons commenc´e par d´efinir un mod`ele chim-
ique form´e de 46 constituants et de 138 r´eactions photochimiques. La m´ethode
de r´esolution du syst`eme diff´erentiel d’´equations chimiques non-lin´eaires est celle
d’Euler implicite.
L’advection est r´esolue par un sch´ema semi-lagrangien utilisant la m´ethode des

172. 172 Chapitre 6: D´eveloppement d’un mod`ele de chimie-transport
´el´ements finis. Ce sch´ema a ´et´e ´evalu´e `a l’aide de plusieurs tests standards.
La diffusion horizontale est r´esolue par une technique explicite dans le temps et
par la m´ethode des ´el´ements finis pour les termes d’espace. La diffusion verticale
utilise une m´ethode implicite dans le temps et les diff´erences finies suivant la
verticale.
La convection par les nuages convectifs profonds est param´etris´ee par la m´ethode
de Feichter et Crutzen [77].
Les conditions initiales du mod`ele de chimie-transport proviennent d’un
mod`ele tridimensionnel de chimie-transport de la troposph`ere globale IMAGES
d´evelopp´e par M¨uller et Brasseur [179]. Les conditions aux limites seront dis-
cut´ees au chapitre suivant.
Remarque: Il est ´evident que la param´etrisation de certaines ´equations et con-
ditions au limites introduit un certain empirisme qui peut affecter les r´esultats
num´eriques finaux. Cependant la m´ethode de r´esolution num´erique ´etablie pour-
rait ˆetre facilement utilis´ee sans modification majeure lorsque des param´etrisations
plus rigoureuse seront disponibles.

173. Chapter 7
Conditions aux limites du mod`ele
de Chimie-Transport
7.1 Introduction
Les flux turbulents des compos´es chimiques `a la surface (w ni )s sont
d´ecompos´es en un flux d’´emission et une perte par d´epˆot sec:
(w ni )s = −vdini + ϕi (7.1)
o`u vdi est appel´e la vitesse de d´epˆot sec (cm.s−1
), ϕi est l’´emission du com-
pos´e i (molec.cm−2
.s−1
), et ni est la concentration du compos´e i `a l’altitude
z (molec.cm−3
).
Pour les ´emissions nous nous sommes servis des cartes d’´emission `a l’´echelle glob-
ale, d´evelopp´ees par M¨uller [178] et des cartes `a haute r´esolution que nous avons
´etablies pour la r´egion d’Hawaii. En nous servant d’une analogie avec les cir-
cuits ´electriques propos´ees par Wesely [239], les vitesses de d´epˆot sec ont ´et´e
param´etris´ees en tous points du domaine.
Dans ce chapitre, nous d´ecrivons l’obtention des cartes d’´emission `a Hawaii et
la m´ethode de param´etrisation de la vitesse de d´epˆot sec. Nous terminerons en
donnant la m´ethode d’interpolation des donn´ees sur notre grille.
7.2 Emissions des gaz dans la r´egion d’Hawaii
On distingue en g´en´eral deux cat´egories d’´emissions:
• les sources technologiques
– combustion des mati`eres fossiles et activit´es industrielles
173

174. 174 Chapitre 7: Conditions aux limites
– la combustion de la biomasse qui comprend
∗ la d´eforestation
∗ les feux de savane et de forˆet
∗ les d´echets de l’agriculture
∗ combustion du bois
• les sources naturelles
– par la v´eg´etation
– par les sols
– par les oc´eans
– par les animaux
– par les volcans
Nous nous sommes servis des cartes d’´emissions globales ´etablies pour l’ann´ee
1984 par M¨uller [178] sur une grille de 5o
× 5o
qui donnent les valeurs mensuelles
moyennes des principales ´emissions.
Les donn´ees n´ecessaires pour ´etablir les cartes d’´emissions `a Hawaii ont
´et´e recueillies de l’Atlas d’Hawaii [11] et report´ees sur une grille de 2.5’×2.5’
(∼ 4 × 4 km). Certains ´ev´enements particuliers relev´es par le journal de bord
de Ridley (communication personnelle) tels que les feux de broussailles ou les
activit´es volcaniques ont ´et´e pris en compte.
Emissions anthropiques
Les ´emissions anthropiques incluent l’utilisation et l’extraction de mati`ere
fossiles, l’activit´e industrielle, et le stockage de d´echets. Elles ont ´et´e d´etermin´ees
par M¨uller [178] `a partir de donn´ees statistiques sur une surface de 5o
×5o
couvrant
Hawaii. La saisonalit´e des ´emissions est li´ee `a celle de la temp´erature de l’air.
Celle-ci ´etant pratiquement constante tout au long de l’ann´ee dans le Pacifique
central nous consid´erons que le flux est constant. Nous avons redistribu´e ces
´emissions en fonction de la densit´e de population ´etablie par cellule de 2.5 ×2.5 :
φ2.5×2.5(x, y) = ∆80−90αh(x, y) (7.2)
o`u
h(x,y) est la densit´e de population (personnes.km−2
) repr´esentative de
1980,
∆80−90 est le facteur de correction qui tient compte du changement total
de la population entre 1980 et 1990,

175. 7.2 Emissions des gaz 175
Table 7.1: Aire et population des ˆıles de l’archipel d’Hawaii.
Iles Surface (km2
) Population
Nord-Ouest 28 31
Kauai 1,624 38,856
Niihau 189 226
Hawaii 10,458 92,053
Maui 1,887 62,823
Molokai 676 6,049
Kahoolawe 116 0
Lanai 361 2,119
Oahu 1,574 762,534
Total 15,072 925,578
α est le facteur de proportionnalit´e, exprim´e en mol´ecules par nombre
d’habitant par seconde (molec.hab−1
.s−1
), d´etermin´e par
α =
φIMAGES × S5×5
Poptot
(7.3)
o`u
φIMAGES est le flux total calcul´e pour le mod`ele IMAGES sur une cellule
de 5o
× 5o
(molec.cm−2
.s−1
),
S5×5 = 2.9 × 105
km2
est l’aire d’une surface de 50
× 5o
`a 20o
de latitude
Nord1
,
Poptot est la population totale des ˆıles d’Hawaii en 1980.
La population et l’aire pour chacune des ˆıles de l’archipel d’Hawaii, obtenues `a
partir de l’Atlas d’Hawaii [11] sont donn´ees au tableau 7.1. En 1990, la popula-
tion totale ´etait de 1,108,229 habitants, soit une augmentation de 15% en dix ans.
En ne consid´erant que les six ˆıles les plus `a l’est, on obtient 925,578 habitants
en 1980 et 1,063,296 en 1990, pour une aire de 15,072 km2
. Le coefficient ∆80−90
vaut donc 1.15. La distribution de la densit´e de population pour chacune des
ˆıles d’Hawaii est donn´ee `a la figure 7.1. La population int´egr´ee sur la grille de
2.5 × 2.5 , en supposant qu’il y a une variation lin´eaire entre points de grille,
est de 929,516 habitants soit une diff´erence de 0.4%. Les valeurs d’´emissions
1
La surface S d’une partie de sph`ere comprise entre deux longitudes et deux latitudes dis-
tantes de α radians est donn´ee par:
S = R2
α sin(α) cos(Φ) (7.4)
o`u R=6371 km et Φ est la latitude en radians.

176. 176 Chapitre 7: Conditions aux limites
Figure 7.1: Densit´e de la population (hab./km2
) sur les ˆıles d’Hawaii.

177. 7.2 Emissions des gaz 177
Table 7.2: Facteurs d’´emissions anthropiques des compos´es gazeux.
Compos´e ΦIMAGES α
(molec.cm−2
.s−1
) (molec.hab−1
.s−1
)
C2H6 5.681 × 107
1.549 × 107
CO 9.1 × 1010
2.7 × 1010
CH4 1.9 × 1010
5.4 × 109
NOx 2.3 × 109
6.2 × 108
Table 7.3: Facteur d’´emission des feux de broussailles exprim´e en grammes
d’atomes de carbone par kilogramme de mati`ere brˆul´ee (g C.kg−1
) d’apr`es An-
dreae 1991.
Compos´e Emission (g C.kg−1
)
CO 100
CH4 11
NMHC 7
NOx 2.1
´etablies par M¨uller [178] pour cinq compos´es gazeux et les coefficients α corre-
spondants sont donn´es au tableau 7.2. La figure 7.2 donne la distribution du flux
de m´ethane par les ´emissions anthropiques. Les valeurs ´etant proportionnelles `a
la densit´e de population, nous notons imm´ediatement les maxima associ´es aux
centres urbains tels qu’`a Honolulu (Oahu), Wailuku (Maui) et dans une moindre
mesure Hilo (Hawaii). A l’oppos´e, nous constatons un minimum sur les deux
volcans principaux d’Hawaii.
Emissions due `a la combustion de la biomasse
A Hawaii, la combustion de la biomasse concerne principalement les feux
de broussailles et la combustion des d´echets de l’agriculture. Le 7 mai 1992
(troisi`eme s´erie de mesures MLOPEX-II), il y eut un important feu de broussailles
qui a d´ebut´e vers 13h00 et fut circonscrit vers minuit, brˆulant 768 hectares dans
la r´egion de Kawaihae (nord-ouest de l’ˆıle d’Hawaii). Pour ´evaluer les flux de gaz
´emis par les feux de broussailles, nous consid´erons, d’apr`es Seiler et Crutzen [211],
que 25% de la mati`ere s`eche de la biomasse au-dessus du sol, qui repr´esente 75%
de la biomasse totale, brˆule avec un facteur d’´emission constant (tableau 7.3).
La biomasse totale de chaque ´ecosyst`eme de la classification de Henderson-Sellers

178. 178 Chapitre 7: Conditions aux limites
Figure 7.2: Emission anthropique du monoxyde de carbone pour les ˆıles d’Hawaii
[molec.cm−2
.s−1
].

179. 7.2 Emissions des gaz 179
[110] a ´et´e estim´ee par Box [30] et est donn´ee au tableau 7.4. La figure 7.3 donne
le flux d’´emission de CO par les feux de broussailles lors de l’incendie du 7 mai
1992.
Figure 7.3: Emission du monoxyde de carbone par le feu de broussailles `a Hawaii
en mai 1992 en [molec.cm−2
.s−1
].
Hawaii est le premier producteur des Etats-Unis de canne `a sucre. Les
champs de canne `a sucre sont brˆul´es juste avant la r´ecolte pour d´etruire les
tiges et les feuilles. La p´eriode de moissonnage a lieu tous les quatre ans [29].
Nous donnons au tableau 7.5 la surface d’exploitation de la canne `a sucre et la
production annuelle pour chacune des ˆıles, ainsi que le flux de CO correspondant.
Nous voyons que l’ˆıle d’Hawaii est le principal producteur. Pour calculer le flux
de CO nous avons suppos´e que 5% de la production anuelle a ´et´e brˆul´ee, et que le
facteur d’´emission du monoxyde de carbone (CO) est de 35 kg de CO par tonne
de mati`ere brˆul´ee [54]. Les flux sont ensuite pond´er´es par un facteur mensuel
qui est proportionnel `a la temp´erature moyenne et inversement proportionnel `a

180. 180 Chapitre 7: Conditions aux limites
Table 7.4: Biomasse s`eche des 14 ´ecosyst`emes de Henderson-Sellers, 1986.
Ecosyst`emes Biomasse (kg.m−2
)
D´esert 0.02
Tundra 0.6
Prairie 1.6
Prairie broussailleuse 6
Prairie arbor´ee 15
Forˆet de feuillus 35
Forˆet d’´epineux 35
Forˆet tropicale 45
Glace 0
Culture 1
Marais 15
Semi-d´esert 0.7
Sol nu 0.5
Surface d’eau 0
Table 7.5: Emissions de CO par la combustion des champs de canne `a sucre pour
chacune des ˆıles.
Iles Surface des champs Production annuelle Flux de CO
de canne `a sucre (km2
) de canne `a sucre (106
kg.an−1
) (molec.cm−2
.s−1
)
Hawaii 990 3,718 4.48 × 1011
Maui 240 2,278 2.9 × 1011
Molokai 0 0 0
Kahoolawe 0 0 0
Lanai 0 0 0
Oahu 220 33 4.6 × 109

181. 7.2 Emissions des gaz 181
l’accumulation des pr´ecipitations sur un mois. Nous avons repris `a la figure 7.4
le taux d’´emission du CO par la combustion des d´echets de canne `a sucre. Les
´emissions sont localis´ees dans les r´egions cˆoti`eres, et celles au nord-est d’Hawaii
peuvent directement influencer les mesures `a l’Observatoire de Mauna Loa par
les vents dominants du nord-est.
Figure 7.4: Emission du CO par la combustion des d´echets de canne `a sucre
exprim´ee en [molec.cm−2
.s−1
].
Emissions d’hydrocarbures par la v´eg´etation
Les ´emissions d’hydrocarbures par la v´eg´etation sont reli´ees `a la biomasse,
et sont affect´ees par des facteurs d´ependant de l’environnement. Chaque type
d’´ecosyst`eme est suppos´e avoir, dans des conditions similaires de temp´erature,
de pr´ecipitation et d’ensoleillement, le mˆeme taux d’´emission et le mˆeme taux
de croissance (productivit´e primaire nette). Nous appelerons ces conditions stan-

182. 182 Chapitre 7: Conditions aux limites
dards. La productivit´e primaire nette standard (NPPstd
) a ´et´e ´etablie par Guen-
ther et al. [97] pour les 72 types de v´eg´etation de la classification d’Olson
[185]. En utilisant une table de conversion de la classification d’Olson vers nos
14 ´ecosyst`emes ´etablie par Henderson-Sellers et al. [110], et en connaissant la
r´epartition de ces 14 ´ecosyst`emes `a Hawaii, nous pouvons d´eterminer la NPPstd
en chaque point de grille. L’effet climatique est alors pris en compte en calculant
une NPP annuelle non-standard qui est le minimum entre deux fonctions [142]:
NPP = 3000 × min(f1, f2) (g.m−2
.an−1
) (7.5)
Nous avons modifi´e les formules de Lieth [142] pour tenir compte d’une variation
mensuelle. Pour ce faire nous calculons une NPP mensuelle par la formule de
Lieth divis´ee par 12. Les fonctions f1 et f2 sont respectivement d´ependantes
de la temp´erature mensuelle moyenne Tm (o
C) et de l’accumulation mensuelle
moyenne Precm (mm.an−1
)2
et sont donn´ees par
f1 =
1
1 + exp(1.315 − 0.119 × Tm)
f2 = 1 − exp(−0.000664 × Precm) (7.6)
Les ´emissions d’isopr`ene (C5H8) et de monoterp`ene (C10H16) par la v´eg´etation
d´ependent de chaque esp`ece v´eg´etale: les arbres `a feuilles caduques ´emettent prin-
cipalement de l’isopr`ene alors que les conif`eres lib`erent des monoterp`enes [65].
Certains arbres, tels que le pin et l’eucalyptus produisent tout autant d’isopr`ene
que de monoterp`ene [199]. L’isopr`ene est ´emis quand les stomates sont ouverts
c’est-`a-dire pendant la journ´ee, alors que les terp`enes sont ´emis au travers des cu-
ticules quand ceux-ci sont secou´es soit par un pr´edateur soit par le vent. Le feuil-
lage faisant partie de la NPP, il semble logique de relier les flux d’hydrocarbures `a
la NPP. Pour tenir compte des facteurs climatiques, on distingue un flux standard
`a 30o
C correspondant `a NPPstd
, et le flux moyen mensuel associ´e `a la NPP. Ces
variables sont reli´ees par les formules de Lamb [135]:
φC5H8 = φstd
C5H8
NPP
NPPstd
100.0416(T−30)
(7.7)
φC10H16 = φstd
C10H16
NPP
NPPstd
100.0568(T−30)
(7.8)
o`u
T est la temp´erature instantan´ee en degr´e Celsius,
NPPstd
et φstd
sont respectivement la production primaire nette et le
flux d’un compos´e gazeux dans les conditions standards `a 30o
C.
2
Les formules de Lieth ont ´et´e ´etablies en tant que valeur annuelle moyenne. C’est pourquoi
nous gardons les mˆemes unit´es bien qu’il s’agisse de valeurs mensuelles moyennes.

183. 7.2 Emissions des gaz 183
Les flux de C5H8 et C10H16 dans les conditions standards ont ´et´e calcul´es suivant
la formulation de M¨uller et Brasseur [179] qui tient compte du type d’´ecosyst`eme.
Les valeurs de Tm et de Precm sont d´eduites des moyennes observ´ees en 67 stations
[11]. A ces stations nous avons joint des points qui encadrent toute la r´egion pour
permettre les interpolations spatiales (figure 7.5). En ces points nous utilisons les
valeurs mensuelles moyennes sur 10 ans `a 1000 mb de la temp´erature calcul´ees par
Trenberth [226], et les valeurs de pr´ecipitation moyenne compil´ees par Shea [212].
Les figures 7.6 et 7.7 donnent respectivement la distribution des pr´ecipitations et
de la temp´erature mensuelles moyennes. Les valeurs de NPP sont contraintes par
les valeurs minimales de ces deux distributions, comme nous le constatons sur la
figure 7.8 donnant la production primaire nette pour le mois de mai.
Figure 7.5: Triangulation pour l’interpolation de donn´ees n´ecessaires au calcul
de la temp´erature et des pr´ecipitations mensuelles et annuelles moyennes. Les
points correspondent aux 67 stations de mesure dispers´ees sur les ˆıles d’Hawaii
et 8 points sur les cˆot´es correspondant aux points de grille du ECMWF.
La variation diurne des flux d’isopr`ene (figure 7.9), li´ee `a la photo-
synth`ese, est simul´ee suivant M¨uller et Brasseur [179] par une fonction sinusoidale

184. 184 Chapitre 7: Conditions aux limites
Figure 7.6: Pr´ecipitation mensuelle moyenne [mm.mois−1
] pour le mois de mai `a
Hawaii.

185. 7.2 Emissions des gaz 185
Figure 7.7: Temp´erature mensuelle moyenne [K] pour le mois de mai `a Hawaii.

186. 186 Chapitre 7: Conditions aux limites
Figure 7.8: Production primaire nette [g.mois−1
.m−2
] pour le mois de mai `a
Hawaii.

187. 7.2 Emissions des gaz 187
`a la quatri`eme puissance. Quant `a l’α-pin`ene, ses ´emissions ne d´ependent pas de
la photosynth`ese et elles sont fix´ees la nuit `a 70% de leur valeur de jour.
Figure 7.9: Emission d’isopr`ene moyenn´ee sur une journ´ee pour le mois de mai
[molec.cm−2
.s−1].
Les ´emissions des autres hydrocarbures sont ´evalu´ees en supposant qu’elles
sont ´egalement proportionnelles `a la NPP mais corrig´ees par un facteur tel que
l’´emission globale corresponde `a des valeurs ´etablies dans la litt´erature. Les fac-
teurs de correction donn´es au tableau 7.6 sont dimensionnels car non seulement
ils assurent la valeur de l’´emission globale mais ´egalement convertissent les unit´es
de la NPP (kg.m−2
.mois−1
) en flux de mol´ecules (molec.cm−2
.s−1
).
Autres ´emissions naturelles
Les autres sources d’´emissions naturelles que nous consid´erons sont les
sols, les oc´eans et le b´etail. Les activit´es biologiques (nitrification et d´enitrification)

188. 188 Chapitre 7: Conditions aux limites
Table 7.6: Facteurs d’´emission biog´enique de certains hydrocarbures.
Compos´e Facteur d’´emission
(molec.kg−1
)
CH4 1.07 × 109
C2H4 3.07 × 1010
C3H6 4.09 × 109
C2H6 5.73 × 109
et non-biologiques (d´ecomposition du dioxyde d’azote) dans les sols produisent
et d´egagent vers l’atmosph`ere du NO. L’intensit´e de ces activit´es d´epend essen-
tiellement de la temp´erature, du contenu en eau et du type de sol, ainsi que de
la v´eg´etation. Pour rendre compte de la production de NO par les sols il serait
n´ecessaire d’utiliser un mod`ele tr`es complexe de chimie h´et´erog`ene. Nous avons
pr´ef´er´e utiliser des param´etrisations simples qui rendent compte correctement de
la production globale, en particulier celles d´evelopp´ees par M¨uller et Brasseur
[179]. Suivant ces param´etrisations il faut distinguer entre la forˆet tropicale et
les autres ´ecosyst`emes. Le flux de NO ´emis par les sols dans les forˆets tropicales
pour un mois m est param´etris´e par la formule
φm = 1.14 × 1011
× 12 × NPP
12
k=1
1
P reck
1
P recm
(molec.cm−2
.s−1
) (7.9)
o`u
Preck est le taux de pr´ecipitation pendant le mois k (mm.mois−1
),
NPP est la productivit´e primaire nette (kg.m2
.mois−1
).
Les valeurs d’´emission sont des moyennes mensuelles et leurs variations diurnes
sont n´eglig´ees. La figure 7.10 donne les ´emissions de NO pour le mois de mai,
dont les maxima co¨ıncident avec les zones de forˆet tropicale. Pour les autres types
d’´ecosyst`emes, la param´etrisation utilis´ee est la suivante
φm = 4.3 × 109
× 10(0.049Tm−0.83)
(molec.cm−2
.s−1
) (7.10)
o`u Tm est la temp´erature mensuelle moyenne au cours du mois m exprim´e en
degr´e Celsius.
Le volcan actif de Kilauea au sud-est de Mauna Loa ´emet en perma-
nence un certain nombre de gaz. Les valeurs d’´emissions utilis´ees proviennent
des valeurs moyennes observ´ees pendant 27 ann´ees par Gerlach et Graeber [87].
Nous avons repris la liste des gaz ´emis par le volcan ainsi que le flux d’´emission
au tableau 7.7. Except´e pour la vapeur d’eau, aucun des gaz de cette liste n’est

189. 7.2 Emissions des gaz 189
Figure 7.10: Emission de NO par les sols pour le mois de mai [molec.cm−2
.s−1].
Table 7.7: Flux moyen d’´emission de quelques gaz par le volcan de Kilauea
(Hawaii).
Compos´e Emission (tonne.jour−1
)
H2O 560
CO2 3740
S 470
Cl 2
F 1

190. 190 Chapitre 7: Conditions aux limites
Table 7.8: Flux de m´ethane par la production ent´erique du b´etail pour chacune
des ˆıles et les donn´ees utilis´ees pour leur calcul.
Iles Surface des Production annuelle Nombre de Flux de CH4
pˆaturages (km2
) de viande (kg.an−1
) boeufs (molec.cm−2
.s−1)
Hawaii 1513.2 8.26 × 106
27, 500 2.37 × 1010
Maui 742.7 1.84 × 106
6000 2.84 × 1010
Molokai 320.3 0.79 × 106
2500 2.6 × 1010
Kahoolawe 0 0 0 0
Lanai 0 0 0 0
Oahu 99.8 7.26 × 106
24, 000 3.34 × 1011
consid´er´e dans notre mod`ele. D’autre part le calcul de la concentration de la
vapeur d’eau par le mod`ele `a m´eso-´echelle MM5 ne tient pas compte de la source
volcanique. Nous ne consid´erons donc pas l’effet des ´emissions du volcan Kilauea
sur la composition chimique dans notre mod`ele.
La production ent´erique du m´ethane par le b´etail est reconnue comme
une source non-n´egligeable (15 `a 25% de toutes les sources de CH4) `a l’´echelle
globale [52]. La production par tˆete de b´etail est estim´ee `a 55 kg par ann´ee. Nous
connaissons la distribution des pˆaturages sur une grille de 2.5 × 2.5 `a partir de
l’Atlas d’Hawaii [11]. D’autre part, ce mˆeme Atlas fournit la production de viande
de boeuf annuelle pour chacune des ˆıles exprim´ee en (kg.an−1
). En estimant que
300 kg de viande sont utilis´es par boeuf, nous pouvons estimer le nombre de
boeufs pour chacune des ˆıles qui sont distribu´es en fonction de la surface des
pˆaturages. Connaissant alors la fraction non enti`ere de boeufs en chaque point
de la grille et le flux par boeuf (55 kg.an−1
), nous pouvons ´etablir la distribution
du flux de m´ethane (molec.cm−2
.s−1
) par point de grille. Le tableau 7.8 r´esume
l’ensemble des donn´ees utilis´ees ainsi que le flux de CH4 pour chacune des ˆıles.
En combinant les ´emissions globales de M¨uller [178] et nos cartes d’´emission,
nous obtenons pour le CO les distributions globales, en tenant compte de toutes
les sources, repr´esent´ees `a la figure 7.11 pour les quatre mois simul´es. Nous con-
statons que les maxima sont localis´es sur les r´egions industrielles d’Europe, de
l’Est de l’Asie et des Etats-Unis o`u les valeurs avoisinnent 1.5× 10−3
g.m−2
.h−1
(∼ 9 molec.cm−2
.s−1
).
7.3 Vitesse de d´epˆot sec
La destruction de l’ozone `a la surface terrestre est un facteur d´eterminant
la concentration de l’ozone dans la basse atmosph`ere [82]. Les conditions qui

191. 7.3 Vitesse de d´epˆot sec 191
Figure 7.11: Emission du CO `a la surface terrestre (mg.m−2
.heure−1
) pour les
mois de: a) Octobre, b) Janvier, c) Mai et d) Juillet.

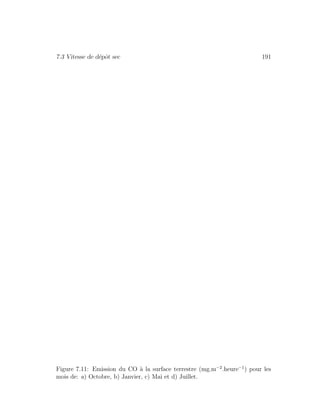
192. 192 Chapitre 7: Conditions aux limites
Figure 7.12: Diagramme sch´ematique des diff´erentes r´esistances au transfert d’un
gaz vers la v´eg´etation (A), la partie basse de la canop´ee (B) et le sol (C), d’apr`es
Wesely (1989)
d´eterminent la destruction d’ozone par d´epˆot sec ont ´et´e d´ecrites par Regener
(1975): le taux de destruction est proportionnel `a la concentration de l’ozone et
`a l’altitude au-dessus de la surface. La constante de proportionnalit´e est appel´ee
vitesse de d´epˆot sec [82] et est invariante pour un type de surface dans une con-
dition atmosph´erique donn´ee. Nous allons au cours de ce paragraphe d´ecrire la
param´etrisation de cette vitesse due `a Wesely [239].
L’approche g´en´eralement adopt´ee consiste `a d´evelopper un mod`ele ´electrique
analogique o`u la vitesse de d´epˆot sec est inversement proportionnelle `a la somme
de trois r´esistances en s´erie, elles-mˆemes compos´ees de r´esistances en s´erie et en
parall`ele (figure 7.12):
vd =
1
ra + rb + rc
(7.11)
La r´esistance a´erodynamique (ra) au transport des compos´es chimiques est
contrˆol´ee principalement par la turbulence dans la couche de surface. La r´esistance
au transport au travers de la couche visqueuse (rb) est d´etermin´ee par le taux
de transport par diffusion turbulente effective. La valeur mesur´ee de vd est en
g´en´eral consid´erablement plus faible que celle calcul´ee en consid´erant (ra + rb).
Pour r´esoudre ce d´esaccord, on ajoute une r´esistance r´esiduelle rc (r´esistance de
la canop´ee) qui s’obtient en prenant la diff´erence entre les valeurs mesur´ees de

193. 7.3 Vitesse de d´epˆot sec 193
ra + rb et de ra + rb + rc. Un nouveau probl`eme se pose par le manque de valeurs
mesur´ees except´e pour l’ozone et le dioxyde de soufre. La m´ethode propos´ee
par Wesely et Hicks [238] consiste `a obtenir les valeurs vd pour tous les compos´es
chimiques `a partir de celles calcul´ees pour O3 et SO2, en fonction de leur r´eactivit´e
par rapport `a O3 et de leur solubilit´e par rapport `a SO2.
R´esistance a´erodynamique
La r´esistance a´erodynamique peut ˆetre d´efinie en fonction du coefficient de diffu-
sion tourbillonnaire:
ra =
z
z0
dz
Km(z)
=
zSL
z0
dz
Km(z)
+
z
zSL
dz
Km(z)
(7.12)
o`u
z0 est la longueur de rugosit´e de la surface,
zSL = 0.1hCLP est la hauteur de la couche de surface qui par d´efinition
est ´egale au dixi`eme de la hauteur de la couche limite plan´etaire [222].
R´esistance de la couche visqueuse
Wesely et Hicks [238] ont propos´e la formule suivante pour calculer rb:
rb =
2
ku
(
κ
Di
)2/3
(7.13)
o`u
k est la constante de von Karman,
κ est la diffusivit´e thermique de l’air,
Di est la diffusivit´e mol´eculaire du compos´e gazeux i,
u est l’´echelle de vitesse. Except´e dans le cas de conditions extrˆemement
instables au dessus d’un terrain tr`es rugueux, rb est habituellement inf´erieure `a ra.
En cons´equence, vd est relativement peu sensible au choix de la param´etrisation
de rb et Walcek et al. [233] calculent le rapport κ/Di en prenant le rapport de la
diffusivit´e de la vapeur d’eau et du gaz i.
R´esistance de la canop´ee
Au dessus d’une r´egion donn´ee, il existe diff´erents types de plantes, de sol, de
surfaces d’eau qui ont leur propres caract´eristiques. La r´esistance de la canop´ee
est par cons´equent d´ecompos´ee en trois r´esistances en parall`ele, correspondant `a:
• la v´eg´etation: le transfert se fait soit au travers des ouvertures (stomates)
suivi d’une diffusion dans la partie interne (m´esophyle), soit au travers de
la pellicule (cuticule)

194. 194 Chapitre 7: Conditions aux limites
• la partie basse de la v´eg´etation: le tronc des arbres, les tiges des broussailles,
etc.
• le sol, auquel il faut ajouter une r´esistance qui tient compte du transfert
dynamique au travers de la canop´ee.
Pour simplifier le calcul de vd, on consid`ere que les r´esistances sont constantes
par saison, contrairement `a un v´eritable mod`ele de la biosph`ere, except´e pour la
r´esistance stomatale qui subit une forte variation diurne.
R´esistance de surface
La r´esistance de surface volumique rc est donn´ee par la relation, si on se r´ef`ere `a
la figure 7.12:
rc =
1
1
rs+rm
+ 1
rlu
+ 1
rdc+rcl
+ 1
rac+rgs
(7.14)
Nous allons `a pr´esent donner la param´etrisation utilis´ee pour chacune de ces
r´esistances.
1. R´esistance stomatale: L’ouverture de jour des stomates, pour permet-
tre la photosynth`ese, d´epend de l’ensoleillement et de la temp´erature. La
r´esistance stomatale peut ˆetre param´etris´ee en fonction de ces 2 variables
selon:
rs =
400 1 + ( 200
Qs+0.1
)2
Ts(40 − Ts)
DH2O
Dg
ri (7.15)
o`u
Qs est la radiation solaire (W.m−2
) calcul´ee `a partir de l’´equilibre radiatif
`a la surface (5.19),
Ts est la temp´erature de surface (o
C) entre 0 et 40o
C,
DH2O/Dg est le rapport de la diffusivit´e de la vapeur d’eau dans l’air `a celle
du compos´e gazeux g et dont les valeurs sont donn´ees au tableau 7.9,
ri est la r´esistance stomatale volumique minimum de la canop´ee pour la
vapeur d’eau et est une donn´ee ´etablie `a partir des observations [239].
2. R´esistance m´esophyllique: La r´esistance m´esophyllique pour un com-
pos´e gazeux est param´etris´ee de la mani`ere suivante [239]:
rm =
1
H
3000
+ 100fo
(7.16)
o`u

195. 7.3 Vitesse de d´epˆot sec 195
H est la constante effective de Henry (tableau 7.9),
f0 est le taux de r´eactivit´e (tableau 7.9).
3. R´esistance cuticulaire: La r´esistance cuticulaire dans la partie haute de
la canop´ee et pour chaque compos´e gazeux est param´etris´ee selon Wesely
[239]
rlu =
1
10−5H + f0
rlu0 (7.17)
o`u rlu0 est la r´esistance cuticulaire pour la vapeur d’eau.
4. R´esistance au transport vers le sol dans la partie basse de la v´eg´etation La
r´esistance rdc correspond `a l’efficacit´e du transport par convection libre et
forc´ee sur les pentes de montagne. La formule simple d´evelopp´ee par Wesely
[239] est utilis´ee
rdc =
100(1 + 1000
Qs+10
)
1 + 1000ψ
(7.18)
o`u ψ est l’inclinaison du terrain en radians.
5. R´esistance de la partie basse de la canop´ee: La r´esistance rcl des
compos´es gazeux au transfert vers les tiges, le tronc et autres surfaces de la
partie basse de la canop´ee est param´etris´ee suivant Wesely [239]:
rcl =
1
H
105rSO2
cl
+ f0
rO3
cl
(7.19)
o`u rSO2
cl et rO3
cl sont respectivement les r´esistances au transfert de SO2 et O3
vers la partie basse de la v´eg´etation.
6. R´esistance au transfert vers le sol: La r´esistance rac au transfert des
compos´es gazeux ne d´epend que de la hauteur et de la densit´e de la canop´ee.
7. R´esistance du sol: La r´esistance du sol rgs au transfert des compos´es
gazeux vers le sol et les ´el´ements jonchant le sol est calcul´ee de la mˆeme
mani`ere que Wesely [239]
rgs =
1
H
105rSO2
gs
+ f0
rO3
gs
(7.20)
o`u rSO2
gs et rO3
gs sont respectivement les r´esistances au transfert de SO2 et O3
vers le sol.

196. 196 Chapitre 7: Conditions aux limites
7.3.1 Les variables d’entr´ee
Pour calculer le d´epˆot sec des compos´es gazeux, il est n´ecessaire d’avoir les valeurs
des r´esistances suivantes:
• R´esistance stomatale de la vapeur d’eau: ri
• R´esistance cuticulaire de la vapeur d’eau: rlu
• R´esistance au transfert convectif: rac
• R´esistance de la partie basse au transfert de SO2: rSO2
cl
• R´esistance de la partie basse au transfert de O3: rO3
cl
• R´esistance du sol au transfert de SO2: rSO2
gs
• R´esistance du sol au transfert de O3: rO3
gs
Ces diff´erentes r´esistances sont calcul´ees pour les diff´erents types d’´ecosyst`eme et
aux diff´erentes saisons. Nous nous sommes servis des valeurs calcul´ees par Wesely
[239] pour onze ´ecosyst`emes et au cours de cinq p´eriodes de l’ann´ee. Nous avons
converti ces valeurs `a nos quatorze ´ecosyst`emes et pour les mˆemes p´eriodes.
7.3.2 Effets de la pluie et de la ros´ee
Un des effets de la pluie et de la ros´ee est de couvrir les stomates et d’empˆecher
les ´echanges feuille/atmosph`ere. Cet effet est surtout sensible pour l’ozone. Par
contre pour SO2 qui est soluble, la pluie et la ros´ee augmentent son taux de
d´epˆot `a la surface terrestre. Ces effets ont ´et´e introduits `a l’aide d’une simple
param´etrisation.
7.3.3 Extension aux autres gaz
Nous avons donn´e au tableau 7.9, la liste des gaz qui se d´eposent `a la surface avec
certaines de leurs propri´et´es:
• R´eactivit´e du gaz compar´ee `a celle de l’ozone (f0/fO3)
• Solubilit´e exprim´ee par la constante efficace de Henry (H ) pour un ph=7
• Diffusivit´e de la vapeur d’eau compar´ee `a celle du gaz (DH2O/Dg)

197. 7.4 Liste des param`etres 197
Table 7.9: Propri´et´es relatives au d´epˆot sec de certains compos´es gazeux. Les
valeurs proviennent de Wesely (1989) et Finlayson-Pitss et Pitts, 1986.
Gaz f0/fO3 H (mole.atm−1
.l−1
) DH2O/Dg
SO2 0.0 1 × 105
1.9
O3 1.0 0.01 1.6
NO2 0.1 0.01 1.6
NO 0.0 2×10−3
1.3
HNO3 0.0 1×1014
1.9
H2O2 1.0 1×105
1.4
CH3CHO 0.0 15 1.6
CH2O 0.0 6×103
1.3
CH3O2H 0.1 240 1.6
CH3CO3H 0.1 540 2.0
HCOOH 0.0 4×106
1.6
PAN 0.1 3.6 2.6
MPAN 0.1 3.6 2.9
ONIT 0.1 3.6 2.8
CH4 0.0 0.1 0.9
CO 0.0 0.1 1.2
Les gaz r´eactifs et peu solubles se comporteront comme l’ozone et les gaz tr`es
solubles auront des valeurs de vitesse de d´epˆot proches de celles de SO2.
Les valeurs moyennes de la d´eposition s`eche de HNO3 calcul´ees pendant
les quatre simulations que nous avons effectu´ees sont donn´ees `a la figure 7.13. Les
valeurs avoisinent 1 `a 2 cm.s−1
avec un maximum en octobre sur les continents
(∼ 5 cm.s−1). Dans la r´egion d’Hawaii les vitesses de d´epˆot varient entre 0.5 et 2
cm.s−1
. La valeur moyenne mesur´ee entre aoˆut et septembre 1991 [140] `a Hawaii
est de 1.25 cm.s−1
. Walcek et al. [233] obtiennent, `a l’aide d’un mod`ele r´egional,
au printemps sur la cˆote Est des Etats-Unis, une valeur moyenne de 2.5 cm.s−1
pendant la journ´ee et 1.75 cm.s−1
pendant la nuit. Ce qui correspond `a la valeur
que nous calculons en Mai sur la mˆeme r´egion (figure 7.13c).
7.4 Liste des param`etres
Nous avons r´esum´e l’ensemble des param`etres `a d´eterminer avant de pou-
voir r´esoudre les ´equations au tableau 7.10. Les valeurs qui font r´ef´erence `a la
surface sont d´etermin´ees pour les quatorze types d’´ecosyst`emes (´ecosyst`emes de
Henderson-Sellers [110]) et pour deux saisons diff´erentes. Les param`etres relatifs
au sol, pour le calcul de l’humidit´e sp´ecifique `a la surface terrestre (cf. ´equation

198. 198 Chapitre 7: Conditions aux limites
Figure 7.13: Distribution des vitesses de d´epˆot sec de HNO3 calcul´ee par notre
mod`ele pour les mois de: a) Octobre 1991, b) Janvier 1992, c) Mai 1992 et d)
Juillet 1992.

199. 7.5 Liste des donn´ees 199
Table 7.10: Liste des param`etres.
z0m Rugosit´e a´erodynamique m
Fl, Fm, Fh, Fcb Fraction des nuages de type %
bas, moyen, haut et cumulonimbus
ω Porosit´e du sol m3.m−3
ωk Contenu maximum en eau du sol kg.kg−1
Ks Diffusivit´e thermique du sol m2.s−1
Kw Perm´eabilit´e du sol m.s−1
Prec Pr´ecipitation kg.m2.s−1
zs Orographie m
aUV Alb´edo de surface dans l’ultra-violet -
aV I Alb´edo de surface dans le visible
et l’infrarouge -
Emissivit´e radiative de surface -
5.42), ont ´et´e calcul´es en d´eterminant pour chaque type de sol le pourcentage
de sable, d’argile et de limon. Ces pourcentages ont ´et´e obtenus en effectuant
des moyennes statistiques sur de multiples sondages entrepris par le d´epartement
am´ericain de l’agriculture [231]. De ces sondages nous n’avons gard´e que les
mesures `a moins d’un m`etre de profondeur. Nous avons obtenu ainsi les pour-
centages des trois composantes du sol suivant la classification am´ericaine. La
distribution globale des sols qui nous est accessible provient de la FAO/Unesco
[255] qui utilise une classification diff´erente. Nous nous sommes alors servis des
corr´elations ´etablies par Bouwman [28] entre la classification am´ericaine et celle
de la FAO/Unesco r´eduite de 27 classes `a 22 classes. La classification am´ericaine
ne couvrant que les Etats-Unis certains sols d´etermin´es par la FAO n’ont donc
pas d’´equivalent. Dans ce cas, nous consid´erons qu’il y a 33 % de sable, de limon
et d’argile. Connaissant les % de sable, argile et limon des 22 classes de sol de
l’USDA et le num´ero de la classe en chaque point de la surface terrestre il est
possible pour chacun de ces points d’attribuer une valeur des param`etres. Celles-
ci ayant ´et´e ´evalu´ees dans le cas de sol purement sableux, limoneux et argileux
[114]; [115], elles se calculent `a partir d’un diagramme ternaire (figure 7.14). Ces
valeurs sont donn´ees pour les 22 classes au tableau 7.12.
7.5 Donn´ees additionnelles
Pour calculer `a l’´echelle globale les valeurs des param`etres donn´ees au
tableau 7.10, nous utilisons les distributions globales suivantes:

200. 200 Chapitre 7: Conditions aux limites
Figure 7.14: D´etermination d’une propri´et´e d’un sol connaissant d’une part la
fraction de sable, d’argile et de limon et d’autre part la valeur de la propri´et´e
pour un sol compos´e de 100% de sable, d’argile et de limon (sur cet exemple 40,
20 et 40%).
Table 7.11: Valeurs des param`etres de surface pour les 14 ´ecosyst`emes de
Henderson-Sellers (1986) et pour deux saisons.
Ecosyst`eme Ls (m) aUV aV I
1 D´esert 0.002 0.35 0.04 0.85
2 Tundra 0.02 0.14 0.05 0.92
3 Prairie 0.01 0.19 0.04 0.92
4 Prairie broussailleuse 0.1 0.2 0.04 0.92
5 Prairie arbor´ee 0.15 0.19 0.04 0.92
6 Forˆet de feuillus 0.75 0.19 0.02 0.93
7 Forˆet de conif`eres 1.0 0.13 0.06 0.95
8 Forˆet vierge 2.0 0.11 0.08 0.95
9 Glace 0.005 0.7 0.70 0.95
10 Champs de culture 0.01 0.2 0.04 0.92
11 Etangs et marais 0.02 0.12 0.08 0.95
12 Semi-d´esert 0.04 0.29 0.04 0.92
13 Sol nu 0.005 0.15 0.04 0.92
14 Surface d’eau 0.001 0.8 0.075 0.98

201. 7.5 Liste des donn´ees 201
Table 7.12: Valeurs des param`etres des 22 types de sol de la classification de
l’USDA.
USDA Kw (×10−6m.s−1) ω ωk Ks (×10−7m2.s−1)
1 Alfisol 8.3 0.46 0.16 6.5
2 Aridosol 16.3 0.44 0.14 9.0
3 Endisol 9.3 0.45 0.15 6.7
4 Histosol 9.3 0.45 0.15 6.7
5 Inceptisol 8.8 0.47 0.17 7.1
6 Mollisol 9.7 0.46 0.16 7.2
7 Oxisol 5.4 0.56 0.24 7.9
8 Spodosol 16.0 0.43 0.13 8.6
9 Ultisol 15.6 0.44 0.14 8.8
10 Vertisol 7.1 0.49 0.19 7.1
11 Euroboralf 10.9 0.45 0.15 7.3
12 Salorthid 4.6 0.5 0.2 6.5
13 Psamment 26.2 0.41 0.11 11.6
14 Andept 7.2 0.47 0.17 6.6
15 Aquept 14.5 0.45 0.15 8.5
16 Natr-groupes 4.3 0.49 0.19 6.0
17 Cryo-Alfisol 13.1 0.45 0.15 8.0
18 Cryo-Inceptisol 20.0 0.42 0.12 9.7
19 Cryo-Molissol 11.5 0.46 0.16 7.9
20 Cryo-Spodosol 17.1 0.43 0.13 8.8
21 Cryo-Psamment 26.3 0.4 0.1 11.6
22 Glace 10.0 0.5 0.01 9 × 105

202. 202 Chapitre 7: Conditions aux limites
1. Ecosyst`emes: Les 14 types d’´ecosyst`emes de Henderson-Sellers et al. [110]
sont d´eduits `a partir d’une classification plus compl`ete contenant 32 types
[169]. Henderson-Sellers [110] fournit la table de conversion d’une classi-
fication `a l’autre. La distribution globale de Matthews a ´et´e ´etablie sur
une grille de 1o
× 1o
pour le mod`ele du GISS (Goddard Institute for Space
Science) par Matthews [170].
2. Types de sol: Les 22 types de sol de la classification am´ericaine de l’USDA
(United-States Department of Agriculture) [231] sont d´etermin´es `a partir
des 27 types de la classification de la FAO ´etablie par Zobler [255] sur une
grille 1o
× 1o
pour le mod`ele du GISS. La correspondance entre les deux
classifications a ´et´e d´ecrite par Bouwman [28].
3. Distribution des nuages: La distribution des fractions de couverture
nuageuse est obtenue `a partir de la base C2 de l’ISCCP (International Satel-
lite Cloud Climatology Project) ´etablie par le World meteorological organi-
zation [209]. Les donn´ees globales C2 fournissent des moyennes mensuelles,
´etablies depuis juillet 1983, des nombreux param`etres li´es aux nuages sur
une grille de 2.5o
× 2.5o
. Le centre de traitement des donn´ees de l’ISCCP a
chang´e d’algorithme de d´etection de nuage pour am´eliorer celle-ci dans les
r´egions polaires. Les nouvelles donn´ees de la base D2 n’ont ´et´e accessibles
qu’`a partir de juin 1996. Nous avons donc dˆu utiliser la base C2 qui est
disponible jusqu’en en septembre 1991, juste avant le d´ebut de la campagne
MLOPEX-II. En cons´equence, les donn´ees relatives aux ann´ees 1990 et 1991
ont ´et´e arbitrairement selectionn´ees; ce qui signifie que la distribution des
fractions de couverture nuageuse ne correspondent pas aux observations.
La d´etection des nuages r´ealis´ee dans le visible a le d´esavantage d’avoir
de multiples donn´ees manquantes notamment dans les r´egions de nuit po-
laire. Pour combler ces d´eficiences nous effectuons une interpolation par
spline cubique dans chaque direction. Les valeurs ainsi obtenues sont alors
multipli´ees par un coefficient de pond´eration inversement proportionnel au
nombre de donn´ees manquantes suivant une direction. Ces coefficients sont
pris `a la quatri`eme puissance pour attacher plus de poids `a la direction qui a
le plus de donn´ees. L’algorithme correspondant est similaire `a l’expression
suivante
X =
Ci
Ci + Cj
× Xi +
Cj
Ci + Cj
× Xj (7.21)
o`u
Xi et Xj sont les valeurs interpol´ees suivant les directions i et j.
Ci et Cj sont les coefficients de pond´eration suivant les directions i et j et

203. 7.6: Conditions aux limites 203
sont calcul´es par une expression de la forme
Ci = (
ni
Ni
)4
(7.22)
o`u ni et Ni sont respectivement les nombres de points o`u les valeurs des
param`etres sont donn´es et le nombre total de points suivant la direction i.
4. Orographie: L’´el´evation du relief par rapport au niveau de la mer est
obtenue `a partir de la distribution globale de l’orographie ´etablie par le
GISS sur une grille de 1o
× 1o
.
5. Pr´ecipitations: Les donn´ees de pr´ecipitations utilis´ees sont des moyennes
mensuelles climatiologiques ´etablies par Shea [212] et distribu´ees sur une
grille de 5o
× 5o
par M¨uller et Brasseur [179]. Il est important de noter
qu’il peut exister pour certains points de grille une incoh´erence entre les
nuages qui sont observ´es et les pr´ecipitations qui sont des donn´ees clima-
tologiques. En cons´equence, il peut exister des r´egions avec pr´ecipitations
sans couverture nuageuse. Cependant seul le produit des deux est utilis´e
dans la param´etrisation de la convection.
7.6 Interpolation des donn´ees
La plupart des donn´ees sont fournies sur une grille diff´erente de celle du
mod`ele et exprim´ee dans des axes diff´erents. En cons´equence, nous effectuons
toutes les interpolations sur la sph`ere o`u nous d´efinissons un syst`eme d’axes
(x, y) dont l’origine est localis´ee `a l’intersection entre l’´equateur et le m´eridien de
Greennwich et l’axe x est dirig´e vers l’est et l’axe y vers le nord. La technique
d’interpolation utilis´ee consiste `a moyenner les donn´ees en fonction de la fraction
de recouvrement des surfaces attach´ees aux points de la grille de donn´ees et de
notre mod`ele. Ces surfaces sont obtenues en reliant les centres de gravit´e des
mailles qui entourent un point donn´e. Comme indiqu´e `a la figure 7.15, en un
point i de la grille de calcul une variable Vj donn´ee en un point j de la grille des
donn´ees contribue `a la valeur de vi au point i comme:
vi = Vj
Sk
k Sk
(7.23)
o`u k est l’indice sur le nombre de mailles auquel le point i est attach´e et Sk est la
portion de la surface du polygone joignant les centres de gravit´e des diff´erentes
mailles entourant le point i et recouvrant une partie de la maille entourant le
point de donn´ee j. Cette m´ethode permet de conserver une propri´et´e en passant
d’une grille `a l’autre ce qui est particuli`erement important dans le cas d’´emissions.

204. 204 Chapitre 7: Aspects num´eriques
Figure 7.15: Interpolation des donn´ees sur la grille de calcul. En un point i de la
grille de calcul form´ee de triangles, le polygone passant par les centres de gravit´e
des mailles recouvre (partie hachur´ee) une fraction du polygone form´e par les
centres de gravit´e des mailles passant par le point de donn´ee j. Le rapport entre
cette surface de recouvrement et la surface du polygone sur la grille de calcul
donne le poids relatif des donn´ees au point j pour le point i.

205. 7.7: Conclusions 205
7.7 Conclusions
Nous avons d´ecrit dans ce chapitre la m´ethode d’obtention des cartes
d’´emission des constituants gazeux et des vitesses de d´epˆot sec `a la surface ter-
restre. Celles-ci sont param´etris´ees par analogie avec un circuit ´electrique en
combinant des r´esistances en s´erie et en parall`ele. Cette param´etrisation fait ap-
pel `a de multiples param`etres caract´eristiques du sol et de la v´eg´etation ainsi que
des caract´eristiques m´et´eorologiques. Nous avons donn´e les valeurs moyennes de
ces param`etres et leur variation saisonni`ere.
Une caract´eristique frappante est la dissym´etrie des ´emissions anthropiques et
naturelles sur l’ˆıle d’Hawaii o`u elles sont nettement plus ´elev´ees sur la cˆote est
que sur la cˆote ouest. Ceci en raison d’une part de la localisation des activit´es hu-
maines associ´ees avec le seul centre urbain (Hilo) et l’abondance des pr´ecipitations
en relation avec les nuages orographiques sur le versant est face au vent. Cepen-
dant les ´emissions anthropiques `a Hilo sont nettement inf´erieures `a celles obtenues
pour la ville d’Honolulu localis´ee sur l’ˆıle d’Ohau `a l’ouest d’Hawaii. Ces donn´ees
locales d’´emission ont ´et´e combin´ees avec les cartes globales ´etablies par M¨uller
[178] pour le mod`ele IMAGES, `a l’aide d’une m´ethode d’interpolation qui pond`ere
chaque donn´ee suivant une technique de recouvrement de surfaces.

206. 206 Chapitre 7: Conditions aux limites

207. Chapter 8
Analyse et interpr´etation des
donn´ees MLOPEX-II
8.1 Introduction
Au cours des pr´ec´edents chapitres nous avons d´ecrit le d´eveloppement
d’un mod`ele tridimensionnel de chimie-transport de la troposph`ere. Nous allons
`a pr´esent appliquer ce mod`ele `a l’analyse des donn´ees de la campagne MLOPEX-
II. Nous avons envisag´e trois ´etapes:
La premi`ere consiste `a classifier les masses d’air arrivant `a l’Observatoire
de Mauna Loa en se servant de r´etro-trajectoires. Certaines de leurs caract´eristiques
permettent d’interpr´eter les variations diurne, journali`ere et saisonni`ere des con-
centrations des gaz composant l’air analys´e `a Hawaii.
Dans une deuxi`eme ´etape nous avons cherch´e `a d´eterminer la contribution
des diff´erentes sources d’´emission tant continentales que locales sur la composition
de l’air `a l’Observatoire de Mauna Loa. Pour ce faire nous avons simul´e l’´evolution
d’un traceur passif auquel est attribu´e une couleur en fonction de la r´egion de
son ´emission. La coloration du traceur fournit non seulement la contribution
de chaque source en n’importe quel point du domaine et `a chaque instant mais
´egalement le cheminement.
Lors de la troisi`eme ´etape, nous avons simul´e l’´evolution de 46 consti-
tuants chimiques sur quatre p´eriodes de huit jours en focalisant notre ´etude sur
une partie de chacune des p´eriodes de mesure de la campagne MLOPEX-II (cf.
tableau 8.1). Les r´esultats des simulations ont ´et´e compar´es aux observations
prises non seulement `a l’Observatoire de Mauna Loa mais ´egalement lors de
mesures par avion. Nous avons ensuite interpr´et´e l’´evolution de quelques com-
pos´es chimiques au-dessus de l’Observatoire. Enfin les bilans d’un certain nombre
de compos´es gazeux ont ´et´e ´etablis sur un ensemble de r´egions couvrant le do-
maine du mod`ele et pour chacune des simulations. Nous avons distingu´e les con-
207

208. 208 Chapitre 8: Analyse des donn´ees MLOPEX-II
Table 8.1: Dates de d´ebut et de fin des p´eriodes de mesure de la campagne
MLOPEX-II et des simulations correspondantes effectu´ees avec notre mod`ele
P´eriode MLOPEX-II Simulations
D´ebut Fin D´ebut Fin
IIa 15 Octobre 91 23 Novembre 91 15 Octobre 91 23 Octobre 91
IIb 15 Janvier 92 15 F´evrier 92 21 Janvier 92 29 Janvier 92
IIc 15 Avril 92 15 Mai 92 1 Mai 92 9 Mai 92
IId 15 Juillet 92 15 Aoˆut 92 22 Juillet 92 30 Juillet 92
tinents des zones cˆoti`eres et des oc´eans, les latitudes ´elev´ees des r´egions tropicales
et ´equatoriales, et la couche limite plan´etaire de la troposph`ere libre.
8.2 Etude de r´etro-trajectoires
Les r´etro-trajectoires d´ecrivent le chemin suivi par une parcelle d’air dont
la position d’arriv´ee est donn´ee. Connaissant les champs de vitesse (chapitre
4) pour chacune des p´eriodes du tableau 8.1 et ayant transform´e notre algo-
rithme semi-lagrangien (chapitre 6) en un algorithme lagrangien, nous avons cal-
cul´e toutes les douze heures une r´etro-trajectoire pendant deux jours, en fixant
la position de l’Observatoire de Mauna Loa comme point d’arriv´ee. Les temps
d’arriv´ee sont fix´es `a 2 heures et 14 heures (heure locale d’Hawaii ou HST) pour
les six derniers jours de chaque simulation. Le trac´e en plan des trajectoires est
repris `a la figure 8.1. L’altitude et la date de d´epart sont indiqu´ees.
8.2.1 Variations saisonni`ere
Les caract´eristiques moyennes des trajectoires pour les quatre p´eriodes
sont r´esum´ees au tableau 8.2. De ce tableau il ressort que les trajectoires restent
au voisinage d’Hawaii en octobre et en juillet et s’´etendent jusqu’en Asie en janvier
et en mai. En comparant nos r´esultats `a ceux obtenus `a partir d’une climatologie
[103], il apparait une similarit´e dans la direction moyenne des trajectoires et dans
leur variation saisonni`ere.
L’altitude moyenne est la plus ´elev´ee en janvier, ce qui signifie que la
subsidence est la plus forte durant cette p´eriode. Par contre en mai, l’altitude
moyenne est la plus faible. Hess et al. [112] dans leur ´etude de trajectoires sur

209. 8.2: Etude de r´etro-trajectoires 209
Figure 8.1: Trac´e des six trajectoires pour chacune des 4 p´eriodes: (a) Octobre
1991, (b) Janvier 1992, (c) Mai 1992 et (d) Juillet 1992. L’altitude, en kilom`etres,
et la date de d´epart sont indiqu´ees pour chacune des trajectoires.

210. 210 Chapitre 8: Analyse des donn´ees MLOPEX-II
Table 8.2: Caract´eristiques moyennes des trajectoires arrivant `a l’Observatoire de
Mauna Loa (204.42oE, 19.54oN, 3.4 km d’altitude) pour les mois d’octobre, janvier, mai,
juillet: longitude minimum en oE (λi), longitude maximum en oE (λa), latitude mini-
mum en oN (Φi), latitude maximum en oN (Φa), altitude minimum en kilom`etres (zi),
altitude moyenne en kilom`etres (z), altitude maximum en kilom`etres (za), diff´erence
moyenne de temp´erature entre deux intervalles de temps successifs en degr´e Kelvin
(∆T), vitesse moyenne en kilom`etres par heure (v), chemin parcouru minimum en
kilom`etres (si), chemin parcouru moyen en kilom`etres (s), chemin parcouru maximum
en kilom`etres (sa).
P´eriode λi λa Φi Φa zi z za Ti T Ta v si s sa
Octobre 204 210 19 24 1.7 3.2 5.5 267 282 291 13 231 605 1060
Janvier 178 205 18 31 1.2 3.3 6.3 254 280 291 37 601 1760 4340
Mai 197 210 19 35 0.5 2 4.8 264 286 296 20 287 965 1773
Juillet 204 211 19 24 2.0 3.2 4.9 270 282 291 16 537 771 1070
dix jours obtiennent les pressions minimums les plus faibles en mai. Cependant
ils indiquent ´egalement que le temps pass´e `a des pressions sup´erieures `a 640
mb (altitudes inf´erieures `a environ 4 kilom`etres) est plus du double de ce qu’ils
obtiennent en janvier. Ce qui signifie que l’altitude moyenne des trajectoires est
plus ´elev´ee en janvier qu’en mai. La pr´esence de perturbations cycloniques et de
la position `a l’Ouest de l’anticyclone du Pacifique peuvent en expliquer la raison.
La diff´erence moyenne de temp´erature est un param`etre d´eterminant
pour l’analyse de compos´es chimiques sensibles `a la d´ecomposition thermique,
tel que le nitrate de peroxy-ac´etyle (PAN) qui est un r´eservoir pour les oxydes
d’azote. La temp´erature moyenne peut ˆetre reli´ee `a l’altitude moyenne. Si la
temp´erature est basse, la d´ecomposition thermique du PAN sera lente et donc
une masse d’air continentale transport´ee `a haute altitude aura une concentration
de PAN ´elev´ee. Les temp´eratures moyenne et extrˆeme sont les plus faibles en
janvier. La temp´erature moyenne maximum est atteinte en mai lorsque l’atitude
moyenne est la plus basse.
8.2.2 Variations journali`eres
Trajectoires en octobre Nous pouvons distinguer deux p´eriodes durant les
huit jours de simulation (du 15 octobre au 22 octobre), la premi`ere couvre les
trois premiers jours et est caract´eris´ee par une circulation cyclonique faible li´ee
`a une basse pression `a l’Ouest d’Hawaii avec des masses d’air venant du Sud.
Durant la deuxi`eme p´eriode, qui d´ebute le 19 octobre jusqu’`a la fin de la simu-

211. 8.2: Etude de r´etro-trajectoires 211
lation, le r´egime d’´ecoulement est caract´eris´e par le d´eveloppement d’une haute
pression au Nord Nord-Est d’Hawaii. Les trajectoires proviennent alors du Nord-
Est en relation avec une circulation anticyclonique. Les trajectoires restent dans
le voisinage de Hawaii avec une distance parcourue minimum le 21 octobre `a 14
heures. Les trajectoires du 17 et 18 octobre refl`etent la transition entre les deux
r´egimes avec une direction g´en´erale qui passe du Sud au Nord-Est. La distance
parcourue maximum correspond `a la trajectoire du 18 octobre. En r`egle g´en´erale
les trajectoires arrivent `a l’Observatoire du Sud Sud-Ouest jusqu’au 17 octobre et
de l’Est Sud-Est jusqu’au 21 `a 14 heures quand les trajectoires arrivent de plein
Nord.
Trajectoires en janvier Durant le mois de janvier, l’anticylone est situ´e au
Sud-Ouest d’Hawaii et les trajectoires traversent le Pacifique `a altitude ´elev´ee.
Le 24 janvier, les masses d’air arrivent en deux jours de l’Est du Japon `a Hawaii.
Jusqu’au 26 janvier, les trajectoires arrivent en g´en´eral de l’Est `a l’Observatoire.
Apr`es cette date les vents s’affaiblissent et les trajectoires restent dans la r´egion
d’Hawaii et arrivent `a l’Observatoire du Nord-Est. Il faut donc s’attendre `a une
transition le 26 janvier entre des masses d’air continental et des masses d’air
essentiellement oc´eanique.
Trajectoires en mai Durant le mois de mai, la distinction entre les trajec-
toires de jour et de nuit est la plus marqu´ee. Les trajectoires arrivant `a 14h00 `a
l’Observatoire, restent confin´ees dans la couche limite plan´etaire. La variabilit´e
des syst`emes synoptiques se refl`ete dans la variabilit´e des trajectoires. Jusqu’au
4 mai, les trajectoires restent dans l’entourage des ˆıles et prennent des directions
tr`es variables alors que l’anticyclone du Pacifique occupe une position au Sud-
Ouest d’Hawaii. A partir du 5 mai, Hawaii est situ´e entre une basse pression
`a l’est et une haute pression `a l’Ouest cr´eant des trajectoires de direction plein
Nord. C’est durant cette p´eriode que les trajectoires viennent de latitudes les
plus ´elev´ees. Nous pouvons donc distinguer deux types de masse d’air durant ce
mois, avant le 5 mai l’air est contamin´e par les ´emissions locales et apr`es le 5 mai
les masses d’air seront un m´elange d’air continental asiatique et d’air oc´eanique.
Trajectoires en juillet Durant le mois de juillet, l’anticyclone occupant sa
position au Nord-Ouest d’Hawaii, les trajectoires viennent en g´en´eral de l’Est.
Cependant, du 20 au 24 juillet, les trajectoires ont des origines diverses et peu
´eloign´ees des ˆıles. Par contre du 25 au 27 juillet, les trajectoires se d´eplacent
rapidement de l’Est alors que l’anticyclone se renforce au Nord d’Hawaii. Enfin du
28 au 30 juillet, le d´eplacement plus au Nord de l’anticylone affaiblit de nouveau
la circulation et conduit `a des trajectoires venant du Nord.

212. 212 Chapitre 8: Analyse des donn´ees MLOPEX-II
8.2.3 Variations diurnes
En s´eparant les trajectoires arrivant `a 2 heures de celles arrivant `a 14
heures, il est possible de constater que les premi`eres restent dans la couche limite
plan´etaire o`u elles suivent un trac´e complexe qui reste au voisinage de l’ˆıle, alors
que les secondes d´ecrivent des courbes rectilignes dans la troposph`ere libre o`u
les vitesses des vents sont plus ´elev´ees. Nous avons repris `a la figure 8.2 le trac´e
d’une trajectoire arrivant le 6 mai 1992 `a 14 heures (heure locale) `a l’Observatoire
de Mauna Loa. La complexit´e de la trajectoire est frappante, mais au-del`a il
est int´eressant de constater les effets des vents montants diurnes et descendants
nocturnes sur le trac´e de la trajectoire. En effet une masse d’air arrivant du Nord
le 4 mai `a 14 heures est entraˆın´ee rapidement au Sud-Ouest d’Hawaii dans une
r´egion sous le vent en passant par le col entre les volcans Kohala et Mauna Kea.
La parcelle stagne pendant un jour dans cette zone avant d’ˆetre prise par les vents
montants dans la matin´ee du 6 mai pour arriver `a l’Observatoire `a 14 heures.
8.3 Etude de traceurs passifs
Pour d´eterminer l’origine des masses d’air il est g´en´eralement fait appel
`a l’´etude d’un traceur dont le temps de vie est proche du temps caract´eristique
au transport. Le temps mis depuis le continent asiatique jusqu’`a Hawaii est
d’environ une semaine. C’est pourquoi nous avons choisi comme traceur le radon
isotopique 222, 222
Rn, qui a un temps de vie de 5.5 jours et est ´emis `a un taux
quasiment constant de 1 atome.cm−2
.s−1
par les sols non-gel´es [77], [128], [17],
[86]. Cependant, il existe un d´esaccord entre les mod`eles et les observations en
ce qui concerne les concentrations de 222
Rn dont l’origine proviendrait de fluctu-
ations importantes dans les ´emissions [164]. En effet les mesures de Wilkening
[242] ont montr´e que les ´emissions de 222
Rn variaient d’un facteur 10 suivant le
type de sol `a Hawaii. Nous nous sommes servis de cette ´etude pour fixer le taux
d’´emission `a Hawaii. Nous ne l’avons cependant pas ´etendu aux continents o`u
nous maintenons une ´emission de 1 atome.cm−2
.s−1
. Les valeurs d’´emission du
222
Rn pour la r´egion d’Hawaii sont donn´ees `a la figure 8.3. Nous remarquons un
maximum de 1.5 atomes.cm−2
.s−1
pour les sols organiques et un minimum de 0.1
atomes.cm−2
.s−1
pour les laves sur les pentes des volcans et z´ero en altitude.
8.3.1 Comparaison des simulations avec les observations
La distribution du 222
Rn a ´et´e simul´ee durant les p´eriodes donn´ees au
tableau 8.1 en sp´ecifiant une concentration nulle comme condition initiale et un
flux constant de 1 atome.cm−2
.s−1
pour les sols dont la temp´erature est sup´erieure

213. 8.3: Etude de traceurs 213
Figure 8.2: Trac´e d’une trajectoire arrivant le 6 mai 1992 `a 14 heures `a
l’Observatoire de Mauna Loa. L’altitude et la date sont indiqu´ees toutes les
douze heures le long de la trajectoire.

214. 214 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.3: Distribution des ´emissions de 222
Rn par les sols de l’archipel d’Hawaii,
exprim´ees en atomes.cm−2
.s−1
.
Table 8.3: Valeurs moyennes et variances des concentrations (pCi/SCM) du 222
Rn
observ´ees et simul´ees pour les quatre saisons.
P´eriode Mesures Simulations
IIa 3 ± 1.7 2 ± 1.8
IIb 6 ± 5.8 7.3 ± 6.6
IIc 12 ± 6.2 9.1 ± 7.1
IId 3.3 ± 2.1 3.8 ± 3.2
`a -5o
C, `a l’exception d’Hawaii o`u la distribution d´epend du type de sol (cf. figure
8.3).
L’´evolution de la concentration du 222
Rn pour les quatre p´eriodes est
compar´ee aux valeurs observ´ees `a l’Observatoire de Mauna Loa `a la figure 8.4.
Les valeurs moyennes et les variances sont donn´ees au tableau 8.3. Le
mod`ele reproduit bien le maximum au printemps et le minimum en automne
qui sont li´es `a l’efficacit´e du transport `a grande ´echelle depuis les continents.
Les variations diurnes des concentrations calcul´ees et mesur´ees sont relativement
similaire, marqu´ees par un minimum de jour due aux ´emissions locales et un
minimum de nuit. Mais certains maxima observ´es de jour ne sont pas aussi
prononc´es dans les simulations.

215. 8.3: Etude de traceurs 215
Figure 8.4: Evolution de la concentration (activit´e isotopique) du 222
Rn `a
l’Observatoire de Mauna, exprim´ee en pico Curie dans les conditions standards
[pCi/SCM], pour les 4 simulations en (a) octobre 1991, (b) janvier 1992, (c) mai
1992 et (d) juillet 1992. Les valeurs observ´ees sont repr´esent´ees par les lignes dis-
continues et les valeurs calcul´ees au niveau 22 (σ=0.95) par les lignes continues.

216. 216 Chapitre 8: Analyse des donn´ees MLOPEX-II
8.3.2 Origines des masses d’air `a MLO
Pour distinguer l’origine des diff´erentes masses d’air arrivant `a l’Observatoire
de Mauna Loa (MLO), nous avons ajout´e une marque distinctive (couleur) au
traceur en fonction de la position de sa source d’´emission. Nous avons ainsi
distingu´e cinq sources diff´erentes:
1. Europe: toute partie de terre dont la temp´erature de surface est sup´erieure
`a -5o
C, et situ´ee entre 340o
et 60o
de longitude. Les ´emissions sont con-
stantes et de 1 atom.cm−2
.s−1
.
2. Asie: toute partie de terre dont la temp´erature de surface est sup´erieure `a
-5o
C, et situ´ee entre 60o
et 200o
de longitude. Les ´emissions sont constantes
et de 1 atom.cm−2
.s−1
.
3. Am´erique: toute partie de terre dont la temp´erature de surface est sup´erieure
`a -5o
C, et situ´ee entre 200o
et 340o
de longitude. Les ´emissions sont con-
stantes et de 1 atome.cm−2
.s−1
.
4. Archipel d’Hawaii: les portions des ˆıles de Oahu, Lanai, Maui, Molokai
et Kahoolawe dont l’altitude est inf´erieure `a 2000 m`etres. Les ´emissions sont
bas´ees sur l’´etude de Wilkening [242] et varient entre 1.5 et 0.1 atom.cm−2
.s−1
.
5. Hawaii: la portion d’Hawaii dont l’altitude est inf´erieure `a 2000 m`etres.
Les ´emissions sont bas´ees sur l’´etude de Wilkening [242] et varient entre 1.5
et 0.1 atom.cm−2
.s−1
.
Comme pour la simulation pr´ec´edente, nous avons initialis´e les concentrations
`a z´ero et int´egr´e les ´equations pendant vingt-quatre jours en gardant la mˆeme
m´et´eorologie tous les huit jours et en ne gardant pour r´esultats que les derniers
huit jours. Le temps de vie de ces traceurs color´es est identique au 222
Rn.
Le profil vertical de la fraction moyenne de chacune des couleurs du
222
Rn au-dessus de l’observatoire de Mauna Loa est repr´esent´e pour les quatre
simulations `a la figure 8.5. De cette figure, il ressort que pr`es de la surface
terrestre les sources locales dominent tr`es largement. Un peu plus haut le 222
Rn
am´ericain domine en octobre et en juillet alors qu’en janvier et en mai c’est plutˆot
le 222
Rn asiatique. Dans la troposph`ere sup´erieure le 222
Rn asiatique pr´edomine
except´e en janvier quand il est originaire d’Am´erique.
La contribution des autres ˆıles de l’Archipel d’Hawaii est g´en´eralement
n´egligeable, except´e en juillet, ce qui s’explique par la direction des vents domi-
nants du Nord-Est qui chassent les ´emissions loin d’Hawaii. Ceci signifie que la
ville industrielle de Honolulu et ses ´emissions de polluants n’affecteront pas les
mesures.

217. 8.3: Etude de traceurs 217
Figure 8.5: Profil vertical de la fraction (%) de chacune des sources de 222
Rn. A
chaque type de trait est associ´e une origine diff´erente: pointill´e (Europe), plein
(Asie), traits (Am´erique), traits suivis d’un point (Archipel de Hawaii en excluant
l’ˆıle de Hawaii), traits suivis de trois points (Ile de Hawaii). Les pourcentages
sont des valeurs moyennes sur les huit jours de simulation pour: a) Octobre 1991,
b) Janvier 1992, c) Mai 1992 et d) Juillet 1992.

218. 218 Chapitre 8: Analyse des donn´ees MLOPEX-II
L’influence des ´emissions europ´eennes est insignifiante except´e `a haute
altitude en janvier. Ceci s’explique par l’activit´e convective plus ´elev´ee en Europe
qu’en Asie idurant le mois de janvier (cf. figure 5.6).
8.3.3 Influence des sources am´ericaines en janvier
Il est g´en´eralement admis [175], [103], [101], [112] que les masses d’air
en janvier `a l’Observatoire de Mauna Loa sont en provenance d’Asie puisque les
vents sont d’Ouest. Le 222
Rn ´emis par les sols am´ericains devrait passer au-dessus
de l’Europe puis de l’Asie pour arriver `a Hawaii. Comme le 222
Rn ´emis par les
sols europ´eens est n´egligeable, il semblerait normal que l’influence am´ericaine soit
nulle. Or d’apr`es notre ´etude, il semble qu’il y ait une influence ´equivalente des
masses d’air am´ericaines. Il faut noter qu’`a l’exception de celle de Balkanski et al.
[17], les ´etudes de traceurs ne distinguent pas les diff´erentes sources continentales
mais se basent uniquement sur des ´etudes de trajectoires. Or de telles ´etudes ne
tiennent pas compte des ph´enom`enes `a sous-´echelle telles que la turbulence et la
convection par les nuages cumuliformes. Or ce sont justement ces ph´enom`enes,
plus leur distribution que leur intensit´e, qui diminuent l’importance des ´emissions
asiatiques au profit de celles en Am´erique du Nord.
Si nous analysons les colonnes de 222
Rn sur toute la troposph`ere, nous
constatons que des valeurs ´elev´ees sont distribu´ees depuis le continent am´ericain
jusqu’`a l’Ouest de l’ˆıle d’Hawaii en passant au Nord de celle-ci (figure 8.7). La
distribution de la source asiatique forme une langue depuis le continent asiatique
jusqu’au Canada (figure 8.6). La distribution de la colonne de 222
Rn forme un
´etau autour de la langue asiatique. Cependant, l’analyse indique que la partie
Nord se trouve `a une altitude avoisinant 300 mb alors que la partie sud est situ´ee
dans la couche limite plan´etaire. Nous constatons ´egalement une bande qui part
de l’Est am´ericain, qui passe au-dessus du pˆole Nord et s’avance sur la Sib´erie.
Pour d´eterminer le cheminement pris par les masses d’air d’origine am´ericaine
arrivant au-dessus de l’Observatoire de Mauna Loa, nous avons effectu´e une sim-
ulation pour laquelle les concentrations du 222
Rn am´ericain passant au-dessus du
continent asiatique sont annul´ees. Si la contribution dans la troposph`ere moyenne
et sup´erieure ne se modifie pas, cela signifie que les masses d’air en provenance
du Canada sont prises dans un mouvement cyclonique jusqu’`a l’est du Japon o`u
elles se m´elangent aux masses d’air asiatique avant d’ˆetre prises par les nuages
convectifs `a haute altitude vers Hawaii. Par contre s’il n’y a plus de contribution
cela veut dire que les masses d’air am´ericaines passent par le pˆole Nord. Pr`es de
la surface, il ne devrait pas y avoir de modification car il s’agit de masses d’air
provenant en droite ligne de la cˆote Ouest am´ericaine.
. .
Nous avons ´egalement effectu´e une ´etude de sensibilit´e en modifiant

219. 8.3: Etude de traceurs 219
Figure 8.6: Distribution du logarithme de la colonne de 222
Rn ´emis par le con-
tinent asiatique pour les mois d’Octobre 1991, de Janvier 1992, de Mai 1992 et
Juillet 1992

220. 220 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.7: Distribution du logarithme de la colonne de 222
Rn ´emis par le con-
tinent am´ericain pour les mois d’Octobre 1991, de Janvier 1992, de Mai 1992 et
Juillet 1992

221. 8.3: Etude de traceurs 221
l’intensit´e du transport convectif et turbulent. La figure 8.8 reprend le profil ver-
tical de la fraction du 222
Rn am´ericain dans le cas standard, en multipliant le flux
massique par convection dans les cumulonimbus par deux et par un demi, et en
augmentant par cinq la valeur du coefficient de diffusion turbulente. La fraction
ne variant quasiment pas il apparait qu’elle est peu sensible `a la param´etrsiation
de la convection et de la turbulence. Par contre, en annulant toute concentra-
tion de 222
Rn provenant d’Am´erique au-dessus du continent asiatique, la fraction
descend en-dessous de 50%.
Nous pouvons en conclure que dans la r´egion d’Hawaii, les masses d’air
pr`es de la surface sont un m´elange d’airs d’origines asiatique et am´ericaine alors
qu’en altitude il s’agit essentiellement de masses d’air d’origine am´ericaine qui
passe au-dessus du pˆole Nord et ensuite au-dessus du continent asiatique .
8.3.4 Cheminement des polluants locaux vers MLO
Nous d´esirons savoir comment les polluants ´emis sur la cˆote Est d’Hawaii
montent `a l’Observatoire, en particulier s’ils sont entraˆın´es par une voie directe ou
s’ils contournent l’ˆıle avant d’atteindre l’Observatoire sur le versant oppos´e. Nous
avons repris uniquement deux ´etudes caract´eristiques, l’une o`u l’on consid`ere une
source de 222
Rn `a Hilo (204.953o
E, 19.73o
N) qui est une ville sur la cˆote Est
d’Hawaii, et l’autre, pour le mois d’Octobre, au crat`ere de Kilauea (204.73o
E,
19.43o
N) au Sud-Est de Mauna Loa.
Source de 222
Rn au crat`ere de Kilauea
L’´evolution, entre le 14 octobre 1991 `a 14 heures et le 17 octobre 1991 `a
2 heures, des concentrations de 222
Rn en ne consid´erant qu’une source au crat`ere
de Kilauea est donn´ee `a la figure 8.9. Les concentrations sont des valeurs instan-
tan´ees repr´esent´ees toutes les quatre heures et moyenn´ees entre les niveaux σ=1
et 0.875 (0 `a 2 kilom`etres d’altitude). La valeur initiale est nulle. Pour compren-
dre l’´evolution de la distribution il est n´ecessaire de se reporter `a l’´evolution de
la direction du vent `a Hilo (figure 4.9).
En octobre, les vents sont initialement du Sud et donc les gaz ´emis `a
Kilauea sont pouss´es vers le Nord. A partir du 16 octobre `a midi les vents
tournent `a l’Est et les masses d’air sont pouss´ees vers l’Ouest. Ensuite les vents
sont du Nord-Est `a partir du 18 octobre et ce jusqu’`a la fin de la simulation.
En d´ebut de simulation, les vents ascendants le long des pentes des volcans sont
dans leur phase d’affaiblissement et font place `a partir de 22 heures (troisi`eme
panneau) `a des vents descendants qui poussent les gaz ´emis vers l’oc´ean. A partir
de 10 heures le 15 octobre, il y a une faible mont´ee du 222
Rn vers le col depuis
Hilo. Mais une fraction de l’isotope n’arrive `a l’Observatoire qu’`a partir du 16

222. 222 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.8: Sensibilit´e du profil vertical de la fraction (%) de 222
Rn provenant
d’Am´erique: cas standard (ligne continue), deux fois plus d’activit´e convective
(traits), cinq fois plus de diffusion turbulente (ligne pointill´ee), et en annulant la
concentration du 222
Rn qui passe au-dessus du continent asiatique (traits altern´es
par un point).

223. 8.3: Etude de traceurs 223
Figure 8.9: Evolution, entre le 14 octobre 1991 `a 14 heures et le 17 octobre 1991
`a 2 heures, de la distribution de la concentration dans la couche limite plan´etaire
du 222
Rn en ne consid´erant qu’une source au crat`ere de Kilauea. Les valeurs
sont des valeurs instantan´ees et correspondent `a des instants successifs espac´es
de quatre heures.

224. 224 Chapitre 8: Analyse des donn´ees MLOPEX-II
octobre alors que les masses d’air ont contourn´e l’ˆıle par le Nord pour ensuite
passer le col entre les volcans Mauna Kea et Kohala. Au treizi`eme pas de temps,
on voit clairement que la mont´ee des vents ascendants se fait depuis le versant
ouest et redescendent en partie sur le versant est. Nous voyons donc que c’est
l’´ecoulement de retour dans la partie de l’ˆıle sous le vent qui est responsable du
transport depuis la cˆote jusqu’`a l’Observatoire.
Sources de 222
Rn `a Hilo
La figure 8.10 reprend l’´evolution du 222
Rn en consid´erant une seule
source `a Hilo pour les mˆemes instants que pr´ec´edemment. Bien que les dis-
tributions soient diff´erentes il existe une similarit´e dans le cheminement des gaz
vers l’Observatoire avec le cas pr´ec´edent. Ceci signifie que durant cette p´eriode
les polluants acc`edent `a l’Observatoire par une voie indirecte relativement longue
et ils seront ,pour les plus r´eactifs, en grande partie oxyd´es ou d´etruits par d´epˆot
sec.
En ce qui concerne les autres p´eriodes, nous arrivons `a un r´esultat simi-
laire pour le mois de juillet mais variable en janvier et en mai, p´eriodes pendant
lesquelles en fonction de la direction des vents dominants, il y aura acc`es direct
ou indirect des polluants de la cˆote Est de l’ˆıle d’Hawaii vers l’Observatoire.
8.4 Analyse de la chimie
L’analyse des donn´ees et des r´esultats de nos simulations comporte trois
parties. Au cours de la premi`ere nous comparerons les valeurs calcul´ees `a celles
mesur´ees. Ensuite nous analyserons les variations diurne, journali`ere et saisonni`ere
en nous aidant des ´etudes de trajectoires et de traceurs passifs. Nous terminerons
en calculant les bilans tant chimiques que dynamiques de quelques constituants
gazeux.
Mais avant de commencer l’analyse nous discuterons bri`evement des
mesures MLOPEX-II, en particulier les diff´erentes donn´ees qui ont ´et´e prises
`a l’Observatoire de Mauna Loa et par avion.
8.4.1 Donn´ees relatives `a MLOPEX-II
Mesures `a l’Observatoire de Mauna Loa
La liste des compos´es mesur´es `a l’Observatoire de Mauna Loa a ´et´e
donn´ee dans le chapitre d’introduction au tableau 1.1. Nous discuterons ici
bri`evement des instruments utilis´es et leurs marges d’erreur dans la mesure de
quelques compos´es (pour les autres compos´es et une description d´etaill´ee nous

225. 8.4: Analyse de la chimie 225
Figure 8.10: Evolution, entre le 14 octobre 1991 `a 14 heures et le 17 octobre 1991 `a
2 heures, de la distribution de la concentration dans la couche limite plan´etaire du
222
Rn en ne consid´erant qu’une source sur la ville de Hilo. Les mˆemes remarques
qu’`a la figure 8.9 s’appliquent ici.

226. 226 Chapitre 8: Analyse des donn´ees MLOPEX-II
renvoyons le lecteur au num´ero sp´ecial du Journal of Geophysical Research, vol-
ume 101, publi´e en juin 1996).
• Ozone. L’ozone (O3) a ´et´e mesur´e `a l’aide d’un instrument commercial
(TECO mod`ele 49) d’absorption dans l’ultra-violet [234]. L’instrument a
´et´e calibr´e deux `a trois fois pour chaque p´eriode de mesure avec un instru-
ment identique calibr´e, quant `a lui, sur les valeurs standards d´efinies par le
CMDL (Climate Monitoring and Diagnostics Laboratory) de la NOAA (Na-
tional Oceanographic and Atmospheric Administration) `a Boulder (USA).
La pr´ecision des mesures, sur l’intervalle de 20 s entre deux mesures, est
de 2 ppb. En moyennant les valeurs mesur´ees sur une heure, la pr´ecision
augmente et l’incertitude devient inf´erieure `a 1 ppb.
• Oxydes d’azote. Les oxydes d’azote NO, NO2 ont ´et´e mesur´es simul-
tan´ement avec un nouvel appareil `a trois d´etecteurs de NO/O3 et un con-
vertisseur photolytique mont´e en amont d’un des d´etecteurs pour mesurer
NO2 [234], [205]. La limite de d´etection de l’appareil est de 2 ppt pour
NO et de 4 ppt pour NO2. La p´eriode d’int´egration est de 10 secondes et
les valeurs moyennes sont extraites toutes les minutes. L’incertitude des
mesures sur une minute est de l’ordre de 31% pour NO et 25% pour NO2.
Pour ´eviter que les ´echantillons d’air soient contamin´es par les ´emissions lo-
cales, les mesures effectu´ees avec une vitesse de vent inf´erieure `a 0.5 m.s−1
ont ´et´e supprim´ees.
• Famille azot´ee. La somme de tous les compos´es azot´es impairs (NOy) a
´et´e mesur´ee `a l’aide d’une technique de conversion Au/CO d´evelopp´ee par
Bollinger et al. [25] et Fahey et al. [72].
• Radical hydroxyle. Les faibles concentrations (∼ 106
molec.cm−3
) et
le temps de vie tr`es court (1 seconde) du radical hydroxyle (OH) rend
sa mesure particuli`erement difficile. Eisele et al. [69] ont mesur´e OH au
printemps et en ´et´e `a l’aide d’un instrument qui convertit OH en H34
2 SO4
qui est ensuite ionis´e par NO−
3 . Le rapport H34
SO−
4 /NO−
3 est mesur´e `a
l’aide d’un spectrom`etre de masse et permet de d´eterminer la concentration
de H34
2 SO4 et donc OH. Une description de la technique plus d´etaill´ee est
donn´ee par Eisele et Tanner [67], [68]. Eisele et al. [69] estiment que l’erreur
de mesure est ± 50%.
• Radicaux peroxydes. Les radicaux peroxydes (RO2) ont ´et´e mesur´es [36]
`a l’aide d’un amplificateur chimique. En utilisant la r´eaction en chaˆıne NO
+ HO2 → OH + NO2 et OH + CO → HO2 + CO2, il est possible d’amplifier
les concentrations de HO2 en ajoutant une grande quantit´e de NO et CO

227. 8.4: Analyse de la chimie 227
`a l’air ambiant. Les auteurs estiment que les incertitudes sont en g´en´eral
inf´erieures `a 65%.
• Monoxyde de carbone. Le monoxyde de carbone a ´et´e mesur´e toute les
vingt minutes par Greenberg et al. [95] en r´eduisant HgO par CO dans une
enceinte chauff´ee et en d´etectant la vapeur de Hg par l’absorption atomique
de lumi`ere d´egag´ee par une source de Hg. L’incertitude sur la mesure est
de quelques pourcents.
• Hydrocarbures non-m´ethaniques. Les concentrations des hydrocar-
bures non-m´ethaniques (NMHC) ont ´et´e mesur´ees toutes les deux heures
[95]. La mesure proc`ede en une premi`ere ´etape de pi´egage cryog´enique des
mol´ecules `a plusieurs atomes de carbone, suivie d’une ´etape de chauffage
rapide pour ´eliminer la vapeur d’eau avant le transfert vers un chromatographe.
Les incertitudes sont approximativement de 5% pour des rapports de m´elange
sup´erieurs `a 50 ppt, 7% `a 10 ppt et 10% `a 3 ppt.
• Formald´ehyde. Le formald´ehyde a ´et´e mesur´e par cinq techniques diff´erentes
et leur intercomparaison a ´et´e r´ealis´ee par Heikes et al. [109]. L’incertitude
des mesures `a 200 ppt de CH2O varient de 110 ppt `a 40 ppt en fonction
de l’instrument employ´e. Nous avons utilis´e les mesures effectu´ee `a l’aide
d’une bobine de pi´egage en phase aqueuse [139], [108] dont l’incertitude est
de l’ordre de 40%.
Mesures par avion
A l’ensemble des mesures effectu´ees `a l’Observatoire de Mauna Loa se
sont ajout´ees un certain nombre de mesures par avion qui nous offrent l’opportunit´e
d’´evaluer les profils verticaux des concentrations calcul´ees par notre mod`ele:
• Les 10 vols du King Air de l’Universit´e du Wyoming ont ´et´e effectu´es entre
le 22 Avril et le 11 mai 1992. Les diff´erents constituants chimiques mesur´es
ainsi que la technique utilis´ee et les personnes et les institutions impliqu´ees
sont reprises au tableau 8.4.
• Le vol num´ero 20 de la campagne Global Tropospheric Experiment (GTE)
de la Pacific Exploratory Mission (PEM-WEST A) organis´e par la NASA le
20 octobre 1991. Le tableau (8.5) reprend la liste des constituants mesur´es,
des exp´erimentateurs et de la technique utilis´ee.
8.4.2 Simulations
A l’aide de notre mod`ele nous avons simul´e la distribution des concen-
trations de 46 constituants pour les p´eriodes donn´ees au tableau 8.1. Le pas de

228. 228 Chapitre 8: Analyse des donn´ees MLOPEX-II
Table 8.4: R´esum´e des mesures effectu´ees `a bord du King Air de l’Universit´e du
Wyoming pendant la campagne MLOPEX-II, entre le 22 Avril et le 11 mai 1992.
Compos´es Exp´erimentateurs Institution
HOOH, CO, O3, NOy, B. Ridley
Noyaux de condensation, T. Staffelbach, J. Walega
NMHC F. Grahek, G. Kok
et nitrates organiques J.Greenberg, E. Atlas NCAR
NCAR= National Center for Atmospheric Research, Colorado
temps pour le transport advectif est de une heure et de vingt minutes pour la
chimie et le transport diffusif et convectif. Les concentrations sont d´etermin´ees
en 3027 points suivant l’horizontale et pour chacun des 23 niveaux et sont sauve-
gard´ees toutes les quatre heures. Une simulation n´ecessite approximativement
une heure CPU pour deux jours simul´es sur un CRAY-YMP8/864.
Nous avons repris, `a titre d’exemple, l’´evolution des rapports de m´elange
calcul´es au dessus de l’Observatoire de Mauna Loa pour le mois d’octobre 1991 `a
la figure 8.11. Il apparaˆıt clairement que le changement dans la direction du vent
le 18 octobre, observ´e par l’´etude de trajectoires, conduit en d´ebut de simulation `a
une composition chimique ”propre” avec peu de NOx, de CO et d’autres hydrocar-
bures, ainsi que d’O3. Par contre quand les masses d’air viennent du Nord, nous
constatons une brusque augmentation dans leurs rapports de m´elange. L’origine
continentale de ces polluants est visible sur la figure 8.12 qui donne la distribution
moyenne du CO `a 700 mb pour la p´eriode de simulation en octobre.
8.4.3 Comparaison entre les r´esultats du mod`ele et les
observations
Comparaison avec les mesures `a MLO
L’´evolution temporelle observ´ee `a MLO (ligne pointill´ee) et calcul´ee (ligne
continue) pour chacune des quatre simulations (tableau 8.1) de quelques consti-
tuants chimiques est repr´esent´ee aux figures 8.13 et 8.14. Pour distinguer les deux
r´egimes de vent (montant et descendant), nous avons repris pour chacun d’eux
les valeurs moyennes des rapports de m´elange de la plupart des concentrations
de gaz mesur´ees et calcul´ees au tableau 8.6.
Les variations diurne, journali`ere et saisonni`ere des concentrations sont
dues respectivement aux changements de r´egime des vents locaux, de la direction
des vents dominants et de la position de l’anticylone du Pacifique en mˆeme temps

229. 8.4: Analyse de la chimie 229
Table 8.5: R´esum´e des mesures effectu´ees `a bord du DC-8 de la NASA durant le
vol no
20 de la campagne PEM-West A, le 20 octobre 1991.
Compos´es Instruments Incertitude Exp´erimentateurs Institutions
O3 CL ± 2 ppb G. Gregory Univ of RI
NOy LIF 10-20% J. Bradshaw Georgia Tech
CL 10-20% Y. Kondo STEL
HNO3 Mist/IC 15-25% R. Talbot IEOS
NO LIF 15-20% J. Bradshaw Georgia Tech
CL 15-20% Y. Kondo STEL
NO2 LIF 15-20% J. Bradshaw Georgia Tech
PAN GC/ECD 8-15% H. Singh NASA Ames
HOOH PF ± 15% B. Heikes Georgia Tech
ROOH PF ± 15% B. Heikes Georgia Tech
NMHC GC/FID ? D. Blake Univ of Cal
CH4 ± 1.5% TDL G. Sachse NASA Langley
CO TDL ± 15 ppb G. Sachse NASA Langley
C2Cl4 GC/ECD ? D. Blake Univ of Cal
Halocarbones ± 1% GC/ED D. Blake Univ of Cal
N2O TDL ± 0.4% G. Sachse NASA Langley
SO2 GC/MS ± 20% A. Bandy Univ Drexel
LIF=Laser Induced Florescence;
Mist/IC= Mist Chamber with Ion Chromatography; CL= ChemiLumiscence;
GC/ECD= Gas Chromatography with Electron Capture Detection;
GC/FID= Gas Chromatography with Flame Ionization Detection;
PF= Photo-Fluorescence; TDL= Tunable Diode Laser;
GC/MS= Gaz Chromatography and Mass Spectrometry for sulfur;
STEL= Solar Terrestrial Environmental Laboratory, Toyokawa, Japan;
IEOS= Institute for Earth, Oceans, and Space, University of New Hamphshire;
NASA Langley= NASA Langley Research Center, Virginia;
NASA Ames= NASA Ames Research Center, California;
Univ of RI= University of Rhode Island;
Georgia Tech= Georgia Institute of Technology, Atlanta;
Univ of Cal= University of California, Irvine;
Univ Drexel= Drexel University, Philadelphia, Pennsylvania

230. 230 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.11: Evolution du rapport de m´elange au-dessus de l’Observatoire de
Mauna Loa pour les huit jours de simulation en octobre 1991 pour les douze
gaz suivants: (a) le nitrate de peroxy-ac´etyle (PAN), (b) isopr`ene (ISO), (c) α-
pin`ene (APIN), (d) acide nitrique (HNO3), (e) monoxyde de carbone (CO), (f)
ozone (O3), (g) ´ethane (C2H6), (h) ´ethyl`ene (C2H4), (i) propyl`ene (C3H6), (j) bu-
tane (C4H10), (k) peroxyde d’hydrog`ene (H2O2), (l) nitrate peroxym´ethacrylique
(MPAN).

231. 8.4: Analyse de la chimie 231
Figure 8.12: Distribution calcul´ee du rapport de m´elange du CO `a 700 mb
moyenn´ee sur les huit jours de simulation au mois d’octobre 1991.

232. 232 Chapitre 8: Analyse des donn´ees MLOPEX-II
Table 8.6: Valeurs moyennes des concentrations des compos´es chimiques mesur´es
et calcul´es pour chacune des 4 simulations et pour les conditions de vents ascen-
dant et descendant.
Octobre 1991 Janvier 1992 Mai 1992 Juillet 1992
Gaz Asc Dsc Ttes Asc Dsc Ttes Asc Desc Ttes Asc Dsc Ttes
Mesures
O3 26 31 28 38 39 39 54 61 57 31 34 31
HNO3 68 68 68 35 26 30 96 113 75 85 70 85
CO 88 87 87 98 97 98 126 123 125 68 63 67
C2H4 22 12 17 17 9 13 11 4 8 11 4 10
C2H6 479 491 485 1011 924 970 1124 1029 1083 428 445 430
C3H6 10 7 8 6 3 5 4 2 3 4 2 4
C5H8 46 12 28 32 1 15 6 0 4 18 0 16
222
Rn 4 2 3 8 3 5 13 10 12 4 1 3
RO2 12 13 12 17 13 15 14 9 12 8 10 9
H2O 9 4 7 4 2 3 6 2 4 10 6 9
NO 8 3 6 9 5 7 12 6 10 20 6 19
NO2 30 19 25 31 27 29 45 42 44 51 27 49
H2O2 740 791 763 688 740 716 1249 1406 1322 985 1901 1129
CH3O2H 391 389 390 236 263 250 460 476 436 536 633 550
Mod`ele
O3 21 22 21 31 29 30 18 21 20 18 20 18
HNO3 15 19 17 37 30 32 41 49 46 38 51 41
CO 86 86 86 182 181 181 110 100 104 85 79 84
C2H4 20 14 17 10 7 8 84 45 61 40 30 38
C2H6 506 522 513 644 643 643 632 625 628 349 325 345
C3H6 3 2 3 3 1 2 8 6 7 5 5 5
C5H8 16 2 10 0 0 0 3 4 4 7 8 7
222
Rn 2 1 2 7 8 8 19 7 8 4 2 4
RO2 9 3 7 30 1 11 24 1 10 12 1 10
H2O 9 4 7 7 3 4 6 3 4 9 5 9
NO 5 1 3 9 0 3 24 0 10 7 0 6
NO2 16 18 16 15 21 19 20 33 28 21 22 21
H2O2 390 449 417 661 663 662 764 795 782 732 799 743
CH3O2H 418 460 437 623 648 636 585 617 604 625 694 636
N.B. Toutes les concentrations sont exprim´ees en ppt sauf pour O3 et CO pour lesquels elles sont exprim´ees en
ppb et pour H2O dont les unit´es sont des ppth. OH est exprim´e en molec.cm−3.

233. 8.4: Analyse de la chimie 233
Figure 8.13: Evolution sur huit jours du rapport de m´elange de l’ozone `a
l’Observatoire de Mauna Loa calcul´e (ligne continue) et observ´e (ligne pointill´ee)
pour les quatre p´eriodes (a) Octobre 1991, (b) Janvier 1992, (c) Mai 1992 et (d)
Juillet 1992.

234. 234 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.14: Identique `a la figure 8.13 mais pour les oxydes d’azote NOx (parties
par 1012
).

235. 8.4: Analyse de la chimie 235
Figure 8.15: Identique `a la figure 8.13 mais pour l’oxyde d’azote NO (parties par
1012
). Les pics des valeurs mesur´ees sont dus `a une pollution dans le voisinnage
de l’instrument de mesure.

236. 236 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.16: Identique `a la figure 8.13 mais pour les radicaux peroxydes RO2
(parties par 1012
).

237. 8.4: Analyse de la chimie 237
Figure 8.17: Identique `a la figure 8.13 mais pour le radical hydroxyle (105
molec.cm−3
).

238. 238 Chapitre 8: Analyse des donn´ees MLOPEX-II
que de la radiation solaire.
Les variations diurnes sont clairement visibles sur la figure 8.14 pour le
NOx avec des maxima vers midi li´es au transport local de NOx ´emis localement
tant par les sols que par l’activit´e anthropique. En juillet, les maxima dans
l’apr`es-midi sont mal simul´es, en raison sans doute d’un taux d’´emissions locales
insuffisant. Les variations diurne et saisonni`ere de la concentration du monoxyde
d’azote (figure 8.15) sont simul´ees correctement avec un minimum en janvier et
un maximum en juillet qui sont dus aux variations saisonni`eres des ´emissions.
En ce qui concerne l’ozone (figure 8.13) le mod`ele est capable de re-
produire les variations diurnes qui sont marqu´ees par le passage entre de l’air
maritime pauvre en ozone la journ´ee et les valeurs plus ´elev´ees de la troposph`ere
libre la nuit. Les ´emissions locales des pr´ecurseurs d’ozone att´enuent les minima
relatifs de jour. Les variations journali`eres marqu´ees par les changements de di-
rection des vents dominants sont ´egalement bien simul´ees. En ce qui concerne les
variations saisonni`eres, les r´esultats du mod`ele suivent bien l’augmentation des
concentrations en janvier et en mai comparativement `a octobre et juillet alors que
le transport `a grande ´echelle influence le plus la composition chimique `a Hawaii.
Cependant en mai, les valeurs du rapport de m´elange calcul´ees sont significative-
ment plus faibles que celles observ´ees (cf. tableau 8.6), nous analyserons ceci en
´etudiant les bilans par r´egions. Aux environs du 23 juillet, le maximum observ´e
d’ozone (∼ 70 ppb) n’est pas reproduit par le mod`ele. Ce maximum apparait
un jour apr`es le d´ebut de la simulation et il doit son origine `a un ph´enom`ene de
transport particulier qui a du se d´evelopper quelques jours avant le 23 juillet.
Comparaison avec les mesures PEM-WEST
Durant la journ´ee du 20 octobre 1991, un vol de la mission Global Tro-
pospheric Experiment (GTE) Pacific Exploratory Mission (PEM-West A) de la
NASA a survol´e l’ˆıle d’Hawaii dans le but de r´ealiser une intercomparaison entre
les instruments de mesure `a bord et `a l’Observatoire de Mauna Loa [14]. Le vol a
quitt´e Honolulu le 20 octobre `a 3 heures 38 minutes (3H38). Le premier passage
Ouest-Est au-dessus de l’ˆıle a ´et´e effectu´e `a une altitude de 6 kilom`etres, suivi
d’un contournement de l’ˆıle vers le Sud `a 400 m`etres d’altitude. A partir de la
pointe sud, atteinte `a 5H34, l’avion est mont´e `a 3.3 kilom`etres d’altitude et a
effectu´e un cercle autour de l’ˆıle dans le sens anti-horlogique (5H48-6H52). Un
deuxi`eme cercle fut ensuite r´ealis´e `a 4.8 kilom`etres d’altitude (7H00-7H32). A la
pointe Nord, l’avion a r´ealis´e un passage Nord-Sud `a 3.6 kilom`etres d’altitude, en
passsant `a 20 kilom`etres de MLO vers environ 7H50. Un dernier passage `a basse
altitude fut r´ealis´e avant le retour vers Honolulu.
Nous avons compar´e les r´esultats de notre mod`ele (trait plein) avec les
valeurs des concentrations mesur´ees par l’avion (trait interrompu ou croix) sur

239. 8.4: Analyse de la chimie 239
Figure 8.18: Evolution du rapport de m´elange mesur´e (trait interrompu ou croix)
et calcul´e (trait continu) le long de la trajectoire prise par l’avion de la NASA
lors de la campagne PEM-West A pour: (b) l’ ozone (O3), (c) le monoxyde
de carbone (CO), (d) le peroxyde d’hydrog`ene (H2O2). La courbe (a) donne
l’altitude en m`etres en fonction du temps.

240. 240 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.19: Idem `a la figure 8.18 mais pour: (a) le nitrate de peroxy-ac´etyle
(PAN), (b) la somme des compos´es azot´es impairs (NOy), (c) le monoxyde d’azote
(NO) et (d) l’acide nitrique (HNO3).

241. 8.4: Analyse de la chimie 241
Figure 8.20: Idem `a la figure 8.18 mais pour: (a) le peroxyde de m´ethyle
(CH3O2H), (b) l’´ethane (C2H6), (c) l’´ethyl`ene (C2H4) et (d) le propyl`ene (C3H6).

242. 242 Chapitre 8: Analyse des donn´ees MLOPEX-II
les figures 8.18-8.20. Les valeurs du mod`ele sont obtenues en interpolant les
concentrations dans le temps et l’espace le long de la trajectoire prise par l’avion.
Nous constatons un bon accord entre les valeurs du mod`ele et les observations,
en particulier pour les compos´es azot´es. La structure verticale de l’ozone avec
des valeurs ´elev´ees (30-40 ppb) dans la troposph`ere libre et faibles (10-20 ppb)
dans la couche limite plan´etaire sont bien simul´ees. Les structures verticales
de plus petite ´echelle sont par contre absentes de nos simulations. En effet, les
mesures indiquent des valeurs proches de 50 ppb d’ozone vers 6 heures (7.25 sur
les graphiques) alors que le mod`ele indique un minimum secondaire `a 25 ppb
pendant que l’avion se situe sur la cˆote Est `a 3.3 kilom`etres d’altitude. Cette
diff´erence se retrouve ´egalement pour les compos´es azot´es. Lors du survole de
l’ˆıle le mod`ele indique un maximum pour O3 (> 50 ppb) et le PAN (50 ppt) qui
est absent des mesures. Ces maxima se retrouvent dans l’´evolution des profils
verticaux du PAN (figure 8.11a) et de O3 (figure 8.11f) dans la matin´ee du 20
octobre quand une langue riche en ozone descend jusqu’`a 4-5 kilom`etres d’altitude
(1-σ=0.2). L’´etude de r´etro-trajectoire indique que le 20 octobre `a 2 heures du
matin (figure 8.21) les masses d’air ont subi la plus forte descendance (3 kilom`etres
en deux jours) et venaient du Nord-Est alors que les directions g´en´erales des
trajectoires sont du Sud au d´ebut de la simulation et puis de l’Est. Pour le
monoxyde de carbone, un probl`eme avec l’instrument de mesure a surestim´e la
valeur de sa concentration de 25% [14], ce qui correspond alors `a la valeur calcul´ee
par notre mod`ele. En ce qui concerne les hydrocarbures non-m´ethaniques, les
valeurs de concentration calcul´ees pr´esentent une plus grande variabilit´e que dans
les mesures. La concentration de l’´ethyl`ene calcul´ee est 5 fois trop ´elev´es dans
la couche limite ce qui indique une surestimation de ses ´emissions locales. La
brusque augmentation des concentrations calcul´ees des hydrocarbures en fin de
vol traduit la travers´ee d’un nuage de pollution autour de Honolulu.
Comparaison avec les mesures du King-Air
Entre le 22 avril et le 11 mai 1992, dix vols de l’avion King Air de
l’Universit´e du Wyoming ont ´et´e entrepris lors du maximum d’ozone troposph´erique
sur le Pacifique Nord. Nous avons compar´e les mesures des vols du 2, 5 et 7 mai
1992 qui s’ins`erent dans la p´eriode simul´ee. Nous n’analyserons ici que le vol du 7
mai dont les mesures ont ´et´e compar´ees aux r´esultats de notre mod`ele aux figures
8.22-8.23. D’une mani`ere g´en´erale, il existe un bon accord entre les r´esultats du
mod`ele et les valeurs calcul´ees pour la plupart des constituants chimiques except´e
le CO. Mais comme pour le vol PEM-West A, le CO est surestim´e de 25% [206],
ce qui rapproche la valeur mesur´ee de celle calcul´ee. Le mod`ele est capable de
reproduire les variations verticales principales, mais il ne parvient pas `a simuler
les structures verticales plus fines.

243. 8.4: Analyse de la chimie 243
Figure 8.21: R´etro-trajectoire sur deux jours d’une parcelle d’air arrivant `a
l’Observatoire de Mauna Loa le 20 octobre 1991 `a 2 heures du matin. L’altitude
en kilom`etres et la date sont indiqu´ees toutes les 12 heures le long de la trajectoire.

244. 244 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.22: Evolution du rapport de m´elange mesur´e (trait interrompu ou croix)
et calcul´e (trait continu) le long de la trajectoire prise par l’avion King Air de
l’Universit´e du Wyoming lors du vol du 7 mai 1992 pour: (b) l’ ozone (O3), (c)
le monoxyde de carbone (CO), (d) la somme des compos´es azot´es impairs (NOy)

245. 8.4: Analyse de la chimie 245
Figure 8.23: Idem `a la figure 8.22 mais pour: (a) l’´ethyl`ene (C2H4), (b) l’´ethane
(C2H6), (c) le m´ethyle de peroxyde (CH3O2H) et (d) le peroxyde d’hydrog`ene.

246. 246 Chapitre 8: Analyse des donn´ees MLOPEX-II
8.5 Analyse des r´esultats du mod`ele
La comparaison des r´esultats du mod`ele avec les diff´erentes observations
effectu´ees aux paragraphes pr´ec´edents a montr´e que les simulations de la dis-
tribution des constituants chimiques et leurs variations diurne, journali`ere et
saisonni`ere montre en g´en´eral un accord satisfaisant avec les observations. Nous
sommes par cons´equent `a mˆeme de mieux comprendre les effets de l’activit´e hu-
maine sur la composition chimique de l’atmosph`ere au-dessus du Pacifique en
analysant les r´esultats du mod`ele. Nous limiterons notre analyse aux ´echelles
locales, en ´etudiant l’influence des ´emissions locale, et r´egionale, en analysant
l’influence des ´emissions continentales.
8.5.1 Analyse locale
La production photochimique nette de l’ozone est donn´ee par la diff´erence
entre le terme de production (relation 2.1) et de destruction (relation 2.2) si l’on
ne tient pas compte des cycles nuls de r´eactions. Elle d´epend donc des radicaux
hydroxyle (OH) et peroxyde (RO2), et du monoxyde d’azote (NO). Le NOx limite
la production d’ozone et il existe une valeur limite de sa concentration (∼ 60ppt)
en de¸c`a de laquelle il y a destruction et au-del`a de laquelle il y a production
d’ozone (cf. figure 2.17). Nous avons vu `a la figure 8.14 que la concentration de
nuit ´etait g´en´eralement plus faible que cette valeur limite et celle de jour plus
´elev´ee. La nuit, l’air `a l’Observatoire appartient `a la troposph`ere libre et est
soumis au transport `a grande ´echelle. Par contre, le jour il y a m´elange des
masses d’air de la couche limite plan´etaire et de la troposph`ere libre. C’est cette
production que nous d´esirons `a pr´esent analyser.
Des r´esultats du mod`ele, nous avons extrait les valeurs moyennes vers
500 m`etres d’altitude (mi-hauteur de la couche limite) `a deux heures de l’apr`es-
midi au-dessus de l’ˆıle d’Hawaii. La production nette d’ozone, exprim´ee en 105
molec.cm−3
.s−1
, est repr´esent´ee pour les quatre simulations `a la figure 8.24. Nous
constatons sur l’oc´ean, une perte assez importante de l’ordre de 106
molec.cm−3
.s−1
(∼ 4 ppb.jour−1
), alors que sur les parties basses des volcans il y a production
d’ozone. Celle-ci varie tr`es fort avec les saisons: en janvier elle reste inf´erieure `a 2
molec.cm−3
.s−1
(1 ppb.jour−1
) alors qu’en juillet elle atteint 70 molec.cm−3
.s−1
(30 ppb.jour−1
), ce qui est comparable aux valeurs continentales. Les valeurs at-
teintes `a l’Observatoire de Mauna Loa pour les quatre p´eriodes sont d’environ 0.4,
-3, +2, +4 ppb.jour−1
. L’analyse des mesures pour les quatre p´eriodes durant
MLOPEX-II [106] indique des valeurs de production d’ozone `a l’Observatoire
de respectivement -0.4, -1, +2, +2 ppb.jour−1
, avec une incertitude de ± 2
ppb.jour−1
. Nos r´esultats sont donc dans les limites d’incertitude. Si l’on com-
pare la production nette d’ozone avec la concentration de NO, exprim´ee en ppt,

247. 8.5: Analyse des r´esultats du mod`ele 247
Figure 8.24: Production moyenne nette d’ozone, exprim´ee en 105
molec.
cm−3
.s−1, `a deux heures de l’apr`es-midi et `a 500 m`etres d’altitude, pour les
simulations d’octobre 1991, janvier 1992, mai 1992 et juillet 1992.

248. 248 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.25: Distribution moyenne du rapport de m´elange, exprim´e en parties
par 1012
(ppt), `a 14 heures et `a 500 m`etres d’altitude pour les quatre simulations
d’octobre 1991, janvier 1992, mai 1992 et juillet 1992.

249. 8.5: Analyse des r´esultats du mod`ele 249
donn´ee `a la figure 8.25, on constate imm´ediatement leur similarit´e. Les valeurs
´elev´ees de la concentration du NO dans les parties basses de l’ˆıle sont li´ees aux
activit´es biologiques par les sols des zones humides.
La destruction d’ozone est essentiellement due `a la r´eaction entre un
atome d’oxyg`ene `a l’´etat excit´e O(1
D) et la vapeur d’eau, et les r´eactions de
O3 avec les radicaux peroxydes (RO2). En ce qui concerne la vapeur d’eau son
rapport de m´elange diminue avec l’altitude. Cependant durant l’apr`es-midi, l’air
maritime est transport´e vers le col entre Mauna Kea et Mauna Loa, comme il ap-
paraˆıt clairement sur la figure 8.26. De plus, en mai la pr´esence quasi-permanente
de nuages orographiques maintient une valeur maximum `a mi-hauteur des vol-
cans. En cons´equence la r´eaction entre H2O et O(1
D) compte pour environ 40%
`a 60% dans la perte d’ozone [106].
La distribution de l’ozone (figure 8.27) refl`ete l’interaction du transport
et de la production photochimique. La pr´edominance des vents du Nord-Est en
mai et de l’Est en juillet qui entraˆınent les masses d’air riche en ozone, produites
localement, est clairement visible. L’ascension, pendant la journ´ee, de ces masses
d’air att´enue les variations diurnes `a l’Observatoire de Mauna Loa (cf. figure
8.13). En mai, alors que les valeurs de surface sont de 35 ppb au Nord-Est, elles
atteignent 55 ppb dans le sillage de l’ˆıle au Sud-Ouest.
8.5.2 Analyse r´egionale
Dans ce paragraphe, nous allons analyser le bilan de l’ozone, du NOx et
du CO par r´egions en distinguant les continents, des zones cˆoti`eres et les oc´eans.
Le Pacifique a ´et´e de plus subdivis´e en sous-domaines. Le but est de caract´eriser
chacune des r´egions en fonction de l’importance relative des ph´enom`enes de trans-
port et de la chimie. Nous avons ainsi s´electionn´e 21 r´egions qui sont repr´esent´ees
`a la figure 8.28.
Bilan sur tout le domaine
• Le m´ethane Le temps de vie photochimique 1
du m´ethane d´epend unique-
ment de la r´eaction avec OH. Il est donc un bon indicateur du contenu
total en radical hydroxyle et de la capacit´e oxydante de l’atmosph`ere. Sa
valeur est de l’ordre de 8 `a 10 ans [246] `a l’´echelle globale et il est par
cons´equent bien m´elang´e au sein de la troposph`ere. Sa source ´etant situ´ee
dans l’h´emisph`ere Nord, il existe un gradient interh´emisph´erique avec des
valeurs de 6% plus ´elev´ees dans l’h´emisph`ere Nord [246]. La variation
1
Le temps de vie photochimique est calcul´e en prenant le rapport des int´egrales d’espace de
la masse et de la destruction par photochimie.

250. 250 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.26: Distribution moyenne du rapport de m´elange de la vapeur d’eau,
exprim´ee en parties par milliers, `a 14 heures et `a 500 m`etres d’altitude, pour les
simulations d’octobre 1991, janvier 1992, mai 1992 et juillet 1992.

251. 8.5: Analyse des r´esultats du mod`ele 251
Figure 8.27: Distribution moyenne du rapport de m´elange de l’ozone, exprim´ee
en parties par millions (ppb), `a 14 heures et `a 500 m`etres d’altitude, pour les
simulations d’octobre 1991, janvier 1992, mai 1992 et juillet 1992.

252. 252 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.28: R´epartition des 21 r´egions composant le domaine du mod`ele pour
l’´etude des bilans r´egionaux, et suivant deux points de vue qui sont centr´es: a)
sur le Pacifique et b) sur l’Atlantique.
Table 8.7: Temps de vie de l’ozone et du m´ethane et bilan photochimique pour
l’ozone.
O3
Octobre 1991 Mai 1992 Juillet 1992
τres (jours) 56 13 23
Masse (Tg) 132 161 126
Production (Tg.an−1
) 162 436 402
D´epˆot sec (Tg.an−1
) 308 169 577
CH4
τres (ans) 19.2 9.6 8.9

253. 8.5: Analyse des r´esultats du mod`ele 253
saisonni`ere est due `a la variation de la concentration du radical hydrox-
yle et donc de la radiation solaire. Ceci explique la valeur de presque 20
ans que nous obtenons pour le mois d’octobre: la concentration du radical
hydroxyle est faible durant ce mois. En juillet et en mai, la concentration
est plus ´elev´ee dans l’h´emisph`ere Nord et nous obtenons alors une valeur
proche de 10 ans.
• L’ozone La dur´ee de vie de l’ozone varie entre 1 mois en juillet et 2 mois et
demi en octobre. M¨uller et Brasseur [179] obtiennent une moyenne globale
de 4 mois avec un domaine qui s’´etend jusqu’`a 50 mb. Or la concentration
d’ozone croˆıt rapidement au-dessus de la tropopause (200 mb) et si nous
calculons la dur´ee de vie en int´egrant jusqu’`a 100 mb nous obtenons alors
3 mois en juillet et 7 mois en janvier. La mˆeme remarque s’applique pour
le calcul du temps de r´esidence2
, alors que les valeurs sont inf´erieures `a un
mois M¨uller et Brasseur [179] obtiennent 3 mois.
La variation spatiale du temps de vie en fonction des saisons est donn´ee `a la
figure 8.29 pour la couche limite (de 1000 `a 850 mb) et `a la figure 8.30 pour
la troposph`ere libre (de 850 `a 200 mb). Dans la couche limite plan´etaire, le
temps de r´esidence pr´esente peu de variabilit´e spatiale en juillet avec une
valeur proche de 15 jours. Par contre en octobre, le temps de r´esidence passe
de 3 mois et demi au pˆole Nord `a 15 jours `a l’´equateur. La perte d’ozone
par d´epˆot sec a principalement lieu sur les feuillages, ce qui explique des
temps de r´esidence plus faibles sur les continents que sur les oc´eans.
Le temps de vie photochimique dans la troposph`ere libre pr´esente ´egalement
une forte variation saisonni`ere d’autant plus marqu´ee que les latitudes sont
´elev´ees. Il y a peu de variation en longitude sur le Pacifique et le temps de
vie `a Hawaii est d’environ 1 mois et demi.
La masse totale d’ozone dans la troposph`ere oscille entre 125 Tg en octo-
bre et 163 en mai en bon accord avec les valeurs que calculent Roelofs et
Lelieveld [207] pour l’h´emisph`ere Nord: 123 Tg et 153 Tg. Les productions
nettes varient d’un facteur trois entre octobre (150 Tg.an−1
) et juillet (430
Tg.an−1
) ce qui correspond au facteur calcul´e par les mˆemes auteurs: 140
en automne et 420 en ´et´e. Les taux de d´epˆot sec sont de 300 Tg.an−1
en
octobre et 575 Tg.an1
en juillet ce qui est comparable aux valeurs corre-
spondantes de Roelofs et Lelieveld [207]: 196 Tg.an−1
en automne et 588
Tg.an−1
en ´et´e.
2
Le temps de r´esidence est calcul´e comme pour le temps de vie photochimique mais en tenant
compte ´egalement de la destruction par d´epˆot sec.

254. 254 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.29: R´epartition par r´egion du temps de r´esidence, exprim´e en mois, de
l’ozone dans la couche limite plan´etaire pour les mois de a) Octobre 1991, b)
Janvier 1992, c) Mai 1992 et d) Juillet 1992.

255. 8.5: Analyse des r´esultats du mod`ele 255
Figure 8.30: R´epartition par r´egion du temps de vie photochimique, exprim´e en
mois, de l’ozone dans la troposph`ere libre pour les mois de a) Octobre 1991, b)
Janvier 1992, c) Mai 1992 et d) Juillet 1992.

256. 256 Chapitre 8: Analyse des donn´ees MLOPEX-II
Bilan photochimique.
Pour pouvoir comparer les r´egions continentales et oc´eaniques, nous
avons subdivis´e le domaine en 8 sous-domaines qui incluent les r´egions d´efinies `a
la figure 8.28:
1. Le Pacifique: r´egions 3,6,7,8,9,10,11,12,13,14,16,17,18,19,21
2. L’Atlantique Nord: r´egion 4
3. L’Europe: r´egion 5
4. L’Asie centrale: r´egion 2
5. L’Asie de l’Est: r´egion 3
6. L’Am´erique du Nord: r´egion 20
7. L’Am´erique centrale: r´egion 1
8. Le Pˆole Nord: r´egion 15
Les masse, production photochimique nette et la perte par d´epˆot sec sont donn´ees
pour l’ozone au tableau 8.8, pour les oxydes d’azote impairs au tableau 8.9, pour
l’acide nitrique au tableau 8.10 et pour le nitrate de peroxy-ac´etyle au tableau
8.11.
• L’ozone. En ce qui concerne l’ozone, nous constatons qu’au dessus des
continents il y a production d’ozone, avec un maximum relatif en Am´erique
centrale. Sur le Pacifique qui repr´esente 25% de la masse d’ozone, il y a pro-
duction chimique nette en mai et en juillet et une destruction importante
en octobre. C’est l’abondance des oxydes d’azote qui contrˆole la production
d’ozone, par les r´eactions entre NO et les radicaux peroxydes (principale-
ment HO2 et CH3O2). Or nous avons calcul´e une augmentation des NOx
de pr`es de 50% entre octobre et juillet. Si l’on tient ´egalement compte du
d´epˆot sec, on voit que le Pacifique agit comme un puits d’ozone pour les
trois p´eriodes. La quantit´e d´etruite compte pour pr`es de la moiti´e de ce qui
est produit en Asie de l’Est. Il est difficile de comparer les valeurs pour le
Pacifique avec celles sur l’Atlantique Nord car ce dernier ne couvre, dans
notre cas, que la partie au Nord de 30o
de latitude. Pour cette r´egion, il y
a production nette d’ozone en raison du flux ´elev´e de pr´ecurseurs en prove-
nance d’Am´erique du Nord [9]. Le temps de vie de l’ozone est plus ´elev´e
sur le Pacifique que sur les continents en juillet quand le feuillage est le plus
abondant et inversement pour les deux autres mois.

257. 8.5: Analyse des r´esultats du mod`ele 257
La distribution de la concentration moyenne d’ozone `a la surface (figure
8.31) refl`ete la production photochimique continentale, la d´eposition s`eche
et le transport. Les maxima ont lieu en mai et en juillet quand la radiation
solaire est la plus intense dans l’h´emisph`ere Nord. Le minimum oc´eanique
est principalement du `a la r´eaction de d´esactivation de l’atome O(1
D) avec
la vapeur d’eau.
• Les oxydes d’azote impair. Les oxydes d’azote sont principalement
d´etruits par la r´eaction avec le radical OH qui forme du HNO3 et avec le radi-
cal peroxy-ac´etyle (CH3CO3) qui forme du nitrate de peroxy-ac´etyle (PAN).
Leur destruction a lieu essentiellement au-dessus des r´egions pollu´ees, de
l’Europe et de l’Am´erique du Nord. Le taux de destruction est le plus ´elev´ee
en juillet en raison de l’abondance plus ´elev´ee des radicaux OH durant ce
mois (la radiation solaire est alors plus intense). Au-dessus de l’Atlantique
et du Pacifique, il y a une production nette qui est due principalement `a
la d´ecomposition du PAN. Le taux de production par le PAN va d´ependre
de son abondance et de la temp´erature ambiante. Plus la temp´erature
est ´elev´ee et moins longtemps le PAN est transport´e. La perte par d´epˆot
sec ´etant peu ´elev´ee sur les surfaces d’eau, le Pacifique agit donc comme
une source photochimique de NOx. Sa fraction de la famille des compos´es
azot´es3
(NOy) est g´eographiquement variable avec un minimum (10%) au-
dessus des r´egions pollu´ees et un maximum loin des sources (30%).
• L’acide nitrique. L’acide nitrique HNO3 est form´e principalement par
NO2+OH ce qui explique les valeurs maxima de sa production nette au-
dessus de l’Europe et de l’Am´erique du Nord, l`a o`u les ´emissions de com-
pos´es azot´es sont les plus ´elev´ees. A l’inverse, au-dessus du Pacifique et
de l’Atlantique, l’abondance des oxydes d’azote est insuffisante pour com-
penser la perte de l’acide nitrique par d´epˆot sec et humide. Le Pacifique agit
donc comme un puits pour l’acide nitrique qui est aussi un puits important
pour NOy puisque HNO3 repr´esente pr`es de 50% de NOy.
• Le nitrate de peroxy-ac´etyle. Le nitrate de peroxy-ac´etyle (PAN) est
form´e en pr´esence de NOx et du radical de peroxy-ac´etyle (CH3CO3). Ce
radical est le produit de la d´ecomposition des hydrocarbures non-m´ethaniques.
Sa destruction par d´ecomposition thermique qui est une fonction croissante
de la temp´erature ne permet son transport `a grande ´echelle que dans les
parties hautes de la troposph`ere. Son temps de vie moyen n’est que d’un
jour, mais il est de plusieurs jours au-dessus de la couche limite plan´etaire.
Au-dessus du Pacifique, il constitue une source de NOx qui d´ecroˆıt rapide-
ment lorsque l’on s’´eloigne de la cˆote industrielle asiatique.
3
NOy=HNO3+NO+NO2+2 × N2O5+PAN+MPAN+ONIT.

258. 258 Chapitre 8: Analyse des donn´ees MLOPEX-II
Figure 8.31: Distibution de la concentration moyenne de l’ozone `a la surface pour
les mois de: a) Octobre 1991, b) Janvier 1992, c) Mai 1992 et d) Juillet 1992

259. 8.5: Conclusions 259
Table 8.8: Bilan photochimique par sous-domaine de l’ozone.
Octobre 1991
Pac Atl Eu As C As E Am N Am C Pˆole N
τres (jours) 47 79 56 102 54 83 18 1400
Masse (Tg) 32 9.5 18 28 10 15 6 14
Production (Tg.an−1
) -8.5 15 40 16 32 25 43 -0.8
D´epˆot (Tg.an−1
) 27 6 61 63 33 50 64 3
O3/NOy 335 279 232 349 324 272 245 363
Mai 1992
τres (jours) 6 30 23 34 25 26 14 118
Masse (Tg) 38 12 23 32 12 19 7 18
Production (Tg.an−1
) 2.2 3.9 29 24 12 23 13 1
D´epˆot (Tg.an−1
) 12 3 41 42 17 33 19 2
O3/NOy 215 186 160 216 209 198 160 277
Juillet 1992
τres (jours) 26 32 21 23 17 20 14 92
Masse (Tg) 30 8.6 19 27 7.6 15 6.4 13
Production (Tg.an−1
) 4.6 6.7 59 70 37 74 41 9
D´epˆot (Tg.an−1
) 31 7 128 158 51 122 58 21
O3/NOy 243 261 272 226 230 244 171 328
8.6 Conclusions
Au cours de ce chapitre nous avons analys´e les donn´ees de la campagne
de mesure MLOPEX-II et les r´esultats de notre mod`ele pour quatre p´eriodes de
8 jours.
En ´etudiant les r´etro-trajectoires, nous avons pu interpr´eter les variations
saisonni`ere, journali`ere et diurne de la composition chimique au-dessus du site de
mesure. La variation saisonni`ere indique clairement l’importance du transport `a
grande ´echelle depuis l’Asie en janvier et en mai, et dans une moindre mesure en
juillet. Pour les deux premi`eres p´eriodes les masses d’air subissent une descente
rapide vers Hawaii, alors qu’en juillet le transport a lieu pr`es de la surface. La
variation journali`ere des vents dominants, en g´en´eral du Nord-Est, provoque une
profonde modification de la composition chimique: les masses d’air venant du sud
sont pauvres en CO, NOx, O3 et riches en H2O2, et inversement quand les masses
d’air viennent du Nord ou du Nord-Est.
Une ´etude de traceur color´e en fonction de la position de la source

260. 260 Chapitre 8: Analyse des donn´ees MLOPEX-II
Table 8.9: Bilan photochimique par sous-domaine des oxydes d’azote impairs
(NOx).
Octobre 1991
Pac Atl Eu As C As E Am N Am C Pˆole N
τres (heures) 5 5 8 8 4 6 1 34
Masse (Tg) 0.03 0.008 0.02 0.01 0.007 0.01 0.01 0.001
Production (Tg.an−1
) 0.05 0.05 -1 -0.02 -0.4 -0.9 -0.1 -0.1
D´epˆot (Tg.an−1
) 0.032 0.004 0.45 0.275 0.91 0.29 0.07 0.005
NOx/NOy 0.3 0.25 0.27 0.14 0.23 0.22 0.45 0.04
Mai 1992
τres (heures) 2 2 2 3 2 2 1 6
Masse (Tg) 0.03 0.008 0.02 0.01 0.006 0.01 0.01 0.006
Production (Tg.an−1
) 0.07 0.02 -0.33 -0.1 -0.12 -0.28 -0.05 -0.009
D´epˆot (Tg.an−1
) 0.2 0.03 0.06 0.08 0.03 0.04 0.06 0.02
NOx/NOy 0.15 0.12 0.11 0.1 0.11 0.11 0.25 0.09
Juillet 1992
τres (heures) 3 3 2 2 1 1 1 5
Masse (Tg) 0.046 0.008 0.01 0.03 0.008 0.01 0.01 0.004
Production (Tg.an−1
) 0.025 0.045 -1.16 -0.15 -0.17 -0.8 -0.18 -0.08
D´epˆot (Tg.an−1
) 0.03 0.002 0.34 0.17 0.08 0.2 0.08 0.01
NOx/NOy 0.37 0.25 0.21 0.17 0.25 0.19 0.4 0.11

261. 8.5: Conclusions 261
Table 8.10: Bilan photochimique par sous-domaine de l’acide nitrique HNO3.
Octobre 1991
Pac Atl Eu As C As E Am N Am C Pˆole N
Masse (Tg) 0.04 0.02 -.03 0.04 0.01 0.02 0.008 0.02
Production (Tg.an−1
) -0.12 -0.02 0.69 0.8 0.21 0.43 0.14 0.01
D´epˆot (Tg.an−1
) 0.23 0.1 -1.54 0.6 0.6 1.3 0.49 0.1
HNO3/NOy 0.44 0.48 0.42 0.47 0.45 0.47 0.33 0.6
Mai 1992
Masse (Tg) 0.1 0.04 0.08 0.08 0.03 0.05 0.02 0.04
Production (Tg.an−1
) -0.24 -0.01 0.7 0.2 0.2 0.38 0.16 -0.03
D´epˆot (Tg.an−1
) 0.19 0.08 1.4 0.53 0.42 1.1 0.31 0.02
HNO3/NOy 0.58 0.57 0.53 0.53 0.52 0.53 0.44 0.62
Juillet 1992
Masse (Tg) 0.06 0.02 0.04 0.05 0.01 0.03 0.01 0.02
Production (Tg.an−1
) -0.3 -0.05 0.77 0.06 0.09 0.47 0.07 -0.02
D´epˆot (Tg.an−1
) 0.21 0.14 2.1 0.95 0.5 1.6 0.44 0.08
HNO3/NOy 0.47 0.53 0.53 0.43 0.45 0.5 0.36 0.54

262. 262 Chapitre 8: Analyse des donn´ees MLOPEX-II
Table 8.11: Bilan photochimique par sous-domaine du nitrate de peroxy-ac´etyle
(PAN).
Octobre 1991
Pac Atl Eu As C As E Am N Am C Pˆole N
τres (heures) 14 10 7 12 7 13 3 359
Masse (Tg) 0.006 0.002 0.005 0.007 0.003 0.003 0.002 0.003
Production (Tg.an−1
) -0.1 -0.05 0.03 0.11 -0.05 0.01 -0.07 0.002
D´epˆot (Tg.an−1
) 0.03 0.03 0.12 0.14 0.1 0.16 0.06 0.01
PAN/NOy 0.06 0.07 0.07 0.08 0.1 0.06 0.08 0.09
Mai 1992
τres (heures) 28 24 10 20 11 17 4.5 543
Masse (Tg) 0.03 0.01 0.03 0.04 0.01 0.02 0.009 0.01
Production (Tg.an−1
) -0.18 -0.14 -0.45 -0.47 -0.11 -0.04 -0.11 0.002
D´epˆot (Tg.an−1
) 0.04 0.17 0.77 2.0 0.08 0.1 0.47 0.14
PAN/NOy 0.18 0.18 0.22 0.24 0.26 0.22 0.21 0.2
Juillet 1992
τres (heures) 21 20 4 6 4 5 4 46
Masse (Tg) 0.006 0.002 0.005 0.006 0.002 0.005 0.003 0.003
Production (Tg.an−1
) -0.03 -0.04 -0.006 -0.12 -0.07 0.006 0.005 -0.02
D´epˆot (Tg.an−1
) 0.02 0.002 0.14 0.19 0.05 0.25 0.061 0.02
PAN/NOy 0.04 0.06 0.07 0.05 0.05 0.08 0.08 0.07

263. 8.5: Conclusions 263
d’´emission a mis en ´evidence deux aspects interessants:
1. L’abondance, en janvier, de traceur venant d’Am´erique est plus importante
que celle venue d’Asie mˆeme si Hawaii est sous l’influence des vents d’Ouest.
Une ´etude de sensibilit´e a montr´e que la position g´eographique des nuages
de types cumulonimbus ´etait `a l’origine d’un accroissement du transport
par les courants jets du traceur d’origine am´ericaine alors que le traceur
venu d’Asie doit se d´eplacer longtemps `a la surface.
2. Le transport des polluants locaux depuis leur source d’´emission, principale-
ment sur la cˆote Est, jusqu’`a l’Observatoire ne se fait pas toujours par voie
directe. En fonction de la direction des vents dominants, les polluants sont
transport´es de l’autre cˆot´e de l’ˆıle en la contournant par le Nord ou le Sud.
Pour des conditions de vents montants les polluants atteignent apr`es deux
jours l’Observatoire.
Cette ´etude a ´egalement montr´e que l’influence des ´emissions des autres ˆıles de
l’Archipel ´etaient insignifiante sur les r´esultats `a l’Observatoire.
Nous avons compar´e les r´esultats du mod`ele aux donn´ees prises au sol,
`a l’Observatoire de Mauna Loa (MLO), et par avion (DC8 de la NASA en oc-
tobre et King-Air de l’Universit´e du Wyoming en mai). Il en est ressorti que
les valeurs calcul´ees sont en bon accord avec les mesures par avion mais sont
syst´ematiquement trop faibles `a MLO. Le mod`ele simule bien la structure verti-
cale et horizontale de la chimie atmosph´erique `a Hawaii. Mais il semble que les
vitesses de d´epˆot y soient trop ´elev´ees.
La production d’ozone par les ´emissions locales de NOx varie de 1 (jan-
vier) `a 30 ppb par jour (juillet) pr`es des sources et d´ecroˆıt jusqu’`a 0.4 (janvier)
`a 4 ppb par jour (juillet) `a l’Observatoire. La dur´ee de vie de plusieurs jours de
l’ozone permet son transport par les vents dominants du Nord-Est mais seule une
faible fraction atteint l’Observatoire, le restant ´etant repouss´e au Sud-Ouest de
l’ˆıle.
Finalement, les bilans r´egionaux de l’ozone et des compos´es azot´es ont
permis de diff´erencier les productions et les pertes chimiques sur les continents
et les oc´eans. L’oc´ean Pacifique agit comme un puits d’ozone dont la masse
d’environ 33 Tg est d´etruite `a raison de 24 Tg par an. Cette perte est compens´ee
par le transport depuis les r´egions continentales, le temps de vie de l’ozone ´etant
proche d’un mois. Les oxydes d’azote qui limitent la production d’ozone ont
une dur´ee de vie trop courte (moins d’une journ´ee) pour ˆetre transport´es sur le
Pacifique. Leur faible abondance conduit `a une destruction de 8.5 Tg par an en
octobre, et une faible production en mai (2.2 Tg.an−1
) et en juillet (4.6 Tg.an−1
).

264. 264 Chapitre 8: Analyse des donn´ees MLOPEX-II

265. Chapter 9
Conclusions
L’objectif de notre travail ´etait de d´evelopper un mod`ele atmosph´erique
de chimie et transport destin´e `a l’´etude de l’impact des activit´es humaines sur la
composition chimique de la troposph`ere non-pollu´ee. Ce mod`ele a ´et´e appliqu´e au
cas particulier de l’oc´ean Pacifique o`u nous avons pu estimer l’effet des ´emissions
continentales sur la photochimie des r´egions ´eloign´ees de l’Archipel d’Hawaii.
Dans ce but, nous avons analys´e plus particuli`erement les mesures effectu´ees dans
le cadre de la campagne Mauna Loa Observatory Photochemistry EXperiment
(MLOPEX).
Durant cette campagne qui s’est d´eroul´ee au cours de quatre p´eriodes
d’un mois caract´erisant les saisons des ann´ees 1991-1992, un grand nombre de
compos´es gazeux ont ´et´e simultan´ement mesur´es `a l’Observatoire de Mauna Loa
sur l’ˆıle d’Hawaii. La situation isol´ee de l’ˆıle et l’altitude ´elev´ee du site des mesures
(troposph`ere libre pendant une partie de la journ´ee) ont permis d’´evaluer l’effet
des ´emissions continentales sur la composition chimique de la troposph`ere libre `a
Hawaii.
Pour mener `a bien celui-ci, nous avons proc´ed´e aux ´etapes suivantes:
1. Nous avons analys´e les processus chimiques et dynamiques en relation avec
les donn´ees MLOPEX. Nous pouvons en d´eduire que le transport `a grande
´echelle des polluants continentaux jusqu’`a Hawaii se produit par la succes-
sion des ph´enom`enes suivants:
(a) ´emission par les sources biog´eniques et anthropiques,
(b) d´epˆot sec `a la surface terrestre et humide dans les pr´ecipitations,
(c) m´elange dans la couche limite plan´etaire par la turbulence
(d) leur d´etraˆınement dans la troposph`ere libre par convection au sein des
cumulonimbus,
265

266. 266 Chapitre 9: Conclusions
(e) transport horizontal dans les couches sup´erieures de la troposph`ere par
les vents rapides d’ouest,
(f) la subsidence tropicale associ´ee `a la branche descendante de la cellule
de Hadley.
En outre, il semblait n´ecessaire d’´evaluer l’impact des ´emissions locales de
ces polluants, ce qui n´ecessitait de connaˆıtre:
(a) le taux d’´emission locale,
(b) le m´elange avec les masses d’air maritime dans la couche limite et les
masses d’air continental dans la troposph`ere libre,
(c) le transport jusqu’`a l’Observatoire qui est le r´esultat d’une interaction
entre les vents dominants du Nord-Est, les brises de mer et de terre et
d’un ´ecoulement de montagne.
2. Nous avons ´etabli un ensemble d’´equations aux d´eriv´ees partielles non-
lin´eaires pour les variables chimiques et dynamiques. Les termes relatifs
aux ph´enom`enes de transport `a sous-´echelle (turbulence dans la couche
limite plan´etaire et convection par les cumulonimbus) ont ´et´e param´eteris´e.
3. Pour simplifier cet ensemble, nous avons d´ecoupl´e les ´equations de la dy-
namique et de la chimie. Les variables dynamiques sont obtenues en com-
binant les donn´ees globales analys´ees du European Center for Medium
Weather Forecasting (ECMWF) et les r´esultats de simulations effectu´ees
`a l’aide du mod`ele Mesoscale Model version 5 (MM5). Les valeurs de ces
variables ont ´et´e compar´ees avec les observations en de multiples stations.
De cette comparaison il apparait que nous sommes capables de simuler cor-
rectement les variations diurne, journali`ere et saisonni`ere de la circulation
`a l’´echelle r´egionale.
4. A l’´echelle synoptique, l’absence de donn´ees `a la surface terrestre nous a
contraint `a d´eveloper un mod`ele de surface terrestre pour le calcul de la
temp´erature et de l’humidit´e sp´ecifique
5. La discr´etisation des ´equations a ´et´e effectu´ee sur une grille `a maille variable.
Cette approche num´erique fournit une solution efficace `a l’´etude r´egionale
de la composition chimique de l’atmosph`ere. En effet, la r´esolution variable
permet de conjuguer une vision t´el´escopique sur une r´egion sp´ecifique en
y concentrant les points de grille et une vision globale par l’´elargissement
progressif des mailles `a mesure que l’on s’en ´eloigne. Cette approche nous a
cependant contraints `a d´evelopper des sch´emas num´eriques, en particulier
pour la r´esolution de l’advection. Ces m´ethodes ont fait l’objet de multiples
tests qui ont montr´e leur efficacit´e.

267. Conclusions 267
Nous avons d´evelopp´e un mod`ele original de chimie-transport tridimen-
sionnel de la troposph`ere qui simule la distribution de 46 compos´es gazeux,
r´eagissant suivant 138 r´eactions photochimiques, en 3027 points r´epartis
horizontalement sur l’h´emisph`ere Nord avec une r´esolution qui varie de
quelques kilom`etres au-dessus d’Hawaii `a plusieurs centaines de kilom`etres
sur les bords du domaine. Suivant la verticale, le domaine s’´etend depuis
la surface terrestre jusqu’`a 100 mb et est subdivis´e en 23 niveaux.
6. Comme conditions aux limites inf´erieures, les flux d’´emissions `a la surface
terrestre sont sp´ecifi´es. L’absence de telles donn´ees `a haute r´esolution pour
Hawaii nous a oblig´e `a cr´eer nos propres cartes avec une r´esolution de 2.5
minutes (∼ 5 km). A la limite sup´erieure, les gradients observ´es de l’ozone
et de l’acide nitrique sont impos´es. Les r´esultats du mod`ele global tri-
dimensionel de la troposph`ere IMAGES servent de conditions initiales pour
les concentrations des compos´es gazeux.
7. L’analyse des donn´ees MLOPEX a fait l’objet de cinq ´etudes distinctes:
(a) Une ´etude de r´etro-trajectoires calcul´ees sur deux jours depuis l’Observatoire
de Mauna Loa dans le but d’interpr´eter les variations journali`eres et
saisonni`eres des concentrations mesur´ees
(b) Une ´etude de traceurs dont la localisation des ´emissions est sp´ecifi´ee
pour connaˆıtre l’origine des masses d’air arrivant `a l’Observatoire de
Mauna Loa.
(c) Une comparaison des r´esultats du mod`ele non seulement avec les donn´ees
`a l’Observatoire mais ´egalement avec les mesures avions de la cam-
pagne PEM-West et de l’avion King-Air de l’Universit´e du Wyoming.
(d) Une ´etude de la chimie au-dessus d’Hawaii et en particulier de la pro-
duction d’ozone par les ´emissions locales.
(e) Une ´etude des bilans chimiques sur 21 r´egions couvrant le domaine et
en distinguant la couche limite plan´etaire de la troposph`ere libre.
De l’analyse des donn´ees MLOPEX, nous avons mis `a jour les points suivants:
1. En ce qui concerne la contribution des diff´erentes sources d’´emission
(a) L’influence des ´emissions continentales sur l’atmosph`ere d’Hawaii varie
d’une saison `a l’autre:

268. 268 Chapitre 9: Conclusions
• En octobre 1991, l’influence continentale est la plus faible: les
masses d’air se d´eplacent lentement, arrivant `a Hawaii du Sud
durant les trois premiers jours de la simulation ensuite du Nord,
• En janvier 1992, l’influence continentale est la plus importante
avec des masses d’air se d´epla¸cant rapidement depuis la cˆote asi-
atique jusqu’`a Hawaii. La localisation des cumulonimbus `a prox-
imit´e des sources d’´emission d’Am´erique du Nord, contrairement
aux sources asiatiques, favorise le transport jusqu’`a Hawaii de
traceur d’origine am´ericaine. La trajectoire de ce traceur passe
par le pˆole Nord pour arriver au-dessus de l’Asie et continuer vers
Hawaii.
• En mai 1992, l’influence des ´emissions asiatiques est pr´epond´erante
avec des masses d’air arrivant du Pacifique Nord le long d’un
m´eridien en subissant une descente de plusieurs kilom`etres en deux
jours.
• En juillet 1992, Hawaii est sous l’influence des vents d’Est qui se
d´eplacent en quelques jours depuis la cˆote californienne.
(b) L’influence des ´emissions locales sur l’air pr´elev´e `a l’Observatoire a
lieu principalement pendant la journ´ee durant les p´eriodes de vents
montants. Le chemin parcouru depuis la source d’´emission jusqu’`a
l’Observatoire d´epend de la position de la source par rapport aux zones
de divergence du vent. Si la source est en aval de cette zone le chemin
suit un trac´e complexe qui d´ebute par une mont´ee vers l’Observatoire
suivie d’un contournement de l’ˆıle par le Nord ou le Sud et enfin une
mont´ee vers l’Observatoire si les vents sont montants.
(c) L’influence des ´emissions des autres ˆıles de l’archipel d’Hawaii est en
g´en´eral insignifiante en raison de la direction des vents dominants du
Nord-Est.
2. Alors que sur l’oc´ean il y a une destruction nette d’ozone de 4 ppb par jour,
les ´emissions d’oxyde d’azote provoquent une production nette maximum
d’ozone de 30 ppb par jour `a 14 heures. La longueur du trajet entre la zone
de production et l’Observatoire r´eduit cette production `a quelques ppb par
jour voire mˆeme `a une faible destruction.
3. L’´etude des bilans par r´egion a montr´e que le Pacifique est un puits d’ozone
de l’ordre de 36 Tg.an−1
en octobre, 10 Tg.an−1
en mai et 26 Tg.an−1
en juillet. Le temps de r´esidence de l’ozone d’environ un mois permet son
transport depuis les sources continentales jusqu’au Pacifique. Les oxydes
d’azote ont une dur´ee de vie de moins d’une journ´ee et leur transport depuis
les sources continentales d’´emission est limit´e. Le principal compos´e azot´e

269. Conclusions 269
sur le Pacifique est l’acide nitrique (50%) dont le d´epˆot sec et humide sur
le Pacifique contribue `a la perte nette d’azote. Le nitrate de peroxy-ac´etyle
est peu abondant sur le Pacifique et sa faible dur´ee de vie ne permet pas
un transport efficace d’azote.
Pour terminer nous pouvons estimer que nos objectifs qui consistaient
`a d´evelopper un mod`ele de chimie-transport tridimensionnel pour l’analyse
et l’interpr´etation de donn´ees observ´ees, ont ´et´e atteints. Ce mod`ele est
actuellement le seul, `a notre connaissance, qui permette d’effectuer une
analyse r´egionale de la chimie troposph´erique en tenant compte tout `a la
fois du transport `a macro (> 1000 km) et m´eso (< 100 km) ´echelle.
Nous avons donc pu mettre en ´evidence l’influence des ´emissions continen-
tales sur une partie recul´ee de la troposph`ere qu’il est donc incorrect de qualifier
de non-pollu´ee. En extrapolant les taux d’´emission asiatique, si l’on consid`ere
le d´eveloppement industriel de la Chine, il serait int´eressant de voir si le Paci-
fique agit toujours comme un puits d’ozone. Une telle recherche constituerait un
prolongement int´eressant pour notre ´etude.

270. 270 Chapitre 9: Conclusions

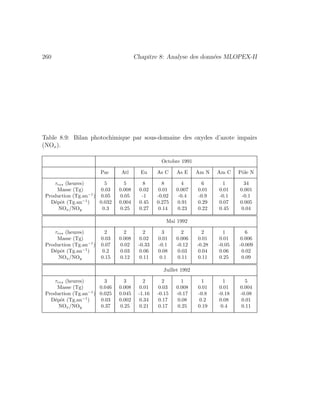
271. Annexe 1
9.1 Param´eterisation du transport convectif de
constituants gazeux par un ensemble de nu-
ages cumuliformes.
Le transport convectif d’une grandeur X peut s’exprimer par comme un flux
turbulent:
Transport convectif = w X (9.1)
o`u w et X sont les fluctuations `a petites ´echelles respectivement de la vitesse
verticale et de la grandeur X.
Ce flux est approch´e par l’expression, due `a Yanai [249], suivante
−w X ≈
i
Mci(Xci − X) (9.2)
o`u
Mci est le flux vertical massique dans le ieme
nuage convectif,
Xci est la valeur de X dans le nuage.
9.1.1 Param´eterisation du flux massique Mc
La param´eterisation de Mc est formul´ee en ´etablissant un bilan de la vapeur
d’eau. L’´equation de conservation de masse de la vapeur d’eau pour une tranche
(z, z + dz) d’un nuage est (figure 9.1):
Mcqc − (Mc + dMe
− dMd
)(qc + dqc) − dMd
(qc + 0.5dqc) + dMe
(qe + 0.5dqe) = dC
(9.3)
o`u
Mc est le flux de masse au travers de la surface z,
dMe
est le flux d’entraˆınement vers le nuage,
dMd
est le flux de d´etraˆınement vers l’environnement,
271

272. 272 Annexe 1: Param´eterisation du transport convectif
Figure 9.1: Balance de la vapeur d’eau au sein d’une tranche infinit´esimale d’un
nuage convectif.
qc est l’humidit´e sp´ecifique dans le nuage1
qe est l’humidit´e sp´ecifique dans l’environnement, et
dC est la masse d’eau condens´ee dans la couche z, z + dz par unit´e de
surface.
En n´egligeant les produits de diff´erentielles, on obtient:
dMe
(qe − qc) − Mcdqc = dC (9.5)
Si on d´efinit le taux d’entraˆınement2
par,
E =
1
Mc
dMe
dz
(9.7)
l’´equation (9.5) devient:
McE(qe − qc) − Mc
dqc
dz
=
dC
dz
(9.8)
1
Les nuages sont suppos´es satur´es en vapeur d’eau, et la valeur de qc(Tc) s’obtient `a partir
de la formule (5.30). La temp´erature dans le nuage Tc est ´etablie `a partir de l’´equation de
flottabilit´e [15]:
Tc =
1
1 − wc
g (Ewc + dwc
dz ) (1 + 0.608qc)
(9.4)
o`u wc est la vitesse verticale dans le nuage et se calcule `a partir de la relation wc(z) = wmaxΦ(z),
avec Φ(z) qui est donn´e par la relation (9.11) et wmax est tabul´ee en fonction de la pression au
sommet du nuage [15].
2
Le taux d’entraˆınement E est suppos´e constant avec l’altitude z et est donn´e par la relation
[15]:
E =
0.2
0.13(zT − zB − 103)
[m−1
] (9.6)

273. Annexe 1 273
En int´egrant l’´equation 9.8 entre la base3
zB et le sommet 4
zT du nuage, la
condensation totale dans la colonne de nuage est donn´ee par:
C =
zT
zB
Mc E(qe − qc) −
dqc
dz
dz (9.9)
Pour r´esoudre cette int´egrale, Mc(z) suit un profil vertical fix´e tel que
Mc(z) = Mc(ξ)Φ(z) (9.10)
o`u
ξ est l’altitude5
correspondant au maximum du flux Mc,
Φ est une fonction de forme6
.
La valeur Mc(ξ) peut ˆetre extraite de l’int´egrale (9.9):
Mc(ξ) =
C
zT
zB
Φ(z) E(qe − qc) − dqc
dz
dz
(9.12)
Cette derni`ere expression est ´evalu´ee pour chacun des nuages, en consid´erant
que la masse d’eau condens´ee vaut trois fois la masse d’eau pr´ecipit´ee [15], ce
qui correspond `a une ”efficacit´e” de pr´ecipitation de 33% et est calcul´ee par la
relation suivante:
C = 0.33 Prec Fconv FD (9.13)
o`u
Prec est la quantit´e d’eau pr´ecipit´ee (kg.m−2
.s−1
)
Fconv est la fraction de couverture par les nuages convectifs
FD est la fraction de couverture de nuages de hauteur donn´ee 7
.
Le flux massique maximum Mj
c (ξ) pour un nuage j peut `a pr´esent se calculer
3
La base des nuages est suppos´ee coˆıncider avec le 1er
point de grille au-dessus de la hauteur
de la PBL
4
Les pressions aux sommets des nuages cumuliformes sont obtenues `a partir des donn´ees glob-
ales satellitaires de l’ISCCP et des r´esultats du mod`ele `a m´eso-´echelle pour la r´egion d’Hawaii.
5
La valeur de ξ est approch´ee par l’expression [77]: ξ = zB + α(zT − zB), avec α =0.75 aux
tropiques et 0.5 aux latitudes moyennes
6
La fonction de forme Φ est fournie par les expressions [15]:
Φ(z) =
⎧
⎪⎨
⎪⎩
0.002
0.002−E eE(z−ξ)
− E
0.002−E e2(z−ξ)
zB < z < ξ,
zT −z
zT −ξ
2
ξ < z < zT .
(9.11)
7
La d´etermination de FD se base sur les trois hypoth`eses simplificatrices suivantes:
1. Il y a autant de nuages de hauteurs diff´erentes qu’il y a de points de grille entre le
sommet de la couche limite et la pression du nuage le plus haut (cette pression d´epend

274. 274 Annexe 1: Param´eterisation du transport convectif
par,
Mj
c (ξ) =
Cj
(Fj
D)
zj
T
zj
B
Φj(z)[Ej(qe − qc) − dqc
dz
]dz
(9.14)
Le flux massique pour l’ensemble des nuages s’obtient en sommant les contribu-
tions Mj
c de chaque nuage j:
Mc(z) =
j
Mj
c (ξ)Φj
(z) (9.15)
9.1.2 D´etermination de Xci
En ´etablissant un bilan pour un compos´e gazeux de rapport de m´elange
f, de la mˆeme mani`ere que pour la vapeur d’eau, au travers d’un nuage convectif
moyen repr´esentant l’ensemble des nuages de sommet d’altitudes diff´erentes, on
obtient:
dfc
dz
+ Efc = Efe (9.16)
dont la solution analytique pour fc est donn´ee par la formule:
fc = fB + (Efee Edz
)dz e− Edz
(9.17)
o`u
fB est le rapport de m´elange `a l’altitude zB et
E = j Ej.
Connaissant Mc et fc, le gradient vertical du transport convectif peut se calculer
ais´ement en remarquant que:
∂w f
∂z
= − ∂
∂z
Mc(fc − fe)
= −Mc
∂fc
∂z
+ Mc
∂fe
∂z
− (fc − fe)∂Mc
∂z
= Mc
∂fe
∂z
− δ(fc − fe) (9.18)
de la latitude),
2. Les sommets des nuages convectifs coˆıncident avec un point de grille qui a une pression
inf´erieure `a 700mb
3. La base des nuages coˆıncide avec le premier point de grille situ´e au-dessus de la couche
limite et correspondant `a une pression inf´erieure `a 900mb
En se basant sur l’article de Houze et al. [120], nous supposons que FD suit une variation
sinusoˆıdale avec l’altitude z telle que FD = 1
NP +1 (1 + cos(i−1
NP π)) avec i variant de 1 `a NP+1,
et NP est le nombre de points de grille entre 700mb et la pression du nuage convectif le plus
´elev´e. On constate que l’int´egrale de FD entre 1 et NP+1 est bien ´egale `a 1

275. Annexe 1 275
avec δ qui repr´esente le taux de d´etraˆınement8
.
Dans l’´equation (9.18) le premier terme du membre de droite repr´esente une
source due `a l’affaissement de l’air dans l’environnement entourant les nuages, le
deuxi`eme terme correspond `a une perte par d´etraˆınement de l’air hors du nuage.
8
δ = McE − ∂Mc
∂z

276. 276 Annexe 1: Param´eterisation du transport convectif

277. Annexe 2
9.2 Approximation par ´el´ements finis
L’approximation par ´el´ements finis consiste `a approcher une fonction sur
un sous-domaine tel que
• L’approximation sur un ´el´ement fini ne fait intervenir que les variables aux
noeuds de cet ´el´ement,
• Les fonctions approch´ees sont continues sur chaque ´el´ement fini et satisfont
des conditions de continuit´e entre ´el´ements
La g´eom´etrie de tous les ´el´ements finis est d’abord d´efinie analytiquement. En-
suite les fonctions d’interpolation Ni(˜x, ˜y, σ) en chaque noeud de chaque ´el´ement
sont construites. De mani`ere `a simplifier la d´efinition analytique des ´el´ements
finis et `a r´eduire le nombre de fonctions Ni, on pr´ef`ere travailler sur des ´el´ements
de r´ef´erence: un ´el´ement de r´ef´erence V r
est un ´el´ement de forme tr`es simple
(segment, carr´e, triangle, cube, pyramide) et de dimension unitaire, rep´er´e dans
un espace de r´ef´erence, qui peut ˆetre transform´e en chaque ´el´ement r´eel V e
par
une transformation g´eom´etrique τe
(figure 9.2). La transformation τe
d´efinit
les coordonn´ees (˜x, ˜y, σ) de chaque point de l’´el´ement r´eel `a partir des coor-
donn´ees (ξ, η, ζ) du point correspondant de l’´el´ement de r´ef´erence. Les ´el´ements
de r´ef´erence sont d´efinis `a partir d’un nombre de noeuds identique `a celui de
l’´el´ement r´eel. Donc un ´el´ement r´eel parall´elipip´edique `a 4 noeuds aura un ´el´ement
de r´ef´erence diff´erent qu’un ´el´ement de mˆeme forme mais `a 9 noeuds. Une fonction
X est approch´ee sur l’´el´ement de r´ef´erence par l’approximation:
X(ξ, η, ζ) =
n
i=1
Ni(ξ, η, ζ)Xi (9.19)
o`u
Xi est la valeur de la fonction X au noeud i,
Ni(ξ, η, ζ) est la fonction d’interpolation au noeud i de l’´el´ement de
r´ef´erence,
277

278. 278 Annexe 2: Approximation par ´el´ements finis
Figure 9.2: Transformation τe
d’un ´el´ement de r´ef´erence vers un ´el´ement r´eel.
n est le nombre de noeud de l’´el´ement.
La construction des fonctions d’interpolation N est faite `a partir de polynˆomes
formant une base orthonormale et dont le nombre est ´egal au nombre de noeuds
de l’´el´ement fini. Ces polynˆomes sont tels qu’en chaque point d’un ´el´ement fini la
somme des fonctions d’interpolation vaut 1 et elles s’annulent en chaque noeud
except´e au noeud auquel elle sont attach´ees o`u elles valent 1. La m´ethode de
construction des fonctions d’interpolation pouvant ˆetre trouv´ee dans l’ouvrage
de Zienkiewicz et Taylor [253], nous nous limiterons `a donner les expressions des
fonctions d’interpolation, de leurs d´eriv´ees et du jacobien de la transformation τe
pour les types d’´el´ements finis que nous avons utilis´es.
9.2.1 El´ement rectiligne lin´eaire
Les ´el´ements rectilignes lin´eaires (figure 9.3) sont d´efinis par les deux noeuds
aux extr´emit´es. Une fonction et ses d´eriv´ees premi`eres sont continues sur cet
´el´ement mais seule la fonction est continue sur la fronti`ere de l’´el´ement. Le
d´eterminant du jacobien est ´egal `a la moiti´e de la longueur de l’´el´ement. Les
fonctions d’interpolation et les d´eriv´ees premi`eres aux 2 noeuds sont donn´ees au
tableau 9.2. L’erreur d’approximation est du deuxi`eme ordre et est donn´ee par
la relation:
e(ξ) ≤
1
2
(1 − ξ2
) Max(
∂2
fex
∂ξ2
) (9.20)

279. Annexe 2 279
Table 9.1: Fonctions d’interpolation et ses d´eriv´ees premi`eres de l’´el´ement trian-
gulaire `a 3 noeuds, exprim´ees dans l’espace de r´ef´erence
{N} {∂N/∂ξ} {∂N/∂η}
1 1 − ξ − η -1 -1
2 ξ 1 0
3 η 0 1
o`u fex est la valeur exacte de la fonction.
L’erreur est donc de forme parabolique avec un maximum au milieu de l’´el´ement
et s’annule aux deux noeuds o`u la solution est exacte.
Figure 9.3: Transformation d’un el´ement lin´eaire.
9.2.2 El´ement triangulaire lin´eaire
Les ´el´ements triangulaires lin´eaires sont d´efinis par les 3 noeuds des sommets.
Les fonctions d’interpolation et ses d´eriv´ees exprim´ees dans l’espace de r´ef´erence
sont donn´ees au tableau 9.1. Les noeuds sont num´erot´es tant dans l’´el´ement
de r´ef´erence que dans l’´el´ement r´eel dans le sens anti-horlogique (figure 9.2. Le
d´eterminant du jacobien de la transformation est ´egal `a deux fois l’aire du triangle.
L’erreur d’approximation e(ξ, η) est donn´ee par la formule suivante
e(ξ, η) =
1
2
ξ(1 − ξ)
∂2
fex
∂ξ2
− 2ξη
∂2
fex
∂ξ∂η
+ η(1 − η)
∂2
fex
∂η2
(9.21)
o`u l’on voit que l’erreur est du deuxi`eme ordre et s’annule aux trois sommets
du triangle. La fonction inconnue et ses d´eriv´ees premi`eres sont continues sur

280. 280 Annexe 2: Approximation par ´el´ements finis
Table 9.2: Fonctions d’interpolation et ses d´eriv´ees premi`eres pour l’´el´ement rect-
angulaire quadratique `a 9 noeuds, exprim´ees dans l’espace de r´ef´erence.
{N} {∂N/∂ξ} {∂N/∂η}
1 0.25(1 − ξ)(1 − η)ξη 0.25(1 − 2ξ)(1 − η)η 0.25(1 − ξ)(1 − 2η)ξ
2 −0.5(1 − ξ2
)(1 − η)η (1 − η)ξη −0.5(1 − ξ2
)(1 − 2η)
3 −0.25(1 + ξ)(1 − η)ξη −0.25(1 + 2ξ)(1 − η)η −0.25(1 + ξ)(1 − 2η)ξ
4 0.5(1 + ξ)(1 − η2
)ξ 0.5(1 + 2ξ)(1 − η2
) −(1 + ξ)ξη
5 0.25(1 + ξ)(1 + η)ξη 0.25(1 + 2ξ)(1 + η)η 0.25(1 + ξ)(1 + 2η)
6 (1 − ξ2
)(1 + η)η −(1 + η)ξη 0.5(1 − ξ2
)(1 + 2η)
7 −0.25(1 − ξ)(1 + η)ξη −0.25(1 − 2ξ)(1 + η)η −0.25(1 − ξ)(1 + 2η)ξ
8 −0.5(1 − ξ)(1 − η2
)ξ −0.5(1 − 2ξ)(1 − η2
) (1 − ξ)ξη
9 (1 − ξ2
)(1 − η2
) −2(1 − η2
)ξ −2(1 − ξ2
)η
l’´el´ement. La fonction inconnue est continue sur la fronti`ere de l’´el´ement, mais
ses d´eriv´ees premi`eres ne le sont pas: la d´eriv´ee tangentielle est continue et seule
la d´eriv´ee normale est discontinue.
9.2.3 El´ement quadratique complet
L’´el´ement quadrilat´eral quadratique complet est d´efini par 9 noeuds (figure 9.4).
Une fonction et ses d´eriv´ees premi`eres et secondes sont continues sur l’´el´ement
mais seule la fonction est continue sur les cˆot´es. Les fonctions d’interpolation
et ses d´eriv´ees premi`eres exprim´ees sur l’´el´ement de r´ef´erence sont donn´ees au
tableau 9.2. L’erreur d’approximation sur cet ´el´ement est du troisi`eme ordre. Les
noeuds sont num´erot´es tant dans l’´el´ement de r´ef´erence que dans l’´el´ement r´eel
dans le sens anti-horlogique. La matrice du jacobien peut s’exprimer en fonction
des fonctions d’interpolation d´ependant des coordonn´ees de r´ef´erence (ξ, η) et des
coordonn´ees des noeuds dans l’espace r´eel (xi, yi), en remarquant que
(J) =
∂x
∂ξ
∂y
∂ξ
∂x
∂η
∂y
∂η
=
9
i=1
∂Ni
∂ξ xi
9
i=1
∂Ni
∂ξ yi
9
i=1
∂Ni
∂η xi
9
i=1
∂Ni
∂η yi
9.2.4 El´ements tridimensionnels
Les ´el´ements `a trois dimensions sont construits en scindant les fonctions d’interpolation
suivant la verticale et l’horizontale. Une fonction X sera interpol´ee `a 3 dimensions
par une relation du type,
X =
k i
Ni(ξ, η)Nk(ζ) (9.22)

281. Annexe 2 281
Figure 9.4: Transformation d’un ´el´ement rectangulaire `a 9 noeuds.
o`u les indices i et k portent respectivement sur les noeuds horizontalement (3 ou
9) et verticalement (toujours 2).

282. 282 Annexe 2: Approximation par ´el´ements finis

283. Bibliography
[1] Abe, M., et S. Abe, Trends in the chemical state of Polonium-210 in the
atmosphere, NRE III, Houston, Texas, USA, 430-439, 1978.
[2] ACD Textbook, Atmospheric Chemistry and Global Change, A textbook
prepared by scientists at the NCAR, Boulder, Colorado, en pr´eparation.
[3] Akimoto, H., N. Nakane, et Y. Matsumoto, The chemistry of oxidant gen-
eration: Tropospheric ozone increase in Japan, The Chemistry of the At-
mosphere: Its impact on Global Change, J.G. Calvert Edition, Blackwell
Sc. Publ., Oxford, 261-273, 1994.
[4] Anderson, B. E., J. E. Collins, G. W. Sachse, G. W. Whiting, D. R. Blake,
et F. S. Rowland, AASE-II observations of trace carbon species distributions
in the mid to upper troposphere, Geophys. Res. Lett., 20, 2539-2542, 1993.
[5] Anderson, W. K., A grid generation and flow solution method for the Euler
equations on unstructured grids, J. Comput. Phys., 110, 23-38, 1994.
[6] Almanac of the 50 States, Basic data profiles with comparative tables, Edi-
tion E.R. Hornor, Information Publications, Palo Alto, 1992.
[7] Andreae, M.O., Biomass burning: its history, and distribution and its im-
pact on environmental quality and global climate, Global biomass burning,
Atmospheric, climatic and biosphere implications, Edition J.S. Levine, MIT
Press, Cambridge, 1991.
[8] Anthes, R. A., E.-Y. Hsie, et Y.-H. Kuo, Description of the Penn
State/NCAR Mesoscale Model version 4 (MM4), NCAR Technical note,
NCAR/TN-282+STR, Boulder, Colorado, 1987.
[9] Atherton, C. S., S. Sillman, et J. Walton, Three-dimensional global modeling
studies of the transport and photochemistry over the North Atlantic Ocean,
J. Geophys. Res., 101, 29289-29304, 1996.
283

284. 284 Bibliographie
[10] Atkinson, B. W., Introduction to the fluid mechanic of meso-scale flow
fields, dans Diffusion and Transport of pollutants in atmospheric mesoscale
flow fields, Kluwer Acadenic Publishers, Dordrecht, 1-20, 1995.
[11] Atlas of Hawaii, 2d
Edition, Department of Geography, University of Hawaii
Press, Honolulu, 1983.
[12] Atlas, E. L., B. A. Ridley, G. H¨ubler, J. G. Walega, M. A. Carroll, D.
D. Montzka, B. J. Huebert, R. B. Norton, F. E. Grahek, et S. Schauffler,
Partitioning and budget of NOy species during the Mauna Loa Observatory
Experiment, J. Geophys. Res., 97, 10449-10462, 1992.
[13] Atlas, E. L., et B. A. Ridley, The Mauna Loa Observatory Photochemistry
Experiment: Introduction, J. Geophys. Res., 101, 14531-14541, 1996.
[14] Atlas, E., B. A. Ridley, J. G. Walega, J. Greenberg, G. Kok, T. Staffel-
bach, S. Schauffler, J. Lind, G. H¨ubler, R. Norton, GTE PEM-West Science
Team, E. Dlugokencky, J. Elkins, S. Oltmans, G. Mackay, et D. Karecki, A
comparison of aircraft and ground-based measurements at Mauna Loa Ob-
servatory, Hawaii, during GTE PEM-West and MLOPEX-2, J. Geophys.
Res., 101, 14599-14612, 1996.
[15] Austin, P.M. et R. A. Houze, A technique for computing vertical transports
by precipitating cumuli, J. Atmos. Sci, 30, 1100-1111, 1973.
[16] Bachmeier, A. S., R. E. Newell, M. C. Shipham, Y. Zhu, D. R. Blake, et E.
V. Browell, PEM-West A: Meteorological overview, J. Geophys. Res., 101,
1655-1678, 1996.
[17] Balkanski Y., D. J. Jacob, R. Arimoto, M. A. Kritz, Distribution of 222
Rn
over the North Pacific: Implications for continental influences, J. Atm.
Chem., 14, 353-374, 1992.
[18] Barry, R. G., Mountain weather and climate, Methuen, London, England,
1981.
[19] Baughcum, S.L., M. Metwally, R.K. Seals, et D.J. Wuebbles, Emissions
scenarios development: Complete scenario database (subchapter 3-4), dans
The Atmospheric Effets of Stratospheric Aircraft: A third Program Report,
Edition R.S.Stolarski et H.L. Wesoky, NASA Ref. Publ. 1313, 185-208,
1993.
[20] Benoit, R., J. Cote, et J. Mailhot, Inclusion of a TKE boundary layer
parameterization in the Canadian regional finite-element model, Mon. Wea.
Rev., 1117, 1726-1750, 1989.

285. Bibliographie 285
[21] Blackadar, A. K., Modeling the nocturnal boundary layer, Third Symposium
on Atmospheric Turbulence, Diffusion and Air Quality, Raleigh, Amer. Me-
teor. Soc., 46-49, 1976.
[22] Blackadar, A. K., High resolution model of the planetary boundary layer,
Advances in Environmental Science and Engineering, Gordon and Breach
Sci. Pub., New York, 50-85, 1979.
[23] Blunier, T. , Chappellaz J., J. Schwander, J. Barnola, T. Desperts, B.
Stauffer et D. Raynaud, Atmospheric methane record from a Greenland ice
core over the past 1000 years, Geophys. Res. Lett., 20, 2219-2222, 1993.
[24] Bodhaine, B. A., B. G. Mendonca, J. M. Harris, et J. M. Miller, Seasonal
variations in aerosols and atmospheric transmission at Mauna Loa Obser-
vatory, J. Geophys. Res., 86, 7395-7398, 1981.
[25] Bollinger, M. J., R. E. Sievers, D. W. Fahey, et F. C. Fehsenfeld, Conver-
sion of nitrogen dioxide, nitric acid, and n-propyl nitrate to nitric oxide by
gold catalyzed reduction with carbon monoxide, Anal. Chem., 55, 1980-1986,
1983.
[26] Borucki, W. J., et W. L. Chameides, Lightning: Estimates of the rates of
energy dissipation and nitrogen fixation, Rev. Geophys. Space Phys., 22,
363-372, 1984.
[27] Boubel, R. W., D. L. Fox, D. B. Turner, A. C. STern, Fundamentals of air
pollution, 3d
Edition, Academic Press, San Diego, California, USA, 1994.
[28] Bouwman, A. F., Soils and the greenhouse effect, Edition A. F. Bouwman,
John Wiley and Sons, 1990.
[29] Bowen, J.E. et D. Anderson, Sugar-cane cropping systems, Ecosystems of
the World: Field crop ecosystem, vol. 18, Edition C.J. Pearson, Elsevier,
Amsterdam, 1992.
[30] Box, E.O., Foliar Biomass: Data base of the International Program and
other sources, 1981.
[31] Brasseur, G. P. and S. Solomon, Aeronomy of the Middle Atmosphere, 2d
Edition, Kluwer Academic Publishers, Dordrecht, Holland, 1986.
[32] Brasseur, G. P., D. A. Hauglustaine, et S. Walters, Chemical compounds
in the remote Pacific troposphere: comparison between MLOPEX measure-
ments and chemical- transport-model calculations, J. Geophys. Res., 1996.

286. 286 Bibliographie
[33] Businger, J. A., J. C. Wyngaard, Y. Izum, et E. F. Bradley, Flux-profile
relationships in the atmospheric surface layer, J. Atm. Sci., 28, 181-189,
1971.
[34] Carbone, R. E., W. A. Cooper, et W-Ch. Lee, Forcing of flow reversal along
the windward slopes of Hawaii, Mon. Wea. Rev., 123, 3466-3480, 1995.
[35] Carroll, M. A., B. A. Ridley, D. Montzka, G. Hubler, J. G. Walega, R.
B. Norton, B. J. Huebert, et F. E. Grahek, Measurements of nitric oxide
and nitrogen dioxide during the Mauna Loa Observatory Photochemistry
Experiment, J. Geophys. Res., 97, 10361-10374, 1992.
[36] Cantrell, C. A., R. E. Shetter, T. M. Gilpin, J. G. Calvert, F. L. Eisele, et
D. J. Tanner, Peroxy radical concentrations measured and calculated from
trace gas measurements in the Mauna Loa Observatory Photochemistry Ex-
periment 2, J. Geophys. Res., 101, 14653-14664, 1996.
[37] Chamberlain, A. C., Roughness length of sea, sand and snow, Bound. Layer
Meteo., 25, 405-409, 1983.
[38] Chameides, W. L., Effect of variable energy input on nitrogen fixation in
instantaneous linear discharges, Nature, 277, 123-125, 1979.
[39] Chang, J. S., R. A. Brost, I. S. A. Isaksen, S. Madronich, P. Middleton, W.
R. Stockwell, et C. J. Walcek, A three-dimensional eulerian acid deposition
model: Physical concepts and formulation, J. Geophys. Res., 92, 14681-
14700, 1987.
[40] Chatfield, R. B., et P. J. Crutzen, Sulfur dioxide in remote oceanic air:
Cloud transport of reactive precursors, J. Geophys. Res., 89, 7111-7132,
1984.
[41] Chatfield, R. B., Anomalous HNO3/NOx ratio of remote tropospheric air:
Conversion of nitric acid to formic acid and NOx, Geo. Res. Let., 21, 2705-
2708, 1994
[42] Chen, Y.-L., et A. J. Nash, Diurnal variation of surface airflow and rainfall
frequencies on the island of Hawaii, Mon. Wea. Rev., 122, 34-56, 1994.
[43] Chen, Y.-L., et J.-J. Wang, Diurnal variation of surface thermodynamic
fields on the island of Hawaii, Mon. Wea. Rev., 122, 2125-2138, 1994.
[44] Chen, Y.-L., et J. Feng, The influences of inversion height on precipitation
and airflow over the island of Hawaii, Mon. Wea. Rev., 123, 1660-1676,
1995.

287. Bibliographie 287
[45] Chock, D.P. et A.M. Dunker, A comparison of numerical methods for solv-
ing the advection equation, Atm. Envir., 17, 11-24, 1983.
[46] Chock, D.P., A comparison of numerical methods for solving the advection
equation-II, Atm. Evir., 19, 571-586, 1985.
[47] Chock, D.P., A comparison of numerical methods for solving the advection
equation-III, Atm. Envir., 25A, 853-871, 1991.
[48] Chock, D.P. et S.L. Winkler, A comparison of advection algorithms coupled
with chemistry, Atm. Envir., 28, 2659-2675, 1994.
[49] Clarke, R.H., A. J. Dyer, R. R. Brook, D. G. Reid, et A. J. Troup, The
Wangara experiment: Boundary layer data, Tech. Paper 19, Div. Meteor.
Phys., CSIRO, Australia, 1971.
[50] Coiffier, J., Y. Ernie, J.-F. Geleyn, J. Clochard et F. Dupont, The
operational hemispheric model at the French Meteorological Service,
WMO/IUGG International Symposium on Short- and Medium-Range
NWP, Tokyo, WMO Tech. Doc. 114, 265-268, 1986.
[51] Crutzen, P. J., The role of NO and NO2 in the chemistry of troposphere
and stratosphere, Annu. Rev. Earth Planet. Sci., 7, 443-472, 1979.
[52] Crutzen, P.J., I. Anselman et W Seiler, Methane production by domestic
animals, wild ruminants, other herbivorous fauna, and humans, Tellus, 38B,
271-284, 1986.
[53] Crutzen, P.J., W.M. Hao, M. H. Liu, J. M. Lobert, et D. SCharffe, Emis-
sions of CO2 and other trace gases to the atmosphere from fires in the
tropics, Li`ege International Astrophysical Colloquium ”Our Changing At-
mosphere”, Universit´e de Li`ege, Belgique, 1989.
[54] Cullis, C. F., et M. H. Hirschler, Man’s emissions of carbon monoxide and
hydrocarbons into the atmosphere, Atm. Envir., 23, 1195-1203, 1989.
[55] Dalu, G. et G. A. Dalu, An experimental check on the removal of radon,
Rap. 32, Instituto Di Fisica Dell’Atmosfira, Rome, 1970.
[56] Davis, J. J., er P. Rabinowitz, Methods of Numerical Integration, Academic
Press, 1975.
[57] Dawson, G. A., Nitrogen fixation by lightning, J. Atmos. Sc., 37, 174-178,
1980.

288. 288 Bibliographie
[58] Deardroff, J. W., Efficient prediction of ground surface temperature and
moisture with inclusion of a layer of vegetation, J. Geophys. Res., 83, 1978.
[59] Defant, F., Local winds, Compendium of Meteorology, pp. 655-672. Ameri-
can Meteorological Society, Boston. 1951.
[60] Delaunay B., Neue darstellung der geometrischen krystallographie,
Zeitschrift Krystallographie, 84, 109-149, 1932.
[61] DeMore, W. B., S. P. Sander, D. M. Golden, M. J. Molina, R. F. Hampson,
M. J. Kurylo, C. J. Howard, et A. R. Ravishankara, Chemical kinetics and
photochemical data for use in stratospheric modeling, JPL Publication 90-1,
Pasadena, 1990.
[62] Devloo, P., Oden J.T. et T. Strouboulis, Implementation of an adaptative
refinment technique for the SUPG algorithm, Comp. Meth. appl. Mech.
Engng., 61, 339-358, 1987.
[63] Dlugokencky, E. J., L. P. Steele, P. M. Lang, et K. A. Masarie, Atmospheric
methane at Mauna Loa and Barrow observatories: presentation and analy-
sis of in situ measurements, J. Geophys. Res., 100, 23103-23113, 1995.
[64] Duce, R., C. K. Unni, B. Ray, J. M. Prospero, et J. Merrill, Long-range
transport of soil dust from Asia to the tropical North Pacific, Science, 209,
1522-1524, 1980.
[65] Duce, R. A., V. A. Mohnen, P. R. Zimmerman, D. Grosjean, W. Cautreels,
R. B. Chatfield, R. Jaenicke, J. A. Ogren, E. D. Pellizari, et G. T. Wallace,
Organic material in the global troposphere, Rev. Geophys. Space Phys., 21,
921-952, 1983.
[66] Dudhia, J., A nonhydrostatic version of the Penn State-NCAR mesoscale
model: validation tests and simulation of an Atlantic cyclone and cold front,
Mon. Wea. Rev., 121, 1493-1513, 1993.
[67] Eisele, F. L., et D. J. Tanner, Ion-assisted tropospheric OH measurements,
J. Geophys. Res., 96, 9295, 1991.
[68] Eisele, F. L., et D. J. Tanner, Measurement of the gas phase concentration
of H2SO4 and methane sulfonic acid and estimates of H2SO4 production
and loss in the atmosphere, J. Geophys. Res., 98, 9001, 1993.
[69] Eisele, F. L. D. J. Tanner, C. A. Cantrell, et J. G. Calvert, Measurements
and steady state calculations of OH concentrations at Mauna Loa Observa-
tory, J. Geophys. Res., 101, 14665-14679, 1996.

289. Bibliographie 289
[70] Erickson, D.J., Ocean to atmosphere carbon monoxide flux: Global inven-
tory and climate implications, Global Biogeochem. Cycles., 3, 305-314,
1989.
[71] Etheridge, D. M., Pearman, G. I., et P. J. Fraser, Changes in tropospheric
methane between 1841 and 1978 from a high accumulation rate Antarctic
ice core, Tellus, 44B, 282-294, 1992.
[72] Fahey, D. W., C. S. Eubank, G. H¨ubler, et F. C. Fehsenfeld, Evaluation
of a catalytic reduction technique for the measurement of total reactive odd
nitrogen NOy in the atmosphere, J. Atmos. Chem., 3, 435-468, 1985.
[73] Fahey, D. W., G. H¨ubler, D. D. Parrish, E. J. Williams, R. B. Norton, B. A.
Ridley, H. B. Singh, S. C. Liu, et F. C. Fehsenfeld, Reactive nitrogen species
in the troposphere: Measurements of NO, NO2, HNO3, particulate nitrate,
peroxyacetyl nitrate (PAN), O3, and total reactive odd nitrogen (NOy) at
Niwot Ridge, Colorado, J. Geophys. Res., 91, 9781-9783, 1986.
[74] Fang T.-P. et L.A. Piegl, Delaunay triangulation using a uniform grid, IEEE
Comp. Graphic and Appl., 272, 36-47, 1993
[75] FAO/UNESCO: Soil Map of the World. 1:5,000,000, FAO, Roma, Italie,
1974.
[76] Feely, H. W., R. J. Larsen, et C. G. Sanderson, Annual report of the sur-
face air sampling program, EML Report-497, Environmental Measurements
Laboratory, U.S. Department of Energy, New York, 1988
[77] Feichter, J. et P.J. Crutzen, Parameterization of vertical tracer transport
due to deep cumulus convection in a global transport model and its evalua-
tion with 222
Radon measurements, Tellus, 42B, 100-117, 1990.
[78] Fiedler, F. et H. A. Panofsky, The geostrophic drag coefficient and the ef-
fective roughness length, Quart. J. Roy. Meteor. Soc., 98, 213-220, 1972.
[79] Fishman, J., S. Solomon, et P. J. Crutzen, Observational and theoratical
evidence in support of a significant in-situ photochemistry source of tropo-
spheric ozone, Tellus, 31, 432-446, 1979.
[80] Finlayson-Pitts, B. J., et J. N. Pitts Jr., Atmospheric Chemistry: funda-
mentals and experimental techniques, Edition John Wiley and Sons, New-
York, 1986.
[81] Fletcher C.A.J., Computational Techiques for fluid dynamics, vol. 2,
Springer Verlag, Berlin, 1988.

290. 290 Bibliographie
[82] Galbally, I. E.,Ozone profiles and ozone fluxes in the atmospheric surface
layer, Quart. J. Roy. Meteor. Soc., 97, 18-29, 1971.
[83] Galbally, I. E., The emissions of nitrogen to the remote atmosphere, Bio-
gemical Cycling of Sulfur and Nitrogen in the Remote Atmosphere, J. N.
Galloway et al. (eds.), D. Reidel Publishing Company, Hingham, Mas-
sachusetts, 1985.
[84] Garrett, A. J., Orographic cloud over the Eastern slopes of Mauna Loa
volcano, Hawaii, related to insolation and wind, Mon. Wea. Rev., 108, 931-
941, 1980.
[85] Gear, C. W., Numerical value problems in ordinary differential equations,
Prentice-Hall, Englewood Cliffs, N.J., 1971.
[86] Genthon, Ch., et A. Armengaud, Radon 222 as a comparative tracer of
transport and mixing in two general circulation models of the atmosphere,
J. Geophys. Res, 100, 2849-2866, 1995.
[87] Gerlach, T.M. et E.J. Graeber, Volatile budget of Kilauea volcano, Nature,
31, 273-277, 1985.
[88] Giambelluca, T. W., M. A. Nullet, et T. A. Schroeder, Rainfall Atlas of
Hawaii, Report R76, Dept. of Land and Natural Resources, State of Hawaii,
1986.
[89] Gidel L., Cumulus transport of transient tracers, J. Geophys. Res., 88, 6587-
6594, 1983.
[90] Graedel, T. E., et P. J. Crutzen, Atmospheric Change. An earth system
perspective, W. H. Freeman and Company, New York, 1993.
[91] Gray, W. G. et M. Th. van Genuchten, Economical alternatives to Gaussian
quadrature over isoparametric quadrilaterals, Int. J. Num. Meth. Engng.,
12, 1478-1484, 1978.
[92] Greenberg, J. P., P. R. Zimmerman, W. F. Pollock, R. A. Lueb, et L. E.
Heidt, Diurnal variability of atmospheric methane, nonmethane hydrocar-
bons, and carbon monoxide at Mauna Loa, J. Geophys. Res., 97, 10395-
10413, 1992.
[93] Grell, G. A., Dudhia, J. et D. R. Stauffer, A description of the fifth-
generation PENN STATE/NCAR MESOSCALE MODEL (MM5), NCAR
Technical Note, NCAR/TN-398+IA, Boulder, Colorado, 1993.

291. Bibliographie 291
[94] Greenberg, J. P., P. R. Zimmerman, W. F. Pollock, R. A. Lueb, et L. E.
Heidt, Diurnal variability of atmospheric methane, nonmethane hydrocar-
bons, and carbon monoxide at Mauna Loa, J. Geophys. Res., 97, 10395-
10413, 1992.
[95] Greenberg, J. P., D. Helmig, et P. R. Zimmerman, Seasonal measurements
of nonmethane hydrocarbons and carbon monoxide at the Mauna Loa Ob-
servatory during the Mauna Loa Observatory Photochemistry Experiment
2, J. Geophys. Res., 101, 14581-14598, 1996.
[96] Guenther, A.G., R.K. Monson, et R. Fall, Isoprene and monoterpene emis-
sion rate variability: Observations with Eucalyptus and emission rate algo-
rithm development, J. Geophys. Res., 96, 10,799-10,808, 1991.
[97] Guenther, A.G., C.N. Hewitt, D. Erickson, R. Fall, Ch. Geron, T. Graedel,
P. Harley, L. Klinger, M. Lerdau, W.A. McKay, T. Pierce, B. Scholes, R.
STeinbrechter, R. Tallamraju, J. Taylor, P. Zimmerman, A global model of
natural volatil organic compound emissions, J. Geophys. Res.,1996
[98] Guo, Y.-R. et S. Chen, Terrain and Land Use for the Fifth-Generation Penn
State/NCAR Mesoscale Modeling System (MM5): Program TERRAIN,
NCAR Technical Note NCAR/TN-397+IA, Boulder, Colorado, 1994.
[99] Haagenson, Ph. L., J. Dudhia, The Penn State/NCAR Mesoscale Model
(MM5) Source code documentation, NCAR technical Note NCAR/TN-392,
Boulder, Colorado, 1993.
[100] Haagenson Ph. L., J. Dudhia, G. A. Grell et D. R. Stauffer, The Penn
State/NCAR Mesoscale Model (MM5) Source Code Documentation, NCAR
Technical Note, NCAR/TN-392+STR, Boulder, Colorado, 1994.
[101] Hahn, C. J., J. T. Merrill, et B. G. Mendonca, Meteorological influences
during MLOPEX, J. Geophys. Res., 97, 10291-10309, 1992.
[102] Hansen, J., G. Russell, D. Rind, P. Stone, A. Lacis, S. Lebedeff, R. Ruedy,
et L. Travis, Efficient Three-dimensional global models for climate studies:
models I and II, Mon. Wea. Rev., 111, 609-662, 1983.
[103] Harris, J. M., et J. D. Kahl, A descriptive atmospheric transport climatology
for the Mauna Loa Observatory, using clustered trajectories, J. Geophys.
Res., 95, 13651-13667, 1990.
[104] Harris, J. M., P. P. Tans, E. J. Dlugokencky, K. A. Masarie, P. M. Lang, S.
Whittlestone, et L. P. Stelle, Variations in atmospheric methane at Mauna

292. 292 Bibliographie
Loa Observatory related to long-range transport, J. Geophys. Res., 97, 6003-
6010, 1992.
[105] Hasbani, Y., E. Levine, et M. Bercovier, Finite elements and characteristics
applied to advection-diffusion equations, Comp. Fluids, 11, 71-83, 1983.
[106] Hauglustaine, D. A., S. Madronich, B. A. Ridley, J. G. Walega, C. A.
Cantrell, et R. E. Shetter, Observed and model-calculated phtostationary
state at Mauna Loa Observatory during MLOPEX 2, J. Geophys. Res.,
101, 14681-14696, 1996.
[107] Haurwitz B., A linear sea breeze model, Quarterly Progress Report no. 3,
Project no. 3-36-05-401, College of Engineering, Research Division, New
York University, 1959.
[108] Heikes, B., Formaldehyde and hydroperoxides at Mauna Loa Observatory,
J. Geophys. Res., 97, 18001-19013, 1992.
[109] Heikes, B., B. McCully, X. Zhou, Y.-N. Lee, K. Mopper, X. Chen, G.
Mackay, D. Karecki, H. Schiff, T. Campos, et E. Atlas, Formaldehyde meth-
ods comparison in the remote lower troposphere during the Mauna Loa Pho-
tochemistry Experiment 2, J. Geophys. Res., 101, 14741-14755, 1996.
[110] Henderson-Sellers, A., Wilson, M. F., Thomas G. et R. E. Dickinson, Cur-
rent Global land-surface data sets for use in climate-related studies, NCAR
Technical Note NCAR/TN-272+STR, Boulder, Colorado, 1986.
[111] Hess, S. L., Introduction to theoretical meteorology, Holt, Rinehart and Win-
ston, 1959.
[112] Hess, P. G., N. Srimani, et S. J. Flocke, Trajectories and related variations
in the chemical composition of air for the Mauna Loa Observatory during
1991 and 1992, J. Geophys. Res., 101, 14543-14568, 1996.
[113] Hill, R. D., R. G. Rinker, et H. Dle Wilson, Atmospheric nitrogen fixation
by lightning, J. Atmos. Sci., 37, 179-192, 1980.
[114] Hillel, D., Fundamentals of soil physics, Academic Press, London, England,
1980a.
[115] Hillel, D., Applications of soil physics, Academic Press, London, England,
1980b.
[116] Hillel, D., Introduction to soil physics, Academic Press, London, England,
1982.

293. Bibliographie 293
[117] Holton, J. R., An introduction to dynamic meteorology, Acadenic Press, San
Diego, 1979.
[118] Hoell, J. M., D. D. Davis, S. C. Liu, R. Newell, M. Shipham, H. Akimoto, R.
J. McNeal, R. J. Bendura, et J. W. Drewry, Pacific Exploratory Missions-
Est A (PEM-West A): September-October 1991, J. Geophys. Res., 101,
1641-1653, 1996.
[119] Holtslag, A. A. M. et A. C. M. Beljaars, Surface flux parameterization
schemes; developments and experiences at KNMI, ECMWF workshop on
parameterization of fluxes and land surfaces, 121-147, Reading, 1989.
[120] Houze R.A., Ch.-P. Cheng, C.A. Leary, et J.F. Gamache, Diagnosis of
cloud mass and heat fluxes from radar and synoptic data, J. Atmos. Sci.,
37, 754-773, 1979.
[121] Houze, R. A., Cloud dynamics, Academic Press, San Diego, California,
USA, 1993.
[122] Hov, O., Z. Zlatev, R. Berkowicz, A. Eliassen, et L. P. Prahm, Compari-
son of numerical techniques for use in air pollution models with nonlinear
chemical reactions, Atmos. Environ., 23, 967-983, 1989.
[123] H¨ubler, G., D. D. Montzka, R. B. Norton, P. C. Murphy, F. C. Fehsenfeld,
S. C. Liu, B. A. Ridley, J. G. Walega, E. Atlas, F. E. Grahek, L. E. Heidt, J.
Merrill, B. J. Huebert, et B. A. Bodhaine, Total reactive oxidized nitrogen
(NOy) in the remote Pacific troposphere and its correlation with O3 and
CO; Mauna Loa Observatory Experiment 1988, J. Geophys. Res., 97, 10427-
10447, 1992.
[124] Hughes, T.J.R. et A.N. Brooks, A multidimensional upwind scheme with
no crosswind diffusion, Edition T.J.R. Hughes, Finite Element Methods for
Convection Dominated Flows, ASME, New-York, 19-35, 1979.
[125] Hughes, T.J.R., R. Mallet et A. Mizukami, A new finite element formulation
for computational fluid dynamics: II. Beyond SUPG, Comput. Methods
appl. mech. Engng., 54, 341-355, 1986.
[126] Hunt, C. R.,et W. H. Snyder, Experiments on stably and neutrally stratified
flow over a model three-dimensional hill, J. Fluid Mech., 96, 671-704, 1980.
[127] Isaksen, I. S. A., et O. Hov, Calculations of trends in the tropospheric
concentrations of O3, OH, CO, CH4, NOx, Tellus, 396, 271-285, 1987.

294. 294 Bibliographie
[128] Jacob, D. J. et M. J. Prather, Radon-222 as a test of convective transport
in a general circulation model, Tellus, 42B, 118-134, 1990.
[129] Joseph, J. H., W. J. Wiscombe, et J. A. Weiman, The delta-Eddington
approximation for radiative flux transfer, J. Atmos. Sci., 33, 2452-2458,
1976.
[130] Kasibhatla, P. S., H. Levy II et W. J. Moxim, Global NOx, HNO3, PAN, and
NOy distributions from fossil fuel combustion emissions: A model study, J.
Geophys. Res., 98, 7165-7180, 1993.
[131] Komhyr, W. D., S. J. Oltmans, P. R. Franchois, W. F. J. Evans, et W.
A. Matthews, The latitudinal distribution of ozone to 35 km altitude from
ECC ozonesonde observations, 1985-1987,
[132] Kondo, J. et S. Akashi, Numerical studies on the two-dimensional flow in
horizontally homogeneous canopy layers, Bound. Layer Meteo., 10, 255-272,
1976.
[133] Kondo, J., et H. Yamazawa, Aerodynamic roughness over inhomogeneous
ground surface, Bound. Layer Meteo., 35, 331-348, 1986.
[134] Lamarque, J.-F., G. P. Brasseur, P. G. Hess, et J.-F. M¨uller, Three-
dimensional study of the relative contributions of the different nitrogen
sources in the troposphere, J. Geophys. Res., 101, 22955-22968, 1996.
[135] Lamb, B., A. Guenther, D. Gay, et H. Westberg, A national inventory of
biogenic hydrocarbon emissions, Atmos. Environ., 21, 1695-1705, 1987.
[136] Lambert, G., G. Polian, J. Sanak, B. Ardouin, A. Buisson, A. Jegou, et
J.C.Le Roulley, Cycle dur radon et de ses descendants: application `a l’´etude
des ´echanges troposph`ere- stratosph`ere, Annales de Geophys., 38, 497-531,
1982.
[137] Larsen, R. J., et C. G. Sanderson, Annual report of the surface air sampling
program, Environmental Measurements Laboratory, EML Report 524, U.S.
Department of Energy, New York, 1990.
[138] Lavoie, R. L., Background data for the warm rain project, Tellus, 19, 348-
353, 1967.
[139] Lazrus, A. L., K. L. Fong, et J. A. Lind, Automated fluorometric determi-
nation of formaldehyde in air, Anal. Chem., 60, 1074-1078, 1988.

295. Bibliographie 295
[140] Lee, G., L. Zhuang, B. Huebert, et T. P. Meyers, Concentration gradients
and dry deposition of nitric acid vapor at the Mauna Loa Observatory,
Hawaii, J. Geophys. Res., 98, 12661-12671, 1993.
[141] Lee, H. N., J. Feichter, An intercomparison of wet precipitation scavenging
schemes and the emission rates of 222
Rn for the simulation of global trans-
port and deposition of 210
Pb, J. Geophys. Res., 100, 23253-23270, 1995.
[142] Lieth, H., Modeling the primary productivity of the world, Primary produc-
tivity of the Biosphere, Edition H. Lieth and R.H. Whittaker, p237-263,
Springer-Verlag, 1975.
[143] Lettau, H., Note on aerodynamic roughness-parameter estimations on the
basis of roughness element description, J. Appl. Meteo., 8, 828-832, 1969.
[144] Levy II, H., J. D. Mahlman, W. J. Moxim, et S. C. Liu, Tropospheric ozone:
the role of tranpsort, J. Geophys. Res., 90, 3753-3772, 1985.
[145] Levy II, H., et W. J. Moxim, Influence of long-range transport of combustion
emissions on the chemical variability of the background atmosphere, Nature,
338, 326-328, 1989a.
[146] Levy II, H., et W. J. Moxim, Simulated global distribution and deposition
of reactive nitrogen emitted by fossil fuel combustion, Tellus, 41, 256-271,
1989b.
[147] Liaw, Y.P., D.L. Sisterson, et N.L. Miller, Comparison of field, laboratory,
and theoretical estimates of global nitrogen fixation by lightning, J. Geophys.
Res., 95, 22489-22494, 1990.
[148] Lindley, S.J., J.W.S. Longhurst, A.F.R. Watson et D.E. Conlan, Procedures
for the estimation of regional scale atmospheric emissions-An example from
the North West region of England, Atm. Envir., 30, 3079-3091, 1996.
[149] Liu, S.C., M. McFarland, J. D. Mahlman, et H. Levy II, On the origin of
tropospheric ozone, J. Geophys. Res., 85, 7546-7552, 1980.
[150] Liu, S. C., J. R. McAfee, et R. J. Cicerone, Radon 222 and tropospheric
vertical transport, J. Geophys. Res., 89, 7291-7297, 1984.
[151] Liu, S. C., M. Trainer, F. C. Fehsenfeld, D. D. Parrish, E. J. Williams,
D. W. Fahey, G. H¨ubler, et P. C. Murphy, Ozone production in the rural
troposphere and the implications for regional and global ozone distributions,
J. Geophys. Res., 92, 4191-4207, 1987.

296. 296 Bibliographie
[152] Liu, S. C., M. Trainer, M. A. Carroll, G. H¨ubler, D. D. Montzka, R. B.
Norton, B. A. Ridley, J. G. Walega, E. L. Atlas, B. G. Heikes, B. J. Huebert,
et W. Warren, A study of the photochemistry and ozone budget during the
Mauna Loa Observatory Photochemistry Experiment, J. Geophys. Res., 97,
10463-10471, 1992.
[153] Logan, J. A., M. J. Prather, S. C. Wofsy, et M. B. McElroy, Tropospheric
chemistry: A global perspective, J. Geophys. Res., 86, 7210-7254, 1981.
[154] Logan, J. A., Nitrogen oxides in the troposphere: global and regional budgets,
J. Geophys. Res., 88, 10785-10807, 1983.
[155] Long, R. R., Some aspects of the flow of stratified fluids. II. Experiments
with two-fluid systems, Tellus, 6, 97-115, 1954.
[156] Long, P.E. et D.W. Pepper, An examination of some simple numerical
schemes for calculating scalar advection, J. Appl. Met., 20, 146-156, 1981.
[157] Louis, J.-F., The parameterization of the planetary boundary layer, Lec-
ture note No. 9, European Centre for Medium Range Weather Forecasts,
Reading, England, 1979.
[158] Lowenthal, D. H., R. D. Borys, J. C. Chow, F. Rogers, et G. E. Shaw,
Evidence for long-range transport of aerosol from the Kuwaiti oil fires to
Hawaii, J. Geophys. Res., 97, 14,573-14,580, 1992.
[159] Ludlam, F. H., Clouds and storms, The behavior and effect of water in
the atmosphere, Pennsylvania State University Press, Pennsylvania, USA,
1980.
[160] Luria, M, J. F. Boatman, J. Harris, J. Ray, T. Straube, J. Chin, R. L.
Gunter, G. Herbert, T. M. Gerlach, et Ch. C. Van Valin, Atmospheric sulfur
dioxide at Mauna Loa, Hawaii, J. Geophys. Res., 97, 6011-6022, 1992.
[161] Madronich, S., Photodissociation in the atmosphereI, Actinic flux and the
effects of ground reflections and clouds, J. Geophys. Res., 92, 9740-9752,
1987.
[162] Madronich, S. et J. G. Calvert, The NCAR Master Mechanism of the gas
phase chemistry-Version 2.0, NCAR Technical Note NCAR/TN-333+STR,
Boulder, Colorado, 1989.
[163] Madronich, S., UV Radiation in the natural and perturbed atmosphere, UV-
B radiation and ozone depletion, 17-69, Lewis Publishers, Boca Raton,
1993.

297. Bibliographie 297
[164] Mahowald, N., Development of a 3-dimensional chemical transport model
based on observed winds and use in inverse modeling of the source of CCl3F,
Report No. 42, Center for Meteorology and Physical Oceanography, Mas-
sachusetts Institue of Technology, Massachusetts, 1996.
[165] Mahrt, L., Grid averaged surface fluxes, Mon. Wea. Rev., 115, 1550-1560,
1987.
[166] Mahrt, L., M. Ek, J. Kim et A. A. M. Holtslag, Boundary layer parame-
terization for a global spectral model, Phillips Laboratory Technical Note,
PL-TR-91-2031, Hanscom Air Force Base, USA, 1991.
[167] Manning, K. W. et Ph. L. Haagenson, Data ingest and objective analysis for
the PSU/NCAR modeling system: Programs DATAGRID and RAWINS,
NCAR Technical Note NCAR/TN-376+IA, Boulder, Colorado, 1992.
[168] Martin, C. L. et R. A. Pielke, The adequacy of the hydrostatic assumption
in sea-breeze modelling over flat terrain, J. Atm. Sci., 40, 1472-1481, 1983.
[169] Matthews, E., Global vegetation and land use: New high-resolution data
bases for climate studies, J. Clim. Appl. Meteor., 22, 474-487, 1983.
[170] Matthews, E., 1984, Prescription of land-surface boundary conditions in
GISS GCM II: a simple method based on high-resolution vegetation data
sets, NASA Technical Memorandum 86096, Juin 1984.
[171] Mellor, G. L., et T. Yamada, A hierarchy of turbulence closure models for
planetary boundary layers, J. Atm. Sci., 31, 1791-1806, 1974.
[172] Mendonca, B. C., Local wind circulation on the slopes of Mauna Loa, J.
Appl. Meteo., 8, 533-541, 1969.
[173] Merrill, J. T., M. Uematsu, et R. Bleck, Meteorological analysis of long
range transport of mineral aerosols over the North Pacific, J. Geophys.
Res., 94, 8584-8598, 1989.
[174] M´esz´aros E., Global and regional changes in atmospheric composition, Lewis
Publishers, 1993.
[175] Miller, J. M., A five-year climatology of back trajectories from the Mauna
Loa Observatory, Hawaii, Atmos. Environ., 15, 1533-1558, 1981.
[176] Mishra, U. O., O. Ransarajan, et C. D. Eapen, Natural radioactivity of
the atmosphere over the indian land mass, inside deep mines, and over
adjoining oceans, NRE III, US DOE Symposium Series 51, 327-346, 1978.

298. 298 Bibliographie
[177] Moore, H. E., S. E. Poet, et E. A. Martell, Origin of 222
Rn and its long-lived
daughters in air over Hawaii, J. Geophys. Res., 79, 5019-5024, 1974.
[178] M¨uller, J.-F., Geographical distribution and seasonal variation of surface
emissions and deposition velocities of atmospheric trace gases, J. Geophys.
Res., 97, 3787-3804, 1992.
[179] M¨uller, J.-F. et G. Brasseur, IMAGES: A three-dimensional chemical trans-
port model of the global troposphere, J. Geophys. Res., 100, 16,445-16,490,
1995.
[180] Nakazawa, T., T. Machida, M. Tanaka, Y. Fujii, S. Aoki, et O. Watanabe,
Differences of the atmospheric CH4 concentration between the Arctic and
Antarctic regions in preindustrial/agricultural era, Geophys. Res. Lett., 20,
943-946, 1993.
[181] Nicholls, J.M., The airflow over mountains. Research 1958-1972, WMO
Tech. Note No. 127, Geneva, World Meteorological Organization, 1973.
[182] Nicolet, M., Etude des r´eactions chimiques de l’ozone dans la stratosph`ere,
IRMB/KMIB, Bruxelles, 1978.
[183] Odman, M.T. et A.G. Russell, A multiscale finite element pollutant trans-
port scheme for urban and regional modeling, Atm. Envir., 25A, 2385-2394,
1991.
[184] Oliger, J. et A. Sundstr¨om, Theoretical and practical aspects of some initial-
boundary value problems in fluid dynamics, Rep. STAN-CS-76-578, Com-
puter Science Department, Stanford University, 1976.
[185] Olson, J.S., J.A. Watts et L.J. Allison, Carbon in Live vegetation of ma-
jor world ecosystems, DOE/NBB Report No. TR004, Oak Ridge National
Laboratory, Oak Ridge, TN 37830, 1983.
[186] Oltmans, S. J., et W. D. Komhyr, Surface ozone distributions and varia-
tions from 1973-1984 measurements at the NOAA geophysical monitoring
for climatic change baseline observatories, J. Geophys. Res., 91, 5229-5236,
1986.
[187] Pasquil, F., Atmospheric diffusion, Ellis Horwood Limited, Chichester, Eng-
land, 2d
Edition, 1983.
[188] Penkett, S. A., N. J. Blake, P. Lightman, A. R. W. Marsh, P. Anwyl, et
G. Butcher, The seasonal variation of nonmethane hydrocarbons in the free
troposphere over the North Atlantic Ocean: Possible evidence for extemsive

299. Bibliographie 299
reaction of hydrocarbons with the nitrate radical, J. Geophys. Res., 98, 2865-
2885, 1993.
[189] Peraire, J., M. Vahdati, K. Morgan et O.C. Zienkiewicz, Adaptative remesh-
ing for compressible flow computation, J. Comp. Phys., 72, 449-466, 1987.
[190] Perry, R.H., C.H. Chilton, et S. D. Kirkpatrick, Perry’s Chemical Engi-
neer’s Handbook, 4th
Edition, McGraw Hill, New-York, 1963.
[191] Peters, L.K., C.M. Berkowitz, G.R. Carmichael, R.C.Easter, G. Fair-
weather, S.J. Ghan, J.M. Hales, L.R. Leung, W.R. Pennell, F.A. Potra,
R.D. Saylor et T.T. Tsang, The current state and future direction of eule-
rian models in simulating the tropospheric chemistry and transport of trace
species: A review, Atm. Envir., 29, 189-222, 1995.
[192] Pham M., J.-F. M¨uller, G. P. Brasseur, C. Granier, et G. M´egie, A three-
dimensional study of the tropospheric sulfur cycle, J. Geophys. Res., 100,
26061-26092, 1995.
[193] Pielke, R. A., Mesoscale meteorological modeling, Academic Press, Orlando,
1984.
[194] Pleim, J.E., Chang J.S. et K. Zhang, A nested grid meso-scale atmospheric
chemistry model, J. Geophys. Res., 96D, 3065-3084, 1991.
[195] Press, W.H., B. P. Flannery, S. A. Teukolsky et W. T. Vetterling, Numerical
recipes, Cambridge University Press, 1986.
[196] Price, C. et D. Rind, A simple lightning parameterization for calculating
global lightning distributions, J. Geophys. Res., 97, 9919-9933, 1992.
[197] Pudykiewicz, J., R. Benoit et A. Staniforth, Preliminary results from a
partial LRTAP model based on an existing meteorological forecast model,
Atm.-Ocean, 23, 267-303, 1985.
[198] Rao, A. et T.H. Tsang, A mnoving finite element method for the population
balance equation, Int. J. numer. Meth. Fluids, 10, 753-770, 1990.
[199] Rasmussen, R. A., A review of the natural hydrocarbon issue, Atmospheric
Biogenic Hydrocarbons, vol. 1, Emissions, Ann Arbor Science Publishers,
Michigan, 3-14, 1981.
[200] Rasmussen, R. A., P. Smolarkiewicz, et J. Warner, On the dynamics of
Hawaiian cloud bands: comparison of model results with observations and
island climatology, J. Atmos. Sci., 46, 1589-1608, 1989.

300. 300 Bibliographie
[201] Rasmussen, R. A. et P. K. Smolarkiewicz, On the dynamics of Hawaiian
cloud bands. Part III: local aspects, J. Atmos. Sci., 50, 15601572, 1993.
[202] Ridley, B. A., et al., The behavior of some organic nitrate at Boulder and
Niwot Ridge, Colorado, J. Geophys. Res., 95, 13949-13961, 1990.
[203] Ridley, B. A. et E. Robinson, The Mauna Loa Observatory Photochemistry
Experiment, J. Geophys. Res., 97, 10285-10290, 1992.
[204] Ridley, B. A., S. Madronich, R. B. Chatfield, J. G. Walega, R. E. Shetter,
M. A. Carroll, et D. D. Montzka, Measurements and model simulations of
the photostationary state during the Mauna Loa Observatory Experiment:
Implications for radical concentrations and ozone production and loss rates,
J. Geophys. Res., 97, 10375-10387, 1992.
[205] Ridley, B. A., J. G. Walega, J. E. Dye, et F. E. Grahek, Distributions of NO,
NOx, NOy and O3 to 12 km altitude during the summer monsoon season
over New Mexico, J. Geophys. Res., 99, 25519-25534, 1994.
[206] Ridley, B. A., E. L. Atlas, J. G. Walega, G. L. Kok, T. A. Staffelbach, J. P.
Greenberg, F. E. Grahek, P. G. Hess, et D. D. Montzka, Aircraft measure-
ments made during the spring maximum of ozone over Hawaii: Peroxides,
CO, O3, NOy, condensation nuclei, selected hydrocarbons, halocarbons, and
alkyl nitrates between 0.5 and 9 km altitude, submitted to J. Geophys. Res.,
1997.
[207] Roelofs, G.-J., et J. Lelieveld, Distribution and budget of O3 in the tropo-
sphere calculated with a chemistry general circulation model, J. Geophys.
Res., 100, 20983-20998, 1995.
[208] Roffman, A., Short-lived daughter ions of Radon 222 in relation to some
atmospheric processes, J. Geophys. Res., 77, 5883-5899, 1972.
[209] Rossow, W. B., L. C. Garder, et P.-J. Lu, International Satellite Cloud
Climatology Project (ISCCP). Documentation of cloud data, World Cli-
mate Research Programme, WMO/TD-No. 266, NCAR, Boulder, Colorado,
1991.
[210] Schery, S. D., S. Whittlestone, Evidence of high deposition of ultrafine par-
ticles at Mauna Loa Observatory, Atm. Envir., 29, 3319-3324, 1995.
[211] Seiler, W., et P.J. Crutzen, Estimates of gross and net fluxes of carbon
between the biosphere and the atmosphere from biomass burning, Clim.
Change, 2, 207-247, 1980.

301. Bibliographie 301
[212] Shea, D. J., Climatological atlas: 1950-1979, NCAR Tech. Note,
NCAR/TN-269+STR, Boulder, Colorado, 1986.
[213] Shwartz, S. E., Use of tracers for the study of atmospheric chemical and
physical transformation processes, Atmospheric tracer technology and Aplli-
cations, J. H. Heiken Edition, Noyes Publications, Park Ridge, New Jersey,
USA, pp.241-280, 1986.
[214] Smolarkiewicz, P.K., A fully multi-dimensional positive definite algorithm
with small implicit diffusion, J. Comp. Phys., 54, 325-362, 1984.
[215] Smolarkiewicz, P. K., R. M. Rasmussen et T. L. Clark, On the dynamics of
hawaiian cloud bands: island forcing, J. Atmos. Sci., 45, 1872-1905, 1988.
[216] Smolarkiewicz, P. K., et R, Rotunno, Low Froude number flow past three-
dimensional obstacles. Part I: Baroclinically generated lee vortices, J. At-
mos. Sci. 46, 1154-1164, 1989.
[217] Smolarkiewicz, P. K., et R. Rotunno, Low Froude number flow past a three-
dimensional obstacles. Part II: Upwind flow reversal zone, J. Atmos. Sci.,
47, 1498-1511, 1990.
[218] Smolarkiewicz, P. K., et P. J. Rash, Monotone advection on the sphere: An
eulerian versus semi-lagrangian approach, J. Atmos. Sci., 48, 793-810, 1991.
[219] Staniforth A.N. et H.L. Mitchell, A variable-resolution finite-element tech-
nique for regional forecasting with primitive equations, Mon. Wea. Rev.,
106, 439-447, 1978.
[220] Staley, D. O. et G. M. Jurica, Effective atmospheric emissivity (under clear
skies), J. Appl. Meteor., 11, 349-356, 1972.
[221] Statistical abstract of the United States, 112th
Edition, US Department of
Commerce, 1992.
[222] Stull, R., An introduction to boundary layer meteorology, Kluwer Academic
Publishers, Dordrecht, Holland, 1988.
[223] Taylor, J.A., G. Brasseur, P.R. Zimmerman, et R.J. Cicerone, A study of
the sources and sinks of methane and methyl chloroform using a global 3-
dimensional Lagrangian tropospheric tracer transport model, J. Geophys.
Res., 96, 3013-3044, 1991.

302. 302 Bibliographie
[224] Thompson J.F., F.C. Thomas et C.W. Mastin, TOMCAT- A code for
numerical generation of boundary-fitted curvilinear coordinate systems on
fields containing any number of arbitrary two-dimensional bodies, J. Comp.
Phys., 24, 274-302, 1977.
[225] Trenberth, K. E., et J. G. Olson, Intercomparison of NMC and ECMWF
global analyses, NCAR Technical Note NCAR/TN-229+STR, Boulder, Col-
orado, 1988.
[226] Trenberth, K. E., Global analyses from ECMWF and Atlas of 1000 to 10 mb
circulation statistics, NCAR technical Note NCAR/TN-373+STR, Boulder,
Colorado, 1992.
[227] Tuck, A. F., Production of nitrogen oxides by lightning discharges, Quart.
J. Roy. Meteor. Soc., 102, 749-755, 1976.
[228] Turco, R. P., et R. C. Whitten, A comparison of several computational
techniques for solving some common aeronomic problems, J. Geophys. Res.,
79, 3179-3185, 1974.
[229] Turman, B. N., et B. C. Edgar, Global lightning distributions at dawn and
dusk, J. Geophys. Res., 87, 1191-1206, 1982.
[230] Troen, I. et L. Mahrt, A simple model of the atmospheric boundary layer;
Sensitivity to surface evaporation, Bound. Layer Meteor., 37, 129-148, 1986.
[231] USDA, Soil Taxonomy, Washington DC: Soil Conservation Service, Serie
no. 436.n1, US Department of Agriculture, 1975.
[232] Wahner, A., F. Rohrer, D. H. Ehhalt, E. Atlas, et B. Ridley, Global
Measurements of photochemically active compounds, Global Atmospheric-
Biospheric Chemistry, R.G. Prinn Edition, Plenum Press, New York, 1994.
[233] Walcek, C. J., R. A. Brost, J. S. Chang, et M. L. Wesely, SO2, sulfate and
HNO3 deposition velocities computed using regional landuse and meteoro-
logical data, Atmos. Environ., 20, 949-964, 1986.
[234] Walega, J. G., B. A. Ridley, S. Madronich, F. E. Grahek, J. D. Shetter,
T. D¿ Sauvain, C. J. Hahn, J. T. Merill, B. Bodhaine, et E. Robinson,
Observations of peroxyacetyl nitrate, peroxypropionyl nitrate, methyl nitrate
and ozone during the Mauna Loa Observatory Photochemistry Experiment,
J. Geophys. Res., 97, 10311-10330, 1992.

303. Bibliographie 303
[235] Wang, J.-J., et Y.-L. Chen, Characteristics of near surface winds and ther-
mal profiles on the windward slopes of the island of Hawaii, Mon. Wea.
Rev., 123, 3481-3501, 1995.
[236] Wayne R., Chemistry of atmospheres, 2d
Edition, Clarendon Press, Oxford,
USA, 1991.
[237] Weatherill N.P., Numerical grid generation, Lecture Series 1990-06, von
Karman Institute for fluid dynamics, Rhodes-St,-Gen`ese, 1990.
[238] Wesely, M. L., et B. B. Hicks, Some factors that affect the deposition rates
of sulfur dioxide and similar gases on vegetation, J. Air Pollut. Control
Ass., 27, 1110-1116, 1977.
[239] Wesely, M. L., Parameterization of surface resistances to gaseous dry de-
position in regional scale numerical models, Atm. Envir., 23, 1293-1304,
1989.
[240] Wieringa, J., Representative roughness parameters for homogeneous terrain,
Bound. Layer Meteo., 63, 323-363, 1993.
[241] Whittlestone, S., E. R. Ryan, et S. Ryan, Radon at the Mauna Loa Ob-
servatory: Transport from distant continents, Atm. Envir., 26A, 251-260,
1992.
[242] Wilkening, M. H., Radon-222 from the island of Hawaii: Deep soils are
more important than lava fields or volcanoes, Science, 183, 413-415, 1974.
[243] Wilkening, M. H. et W. E. Clements, Radon-222 from the ocean surface, J.
Geophys. Res., 80, 3828-3830, 1975.
[244] World Meteorological Organization, Reports of the International Ozone
Trends Panel: 1988, Global Ozone Research and Monitoring Project, Re-
port 18, Gen`eve, Suisse, 1995.
[245] World Meteorological Organization, Scientific Assessment of Ozone Deple-
tion: 1991, Global Ozone Research and Monitoring Project, Report 25,
Gen`eve, Suisse, 1992.
[246] World Meteorological Organization, Scientific Assessment of Ozone Deple-
tion: 1994, Global Ozone Research and Monitoring Project, Report 37,
Gen`eve, Suisse, 1995.
[247] Wu, J., Wind stress and surface roughness at air-sea interface, J. Geophys.
Res., 5, 285-308, 1969.

304. 304 Bibliographie
[248] Yamada, T. et G. Mellor, A simulation of the Wangara Atmospheric Bound-
ary Layer Data, J. Atm. Sci., 32, 2309-2329, 1975.
[249] Yanai, M., Esbensen S. et J.-H. Chu, Determination of bulk properties of
tropical cloud clusters from large-scale heat and moisture budgets, J. Atmos.
Sci., 30, 611-627, 1973.
[250] Yanenko N.N., The method of fractional steps, Springer, Berlin, 1971.
[251] Yienger, J. J. et H. Levy II, Empirical model of global soil-biogenic NOx
emissions, J. Geophys. Res., 100, 11447-11464, 1995.
[252] Zhang, D.-L., et R. A. Anthes, A high resolution model of the planetary
boundary layer-sensitivity tests and comparisons with SESAME-79 data, J.
Appl. Meteor., 21, 1594-1609, 1982.
[253] Zienkiewicz, C. O. et R. L. Taylor, The finite element method, vol. 1, 4th
Edition, McGraw-Hill Book Company, London, 1989.
[254] Zienkiewicz, C. O. et R. L. Taylor, The finite element method, vol. 2, 4th
Edition, McGraw-Hill Book Company, London, 1991.
[255] Zobler, L., World soil file for global climate modeling, NASA Technical
Memorandum 87802, 1986.